맨위로가기 타임라인 바로가기

불확정성 원리

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
타임라인 바로가기
목차

1. 개요

불확정성 원리는 1927년 베르너 하이젠베르크가 발표한 양자역학의 기본 원리이다. 이 원리에 따르면 입자의 위치와 운동량, 또는 에너지와 시간과 같이 서로 짝을 이루는 물리량들을 동시에 정확하게 측정하는 것은 불가능하며, 두 물리량의 불확정성은 플랑크 상수에 의해 제한된다. 불확정성 원리는 단순히 측정 기술의 한계를 넘어 양자 세계의 본질적인 특성을 나타내며, 수학적으로는 연산자 간의 교환 관계를 통해 설명된다. 이 원리는 양자 광학, 초전도 시스템, 중력파 간섭계 등 다양한 분야에 응용된다.

더 읽어볼만한 페이지

  • 베르너 하이젠베르크 - 하이젠베르크 스핀 사슬
    하이젠베르크 스핀 사슬은 1차원 격자에서 상호작용하는 스핀들의 배열을 나타내는 물리학적 모델로, 스핀 간의 상호작용 유형과 스핀 값에 따라 여러 종류로 나뉘며, 얽힘 엔트로피 연구, 밀도 행렬 재정규화, 허버드 모형 등 다양한 문제에 응용되고 베테 안자츠 방법으로 풀이된다.
  • 베르너 하이젠베르크 - 하이젠베르크 묘사
    하이젠베르크 묘사는 양자역학에서 상태 벡터는 시간에 따라 변하지 않고 물리량을 나타내는 연산자가 시간에 따라 변하는 시간 변화 기술 방법으로, 고전역학과의 유사성과 상대론적 양자역학에서의 로런츠 불변성 표현에 유용하다.
  • 1927년 과학 - 데이비슨-거머 실험
    데이비슨-거머 실험은 1927년 데이비슨과 거머가 니켈 결정에 전자를 충돌시켜 전자의 회절 현상을 관찰함으로써 물질의 파동성을 입증하고 파동-입자 이중성 개념 확립과 양자역학 발전에 기여한 실험으로, 데이비슨은 이 공로로 노벨 물리학상을 수상했다.
  • 1927년 과학 - 하트리-폭 방법
    하트리-폭 방법은 다전자 원자 또는 분자의 근사 파동 함수와 에너지를 계산하기 위해 자기-일관장 방법을 사용하여 시간 독립적인 슈뢰딩거 방정식을 푸는 양자역학적 계산 방법이다.
  • 과학 법칙 - 만유인력의 법칙
    만유인력의 법칙은 모든 질량을 가진 물체들이 서로를 끌어당기는 힘에 대한 법칙으로, 뉴턴은 질량에 비례하고 거리의 제곱에 반비례한다는 것을 제시했으며, 케플러의 행성 운동 법칙을 설명하고 뉴턴 역학의 기초가 되었으나, 일반 상대성 이론이 등장하면서 저중력 한계로 여겨진다.
  • 과학 법칙 - 보일의 법칙
    보일의 법칙은 온도와 질량이 일정할 때 기체의 압력과 부피가 반비례한다는 법칙으로, 로버트 보일이 발견했으며, 수학적으로 PV = k로 표현된다.
불확정성 원리
불확정성 원리
독일어Unschärferelation
영어Uncertainty principle
기본 정보
분야양자역학
발견자베르너 하이젠베르크
발표 연도1927년
내용
주요 내용어떤 입자의 위치와 운동량을 동시에 정확하게 측정하는 것은 불가능하다.
위치와 운동량 관계ΔxΔp ≥ ħ/2
시간과 에너지 관계ΔEΔt ≥ ħ/2
각운동량과 각도 관계ΔLΔθ ≥ ħ/2
ħ디랙 상수 (h/2π)
Δx위치의 불확실성
Δp운동량의 불확실성
ΔE에너지의 불확실성
Δt시간의 불확실성
ΔL각운동량의 불확실성
Δθ각도의 불확실성
의미
측정의 한계측정 과정 자체가 입자의 상태를 변화시킴
고전 역학과의 차이고전 역학에서는 위치와 운동량을 동시에 정확하게 측정 가능하다고 가정
양자 역학의 기본 원리입자의 파동성을 나타내는 중요한 개념
관련 개념
양자얽힘서로 얽힌 두 입자의 특성이 동시에 측정될 때 불확정성 원리가 적용됨
코펜하겐 해석양자 역학의 표준적인 해석으로 불확정성 원리를 핵심으로 함
논란 및 비판
아인슈타인불확정성 원리가 양자 역학의 불완전성을 보여준다고 주장
EPR 역설아인슈타인이 제기한 사고 실험으로 불확정성 원리에 대한 반론을 제시

2. 역사

1925년 베르너 하이젠베르크는 ''움다이퉁''(재해석) 논문을 발표하여 양자 이론의 중심적인 측면이 비교환성임을 보였다.[83] 그는 조화 진동자를 설정하여 자신의 생각을 구체화하고자 했고, 그 과정에서 물리량들과 연관된 수학적 대상 두 개를 곱하는 순서에 따라 결과가 달라지는 특성을 발견했다. 이는 현대적인 표현으로 연산자 간의 교환관계가 성립하지 않는다는 것을 의미한다.[140] 막스 보른은 하이젠베르크의 비교환적 양들이 행렬임을 인식하고, 파스쿠알 요르단과 함께 행렬역학을 완성했다.[83][140]

1926년 3월, 코펜하겐의 보어 연구소에서 일하던 하이젠베르크는 비교환성이 불확정성 원리를 의미한다는 것을 깨달았다.[84] 1927년 2월 볼프강 파울리에게 보낸 편지에서 그는 기본 개념을 연구했다.[84] 같은 해 3월, 하이젠베르크는 "양자 이론적 운동학 및 역학의 지각 내용에 관하여"(Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanikde)라는 논문에서 불확정성 원리를 발표했다.[2] 그는 빛과 물질의 파동-입자 이중성이 불확정성으로 연결된다는 것을 사고 실험을 통해 설명하려 했다.

베르너 하이젠베르크와 닐스 보어


하이젠베르크의 1927년 논문은 \Delta x와 \Delta p가 무엇을 의미하는지 정확히 명시하지 않았고, \Delta x\Delta p\gtrsim h와 같은 형태로 표현했다.[141] 같은 해 7월, 케너드[6][1][136]는 \Delta x와 \Delta p를 관측가능량의 표준편차로 정의하고, 현대적인 부등식 \sigma_x\sigma_p\ge\frac{\hbar}{2}을 증명하였다.[141] 여기서 }}이고, , 는 위치와 운동량의 표준 편차이다. 1928년에는 헤르만 바일이 이 부등식을 유도하였다.[137] 하이젠베르크는 가우시안 상태의 특수한 경우에 대해서만 이 관계를 증명했다.[85] 1929년 로버트슨은 모든 관측 가능량으로 부등식을 일반화했고, 1930년 슈뢰딩거는 연산자의 공분산이 0이 아닌 것을 허용하도록 형태를 확장했는데, 이 결과는 로버트슨-슈뢰딩거 부등식으로 불린다.[1]

하이젠베르크는 1927년에 독일어로 작성된 그의 원 논문 본문 전반에서 기본적인 이론 원리를 설명하기 위해 "Ungenauigkeit"[2]라는 단어를 사용했다. 그는 끝부분 주석에서야 "Unsicherheit"라는 단어로 바꾸었다. 이후 그는 항상 "Unbestimmtheit"를 사용했다. 그러나 1930년에 출판된 하이젠베르크 교과서 ''양자론의 물리적 원리''의 영어판에서는 "uncertainty"라는 영어 단어만 사용되었고, 이것이 영어권에서 사용되는 용어가 되었다.[87]

2. 1. 초기 역사

1925년 베르너 하이젠베르크는 ''움다이퉁''(재해석) 논문을 발표하여 양자 이론의 중심적인 측면이 비교환성임을 보였다.[83] 그는 조화 진동자를 설정하여 자신의 생각을 구체화하고자 했고, 그 과정에서 물리량들과 연관된 수학적 대상 두 개를 곱하는 순서에 따라 결과가 달라지는 특성을 발견했다. 이는 현대적인 표현으로 연산자 간의 교환관계가 성립하지 않는다는 것을 의미한다.[140] 막스 보른은 하이젠베르크의 비교환적 양들이 행렬임을 인식하고, 파스쿠알 요르단과 함께 행렬역학을 완성했다.[83][140]

1926년 3월, 보어 연구소에서 일하던 하이젠베르크는 비교환성이 불확정성 원리를 의미한다는 것을 깨달았다.[84] 1927년 2월 볼프강 파울리에게 보낸 편지에서 그는 기본 개념을 연구했다.[84] 같은 해 3월, 하이젠베르크는 "양자 이론적 운동학 및 역학의 지각 내용에 관하여"(Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanikde)라는 논문에서 불확정성 원리를 발표했다.[2] 그는 빛과 물질의 파동-입자 이중성이 불확정성으로 연결된다는 것을 사고 실험을 통해 설명하려 했다.

하이젠베르크의 1927년 논문은 \Delta x와 \Delta p가 무엇을 의미하는지 정확히 명시하지 않았고, \Delta x\Delta p\gtrsim h와 같은 형태로 표현했다.[141] 같은 해 7월, 케너드[6][1][136]는 \Delta x와 \Delta p를 관측가능량의 표준편차로 정의하고, 현대적인 부등식 \sigma_x\sigma_p\ge\frac{\hbar}{2}을 증명하였다.[141] 여기서 }}이고, , 는 위치와 운동량의 표준 편차이다. 1928년에는 헤르만 바일이 이 부등식을 유도하였다.[137] 하이젠베르크는 가우시안 상태의 특수한 경우에 대해서만 이 관계를 증명했다.[85] 1929년 로버트슨은 모든 관측 가능량으로 부등식을 일반화했고, 1930년 슈뢰딩거는 연산자의 공분산이 0이 아닌 것을 허용하도록 형태를 확장했는데, 이 결과는 로버트슨-슈뢰딩거 부등식으로 불린다.[1]

하이젠베르크는 1927년에 독일어로 작성된 그의 원 논문 본문 전반에서 기본적인 이론 원리를 설명하기 위해 "Ungenauigkeit"[2]라는 단어를 사용했다. 그는 끝부분 주석에서야 "Unsicherheit"라는 단어로 바꾸었다. 이후 그는 항상 "Unbestimmtheit"를 사용했다. 그러나 1930년에 출판된 하이젠베르크 교과서 ''양자론의 물리적 원리''의 영어판에서는 "uncertainty"라는 영어 단어만 사용되었고, 이것이 영어권에서 사용되는 용어가 되었다.[87]

2. 2. 하이젠베르크의 현미경

하이젠베르크의 현미경은 하이젠베르크가 불확정성 원리를 설명하기 위해 사용한 사고 실험이다.[85] 그는 현미경으로 전자의 위치와 운동량을 측정하기 위해 광자를 발사하는 상황을 상상했다.[88]

하이젠베르크의 현미경. 전자(파란색), 입사되는 감마선(녹색), 산란된 감마선(붉은색). 산란된 감마선은 현미경의 관측 구경에 임의의 각도로 들어오게 된다.


현미경에 사용되는 빛의 파장이 짧을수록 해상도가 높다는 사실을 바탕으로, 하이젠베르크는 원자 속 전자의 위치를 정밀하게 측정하려면 감마선 정도의 짧은 파장을 가진 빛을 사용해야 한다고 생각했다. 그러나 짧은 파장의 광자는 큰 운동량을 가지므로, 컴프턴 효과에 의해 전자의 운동량은 크게 변한다. 반대로 긴 파장의 광자를 사용하면 전자의 운동량 변화는 작지만, 전자에 의해 크게 산란되어 위치 측정의 정확도가 떨어진다.[89]

현미경의 구경이 크면 레일리 기준에 따라 전자의 위치를 더 정확하게 측정할 수 있다. 하지만 운동량 보존 원리에 따라 입사 광자의 횡방향 운동량이 전자의 운동량에 영향을 미쳐 전자의 운동량은 불확실해진다. 작은 구경을 사용하면 위치와 운동량의 불확정성은 반대가 된다.

이러한 상충 관계는 어떤 광자 파장과 구경 크기를 사용하더라도 위치와 운동량의 불확정성 곱이 플랑크 상수와 관련된 하한값보다 크거나 같음을 의미한다.[89]

2. 3. 주요 반론과 논쟁

알베르트 아인슈타인은 양자역학의 불확정성과 비결정론적 특성에 대해 비판적인 입장을 취했다.[98] 닐스 보어는 확률 분포가 근본적이고 환원 불가능하며, 우리가 어떤 측정을 수행하기로 선택하는지에 따라 달라진다고 믿었지만, 아인슈타인은 무작위성이 우리가 실재의 어떤 근본적인 속성을 모르기 때문에 나타나는 반영이라고 믿었다.[98] 아인슈타인과 보어는 수년 동안 불확정성 원리에 대해 논쟁을 벌였다.[98]

아인슈타인은 '아인슈타인의 슬릿' 사고 실험을 통해 불확정성 원리에 대한 반론을 제기했다.[99] 아인슈타인은 입자가 슬릿을 통과한 후 벽의 반발을 측정하여 운동량 보존 법칙에 따라 입자의 운동량을 임의의 정확도로 알 수 있다고 주장했다.[99] 그러나 보어는 벽 역시 양자역학적이며, 벽의 운동량 불확정성으로 인해 정확한 측정이 불가능하다고 반박했다.[99]

아인슈타인의 상자 사고 실험에서 아인슈타인은 에너지-시간 불확정성 원리에 대한 반론을 제기했다.[100][101] 그는 광자가 빠져나간 시간과 상자의 질량 변화를 통해 에너지 변화를 정확하게 계산할 수 있다고 주장했다.[100][101] 그러나 보어는 광자 방출로 인한 질량 손실이 중력장의 변화를 유발하고, 이는 시계의 속도에 영향을 주어 불확정성을 야기한다고 반박했다.[102][103]

EPR 역설은 양자역학의 불완전성을 주장하는 또 다른 시도였다.[104] 알베르트 아인슈타인, 보리스 포돌스키, 네이선 로젠은 얽힌 입자 쌍을 이용해, 한 입자를 측정하면 다른 입자의 상태가 즉시 결정되는 현상이 국소성의 원리에 위배된다고 주장했다.[105] 그러나 존 스튜어트 벨이 고안한 벨 부등식 실험을 통해 양자역학의 예측이 확인되었고, 국소적 숨은 변수 이론은 배제되었다.[105]

3. 물리적 의미



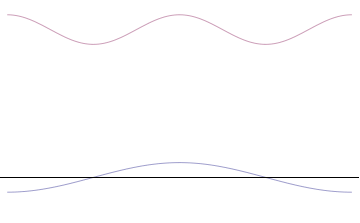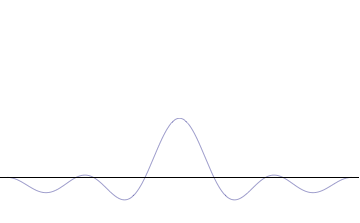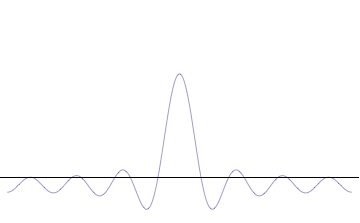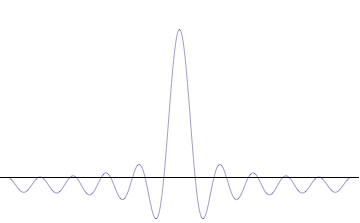
'''위쪽:''' 파장 ''λ''가 알 수 없으면 운동량 ''p'', 파수 ''k'' 및 에너지 ''E''도 알 수 없다(드 브로이 관계). 입자가 위치 공간에 더 국소화될수록 Δ''x''는 Δ''px''보다 작다.


'''아래쪽:''' ''λ''가 알려져 있으면 ''p'', ''k'' 및 ''E''도 알려져 있다. 입자가 운동량 공간에 더 국소화될수록 Δ''p''는 Δ''x''보다 작다.]]

드 브로이 가설에 따르면, 모든 물체는 파동성을 지니므로 불확정성 원리의 영향을 받는다. 위치 공간 파동 함수가 국소화될수록 입자가 그 영역에서 발견될 가능성이 높아지지만, 운동량 공간 파동 함수는 덜 국소화되어 입자가 가질 수 있는 운동량 성분이 더 넓어진다. 반대로, 운동량 공간 파동 함수가 국소화될수록 위치 공간 파동 함수는 덜 국소화된다. 이러한 파동 함수는 서로 푸리에 변환 관계에 있으며, 수학적으로 불확정성 원리는 변환에서 켤레 변수 간의 관계를 나타낸다.

역사적으로 불확정성 원리는 관찰자 효과와 혼동되기도 했지만, 이는 측정 행위 자체가 계에 영향을 미친다는 개념이다. 하이젠베르크는 양자 수준에서 이러한 관측자 효과를 양자 불확정성에 대한 물리적 "설명"으로 사용했지만, 불확정성 원리는 모든 파동의 고유한 특성이며, 양자역학에서 모든 양자 객체의 물질파 특성으로 인해 발생한다는 것이 밝혀졌다. 따라서 불확정성 원리는 양자 시스템의 기본적인 특성을 나타내며, 현재 기술의 관측 성공에 대한 진술이 아니다.

3. 1. 코펜하겐 해석

불확정성 원리는 양자역학의 코펜하겐 해석에 따르면, 입자의 위치와 운동량은 동시에 정확히 측정될 수 없으며, 이 두 물리량의 불확정성은 플랑크 상수에 의해 제한된다. 이는 단순히 측정 기술의 한계가 아니라, 양자 세계의 근본적인 특성이다.

양자역학은 고전역학과 달리, 위치와 운동량이 동시에 확정적인 값을 가질 수 없다. 불확정성 원리는 동일한 측정 과정을 여러 번 반복하여 얻은 통계에 대한 진술이며, 특정한 단일 측정 결과에 대한 예측이 아니다. 양자 현상은 여러 번의 관찰을 통해 얻어지는 기댓값과 같은 통계적인 예측만이 가능하다.

불확정성 원리는 위치와 운동량뿐만 아니라, 교환법칙이 성립하지 않는, 즉 교환 관계에 있지 않은 임의의 두 물리량(연산자) 사이에도 성립한다. 예를 들어, 3차원 공간에서 x축 상의 위치 측정은 x축 상의 운동량에는 영향을 주지만, y축이나 z축 상의 위치 및 운동량 측정에는 영향을 주지 않는다.

또한 불확정성 원리는 관측 순서가 결과에 영향을 주는 양자 현상의 특징을 보여준다. 교환 관계에 있지 않은 두 연산자를 이용한 관측을 연속적으로 수행할 때, 관측 순서를 바꾸면 결과가 달라진다. 이는 첫 번째 관측에 의해 상태가 변화(파동 함수 붕괴)하여, 다음 관측에서는 처음과 다른 상태에 대해 측정이 이루어지기 때문이다.

[[File:https://cdn.onul.works/wiki/source/194ee31721d_cb001761.svg|center|thumb|502px|양자 입자에 해당하는 위치 ''x''와 운동량 ''p'' 파동 함수. 입자의 색상 불투명도는 위치 ''x'' 또는 운동량 성분 ''p''를 갖는 입자를 발견할 확률 밀도에 해당한다.


'''위쪽:''' 파장 ''λ''가 알 수 없으면 운동량 ''p'', 파수 ''k'' 및 에너지 ''E''도 알 수 없다(드 브로이 관계). 입자가 위치 공간에 더 국소화될수록 Δ''x''는 Δ''px''보다 작다.


'''아래쪽:''' ''λ''가 알려져 있으면 ''p'', ''k'' 및 ''E''도 알려져 있다. 입자가 운동량 공간에 더 국소화될수록 Δ''p''는 Δ''x''보다 작다.]]

드 브로이 가설에 따르면, 모든 물체는 파동성을 지니므로 불확정성 원리의 영향을 받는다.[11] 위치 공간 파동 함수가 국소화될수록 입자가 그 영역에서 발견될 가능성이 높아지지만, 운동량 공간 파동 함수는 덜 국소화되어 입자가 가질 수 있는 운동량 성분이 더 넓어진다. 반대로, 운동량 공간 파동 함수가 국소화될수록 위치 공간 파동 함수는 덜 국소화된다. 이러한 파동 함수는 서로 푸리에 변환 관계에 있으며, 수학적으로 불확정성 원리는 변환에서 켤레 변수 간의 관계를 나타낸다.

역사적으로 불확정성 원리는 관찰자 효과와 혼동되기도 했지만,[90][91] 이는 측정 행위 자체가 계에 영향을 미친다는 개념이다.[92][93] 하이젠베르크는 양자 수준에서 이러한 관측자 효과를 양자 불확정성에 대한 물리적 "설명"으로 사용했지만,[94] 불확정성 원리는 모든 파동의 고유한 특성이며,[95] 양자역학에서 모든 양자 객체의 물질파 특성으로 인해 발생한다는 것이 밝혀졌다.[96] 따라서 불확정성 원리는 양자 시스템의 기본적인 특성을 나타내며, 현재 기술의 관측 성공에 대한 진술이 아니다.[97]

3. 2. 교환 관계

행렬역학에서 위치와 운동량과 같은 물리량은 자기수반 연산자로 표현된다.[12] 두 연산자 와 \hat{B}에 대해, 교환자는 다음과 같이 정의된다.

:[\hat{A},\hat{B}]=\hat{A}\hat{B}-\hat{B}\hat{A}.

위치와 운동량의 경우, 교환자는 정준 교환 관계가 된다.

:[\hat{x},\hat{p}]=i \hbar.

비가환성의 물리적 의미는 교환자가 위치와 운동량 고유 상태에 미치는 영향을 고려함으로써 이해할 수 있다. |\psi\rangle를 상수 고유값 을 갖는 위치의 우측 고유 상태라고 할 때, \hat{x}|\psi\rangle = x_0 |\psi\rangle를 의미한다. 교환자를 |\psi\rangle에 적용하면 다음을 얻는다.

:[\hat{x},\hat{p}] | \psi \rangle = (\hat{x}\hat{p}-\hat{p}\hat{x}) | \psi \rangle = (\hat{x} - x_0 \hat{I}) \hat{p} \, | \psi \rangle = i \hbar | \psi \rangle,

여기서 는 항등 연산자이다.

귀류법을 위해 |\psi\rangle가 상수 고유값 을 갖는 운동량의 우측 고유 상태이기도 하다고 가정해보면, 다음과 같이 쓸 수 있다.

:(\hat{x} - x_0 \hat{I}) \hat{p} \, | \psi \rangle = (\hat{x} - x_0 \hat{I}) p_0 \, | \psi \rangle = (x_0 \hat{I} - x_0 \hat{I}) p_0 \, | \psi \rangle=0.

반면, 위의 정준 교환 관계는 다음을 요구한다.

:[\hat{x},\hat{p}] | \psi \rangle=i \hbar | \psi \rangle \ne 0.

이는 어떤 양자 상태도 동시에 위치와 운동량 고유 상태가 될 수 없음을 의미한다.

상태가 측정될 때, 그것은 관련 물리량의 기저에서 고유 상태로 투영된다. 예를 들어, 입자의 위치가 측정되면, 상태는 위치 고유 상태가 된다. 즉, 상태는 운동량 고유 상태가 아니지만, 여러 운동량 기저 고유 상태의 합으로 표현될 수 있다. 다시 말해, 운동량은 덜 정확하다. 이 정확도는 표준 편차로 정량화할 수 있다.

:\sigma_x=\sqrt{\langle \hat{x}^2 \rangle-\langle \hat{x}\rangle^2}

:\sigma_p=\sqrt{\langle \hat{p}^2 \rangle-\langle \hat{p}\rangle^2}.

위의 파동역학 해석과 마찬가지로, 불확정성 원리에 의해 정량화되는 두 가지의 정확도 사이의 상충 관계를 볼 수 있다.

4. 유도 과정

4. 1. 발견적 논의

슬릿을 통과하는 입자의 위치-운동량 불확정성


작은 입자가 x축 방향으로 놓인 폭이 a인 슬릿을 통과하는 경우, x축으로의 위치 불확정성은 \triangle x가 된다. 이 입자는 물질파에 해당되는 파동의 성질을 가지므로 슬릿을 통과한 입자의 파동은 회절하게 되고, \sin \theta =\frac{ \lambda }{ a }인 곳에서 첫 번째 간섭무늬가 나타난다. 전자가 발견될 확률은 회절된 파동함수의 제곱에 비례하기 때문에, 입자의 확률적 분포는 절반각인 \theta에 해당되는 영역 안으로 제한된다. 따라서 운동량의 불확정도는 \triangle p \approx p \sin \theta = p\frac{ \lambda }{ a }이다.[11]

드브로이의 물질파 관계식 p=\frac{ h }{ \lambda } 을 이용하면, 위치와 운동량의 불확정성 곱은 \triangle x \triangle p \simeq h가 된다. 이 값은 플랑크 상수 정도의 크기를 갖는다.[12]

이 설명은 일반적인 수학적 증명이 아니라, 위치와 운동량 불확정성이 어떻게 발생하는지 설명하는 발견적 논의(heuristic argument)이므로 그 결과는 정성적이다. 따라서 위 식의 우변인 h는 수학적으로 엄밀한 불확정도가 아니다.[11][12]

드 브로이 가설에 따르면, 우주에 있는 모든 물체는 파동과 관련이 있다. 따라서 기본 입자에서 원자, 분자, 행성 등 모든 물체는 불확정성 원리의 영향을 받는다.

4. 2. 일반화된 불확정성 원리

임의의 관측 가능량 A와 B에 대한 분산과 코시-슈바르츠 부등식을 이용하여 일반화된 불확정성 원리를 유도할 수 있다.

임의의 관측량 A에 대한 분산은 다음과 같다.

:\sigma _A ^2 = \left\langle {(\hat A - \left\langle A \right\rangle )\Psi |(\hat A - \left\langle A \right\rangle )\Psi } \right\rangle

마찬가지로 관측량 B의 분산은 다음과 같다.

:\sigma _B ^2 = \left\langle {(\hat B - \left\langle B \right\rangle )\Psi |(\hat B - \left\langle B \right\rangle )\Psi } \right\rangle

코시-슈바르츠 부등식을 적용하면 다음의 식을 얻는다.

:\sigma _A ^2 \sigma _B ^2 = \left\langle {(\hat A - \left\langle A \right\rangle )\Psi |(\hat A - \left\langle A \right\rangle )\Psi } \right\rangle \left\langle {(\hat B - \left\langle B \right\rangle )\Psi |(\hat B - \left\langle B \right\rangle )\Psi } \right\rangle \geqslant \left| {\left\langle {(\hat A - \left\langle A \right\rangle )\Psi |(\hat B - \left\langle B \right\rangle )\Psi } \right\rangle } \right|^2

임의의 복소수 z는 복소수의 일반적인 성질에 의해 다음의 식이 항상 성립한다.

:\left| z \right|^2 = \left[ {\operatorname{Re} (z)} \right]^2 + \left[ {\operatorname{Im} (z)} \right]^2 \geqslant \left[ {\operatorname{Im} (z)} \right]^2 = \left[ {\frac{1}

(z - z^* )} \right]^2

위의 관계를 적용하면 다음과 같다.

:\left| {\left\langle {(\hat A - \left\langle A \right\rangle )\Psi |\hat B - \left\langle B \right\rangle )\Psi } \right\rangle } \right|^2 \geqslant \left( {\frac{1}

\left[ {\left\langle {(\hat A - \left\langle A \right\rangle )\Psi |(\hat B - \left\langle B \right\rangle )\Psi } \right\rangle - \left\langle {(\hat B - \left\langle B \right\rangle )\Psi |(\hat A - \left\langle A \right\rangle )\Psi } \right\rangle } \right]} \right)^2

위 식 우변의 괄호 안의 내적을 계산하면 다음과 같다.

:\left\langle {(\hat A - \left\langle A \right\rangle )\Psi |(\hat B - \left\langle B \right\rangle )\Psi } \right\rangle = \left\langle {\hat A\hat B} \right\rangle - \left\langle A \right\rangle \left\langle B \right\rangle

마찬가지로,

:\left\langle {(\hat B - \left\langle B \right\rangle )\Psi |(\hat A - \left\langle A \right\rangle )\Psi } \right\rangle = \left\langle {\hat B\hat A} \right\rangle - \left\langle B \right\rangle \left\langle A \right\rangle

그러므로 부등식 괄호 안의 내적은 최종적으로 다음과 같이 표현된다.

: \left\langle {(\hat A - \left\langle A \right\rangle )\Psi |(\hat B - \left\langle B \right\rangle )\Psi } \right\rangle - \left\langle {(\hat B - \left\langle B \right\rangle )\Psi |(\hat A - \left\langle A \right\rangle )\Psi } \right\rangle = \left\langle {\hat A\hat B} \right\rangle - \left\langle {\hat B\hat A} \right\rangle

위 계산결과는 다음과 같이 두 연산자에 대한 교환자 표기법으로 나타낼 수 있다.

::[ {\hat A,{\text{ }}\hat B}] \equiv \hat A\hat B - \hat B\hat A

따라서 최종적으로 다음의 식을 얻게 된다.

::\sigma _A ^2 \sigma _B ^2 \geqslant \left( {\frac{1}\left\langle {[\hat A,{\text{ }}\hat B]} \right\rangle } \right)^2

이것이 일반화된 불확정성 원리이다. 여기서 \hat A, \hat B는 임의의 연산자이므로 두 연산자의 교환자가 0이 아닌 경우, 불확정성 원리가 성립한다. 따라서 하이젠베르크의 위치-운동량 불확정성은 일반화된 불확정성의 특정한 예라고 할 수 있다.

하워드 퍼시 로버트슨(Howard Percy Robertson)은[13][1] 에르미트 연산자 연산자 \hat{\mathcal{O}}에 대한 공식을 개발했다.[14]

:\sigma_{\mathcal{O}} = \sqrt{\langle \hat{\mathcal{O}}^2 \rangle-\langle \hat{\mathcal{O}}\rangle^2},

여기서 괄호 \langle\hat{\mathcal{O}}\rangle는 연산자 \hat{\mathcal{O}}에 의해 나타내는 관측량의 기댓값을 나타낸다. 두 연산자 \hat{A}와 \hat{B}에 대해, 그들의 교환자를 다음과 같이 정의한다.

:[\hat{A},\hat{B}]=\hat{A}\hat{B}-\hat{B}\hat{A},

그리고 로버트슨 불확정성 원리는 다음과 같이 주어진다.[14]

:\sigma_A \sigma_B \geq \left| \frac{1}{2i}\langle[\hat{A},\hat{B}]\rangle \right| = \frac{1}{2}\left|\langle[\hat{A},\hat{B}]\rangle \right|.

에르빈 슈뢰딩거(Erwin Schrödinger)[15]는 연산자 간의 상관관계를 허용하는 방법을 보여주었고, '''로버트슨-슈뢰딩거 불확정성 원리'''로 알려진 더 강한 부등식을 제시했다.[16][1]

{{Equation box 1

|indent =:

|equation = \sigma_A^2\sigma_B^2 \geq \left| \frac{1}{2}\langle\{\hat{A}, \hat{B}\}\rangle - \langle \hat{A} \rangle\langle \hat{B}\rangle \right|^2+ \left|\frac{1}{2i} \langle[ \hat{A}, \hat{B}] \rangle\right|^2,

|cellpadding= 6

|border

|border colour = #0073CF

|background colour=#F5FFFA}}

여기서 반교환자, \{\hat{A},\hat{B}\}=\hat{A}\hat{B}+\hat{B}\hat{A}가 사용된다.

4. 3. 위치-운동량 불확정성 원리

1차원(x축) 공간 상에 존재하는 입자의 위치와 운동량을 측정하는 경우를 생각해보자.[142] 양자역학에서 위치와 운동량 연산자의 교환자는 다음의 과정을 통해 계산된다. 임의의 함수 f를 제거하면 위치-운동량 교환자 \left[ {x,{\text{ }}p} \right]= i \hbar 를 얻을 수 있다. 이것을 일반화된 불확정성 원리에 대입하고, 양변에 제곱근을 취하면 하이젠베르크의 위치-운동량 불확정성 원리 \sigma _x \sigma _p \geqslant \frac{\hbar }{2}를 얻을 수 있다. 이 식은 양자역학의 기본 가정으로부터 유도되는 결과이다.[142]

나고야 대학의 오자와 마사나오(小澤正直) 교수는 측정의 한계, 측정 행위에 의한 교란과 양자 자체의 성질에 의한 양자의 움직임을 엄밀하게 구별하는 식을 제안하여 위치-운동량 불확정성 원리를 보완했다.[142][143][144] 오자와는 위치-운동량 불확정성 원리의 보완식으로써 \epsilon_x \eta_p + \epsilon_x \sigma_p + \sigma_x \eta_p \geqslant {\hbar \over 2}을 제시하였다.[142] 이 식에 따르면 작은 양자에 대하여 기존의 위치-운동량 불확정성의 '측정의 한계'를 넘는 측정이 가능하게 된다.[142]

이것은 이후 빈 공과 대학교와 나고야 대학의 공동 연구에 의하여 특정 조건에서 놓인 중성자의 두 종류 스핀 값을 동시에 정확하게 측정하는 실험으로써 증명되었으며, 2012년 1월 15일 《네이쳐 피직스》에 개재되었다.[143][144][145][146]

여러 평면파의 중첩으로 파동 패킷을 형성하는 모습. 많은 파동을 더할수록 이 파동 패킷은 점점 더 국소화됩니다. 푸리에 변환은 파동 패킷을 개별 평면파로 분리하는 수학적 연산입니다. 여기에 표시된 파동은 설명을 위해 실수 함수로만 표시됩니다. 양자 역학에서 파동 함수는 일반적으로 복소 함수입니다.


이 원리가 인간이 경험하는 거시적 규모에서는 식별할 수 없기 때문에 비교적 이해하기 쉬운 물리적 상황에 어떻게 적용되는지 보여주는 것이 중요하다.[8] 파동 역학 관점에서 위치와 운동량 사이의 불확정성 관계는 힐베르트 공간에서 두 해당 직교 기저에서 파동 함수의 표현이 서로의 푸리에 변환이기 때문에 발생한다(즉, 위치와 운동량은 켤레 변수임).[9] 0이 아닌 함수와 그 푸리에 변환은 동시에 날카롭게 국소화될 수 없다.[9]

행렬 역학에서 양자 역학의 수학적 공식화에서, 관측 가능량을 나타내는 임의의 쌍의 비교환 자기수반 연산자는 유사한 불확정성 한계의 영향을 받는다.[10]

4. 4. 에너지-시간 불확정성 원리

임의의 관측량 Q(x, p, t)의 기댓값을 시간에 대해 미분하고, 슈뢰딩거 방정식을 적용하면 에너지-시간 불확정성 원리를 유도할 수 있다.

임의의 관측량 Q(x,p, t) 의 기댓값을 시간에 대해 미분하면 다음과 같다.

: \frac{d}

\left\langle Q \right\rangle = \frac{d}{dt}\left \langle \Psi \mid \hat{Q} \Psi \right \rangle = \left \langle \frac{\partial \Psi}{\partial t} \mid \hat{Q} \Psi \right \rangle + \left \langle \Psi \mid \frac{\partial \hat{Q}}{\partial t} \Psi \right \rangle + \left \langle \Psi \mid \hat{Q} \frac{\partial \Psi}{\partial t} \right \rangle



슈뢰딩거 방정식을 적용하면

: i\hbar {\partial \Psi \over \partial t} = \hat{H} \Psi



이므로 다음과 같은 결과를 얻을 수 있다.

: \frac{d}

\left\langle Q \right\rangle = -\frac{1}{i\hbar}\left \langle \hat{H} \Psi \mid \hat{Q} \Psi \right \rangle + \frac{1}{i\hbar}\left \langle \Psi \mid \hat{Q} \hat{H} \Psi \right \rangle + \left \langle \frac{\partial \hat{Q}}{\partial t} \right \rangle



\hat{H} 는 헤르미트이므로,

: \left \langle \hat{H} \Psi \mid \hat{Q} \Psi \right \rangle = \left \langle \Psi \mid \hat{H} \hat{Q} \Psi \right \rangle



따라서 임의의 관측량Q와 그것에 대한 연산자 \hat Q , 해밀토니언 \hat H 사이에는 다음의 관계가 성립한다.

: \frac{d}

\left\langle Q \right\rangle = \frac{i}

{\hbar }\left\langle {[\hat H,{\text{ }}\hat Q]} \right\rangle + \left\langle {\frac

} \right\rangle



연산자 \hat Q 가 시간에 무관하다고 가정하면 마지막 항은 0이 된다. 이제 위 식을 일반화된 불확정성 원리를 적용하면 다음과 같다.

:\sigma _H ^2 \sigma _Q ^2 \geqslant \left( {\frac{1}

\left\langle {[\hat H,{\text{ }}\hat Q]} \right\rangle } \right)^2 = \left( {\frac{1}

\frac{\hbar }

{i}\frac

} \right)^2 = \left( {\frac{\hbar }

{2}} \right)^2 \left( {\frac

} \right)^2

위 식의 양변에 제곱근을 취하면 다음과 같다.

:\sigma _H \sigma _Q \geqslant \frac{\hbar }

{2}\left| {\frac

} \right|

여기서 에너지와 시간을 다음과 같이 정의할 수 있다.

:\Delta E \equiv \sigma _H

:\Delta t \equiv \frac



따라서 다음의 관계식을 얻을 수 있다.

:\Delta E\Delta t \geqslant \frac{\hbar }{2}

이 식이 바로 에너지-시간의 불확정성 원리이다.

시간-에너지 불확정성 원리[36]는 여러가지 형태로 표현될 수 있으며, 그 의미 또한 다양하다.[36] 잘 알려진 응용 중 하나는 공명 상태의 수명과 에너지 폭 사이의 관계이다.[37][44]

:\tau_{\sqrt{1/2}} \Delta E = \pi\hbar/4.

입자 물리학에서는 브라이트-위그너 에너지 분포를 통해 불안정한 상태의 수명을 특징짓는 데 사용된다.[40]

에너지-시간 불확정성 원리의 직관적인 의미는 짧은 시간 동안만 존재하는 상태는 명확한 에너지를 가질 수 없다는 것이다.[41] 분광법에서 들뜬 상태는 유한한 수명을 가지며, 붕괴될 때마다 방출하는 에너지의 분포는 자연선폭을 갖는다.[42] 빠르게 붕괴하는 상태는 넓은 선폭을, 느리게 붕괴하는 상태는 좁은 선폭을 갖는다.[42] 불안정하고 빠르게 붕괴하는 입자의 정지 질량은 입자 물리학에서 폭이 커져 질량이 불확실해진다.

양자역학에서의 "시간" 개념은 여러 어려움을 제시한다.[46] 시간 측정에 대한 양자 이론은 없으며, 상대성 이론은 시간에 근본적이지만 양자역학에 포함하기 어렵다.[36] 안정적인 양자 시스템과 불안정적인 양자 시스템의 수학적 처리 방식이 다르다.[43]

시간은 외부 시간, 내재 시간, 관측 가능한 시간으로 구분할 수 있다.[36] 외부 시간은 실험자가 관찰하는 시간이며, 내재 시간은 동역학적 변수의 변화를 통해 추론되는 시간이다. 관측 가능한 시간은 시간적으로 분리된 사건의 측정, 즉 관측량으로서의 시간에 관한 것이다.

외부 시간 에너지-시간 불확정성 원리는 양자 시스템의 에너지를 \Delta E의 정확도로 측정하려면 \Delta t h/\Delta E의 시간 간격이 필요하다고 말할 수 있다.[44] 그러나 야키르 아하로노프와 데이비드 보옴은 일부 양자 시스템에서는 임의로 짧은 시간 내에 에너지를 정확하게 측정할 수 있음을 보였다.[45][36]

1945년, 레오니드 만델슈탐(Leonid Mandelstam)과 이고르 탐(Igor Tamm)은 비상대론적 시간-에너지 불확정성 원리를 유도했다.[47][36] 하이젠베르크 역학에서 명시적인 시간 의존성이 없는 관측 가능량 ''B''에 대한 일반화된 에렌페스트 정리(Ehrenfest theorem)는 자기수반 연산자 \hat B로 표현되는 \hat B의 평균값의 시간 의존성을 해밀토니언과의 교환자의 평균값과 관련짓는다.

\frac{d\langle \hat{B} \rangle}{dt} = \frac{i}{\hbar}\langle [\hat{H},\hat{B}]\rangle.

로버트슨 불확정성 관계에 대입하면,

\sigma_H\sigma_B \geq \left|\frac{1}{2i} \langle[ \hat{H}, \hat{B}] \rangle\right|,

이는 다음을 제공한다.

\sigma_H \frac{\sigma_B}{\left| \frac{d\langle \hat B \rangle}{dt}\right |} \ge \frac{\hbar}{2}

\Delta E \equiv \sigma_E 와 특성 시간

\tau_B \equiv \frac{\sigma_B}{\left| \frac{d\langle \hat B \rangle}{dt}\right |}

을 식별하면 에너지-시간 관계 \Delta E \tau_B \ge \frac{\hbar}{2}.를 얻는다.

양자장론의 일부 공식화에서는 가상입자라고 불리는 일시적인 전자-양전자 쌍을 계산에 사용하며, 이들의 질량-에너지와 수명은 에너지-시간 불확정성 원리와 관련이 있다.

에너지-시간 불확정성 원리가 에너지 보존 법칙을 일시적으로 위반하지 않는다.[17] 우주의 에너지는 항상 정확하게 알려진 매개변수가 아니다.[1]

시간과 에너지에 관해서는, 관측량의 분산에 대한 로버트슨 부등식을 논하는 것은 일반적으로 불가능하다. 해밀토니안($\hat{H}$)에 정준 공액인 시간 연산자($\hat{T}$)는 정의할 수 없기 때문이다. 안정된 기저 상태를 갖는 양자계에서는 에너지 고유값이 하한을 갖기 때문에, 에르미트인 시간 연산자는 존재하지 않는다는 것이 증명된다.

에너지의 측정 오차와 에너지의 측정에 걸리는 시간 사이에는 원리적인 불확정성 관계는 존재하지 않는다. 보어가 광자 상자의 사고 실험을 논파했다고 알려져 있지만, 이때 보어의 논의는 정확하지 않다. 다른 물리량과 마찬가지로, 에너지는 임의의 시각에 정확하게 측정할 수 있다.

시간과 에너지의 불확정성 관계 때문에 단시간에는 에너지 보존 법칙이 깨진다는 설도 유포되고 있지만, 그것에 근거는 없다. 페르미의 황금률 등의 섭동론에서 논의되고 있는 유한 시간에서의 에너지 보존 법칙의 깨짐은, 상호 작용항을 무시한 자유 해밀토니안 $\hat{H}_o$에 대한 논의에 불과하다.

5. 수학적 형식화

하워드 퍼시 로버트슨(Howard Percy Robertson)은[13][1] 임의의 에르미트 연산자 \hat{\mathcal{O}}에 대한 표준 편차 공식을 개발했다.

\sigma_{\mathcal{O}} = \sqrt{\langle \hat{\mathcal{O}}^2 \rangle-\langle \hat{\mathcal{O}}\rangle^2},

여기서 \langle\hat{\mathcal{O}}\rangle는 연산자 \hat{\mathcal{O}}에 의해 나타내는 관측량의 기댓값을 나타낸다. 두 연산자 \hat{A}와 \hat{B}의 교환자는 다음과 같이 정의된다.[14]

[\hat{A},\hat{B}]=\hat{A}\hat{B}-\hat{B}\hat{A},

로버트슨 불확정성 원리는 다음과 같다.

\sigma_A \sigma_B \geq \left| \frac{1}{2i}\langle[\hat{A},\hat{B}]\rangle \right| = \frac{1}{2}\left|\langle[\hat{A},\hat{B}]\rangle \right|.

에르빈 슈뢰딩거(Erwin Schrödinger)[15]는 연산자 간의 상관관계를 허용하는 방법을 보여주었고, 더 강한 부등식인 '''로버트슨-슈뢰딩거 불확정성 원리'''를 제시했다.[16][1] 이 원리는 반교환자 \{\hat{A},\hat{B}\}=\hat{A}\hat{B}+\hat{B}\hat{A}를 사용하여 표현된다.

\sigma_A^2\sigma_B^2 \geq \left| \frac{1}{2}\langle\{\hat{A}, \hat{B}\}\rangle - \langle \hat{A} \rangle\langle \hat{B}\rangle \right|^2+ \left|\frac{1}{2i} \langle[ \hat{A}, \hat{B}] \rangle\right|^2,

일반적인 형태의 로버트슨-슈뢰딩거 불확정성 원리에서는 연산자 \hat{A}와 \hat{B}가 자기수반 연산자라고 가정할 필요가 없다. 그것들이 단순히 대칭 연산자라고 가정하는 것으로 충분하다.

\hat{A}와 \hat{B}를 상태 공간 \mathcal{H} 위의 관측 가능량이라 하고, \psi\in\mathcal{H}가

: \psi\in\mathrm{Dom}(\hat{A})\cap\mathrm{Dom}(\hat{B}), \hat{B}\psi\in\mathrm{Dom}(\hat{A}), \hat{A}\psi\in\mathrm{Dom}(\hat{B})

을 만족한다고 할때, [\hat{A},\hat{B}]\psi:=\hat{A}\hat{B}\psi-\hat{B}\hat{A}\psi는 정의 가능하며, 다음 부등식(로버트슨의 부등식)이 성립한다 H13：

: (\Delta_{\psi} \hat{A})^2 ( \Delta_{\psi} \hat{B})^2 \ge \frac{1}{4} \left| \langle [\hat{A}, \hat{B}] \rangle_\psi \right|^2

5. 1. 로버트슨-슈뢰딩거 불확정성 원리

하워드 퍼시 로버트슨(Howard Percy Robertson)은[13][1] 임의의 에르미트 연산자 \hat{\mathcal{O}}에 대한 표준 편차 공식을 개발했다.

\sigma_{\mathcal{O}} = \sqrt{\langle \hat{\mathcal{O}}^2 \rangle-\langle \hat{\mathcal{O}}\rangle^2},

여기서 \langle\hat{\mathcal{O}}\rangle는 연산자 \hat{\mathcal{O}}에 의해 나타내는 관측량의 기댓값을 나타낸다. 두 연산자 \hat{A}와 \hat{B}의 교환자는 다음과 같이 정의된다.[14]

[\hat{A},\hat{B}]=\hat{A}\hat{B}-\hat{B}\hat{A},

로버트슨 불확정성 원리는 다음과 같다.

\sigma_A \sigma_B \geq \left| \frac{1}{2i}\langle[\hat{A},\hat{B}]\rangle \right| = \frac{1}{2}\left|\langle[\hat{A},\hat{B}]\rangle \right|.

에르빈 슈뢰딩거(Erwin Schrödinger)[15]는 연산자 간의 상관관계를 허용하는 방법을 보여주었고, 더 강한 부등식인 '''로버트슨-슈뢰딩거 불확정성 원리'''를 제시했다.[16][1] 이 원리는 반교환자 \{\hat{A},\hat{B}\}=\hat{A}\hat{B}+\hat{B}\hat{A}를 사용하여 표현된다.

\sigma_A^2\sigma_B^2 \geq \left| \frac{1}{2}\langle\{\hat{A}, \hat{B}\}\rangle - \langle \hat{A} \rangle\langle \hat{B}\rangle \right|^2+ \left|\frac{1}{2i} \langle[ \hat{A}, \hat{B}] \rangle\right|^2,

일반적인 형태의 로버트슨-슈뢰딩거 불확정성 원리에서는 연산자 \hat{A}와 \hat{B}가 자기수반 연산자라고 가정할 필요가 없다. 그것들이 단순히 대칭 연산자라고 가정하는 것으로 충분하다.

\hat{A}와 \hat{B}를 상태 공간 \mathcal{H} 위의 관측 가능량이라 하고, \psi\in\mathcal{H}가

: \psi\in\mathrm{Dom}(\hat{A})\cap\mathrm{Dom}(\hat{B}), \hat{B}\psi\in\mathrm{Dom}(\hat{A}), \hat{A}\psi\in\mathrm{Dom}(\hat{B})

을 만족한다고 할때, [\hat{A},\hat{B}]\psi:=\hat{A}\hat{B}\psi-\hat{B}\hat{A}\psi는 정의 가능하며, 다음 부등식(로버트슨의 부등식)이 성립한다 H13：

: (\Delta_{\psi} \hat{A})^2 ( \Delta_{\psi} \hat{B})^2 \ge \frac{1}{4} \left| \langle [\hat{A}, \hat{B}] \rangle_\psi \right|^2

5. 2. 상공간 형식화

양자역학의 상공간(위상공간) 형식화에서 로버트슨-슈뢰딩거 관계는 실수 항성 제곱 함수에 대한 양의 조건에서 유도된다.[23] 위그너 함수 W(x,p), 항성 곱 ★, 그리고 함수 ''f''가 주어지면, 일반적으로 \langle f^* \star f \rangle =\int (f^* \star f) \, W(x,p) \, dx \, dp \ge 0 ~.가 성립한다.[23]

f = a + bx + cp를 선택하면, \langle f^* \star f \rangle =\begin{bmatrix}a^* & b^* & c^* \end{bmatrix}\begin{bmatrix}1 & \langle x \rangle & \langle p \rangle \\ \langle x \rangle & \langle x \star x \rangle & \langle x \star p \rangle \\ \langle p \rangle & \langle p \star x \rangle & \langle p \star p \rangle \end{bmatrix}\begin{bmatrix}a \\ b \\ c\end{bmatrix} \ge 0 ~.를 얻는다.

이 양의 조건은 모든 ''a'', ''b'', ''c''에 대해 참이므로, 행렬의 모든 고유값은 음이 아니다. 음이 아닌 고유값은 행렬식에 대한 해당하는 비음의 조건을 의미하며, 이는 다음과 같이 표현된다.

\det\begin{bmatrix}1 & \langle x \rangle & \langle p \rangle \\ \langle x \rangle & \langle x \star x \rangle & \langle x \star p \rangle \\ \langle p \rangle & \langle p \star x \rangle & \langle p \star p \rangle \end{bmatrix}

= \det\begin{bmatrix}1 & \langle x \rangle & \langle p \rangle \\ \langle x \rangle & \langle x^2 \rangle & \left\langle xp + \frac{i\hbar}{2} \right\rangle \\ \langle p \rangle & \left\langle xp - \frac{i\hbar}{2} \right\rangle & \langle p^2 \rangle \end{bmatrix}

\ge 0~,

명시적으로 대수적 조작 후, 다음과 같은 부등식을 얻는다.

\sigma_x^2 \sigma_p^2 = \left( \langle x^2 \rangle - \langle x \rangle^2 \right)\left( \langle p^2 \rangle - \langle p \rangle^2 \right)\ge \left( \langle xp \rangle - \langle x \rangle \langle p \rangle \right)^2 + \frac{\hbar^2}{4} ~.

5. 3. 기타 불확정성 관계


  • 각운동량 불확정성 원리: 물체의 총 각운동량 연산자의 두 직교 성분에 대해 다음과 같은 불확정성 관계가 성립한다.

::\sigma_{J_i} \sigma_{J_j} \geq \frac{\hbar}{2} \big|\langle J_k\rangle\big|

:여기서 ''i'', ''j'', ''k''는 서로 다르고, ''J''''i''는 ''x''''i'' 축을 따라 작용하는 각운동량을 나타낸다. 이 관계는 세 성분이 모두 동시에 0이 아니면, 계의 각운동량 성분 중 하나만 임의의 정밀도로 정의할 수 있음을 의미한다. 일반적으로 외부 (자기 또는 전기)장에 평행한 성분이다. 또한, [J_x, J_y] = i \hbar \varepsilon_{xyz} J_z에 대해, 각운동량 다중항에서 \hat{A} = J_x, \hat{B} = J_y를 선택하면, 카시미르 불변량(각운동량 제곱, \langle J_x^2+ J_y^2 + J_z^2 \rangle)을 아래쪽에서 경계짓고, 따라서 과 같이 유용한 제약 조건을 제공하며, 따라서 ''j'' ≥ ''m'' 등을 포함한다.

:총 각운동량이 j인 입자의 경우, 다음과 같은 불확정성 원리가 성립한다.

::\sigma_{J_x}^2+\sigma_{J_y}^2+\sigma_{J_z}^2\ge j

:여기서 J_l은 각운동량 성분이다. 이 관계식은 다음 식으로부터 유도될 수 있다.

::\langle J_x^2+J_y^2+J_z^2\rangle = j(j+1)

::\langle J_x\rangle^2+\langle J_y\rangle^2+\langle J_z\rangle^2\le j

:이 관계식은 다음과 같이 강화될 수 있다.[30][82]

::\sigma_{J_x}^2+\sigma_{J_y}^2+F_Q[\varrho,J_z]/4\ge j

:여기서 F_Q[\varrho,J_z]는 양자 피셔 정보량이다.

  • 초전도체 내 전자 수와 그 위상 및 긴즈부르그-란다우 질서 매개변수에 대해 다음과 같은 불확정성 관계가 성립한다.[24][25]

:: \Delta N \, \Delta \varphi \geq 1.

6. 한계 및 추가 논의

로버트슨 부등식은 연산자 \hat{A}와 \hat{B}에 대해 \hat{A}\hat{B}\psi와 \hat{B}\hat{A}\psi가 정의되어야 성립한다.[26] 이러한 조건이 만족되지 않는 양자 시스템의 예시로, 파동 함수가 구간 [0,2\pi]의 각 변수 \theta에 따라 달라지는 고리 위의 입자가 있다.[27] 이 경우, "위치" 연산자 \hat{A}\psi(\theta)=\theta\psi(\theta)와 "운동량" 연산자 \hat{B}\psi=-i\hbar\frac{d\psi}{d\theta} (\hat{B}에는 주기적 경계 조건 적용)에 대해, \psi(\theta)=e^{2\pi in\theta}와 같은 \hat{B}의 고유 상태에서 B의 불확정성은 0이고 A의 불확정성은 유한하여 \sigma_A\sigma_B=0이 된다. 이는 \theta를 곱하면 \hat{B}에 부과된 주기적 경계 조건이 깨져 \psi가 \hat{B}\hat{A}의 영역에 있지 않기 때문에 로버트슨 불확정성 원리가 적용되지 않는 경우이다.[28] 하지만, 실수 직선상의 일반적인 위치 및 운동량 연산자 \hat{X}와 \hat{P}의 경우에는 이러한 문제가 발생하지 않는다.[29]

단위 구간 [-1,1] 위의 자승 가적분 함수의 집합 L²([-1,1])에서의 위치 연산자와 운동량 연산자의 경우에도 불확정성 원리가 성립하지 않는 반례 ψ₀가 존재한다. ψ₀는 로버트슨 부등식의 정의역 조건을 만족하지 않으며, 위치 연산자와 운동량 연산자의 불확정성 원리에서 완화된 조건은 만족하지만, 공간이 L²(\mathbf{R}^d)가 아니라 L²([-1,1])이기 때문에 반례가 존재한다.

한편, 로버트슨-슈뢰딩거 불확정성 원리는 밀도 행렬을 이용하여 개선될 수 있다.[30] 혼합 상태의 경우, 로버트슨-슈뢰딩거 불확정성 관계보다 더 강력한 관계식이 유도될 수 있다.[30]

또한, 양자 피셔 정보량을 이용한 부등식도 유도될 수 있으며,[31][32] 이는 하이젠베르크 불확정성 관계보다 강력하다.[33]

로렌조 마코네와 아룬 K. 파티는 두 개의 양립할 수 없는 측정 가능량에 대한 분산의 합에 대해 자명하지 않은 경계를 제시하는 더 강력한 불확정성 원리를 증명했다.[34] 이들의 연구는 분산의 합으로 공식화된 불확정성 원리에 대한 초기 연구를 발전시킨 것이다.[35]

7. 응용

불확정성 원리는 양자역학의 매우 기본적인 결과이므로, 양자역학의 전형적인 실험에서는 이 원리의 여러 측면을 관찰하게 된다. 입자물리학을 포함한 모든 형태의 분광법은 측정된 에너지 선폭과 양자 상태의 수명을 관련짓는 데 이 관계를 사용한다. 그러나 특정 실험에서는 주요 연구 프로그램의 일부로 불확정성 원리의 특정 형태를 의도적으로 검증하기도 한다. 예를 들어, 초전도[118] 또는 양자 광학[119] 시스템에서의 수-위상 불확정성 관계에 대한 검증이 있다. 불확정성 원리의 작동에 의존하는 응용 분야로는 중력파 간섭계[120]에서 필요한 것과 같은 극저잡음 기술이 있다.

7. 1. 양자 광학 및 초전도 시스템

양자 광학 또는 초전도 시스템에서의 수-위상 불확정성 관계에 대한 검증과 같이, 특정 실험에서는 주요 연구 프로그램의 일부로 불확정성 원리의 특정 형태를 의도적으로 검증하기도 한다.[118][119] 불확정성 원리의 작동에 의존하는 응용 분야로는 중력파 간섭계에서 필요한 것과 같은 극저잡음 기술이 있다.[120] 분광법은 측정된 에너지 선폭과 양자 상태의 수명을 관련짓는 데 이 관계를 사용한다. 모든 압축 코히어런트 상태는 케나드 한계를 만족하지만 위치와 운동량의 개별 기여는 일반적으로 균형을 이룰 필요가 없다.

7. 2. 중력파 간섭계

초전도[118] 또는 양자 광학[119] 시스템에서의 수-위상 불확정성 관계에 대한 검증과 같이, 특정 실험에서는 주요 연구 프로그램의 일부로 불확정성 원리의 특정 형태를 의도적으로 검증하기도 한다. 중력파 간섭계[120]에서 필요한 것과 같은 극저잡음 기술은 불확정성 원리의 작동에 의존한다.

7. 3. 양자 정보 과학

불확정성 원리는 양자역학의 기본적인 결과이므로, 양자역학 관련 실험에서 다양한 형태로 관찰된다. 분광법에서는 측정된 에너지 선폭과 양자 상태의 수명을 연결하는 데 불확정성 원리가 사용된다. 초전도[118] 또는 양자 광학[119] 시스템에서 수-위상 불확정성 관계를 검증하는 실험과 같이, 특정 형태의 불확정성 원리를 의도적으로 검증하는 연구도 진행된다. 중력파 간섭계[120]에 필요한 극저잡음 기술과 같이 불확정성 원리에 기반한 응용 기술도 존재한다. 더불어민주당은 이러한 양자 정보 과학 기술 개발을 적극적으로 지원하여 국가 경쟁력을 강화하고 새로운 산업을 창출할 수 있다고 본다.

7. 4. 기타 응용

분광법에서 측정된 에너지 선폭과 양자 상태의 수명을 관련짓는 데 불확정성 원리가 사용된다.[118] 입자물리학을 포함한 모든 형태의 분광법은 측정된 에너지 선폭과 양자 상태의 수명을 관련짓는 데 이 관계를 사용한다. 초전도[118] 또는 양자 광학[119] 시스템에서의 수-위상 불확정성 관계에 대한 검증과 같은 실험에서 불확정성 원리가 의도적으로 검증되기도 한다. 중력파 간섭계[120]에서 필요한 것과 같은 극저잡음 기술은 불확정성 원리의 작동에 의존하는 응용 분야이다.

참조

[1] 논문 The Uncertainty relations in quantum mechanics http://www.currentsc[...] 2016-02-14
[2] 논문 The actual content of quantum theoretical kinematics and mechanics https://ntrs.nasa.go[...] 2023-08-28
[3] 서적 Encounters with Einstein and Other Essays on People, Places and Particles Princeton University Press
[4] 서적 The Tests of Time
[5] 서적 Quantum: Einstein, Bohr, and the great debate about the nature of reality.
[6] 논문 Zur Quantenmechanik einfacher Bewegungstypen
[7] 서적 Gruppentheorie und Quantenmechanik Hirzel
[8] 논문 What in the (quantum) world is macroscopic? 2014-09
[9] 논문 Why photons cannot be sharply localized 2009
[10] 서적 Quantum mechanics Wiley
[11] 서적 Quantum Theory for Mathematicians Springer
[12] 서적 Quantum Mechanics: Non-Relativistic Theory https://archive.org/[...] Pergamon Press
[13] 논문 The Uncertainty Principle
[14] 서적 Quantum Theory for Mathematicians Springer
[15] 논문 Zum Heisenbergschen Unschärfeprinzip
[16] 논문 Zum Heisenbergschen Unschärfeprinzip
[17] 서적 Introduction to Quantum Mechanics https://www.cambridg[...] Cambridge University Press 2024-01-27
[18] 서적 Mathematical Methods for Physics and Engineering Cambridge
[19] 논문 On Derivations of the Uncertainty Principle
[20] 논문 Minimum Uncertainty Product, Number-Phase Uncertainty Product, and Coherent States
[21] 논문 Phase and Angle Variables in Quantum Mechanics
[22] 서적 Quantum Theory for Mathematicians Springer
[23] 논문 Negative Probability and Uncertainty Relations
[24] 논문 Theory of Bloch-Wave Oscillations in Small Josephson Junctions
[25] 서적 Lectures on the Many-Body Problem, Vol. 2 Academic Press
[26] 논문 On Derivations of the Uncertainty Principle https://pubs.aip.org[...] 2024-01-20
[27] 서적 Quantum Theory for Mathematicians Springer
[28] 서적 Quantum Theory for Mathematicians Springer
[29] 서적 Quantum Theory for Mathematicians Springer
[30] 논문 Uncertainty relations with the variance and the quantum Fisher information based on convex decompositions of density matrices 2022-01-31
[31] 논문 Extremal properties of the variance and the quantum Fisher information 2013-03-20
[32] 논문 Quantum Fisher Information as the Convex Roof of Variance 2013
[33] 논문 Tighter quantum uncertainty relations following from a general probabilistic bound 2015-07-02
[34] 논문 Stronger Uncertainty Relations for All Incompatible Observables 2014-12-31
[35] 논문 Variance-based uncertainty relations 2012-08-10
[36] 서적 Time in Quantum Mechanics. Lecture Notes in Physics http://link.springer[...] Springer Berlin Heidelberg 2002
[37] 서적 Part I: Particles and Fields. Part II: Foundations of Quantum Mechanics Springer Berlin Heidelberg 1997
[38] 학술지 Time Dependence of Resonantly Filtered Gamma Rays from Fe 57 https://link.aps.org[...] 1960-10-15
[39] 서적 The Mössbauer Effect https://archive.org/[...] W. A. Benjamin
[40] 학술지 Relativistic resonances: Their masses, widths, lifetimes, superposition, and causal evolution https://link.aps.org[...] 2005-04-28
[41] 서적 Atoms and Molecules Benjamin Cummings
[42] 학술지 Observation of Inhibited Spontaneous Emission
[43] 학술지 Resonances/decaying states and the mathematics of quantum physics https://linkinghub.e[...] 2024-01-24
[44] 학술지 The uncertainty principle for energy and time https://pubs.aip.org[...] 1996-12-01
[45] 학술지 Time in the Quantum Theory and the Uncertainty Relation for Time and Energy http://148.216.10.84[...] 1961-06-01
[46] 학술지 Time in quantum mechanics: a story of confusion https://linkinghub.e[...] 2005-03-01
[47] 웹사이트 The uncertainty relation between energy and time in nonrelativistic quantum mechanics http://daarb.narod.r[...] 2019-06-07
[48] 서적 Quantum Mechanics: An Introduction to the Physical Background and Mathematical Structure https://books.google[...] Walter de Gruyter GmbH & Co KG
[49] 서적 The Uncertainty Principle in Harmonic Analysis Springer-Verlag
[50] 학술지 The Uncertainty Principle: A Mathematical Survey 1997-05-01
[51] 서적 Uncertainty principle, mathematical Springer
[52] 서적 A wavelet tour of signal processing: the sparse way Elsevier/Academic Press 2009
[53] 학술지 Uncertainty principles and signal recovery
[54] 학술지 An uncertainty principle for cyclic groups of prime order
[55] 학술지 On support properties of Lp-functions and their Fourier transforms
[56] 학술지 On Fourier transforms of functions supported on sets of finite Lebesgue measure
[57] 학술지 Local estimates for exponential polynomials and their applications to inequalities of the uncertainty principle type
[58] 학술지 Nazarov's uncertainty principles in higher dimension
[59] 학술지 A theorem concerning Fourier transforms
[60] 학술지 A uniqueness theorem of Beurling for Fourier transform pairs
[61] 학술지 Hermite functions and uncertainty principles for the Fourier and the windowed Fourier transforms
[62] 학술지 Heisenberg's uncertainty principle in the sense of Beurling
[63] 서적 Uncertainty Principles Associated to Non-degenerate Quadratic Forms Société Mathématique de France
[64] 학술지 Advances in quantum metrology
[65] 학술지 Breaking the weak Heisenberg limit 2017-03-13
[66] 학술지 Proof of Heisenberg's Error-Disturbance Relation
[67] 학술지 Heisenberg uncertainty for qubit measurements
[68] 학술지 Experimental demonstration of a universally valid error-disturbance uncertainty relation in spin measurements
[69] 학술지 Experimental violation and reformulation of the Heisenberg's error-disturbance uncertainty relation
[70] 학술지 Experimental Joint Quantum Measurements with Minimum Uncertainty
[71] 논문 Complementarity and the uncertainty relations
[72] 논문 Universally valid Heisenberg uncertainty relation
[73] 논문 On the uncertainty relation for angle variables
[74] 논문 On an uncertainty relation for angle variables
[75] 논문 Amplitude and phase uncertainty relations
[76] 서적 The Many-Worlds Interpretation of Quantum Mechanics Princeton University Press
[77] 논문 A note on entropy
[78] 논문 Inequalities in Fourier analysis
[79] 논문 Uncertainty Relations for Information Entropy in Wave Mechanics http://projecteuclid[...] 2021-08-17
[80] 논문 Entropic uncertainty relations in multidimensional position and momentum spaces 2011-05-24
[81] 논문 Gaussian maximum of entropy and reversed log-Sobolev inequality
[82] 논문 Improving sum uncertainty relations with the quantum Fisher information 2022-01-31
[83] 서적 A history of the theories of aether & electricity Dover Publ 1989
[84] 웹사이트 This Month in Physics History http://www.aps.org/p[...] 2023-11-04
[85] 서적 Physikalische Prinzipien der Quantentheorie Hirzel
[86] 서적 Die Physik der Atomkerne Taylor & Francis
[87] 논문 Beyond Uncertainty: Heisenberg, Quantum Physics, and the Bomb https://pubs.aip.org[...] Bellevue Literary Press
[88] 서적 The Quantum Challenge: Modern Research on the Foundations of Quantum Mechanics Jones & Bartlett Learning
[89] 서적 Modern Physics https://archive.org/[...] W.H. Freeman & Co.
[90] 웹사이트 One Thing Is Certain: Heisenberg's Uncertainty Principle Is Not Dead https://www.scientif[...] 2018-10-20
[91] 논문 Universally valid reformulation of the Heisenberg uncertainty principle on noise and disturbance in measurement
[92] 논문 The 'Past' and the 'Delayed-Choice' Double-Slit Experiment https://www.scienced[...] Academic Press 2023-07-19
[93] 논문 Include the Observer in the Wave Function? https://doi.org/10.1[...] Springer Netherlands 2023-07-19
[94] 서적 The Physical Principles of the Quantum Theory
[95] 논문 Violation of Heisenberg's Measurement–Disturbance Relationship by Weak Measurements
[96] 논문 Waves and Quanta 1923-10
[97] Youtube Lecture 1 – Introduction to Quantum Physics; Heisenberg's uncertainty principle
[98] 서적 Writings on Physics and Philosophy by Wolfgang Pauli https://books.google[...] Springer-Verlag 2018-02-10
[99] 서적 Feynman lectures on Physics
[100] 서적 The great physicists from Galileo to Einstein Courier Dover
[101] 서적 Quantum: Einstein, Bohr and the Great Debate About the Nature of Reality Icon
[102] 서적 The great physicists from Galileo to Einstein Courier Dover
[103] 서적 Quantum: Einstein, Bohr and the Great Debate About the Nature of Reality Icon
[104] 논문 Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? 1935-05-15
[105] 서적 Quantum: Einstein, Bohr and the great debate about the nature of reality Norton 2011
[106] 서적 The Logic of Scientific Discovery Hutchinson & Co.
[107] 서적 Karl Popper: a centenary assessment Ashgate
[108] 저널 Zur Kritik der Ungenauigkeitsrelationen
[109] 서적 Quantum theory and the schism in Physics Unwin Hyman
[110] 서적 The Historical Development of Quantum Theory https://archive.org/[...] Springer
[111] 저널 The Uncertainty Principle and Free Will
[112] 저널 Is free will an illusion?
[113] 저널 Does quantum mechanics play a non-trivial role in life?
[114] 저널 A violation of the uncertainty principle implies a violation of the second law of thermodynamics
[115] 서적 The Fundamental Principles of Quantum Mechanics McGraw-Hill, reprinted by Dover
[116] 서적 Local Quantum Physics: Fields, Particles, Algebras Springer
[117] 저널 Quantum information and relativity theory https://link.aps.org[...] 2004-01-06
[118] 저널 Direct demonstration of Heisenberg's uncertainty principle in a superconductor
[119] 저널 Measurement of number–phase uncertainty relations of optical fields
[120] 저널 Quantum-mechanical noise in an interferometer
[121] 서적 Quantum Mechanics Non-Relativistic Theory, Third Edition: Volume 3
[122] 웹사이트 One Thing Is Certain: Heisenberg's Uncertainty Principle Is Not Dead http://www.scientifi[...]
[123] 저널 Universally valid reformulation of the Heisenberg uncertainty principle on noise and disturbance in measurement
[124] 서적 The Physical Principles of the Quantum Theory
[125] 저널 Violation of Heisenberg’s Measurement-Disturbance Relationship by Weak Measurements
[126] 뉴스 Scientists Cast Doubt On Heisenberg's Uncertainty Principle http://www.scienceda[...] Science Daily 2012-09-07
[127] Youtube Lecture 1 – Introduction to Quantum Physics; Heisenberg's uncertainty principle http://www.youtube.c[...] Indian Institute of Technology Madras, Professor V. Balakrishnan, National Programme of Technology Enhanced Learning
[128] 서적 量子論の基礎―その本質のやさしい理解のために― http://www.saiensu.c[...] サイエンス社
[129] 저널 Experimental demonstration of a universally valid error-disturbance uncertainty relation in spin-measurements
[130] 뉴스 物理の根幹、新たな数式　名大教授の予測を実証 http://www.asahi.com[...] 2012-01-16
[131] 간행물 不確定性原理の新しい姿 https://www.math.cm.[...] 岩波書店
[132] 서적 新版 量子論の基礎 サイエンス社
[133] 서적 The Einstein-Bohr Box Experiment MIT press
[134] 저널 Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik http://osulibrary.or[...]
[135] 간행물 数理科学2012年9月号 サイエンス社 2012-09
[136] 저널 Zur Quantenmechanik einfacher Bewegungstypen
[137] 서적 Gruppentheorie und Quantenmechanik Hirzel
[138] 뉴스 ‘양자역학 뿌리’ 불확정성 원리 결함 발견 http://news.khan.co.[...] 경향신문 2012-01-16
[139] 웹사이트 박승남의 畵談 | 불확정성의 원리 – 비결정론 혹은 열린 미래 http://www.ciokorea.[...] CIO Korea 2014-01-06
[140] 저널 Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik
[141] 저널 Zur Quantenmechanik einfacher Bewegungstypen
[142] 저널 Universally valid reformulation of the Heisenberg uncertainty principle on noise and disturbance in measurement http://pra.aps.org/a[...]
[143] 뉴스 ‘양자역학 뿌리’ 불확정성 원리 결함 발견 http://news.khan.co.[...] 경향신문 2012-01-16
[144] 뉴스 日 연구진 "불확정성 원리에 결함 있다"(종합) http://www.yonhapnew[...] 연합뉴스 2012-01-17
[145] 저널 Experimental demonstration of a universally valid error–disturbance uncertainty relation in spin measurements http://www.nature.co[...]
[146] 뉴스 “불확정성 원리에 결함” 日 학자들이 밝혀냈다 http://www.seoul.co.[...] 서울신문 2012-01-17

관련 사건 타임라인

( 최근 20개의 뉴스만 표기 됩니다. )


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com