고조파
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
고조파는 기본 주파수의 정수배에 해당하는 주파수를 의미하며, 음악, 음향학, 전기공학, 무선공학, 기계공학 등 다양한 분야에서 사용된다. 음악에서는 악기의 음색을 결정하는 중요한 요소이며, 전기공학에서는 전원 주파수의 배수로 발생하여 전자 회로의 오작동을 유발할 수 있다. 무선공학에서는 주파수 체배 및 스퓨리어스 발생과 관련되며, 기계공학에서는 기어, 회전체 등의 진동 및 공진과 관련된다.
더 읽어볼만한 페이지
- 전기통신 - FTTX
FTTx는 광섬유를 활용한 통신 서비스 네트워크 구축 방식으로, 광섬유 연결 위치에 따라 FTTH, FTTB, FTTC, FTTN 등으로 나뉘며, 각 방식은 구축 비용과 제공 대역폭에 차이가 있고, VDSL, PON 기술을 기반으로 초고속 인터넷 서비스 제공에 중요한 역할을 담당하며 미래 기술 발전에 필수적인 인프라로 지속적인 발전과 보급 확대가 예상된다. - 전기통신 - 중계기
중계기는 전기 통신 및 컴퓨터 네트워킹에서 신호를 증폭하거나 재생성하여 통신 거리를 연장하는 장치로, 아날로그 및 디지털 신호를 처리하며 다양한 유형이 존재한다. - 소리 - 음악
음악은 인간이 소리를 재료로 박자, 선율, 화성 등의 요소를 사용하여 감정과 사상을 표현하는 시간 예술로, 다양한 장르로 분류되며 작곡, 연주, 감상의 요소로 구성되어 예술, 오락, 종교 의식 등 다양한 목적으로 활용된다. - 소리 - 의성어
의성어는 사람, 동물, 사물 등의 소리를 흉내 내어 표현하는 단어로, 문화권에 따라 다르게 표현되지만 시각적 효과나 기억술, 언어학적으로 소리와 의미의 관계를 보여주는 예시로 활용된다. - 음향학 - 신시사이저
신시사이저는 전자 회로로 소리를 합성하는 전자 악기로, 1960년대 로버트 무그 등에 의해 현대적인 형태로 발전하여 다양한 음향 합성 방식을 사용하며 여러 장르의 음악과 영화 사운드트랙에 널리 활용된다. - 음향학 - 사인파
사인파는 고조파가 없는 단일 주파수 파형으로, 삼각함수로 표현되며 진폭, 각진동수, 위상 등의 매개변수로 특징지어지고, 푸리에 분석을 통해 복잡한 파형으로 분해 및 합성이 가능하며, 전자공학, 음악, 물리학 등 다양한 분야에서 활용된다.
| 고조파 | |
|---|---|
| 개요 | |
| 정의 | 기본 주파수의 정수배 주파수를 갖는 파동 |
| 관련 용어 | 부분음, 배음, 상음 |
| 특징 | |
| 발생 조건 | 비선형 시스템, 주기 신호 |
| 음향학 | 악기의 음색 결정, 배음렬 형성 |
| 전기 공학 | 전력 시스템 품질 저하, 통신 시스템 간섭 |
| 활용 | 오디오 신호 처리, 전력 시스템 분석 |
| 음향학적 특성 | |
| 악기 음색 | 고조파 구조가 악기 음색을 결정함 |
| 배음렬 | 기본음과 고조파들의 주파수 비율 |
| 전기 공학적 특성 | |
| 전력 품질 | 고조파는 전력 시스템의 전력 품질을 저하시킴 |
| 통신 시스템 | 고조파는 통신 시스템에서 간섭을 유발함 |
| 활용 분야 | |
| 오디오 신호 처리 | 고조파는 오디오 신호의 분석 및 합성에 사용됨 |
| 전력 시스템 분석 | 고조파 분석은 전력 시스템의 문제 진단에 사용됨 |
| 기타 | |
| 주의사항 | 고조파는 시스템에 다양한 문제를 일으킬 수 있으므로 적절한 관리가 필요함 |
2. 용어
고조파는 영어로 하모닉(harmonics)이며, 배음(overtones), 파셜(partials), 어퍼파셜(upper partials) 등과 같은 유의어가 있다. 고조파(하모닉)와 배음(오버톤)의 차이점은 고조파가 기본 주파수를 포함한 모든 음을 포함하는 반면(예: 기타의 개방현), 배음은 기본 주파수 위의 음높이만을 포함한다는 것이다. 일부 음악적 맥락에서 고조파, 배음, 파셜이라는 용어는 서로 바꿔서 사용되기도 한다.[10]
고조파는 "배음", "부분음", 또는 "상위 부분음"이라고도 불린다. 좀 더 정확하게는, "고조파"는 조화로운 음열의 모든 음높이(기본 주파수 포함)를 포함하는 반면, "배음"은 기본 주파수 위의 음높이만 포함한다.
배음은 복합음에서 가장 낮은 부분음보다 높은 모든 부분음을 의미한다. 구성 부분음의 상대적인 세기와 주파수 관계는 악기의 음색을 결정한다. 배음과 부분음이라는 용어의 유사성 때문에 때때로 음악적 맥락에서 서로 바꿔서 느슨하게 사용되지만, 계산 방식이 다르기 때문에 혼란을 야기할 수 있다.
| 주파수 | 순서 (n) | 이름 1 | 이름 2 | 이름 3 |
|---|---|---|---|---|
| 1 × f = 440 Hz | n = 1 | 1번째 부분음 | 기음 | 1번째 배음 |
| 2 × f = 880 Hz | n = 2 | 2번째 부분음 | 1번째 배음 | 2번째 배음 |
| 3 × f = 1320 Hz | n = 3 | 3번째 부분음 | 2번째 배음 | 3번째 배음 |
| 4 × f = 1760 Hz | n = 4 | 4번째 부분음 | 3번째 배음 | 4번째 배음 |
대부분의 음향 악기는 여러 부분음(단순음 또는 정현파)을 포함하는 복합음을 방출하지만, 훈련받지 않은 귀는 이를 별개의 현상으로 인식하지 못하고 하나의 소리, 즉 음색으로 인식한다. 사람의 목소리나 활로 켜는 바이올린과 같은 악기들은 주기 함수 형태의 복합음을 생성하며, 이는 기본 주파수의 정수배에 가까운 부분음들로 구성되어 '조화 부분음' 또는 '배음'이라고 불린다.[2]
3. 음악 및 음향학
기타 현이나 양 끝이 열린 플루트와 같은 1차원 공명기는 조화 부분음을 생성한다. 트럼펫이나 클라리넷처럼 한쪽 끝만 열린 관악기도 배음과 유사한 부분음을 생성하지만, 이론적으로는 홀수 배음에만 일치한다. 실제 악기는 비선형 음향 탄성 등 여러 요인으로 인해 정수가 아닌 부분음을 갖기도 한다.
기본 주파수의 정수배가 아닌 부분음은 비화성 부분음이라고 한다. 피아노, 피치카토 주법의 현악기, 비브라폰, 마림바 등은 조화 및 비화성 부분음이 혼합되어 특정 기본 음고를 인식하게 한다. 반면 심벌즈, 드럼 등은 비화성 부분음이 많아 특정한 음고를 느끼기 어렵다.[3][4]
세타레스의 연구를 바탕으로,[5] 역동적 음조성은 유사 정음 튜닝에서 각 부분음의 주파수를 해당 음표의 음고에 맞춰 유사 조화 음색의 협화음을 최대화하는 유사 조화 부분음 개념을 도입했다.[6][7][8][9]
순정율 체계는 고조파를 기반으로 사용될 수 있다. 아놀드 드레이블라트는 개조된 더블베이스의 단현에서 활을 이용한 독특한 기법으로 다양한 고조파를 만들어냈고, 로렌스 볼은 전자 음악 생성에 고조파를 활용했다.
3. 1. 특징
대부분의 악기는 복합음을 방출하며, 이 복합음은 여러 부분음으로 구성된다. 훈련받지 않은 귀는 부분음을 개별적으로 인식하지 못하고, 하나의 음색으로 인식한다. 사람의 목소리, 현악기, 관악기 등은 기본 주파수의 정수배에 가까운 부분음(조화 부분음 또는 배음)을 생성한다.[2]
비화성 부분음은 기본 주파수의 정수배가 아닌 주파수를 갖는 부분음이다. 피아노, 비브라폰, 마림바 등은 조화 및 비화성 부분음이 혼합되어 특정한 기본 음고를 갖는 소리를 낸다. 심벌즈, 드럼 등은 비화성 부분음이 풍부하여 특정한 음고를 갖지 않는다.[3][4]
다음은 배음, 부분음, 상위 배음의 계산 방식을 나타낸 표이다.
| 주파수 | 순서 | 이름 1 | 이름 2 | 이름 3 | 정상파 표현 | 종파 표현 |
|---|---|---|---|---|---|---|
| 1 × f = 440 Hz | n = 1 | 1번째 부분음 | 기음 | 1번째 배음 | 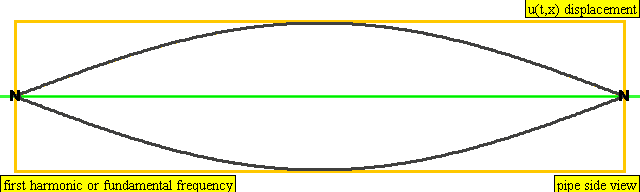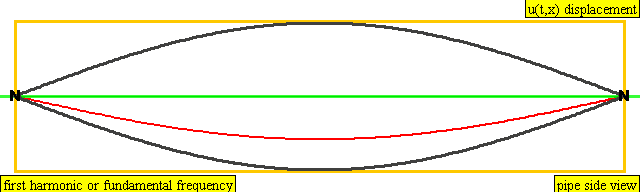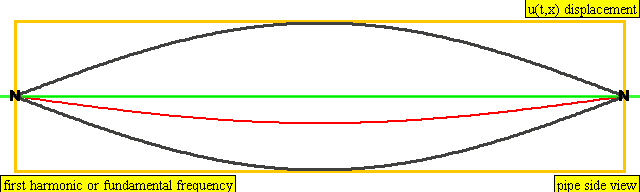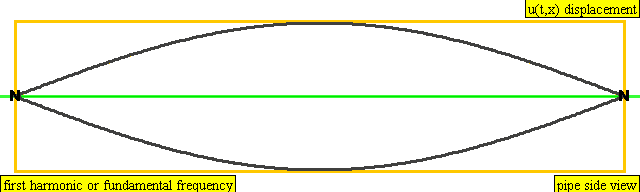 | 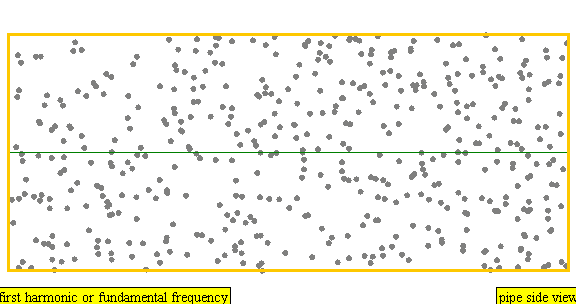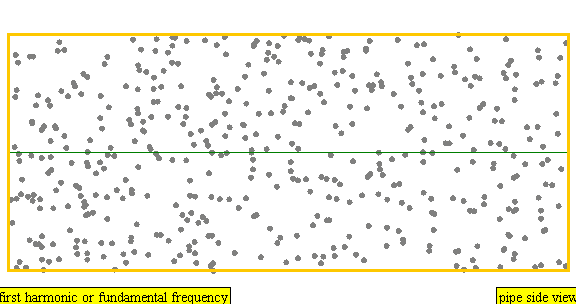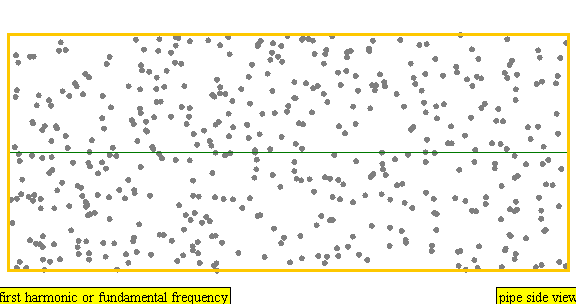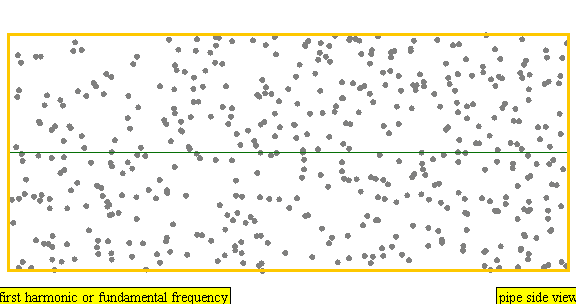 |
| 2 × f = 880 Hz | n = 2 | 2번째 부분음 | 1번째 배음 | 2번째 배음 | 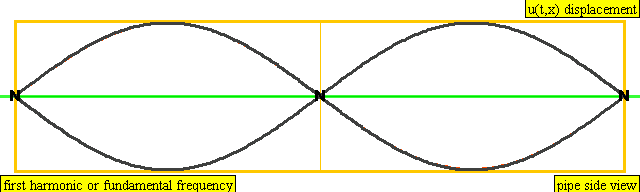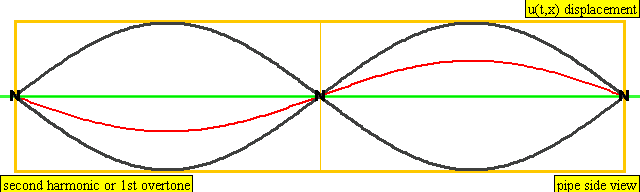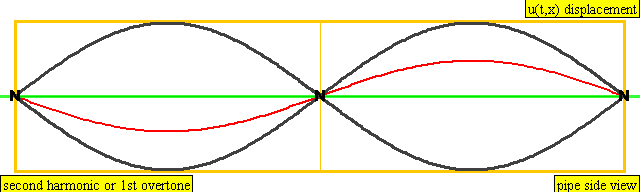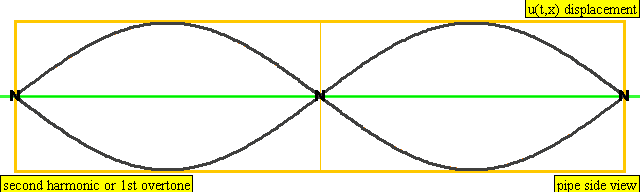 | 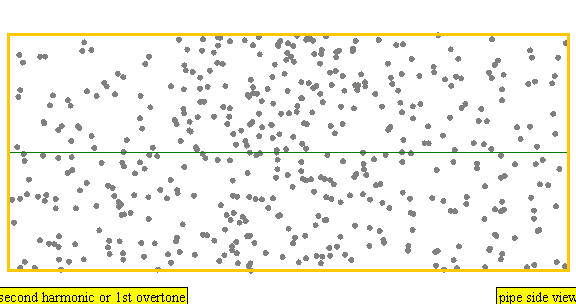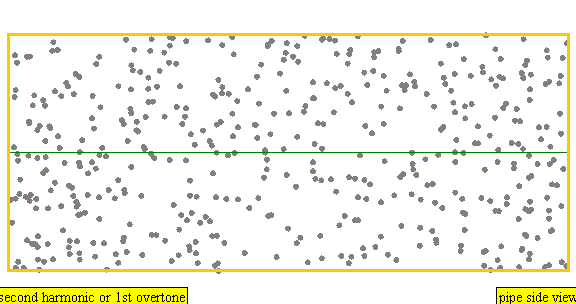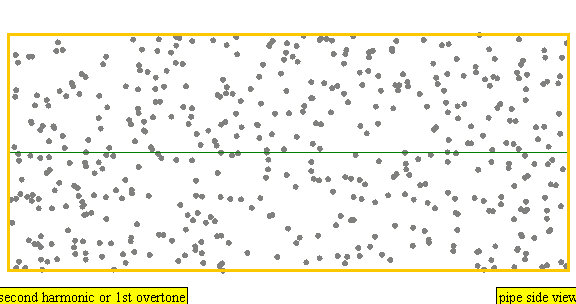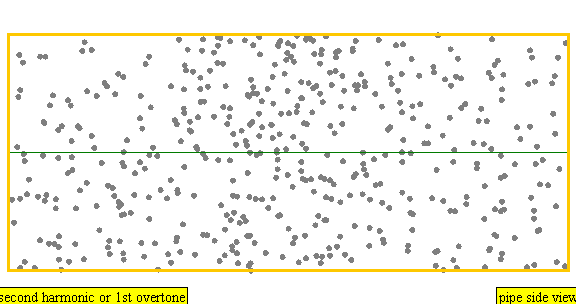 |
| 3 × f = 1320 Hz | n = 3 | 3번째 부분음 | 2번째 배음 | 3번째 배음 | 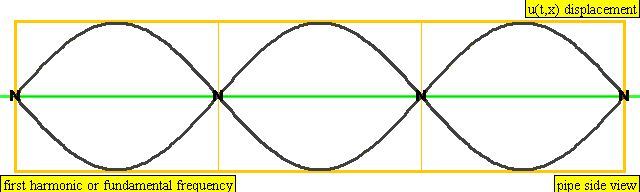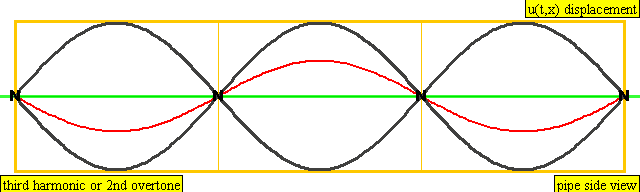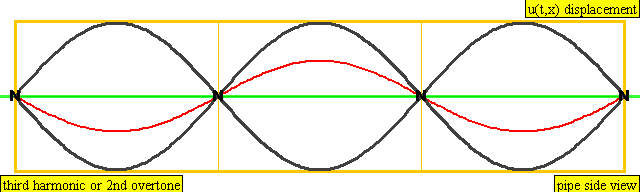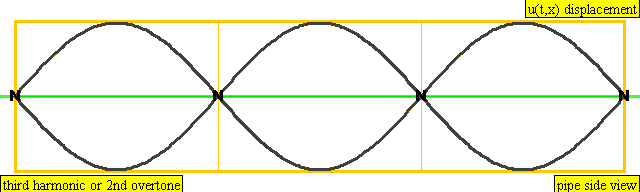 | 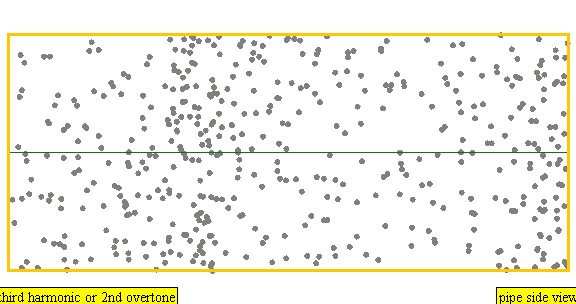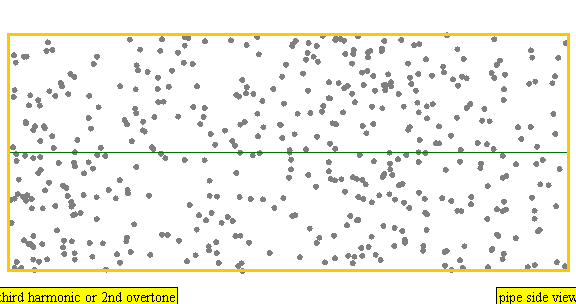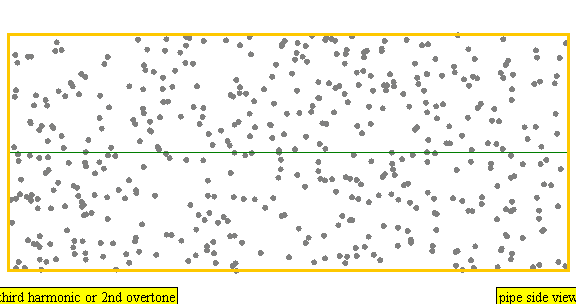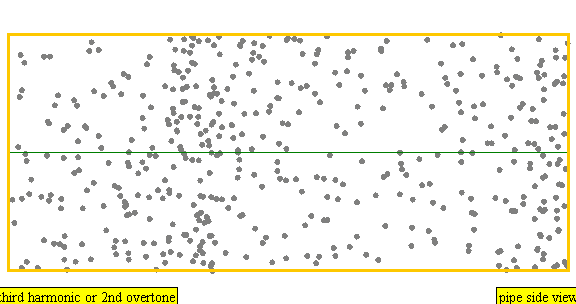 |
| 4 × f = 1760 Hz | n = 4 | 4번째 부분음 | 3번째 배음 | 4번째 배음 | 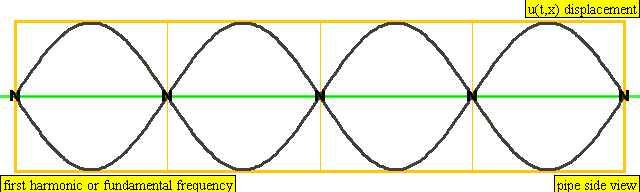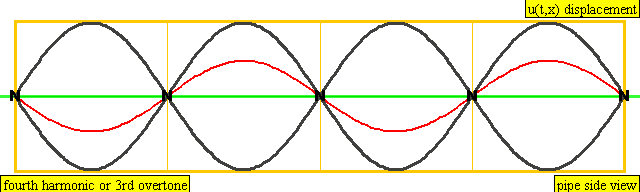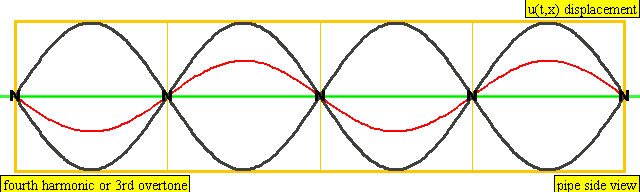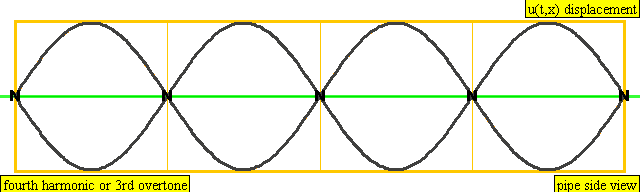 | 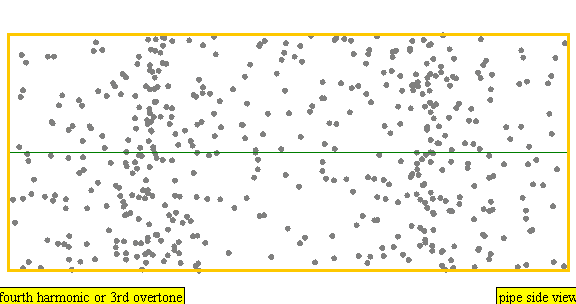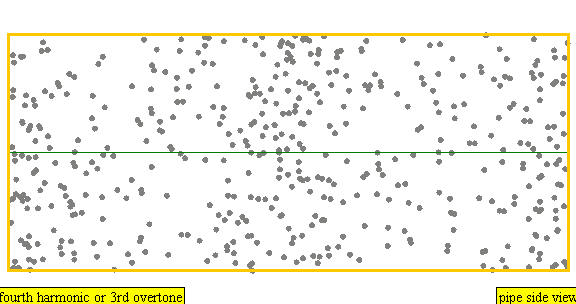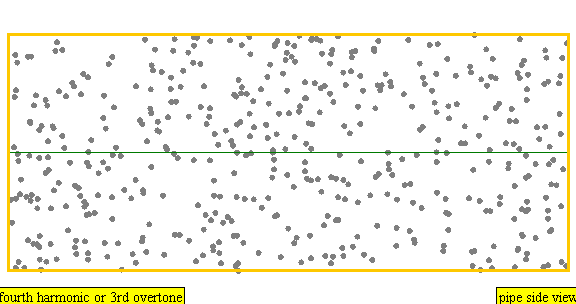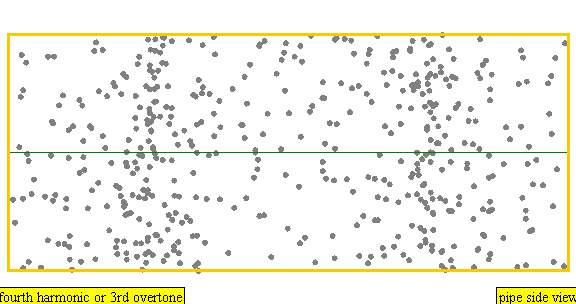 |
많은 악기에서 기본음이 없어도 상위 배음을 연주하는 것이 가능하다. 관악기에서는 ''오버블로잉''이라는 확장 기법을 사용하여 더 높은 음을 얻거나 다중음을 연주하여 배음을 생성한다. 현악기에서는 배음 또는 ''플라젤렛''이라고 불리는 매우 맑은 소리를 생성할 수 있다.
3. 2. 현악기의 고조파
현악기에서는 현의 특정 지점을 가볍게 눌러 고조파를 연주할 수 있다. 이렇게 만들어진 고조파는 플루트와 같은 맑은 음색을 가지며, 관현악에서 특수한 효과를 내기 위해 사용된다.[12]현악기에서 하모닉스(플라조렛 톤)는 현을 가볍게 터치하여 특정 진동 모드를 강제하는 방식으로 만들어진다. 다음 표는 현악기에서 하모닉스를 얻을 수 있는 지점을 보여준다.[12]
| 하모닉스 차수 | 정지점 | 소리나는 음 (개방현 기준) | 오디오 주파수(Hz) | 센트 |
|---|---|---|---|---|
| 1 | 기본 주파수, 완전 일치 | 1 | style="text-align:right;"| | 0.0 |
| 2 | 첫 번째 완전 옥타브 | 8 | style="text-align:right;"| | 0.0 |
| 3 | 완전 5도 | 8 + 5 | style="text-align:right;"| | 702.0 |
| 4 | 두 배의 완전 옥타브 | 28 | style="text-align:right;"| | 0.0 |
| 5 | 순정 장3도, 장3도 | 28 + 3 | style="text-align:right;"| | 386.3 |
| 6 | 완전 5도 | 28 + 5 | style="text-align:right;"| | 702.0 |
| 7 | 하모닉 7도, septimal 단7도 (‘잃어버린 코드’) | 28 + 7 | style="text-align:right;"| | 968.8 |
| 8 | 세 번째 완전 옥타브 | 38 | style="text-align:right;"| | 0.0 |
| 9 | 피타고라스 장2도 하모닉 9도 | 38 + 2 | style="text-align:right;"| | 203.9 |
| 10 | 순정 장3도 | 38 + 3 | style="text-align:right;"| | 386.3 |
| 11 | 작은 십일음 트라이톤, undecimal 반-증4도 | 38 + 4 | style="text-align:right;"| | 551.3 |
| 12 | 완전 5도 | 38 + 5 | style="text-align:right;"| | 702.0 |
| 13 | tridecimal 중립 6도 | 38 + 6 | style="text-align:right;"| | 840.5 |
| 14 | 하모닉 7도, septimal 단7도 (‘잃어버린 코드’) | 38 + 7 | style="text-align:right;"| | 968.8 |
| 15 | 순정 장7도 | 38 + 7 | style="text-align:right;"| | 1088.3 |
| 16 | 네 번째 완전 옥타브 | 48 | style="text-align:right;"| | 0.0 |
| 17 | septidecimal 반음 | 48 + 2 | style="text-align:right;"| | 105.0 |
| 18 | 피타고라스 장2도 | 48 + 2 | style="text-align:right;"| | 203.9 |
| 19 | nanodecimal 단3도 | 48 + 3 | style="text-align:right;"| | 297.5 |
| 20 | 순정 장3도 | 48 + 3 | style="text-align:right;"| | 386.3 |
더블 베이스를 제외하고는 다섯 번째 부분음보다 높은 자연 하모닉스를 사용하는 경우는 드물다.[12]
인공 배음은 이미 짚어진 현에서 배음을 연주하여 만들 수 있다. 연주 기법은 지판에서 두 손가락을 사용하는 것이다. 첫 번째 손가락은 현을 줄여 원하는 기본음을 만들고, 두 번째 손가락은 적절한 배음에 해당하는 마디를 터치한다.
3. 3. 배음 창법
사람의 목소리도 많은 개별 부분음을 포함하는 복합 음을 방출하지만, 훈련받지 않은 인간의 귀는 일반적으로 이러한 부분음을 별도의 현상으로 인식하지 못한다. 오히려 음표는 하나의 소리로 인식되며, 해당 소리의 품질 또는 음색은 개별 부분음의 상대적 강도의 결과이다.[2] 몽골의 흐미와 같이 의도적으로 고조파를 활용하는 창법도 존재한다.4. 전기공학
전기공학에서 고조파는 전원 주파수의 정수배로 발생하며, EMI의 발생원이 된다. 평활 콘덴서를 사용한 DC 전원 회로, 인버터 등에서 사용되는 PWM 스위칭 회로는 파형을 왜곡시킨다. 왜곡된 파형은 전원 주파수의 정수배로 노이즈를 발생시킨다. 이 노이즈는 전원의 역률을 저하시키고, 전자 회로의 오작동이나 정전을 일으킬 수 있기 때문에, 기술 기준에 의해 규제되고 있다. 전원 선로의 중성선(N)은 대지로의 귀선(리턴 패스)이지만, 무효 전력인 고조파 성분을 대지로 되돌리는 역할도 한다.
5. 무선공학
무선 공학에서는 무선기에서 송신하는 전파에 섞이는 목적 신호 이외의 성분(주로 고조파 및 저조파)을 스퓨리어스라고 부른다.[1] 스퓨리어스의 강도는 전파법에 의해 제한되며, 일반적으로 스펙트럼 분석기를 사용하여 측정한다.[1]
무선 통신 등의 발진 회로에서 필요한 주파수의 1/n의 기본파(원 발진, 줄여서 원발)에서 의도적으로 왜곡 특성을 가진 회로를 통과시켜 고조파로서 목적 주파수의 신호를 발생시키는 것을 '''(주파수) 체배'''((frequency) multiplication)라고 한다. PLL에 의해 n배의 주파수 신호를 얻는 것도 체배라고 한다.
6. 기계공학
기계공학에서 평기어나 직선 래핑 기어는 물림 진동(회전수 × 잇수) 외에 고조파가 발생한다. 이를 줄이기 위해 평기어는 사선 톱니 기어나 산형 톱니 기어를 사용하고, 래핑 기어는 사선 래핑 기어나 곡선 래핑 기어, 하이포이드 기어를 사용한다.[16] 톱니에 손상이 있는 경우에는 회전수에 의존하는 큰 진동과 그 고조파가 이상 진동으로 발생할 수 있다.[16] 증기 기관이나 내연 기관 등 링크 기구에서는 지지부가 링크의 진동과 공진하여 고조파가 발생하거나, 고속 회전체에서도 축 주위에서 공진하여 고조파가 나올 수 있다.[16]
7. 대조어
어떤 주파수 성분을 가진 파동에 대해, 그 정수분의 1의 주파수 성분(예: 기본 주파수의 1/2, 1/3, 1/4 ... 주파수)을 저조파라고 한다.
참조
[1]
간행물
Russell Walker
http://dx.doi.org/10[...]
Institute for Operations Research and the Management Sciences
2020-12-21
[2]
site sub-index & mini-bio for Scholz
Category:Scholz, Richard
https://imslp.org/wi[...]
2020-12-21
[3]
간행물
Large grand and small upright pianos
http://www.acoustics[...]
Acoustical Society of America
2024-01-13
[4]
book review
"''Golo und Genovefa'' {{grey|[by]}} Hanna Rademacher"
1927-04
[5]
서적
Tuning, Timbre, Spectrum, Scale
https://books.google[...]
Springer
[6]
학술지
Spectral tools for dynamic tonality and audio morphing
http://muse.jhu.edu/[...]
2009-09-20
[7]
학술지
Tuning continua and keyboard layouts
http://oro.open.ac.u[...]
2008-08-29
[8]
학술지
Invariant fingerings across a tuning continuum
http://oro.open.ac.u[...]
2007-Winter
[9]
보고서
X System
http://oro.open.ac.u[...]
Thumtronics Inc.
2020-05-02
[10]
간행물
https://www.its.bldr[...]
[11]
웹사이트
Free Online Games for Kids
http://doi.org/10.40[...]
2020-12-21
[12]
사전
Oxford University Press
2020-12-21
[13]
문서
https://www.hioki.co[...]
[14]
문서
https://www.emc-ohta[...]
[15]
문서
https://catalog.club[...]
[16]
웹사이트
振動の世界 東京文映製作 - YouTube
https://www.youtube.[...]
2020-12-16
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com