마이어-피토리스 열

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 정의
- 3.1. 경계 사상 (Boundary Map)
4. 성질
5. 응용
6. 다른 호몰로지 이론과의 관계
참조

1. 개요

마이어-피토리스 열은 위상 공간의 호몰로지 군을 계산하기 위한 도구로, 오스트리아의 수학자 발터 마이어와 레오폴트 피토리스에 의해 도입되었다. 두 부분 집합의 내부가 위상 공간을 덮는 경우, 마이어-피토리스 열은 공간, 부분 집합, 그리고 그들의 교집합의 호몰로지 군을 연결하는 긴 완전열을 제공하며, 비축소 및 축소 버전이 존재한다. 이 열은 호몰로지 이론의 기본 공리에서 유도되며, k-구, 클라인 병, 쐐기합, 현수 등 다양한 공간의 호몰로지 군을 계산하는 데 응용된다. 또한, 자이페르트-판 캄펜 정리와 유사한 성질을 가지며, 자연성을 만족한다. 코호몰로지 버전과 상대 호몰로지, 그리고 일반 코호몰로지 이론에서도 성립한다.

더 읽어볼만한 페이지

호몰로지 이론 - 매시 곱
매시 곱은 미분 등급 대수 원소에 대한 연산으로 코호몰로지 곱으로 파악하기 어려운 위상수학적 불변량을 측정하며, 2항 곱과 3항 곱을 일반화한 형태로 불확정성을 가지지만, 브루니안 링크, 보로메오 고리 연구 및 꼬인 K-이론 등 다양한 분야에 응용된다.
호몰로지 이론 - 베유 대수
베유 대수는 체 K 위의 리 대수 g에 대하여 정의되는 미분 등급 대수이며, g의 쌍대 공간과 그 등급 이동으로 생성되는 외대수와 대칭 대수의 텐서곱으로 표현되고, 리 군의 분류 공간의 주다발의 무한소 형태를 나타내는 완전열과 관련이 있다.

마이어-피토리스 열

2. 역사

오스트리아의 수학자 발터 마이어(Walther Mayer^de)와 레오폴트 피토리스(Leopold Vietoris^de)가 도입하였다. 1926~1927년, 마이어는 피토리스의 위상수학 강의를 듣고 마이어-피토리스 열의 초기 형태에 대한 아이디어를 얻었다. 1929년, 마이어는 베티 수에 대한 마이어-피토리스 열을 증명하였다.^[58] 1930년, 피토리스는 호몰로지 군에 대한 마이어-피토리스 열을 완전히 증명하였다.^[59]

이후 사무엘 에일렌베르크와 노먼 스틴로드가 완전열의 개념을 도입하면서, 마이어와 피토리스의 준동형들이 긴 완전열을 이룸을 지적하였다. 1952년, 에일렌베르크와 스틴로드는 공저 "대수적 위상수학의 기초"에서 완전열의 개념을 도입하여 마이어-피토리스 열을 현대적인 형태로 정립하였다.^[7]

3. 정의

위상 공간 $X$ 의 두 부분 집합 $A,B\subset X$ 의 내부가 $X$ 의 열린 덮개를 이룬다고 가정하면, 즉,

: $\operatorname{int}(A)\cup\operatorname{int}(B)=X$

다음과 같은 포함 사상들을 정의할 수 있다.

$i\colon A\cap B\hookrightarrow A$
$j\colon A\cap B\hookrightarrow B$
$k\colon A\hookrightarrow X$
$l\colon B\hookrightarrow X$

이에 따라 호몰로지 군 사이의 군 준동형이 유도된다.

$i_*\colon H_n(A\cap B)\to H_n(A)$
$j_*\colon H_n(A\cap B)\to H_n(B)$
$k_*\colon H_n(A)\to H_n(X)$
$l_*\colon H_n(B)\to H_n(X)$

임의의 닫힌

n

차 특이 호몰로지 사슬

x\in C_n(X)

는

A

에 속한 사슬과

B

에 속한 사슬로 분해 가능하다. (단, 분해는 유일하지 않다.)

:

x=u+v

(

u\in C_n(A)

,

v\in C_n(B)

)

:

\partial u=-\partial v\in C_{n-1}(A\cap B)

이때, 군 준동형

\partial_*\colon H_n(X)\to H_{n-1}(A\cap B)

은 다음과 같이 정의된다.

:

\partial_*\colon [x]\mapsto[\partial u]=-[\partial v]\in H_{n-1}(A\cap B)

이러한 과정을 통해, 특이 호몰로지 사슬 복합체에 대한 짧은 완전열이 존재함을 알 수 있다.

:

0\to C_\bullet(A\cap B)\xrightarrow{(i_*,j_*)}C_\bullet(A)\oplus C_\bullet(B)\xrightarrow{k_*-l_*}C_\bullet(X)\to0

이 짧은 완전열에 지그재그 보조정리를 적용하면, 다음과 같은 긴 완전열이 존재하며, 이를 '''마이어-비토리스 열'''이라고 한다.

:

\cdots\to H_{n+1}(X)\xrightarrow{\partial_*}\,H_{n}(A\cap B)\xrightarrow{(i_*,j_*)}H_{n}(A)\oplus H_{n}(B)\xrightarrow{k_* - l_*}H_{n}(X)\xrightarrow{\partial_*}H_{n-1} (A\cap B)\to\cdots\to H_0(A)\oplus H_0(B)\xrightarrow{k_* - l_*}H_0(X)\to0

축소 호몰로지

\tilde H_n(X)=H_n(X)/H_n(\{\bullet\})

에 대해서도 유사한 긴 완전열이 존재한다.

마이어-비토리스 열은 호몰로지 군 계산에 사용되는 중요한 도구이다. 공간을 더 작은 조각으로 분해하여 각 조각의 호몰로지를 계산하고, 마이어-비토리스 열을 통해 결합하여 전체 공간의 호몰로지를 구한다.

3. 1. 경계 사상 (Boundary Map)

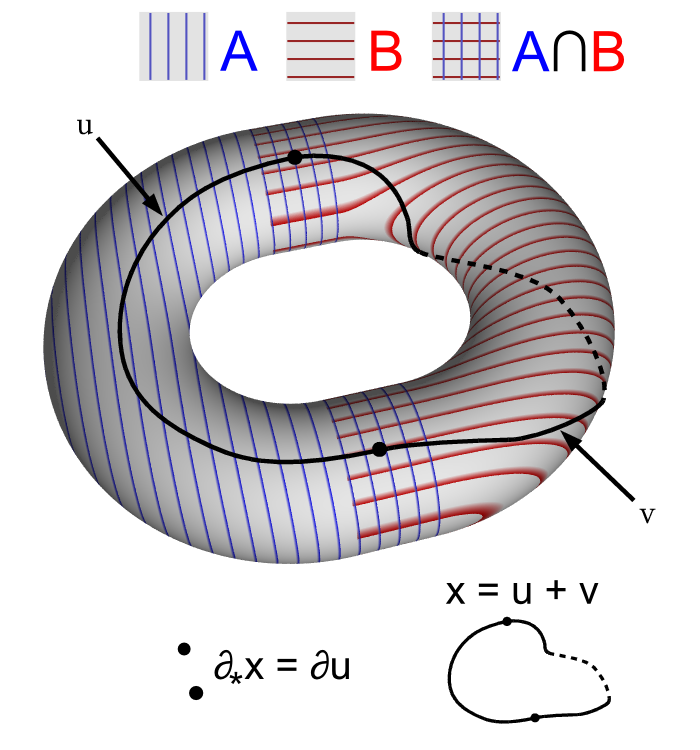
차원을 낮추는 경계 사상 ∂_*는 다음과 같이 정의할 수 있다.^[10] H_n(X)의 원소는 n-사이클 x의 호몰로지류로 나타낼 수 있다. 이 x는 바리 중심 세분을 통해 이미지들이 각각 A와 B에 완전히 속하는 두 개의 n-체인 u와 v의 합으로 쓸 수 있다. 즉, x = u + v로 표현 가능하다.

∂x = ∂(u + v) = ∂u + ∂v이다. x는 사이클이므로 ∂x = 0이고, 따라서 ∂u = -∂v이다. 이는 두 경계 (n - 1)-사이클의 이미지들이 교차점 A∩B에 포함됨을 의미한다.

그러면 ∂_*([x])는 H_n-1(A∩B)에서 ∂u의 호몰로지류로 정의할 수 있다. 다른 분해 x = u′ + v′를 선택해도 [∂u′]에 영향을 미치지 않는다. 왜냐하면 ∂u + ∂v = ∂x = ∂u′ + ∂v′이므로 ∂u - ∂u′ = ∂(v′ - v)가 되어 ∂u와 ∂u′가 같은 호몰로지류에 속하기 때문이다. 또한 다른 대표 x′를 선택해도 영향을 미치지 않는데, 이는 x′ - x = ∂φ가 어떤 φ in H_n+1(X)에 대해 성립하기 때문이다.

마이어-비토리스 수열의 사상은 A와 B의 순서 선택에 의존한다는 점에 유의해야 한다. 특히, A와 B를 교환하면 경계 사상의 부호가 바뀐다.^[39]

4. 성질

마이어-피토리스 열은 다음과 같은 성질을 갖는다.

자이페르트-판 캄펜 정리와의 관계: 마이어-피토리스 열(특히 1차원 호몰로지 군)과 자이페르트-판 캄펜 정리 사이에는 유사성이 있다.^[10]^[12] ''A''∩''B''가 경로 연결 공간일 때, 축소된 마이어-피토리스 열은 다음과 같은 동형 사상을 제공한다.

:

H_1(X) \cong (H_1(A)\oplus H_1(B))/\text{Ker} (k_* - l_*)

정확성에 의해,

:

\text{Ker} (k_* - l_*) \cong \text{Im} (i_*, j_*).

이것은 정확히 자이페르트-판 캄펜 정리의 아벨화된 표현이다. ''X''가 경로 연결 공간일 때 ''H''₁(''X'')가 기본군 π₁(''X'')의 아벨화라는 사실과 비교해 볼 수 있다.^[13]

자연성 (Naturality): 호몰로지 군은 연속 함수 $f:X_1 \to X_2$ 에 대해 자연성을 가진다. 즉, 호몰로지 군의 표준적인 푸시포워드 사상 $f_*: H_k(X_1) \to H_k(X_2)$ 가 존재하며, 푸시포워드의 합성은 합성의 푸시포워드와 같다. 즉, $(g\circ h)_* = g_*\circ h_*$ 이다. 마이어-비토리스 수열 또한 자연성을 가지는데, 만약

:

\begin{matrix} X_1 = A_1 \cup B_1 \\ X_2 = A_2 \cup B_2 \end{matrix} \qquad \text{and} \qquad \begin{matrix} f(A_1) \subset A_2 \\f(B_1) \subset B_2\end{matrix}

이고, 마이어-비토리스 수열의 연결 준동형사상

\partial_*,

가

f_*

와 가환하면,^[20] 즉, 다음의 가환도표가 성립한다.^[21] (수평 사상은 일반적인 사상이다):

:

\begin{matrix}\cdots & H_{n+1}(X_1) & \longrightarrow & H_n(A_1\cap B_1) & \longrightarrow & H_n(A_1)\oplus H_n(B_1) & \longrightarrow & H_n(X_1) & \longrightarrow &H_{n-1}(A_1\cap B_1) & \longrightarrow & \cdots\\& f_* \Bigg\downarrow & & f_* \Bigg\downarrow & & f_* \Bigg\downarrow & & f_* \Bigg\downarrow & & f_* \Bigg\downarrow\\\cdots & H_{n+1}(X_2) & \longrightarrow & H_n(A_2\cap B_2) & \longrightarrow & H_n(A_2)\oplus H_n(B_2) & \longrightarrow & H_n(X_2) & \longrightarrow &H_{n-1}(A_2\cap B_2) & \longrightarrow & \cdots\\\end{matrix}

상대 호몰로지 (Relative Homology): 상대 호몰로지에 대한 마이어-비토리스 열도 존재한다.^[19] ''Y'' ⊂ ''X''이고, ''C'' ⊂ ''A''와 ''D'' ⊂ ''B''의 내부의 합집합일 때, 다음과 같은 정확한 수열이 존재한다.^[48]

:

\cdots\to H_{n}(A\cap B,C\cap D)\,\xrightarrow{(i_*,j_*)}\,H_{n}(A,C)\oplus H_{n}(B,D)\,\xrightarrow{k_* - l_*}\,H_{n}(X,Y)\, \xrightarrow{\partial_*} \,H_{n-1}(A\cap B,C\cap D)\to\cdots

코호몰로지 버전 (Cohomological Versions): 특이 코호몰로지 군에 대한 마이어-비토리스 완전열은 호몰로지 버전과 쌍대 관계이다.^[22] 계수 군 ''G''를 갖는 경우, 다음과 같다.

:

\cdots\to H^{n}(X;G)\to H^{n}(A;G)\oplus H^{n}(B;G)\to H^{n}(A\cap B;G)\to H^{n+1}(X;G)\to\cdots

여기서 차원을 보존하는 사상은 포함에 의해 유도된 제한 사상이고, (코-)경계 사상은 호몰로지 버전과 유사하게 정의된다. 상대적인 공식도 존재한다.

''G''가 실수 '''R'''의 군이고 기본 위상 공간이 매끄러운 다양체의 추가적인 구조를 갖는 중요한 특별한 경우, 드람 코호몰로지에 대한 마이어-비토리스 완전열은 다음과 같다.

:

\cdots\to H^{n}(X)\,\xrightarrow{\rho}\,H^{n}(U)\oplus H^{n}(V)\,\xrightarrow{\Delta}\,H^{n}(U\cap V)\, \xrightarrow{d^*}\, H^{n+1}(X) \to \cdots

여기서 는 의 열린 덮개를 나타내고, 는 제한 사상을, 는 차이를 나타낸다. 사상

d^*

는 위에서

\partial_*

와 유사하게 정의된다. 에서 닫힌 형식 로 표현되는 코호몰로지 클래스 에 대해, 에 종속적인 1의 분할을 통해 를 형식의 차이

\omega_U - \omega_V

로 표현한다. 외미분 및 는 에서 일치하므로, 함께 에 대한 형식 를 정의한다. 그러면 가 성립한다.

콤팩트 지지 드람 코호몰로지의 경우, 위 수열의 "뒤집힌" 버전이 존재한다.

:

\cdots\to H_{c}^{n}(U\cap V)\,\xrightarrow{\delta}\,H_{c}^{n}(U)\oplus H_{c}^{n}(V)\,\xrightarrow{\Sigma}\,H_{c}^{n}(X)\, \xrightarrow{d^*}\, H_{c}^{n+1}(U\cap V) \to \cdots

여기서

U

,

V

,

X

는 위와 같고,

\delta

는 부호가 있는 포함 사상

\delta : \omega \mapsto (i^U_*\omega,-i^V_*\omega)

이며,

i^U

는 콤팩트 지지를 가진 형식을 0으로

U

에 대한 형식으로 확장하고

\Sigma

는 합이다.^[23]

사슬 복합체의 구성 그룹인 사슬 군의 긴 완전열을 고려할 수 있다.

:

0 \to C_n(A\cap B)\,\xrightarrow{\alpha}\,C_n(A) \oplus C_n(B)\,\xrightarrow{\beta}\,C_n(A+B) \to 0

여기서 α(''x'') = (''x'', −''x''), β(''x'', ''y'') = ''x'' + ''y''이고, ''C''_''n''(''A'' + ''B'')는 ''A''의 사슬과 ''B''의 사슬의 합으로 구성된 사슬 군이다.^[9] ''X''의 특이 ''n''-단순체 중 그 이미지들이 ''A'' 또는 ''B''에 포함된 것들은 모든 호몰로지 군 ''H''_''n''(''X'')을 생성한다.^[24] 즉, ''H''_''n''(''A'' + ''B'')는 ''H''_''n''(''X'')와 동형이다.

미분 형식의 벡터 공간의 짧은 완전 시퀀스에 동일한 계산을 적용하면 다음과 같다.

:

0\to\Omega^{n}(X)\to\Omega^{n}(U)\oplus\Omega^{n}(V)\to\Omega^{n}(U\cap V)\to 0

이는 드람 코호몰로지를 위한 마이어-비토리스 시퀀스를 생성한다.^[25]

마이어-비토리스 시퀀스는 호몰로지 이론을 위한 Eilenberg–Steenrod 공리로부터 호몰로지에서 긴 완전 시퀀스를 사용하여 유도될 수 있다.^[26]

4. 1. 자이페르트-판 캄펜 정리와의 관계

마이어-피토리스 열(특히 1차원 호몰로지 군)과 자이페르트-판 캄펜 정리 사이에는 유사성이 있다.^[10]^[12] ''A''∩''B''가 경로 연결 공간일 때, 축소된 마이어-피토리스 열은 다음과 같은 동형 사상을 제공한다.

:

H_1(X) \cong (H_1(A)\oplus H_1(B))/\text{Ker} (k_* - l_*)

정확성에 의해,

:

\text{Ker} (k_* - l_*) \cong \text{Im} (i_*, j_*).

이것은 정확히 자이페르트-판 캄펜 정리의 아벨화된 표현이다. ''X''가 경로 연결 공간일 때 ''H''₁(''X'')가 기본군 π₁(''X'')의 아벨화라는 사실과 비교해 볼 수 있다.^[13]

4. 2. 자연성 (Naturality)

호몰로지 군은 연속 함수

f:X_1 \to X_2

에 대해 자연성을 가진다. 즉, 호몰로지 군의 표준적인 푸시포워드 사상

f_*: H_k(X_1) \to H_k(X_2)

가 존재하며, 푸시포워드의 합성은 합성의 푸시포워드와 같다. 즉,

(g\circ h)_* = g_*\circ h_*

이다. 마이어-비토리스 수열 또한 자연성을 가지는데, 만약

:

\begin{matrix} X_1 = A_1 \cup B_1 \\ X_2 = A_2 \cup B_2 \end{matrix} \qquad \text{and} \qquad \begin{matrix} f(A_1) \subset A_2 \\f(B_1) \subset B_2\end{matrix}

이고, 마이어-비토리스 수열의 연결 준동형사상

\partial_*,

가

f_*

와 가환하면,^[20] 즉, 다음의 가환도표가 성립한다.^[21] (수평 사상은 일반적인 사상이다):

:

\begin{matrix}\cdots & H_{n+1}(X_1) & \longrightarrow & H_n(A_1\cap B_1) & \longrightarrow & H_n(A_1)\oplus H_n(B_1) & \longrightarrow & H_n(X_1) & \longrightarrow &H_{n-1}(A_1\cap B_1) & \longrightarrow & \cdots\\& f_* \Bigg\downarrow & & f_* \Bigg\downarrow & & f_* \Bigg\downarrow & & f_* \Bigg\downarrow & & f_* \Bigg\downarrow\\\cdots & H_{n+1}(X_2) & \longrightarrow & H_n(A_2\cap B_2) & \longrightarrow & H_n(A_2)\oplus H_n(B_2) & \longrightarrow & H_n(X_2) & \longrightarrow &H_{n-1}(A_2\cap B_2) & \longrightarrow & \cdots\\\end{matrix}

4. 3. 상대 호몰로지 (Relative Homology)

상대 호몰로지(relative homology)에 대한 마이어-비토리스 열도 존재한다.^[19] ''Y'' ⊂ ''X''이고, ''C'' ⊂ ''A''와 ''D'' ⊂ ''B''의 내부의 합집합일 때, 다음과 같은 정확한 수열이 존재한다.^[48]

:

\cdots\to H_{n}(A\cap B,C\cap D)\,\xrightarrow{(i_*,j_*)}\,H_{n}(A,C)\oplus H_{n}(B,D)\,\xrightarrow{k_* - l_*}\,H_{n}(X,Y)\, \xrightarrow{\partial_*} \,H_{n-1}(A\cap B,C\cap D)\to\cdots

4. 4. 코호몰로지 버전 (Cohomological Versions)

특이 코호몰로지 군에 대한 마이어-비토리스 완전열은 호몰로지 버전과 쌍대 관계이다.^[22] 계수 군 ''G''를 갖는 경우, 다음과 같다:

:

\cdots\to H^{n}(X;G)\to H^{n}(A;G)\oplus H^{n}(B;G)\to H^{n}(A\cap B;G)\to H^{n+1}(X;G)\to\cdots

여기서 차원을 보존하는 사상은 포함에 의해 유도된 제한 사상이고, (코-)경계 사상은 호몰로지 버전과 유사하게 정의된다. 상대적인 공식도 존재한다.

''G''가 실수 '''R'''의 군이고 기본 위상 공간이 매끄러운 다양체의 추가적인 구조를 갖는 중요한 특별한 경우, 드람 코호몰로지에 대한 마이어-비토리스 완전열은 다음과 같다.

:

\cdots\to H^{n}(X)\,\xrightarrow{\rho}\,H^{n}(U)\oplus H^{n}(V)\,\xrightarrow{\Delta}\,H^{n}(U\cap V)\, \xrightarrow{d^*}\, H^{n+1}(X) \to \cdots

여기서 는 의 열린 덮개를 나타내고, 는 제한 사상을, 는 차이를 나타낸다. 사상

d^*

는 위에서

\partial_*

와 유사하게 정의된다. 에서 닫힌 형식 로 표현되는 코호몰로지 클래스 에 대해, 에 종속적인 1의 분할을 통해 를 형식의 차이

\omega_U - \omega_V

로 표현한다. 외미분 및 는 에서 일치하므로, 함께 에 대한 형식 를 정의한다. 그러면 가 성립한다.

콤팩트 지지 드람 코호몰로지의 경우, 위 수열의 "뒤집힌" 버전이 존재한다.

:

\cdots\to H_{c}^{n}(U\cap V)\,\xrightarrow{\delta}\,H_{c}^{n}(U)\oplus H_{c}^{n}(V)\,\xrightarrow{\Sigma}\,H_{c}^{n}(X)\, \xrightarrow{d^*}\, H_{c}^{n+1}(U\cap V) \to \cdots

여기서

U

,

V

,

X

는 위와 같고,

\delta

는 부호가 있는 포함 사상

\delta : \omega \mapsto (i^U_*\omega,-i^V_*\omega)

이며,

i^U

는 콤팩트 지지를 가진 형식을 0으로

U

에 대한 형식으로 확장하고

\Sigma

는 합이다.^[23]

사슬 복합체의 구성 그룹인 사슬 군의 긴 완전열을 고려할 수 있다.

:

0 \to C_n(A\cap B)\,\xrightarrow{\alpha}\,C_n(A) \oplus C_n(B)\,\xrightarrow{\beta}\,C_n(A+B) \to 0

여기서 α(''x'') = (''x'', −''x''), β(''x'', ''y'') = ''x'' + ''y''이고, ''C''_''n''(''A'' + ''B'')는 ''A''의 사슬과 ''B''의 사슬의 합으로 구성된 사슬 군이다.^[9] ''X''의 특이 ''n''-단순체 중 그 이미지들이 ''A'' 또는 ''B''에 포함된 것들은 모든 호몰로지 군 ''H''_''n''(''X'')을 생성한다.^[24] 즉, ''H''_''n''(''A'' + ''B'')는 ''H''_''n''(''X'')와 동형이다.

미분 형식의 벡터 공간의 짧은 완전 시퀀스에 동일한 계산을 적용하면 다음과 같다.

:

0\to\Omega^{n}(X)\to\Omega^{n}(U)\oplus\Omega^{n}(V)\to\Omega^{n}(U\cap V)\to 0

이는 드람 코호몰로지를 위한 마이어-비토리스 시퀀스를 생성한다.^[25]

마이어-비토리스 시퀀스는 호몰로지 이론을 위한 Eilenberg–Steenrod 공리로부터 호몰로지에서 긴 완전 시퀀스를 사용하여 유도될 수 있다.^[26]

5. 응용

(코)호몰로지 군은 위상 공간의 중요한 위상 불변량으로, 선형대수학 도구를 사용해 계산 가능한 경우도 있지만, 특이 (코)호몰로지론과 같이 정의만으로는 계산이 어려운 경우가 많다. 특이 (코)호몰로지의 경우, (코)체인 군이나 (코)사이클 군이 너무 커서 다루기 어렵기 때문에 간접적인 방법이 필요하다. 마이어-비토리스 완전열은 이러한 간접적인 방법 중 하나로, 공간의 (코)호몰로지 군에 대한 부분적인 정보를 그 공간의 두 부분 공간 및 그 교차점의 (코)호몰로지 군과 연결하여 제공한다.

이러한 관계는 완전열이라는 대수적 개념을 통해 나타낼 수 있다. 완전열은 대상(여기서는 군)과 사상(여기서는 군 준동형)으로 구성된 열로, 각 사상의 상이 다음 사상의 핵과 일치하는 것이다. 마이어-비토리스 완전열이 항상 공간의 (코)호몰로지 군을 완전히 계산해주는 것은 아니지만, 위상다양체, 단순 복체, CW 복체와 같이 위상 기하학에서 중요한 공간들은 간단한 소편들의 붙임으로 구성되는 경우가 많아, 마이어-비토리스 정리는 광범위하고 깊은 응용 가능성을 가진다.

마이어는 1926년과 1927년 빈 대학교 강연에서 비토리스로부터 위상 기하학을 소개받고 베티 수 문제와 해법을 들었으며, 1929년에 이 문제를 해결했다.^[30]^[31] 그는 두 개의 원통 합집합으로 표현되는 토러스에 이 결과를 적용했다.^[32]^[33] 1930년, 비토리스는 토러스의 호몰로지 군에 대한 완전한 결과를 제시했지만, 완전열 형태로 표현하지는 않았다.^[34] 완전열 개념은 1952년 새뮤얼 아일렌버그와 노먼 스틴로드의 저서 ''Foundations of Algebraic Topology''에서 처음 등장했으며, 여기에 마이어-비토리스 결과가 현대적인 형태로 기록되었다.^[35]^[36]

위상 공간 ''X''와 그 부분 공간 ''A'', ''B''의 내부가 ''X''를 덮을 때 (''A'', ''B''의 내부는 서로소일 필요는 없음), 세 묶음 (''X'', ''A'', ''B'')에 대한 특이 호몰로지의 마이어-비토리스 완전열은 공간 ''X'', ''A'', ''B'' 및 교차점 ''A''∩''B''에 관한 (정수 계수) 특이 호몰로지 군으로 구성된 긴 완전열이다. 축약 버전과 비축약 버전이 존재한다.

비축약 호몰로지에 대한 마이어-비토리스 완전열은 다음과 같다.^[38]

: $\begin{align}\cdots\to H_{n+1}(X)&\,\xrightarrow{\partial_*}\,H_{n}(A\cap B)\,\xrightarrow{(i_*,j_*)}\,H_{n}(A)\oplus H_{n}(B)\,\xrightarrow{k_* - l_*}\,H_{n}(X)\,\xrightarrow{\partial_*}\\&\quad\xrightarrow{\partial_*}\,H_{n-1}(A\cap B)\to\cdots\to H_0(A)\oplus H_0(B)\,\xrightarrow{k_* - l_*}\,H_0(X)\to 0\end{align}$

여기서 사상 ''i'': ''A''∩''B'' ↪ ''A'', ''j'': ''A''∩''B'' ↪ ''B'', ''k'': ''A'' ↪ ''X'', ''l'': ''B'' ↪ ''X''는 모두 포함 사상이며, ⊕는 아벨 군의 직합을 나타낸다.

축약 호몰로지에 대해서도 ''A''와 ''B''의 교집합이 공집합이 아니라는 가정 하에 마이어-비토리스 완전열이 존재한다.^[40] 이는 양의 차원의 호몰로지가 이루는 끝점을 갖는 다음과 같은 열과 동일하다.

: $\cdots\to\tilde{H}_0(A\cap B)\,\xrightarrow{(i_*,j_*)}\,\tilde{H}_0(A)\oplus\tilde{H}_0(B)\,\xrightarrow{k_* - l_*}\,\tilde{H}_0(X)\to\,0$

5. 1. k-구 (k-sphere)

''k''-구 ''X'' = ''S''^''k''의 호몰로지를 완전히 계산하기 위해, ''A''와 ''B''를 교차점이 (''k'' - 1)차원 적도 구와 호모토피 동치인 ''X''의 두 반구라고 하자. ''k''차원 반구는 위상 동형인 ''k''-원판과 같으며, 이는 축약 가능하므로 ''A''와 ''B''의 호몰로지 군은 자명군이다. 그런 다음 환원 호몰로지 군에 대한 마이어-비토리스 열은 다음을 산출한다.^[14]

:

\cdots \longrightarrow 0 \longrightarrow\tilde{H}_{n}\!\left(S^k\right)\, \xrightarrow{\overset{}{\partial_*}}\,\tilde{H}_{n-1}\!\left(S^{k-1}\right)\longrightarrow 0 \longrightarrow \cdots

정확성은 맵 ∂_*가 동형 사상임을 즉시 암시한다. 기저 사례로 0-구 (두 점)의 환원 호몰로지를 사용하면 다음이 따른다.^[14]

:

\tilde{H}_n\!\left(S^k\right)\cong\delta_{kn}\,\mathbb{Z}=\begin{cases}\mathbb{Z} & \mbox{if } n=k,   \\0 & \mbox{if } n \ne k,\end{cases}

여기서 δ는 크로네커 델타이다. 구에 대한 호몰로지 군에 대한 이러한 완전한 이해는, 특히 ''n'' > ''k''인 경우에 거의 알려진 바가 없는 구의 호모토피 군에 대한 현재 지식과 매우 대조적이다.^[15]

5. 2. 클라인 병 (Klein bottle)

마이어-피토리스 열을 이용하여 클라인 병 ''X''의 호몰로지 군을 계산할 수 있다. ''X''를 경계 원을 따라 접착된 두 개의 뫼비우스의 띠 ''A''와 ''B''의 합집합으로 사용한다(오른쪽 그림 참조). 그러면 ''A'', ''B'' 및 그들의 교차점 ''A''∩''B''는 원과 호모토피 동치이므로 수열의 비자명한 부분은 다음과 같다.^[16]

:

0 \rightarrow \tilde{H}_{2}(X) \rightarrow\mathbb{Z}\ \xrightarrow{\overset{}{\alpha}} \ \mathbb{Z} \oplus \mathbb{Z}\rightarrow \, \tilde{H}_1(X) \rightarrow 0

그리고 자명한 부분은 2보다 큰 차원에 대해 호몰로지가 사라짐을 의미한다. 중심 사상 α는 1을 (2, -2)로 보낸다. 뫼비우스 띠의 경계 원은 중심 원을 두 번 감싸기 때문이다. 특히 α는 단사이므로 2차원의 호몰로지도 사라진다. 마지막으로, '''Z'''²에 대한 기저로 (1, 0)과 (1, -1)을 선택하면 다음이 따릅니다.

:

\tilde{H}_n\left(X\right)\cong\delta_{1n}\,(\mathbb{Z}\oplus\mathbb{Z}_2)=\begin{cases}\mathbb{Z}\oplus\mathbb{Z}_2 & \mbox{if } n=1,\\0 & \mbox{if } n\ne1.    \end{cases}

5. 3. 쐐기합 (Wedge sums)

두 2-구 ''K''와 ''L''의 쐐기합 ''X''의 이 분해는 ''X''의 모든 호몰로지 군을 생성한다.

''X''가 두 공간 ''K''와 ''L''의 쐐기합이고, 식별된 밑점이 ''K''와 ''L''의 열린 근방 ''U'' ⊆ ''K'' 및 ''V'' ⊆ ''L''의 변형 retract라고 가정하자. ''A'' = ''K'' ∪ ''V'' 및 ''B'' = ''U'' ∪ ''L''로 두면 ''A'' ∪ ''B'' = ''X'' 및 ''A'' ∩ ''B'' = ''U'' ∪ ''V''가 되며, 이는 구성상 수축 가능하다. 그러면 시퀀스의 축소된 버전은 (정확성에 의해)^[17] 모든 차원 ''n''에 대해 다음과 같다.

:

\tilde{H}_n(K\vee L)\cong \tilde{H}_n(K)\oplus\tilde{H}_n(L)

오른쪽 그림은 ''X''를 두 2-구 ''K''와 ''L''의 합으로 나타낸다. 이 특정한 경우, 2-구에 대한 위에서 얻은 결과를 사용하여 다음을 얻는다.

:

\tilde{H}_n\left(S^2\vee S^2\right)\cong\delta_{2n}\,(\mathbb{Z}\oplus\mathbb{Z})=\left\{\begin{matrix}\mathbb{Z}\oplus\mathbb{Z} & \mbox{if } n=2,   \\0 & \mbox{if } n \ne 2.   \end{matrix}\right.

5. 4. 현수 (Suspensions)

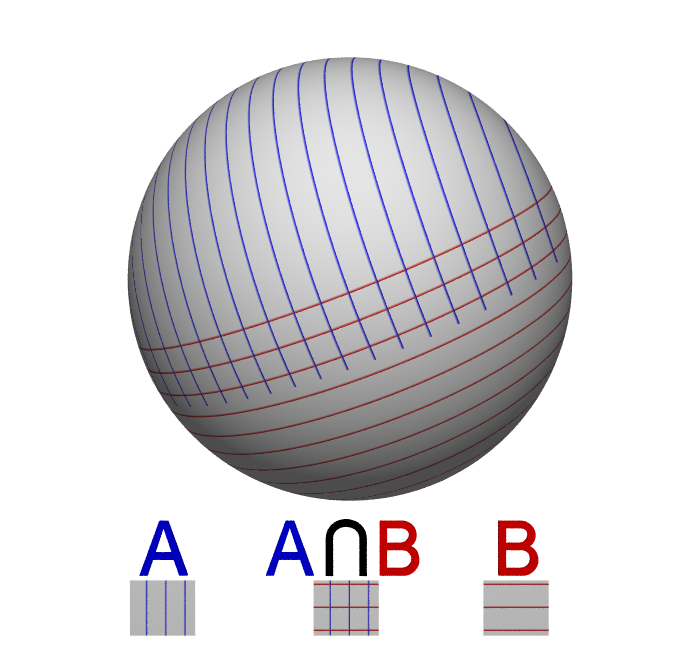
위상 공간 ''X''가 다른 공간 ''Y''의 현수 ''SY''일 때, ''A''와 ''B''를 이중 원뿔의 상단과 하단 꼭짓점의 ''X''에서의 여집합이라고 하면, ''X''는 ''A''∪''B''의 합집합이며, ''A''와 ''B''는 수축 가능하다. 또한, 교집합 ''A''∩''B''는 ''Y''와 호모토피 동치이다. 따라서 마이어-비토리스 수열은 모든 ''n''에 대해 다음을 제공한다.^[18]

:

\tilde{H}_n(SY)\cong \tilde{H}_{n-1}(Y)

오른쪽 그림은 0차원 구 ''Y''의 현수로서 1차원 구 ''X''를 보여준다. 일반적으로 ''k''차원 구가 (''k'' − 1)차원 구의 현수임을 고려하면, 위에서 언급했듯이 귀납법을 통해 ''k''차원 구의 호몰로지 군을 쉽게 유도할 수 있다.

6. 다른 호몰로지 이론과의 관계

마이어-피토리스 열은 에일렌베르크-스틴로드 공리에서 유도되며, 차원 공리를 필요로 하지 않으므로,^[27] 특이 호몰로지뿐만 아니라 일반 호몰로지 이론(예: 위상적 K-이론, 코보디즘)에서도 성립한다.

층 코호몰로지 관점에서, 마이어-비토리스 열은 체흐 코호몰로지와 관련이 있다. 구체적으로, 체흐 코호몰로지를 계산하는 데 사용된 열린 덮개가 두 개의 열린 집합으로 구성된 경우, 체흐 코호몰로지와 층 코호몰로지를 연관시키는 스펙트럼 열(때로는 마이어-비토리스 스펙트럼 열이라고 함)의 퇴화로부터 발생한다.^[28] 이 스펙트럼 열은 임의의 토포스에서 존재한다.^[29]

참조

_[1] 서적
_[2] 서적
_[3] 서적
_[4] 서적
_[5] 서적
_[6] 서적
_[7] 서적
_[8] 서적
_[9] 서적
_[10] 서적
_[11] 서적
_[12] 서적
_[13] 서적
_[14] 서적
_[15] 서적
_[16] 서적
_[17] 서적
_[18] 서적
_[19] 서적
_[20] 서적
_[21] 서적
_[22] 서적
_[23] 서적 Differential forms in algebraic topology https://www.worldcat[...] 1995-05-16
_[24] 서적
_[25] 서적
_[26] 서적
_[27] 서적
_[28] 서적
_[29] 서적
_[30] 서적
_[31] 서적
_[32] 서적
_[33] 서적
_[34] 서적
_[35] 서적
_[36] 서적
_[37] 서적
_[38] 서적
_[39] 서적
_[40] 서적
_[41] 서적
_[42] 서적
_[43] 서적
_[44] 서적
_[45] 서적
_[46] 서적
_[47] 서적
_[48] 서적
_[49] 서적
_[50] 서적
_[51] 서적
_[52] 서적
_[53] 서적
_[54] 서적
_[55] 서적
_[56] 서적
_[57] 서적
_[58] 논문 Über abstrakte Topologie 1929
_[59] 논문 Über die Homologiegruppen der Vereinigung zweier Komplexe 1930

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com