수직 벡터 다발

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 성질
- 3.1. 아티야 완전열
- 3.2. 에레스만 접속과의 관계
4. 예시
5. 추가 성질 (틀 다발)
참조

1. 개요

수직 벡터 다발은 매끄러운 다양체 M 위의 매끄러운 올다발 E가 주어졌을 때, 사영 사상의 미분 Tπ의 커널로 정의되는 E 위의 벡터 다발이다. 수직 벡터 다발은 수직 벡터장, 수평 미분 형식, 에레스만 접속 등과 밀접한 관련이 있으며, 아티야 완전열과 같은 중요한 성질을 갖는다. 뫼비우스 띠, 자명한 올다발, 주다발, 벡터 다발 등 다양한 예시에서 수직 벡터 다발을 찾아볼 수 있으며, 틀 다발의 경우 접속 형식, 솔더 형식, 비틀림 형식 등과의 관계를 통해 레비-치비타 접속을 정의하는 데 사용될 수 있다.

더 읽어볼만한 페이지

접속 (수학) - 비틀림 텐서
비틀림 텐서는 매끄러운 다양체와 코쥘 접속에 대해 정의되며, 접속의 비대칭성을 나타내는 (1,2)차 텐서장이다.
접속 (수학) - 스핀 접속
스핀 접속은 매끄러운 다양체에서 필바인과 코쥘 접속을 사용하여 정의되며, 스피너 다발의 접속 성분을 구성하고 일반화된 텐서에 대한 공변 미분을 정의하며, 비틀림이 없는 경우 카르탕의 구조 방정식을 통해 비틀림과 곡률을 설명하는 데 사용된다.
올다발 - 주다발
주다발은 위상 공간을 밑공간으로, 위상군을 올로 가지며, 연속적인 군 작용을 통해 정의되는 올다발로, 위상수학, 미분기하학, 게이지 이론 등에서 활용된다.
올다발 - 단면 (올다발)
단면은 올다발의 정의를 만족하는 함수로, 함수의 그래프를 일반화한 개념이며, 매끄러운 올다발에서는 매끄러운 단면을 정의할 수 있고, 전역 단면의 존재 여부는 호모토피 이론에서 중요한 연구 대상이다.
미분위상수학 - 벡터장
벡터장은 유클리드 공간이나 미분다양체의 각 점에 벡터를 대응시키는 사상으로, 유클리드 공간에서는 벡터값 함수로 표현되고 미분다양체에서는 접다발의 단면이나 도함수로 정의되며, 물리학, 기상, 유체역학, 전자기학, 컴퓨터 그래픽스 등 다양한 분야에서 응용된다.
미분위상수학 - 법다발
법다발은 다양체 $M$에 매장된 다양체 $N$의 접다발을 $M$의 접다발로 확장한 몫다발로, 리만 다양체에서는 법선 공간들의 모임으로 정의되며 여법선 다발과 관련이 깊다.

수직 벡터 다발
수직 벡터 다발
정의	매끄러운 사상 π: E → M에 대한 벡터 다발의 부분다발
기호	V(E)
다른 이름	접벡터 다발의 수직 부분다발
설명	E의 각 올버의 접공간을 취하여 얻어짐
관련 개념	수평 벡터 다발 벡터 다발
참고 문헌

2. 정의

매끄러운 다양체 $M$ 위의 매끄러운 올다발

: $\pi\colon E\twoheadrightarrow M$

이 주어졌다고 하고, $E$ 및 $E$ 의 각 올이 매끄러운 다양체를 이룬다고 하자. 사영 사상의 미분

: $\mathrm T\pi\colon\mathrm TE\twoheadrightarrow\mathrm TM$

을 정의할 수 있다. 그렇다면, $E$ 위에 다음과 같은 '''수직 벡터 다발''' $\mathrm VE$ 를 정의할 수 있다.

: $\mathrm VE=\ker(\mathrm T\pi)$

즉,

: $\mathrm V_eE=\mathrm T_e(E_{\pi(e)})\qquad\forall e\in E$

: $\forall u\in T_\mathrm eE\colon \left(u\in\mathrm V_eE\iff\forall(\gamma\colon\mathbb R\to E,\;\gamma(0)=e)\colon\frac{\mathrm d\gamma}{\mathrm dt}(0)=u\implies \frac{\mathrm d(\pi\circ\gamma)}{\mathrm dt}(0)=0\right)$

즉, 벡터 다발 $V$ 의 $e\in E$ 에서의 올은 $E$ 의 올의 접공간이다.^[2]

dπ_e가 각 점 ''e''에서 전사적이므로, T''E''의 ''정칙'' 부분다발을 생성한다. 또한, 수직 다발 V''E''는 적분 가능하다.

$E$ 위의 벡터장 $X$ 에 대하여, 만약 $X\in\Gamma(\mathrm TE)$ 라면 (즉, 만약 모든 $x\in M$ 에 대하여 $X_x\in\mathrm V_eE$ 라면) $X$ 를 '''수직 벡터장'''(垂直vector場, vertical vector field^영어)이라고 한다. 마찬가지로, $E$ 위의 $p$ 차 미분 형식 $\alpha\in\Omega^p(E)$ 에 대하여, 만약

: $\alpha(X_1,X_2,\dots,X_p)=0\qquad\forall X_1,\dots,X_p\in\Gamma(\mathrm VE)$

라면, $\alpha$ 를 '''수평 미분 형식'''(水平微分形式, horizontal differential form^영어)이라고 한다.

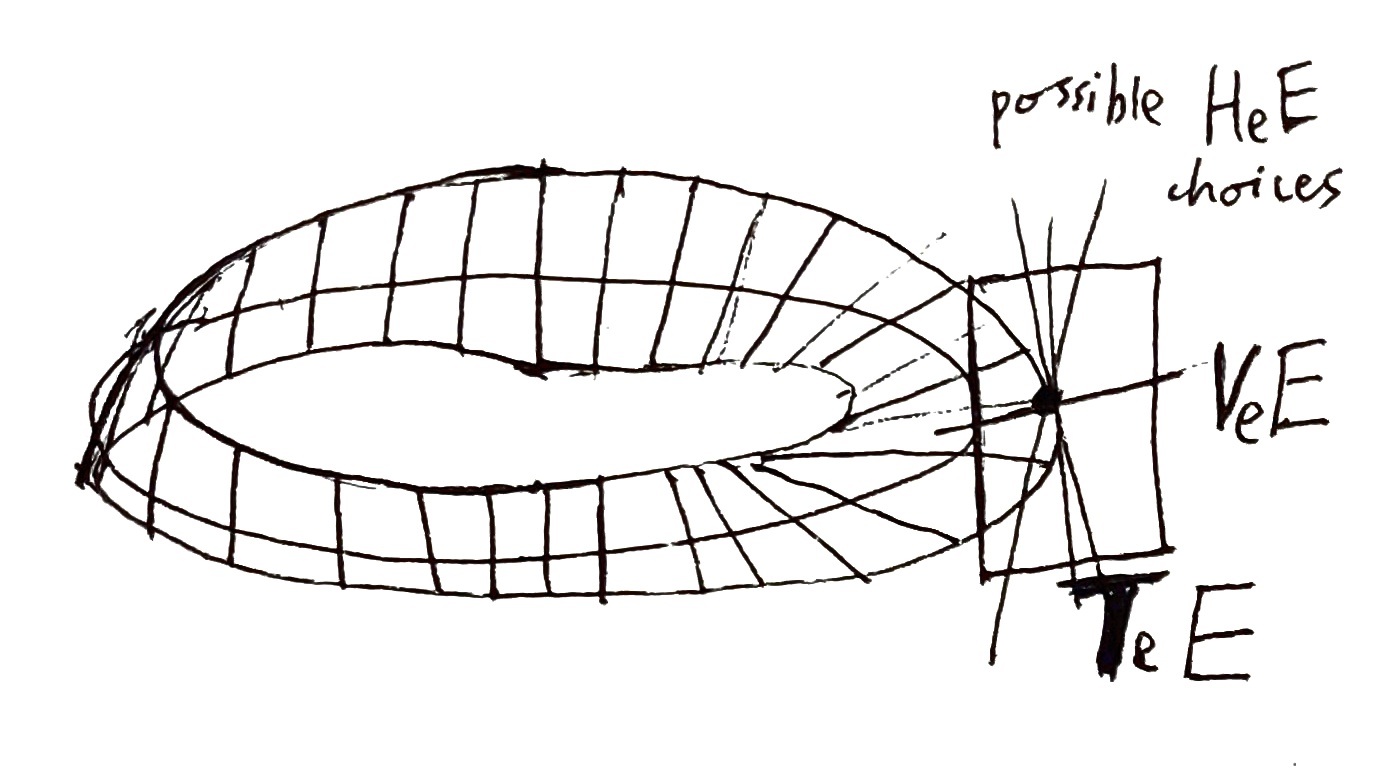
''E'' 위의 에레즈만 접속은 T''E''에서 V''E''에 대한 여부분다발 H''E''를 선택하는 것으로, 이 부분을 접속의 수평 다발이라고 부른다. ''E''의 각 점 ''e''에서, 두 부분 공간은 직합을 형성하여

T_''e''''E'' = V_''e''''E'' ⊕ H_''e''''E''를 만족한다.

2. 1. 수직 벡터 다발

매끄러운 다양체

M

위의 매끄러운 올다발

:

\pi\colon E\twoheadrightarrow M

이 주어졌다고 하고,

E

및

E

의 각 올이 매끄러운 다양체를 이룬다고 하자. 그렇다면, 사영 사상의 미분

:

\mathrm T\pi\colon\mathrm TE\twoheadrightarrow\mathrm TM

을 정의할 수 있다.

E

위에 다음과 같은 '''수직 벡터 다발'''

\mathrm VE

를 정의할 수 있다.^[2]

:

\mathrm VE=\ker(\mathrm T\pi)

즉,

:

\mathrm V_eE=\mathrm T_e(E_{\pi(e)})\qquad\forall e\in E

:

\forall u\in T_\mathrm eE\colon \left(u\in\mathrm V_eE\iff\forall(\gamma\colon\mathbb R\to E,\;\gamma(0)=e)\colon\frac{\mathrm d\gamma}{\mathrm dt}(0)=u\implies \frac{\mathrm d(\pi\circ\gamma)}{\mathrm dt}(0)=0\right)

즉, 벡터 다발

V

의

e\in E

에서의 올은

E

의 올의 접공간이다.

dπ_e가 각 점 ''e''에서 전사적이므로, T''E''의 ''정칙'' 부분다발을 생성한다. 또한, 수직 다발 V''E''는 적분 가능하다.

E

위의 벡터장

X

에 대하여, 만약

X\in\Gamma(\mathrm TE)

라면 (즉, 만약 모든

x\in M

에 대하여

X_x\in\mathrm V_eE

라면)

X

를 '''수직 벡터장'''(垂直vector場, vertical vector field^영어)이라고 한다. 마찬가지로,

E

위의

p

차 미분 형식

\alpha\in\Omega^p(E)

에 대하여, 만약

:

\alpha(X_1,X_2,\dots,X_p)=0\qquad\forall X_1,\dots,X_p\in\Gamma(\mathrm VE)

라면,

\alpha

를 '''수평 미분 형식'''(水平微分形式, horizontal differential form^영어)이라고 한다.

''E'' 위의 에레즈만 접속은 T''E''에서 V''E''에 대한 여부분다발 H''E''를 선택하는 것으로, 이 부분을 접속의 수평 다발이라고 부른다. ''E''의 각 점 ''e''에서, 두 부분 공간은 직합을 형성하여

T_''e''''E'' = V_''e''''E'' ⊕ H_''e''''E''를 만족한다.

2. 2. 수직 벡터장

매끄러운 다양체

M

위의 매끄러운 올다발

\pi\colon E\twoheadrightarrow M

가 주어졌고,

E

및

E

의 각 올이 매끄러운 다양체를 이룬다고 하자. 그렇다면, 사영 사상의 미분

\mathrm T\pi\colon\mathrm TE\twoheadrightarrow\mathrm TM

을 정의할 수 있다.

E

위에 다음과 같은 '''수직 벡터 다발'''

\mathrm VE

를 정의할 수 있다.

:

\mathrm VE=\ker(\mathrm T\pi)

즉,

:

\mathrm V_eE=\mathrm T_e(E_{\pi(e)})\qquad\forall e\in E

:

\forall u\in T_\mathrm eE\colon \left(u\in\mathrm V_eE\iff\forall(\gamma\colon\mathbb R\to E,\;\gamma(0)=e)\colon\frac{\mathrm d\gamma}{\mathrm dt}(0)=u\implies \frac{\mathrm d(\pi\circ\gamma)}{\mathrm dt}(0)=0\right)

즉, 벡터 다발

V

의

e\in E

에서의 올은

E

의 올의 접공간이다.

E

위의 벡터장

X

에 대하여, 만약

X\in\Gamma(\mathrm TE)

라면 (즉, 만약 모든

x\in M

에 대하여

X_x\in\mathrm V_eE

라면)

X

를 '''수직 벡터장'''(vertical vector field^영어)이라고 한다.

2. 3. 수평 미분 형식

3. 성질

수직 벡터 다발의 정의에 따라, 다음과 같은 짧은 완전열이 존재한다.

: $0\to\mathrm VE\hookrightarrow\mathrm TE\;\overset{\pi^*\mathrm T\pi}\twoheadrightarrow\;\pi^*\mathrm TM\to0$

이를 '''아티야 완전열'''(Atiyah完全列, Atiyah exact sequence^영어)이라고 한다. 여기서 $\pi^*\mathrm T\pi\colon(e,u)\mapsto(e,\mathrm T\pi(u))$ 이다. 이는 벡터 다발의 범주이므로 분할 완전열이지만, 이러한 분할은 추가 데이터 없이는 표준적으로 주어지지 않는다. $E$ 위의 에레스만 접속은 이러한 분할을 표준적으로 제시하는 데이터이다.^[2]

수직 및 수평 벡터 다발에서는 미분 기하학의 다양한 중요한 텐서와 미분 형식이 특정 속성을 가지며, 심지어 이러한 다발을 사용하여 정의될 수도 있다. 이러한 속성 중 일부는 다음과 같다.

'''수직 벡터장'''은 수직 벡터 다발에 속하는 벡터장이다. 즉, ''E''의 각 점 ''e''에 대해 $V_eE \subset T_eE = T_e(E_{\pi(e)} )$ 이며 $V_eE$ 는 ''e''에서의 수직 벡터 공간인 벡터 $v_e\in V_eE$ 를 선택한다.
''E''상의 미분 가능한 r-형식 $\alpha$ 는 $\alpha(v_1,...,v_r)=0$ 이며, 벡터 $v_1,..., v_r$ 중 적어도 하나가 수직 벡터일 때, 이를 '''수평 형식'''이라고 한다.
접속 형식은 수평 벡터 다발에서는 0이고 수직 벡터 다발에서만 0이 아니다. 이러한 방식으로, 접속 형식은 수평 벡터 다발을 정의하는 데 사용될 수 있다. 수평 벡터 다발은 접속 형식의 커널이다.
솔더 형식 또는 자명한 1-형식은 수직 벡터 다발에서는 0이고 수평 벡터 다발에서만 0이 아니다. 정의에 따라, 솔더 형식은 그 값을 전적으로 수평 벡터 다발에 둔다.
틀 다발의 경우, 비틀림 형식은 수직 벡터 다발에서 0이며, 임의의 접속을 레비-치비타 접속으로 변환하기 위해, 즉 비틀림이 없도록 만들기 위해, 접속에 추가해야 하는 정확한 부분을 정의하는 데 사용될 수 있다. 실제로 솔더 형식을 θ로 표기하면, 비틀림 텐서 Θ는 Θ = D θ (D는 외미분 공변 미분)로 주어진다. 주어진 접속 ω에 대해, T''E''상에 '''컨토션 텐서'''라고 불리는, 수직 벡터 다발에서 0이 되고 ω+σ가 비틀림이 없는 다른 접속 1-형식이 되도록 하는 ''유일한'' 1-형식 σ가 존재한다. 결과적인 1-형식 ω+σ는 레비-치비타 접속과 다름없다. 이를 정의로 사용할 수 있다. 비틀림은 $\Theta = D\theta = d\theta + \omega \wedge \theta$ 로 주어지므로, 비틀림의 소실은 $d\theta = - (\omega +\sigma) \wedge \theta$ 를 갖는 것과 같으며, σ가 수직 벡터 다발에서 0이 되어야 하고 σ가 각 올에서 ''G''-불변이어야 함을 증명하는 것은 어렵지 않다(보다 정확하게는 σ가 ''G''의 수반 표현으로 변환된다는 것이다). 이는 계량 텐서에 대한 명시적인 언급 없이 레비-치비타 접속을 정의한다(계량 텐서는 솔더 형식의 특수한 경우로 이해될 수 있지만, 이는 밑공간의 접선 다발과 여접선 다발 사이, 즉 틀 다발의 수평 및 수직 부분 공간 사이에 매핑을 설정하기 때문이다).
''E''가 주다발인 경우, 기본 벡터장은 필연적으로 수직 벡터 다발에 존재해야 하며, 모든 수평 벡터 다발에서는 0이어야 한다.

3. 1. 아티야 완전열

수직 벡터 다발의 정의에 따라, 다음과 같은 짧은 완전열이 존재한다.

:

0\to\mathrm VE\hookrightarrow\mathrm TE\;\overset{\pi^*\mathrm T\pi}\twoheadrightarrow\;\pi^*\mathrm TM\to0

이를 '''아티야 완전열'''(Atiyah完全列, Atiyah exact sequence^영어)이라고 한다. 여기서

\pi^*\mathrm T\pi\colon(e,u)\mapsto(e,\mathrm T\pi(u))

이다. 이는 벡터 다발의 범주이므로 분할 완전열이지만, 이러한 분할은 추가 데이터 없이는 표준적으로 주어지지 않는다.

E

위의 에레스만 접속은 이러한 분할을 표준적으로 제시하는 데이터이다.^[2]

3. 2. 에레스만 접속과의 관계

수직 벡터 다발의 정의에 따라, 짧은 완전열

:

0\to\mathrm VE\hookrightarrow\mathrm TE\;\overset{\pi^*\mathrm T\pi}\twoheadrightarrow\;\pi^*\mathrm TM\to0

이 존재한다. 이를 '''아티야 완전열'''(Atiyah完全列, Atiyah exact sequence^영어)이라고 한다. (여기서

\pi^*\mathrm T\pi\colon(e,u)\mapsto(e,\mathrm T\pi(u))

이다.) 이는 (벡터 다발의 범주이므로) 물론 분할 완전열이지만, 이러한 분할은 (추가 데이터 없이) 표준적으로 주어지지 않는다.

E

위의 에레스만 접속은 위 분할을 표준적으로 제시하는 데이터이다.

수직 및 수평 벡터 다발에서는 미분 기하학의 다양한 중요한 텐서와 미분 형식이 특정 속성을 가지며, 심지어 이러한 다발을 사용하여 정의될 수도 있다. 이러한 속성 중 일부는 다음과 같다.^[2]

'''수직 벡터장'''은 수직 벡터 다발에 속하는 벡터장이다. 즉, ''E''의 각 점 ''e''에 대해 $V_eE \subset T_eE = T_e(E_{\pi(e)} )$ 이며 $V_eE$ 는 ''e''에서의 수직 벡터 공간인 벡터 $v_e\in V_eE$ 를 선택한다.^[2]
''E''상의 미분 가능한 r-형식 $\alpha$ 는 $\alpha(v_1,...,v_r)=0$ 이며, 벡터 $v_1,..., v_r$ 중 적어도 하나가 수직 벡터일 때, 이를 '''수평 형식'''이라고 한다.^[2]
접속 형식은 수평 벡터 다발에서는 0이고 수직 벡터 다발에서만 0이 아니다. 이러한 방식으로, 접속 형식은 수평 벡터 다발을 정의하는 데 사용될 수 있다. 수평 벡터 다발은 접속 형식의 커널이다.^[2]
솔더 형식 또는 자명한 1-형식은 수직 벡터 다발에서는 0이고 수평 벡터 다발에서만 0이 아니다. 정의에 따라, 솔더 형식은 그 값을 전적으로 수평 벡터 다발에 둔다.^[2]
틀 다발의 경우, 비틀림 형식은 수직 벡터 다발에서 0이며, 임의의 접속을 레비-치비타 접속으로 변환하기 위해, 즉 비틀림이 없도록 만들기 위해, 접속에 추가해야 하는 정확한 부분을 정의하는 데 사용될 수 있다.^[2] 실제로 솔더 형식을 θ로 표기하면, 비틀림 텐서 Θ는 Θ = D θ (D는 외미분 공변 미분)로 주어진다. 주어진 접속 ω에 대해, T''E''상에 '''컨토션 텐서'''라고 불리는, 수직 벡터 다발에서 0이 되고 ω+σ가 비틀림이 없는 다른 접속 1-형식이 되도록 하는 ''유일한'' 1-형식 σ가 존재한다. 결과적인 1-형식 ω+σ는 레비-치비타 접속과 다름없다. 이를 정의로 사용할 수 있다. 비틀림은 $\Theta = D\theta = d\theta + \omega \wedge \theta$ 로 주어지므로, 비틀림의 소실은 $d\theta = - (\omega +\sigma) \wedge \theta$ 를 갖는 것과 같으며, σ가 수직 벡터 다발에서 0이 되어야 하고 σ가 각 올에서 ''G''-불변이어야 함을 증명하는 것은 어렵지 않다(보다 정확하게는 σ가 ''G''의 수반 표현으로 변환된다는 것이다). 이는 계량 텐서에 대한 명시적인 언급 없이 레비-치비타 접속을 정의한다(계량 텐서는 솔더 형식의 특수한 경우로 이해될 수 있지만, 이는 밑공간의 접선 다발과 여접선 다발 사이, 즉 틀 다발의 수평 및 수직 부분 공간 사이에 매핑을 설정하기 때문이다).^[2]
''E''가 주다발인 경우, 기본 벡터장은 필연적으로 수직 벡터 다발에 존재해야 하며, 모든 수평 벡터 다발에서는 0이어야 한다.^[2]

4. 예시

뫼비우스 띠는 원 위의 선 다발이며, 원은 띠의 중간 고리로 묘사될 수 있다. 띠의 각 점

e

에서, 사영 사상은 중간 고리로 투영되며, 올은 중간 고리에 수직이다. 이 점에서의 수직 다발

V_eE

는 올에 대한 접 공간이다.

매끄러운 올 다발의 간단한 예는 두 다양체의 데카르트 곱이다. 다발 사영 pr₁ : ''M'' × ''N'' → ''M'' : (''x'', ''y'') → ''x''를 갖는 다발 ''B''₁ := (''M'' × ''N'', pr₁)을 고려할 때, ''M'' × ''N''의 점 (m,n)을 pr₁ 아래에서 보면 m이고 m의 역상은 {m} × ''N''이므로 T_(m,n) ({m} × ''N'') = {m} × T''N''이다. 수직 다발은 V''B''₁ = ''M'' × T''N''이며, 이는 T(''M'' ×''N'')의 부분 다발이다. 다른 사영 pr₂ : ''M'' × ''N'' → ''N'' : (''x'', ''y'') → ''y''를 사용하여 올 다발 ''B''₂ := (''M'' × ''N'', pr₂)를 정의하면 수직 다발은 V''B''₂ = T''M'' × ''N''이 된다.

두 경우 모두, 곱 구조는 수평 다발에 대한 자연스러운 선택을 제공하며, 따라서 Ehresmann 연결을 제공한다. ''B''₁의 수평 다발은 ''B''₂의 수직 다발과 같으며 그 반대도 마찬가지이다.

4. 1. 자명한 올다발

두 매끄러운 다양체

M

과

F

가 주어졌고,

E=M\times F

를

M

위의 올다발로 여기면,

:

F\xleftarrow{\operatorname{proj}_2}E\xrightarrow{\operatorname{proj}_1}M

이다. 이 경우,

:

\mathrm T_{(m,f)}E=\mathrm T_mM\oplus\mathrm T_fF\qquad(\forall m\in M,\;,f\in F)

이며, 수직 벡터 다발

\mathrm VE

는 다음과 같다.

:

\mathrm VE=\operatorname{proj}_2^*\mathrm TF\subseteq\mathrm TE

이 경우, "수평 벡터 다발"

\operatorname{proj}_1^*\mathrm TM\subseteq\mathrm TE

역시 존재한다. 그러나 이는 임의의 올다발에 대하여 성립하지 않는다.

매끄러운 올 다발의 간단한 예는 두 다양체의 데카르트 곱이다. 다발 사영 pr₁ : ''M'' × ''N'' → ''M'' : (''x'', ''y'') → ''x''를 갖는 다발 ''B''₁ := (''M'' × ''N'', pr₁)을 생각하면, ''M'' × ''N''의 점 (m,n)에서 pr₁ 아래에서 이 점의 이미지는 m이다. pr₁ 아래에서 m의 역상은 {m} × ''N''이므로 T_(m,n) ({m} × ''N'') = {m} × T''N''이다. 수직 다발은 V''B''₁ = ''M'' × T''N''이며, 이는 T(''M'' ×''N'')의 부분 다발이다. 다른 사영 pr₂ : ''M'' × ''N'' → ''N'' : (''x'', ''y'') → ''y''를 사용하여 올 다발 ''B''₂ := (''M'' × ''N'', pr₂)를 정의하면 수직 다발은 V''B''₂ = T''M'' × ''N''이 된다.

두 경우 모두, 곱 구조는 수평 다발에 대한 자연스러운 선택을 제공하며, 따라서 Ehresmann 연결을 제공한다. ''B''₁의 수평 다발은 ''B''₂의 수직 다발과 같으며 그 반대도 마찬가지이다.

4. 2. 주다발

리 군

G

에 대하여,

\pi\colon E\twoheadrightarrow M

가

G

-주다발이라고 하자. 이 경우, 수직 벡터 다발

\mathrm VE

는 리 대수

\mathfrak g=\mathrm T_1G

에 대한 자명한 벡터 다발과 동형이다.

:

\mathrm VE\cong \mathfrak g\times E

구체적으로, 우선, 임의의

m\in M

에 대하여,

G

의 오른쪽 작용을 생성하는 벡터장의 족을

:

X\colon \mathfrak g\to\Gamma(\mathrm TP)

:

X\colon x\mapsto X_x

로 표기하자. 그렇다면, 위 작용이 정추이적 작용이므로,

X

의 상은

P

의 수직 벡터 다발

\mathrm VP=\ker(\mathrm T\pi)\subseteq\mathrm TP

과 같으며, 이는 벡터 다발의 표준적인 동형 사상

:

P\times\mathfrak g\to\mathrm VP

를 정의한다. (좌변은 올이

\mathfrak g

인 자명한 벡터 다발이다.)

뫼비우스 띠는 원 위의 선 다발이며, 원은 띠의 중간 고리로 묘사될 수 있다. 띠의 각 점

e

에서, 사영 사상은 중간 고리로 투영되며, 올은 중간 고리에 수직이다. 이 점에서의 수직 다발

V_eE

는 올에 대한 접 공간이다.

매끄러운 올 다발의 간단한 예는 두 다양체의 데카르트 곱이다. 다발 사영 pr₁ : ''M'' × ''N'' → ''M'' : (''x'', ''y'') → ''x''를 갖는 다발 ''B''₁ := (''M'' × ''N'', pr₁)을 고려하면, 수직 다발은 V''B''₁ = ''M'' × T''N''이며, 이는 T(''M'' ×''N'')의 부분 다발이다. 다른 사영 pr₂ : ''M'' × ''N'' → ''N'' : (''x'', ''y'') → ''y''를 사용하여 올 다발 ''B''₂ := (''M'' × ''N'', pr₂)를 정의하면 수직 다발은 V''B''₂ = T''M'' × ''N''이 된다.

두 경우 모두, 곱 구조는 수평 다발에 대한 자연스러운 선택을 제공하며, 따라서 Ehresmann 연결을 제공한다. ''B''₁의 수평 다발은 ''B''₂의 수직 다발과 같으며 그 반대도 마찬가지이다.

4. 3. 벡터 다발

매끄러운 다양체

M

위의 매끄러운 벡터 다발

\pi\colon E\twoheadrightarrow M

이 주어졌을 때,

E

의 수직 벡터 다발은 스스로의 당김

\pi^*E=E\times_ME

와 표준적으로 동형이다.^[3]

:

\mathrm VE\cong\pi^*E=E\times_ME

뫼비우스 띠는 원 위의 선 다발이며, 원은 띠의 중간 고리로 묘사될 수 있다. 띠의 각 점

e

에서, 사영 사상은 중간 고리로 투영되며, 올은 중간 고리에 수직이다.

매끄러운 올 다발의 간단한 예는 두 다양체의 데카르트 곱이다. 다발 사영 pr₁ : ''M'' × ''N'' → ''M'' : (''x'', ''y'') → ''x''를 갖는 다발 ''B''₁ := (''M'' × ''N'', pr₁)을 고려하면, 수직 다발은 V''B''₁ = ''M'' × T''N''이며, 이는 T(''M'' ×''N'')의 부분 다발이다. 다른 사영 pr₂ : ''M'' × ''N'' → ''N'' : (''x'', ''y'') → ''y''를 사용하여 올 다발 ''B''₂ := (''M'' × ''N'', pr₂)를 정의하면 수직 다발은 V''B''₂ = T''M'' × ''N''이 된다.

두 경우 모두, 곱 구조는 수평 다발에 대한 자연스러운 선택을 제공하며, 따라서 Ehresmann 연결을 제공한다. ''B''₁의 수평 다발은 ''B''₂의 수직 다발과 같으며 그 반대도 마찬가지이다.

4. 4. 뫼비우스 띠

뫼비우스 띠는 원 위의 선 다발이며, 원은 띠의 중간 고리로 묘사될 수 있다. 띠의 각 점

e

에서, 사영 사상은 중간 고리로 투영되며, 올은 중간 고리에 수직이다. 이 점에서의 수직 다발

V_eE

는 올에 대한 접 공간이다.

매끄러운 올 다발의 간단한 예는 두 다양체의 데카르트 곱이다. 다발 사영 pr₁ : ''M'' × ''N'' → ''M'' : (''x'', ''y'') → ''x''를 갖는 다발 ''B''₁ := (''M'' × ''N'', pr₁)을 고려할 때, ''M'' × ''N''의 점 (m,n)을 pr₁ 아래에서 보면 m이고 m의 역상은 {m} × ''N''이므로 T_(m,n) ({m} × ''N'') = {m} × T''N''이다. 수직 다발은 V''B''₁ = ''M'' × T''N''이며, 이는 T(''M'' ×''N'')의 부분 다발이다. 다른 사영 pr₂ : ''M'' × ''N'' → ''N'' : (''x'', ''y'') → ''y''를 사용하여 올 다발 ''B''₂ := (''M'' × ''N'', pr₂)를 정의하면 수직 다발은 V''B''₂ = T''M'' × ''N''이 된다.

두 경우 모두, 곱 구조는 수평 다발에 대한 자연스러운 선택을 제공하며, 따라서 Ehresmann 연결을 제공한다. ''B''₁의 수평 다발은 ''B''₂의 수직 다발과 같으며 그 반대도 마찬가지이다.

5. 추가 성질 (틀 다발)

접속 형식은 수평 벡터 다발에서는 0이고 수직 벡터 다발에서만 0이 아니다. 이러한 방식으로, 접속 형식은 수평 벡터 다발을 정의하는 데 사용될 수 있다. 수평 벡터 다발은 접속 형식의 커널이다.^[2] 솔더 형식은 수직 벡터 다발에서는 0이고 수평 벡터 다발에서만 0이 아니다. 솔더 형식은 그 값을 전적으로 수평 벡터 다발에 둔다.^[2]

틀 다발의 경우, 비틀림 형식은 수직 벡터 다발에서 0이며, 임의의 접속을 레비-치비타 접속으로 변환하기 위해, 즉 비틀림이 없도록 만들기 위해, 접속에 추가해야 하는 부분을 정의하는 데 사용될 수 있다.^[2] 솔더 형식을 θ로 표기하면, 비틀림 텐서 Θ는 Θ = D θ (D는 외미분 공변 미분)로 주어진다.^[2] 주어진 접속 ω에 대해, ''TE''상에 컨토션 텐서라고 불리는, 수직 벡터 다발에서 0이 되고 ω+σ가 비틀림이 없는 다른 접속 1-형식이 되도록 하는 유일한 1-형식 σ가 존재한다.^[2] 결과적인 1-형식 ω+σ는 레비-치비타 접속과 다름없다.^[2] 비틀림은 $ \Theta = D\theta = d\theta + \omega \wedge \theta $로 주어지므로, 비틀림의 소실은 $ d\theta = - (\omega +\sigma) \wedge \theta $를 갖는 것과 같다.^[2]

리 군 $G$에 대하여, $ \pi\colon E\twoheadrightarrow M $가 $G$-주다발인 경우, 기본 벡터장은 수직 벡터 다발에 존재하며, 모든 수평 벡터 다발에서는 0이어야 한다.^[2]

5. 1. 접속 형식과의 관계

접속 형식은 수평 벡터 다발에서는 0이고 수직 벡터 다발에서만 0이 아니다. 이러한 방식으로, 접속 형식은 수평 벡터 다발을 정의하는 데 사용될 수 있다. 수평 벡터 다발은 접속 형식의 커널이다.^[2] 솔더 형식은 수직 벡터 다발에서는 0이고 수평 벡터 다발에서만 0이 아니다. 솔더 형식은 그 값을 전적으로 수평 벡터 다발에 둔다.^[2]

틀 다발의 경우, 비틀림 형식은 수직 벡터 다발에서 0이며, 임의의 접속을 레비-치비타 접속으로 변환하기 위해, 즉 비틀림이 없도록 만들기 위해, 접속에 추가해야 하는 부분을 정의하는 데 사용될 수 있다.^[2] 솔더 형식을 θ로 표기하면, 비틀림 텐서 Θ는 Θ = D θ (D는 외미분 공변 미분)로 주어진다.^[2] 주어진 접속 ω에 대해, ''TE''상에 컨토션 텐서라고 불리는, 수직 벡터 다발에서 0이 되고 ω+σ가 비틀림이 없는 다른 접속 1-형식이 되도록 하는 유일한 1-형식 σ가 존재한다.^[2] 결과적인 1-형식 ω+σ는 레비-치비타 접속과 다름없다.^[2] 비틀림은

\Theta = D\theta = d\theta + \omega \wedge \theta

로 주어지므로, 비틀림의 소실은

d\theta = - (\omega +\sigma) \wedge \theta

를 갖는 것과 같다.^[2]

5. 2. 솔더 형식과의 관계

솔더 형식은 수직 벡터 다발에서는 0이고 수평 벡터 다발에서만 0이 아니다.^[2] 정의에 따라, 솔더 형식은 그 값을 전적으로 수평 벡터 다발에 둔다.

틀 다발의 경우, 비틀림 형식은 수직 벡터 다발에서 0이다.^[2] 비틀림 텐서 Θ는 외미분 공변 미분 D를 사용하여 Θ = Dθ (여기서 θ는 솔더 형식)로 주어진다. 주어진 접속 ω에 대해, 컨토션 텐서라고 불리는 유일한 1-형식 σ가 존재한다. 이 텐서는 수직 벡터 다발에서 0이 되고, ω + σ가 비틀림이 없는 또 다른 접속 1-형식이 되도록 한다.^[2] 이 1-형식 ω + σ는 레비-치비타 접속과 같다. 비틀림은 $\Theta = D\theta = d\theta + \omega \wedge \theta$로 주어지므로, 비틀림이 없다는 것은 $d\theta = - (\omega +\sigma) \wedge \theta$를 만족하는 것과 같다.^[2]

5. 3. 레비-치비타 접속과의 관계

틀 다발의 경우, 비틀림 형식은 수직 벡터 다발에서 0이며, 임의의 접속을 레비-치비타 접속으로 변환하기 위해, 즉 비틀림이 없도록 만들기 위해, 접속에 추가해야 하는 정확한 부분을 정의하는 데 사용될 수 있다.^[2] 실제로 솔더 형식을 θ로 표기하면, 비틀림 텐서 Θ는 Θ = D θ (D는 외미분 공변 미분)로 주어진다. 주어진 접속 ω에 대해, T''E''상에 '''컨토션 텐서'''라고 불리는, 수직 벡터 다발에서 0이 되고 ω+σ가 비틀림이 없는 다른 접속 1-형식이 되도록 하는 ''유일한'' 1-형식 σ가 존재한다. 결과적인 1-형식 ω+σ는 레비-치비타 접속과 다름없다. 비틀림은

\Theta = D\theta = d\theta + \omega \wedge \theta

로 주어지므로, 비틀림의 소실은

d\theta = - (\omega +\sigma) \wedge \theta

를 갖는 것과 같으며, σ가 수직 벡터 다발에서 0이 되어야 하고 σ가 각 올에서 ''G''-불변이어야 함을 증명하는 것은 어렵지 않다(보다 정확하게는 σ가 ''G''의 수반 표현으로 변환된다는 것이다). 이는 계량 텐서에 대한 명시적인 언급 없이 레비-치비타 접속을 정의한다.^[2]

5. 4. 기본 벡터장과의 관계 (주다발)

리 군

G

에 대하여,

\pi\colon E\twoheadrightarrow M

가

G

-주다발인 경우, 기본 벡터장은 수직 벡터 다발에 존재하며, 모든 수평 벡터 다발에서는 0이어야 한다.^[2]

참조

_[1] 서적 Gauge Theory and Variational Principles https://zulfahmed.fi[...] Addison-Wesely Publishing Company 1981
_[2] 서적 Natural Operations in Differential Geometry http://www.emis.de/m[...] Springer-Verlag 1993
_[3] 서적 Natural operations in differential geometry http://www.emis.de/m[...] Springer-Verlag 1993

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com