양자 홀 효과

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

양자 홀 효과는 2차원 전자계에서 자기장 하에 전류가 흐를 때 나타나는 현상으로, 홀 전도율이 기본 상수의 정수 또는 분수 배수로 양자화되는 특징을 보인다. 1879년 에드윈 홀이 홀 효과를 발견한 이후, 1980년 클라우스 폰 클리칭은 실리콘 기반 MOSFET 샘플을 사용하여 정수 양자 홀 효과를 발견하여 노벨 물리학상을 수상했다. 1982년에는 대니얼 추이, 호르스트 슈퇴르머, 아서 고서드가 분수 양자 홀 효과를 발견했다. 양자 홀 효과는 전기 저항 표준, 위상 양자 컴퓨팅 등 다양한 분야에 응용되며, 특히 폰 클리칭 상수를 이용한 전기 저항의 정확한 정의가 가능하다.

더 읽어볼만한 페이지

1980년 과학 - 급팽창 이론
급팽창 이론은 우주 초기에 초광속으로 팽창하는 현상인 우주 급팽창을 설명하며, 공간의 가속 팽창을 통해 초기 우주의 균질성, 비등방성, 평탄성 문제를 해결하고 자기 홀극과 같은 무거운 입자를 희석시키며, 관측 결과와 일치하는 척도 불변의 원시 밀도 요동을 예측한다.
1980년 과학 - 1980년 8월 10일 일식
1980년 8월 10일 일식은 금환 일식으로, 사로스 주기 135의 일부이며, 18년 11일 주기로 반복되는 일식 중 하나이다.
홀 효과 - 에드윈 홀
에드윈 허버트 홀은 홀 효과를 발견하고 하버드 대학교 물리학 교수로 재직하며 물리학 교과서를 저술한 미국의 물리학자이다.
홀 효과 - 홀 효과 추력기
홀 효과 추력기는 정전기적 전위를 이용해 이온을 가속하여 추력을 발생시키는 전기 추진 시스템으로, 1960년대 소련에서 최초로 실용화되어 위성 궤도 유지 등에 활용되며, 화학 로켓보다 높은 비추력과 효율을 제공한다.
양자전자공학 - 양자 우물
양자 우물은 띠 간격이 다른 반도체 물질을 층층이 쌓아 전하 캐리어를 가두는 퍼텐셜 우물을 형성하는 구조로, 광전자 및 전자 소자, 에너지 수확 분야에 응용되며, 한국은 관련 기술 개발에 힘쓰고 있다.
양자전자공학 - 양자 스핀홀 효과
양자 스핀 홀 효과는 전자의 스핀 방향에 따라 반대 방향으로 흐르는 현상이며, 찰스 케인과 유진 멜레는 그래핀 모델을 기반으로 한 케인-멜레 모델을 제안했다.

양자 홀 효과
양자 홀 효과
개요
분야	응집물질물리학, 물리학, 전자기학
발견자	클라우스 폰 클리칭
발견 년도	1980년
설명	2차원 전자 시스템에서 강한 자기장과 낮은 온도 조건에서 나타나는 현상 홀 전도율이 양자화된 값으로 나타나는 현상
특징
홀 저항 (Rxy)	Rxy = h/(ne²)
홀 전도율 (σxy)	σxy = ne²/h
n	정수 (정수 양자 홀 효과) 또는 분수 (분수 양자 홀 효과)
h	플랑크 상수
e	기본 전하
온도	매우 낮은 온도 (T ≈ 0 K)
자기장	강한 자기장
2차원 전자 시스템	2차원 전자 가스
유형
정수 양자 홀 효과	홀 전도율이 정수 배수로 양자화됨
분수 양자 홀 효과	홀 전도율이 분수 배수로 양자화됨
응용
저항 표준	매우 정확한 저항 표준으로 사용
물질 연구	새로운 물질의 특성 연구에 활용
관련 개념
홀 효과	고전적인 홀 효과
란다우 준위	양자화된 에너지 준위
응집물질물리학	관련 분야

2. 역사

홀 효과는 1879년 에드윈 홀(Edwin Hall)이 발견했다. 1978년, 클라우스 폰클리칭(Klaus von Klitzing)은 고전적 홀 효과와 달리 홀 전도율이 양자화되는 양자 홀 효과를 발견하였다. 고전적 홀 효과에서는 홀 전도율이 대상 물질의 전하 수송자 밀도에 비례했지만, 양자 홀 효과에서는 홀 전도율이 기본상수에만 관련되는 양자의 정수배로 양자화된다.

1957년 벨 연구소의 칼 프로슈(Carl Frosch)와 링컨 데릭(Lincoln Derick)은 최초로 실리콘 이산화물 전계 효과 트랜지스터를 제작했다.^[11] 1960년 벨 연구소 연구팀은 작동하는 MOSFET을 시연했다.^[12]^[13] 이를 통해 물리학자들은 거의 이상적인 2차원 기체 내의 전자 거동을 연구할 수 있게 되었다.^[14] MOSFET에서 전도 전자는 얇은 표면층을 따라 이동하며, "게이트" 전압이 이 층의 전하 운반자 수를 제어한다. 이로써 연구자들은 고순도 MOSFET을 액체 헬륨 온도에서 작동시켜 양자 효과를 탐구할 수 있었다.^[14]

1975년 도쿄대학교 연구진은 홀 전도도의 정수 양자화를 예측하였으나, 그들 자신도 그 결과를 믿지 않았다.^[23] 1978년, 가쿠슈인 대학(Gakushuin University) 연구진은 MOSFET의 반전층에서 수행한 실험에서 이 효과를 관찰했다.^[24]

1982년, 대니얼 추이(Daniel Chee Tsui), 호르스트 슈퇴르머(Horst Störmer), 아서 고서드(Arthur C. Gossard)는 분수 양자 홀 효과를 발견하였다. 이후 로버트 래플린(Robert B. Laughlin)은 양자화된 전도도를 터울리스 전하 펌프(Thouless charge pump)의 양자화된 전하 수송과 연결하여 정확한 양자화와 게이지 불변성 사이의 연관성을 제시했다.^[21]^[26]

대부분의 정수 양자 홀 효과 실험은 현재 갈륨 비소 이종구조에서 수행되지만, 다른 많은 반도체 재료도 사용할 수 있다. 2007년에는 실온에서 그래핀^[27]과 마그네슘 아연 산화물 ZnO–Mg_''x''Zn_1−''x''O^[28]에서 정수 양자 홀 효과가 보고되었다.

2. 1. 고전적 홀 효과

홀 효과는 1879년 에드윈 홀(Edwin Hall)이 발견하였다. 홀이 발견한 홀 효과는 양자 홀 효과와 구분하기 위해 고전적 홀 효과라고 부르기도 한다.

2. 2. 양자 홀 효과

홀 효과는 1879년 에드윈 홀(Edwin Hall)이 발견하였으며, 양자 홀 효과와 구분하기 위해 고전적 홀 효과라고도 불린다. 1978년 클라우스 폰클리칭(Klaus von Klitzing)은 고전적 홀 효과와 달리 홀 전도율이 양자화되는 양자 홀 효과를 발견했다. 1980년, 폰 클리칭은 마이클 페퍼(Michael Pepper)와 게르하르트 도르다(Gerhard Dorda)가 개발한 실리콘 기반 MOSFET 샘플을 사용하여 홀 저항이 정확하게 양자화된다는 것을 발견했다.^[25]^[14] 폰클리칭은 이 연구로 1985년 노벨 물리학상을 수상했다.

양자 홀 효과는 전기 저항 표준을 정하거나, 미세 구조 상수를 결정하는 데 사용된다.

1982년, 대니얼 추이(Daniel Chee Tsui), 호르스트 슈퇴르머(Horst Störmer)와 아서 고서드(Arthur C. Gossard)는 분수 양자 홀 효과를 발견하였다. 이는 전자 간 상호작용에서 기인하며, 정수 양자 홀 효과와는 원인이 다르다. 1998년 슈퇴르머, 추이 및 로버트 B. 러플린은 이 공로로 노벨 물리학상을 수상하였다.

3. 홀 저항

2차원 전자계에서, 전자들은 2차원 평면 위에서 운동한다. 전기장 $\mathbf{E}$ 를 가하면, 전기장의 방향으로 전류가 흐른다. 이 상태에서 자기장 $\mathbf{B}$ 를 평면에 수직으로 가하면 전류는 더 이상 $\mathbf{E}$ 방향으로만 흐르지 않는다. 따라서, 전도율 $\sigma$ 를 스칼라에서 텐서로 일반화한다.

: $\mathbf{J} = \mathbf{\sigma} \mathbf{E}$

:( $\mathbf{J}$ : 전류 밀도)

평면을 $x, y$ 로 데카르트 좌표를 쓰면 다음과 같다.

: $J_{x}=\sigma_{xx}E_{x}+\sigma_{xy}E_{y}$

: $J_{y}=\sigma_{yx}E_{x}+\sigma_{yy}E_{y}$

등방성에 의하여, 전도율은 $\sigma_{xx}=\sigma_{yy}$ , $\sigma_{xy}=-\sigma_{yx}$ 와 같은 성질을 가진다. 전류 밀도와 외부 전기장 $\mathbf{E}$ 의 관계식은 비저항 텐서로 나타낼 수 있다.

: $E_{x}=\rho_{xx}J_{x}+\rho_{xy}J_{y}$

: $E_{y}=\rho_{yx}J_{x}+\rho_{yy}J_{y}$

위의 두 식은 동일해야 하므로 아래의 관계식이 성립한다.

: $\rho_{xx}=\rho_{yy}=\frac{\sigma_{xx}}{\sigma_{xx}^2+\sigma_{xy}^2}$

: $\rho_{xy}=-\rho_{yx}=-\frac{\sigma_{xy}}{\sigma_{xx}^2+\sigma_{xy}^2}$

위의 식에서 $\rho_{xx}=\rho_{yy}$ 를 대각 비저항(diagonal resistivity)(diagonal conductivity^영어)으로 정의하고, $\rho_{xy}=-\rho_{yx}$ 를 홀 저항율(Hall resistivity)로 정의한다. $\sigma_{xx}=\sigma_{yy}$ 는 대각 전도율, $\sigma_{xy}=-\sigma_{yx}$ 는 홀 전도율(Hall conductivity)이다. 2차원으로 표현했기 때문에 홀 저항은 홀 저항율과 같다.

4. 정수 양자 홀 효과

정수 양자 홀 효과는 2차원 전자계에서 나타나는 특이한 현상이다. 1980년 클라우스 폰 클리칭은 마이클 페퍼와 게르하르트 도르다가 개발한 실리콘 기반 MOSFET 샘플을 사용하여 홀 저항이 정확하게 양자화된다는 것을 발견했다.^[25]^[14] 이 발견으로 폰 클리칭은 1985년 노벨 물리학상을 수상했다.

일반적으로 약한 전기장에서 홀 비저항은 $\rho_{xy}=\frac{B}{n_{e}e}$ ( $e$ : 기본 전하, $n_{e}$ : 전자 밀도)로 계산된다. 하지만, 저온의 2차원 전자계에 강한 자기장을 걸면 다음과 같은 현상이 관측된다.^[35]

전자 밀도가 변해도 홀 저항율이 일정한 값을 갖는 구간이 존재하며, 이 구간에서는 대각 저항율이 사라진다.
홀 저항율이 변하지 않는 구간에서 홀 저항율은 정확하게 $h/e^2$ 을 정수로 나눈 값이다. 즉, 홀 전도율이 $e^2/h$ 의 정수배로 양자화된다.

이러한 현상을 정수 양자 홀 효과라고 한다. 폰 클리칭은 Si MOS 계에서 이를 측정했지만, GaAs-AlGaAs 이종 결합 등 다른 계에서도 나타난다.^[36]

정수 양자 홀 효과에서 측정한 홀 저항

h/e^2

는 국제 단위계(S.I.)로 25 812.807 Ω이다. 1957년 벨 연구소의 칼 프로슈와 링컨 데릭은 최초의 실리콘 이산화물 전계 효과 트랜지스터를 제작했고,^[11] 1960년 벨 연구소 연구팀은 작동하는 MOSFET을 시연했다.^[12]^[13] MOSFET에서 전도 전자는 얇은 표면층을 따라 이동하며, '게이트' 전압이 이 층의 전하 운반자 수를 제어한다. 연구자들은 고순도 MOSFET을 액체 헬륨 온도에서 작동시켜 양자 효과를 탐구할 수 있었다.^[14]

홀 전도도의 정수 양자화는 1975년 도쿄대학교의 안도 츠네야, 마쓰모토 유키오, 우에무라 야스타다 연구진이 예측했지만,^[23] 1978년 가쿠슈인 대학의 와카바야시 준이치와 가와지 신지 연구진이 MOSFET의 반전층에서 수행한 실험에서 이 효과를 관찰했다.^[24]

단지 설명을 위한 것입니다. 준위는 자기장이 증가함에 따라 퍼져나갑니다. 준위 사이에서 양자 홀 효과가 관찰됩니다. DOS는 상태 밀도입니다.

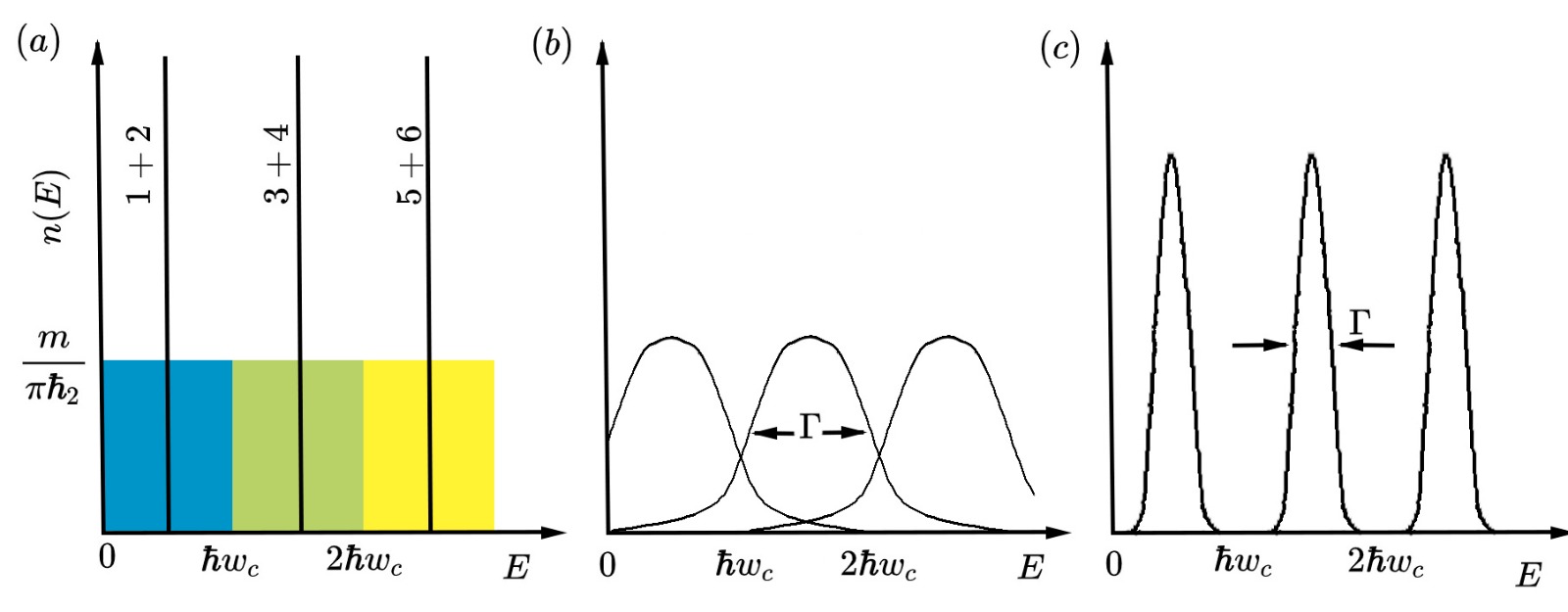
자기장이 걸리면, 2차원 전자 기체의 상태 밀도는 란다우 준위(Landau levels)에 해당하는 일련의 디랙

\delta

함수로 붕괴된다. 란다우 준위는

\Delta\varepsilon_{xy}=\hbar \omega_{\rm c}

만큼 분리되어 있다. 유한 온도에서는 산란 사건 사이의 시간

\tau_i

를 사용하여

\Gamma=\frac{\hbar}{\tau_i}

인 폭을 갖는다. 란다우 준위의 모양은 가우스 분포 또는 로렌츠 분포로 가정한다.

x축을 따라 $x_k$ 에 중심을 둔 포물선 포텐셜과 z 방향의 무한 우물 제한에 해당하는 첫 번째 파동 함수. y 방향에는 진행하는 평면파가 있다.

각 란다우 준위와

k

에 대한 상태의 수는 시료를 통과하는 총 자기 플럭스와 상태에 해당하는 자기 플럭스의 비율로 계산할 수 있다. 단위 면적당 상태 밀도는

n_B=\frac{m^*\omega_{\rm c}}{2\pi \hbar}

이다.

채워진 란다우 준위의 수를 나타내는 채우기 인자

\nu

는

\nu=\frac{n_{\rm 2D}}{n_B}=\frac{hn_{\rm 2D}}{eB}

로 정의된다.

\nu

가 정수일 때, 횡방향 비저항은 전도 양자

e^2/h

의 역수의 배수가 된다.

스핀 분리를 무시한 자기장에서의 상태 밀도. (a) 각 범위 $\hbar \omega_{\rm c}$ 의 상태는 $\delta$ -함수 란다우 준위로 압축된다. (b) 더 현실적인 그림에서 란다우 준위는 0이 아닌 폭 $\Gamma$ 을 가지며, $\hbar \omega_{\rm c}<\Gamma$ 이면 겹친다. (c) $\hbar \omega_{\rm c}>\Gamma$ 이면 준위가 구별된다.

4. 1. 란다우 준위

2차원에서 고전적인 전자가 자기장에 놓이면 원형 사이클로트론 궤도를 따른다. 이 계를 양자역학적으로 다루면 이 궤도는 양자화된다. 에너지 준위의 값을 결정하려면 슈뢰딩거 방정식을 풀어야 한다.

계가 자기장에 놓여 있으므로, 슈뢰딩거 방정식에 전자기 벡터 포텐셜로 도입해야 한다. 고려되는 계는 x와 y 방향으로 자유롭게 움직일 수 있지만 z 방향으로는 단단히 구속된 전자 기체이다. 그런 다음 z 방향으로 자기장을 가하고 란다우 게이지에 따라 전자기 벡터 포텐셜은

\mathbf{A} = (0, Bx, 0)

이고 스칼라 포텐셜은

\phi=0

이다.

이 방정식을 풀기 위해 자기장이 x와 y축을 따라 움직임에만 영향을 미치기 때문에 두 방정식으로 분리할 수 있다. 그러면 총 에너지는 두 기여의 합이 된다.

\varepsilon = \varepsilon_z + \varepsilon_{xy}

. z축에 대한 대응하는 방정식은 다음과 같다.

단순화하기 위해, 해

V(z)

를 무한 우물로 간주한다. 따라서 z 방향에 대한 해는 에너지

\varepsilon_z=\frac{n_z^2\pi^2\hbar^2}{2m^*L^2}

,

n_z=1,2,3...

이고 파동 함수는 사인파이다.

x

와

y

방향에 대해, 슈뢰딩거 방정식의 해는

y

방향의 평면파와

x

의 어떤 미지 함수의 곱으로 선택할 수 있다. 즉,

\psi_{xy}=u(x)e^{ik_yy}

이다. 이는 벡터 포텐셜이

y

에 의존하지 않고, 따라서 운동량 연산자

\hat p_y

가 해밀토니안과 교환하기 때문이다. 이 안자츠를 슈뢰딩거 방정식에 대입하면

x_{k_y}=\frac{\hbar k_y}{eB}

에서 중심을 갖는 1차원 조화 진동자 방정식을 얻는다.

:

\left [- \frac{\hbar^2}{2m^*} {\partial^2\over\partial x^2}+\frac{1}{2}m^*\omega_{\rm c}^2(x-l_B^2k_y)^2\right ]u(x)=\varepsilon_{xy}u(x)

여기서

\omega_{\rm c}=\frac{eB}{m^*}

는 사이클로트론 주파수로 정의되고

l_B^2=\frac{\hbar}{eB}

는 자기 길이이다. 에너지는 다음과 같다.

:

\varepsilon_{xy}\equiv\varepsilon_{n_x}=\hbar \omega_{\rm c} \left ( n_x+\frac{1}{2} \right )

,

n_x=1,2,3...

그리고

xy

평면에서의 운동에 대한 파동 함수는

y

의 평면파와 가우스 함수로 감쇠된 에르미트 다항식의 곱으로 주어지는데, 이는 조화 진동자의 파동 함수이다.

란다우 준위에 대한 식에서 에너지는

n_x

에만 의존하고

k_y

에는 의존하지 않는다는 것을 알 수 있다. 같은

n_x

를 가지지만 다른

k_y

를 갖는 상태는 축퇴되어 있다.

자기장이 0일 때, 스핀에 의한 축퇴를 고려한 2차원 전자 기체의 단위 면적당 상태 밀도는 에너지에 무관하며, 다음과 같다.

:

n_{\rm 2D}=\frac{m^*}{\pi \hbar^2}

자기장이 걸리면, 상태 밀도는 상수에서 디랙 빗살(Dirac comb), 즉

\Delta\varepsilon_{xy}=\hbar \omega_{\rm c}

만큼 분리된 란다우 준위(Landau levels)에 해당하는 일련의 디랙

\delta

함수로 붕괴된다. 그러나 유한 온도에서는 산란 사건 사이의 시간

\tau_i

를 사용하여

\Gamma=\frac{\hbar}{\tau_i}

인 폭을 갖는다. 일반적으로 란다우 준위의 정확한 모양은 가우스 분포 또는 로렌츠 분포로 가정한다.

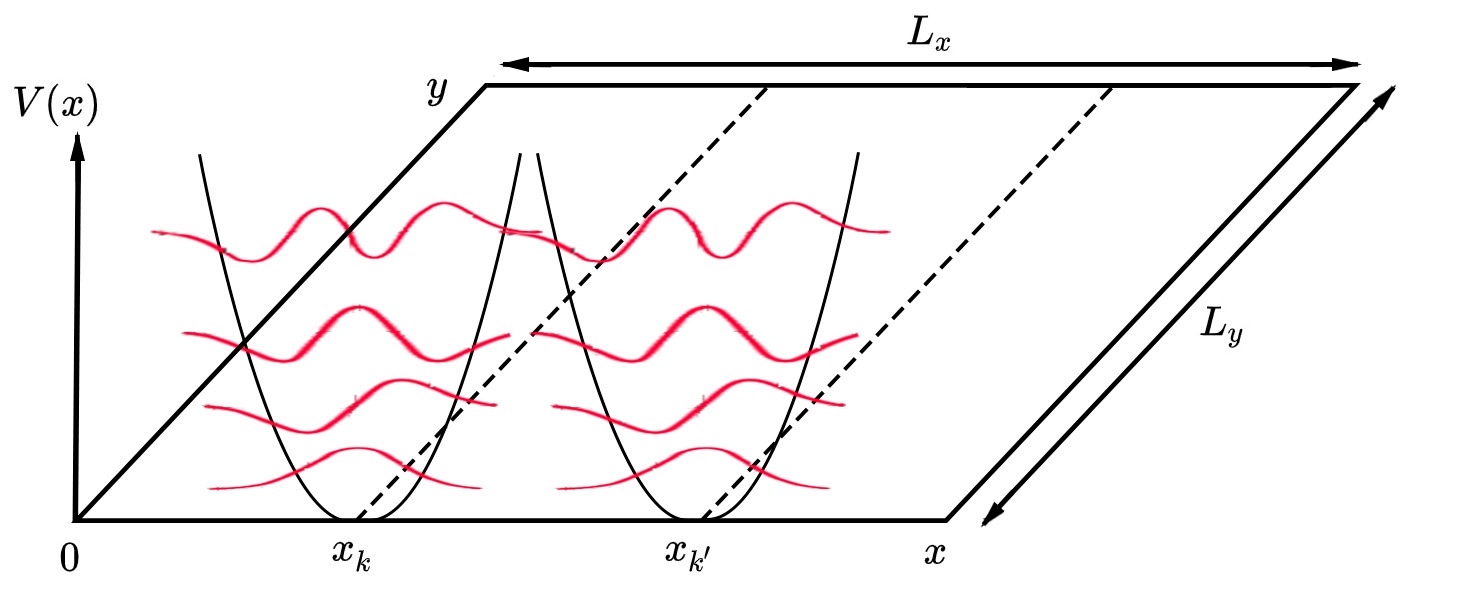
또 다른 특징은 파동 함수가

x

축을 따라 일정하게 간격을 두고

\mathbf{A}

선을 따라

y

방향으로 평행한 띠를 형성한다는 것이다. 벡터 포텐셜이 다르게 선택되면

xy

평면의 어떤 방향도 특별하지 않으므로 원형 대칭성을 찾아야 한다.

L_x \times L_y

크기의 시료에

y

방향으로 주기적 경계 조건

k=\frac{2\pi}{L_y}j

(j는 정수)을 적용하면 각 포물선 포텐셜은

x_k=l_B^2k

값에 위치한다.

각 란다우 준위와

k

에 대한 상태의 수는 시료를 통과하는 총 자기 플럭스와 상태에 해당하는 자기 플럭스의 비율로 계산할 수 있다.

:

N_B=\frac{\phi}{\phi_0}=\frac{BA}{BL_y\Delta x_k}=\frac{A}{2\pi l_B^2}\begin{array}{lcr}& l_B&\\&=&\\ &&\end{array}\frac{AeB}{2\pi \hbar}\begin{array}{lcr}& \omega_{\rm c}&\\&=&\\ &&\end{array} \frac{m^*\omega_{\rm c}A}{2\pi \hbar}

따라서 단위 면적당 상태 밀도는 다음과 같다.

:

n_B=\frac{m^*\omega_{\rm c}}{2\pi \hbar}

상태 밀도의 자기장 의존성에 유의한다. 자기장이 클수록 각 란다우 준위에 더 많은 상태가 존재한다. 결과적으로 더 적은 에너지 준위가 채워지므로 시스템의 구속이 더 강해진다.

마지막 식을

n_B=\frac{\hbar \omega_{\rm c}}{2} \frac{m^*}{\pi \hbar^2}

로 다시 쓰면, 각 란다우 준위에는

\Delta\varepsilon=\hbar \omega_{\rm c}

의 2DEG와 같은 수의 상태가 포함되어 있음을 알 수 있다.

전자가 페르미온이라는 사실을 고려하면, 란다우 준위에서 사용 가능한 각 상태에는 각각 스핀

s=\pm\frac{1}{2}

값을 갖는 두 개의 전자가 해당된다. 그러나 강한 자기장을 가하면, 스핀이 자기장과 정렬하는 것과 관련된 자기 모멘트로 인해 에너지가 두 개의 준위로 분리된다. 에너지 차이는

\Delta E = \pm \frac{1}{2}g\mu_{\rm B}B

이며, 여기서

g

는 재료에 따라 달라지는 인자(

g=2

자유 전자의 경우)이고

\mu_{\rm B}

는 보어 마그네톤이다. 스핀이 자기장과 평행할 때는 부호

+

를, 반평행일 때는

-

를 취한다. 스핀 분리(spin splitting)라고 하는 이 사실은 각 준위의 상태 밀도가 절반으로 감소함을 의미한다.

\Delta E

가 자기장에 비례하므로 자기장이 클수록 분리가 더 중요해진다는 점에 유의한다.

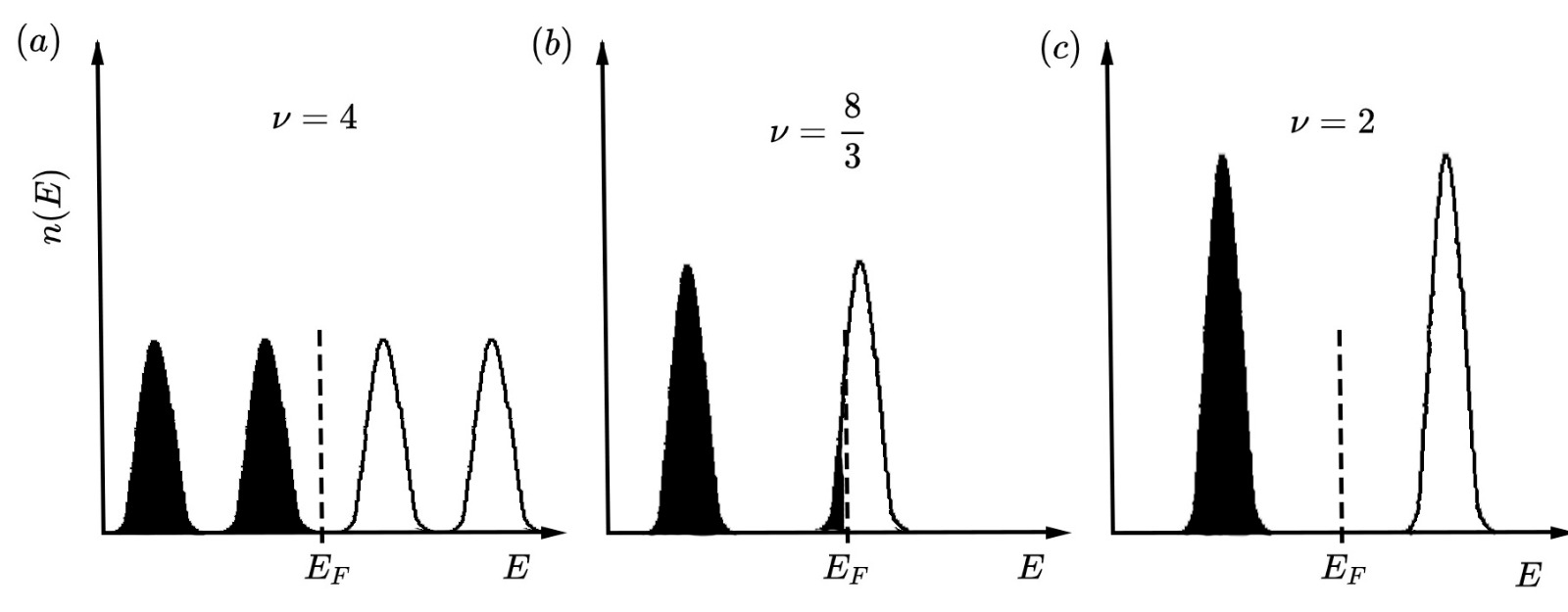
채워진 란다우 준위의 수를 얻기 위해, 2DEG의 상태 밀도와 란다우 준위의 상태 밀도의 비율인 채우기 인자(filling factor)

\nu

를 정의한다.

:

\nu=\frac{n_{\rm 2D}}{n_B}=\frac{hn_{\rm 2D}}{eB}

일반적으로 채우기 인자

\nu

는 정수가 아니다. 채워진 란다우 준위의 수가 정확히 정수일 때 정수가 된다. 대신 최상위 준위가 완전히 채워지지 않으면 비정수가 된다. 실제 실험에서는 자기장을 변화시키고 전자 밀도(페르미 에너지가 아님!)를 고정하거나, 전자 밀도를 변화시키고 자기장을 고정한다. 두 경우 모두 채우기 인자

\nu

의 연속적인 변화에 해당하며

\nu

가 정수일 것이라고 기대할 수 없다.

n_B\propto B

이므로 자기장을 증가시키면 란다우 준위가 에너지가 증가하고 각 준위의 상태 수가 증가하므로 최상위 준위를 점유하는 전자 수가 감소하여 결국 비게 된다. 자기장이 계속 증가하면 결국 모든 전자가 가장 낮은 란다우 준위(

\nu<1

)에 있게 되는데, 이를 자기 양자 한계(magnetic quantum limit)라고 한다.

4. 2. 종방향 및 횡방향 저항률

약한 전기장에서 드루드(Drude) 이론으로 계산한 홀 비저항은 다음과 같다.

:

\rho_{xy}=\frac{B}{n_{e}e}

:(

e

: 기본 전하,

n_{e}

: 전자 밀도)

이는 일반적인 홀 효과와 같지만, 저온의 2차원 전자계에 강한 자기장을 걸면 다른 현상이 나타난다. 폰클리칭은 다음 두 가지 사실을 실험적으로 관찰하였다.^[35]

전자 밀도가 변하는 중에도 홀 저항률이 일정한 값을 갖는 구간이 있고, 이때 대각 저항률이 사라진다.
홀 저항률이 변하지 않는 구간에서 홀 저항률은 정확하게 $h/e^2$ 을 정수로 나눈 값이다. 즉, 홀 전도율이 $e^2/h$ 의 정수배 값을 갖는 형태로 양자화된다.

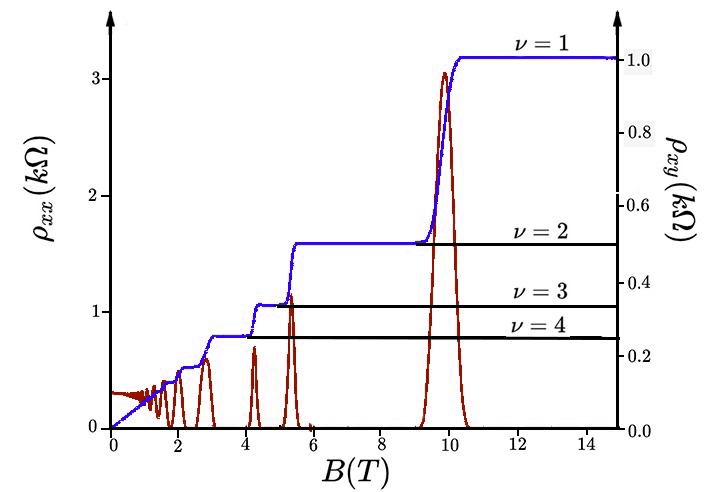
이러한 현상을 정수 양자 홀 효과라고 부른다. 폰클리칭은 Si MOS 계에서 이것을 측정하였는데, 이 현상은 GaAs-AlGaAs 이종 결합과 같은 다른 계에서도 나타난다. 자기장을 변화시키면서 홀 비저항을 측정하면, 자기장이 큰 영역에서 홀 비저항은 자기장이 커짐에 따라 계단 모양으로 증가한다.^[36]

정수 양자 홀 효과는 2차원이기 때문에 홀 비저항이 저항과 같다. 따라서 대상체의 모양에 관계없이 전류와 전압만 측정하면 실험에서 원하는 값을 측정할 수 있다. 또한 대각 저항율이 없기 때문에 홀 저항을 측정하기 위한 장치 배열이 전류 흐름 방향에 정확하게 수직일 필요가 없다. 정수 홀 효과에서 측정한 홀 저항

h/e^2

는 국제 단위계(S.I.)로 25 812.807 Ω이다.

채움 인자(

\nu

)가 정수일 때, 페르미 에너지는 란다우 준위 사이에 위치하여 전도도는 0이 되고, 저항률 또한 0이 된다.^[15] 반대로,

\nu

가 반정수일 때, 페르미 에너지는 어떤 란다우 준위의 밀도 분포의 최댓값에 위치하여 전도도가 최댓값을 갖는다.

최소값과 최댓값의 이러한 분포는 "양자 진동"으로, "슈브니코프-드 하스 진동"이라고 하며, 자기장이 증가함에 따라 더욱 중요해진다.

고전적인 관계식

\rho_{xy}=\frac{B}{en_{\rm 2D}}

에서

n_{\rm 2D}=\nu \frac{eB}{h}

를 대입하면, 횡방향 비저항과 전도도의 양자화를 알 수 있다.

:

\rho_{xy}=\frac{h}{\nu e^2}\Rightarrow \sigma=\nu \frac{e^2}{h}

채움 인수가 정수일 때, 횡방향 비저항은 전도 양자

e^2/h

의 역수의 배수이다. 실험에서는 채움 값

\nu

의 전체 구간에 걸쳐 플래토가 관찰되는데, 이는 란다우 준위 사이에 전자 상태가 존재함을 나타낸다. 이러한 상태는 물질의 불순물에 국소화되어 궤도에 갇히므로 전도도에 기여할 수 없다. 따라서 란다우 준위 사이에서 비저항은 일정하게 유지된다.

5. 분수 양자 홀 효과

추이, 슈퇴르머와 고서드는 홀 비저항이 일정한 구간에서도 정수 양자 홀 효과와 달리 대각 저항율이 남아 있고, 그 위치의 홀 비저항 값도 정수 양자 효과의 $h/e^2$ 이 아닌, 그 값의 $1/3$ 배와 $2/3$ 배한 값이라는 사실을 밝혔다.^[37] 이러한 현상은 정수 양자 홀 효과의 이론으로는 설명할 수 없다. 이후, 분수 양자 홀 효과는 전자 간 상호 작용에 의해 생긴다는 것이 밝혀졌다.

처음으로 발견된 분수 양자 홀 효과의 분수 값은 $1/3$ 과 $2/3$ 였다. 그러나 2차원 전자계의 이동도가 높고, 온도가 낮을수록 분수 양자 홀 효과가 갖는 분수 값의 숫자는 증가한다. 실험에 따르면, 이러한 분수 값의 분모는 홀수이다.^[38]

최근 시료의 품질 향상에 따라 다양한 이종접합 등에서 2차원 전자계가 구현되고 있다. 1979년 후지쓰의 미무라 타카시 등에 의해 고전자이동도 트랜지스터(HEMT)가 개발되었다. 당시 작동 원리는 완전히 해명되지 않았지만, 1982년 다니엘 추이, 호르스트 루트비히 슈퇴르머, 아서 고사드 등은 이 전자계에 강한 자기장(10 T 이상)을 가하고 1 K 이하로 냉각하여 전기 저항률 ρ_xx, ρ_xy를 측정한 결과, 종래의 정수 양자 홀 효과에서 볼 수 있었던 홀 저항률 ρ_xy가 평탄한 영역(이하 플래토라고 한다) 외에 새로운 플래토를 발견했다. 거기서 저항률로부터 홀 전도율 σ_xy를 계산한 결과,

: $\sigma_{xy}=-\frac{p}{q}\cdot\frac{e^2}{h}$

를 얻었다. 여기서 p, q는 정수이며, q가 3 이상의 홀수인 경우(1/3, 2/3, 1/5, 2/5, 3/5, 2/7 등)를 '''분수 양자 홀 효과'''라고 명명했다.

정수 양자 홀 효과의 원인은 불순물 포텐셜에 의한 전자의 국재화이지만, 분수 양자 홀 효과는 전자 간의 쿨롱 포텐셜이 불순물 포텐셜을 압도하는 경우에 발생한다. 따라서 분수 양자 홀 효과가 관측되는 것은 시료가 불순물을 최대한 줄이고 이종접합 계면이 양질인 시료에 한정된다.

1998년 호르스트 루트비히 슈퇴르머, 다니엘 추이와 이론물리학자인 로버트 B. 러플린에게 노벨 물리학상이 수여되었다.

6. 이론적 설명

게이지 불변성 원리와 또 다른 대칭성(이상)의 조합으로 설명되는 부분 양자 홀 효과와 달리, 일반적인 경우의 정확한 양자화는 완전히 이해되지 않았다.^[7] 정수 양자 홀 효과와 분수 양자 홀 효과에 대한 이론적 설명은 아래와 같다.

'''정수 양자 홀 효과''': TKNN 공식과 체르니코프-사이먼스 라그랑지안의 범위 내에서 이해된다.
'''분수 양자 홀 효과''': 전자가 아닌 복합 페르미온으로 알려진 전하-플럭스 복합체의 정수 양자 홀 효과로 이해될 수도 있다.^[9]

분수 양자 홀 효과는 여전히 미해결 연구 문제로 간주된다.^[2] 현재 단일하고 확인되고 합의된 부분 양자수 목록도 없고, 이들을 모두 설명하는 단일 합의된 모델도 없기 때문이다(비록 복합 페르미온과 비 아벨 체르니코프-사이먼스 라그랑지안 범위 내에서 그러한 주장이 있지만).^[10]

홀 효과에 나타나는 정수는 위상 양자수의 한 예이다. 이 수는 수학적으로 제1 차른 수(first Chern number)로 알려져 있으며, 베리 위상과 밀접한 관계가 있다. 이와 관련하여 아벨-하퍼-호프슈타터 모델은 매우 흥미롭다. 이 모델의 양자 위상도는 호프슈타터의 나비(Hofstadter's butterfly)로 표현된다.

세로축은 자기장의 세기이고, 가로축은 전자 밀도에 의해 결정되는 화학 포텐셜이다. 색깔은 정수 양자 홀 전도도를 나타낸다. 따뜻한 색은 양의 정수를 나타내고, 차가운 색은 음의 정수를 나타낸다. 위상도는 프랙탈이며, 명백한 자기 상관성이 관찰된다. 물리적 메커니즘으로는, 불순물이나 국소적인 계(예: 에지 전류) 또는 그 양쪽 모두가 정수 양자 홀 효과와 분수 양자 홀 효과에 중요한 역할을 하고 있다고 생각된다. 덧붙여, 쿨롱 상호작용도 분수 양자 홀 효과를 생각할 때 중요하다. 분수 양자 홀 효과는 정수 양자 홀 효과와 비슷한 현상이며, 짝수 개의 자속 양자와 속박 상태를 형성한 복합 페르미온이라 불리는 전자의 성질에 의한 것이라고 설명할 수 있다.

6. 1. 정수 양자 홀 효과

게이지 불변성 원리와 또 다른 대칭성(이상)의 조합으로 설명되는 부분 양자 홀 효과와 달리, 정수 양자 홀 효과는 해결된 연구 문제로 간주되며^[8]^[21] TKNN 공식과 체르니코프-사이먼스 라그랑지안의 범위 내에서 이해된다.

6. 2. 분수 양자 홀 효과

분수 양자 홀 효과(반정수 양자 홀 효과)는 GaAs를 기본으로 하는 이종결합에서 만들어지는, 이동도가 높은 2차원 전자계에서 나타난다. 추이, 슈퇴르머, 고서드는 홀 비저항이 일정한 구간에서도 정수 양자 홀 효과와 달리 대각 저항율이 남아 있고, 그 위치의 홀 비저항 값도 정수 양자 효과의

h/e^2

이 아닌, 그 값의

1/3

배와

2/3

배한 값이라는 사실을 밝혔다.^[37] 이러한 현상은 정수 양자 홀 효과 이론으로는 설명할 수 없다. 이후, 분수 양자 홀 효과는 전자 간 상호작용에 의해 생긴다는 것이 밝혀졌다.

처음 발견된 분수 양자 홀 효과의 분수 값은

1/3

과

2/3

였다. 그러나 2차원 전자계의 이동도가 높고 온도가 낮을수록 분수 양자 홀 효과가 갖는 분수 값의 숫자는 증가한다. 실험에 따르면, 이러한 분수 값의 분모는 홀수이다.^[38]

부분 양자 홀 효과는 '정확한 양자화'의 일부로 간주된다.^[7] 게이지 불변성 원리와 또 다른 대칭성(이상)의 조합으로 설명되어 왔지만, 일반적인 경우의 정확한 양자화는 완전히 이해되지 않았다. 반면에 정수 양자 홀 효과는 해결된 연구 문제로 간주되며^[8]^[21] TKNN 공식과 체르니코프-사이먼스 라그랑지안 범위 내에서 이해된다.

부분 양자 홀 효과는 여전히 미해결 연구 문제로 간주된다.^[2] 부분 양자 홀 효과는 전자가 아닌 복합 페르미온으로 알려진 전하-플럭스 복합체의 정수 양자 홀 효과로 이해될 수도 있다.^[9] 부분 양자 홀 효과를 설명하는 다른 모델도 존재한다.^[10]

현재 단일하고 확인되고 합의된 부분 양자수 목록도 없고, 이들을 모두 설명하는 단일 합의된 모델도 없기 때문에(비록 복합 페르미온과 비 아벨 체르니코프-사이먼스 라그랑지안 범위 내에서 그러한 주장이 있지만) 미해결 연구 문제로 간주된다.

최근 시료의 품질 향상에 따라 다양한 이종접합 등에서 2차원 전자계가 구현되고 있다. 1979년 후지쓰의 미무라 타카시 등이 고전자이동도 트랜지스터(HEMT)를 개발했다. 당시 작동 원리는 완전히 밝혀지지 않았지만, 1982년 다니엘 추이, 호르스트 루트비히 슈퇴르머, 아서 고사드 등은 이 전자계에 강한 자기장(10 T 이상)을 가하고 1 K 이하로 냉각하여 전기 저항률 ρ_xx, ρ_xy를 측정한 결과, 종래의 정수 양자 홀 효과에서 볼 수 있었던 홀 저항률 ρ_xy가 평탄한 영역(이하 플래토) 외에 새로운 플래토를 발견했다. 거기서 저항률로부터 홀 전도율 σ_xy를 계산한 결과,

:

\sigma_{xy}=-\frac{p}{q}\cdot\frac{e^2}{h}

를 얻었다. 여기서 p, q는 정수이며, q가 3 이상의 홀수인 경우(1/3, 2/3, 1/5, 2/5, 3/5, 2/7 등)를 '''분수 양자 홀 효과'''라고 명명했다.

정수 양자 홀 효과의 원인은 불순물 포텐셜에 의한 전자의 국재화이지만, 분수 양자 홀 효과는 전자 간의 쿨롱 포텐셜이 불순물 포텐셜을 압도하는 경우에 발생한다. 따라서 분수 양자 홀 효과가 관측되는 것은 시료가 불순물을 최대한 줄이고 이종접합 계면이 양질인 시료에 한정된다.

1998년 호르스트 루트비히 슈퇴르머, 다니엘 추이와 이론물리학자인 로버트 B. 러플린에게 노벨 물리학상이 수여되었다.

7. 응용

양자 홀 효과는 매우 정밀한 측정을 가능하게 한다는 특징을 가지고 있다. 실제로 측정된 홀 전도도는 10억 분의 1보다 더 정확하게 e²/h^영어의 정수배 또는 분수배로 나타난다.^[5] 이는 클라우스 폰 클리칭이 발견한 정확한 양자화를 기념하여 이름 붙여진 폰 클리칭 상수( $R_K$ )를 기반으로 한 새로운 실용적인 표준 전기 저항 정의를 가능하게 했다.

1975년 안도 츠네야 등이 양자 홀 효과를 이론적으로 제시했고, 1980년 클라우스 폰 클리칭 등이 처음으로 실험적으로 관측했다. $R_K = \frac{h}{e^2}$ 를 '''폰 클리칭 상수'''라고 한다.

양자 홀 효과는 양자 전기역학에서 기본적으로 중요한 값인 미세구조 상수를 매우 정밀하게 독립적으로 결정할 수 있게 해준다.

1982년 다니엘 추이, 호르스트 루트비히 슈퇴르머, 아서 고사드 등은 분수 양자 홀 효과를 발견했다. 1998년 슈퇴르머, 추이, 로버트 B. 러플린은 이 업적으로 노벨 물리학상을 수상했다.

양자 홀 효과는 이차원 전자계뿐만 아니라 광자에서도 관측될 수 있다. 광자는 고유한 전하가 없지만, 이산적인 광학 공진기와 결합 위상 또는 자리 위상을 조작함으로써 인공적인 자기장을 생성할 수 있다.^[16]^[17]^[18]^[19]^[20]

7. 1. 전기 저항 표준

홀 전도도(

G_{xy} = 1/R_{xy}

)의 양자화는 매우 정밀하다는 중요한 특징을 가지고 있다.^[4] 실제 측정된 홀 전도도는 10억분의 1보다 더 정확하게

\frac{e^2}{h}

의 정수배 또는 분수배로 나타난다.^[5] 이는 '''폰 클리칭 상수'''(

R_K

)를 기반으로 한 새로운 실용적인 표준 전기 저항 정의를 가능하게 했다. 폰 클리칭 상수는 정확한 양자화를 발견한 클라우스 폰 클리칭의 이름을 따서 명명되었다. 양자 홀 효과는 또한 양자 전기역학에서 기본적으로 중요한 값인 미세구조 상수를 매우 정밀하게 독립적으로 결정할 수 있게 해준다.

1990년, 전 세계 저항 보정에 사용하기 위한 고정된 기존 값

R_{K-90}

이 정의되었다. 2018년 11월 16일, 제26차 국제도량형총회는 플랑크 상수(''h'')와 기본 전하량(''e'')의 정확한 값을 고정하기로 결정했고,^[6] 1990년 기존 값을 정확한 영구 값(내재적 표준)

R_K = \frac{h}{e^2}

로 대체했다.

1975년 안도 츠네야 등이 양자 홀 효과를 이론적으로 제시했고, 1980년 클라우스 폰 클리칭 등이 처음으로 실험적으로 관측했다.

R_K = \frac{h}{e^2}

를 '''폰 클리칭 상수'''라고 한다. 플랑크 상수(''h'')와 기본 전하량(''e'')는 2019년 5월 이후로 정의 상수이므로 폰 클리칭 상수에는 불확정도가 없다.^[31]

정수 양자 홀 효과(양자화된 홀 저항을 이용)는 전기 저항 표준으로 정하거나, 미세 구조 상수 결정에 사용된다.

7. 2. 위상 양자 컴퓨팅

1982년, 다니엘 추이, 호르스트 루트비히 슈퇴르머, 아서 고사드 등은 고전자이동도 트랜지스터(HEMT)의 전자계에 강한 자기장(10 T 이상)을 가하고 1 K 이하로 냉각하여 전기 저항률을 측정, 홀 저항률 ρ_xy가 평탄한 영역(플래토) 외에 새로운 플래토를 발견했다. 여기서 저항률로부터 홀 전도율 σ_xy를 계산한 결과,

:

\sigma_{xy}=-\frac{p}{q}\cdot\frac{e^2}{h}

를 얻었다. 여기서 p, q는 정수이며, q가 3 이상의 홀수인 경우(1/3, 2/3, 1/5, 2/5, 3/5, 2/7 등)를 '''분수 양자 홀 효과'''라고 명명했다.

분수 양자 홀 효과는 전자 간의 쿨롱 포텐셜이 불순물 포텐셜을 압도하는 경우에 발생한다. 따라서 이 효과가 관측되는 것은 시료가 불순물을 최대한 줄이고 이종접합 계면이 양질인 시료에 한정된다.

1998년 호르스트 루트비히 슈퇴르머, 다니엘 추이와 이론물리학자인 로버트 B. 러플린에게 노벨 물리학상이 수여되었다.

7. 3. 기타 응용

양자 홀 효과는 이차원 전자계에서 관측될 뿐만 아니라, 광자에서도 관측될 수 있다. 광자는 고유한 전하를 가지고 있지 않지만, 이산적인 광학 공진기와 결합 위상 또는 자리 위상을 조작함으로써 인공적인 자기장을 생성할 수 있다.^[16]^[17]^[18]^[19]^[20] 이 과정은 여러 거울 사이에서 반사되는 광자의 은유를 통해 표현될 수 있다. 여러 거울을 가로질러 빛을 쏘면 광자는 경로가 바뀌고, 각운동량에 비례하는 추가적인 위상을 얻는다. 이는 마치 자기장 속에 있는 것과 같은 효과를 만든다.

8. 수학적 관계

홀 전도도( $G_{xy}= 1/R_{xy}$ )의 양자화는 매우 정밀하다는 중요한 특징을 가지고 있다.^[4] 실제 측정값은 10억분의 1보다 더 정확하게 ''e''²/''h''^영어의 정수배 또는 분수배로 나타난다.^[5] 이는 '''폰 클리칭 상수'''( $R_K$ )에 의해 주어지는 저항 양자를 기반으로 한 새로운 실용적인 표준 전기 저항의 정의를 가능하게 했다. 이 상수는 정확한 양자화를 발견한 클라우스 폰 클리칭의 이름을 따서 명명되었다. 양자 홀 효과는 또한 양자 전기역학에서 기본적으로 중요한 값인 미세구조 상수를 매우 정밀하게 독립적으로 결정할 수 있게 해준다.

1990년, 전 세계 저항 보정에 사용하기 위한 고정된 기존 값 ( $R_{K-90}$ )이 정의되었다. 2018년 11월 16일, 제26차 국제도량형총회는 플랑크 상수( $h$ )와 기본 전하( $e$ )의 정확한 값을 고정하기로 결정했고,^[6] 1990년 기존 값을 정확한 영구 값(내재적 표준) ( $R_K = h/e^2$ )로 대체했다.

1975년 안도 츠네야 등이 이론적으로 제시하였고, 1980년 클라우스 폰 클리칭 등이 처음으로 실험적으로 관측하였다. $R_K = h/e^2$ 를 '''폰 클리칭 상수'''라고 한다. 플랑크 상수( $h$ )와 기본 전하량( $e$ )는 2019년 5월 이후로 정의 상수이므로 폰 클리칭 상수에는 불확정도가 없다.^[31] 15자리 숫자는 $25812.8074593045 \Omega$ 이다.^[32] 2018년 CODATA 권장값은 $25812.80745 \Omega$ 로 10자리로 표시하고 있다.^[33]

정수 양자 홀 효과(양자화된 홀 저항을 이용)는 전기 저항 표준으로 정하거나, 미세 구조 상수의 결정에 사용된다.

정수 양자 홀 효과는 위상 물질에 대한 수리물리학적 접근에서도 기본적인 대상이며, $e^2/h$ 의 짝수 배뿐만 아니라 홀수 배가 허용되는 것은 전자가 수학적으로 스피너(spinor)라는, 360도 회전에서는 원래 상태로 돌아오지 않고 720도 회전에서야 처음으로 원래 상태로 돌아오는 것으로 기술되는 것에 더하여, 4차원 스핀 다양체의 교차 형식이 짝수라는 수학적 사실과 관련이 있다는 것이 알려져 있다.

최근 시료의 품질 향상에 따라 다양한 이종접합 등에서 2차원 전자계가 구현되고 있다. 1979년 후지쓰의 미무라 타카시 등에 의해 고전자이동도 트랜지스터(HEMT)가 개발되었다. 1982년, 다니엘 추이, 호르스트 루트비히 슈퇴르머, 아서 고사드 등은 이 전자계에 강한 자기장(10 T 이상)을 가하고 1 K 이하로 냉각하여 전기 저항률 $\rho_{xx}$ , $\rho_{xy}$ 를 측정한 결과, 종래의 정수 양자 홀 효과에서 볼 수 있었던 홀 저항률 $\rho_{xy}$ 가 평탄한 영역 외에 새로운 플래토를 발견했다. 거기서 저항률로부터 홀 전도율 $\sigma_{xy}$ 를 계산한 결과,

: $\sigma_{xy}=-\frac{p}{q}\cdot\frac{e^2}{h}$

를 얻었다. 여기서 p, q는 정수이며, q가 3 이상의 홀수인 경우(1/3, 2/3, 1/5, 2/5, 3/5, 2/7 등)를 '''분수 양자 홀 효과'''라고 명명했다.

정수 양자 홀 효과의 원인은 불순물 포텐셜에 의한 전자의 국재화이지만, 분수 양자 홀 효과는 전자 간의 쿨롱 포텐셜이 불순물 포텐셜을 압도하는 경우에 발생한다. 따라서 분수 양자 홀 효과가 관측되는 것은 시료가 불순물을 최대한 줄이고 이종접합 계면이 양질인 시료에 한정된다.

1998년 호르스트 루트비히 슈퇴르머, 다니엘 추이와 이론물리학자인 로버트 B. 러플린에게 노벨 물리학상이 수여되었다.

8. 1. 위상 양자수

홀 효과에 나타나는 정수는 위상 양자수의 한 예시이다. 이 수는 수학적으로 제1 체르ㄴ 수로 알려져 있으며, 베리 위상과 밀접한 관계가 있다. 이와 관련하여 매우 흥미로운 모델은 호프슈타터의 나비인 아즈벨-해퍼-호프슈타터 모델이다. 세로축은 자기장의 세기이고, 가로축은 전자 밀도에 의해 결정되는 화학 포텐셜이다. 색깔은 정수 양자 홀 전도도를 나타낸다. 따뜻한 색은 양의 정수를 나타내고, 차가운 색은 음의 정수를 나타낸다.

8. 2. 호프슈타터의 나비

홀 효과에 나타나는 정수들은 위상 양자수의 한 예시이다. 수학적으로는 첫 번째 체르ㄴ 수로 알려져 있으며, 베리 위상과 밀접한 관련이 있다. 이러한 맥락에서 매우 흥미로운 모델은 그림에 표시된 호프슈타터의 나비인 아즈벨-해퍼-호프슈타터 모델이다. 세로축은 자기장의 세기이고, 가로축은 전자 밀도를 고정하는 화학퍼텐셜이다. 색상은 정수 홀 전도도를 나타낸다. 따뜻한 색상은 양의 정수를, 차가운 색상은 음의 정수를 나타낸다. 그러나 이러한 양자화된 홀 전도도 영역에서 상태 밀도는 0이므로 실험에서 관찰되는 플래토를 생성할 수 없다. 상전이 다이어그램은 프랙탈이며 모든 스케일에서 구조를 갖는다. 그림에는 명백한 자기 유사성이 있다.

물리적 메커니즘과 관련하여 불순물 및/또는 특정 상태(예: 에지 전류)는 '정수' 및 '분수' 효과 모두에 중요하다. 또한, 분수 양자 홀 효과에서는 쿨롱 상호작용도 필수적이다. 정수 및 분수 양자 홀 효과 사이의 관찰된 강한 유사성은 전자가 짝수 개의 자기 플럭스 양자와 결합 상태를 형성하는 경향으로 설명되는데, 이를 ''복합 페르미온''이라고 한다.^[1]

8. 3. 보어 원자 모델과의 관계

폰 클리칭 상수의 값은 보어 모형 내의 단일 원자 수준에서 이미 얻을 수 있다. 사이클로트론 운동 중 원형 궤도에서 원심력은 횡방향으로 유도된 전압과 홀 효과를 담당하는 로렌츠 힘에 의해 균형을 이루지만, 보어 원자의 쿨롱 전위차를 단일 원자 홀 전압으로, 원 위의 주기적인 전자 운동을 홀 전류로 볼 수 있다. 단일 원자 홀 전류를 단일 전자 전하

e

가 각속도

\omega

로 케플러 회전을 하는 속도로 정의하면 다음과 같다.

:

I = \frac{\omega e}{2\pi},

유도된 홀 전압은 전자 궤도점과 무한대에서의 수소 원자핵 쿨롱 전위의 차이로 나타낼 수 있다.

:

U=V_\text{C}(\infty) - V_\text{C}(r) = 0 - V_\text{C}(r) = \frac{e}{4\pi\epsilon_0 r}

정의된 보어 궤도 홀 저항의 양자화는 폰 클리칭 상수의 단위로 나타낼 수 있다.

:

R_\text{Bohr}(n) = \frac{U}{I} = n\frac{h}{e^2}

이는 보어 원자의 경우 정수 ''n''에 대해 선형적이지만 역수 관계는 아니다.

참조

_[1] 논문 The quantum Hall effect continues to reveal its secrets to mathematicians and physicists 2020-07-29
_[2] 논문 Quantum Hall physics: Hierarchies and conformal field theory techniques 2017-04-00
_[3] 서적 Quantum Hall Effects: Recent Theoretical and Experimental Developments World Scientific
_[4] 논문 Developments in the quantum Hall effect https://royalsociety[...] 2005-09-15
_[5] 논문 Precision comparison of the quantum Hall effect in graphene and gallium arsenide https://iopscience.i[...] 2012-06-01
_[6] 웹사이트 26th CGPM Resolutions https://www.bipm.org[...] 2018-11-19
_[7] 논문 In Praise of Exact Quantization https://www.science.[...] 2010-00-00
_[8] 웹사이트 Haldane nobel prize Lecture https://www.nobelpri[...]
_[9] 서적 Composite Fermions Cambridge University Press 2012-04-19
_[10] 웹사이트 Quantum Hall Effect http://www.damtp.cam[...]
_[11] 논문 Surface Protection and Selective Masking during Diffusion in Silicon https://iopscience.i[...] 1957-00-00
_[12] 논문 Silicon-Silicon Dioxide Surface Device https://doi.org/10.1[...] 1961-00-00
_[13] 서적 History of Semiconductor Engineering Springer-Verlag Berlin Heidelberg 2007-00-00
_[14] 논문 Focus: Landmarks—Accidental Discovery Leads to Calibration Standard https://physics.aps.[...] 2015-05-15
_[15] 서적 The physics of low-dimension
_[16] 논문 Analogs of quantum-Hall-effect edge states in photonic crystals https://link.aps.org[...] 2008-09-23
_[17] 논문 Realizing effective magnetic field for photons by controlling the phase of dynamic modulation http://www.nature.co[...] 2012-11-00
_[18] 논문 Synthetic Landau levels for photons http://www.nature.co[...] 2016-06-00
_[19] 논문 Haldane quantum Hall effect for light in a dynamically modulated array of resonators https://opg.optica.o[...] 2016-02-20
_[20] 논문 A single photonic cavity with two independent physical synthetic dimensions https://www.science.[...] 2020-01-03
_[21] 논문 Quantized Hall conductivity in two dimensions
_[22] 논문 Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the 'Parity Anomaly'
_[23] 논문 Theory of Hall effect in a two-dimensional electron system
_[24] 논문 Hall effect in silicon MOS inversion layers under strong magnetic fields 1978-00-00
_[25] 논문 New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance
_[26] 논문 Quantization of particle transport
_[27] 논문 Room-temperature quantum Hall effect in graphene
_[28] 논문 Quantum Hall effect in polar oxide heterostructures
_[29] 논문 A Method for simulating chiral fermions on the lattice
_[30] 논문 Chern–Simons currents and chiral fermions on the lattice
_[31] OEIS A248510
_[32] 간행물 改定国際単位系における電気標準 https://unit.aist.go[...] 産総研　計量標準総合センター　物理計測標準研究部門
_[33] 문서 CODATA Value
_[34] 서적 The Quantum Hall Effect Springer
_[35] 논문 New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance
_[36] 논문
_[37] 논문
_[38] 논문

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com