데데킨트 에타 함수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 성질
4. 다른 함수와의 관계
5. 에타 몫
참조

1. 개요

데데킨트 에타 함수는 열린 상반 평면에서 정의되는 복소 함수로, 모듈러 형식의 일종이다. 에타 함수는 무한 곱과 거듭제곱 급수로 표현되며, 함수 방정식, 극점과 영점, 특별한 값, 조합론적 항등식 등 다양한 성질을 갖는다. 특히 모듈러 판별식, 오일러 함수, 야코비 세타 함수 등 다른 함수와의 관계가 깊다. 에타 몫은 에타 함수들의 곱과 몫으로 정의되며, 다양한 모듈러 형식을 표현하는 데 사용된다.

2. 정의

열린 상반평면을 $\mathbb H$ 라고 쓰자. '''데데킨트 에타 함수''' $\eta\colon\mathbb H\to\mathbb C$ 는 다음과 같은 함수이다.

: $\eta(\tau)=\exp(\pi i\tau/12)\prod_{n=1}^\infty\left(1-\exp(2n\pi i\tau)\right)$ .

보통 $q(\tau)=\exp(2\pi i\tau)$ 를 정의한다. 그렇다면 에타 함수의 정의는 다음과 같이 더 간단해진다.

: $\eta(\tau)=q^{1/24}\prod_{n=1}^\infty(1-q^n)$ .

복소수 $\tau$ 에 대해 $\operatorname{Im}(\tau)>0$ 일 때, $q=e^{2\pi i\tau}$ 라고 하자. 그러면 에타 함수는 다음과 같이 정의된다.

: $\eta(\tau) = e^\frac{\pi i \tau}{12} \prod_{n=1}^\infty \left(1-e^{2 n\pi i \tau}\right) = q^\frac{1}{24} \prod_{n=1}^\infty \left(1 - q^n\right) .$

에타 함수는 상반평면에서 정칙 함수이지만, 그 이상으로는 해석적으로 확장될 수 없다.

오일러 함수는 다음과 같이 정의된다.

: $\begin{align}\phi(q) &= \prod_{n=1}^\infty \left(1-q^n\right) \\&= q^{-\frac{1}{24}} \eta(\tau),\end{align}$

오각수 정리에 의해 위 식은 다음과 같은 거듭제곱 급수를 갖는다.

: $\phi(q)=\sum_{n=-\infty}^\infty (-1)^n q^\frac{3n^2-n}{2}.$

$\mathfrak{I} (\tau )>0$ 에 대한 오일러 오각수 정리를 사용하여 에타 함수를 다음과 같이 표현할 수 있다.

: $\eta(\tau)=\sum_{n=-\infty}^\infty e^{\pi i n}e^{3\pi i \left(n+\frac{1}{6}\right)^2 \tau}.$

이것은 에타 함수의 정의와 함께 오일러 오각수 정리에서 $x=2\pi i \tau$ 를 사용하여 증명할 수 있다.

3. 성질

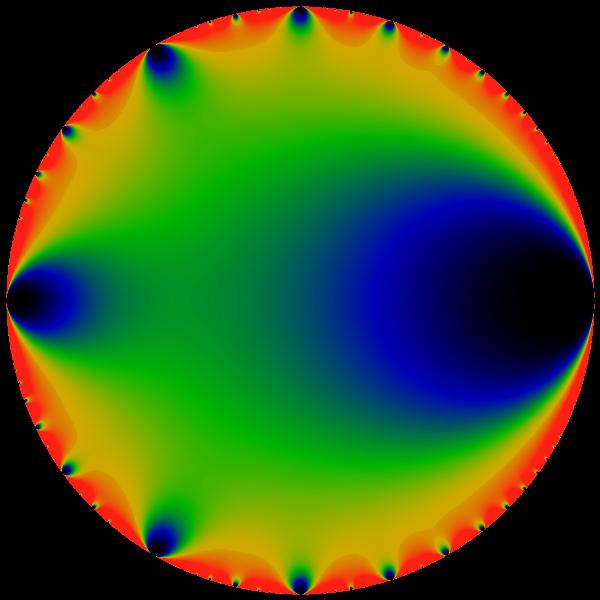
데데킨트 에타 함수는 열린 상반평면에서 정칙함수이나, 복소 평면 전체로 해석적 연속을 할 수 없다.

에타 함수는 다음과 같은 함수 방정식을 만족한다.^[1]

: $\begin{align}\eta(\tau+1) &=e^\frac{\pi i}{12}\eta(\tau),\\\eta\left(-\frac{1}{\tau}\right) &= \sqrt{-i\tau}\, \eta(\tau).\,\end{align}$

이러한 함수 방정식 때문에 에타 함수는 모듈러 군의 메타플렉틱 이중 피복의 어떤 지표에 대해 무게 1/2와 레벨 1을 갖는 모듈러 형식이며, 다른 모듈러 형식을 정의하는 데 사용될 수 있다.

야코비 삼중곱에 따르면 에타 함수는 인수의 특정한 값에 대해 (인자를 제외하고) 야코비 세타 함수와 관련된다.^[2]

: $\eta(\tau) = \sum_{n=1}^\infty \chi(n) \exp\left(\frac {\pi i n^2 \tau}{12}\right),$

여기서 χ(''n'')는 모듈로 12의 디리클레 지표로, χ(±1) = 1이고 χ(±5) = -1이다.

오일러 함수는 다음과 같이 정의되며,

: $\begin{align}\phi(q) &= \prod_{n=1}^\infty \left(1-q^n\right) \\&= q^{-\frac{1}{24}} \eta(\tau),\end{align}$

오각수 정리에 의해 다음과 같은 거듭제곱 급수를 갖는다.

: $\phi(q)=\sum_{n=-\infty}^\infty (-1)^n q^\frac{3n^2-n}{2}.$

에타 함수는 멱급수에서 수치적으로 계산하기 쉽기 때문에, 가능하면 다른 함수를 에타 함수로 표현하는 것이 계산에 도움이 된다. 에타 함수의 곱과 몫(에타 몫)은 다양한 모듈러 형식을 표현하는 데 사용될 수 있다.

오일러 함수와 에타 함수 사이의 추가 인자 q^1/24는 시각적으로 거의 차이가 없으므로, 위 그림은 q의 함수로서 에타 함수를 나타낸다고 간주할 수 있다.

3. 1. 함수 방정식

데데킨트 에타 함수는 무게가 ½이고 준위가 1인 모듈러 형식이다. 즉, 모듈러 군 Γ₀(1)에 대하여 다음과 같은 변환 성질을 만족한다.^[1]

:η(τ+1) = exp(πi/12)η(τ)

:η(-1/τ) = √(-iτ)η(τ)

더 일반적으로, 뫼비우스 변환 τ ↦ (aτ + b) / (cτ + d) (ad - bc = 1, c ≥ 0)에 대해 다음과 같은 성질을 만족한다.

:η((aτ + b) / (cτ + d)) = ε(a, b, c, d)(cτ + d)^½η(τ)

여기서 ε(a, b, c, d)는 다음과 같이 정의된다.

:ε(a, b, c, d) = exp(iπb/12) (c = 0, d = 1인 경우)

:ε(a, b, c, d) = exp(iπ((a + d) / (12c) - s(d, c) - 1/4)) (c > 0인 경우)

이때, s(h, k)는 데데킨트 합(Dedekind sum)으로 다음과 같이 정의된다.^[12]

:s(h,k) = Σ_n=1^k-1 (n/k)(hn/k - ⌊hn/k⌋ - 1/2)

3. 2. 극점과 영점

\image \tau>0

이면

\left|e^{2\pi{i}\tau}\right|<1

이므로, 다음과 같은 식이 성립한다.

:

\begin{align}\left|\log\eta(\tau)\right|&=\frac{\left|\pi{i}\tau\right|}{12}+\sum_{m=1}^{\infty}\left|\log(1-e^{2\pi{i}\tau{m}})\right|\\&=\frac{\left|\pi{i}\tau\right|}{12}+\sum_{m=1}^{\infty}\sum_{n=1}^{\infty}\frac{\left|e^{2\pi{i}\tau{mn}}\right|}{n}\\&=\frac{\left|\pi{i}\tau\right|}{12}+\sum_{n=1}^{\infty}\frac{\left|e^{2\pi{i}\tau{n}}\right|}{n(1-\left|e^{2\pi{i}\tau{n}}\right|)}\\&\le\frac{\left|\pi{i}\tau\right|}{12}+\frac{1}{1-|e^{2\pi{i}\tau}|}\sum_{n=1}^{\infty}\frac

{n}\\&\le\frac{\left|\pi{i}\tau\right|}{12}-\frac{\log(1-|e^{2\pi{i}\tau}|)}{1-|e^{2\pi{i}\tau}|}\\\end{align}

따라서 데데킨트 에타 함수는 상반 평면에서 극점과 영점을 갖지 않는다. 그러나

\tau=q/r

이 유리수이면

1-e^{2\pi{i}\tau{r}}=0

이므로, 에타 함수는 실수 축 위에 조밀한 영점을 가진다.

3. 3. 특별한 값

함수 방정식 등을 사용하여 다음과 같은 특별한 값들을 계산할 수 있다.

:

\eta(i)=\frac{\Gamma(1/4)}{2 \pi ^{3/4}}

:

\eta(i/2)=\frac{\Gamma(1/4)}{2^{7/8} \pi ^{3/4}}

:

\eta(2i)=\frac{\Gamma(1/4)}{2^{11/8} \pi ^{3/4}}

:

\eta(4i)=\frac{\sqrt[4]{-1+\sqrt{2}}\Gamma(1/4)}{2^{29/16} \pi ^{3/4}}

여기서

\Gamma(1/4)\approx3.626

는 감마 함수이다.

위 오일러 함수와의 관계와 오일러 함수의 특수한 값을 통해 다음을 쉽게 유도할 수 있다.

:

\eta(i)=\frac{\Gamma \left(\frac14\right)}{2 \pi ^\frac34}

:

\eta\left(\tfrac{1}{2}i\right)=\frac{\Gamma \left(\frac14\right)}{2^\frac78 \pi ^\frac34}

:

\eta(2i)=\frac{\Gamma \left(\frac14\right)}{2^\frac{11}{8} \pi ^\frac34}

:

\eta(3i)=\frac{\Gamma \left(\frac14\right)}{2\sqrt[3]{3} \left(3+2 \sqrt{3}\right)^\frac{1}{12} \pi ^\frac34}

:

\eta(4i)=\frac{\sqrt[4]{-1+\sqrt{2}}\, \Gamma \left(\frac14\right)}{2^\frac{29}{16} \pi ^\frac34}

:

\eta\left(e^\frac{2 \pi i}{3}\right)=e^{-\frac{\pi i}{24}} \frac{\sqrt[8]{3} \, \Gamma \left(\frac13\right)^\frac32}{2 \pi }

3. 4. 조합론적 항등식

아핀 리 대수의 대수적 지표 이론은 에타 함수에 대한 이전에 알려지지 않은 많은 수의 항등식을 발생시킨다. 이러한 항등식은 바일-카츠 지표 공식, 더 구체적으로는 소위 "분모 항등식"에서 파생된다.^[3] 지표 자체는 야코비 세타 함수의 일반화를 구성할 수 있게 해주며, 이는 모듈러 군에서 변환된다. 이것이 항등식을 유도하는 요인이다. 그러한 새로운 항등식의 예^[3]는 다음과 같다.

:

\eta(8\tau)\eta(16\tau) = \sum_{m,n\in \mathbb{Z} \atop m \le |3n|}(-1)^m q^{(2m+1)^2 - 32n^2}

여기서 ''q''는 모듈의 q-유사체 또는 "변형"이다.

4. 다른 함수와의 관계

에타 함수는 모듈러 판별식, 오일러 함수, 야코비 세타 함수 등 다른 함수들과 밀접하게 관련되어 있다.

에타 함수를 24제곱하고 $(2\pi)^{12}$ 를 곱하면 모듈러 판별식 $\Delta(\tau)$ 를 얻는다.^[1]

: $\Delta(\tau) = (2\pi)^{12}\eta^{24}(\tau)$

이는 모듈러 형식의 한 예이다.

에타 함수는 오일러 함수Euler function^영어 $\phi(q)$ 와 다음과 같은 관계를 갖는다.^[2]

: $\phi(q) = q^{-\frac{1}{24}} \eta(\tau)$

에타 함수는 야코비 세타 함수를 이용하여 다음과 같이 표현할 수 있다.^[2]

: $\eta(\tau) = e^\frac{\pi i \tau}{12}\vartheta\left(\frac{\tau+1}{2}; 3\tau\right).$

4. 1. 모듈러 판별식

에타 함수를 24제곱하고

(2\pi)^{12}

를 곱하면 모듈러 판별식 Δ(τ)를 얻는다.^[11]

:

\Delta(\tau) = (2\pi)^{12}\eta^{24}(\tau)

24라는 수는 24차원 리치 격자 등 다른 경우와의 연관성을 통해 이해할 수 있다.

thumb

4. 2. 오일러 함수

에타 함수는 오일러 함수Euler function^영어 φ(q)와 다음과 같은 관계를 갖는다.

:

\begin{align}\phi(q) &= \prod_{n=1}^\infty \left(1-q^n\right) \\&= q^{-\frac{1}{24}} \eta(\tau),\end{align}

^[2]

오일러 함수의 거듭제곱 급수는 오각수 정리에 의해 다음과 같이 표현된다.

:

\phi(q)=\sum_{n=-\infty}^\infty (-1)^n q^\frac{3n^2-n}{2}.

\mathfrak{I} (\tau )>0

일 때, 오일러 오각수 정리를 사용하여 에타 함수를 다음과 같이 표현할 수 있다.

:

\eta(\tau)=\sum_{n=-\infty}^\infty e^{\pi i n}e^{3\pi i \left(n+\frac{1}{6}\right)^2 \tau}.

이는 에타 함수의 정의와 오일러 오각수 정리에서

x=2\pi i \tau

를 사용하여 증명할 수 있다.

오일러 함수의 절댓값을 나타낸 그림이다. 에타 함수와 오일러 함수는

q^{-\frac{1}{24}}

인자만큼의 차이가 있지만, 그림에서는 거의 차이가 나지 않으므로, 이 그림은 q의 함수로서 에타 함수를 나타낸다고 볼 수 있다.

4. 3. 야코비 세타 함수

에타 함수는 야코비 세타 함수를 이용하여 표현할 수 있다.^[2]

:

\eta(\tau) = e^\frac{\pi i \tau}{12}\vartheta\left(\frac{\tau+1}{2}; 3\tau\right).

오일러 분할 항등식을 사용하면 다음과 같이 표현할 수도 있다.

:

\eta^3\left(\tau\right) = \frac{1}{2}\vartheta_2\left(0,\tau\right)\vartheta_3\left(0,\tau\right)\vartheta_4\left(0,\tau\right)

:

\eta(\tau) = \frac{1}{\sqrt{3}}\vartheta_2\left(\frac{1}{6},\frac{\tau}{3}\right)

5. 에타 몫

에타 몫은 다음과 같은 형식의 몫으로 정의되는 함수이다.

: $\prod_{0$

여기서 `d`는 음이 아닌 정수이고 `r_d`는 임의의 정수이다. 허수 이차 인수를 갖는 에타 몫의 선형 결합은 대수적 수일 수 있으며, 에타 몫의 결합은 심지어 정수일 수도 있다. 예를 들어 다음과 같이 정의한다.

: $\begin{align}j(\tau)&=\left(\left(\frac{\eta(\tau)}{\eta(2\tau)}\right)^{8}+2^8 \left(\frac{\eta(2\tau)}{\eta(\tau)}\right)^{16}\right)^3 \\[6pt]j_{2A}(\tau)&=\left(\left(\frac{\eta(\tau)}{\eta(2\tau)}\right)^{12}+2^6 \left(\frac{\eta(2\tau)}{\eta(\tau)}\right)^{12}\right)^2 \\[6pt]j_{3A}(\tau) &=\left(\left(\frac{\eta(\tau)}{\eta(3\tau)}\right)^{6}+3^3 \left(\frac{\eta(3\tau)}{\eta(\tau)}\right)^{6}\right)^2 \\[6pt]j_{4A}(\tau) &=\left(\left(\frac{\eta(\tau)}{\eta(4\tau)}\right)^{4} + 4^2 \left(\frac{\eta(4\tau)}{\eta(\tau)}\right)^{4}\right)^2 = \left(\frac{\eta^2(2\tau)}{\eta(\tau)\,\eta(4\tau)} \right)^{24}\end{align}$

이것은 베버 모듈 함수의 24제곱으로 표현된다. 그러면,

: $\begin{align}j\left(\frac{1+\sqrt{-163}}{2}\right) &= -640320^3, & e^{\pi\sqrt{163}} &\approx 640320^3+743.99999999999925\dots \\[6pt]j_{2A}\left(\frac{\sqrt{-58}}{2}\right) &= 396^4, & e^{\pi\sqrt{58}}&\approx 396^4-104.00000017\dots \\[6pt]j_{3A}\left(\frac{1+\sqrt{-\frac{89}{3}}}{2}\right) &= -300^3, & e^{\pi\sqrt\frac{89}{3}}&\approx 300^3+41.999971\dots \\[6pt]j_{4A}\left(\frac{\sqrt{-7}}{2}\right)&=2^{12}, & e^{\pi\sqrt{7}}&\approx 2^{12}-24.06\dots\end{align}$

등과 같이 되며, 라마누잔-사토 급수에 나타나는 값들이다.

에타 몫은 직접 계산하고 표현하기 어려운 모듈 형식의 기저를 설명하는 데 유용할 수 있다. 1993년, 바실 고든과 김 휴즈는 위에 주어진 형식의 에타 몫, 즉 $\prod_{0 가 다음을 만족하면$

: $\sum_{0$

합동 부분군 `Γ₀(N)`에 대한 가중치 `k` 모듈 형식이다(단, 정칙성까지). 여기서^[4]

: $k=\frac12\sum_{0$

이 결과는 2019년에 `N`이 6과 서로소 정수일 경우 역이 성립하도록 확장되었으며, 원래 정리가 모든 정수 `N`에 대해 정확한지 여부는 아직 열려 있다.^[5] 또한, 이것은 모든 모듈 에타 몫이 레벨 `n` 합동 부분군에 대한 모든 합동 부분군의 모듈 형식이어야 한다는 것을 나타내도록 확장된다. 이러한 정리는 모듈 에타 몫을 특징짓는 반면, 정칙성의 조건은 제라르 리조와 이브 마틴의 연구에서 나온 정리를 사용하여 별도로 확인해야 한다.^[6]^[7]

`η_g`가 정수 `N`에 대한 위의 조건을 만족하는 에타 몫이고 `c`와 `d`가 서로소 정수이면, 첨점 `c/d`에 대한 소멸 차수는 `Γ₀(N)`에 상대적이다.

: $\frac{N}{24}\sum_{0<\delta|N} \frac{\gcd\left(d,\delta\right)^2r_\delta}{\gcd\left(d,\frac{N}{\delta}\right)d\delta} .$

이러한 정리들은 정칙 모듈 에타 몫을 생성하는 효과적인 수단을 제공하지만, 이것이 벡터 공간의 모듈 형식과 첨점 형식의 기저를 구성하는 데 충분하지 않을 수 있다. 고려할 모듈 에타 몫의 수를 제한하기 위한 유용한 정리는 `Γ₀(N)`에 대한 정칙 가중치 `k` 모듈 에타 몫이 다음을 만족해야 한다고 명시한다.

: $\sum_{0$

여기서 `ord_p(N)`는 `p^m`이 `N`을 나누는 가장 큰 정수 `m`을 나타낸다.^[8]

이러한 결과는 모듈 에타 몫으로 확장될 수 있는 모듈 형식 공간의 여러 특징으로 이어진다.^[8] 모듈 형식의 링에 대한 등급 링 구조를 사용하여, 에타 몫의 ` $\mathbb{C}$ `-선형 결합으로 구성된 모듈 형식의 벡터 공간의 기저를 계산할 수 있다. 예를 들어, `N`이 반소수라고 가정하면 모듈 형식의 에타 몫 기저 `M_k(Γ₀(N))`를 계산하는 데 다음과 같은 과정을 사용할 수 있다.^[5]

# 6과 서로소인 반소수 `N = pq`를 고정한다(즉, `p, q > 3`). 위의 정리를 사용하여 모든 모듈 에타 몫을 찾을 수 있으므로, 이를 알고리즘적으로 계산하는 것이 합리적이다.

# `M_k(Γ₀(N))`의 차원 `D`를 계산한다. 이는 기저를 형성하기 위해 계산해야 하는 선형 독립 모듈 에타 몫의 수를 알려준다.

# 고려할 에타 몫의 수를 줄인다. 반소수의 경우 다음 바운드를 사용하여 분할 수를 줄일 수 있다.

# : $\sum_{0$

# 및 `Γ₀(N)`의 첨점에서의 소멸 차수의 합이

# : $S:=\frac{(p+1)(q+1)}{6}$ 과 같아야 함을 알 수 있다.^[5]

# `S`의 모든 분할을 4-튜플로 찾는다(`Γ₀(N)`의 첨점은 4개이다). 그리고 이 중에서 고든과 휴즈의 조건을 만족하는 분할만 고려한다(소멸 차수를 지수로 변환할 수 있다). 이러한 각 분할은 고유한 에타 몫에 해당한다.

# 요소를 고유하게 식별하는 데 필요한 각 에타 몫의 `q`-확장에서 최소 항의 수를 결정한다(이는 슈름의 경계라고 하는 결과를 사용한다). 그런 다음 선형 대수를 사용하여 이러한 에타 몫 간의 최대 독립 집합을 결정한다.

# 아직 `D` 선형 독립 에타 몫을 찾지 못했다고 가정하고, 에타 몫의 약하게 정칙 에타 몫으로 확장되고, `M_k'−k(Γ₀(N))`가 에타 몫 `η_g`를 포함하는 적절한 벡터 공간 `M_k'(Γ₀(N))`를 찾는다.^[8]

# 가중치 `k`를 갖지만 계산된 에타 몫의 스팬에 없는 모듈 형식 `f`를 가져와서, `f η_g`를 `M_k'(Γ₀(N))`의 에타 몫의 선형 결합으로 계산한 다음 `η_g`로 나눈다. 그 결과는 원하는 대로 `f`를 에타 몫의 선형 결합으로 표현한 것이다. 기저가 형성될 때까지 이것을 반복한다.

데데킨트 에타 함수에 대한 6300개 이상의 곱 항등식 모음은 Michael Somos의 웹사이트의 웨이백 머신에서 표준화된 형식으로 제공된다.^[9]

참조

_[1] 논문 A Simple Proof of ''η''(−1/''τ'') {{error|Error: The retired template {{tn|1==}} has been transcluded; see [[mw:Help:Magic words#Escaped characters]] for details. To fix this, use only the code {{Magic word|1==}} to generate the = character.}} ''η''(''τ''){{sqrt|''τ''/''i''}}
_[2] 서적 Automorphic Forms and Representations Cambridge University Press
_[3] 서적 Affine Lie Algebras and Quantum Groups Cambridge University Press
_[4] 서적 A Tribute to Emil Grosswald: Number Theory and Related Analysis American Mathematical Society 1993
_[5] 논문 Eta-quotients of prime or semiprime level and elliptic curves
_[6] 서적 Courbes modulaires de genre 1 U.E.R. Mathématique, Université Paris XI, Orsay 1974
_[7] 논문 Multiplicative ''η''-quotients
_[8] 논문 On spaces of modular forms spanned by eta-quotients
_[9] 웹사이트 Dedekind Eta Function Product Identities by Michael Somos http://eta.math.geor[...]
_[10] 웹사이트 Wolfram Mathworld: Dedekind Eta Function http://mathworld.wol[...]
_[11] 문서 Apostol 1990
_[12] 문서 Apostol 1990
_[13] 저널 A simple proof of $\eta(-1/\tau)=\eta(\tau)\sqrt{\tau/i}$ 1954-06

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com