맨위로가기

아핀 리 대수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

아핀 리 대수는 여러 가지 방법으로 정의될 수 있는 특수한 종류의 리 대수이다. 카츠-무디 대수의 특별한 경우이며, 단순 리 대수 계수의 로랑 다항식의 리 대수의 중심 확대, 또는 특정 프레셰 리 군의 리 대수의 부분 공간으로 정의될 수 있다. 아핀 리 대수는 유한 차원 단순 리 대수에 대응하는 루프 대수의 중심 확장으로 구성되며, 카르탕 행렬을 통해 카츠-무디 대수로 정의되기도 한다. 아핀 리 대수는 뒤틀린 아핀 리 대수를 포함하며, 기하학적 및 리 군을 통해 정의될 수도 있다.

아핀 리 대수는 대칭화 가능한 카츠-무디 대수이며, 킬링 형식과 근계의 구조를 갖는다. 콕서터 수와 쌍대 콕서터 수, 바일 군 등의 성질을 가지며, 표현론은 베르마 가군을 통해 전개된다. 아핀 리 대수는 딘킨 도표를 사용하여 분류할 수 있으며, 딘킨 도표는 untwisted와 twisted 형태로 나뉜다.

아핀 리 대수는 하이젠베르크 대수와 같은 예시를 가지며, 2차원 등각장론의 대칭 대수로 사용되는 등 끈 이론과 2차원 등각장론과 같은 분야에 응용된다. 아핀 리 대수는 빅토르 카츠와 로버트 무디에 의해 발견되었으며, 스가와라 구성, 공액류 구성 등 표현론과 관련된 연구가 이루어졌다.

더 읽어볼만한 페이지

  • 등각 장론 - 임계점 (열역학)
    임계점은 상평형 그림에서 액체와 기체, 또는 두 액체 상 사이의 경계가 사라지는 특정 온도와 압력의 지점으로, 액체-기체 임계점은 증기압 곡선의 종점에 해당하며, 그 이상의 온도에서는 압력을 가해도 액체 상태를 유지할 수 없는 지점이다.
  • 등각 장론 - 최소 모형 (등각 장론)
    최소 모형 (등각 장론)은 비라소로 대수를 기반으로 하며, 격자 모형의 임계 현상을 나타내는 특정 중심 전하 값을 갖는 2차원 등각장론의 한 종류이다.
  • 리 대수 - 베유 대수
    베유 대수는 체 K 위의 리 대수 g에 대하여 정의되는 미분 등급 대수이며, g의 쌍대 공간과 그 등급 이동으로 생성되는 외대수와 대칭 대수의 텐서곱으로 표현되고, 리 군의 분류 공간의 주다발의 무한소 형태를 나타내는 완전열과 관련이 있다.
  • 리 대수 - 직교 리 대수
    직교 리 대수는 가환환 K 위의 가군 V와 대칭 쌍선형 형식 B가 주어졌을 때, B(v,Mv) = 0을 만족하는 특정 조건을 만족하는 V의 자기 준동형들로 구성된 리 대수이다.
아핀 리 대수
개요
유형리 대수
연구 분야수학, 물리학
역사적 배경
창시자빅토르 카츠
창시 시기1968년
정의 및 성질
정의아핀 리 대수는 카츠-무디 대수의 특수한 경우다.
유한 차원 단순 리 대수에서 확장된 무한 차원 리 대수다.
특징중심 확장(central extension)을 포함한다.
바일 군이 아핀 바일 군이다.
분류꼬임형(twisted) 아핀 리 대수
꼬임없음형(untwisted) 아핀 리 대수
응용
관련 분야끈 이론
공형 장론
적분가능한 계
추가 정보
참고 문헌Infinite dimensional Lie algebras (영어) - Victor G. Kac
Affine Lie algebras and quantum groups: an introduction with applications in conformal field theory (영어) - Jürgen A. Fuchs
Beyond affine Lie algebras (영어) - I. B. Frenkel
Conformal field theory (영어) - P. Di Francesco, P. Mathieu, D. Sénéchal
Conformal field theory and topology (영어) - Toshitake Kohno
Loop groups (영어) - Andrew Pressley, Graeme Segal

2. 정의

아핀 리 대수는 여러 가지 방법으로 정의될 수 있지만, 핵심은 유한 차원 단순 리 대수의 구조를 확장하는 것이다. 이들은 서로 동치이다.

아핀 리 대수는 단순 리 대수 계수의 로랑 다항식의 리 대수의 중심 확대이다. 만약 \mathfrak{g}가 유한 차원 단순 리 대수라면, 이에 대응하는 아핀 리 대수 \hat{\mathfrak{g}}는 루프 대수 \mathfrak{g}\otimes\mathbb{C}[t,t^{-1}]의 중심 확장으로 구성되며, 1차원 중심 \mathbb{C}c를 갖는다. 여기서 \mathbb{C}[t,t^{-1}]는 변수 ''t''에 대한 로랑 다항식의 복소수 벡터 공간이다.

벡터 공간으로서,

:\widehat{\mathfrak{g}}=\mathfrak{g}\otimes\mathbb{C}[t,t^{-1}]\oplus\mathbb{C}c

이다. 리 괄호는 다음 공식으로 정의된다.

:[a\otimes t^n+\alpha c, b\otimes t^m+\beta c]=[a,b]\otimes t^{n+m}+\langle a|b\rangle n\delta_{m+n,0}c

모든 a,b\in\mathfrak{g}, \alpha,\beta\in\mathbb{C} 및 n,m\in\mathbb{Z}에 대해, 여기서 [a,b]는 리 대수 \mathfrak{g}에서의 리 괄호이고 \langle\cdot |\cdot\rangle는 \mathfrak{g}상의 카르탕-킬링 형식이다.

아핀 리 대수의 특정한 미분은 다음과 같이 정의된다.

:\delta (a\otimes t^m+\alpha c) = t{d\over dt} (a\otimes t^m)

대응하는 '''아핀 카츠-무디 대수'''는 [''d'', ''A''] = ''δ''(''A'')를 만족하는 추가 생성자 ''d''를 더하여 반직접 곱으로 정의된다.

2. 1. 카츠-무디 대수로서의 정의

카츠-무디 대수 가운데, 카르탕 행렬 A가 양의 준정부호 행렬이지만 양의 정부호 행렬이 아닌 것들이 아핀 리 대수이다. 즉, 아핀 리 대수 \mathfrak g가 n+1개의 단순근을 갖는다면, 그 카르탕 행렬은 (n+1)\times(n+1) 정사각 행렬이며 그 계수는 l이다.

2. 2. 대수적 구성

아핀 리 대수는 여러 방법으로 정의할 수 있는데, 이들은 서로 동치이다.

여기서는 유한 차원 단순 리 대수와 로랑 다항식을 이용하여 아핀 리 대수를 구성하는 방법을 설명한다. 이 과정에서 중심 확장이 핵심적인 역할을 한다.

복소수체 위의 유한 차원 이차 리 대수 (\stackrel\circ{\mathfrak g}^{\mathbb C},\langle |\rangle \colon\stackrel\circ{\mathfrak g}\otimes_K\stackrel\circ{\mathfrak g}^{\mathbb C}\to\mathbb C)가 주어졌다고 하자. (만약 \stackrel\circ{\mathfrak g}^{\mathbb C}가 반단순 리 대수라면, 이는 킬링 형식으로 잡을 수 있다.)

그렇다면, '''아핀 리 대수''' \hat{\mathfrak g}^{\mathbb C}는 K-벡터 공간으로서 다음과 같다.

:\hat{\mathfrak g}=\stackrel\circ{\mathfrak g}[\mathsf z,\mathsf z^{-1}]\oplus \mathbb C\mathsf k.

즉, \stackrel\circ{\mathfrak g}^{\mathbb C}의 계수를 가진 로랑 다항식 \mathfrak g^{\mathbb C}[\mathsf z,\mathsf z^{-1}]에 중심 확대 \mathsf k를 더한 것이다. \stackrel\circ{\mathfrak g}^{\mathbb C}[\mathsf z,\mathsf z^{-1}]는 대칭의 보존류들을, \mathsf k는 대칭의 변칙을 나타낸다.

\hat{\mathfrak g}^{\mathbb C} 위에는 다음과 같은 리 괄호를 정의한다. a,b\in\stackrel\circ{\mathfrak g}^{\mathbb C}라고 하면,

:[a\mathsf z^m,b\mathsf z^n]=[a,b]\mathsf z^{m+n}+\delta_{m+n,0}m\langle a|b\rangle\mathsf k

:[\mathsf k,a\mathsf z^n]=[\mathsf k,\mathsf k]=0

\mathsf k는 중심 원소이므로, 리 대수의 짧은 완전열

:0 \to \mathbb C\mathsf k \to \hat{\mathfrak g}^{\mathbb C} \to \stackrel\circ{\mathfrak g}^{\mathbb C} \otimes \mathbb C[\mathsf z,\mathsf z^{-1}] \to 0

이 존재한다.

만약 \mathfrak{g}가 유한 차원 단순 리 대수라면, 이에 대응하는 아핀 리 대수 \hat{\mathfrak{g}}는 루프 대수 \mathfrak{g}\otimes\mathbb{\Complex}[t,t^{-1}]의 중심 확장으로 구성되며, 1차원 중심 \mathbb{\Complex}c를 갖는다. 벡터 공간으로서,

:\widehat{\mathfrak{g}}=\mathfrak{g}\otimes\mathbb{\Complex}[t,t^{-1}]\oplus\mathbb{\Complex}c,

여기서 \mathbb{\Complex}[t,t^{-1}]는 변수 ''t''에 대한 로랑 다항식의 복소수 벡터 공간이다. 리 괄호는 다음 공식으로 정의된다.

:[a\otimes t^n+\alpha c, b\otimes t^m+\beta c]=[a,b]\otimes t^{n+m}+\langle a|b\rangle n\delta_{m+n,0}c

모든 a,b\in\mathfrak{g}, \alpha,\beta\in\mathbb{\Complex} 및 n,m\in\mathbb{Z}에 대해, 여기서 [a,b]는 리 대수 \mathfrak{g}에서의 리 괄호이고 \langle\cdot |\cdot\rangle는 \mathfrak{g}상의 카르탕-킬링 형식이다.

2. 2. 1. 실수 형태

\stackrel\circ{\mathfrak g}^{\mathbb C}가 실수 이차 리 대수 \stackrel\circ{\mathfrak g}^{\mathbb R}의 복소화라고 하자. 그렇다면, 복소수 아핀 리 대수 \stackrel\circ{\mathfrak g}^{\mathbb C}는 실수 리 대수로서 다음과 같은 자기 동형을 갖는다.

  • \mathsf z \mapsto \mathsf z^{-1}
  • \mathrm i \mapsto -\mathrm i
  • \mathsf k \mapsto \mathsf k
  • x \mapsto x \qquad\forall x\in \stackrel\circ{\mathfrak g}^{\mathbb R}


즉, 이는 두 복소수 벡터 공간 사이의 반선형(antilinear영어) 사상이다. 이 반선형 사상의 고정점

:\hat{\mathfrak g}^{\mathbb R} = \stackrel\circ{\mathfrak g} \otimes_{\mathbb R}\mathbb R[z+z^{-1},\mathrm i(z-z^{-1})] + \mathbb R\mathsf k

은 실수 리 대수를 이룬다.

2. 2. 2. 미분 연산의 추가

아핀 리 대수는 다음과 같은 리 괄호를 추가하여 확장할 수 있다.

:\tilde{\mathfrak g}^{\mathbb C} = \hat{\mathfrak g}^{\mathbb C} \oplus \mathbb C\mathsf d

:[\mathsf d,az^m]=-\mathrm ima\mathsf z^m \qquad \forall a\in\stackrel\circ{\mathfrak g}^{\mathbb C}

:[\mathsf d,\mathsf c]=0

즉,

:[\mathsf d,-] = -\mathrm i\mathsf z \frac{\mathrm d}{\mathrm d\mathsf z}

이다. 만약 형식적으로 \mathsf z = \exp(\mathrm i\mathsf t)로 놓는다면,

:[\mathsf d,-] = \frac{\mathrm d}{\mathrm d\mathsf t}

가 된다.

또한,

:[\mathsf d,a(z+z^{-1})] = - a\mathrm i(z - \mathsf z^{-1})

:[\mathsf d,\mathrm ia(z-z^{-1})] = a(z + \mathsf z^{-1})

이므로, 이 미분 연산은 실수 형태 \hat{\mathfrak g}^{\mathbb R}에도 잘 정의된다.

아핀 리 대수의 특정한 미분은 다음과 같이 정의된다.

:\delta (a\otimes t^m+\alpha c) = t{d\over dt} (a\otimes t^m).

대응하는 '''아핀 카츠-무디 대수'''는 [''d'', ''A''] = ''δ''(''A'')를 만족하는 추가 생성자 ''d''를 더하여 반직접 곱으로 정의된다.

2. 2. 3. 뒤틀린 아핀 리 대수

\stackrel\circ{\mathfrak g}가 자명하지 않은 자기 동형 \sigma\in\operatorname{Aut}(\stackrel\circ{\mathfrak g})를 가진다면, 다음과 같은 경계 조건을 생각할 수 있다.

:\sigma a(0)=a(2\pi).

이와 같은 경우를 '''뒤틀린 아핀 리 대수'''(twisted affine Lie algebra영어)라고 한다. 마찬가지로 '''뒤틀린 카츠-무디 대수'''(twisted Kač–Moody algebra영어)를 정의할 수 있다.

단순 리 대수가 내부 자기 동형이 아닌 자기 동형을 가질 때, 다른 딘킨 도형을 얻을 수 있으며, 이는 뒤틀린 아핀 리 대수에 대응한다.

뒤틀린 아핀 리 대수의 딘킨 도형
k는 그래프의 정점의 개수. "Twisted" affine forms are named with (2) or (3) superscripts.


2. 3. 기하학적 정의

리 대수 값의 주기 함수를 통해 아핀 리 대수를 기하학적으로 구성할 수 있다.[5]

구체적으로, 킬링 형식이 음의 정부호인 실수 단순 리 대수 \stackrel\circ{\mathfrak g}가 주어졌다고 하자. 그렇다면, \stackrel\circ{\mathfrak g}값의 매끄러운 주기 함수로 구성된 실수 프레셰 공간 \mathrm L\stackrel\circ{\mathfrak g} = \mathcal C^\infty(\mathbb S^1,\stackrel\circ{\mathfrak g})를 정의할 수 있다. 그 위의 실수 벡터 공간 구조는 점별 덧셈이며, 점별 리 괄호를 부여하면 이는 리 대수를 이룬다.

고리 리 대수 \mathrm L\stackrel\circ{\mathfrak g}의 리 대수 코호몰로지에는 다음과 같은 2차 공사슬이 존재한다.

:\alpha \colon \mathrm L\stackrel\circ{\mathfrak g} \times \mathrm L\stackrel\circ{\mathfrak g} \to \mathbb R

:\alpha\colon (x, y) \mapsto \frac{\delta^2}{2\pi}\int_{\mathbb S^1} \langle x(t)|y(t)\rangle \,\mathrm dt

여기서

  • \langle-|-\rangle은 \stackrel\circ{\mathfrak g} 위의 임의의 불변 비퇴화 이차 형식이다. (이는 킬링 형식의 스칼라배이다.)
  • \delta^2는 \stackrel\circ{\mathfrak g}의 근계의 가장 긴 근의 제곱 노름이다.
  • \mathbb S^1의 측도 \mathrm dt에 따르면, \textstyle\int_{\mathbb S^1}\mathrm dt = 2\pi이다.


이 2차 공사슬은 다음과 같은 리 대수의 짧은 완전열을 정의한다.

:0 \to \mathbb R \to \bar{\mathfrak g} \to \mathrm L\stackrel\circ{\mathfrak g} \to 0

만약 \mathfrak{g}가 유한 차원 단순 리 대수라면, 이에 대응하는 아핀 리 대수 \hat{\mathfrak{g}}는 벡터 공간으로서 다음과 같이 구성된다.

:\widehat{\mathfrak{g}}=\mathfrak{g}\otimes\mathbb{\Complex}[t,t^{-1}]\oplus\mathbb{\Complex}c,

여기서 \mathbb{\Complex}[t,t^{-1}]는 변수 ''t''에 대한 로랑 다항식의 복소수 벡터 공간이며, 리 괄호는 다음 공식으로 정의된다.

:[a\otimes t^n+\alpha c, b\otimes t^m+\beta c]=[a,b]\otimes t^{n+m}+\langle a|b\rangle n\delta_{m+n,0}c

이때, a,b\in\mathfrak{g}, \alpha,\beta\in\mathbb{\Complex} 및 n,m\in\mathbb{Z}에 대해, [a,b]는 리 대수 \mathfrak{g}에서의 리 괄호이고 \langle\cdot |\cdot\rangle는 \mathfrak{g}상의 카르탕-킬링 형식이다.

2. 4. 리 군의 기하학적 정의

실수 계수 아핀 리 대수의 프레셰 공간 완비화는 어떤 프레셰 다양체인 리 군의 리 대수이다.[5]

구체적으로, 단일 연결 콤팩트 단순 리 군 \stackrel\circ G와 그 실수 리 대수 \stackrel\circ{\mathfrak g}가 주어졌다고 하자. 그렇다면, 다음과 같은 고리군을 정의할 수 있다.

:\mathrm L\stackrel\circ G = \mathcal C^\infty(\mathbb S^1, \stackrel\circ G)

즉, 이는 \stackrel\circ G값의 매끄러운 주기 함수의 공간이다. 이는 프레셰 다양체를 이루며, 점별 곱셈을 통하여 위상군을 이룬다.

아핀 리 대수는 \mathbb R[\mathsf z+\mathsf z^{-1},\mathrm i(\mathsf z-\mathsf z^{-1})] \otimes_{\mathbb R} \stackrel\circ{\mathfrak g}의 중심 확대이다. 위상군으로서, 이는 짧은 완전열

:1\to \operatorname U(1) \to \hat G \to \mathrm L\stackrel\circ G \to 1

에 해당한다. 위상수학적으로, 이는 U(1) 주다발을 이룬다.

구체적으로, 원판 \mathbb D^2를 생각하자. 이제,

:\mathrm L\stackrel\circ G = G_{\mathbb D^2} / \mathcal G

:G_{\mathbb D^2} = \mathcal C^\infty(\mathbb D^2, G)

:\mathcal G = \{\alpha\in G_{\mathbb D^2} \colon \alpha \restriction \partial\mathbb D^2 = 1_{\stackrel\circ G} \} \cong \mathcal C^\infty_\bullet(\mathbb S^2, \stackrel\circ G)

이다. 여기서 \mathcal G는 일종의 게이지 변환군으로 여길 수 있다. 이제, G_{\mathbb D^2} 위의 다음과 같은 함수를 생각하자.

:\gamma \colon G_{\mathbb D^2} \times G_{\mathbb D^2} \to \mathbb R

:\gamma (g,h) = \frac1{4\pi\delta^2}\int_{\mathbb D^2} \langle g^{-1}\mathrm dg|h^{-1}\mathrm dh\rangle

여기서

  • \langle-|-\rangle는 \stackrel\circ{\mathfrak g} 위의 불변 비퇴화 이차 형식이며, (예를 들어) 딸림표현에서의 대각합 \langle x,y\rangle = \operatorname{tr}(xy)으로 여길 수 있다.
  • \delta^2는 \langle-|-\rangle에 따른, \stackrel\circ{\mathfrak g}의 근계의 가장 긴 근의 제곱 노름이다.

그렇다면,

:\exp(\mathrm il\gamma(-,-)) \colon G_{\mathbb D^2} \times G_{\mathbb D^2} \to \mathbb C\qquad(l\in\mathbb Z)

는 (자명한 계수의) \mathcal C^\infty(\mathbb D^2, G)의 군 코호몰로지의 2차 공사슬을 이루며, 이는 G_{\mathbb D^2}의 중심 확대

:1\to\operatorname U(1) \to \hat G_{\mathbb D^2} \to G_{\mathbb D^2} \to 1

를 정의한다.

이제, 임의의 \alpha\in\mathcal G에 대하여,

:\iota_l \colon \mathcal G \to \hat G_{\mathbb D^2}

:\iota_l \colon \alpha \mapsto \left(\alpha, \exp\left(

\frac{\mathrm il}{12\pi\delta^2}

\int_{\mathbb D^3} \operatorname{tr}(\bar\alpha^{-1} \mathrm d\bar\alpha)^3

\right)\right)

를 정의할 수 있다. 여기서

:\bar\alpha \colon \mathbb D^3 \to\stackrel\circ G

:(\bar\alpha \restriction \partial\mathbb D^3) = \alpha

는 \alpha\colon \mathbb S^2 \to\stackrel\circ G의, 3차원 공 \mathbb D^3으로의 임의의 확장이다. 이 경우, 위 표현이 \bar\alpha의 선택에 의존하지 않음을 보일 수 있다. 이 사상은 사실상 베스-추미노-위튼 모형의 작용의 항에 해당한다.

이 사상은 단사 함수이자 군 준동형이며, \iota_l(\mathcal G)는 \hat G_{\mathbb D^2}의 정규 부분군이다. 따라서, 몫군

:\hat G_l = \frac{\hat G_{\mathbb D^2}}{\iota_l(\mathcal G)}

을 정의할 수 있다. 이는 짧은 완전열

:1 \to \operatorname U(1) \to \hat G_l \to \mathrm LG \to 1

을 구성한다. (정수 l \in \mathbb Z은 \hat{\mathfrak g}의 표현의 준위에 해당한다.) 정의에 따라, \hat G_l의 리 대수는 (l\ne 0일 경우, l의 값에 상관없이) \hat{\mathfrak g}이다.

3. 성질

아핀 리 대수는 항상 대칭화 가능 카츠-무디 대수이다. 카르탕 행렬의 대칭 성분은 중복수 1의 고윳값 0을 가지며, 나머지 고윳값들은 모두 양수이다. 따라서 아핀 리 대수의 카르탕 행렬식은 항상 0이다. 카르탕 행렬의 대칭 성분의 나머지 고윳값들은 그 기본 단순 리 대수의 것들과 같다.

만약 \mathfrak{g}가 유한 차원 단순 리 대수라면, 이에 대응하는 아핀 리 대수 \hat{\mathfrak{g}}는 루프 대수 \mathfrak{g}\otimes\mathbb{\Complex}[t,t^{-1}]의 중심 확장으로 구성되며, 1차원 중심 \mathbb{\Complex}c를 갖는다. 여기서 \mathbb{\Complex}[t,t^{-1}]는 변수 ''t''에 대한 로랑 다항식의 복소수 벡터 공간이다.

유한 차원 반단순 리 대수에 해당하는 아핀 리 대수는 그 단순 성분들에 해당하는 아핀 리 대수들의 직합이다. 아핀 리 대수의 특정한 미분은 다음과 같이 정의된다.

: \delta (a\otimes t^m+\alpha c) = t{d\over dt} (a\otimes t^m).

대응하는 '''아핀 카츠-무디 대수'''는 [''d'', ''A''] = ''δ''(''A'')를 만족하는 추가 생성자 ''d''를 더하여 반직접 곱으로 정의된다.

해당 단순 리 대수의 딘킨 다이어그램에 여분의 노드를 추가하는 것은 아핀 리 대수가 해당 단순 리 대수의 루프 대수의 중심 확장으로 구성될 수 있다는 구성에 해당한다.

3. 1. 콕서터 수와 쌍대 콕서터 수

아핀 리 대수 \mathfrak g의 단순근들이 \alpha_0,\dots,\alpha_n이며, 단순 쌍대근들이 \alpha_0^\vee,\dots,\alpha_n^\vee라고 하자. '''콕서터 라벨'''(Coxeter label영어) a_i와 '''쌍대 콕서터 라벨'''(dual Coxeter label영어) a_i^\vee는 카르탕 행렬 A에 대하여

:0=a^\top A=Aa^\vee

를 만족시키는 벡터이다.[4] 이 경우, a 및 a^\vee의 모든 성분들이 양의 정수이며 최대 공약수가 1이게 정의한다.

아핀 리 대수의 '''콕서터 수'''(Coxeter number영어) h와 '''쌍대 콕서터 수'''(dual Coxeter number영어) h^\vee는 각각 (쌍대) 콕서터 라벨의 성분들의 합이다.

:\mathsf h(\mathfrak g)=\sum_{i=0}^na_i

:\mathsf h^\vee(\mathfrak g)=\sum_{i=0}^na_i^\vee

3. 2. 근계의 구조

아핀 리 대수 \mathfrak g의 근계는 유한 차원 단순 리 대수 \stackrel\circ{\mathfrak g}의 근계와 허근으로 구성된다.[3]

\mathfrak g의 실근(實根, real root)들의 집합 \Delta^{\text{re}}(\mathfrak g)는 다음과 같다.[3]

  • r=1인 경우:

::\Delta^{\text{re}}(\mathfrak g) = \stackrel\circ\Delta+\mathbb Z\delta

  • r\in\{2,3\},\;\mathfrak g\not\cong A_{2n}^{(2)}인 경우:

::\Delta^{\text{re}}(\mathfrak g) = (\stackrel\circ\Delta_\text{short}+\mathbb Z\delta)\cup(\stackrel\circ\Delta_{\text{long}}+r\mathbb Z\delta)

  • \mathfrak g\cong A_{2n}^{(2)}인 경우:

::\Delta^{\text{re}}(\mathfrak g) = \frac12\left(\stackrel\circ\Delta_{\text{long}}+(2\mathbb Z-1)\delta\right)\cup

\left(\stackrel\circ\Delta_{\text{short}}+\mathbb Z\delta\right)\cup

\left(\stackrel\circ\Delta_{\text{long}}+2\mathbb Z\delta\right)

여기서 \stackrel\circ\Delta는 \stackrel\circ{\mathfrak g}의 근계이며, \stackrel\circ\Delta_\text{short}와 \stackrel\circ\Delta_{\text{long}}는 각각 짧은 근과 긴 근의 집합이다. r은 아핀 리 대수를 구성할 때 사용한 자기 동형의 차수이다. 예를 들어, \tilde D_4^{(3)}의 경우 r=3이다.

\mathfrak g의 허근(虛根, imaginary root)들의 집합 \Delta^{\text{im}}(\mathfrak g)는 다음과 같다.[3]

::\Delta^{\text{im}}(\mathfrak g)=(\mathbb Z\setminus\{0\})\delta

영벡터는 정의에 따라 근이 아니며, \delta는 항상 양근(positive root)이다. 따라서 양의 허근들의 집합은 다음과 같다.[3]

::\Delta^{\text{im},+}(\mathfrak g)=\mathbb Z^+\delta

유한 차원 단순 복소 리 대수 \mathfrak{g}를 카르탕 부분 대수 \mathfrak{h}와 특정 근계 \Delta를 사용하여 고정하고, X_n = X\otimes t^n 표기를 도입하면, \mathfrak{g}에 대한 카르탕-바일 기저 \{H^i\} \cup \{E^\alpha|\alpha \in \Delta\}를 \{H^i_n\} \cup \{c\} \cup \{E^\alpha_n\}로 확장할 수 있다. 여기서 \{H^i_0\} \cup \{c\}는 아벨 부분 대수를 형성한다.

E^\alpha_n에 대한 ad(H^i_0) 및 ad(c)의 고유값은 각각 \alpha^i와 0이며 n과 무관하다. 따라서 이 아벨 부분 대수에 대해 근 \alpha는 무한히 축퇴된다. 위에 설명된 미분을 아벨 부분 대수에 추가하면 아벨 부분 대수가 아핀 리 대수에 대한 카르탕 부분 대수로 바뀌고, E^\alpha_n에 대한 고유값은 (\alpha^1, \cdots, \alpha^, 0, n)이 된다.

E^\alpha_n에 연관된 아핀 근을 \hat \alpha = (\alpha;0;n)으로 쓴다. \delta = (0,0,1)로 정의하면, 다음과 같이 다시 쓸 수 있다.

:: \hat \alpha = \alpha + n\delta

전체 근의 집합은 다음과 같다.

:: \hat \Delta = \{\alpha + n\delta|n \in \mathbb Z, \alpha \in \Delta\}\cup \{n\delta|n \in \mathbb Z, n \neq 0\}

이때 \delta는 길이가 0이므로 특이하다. 즉, (\delta, \delta) = 0이며, 여기서 (\cdot,\cdot)은 킬링 형식에 의해 유도된 근 위의 쌍선형 형식이다.

아핀 대수의 단순근 기저를 얻기 위해, 추가적인 단순근이 덧붙여져야 하며, 다음과 같이 주어진다.

::\alpha_0 = -\theta + \delta

여기서 \theta는 \mathfrak{g}의 최고근이며, 이는 근의 일반적인 높이 개념을 사용한다. 이를 통해 확장된 카르탕 행렬과 확장된 딘킨 다이어그램을 정의할 수 있다.

3. 3. 기본 단순 리 대수

아핀 리 대수 \mathfrak g의 슈발레 생성원을 (e_0,f_0),\dots,(e_n,f_n)이라고 하자. 그렇다면, 아핀 리 대수 \mathfrak g의 '''기본 단순 리 대수'''(underlying simple Lie algebra영어) \stackrel\circ{\mathfrak g}\subsetneq\mathfrak g는 \stackrel\circ{\mathfrak h} 및 (e_1,f_1),\dots,(e_n,f_n)으로 생성되는 리 부분 대수이다. 이는 항상 유한 차원 단순 리 대수이며, 기본 단순 리 대수 \stackrel\circ{\mathfrak g}의 카르탕 부분 대수는 \stackrel\circ{\mathfrak h}이다. 근계 및 쌍대 근계는 다음과 같다.

:\stackrel\circ\Delta=\Delta\cap\stackrel\circ{\mathfrak h}^*

:\stackrel\circ\Delta^\vee=\Delta^\vee\cap\stackrel\circ{\mathfrak h}

단순근 및 단순 쌍대근은 각각 다음과 같다.

:\{\alpha_1,\dots,\alpha_n\}

:\{\alpha_1^\vee,\dots,\alpha_n^\vee\}

3. 4. 바일 군

아핀 리 대수 \mathfrak g의 바일 군 \operatorname{Weyl}(\mathfrak g)은 아핀 콕서터 군이며, 그 기본 단순 리 대수 \stackrel\circ{\mathfrak g}의 바일 군 \operatorname{Weyl}(\stackrel\circ{\mathfrak g})과 어떤 자유 아벨 군의 반직접곱이다.[3]

:\operatorname{Weyl}(\mathfrak g)=\operatorname{Weyl}(\stackrel\circ{\mathfrak g}) \rtimes M

여기서

:M=\begin{cases}\operatorname{Span}_{\mathbb Z}\stackrel\circ\Delta&r=1\\

\operatorname{Span}_{\mathbb Z}\stackrel\circ\Delta^\vee&r\in\{2,3\}

\end{cases}

는 \stackrel\circ{\mathfrak h} 속의 격자(의 병진 이동군)이다. 여기서, 단순 리 대수의 근계에 주어진 내적을 사용하여 동형 \circ{\mathfrak h}\cong\circ{\mathfrak h}^*를 암묵적으로 사용하였다.

아핀 리 대수의 바일 군은 0-모드 대수(루프 대수를 정의하는 데 사용되는 리 대수)의 바일 군과 코루트 격자의 반직접곱으로 표현될 수 있다.

아핀 리 대수의 대수적 문자의 바일 문자 공식은 바일-카츠 문자 공식으로 일반화된다.

3. 5. 표현론

아핀 리 대수의 표현론은 베르마 가군을 사용하여 전개되며, 유한 차원 표현은 존재하지 않는다.[1] 이는 유한 차원 베르마 가군의 영벡터가 0이어야 하지만, 아핀 리 대수의 경우에는 그렇지 않기 때문이다.

단순 리 대수 \stackrel\circ{\mathfrak g}에 대응되는 아핀 리 대수 \hat{\mathfrak g}의 표현 V가 주어지면, V에는 다음과 같은 비라소로 대수의 표현이 존재한다.

:\mathsf L_n = \frac1{\mathsf k+\mathsf h^\vee(\mathfrak g)} \sum_{m \in\mathbb Z} \eta_{ab} (x^a\mathsf z^m)(x^b\mathsf z^{-m}) \qquad (n\ne0)

:\mathsf L_0 = \frac2{\mathsf k+\mathsf h^\vee(\mathfrak g)} \sum_{m =0}^\infty \eta_{ab} (x^a\mathsf z^m)(x^b\mathsf z^{-m})

:\mathsf c = \frac{\mathsf k\dim \stackrel\circ{\mathfrak g}}{\mathsf k+\mathsf h^\vee(\stackrel\circ{\mathfrak g})}

이를 '''스가와라 구성'''(菅原構成, Sugawara construction영어)이라고 한다.[9][10] 여기서

  • \mathsf h^\vee(\stackrel\circ{\mathfrak g})는 단순 리 대수 \stackrel\circ{\mathfrak g}의 이중 콕서터 수이다.
  • \eta_{ab}는 \stackrel\circ{\mathfrak g}의 킬링 형식의 스칼라배이다.
  • \mathsf k는 중심 원소이므로, 기약 표현에서 그 값은 상수이다.


보다 일반적으로, 반단순 리 대수 \stackrel\circ{\mathfrak g}의 표현 V 및 부분 단순 리 대수 \stackrel\circ{\mathfrak h}\subseteq\stackrel\circ{\mathfrak g}가 주어졌다고 하자. \hat{\mathfrak g}에 대응하는 스가와라 구성 (\mathsf L'_n,\mathsf c')_{\mathbb Z} 및 \hat{\mathfrak h}에 대응하는 스가와라 구성 (\mathsf L''_n,\mathsf c'')_{\mathbb Z}이 주어진다. 이 경우,

:\mathsf L_n = \mathsf L'_n - \mathsf L''_n

:\mathsf c = \mathsf c' - \mathsf c'' = \frac{\mathsf k\dim \stackrel\circ{\mathfrak g}}{\mathsf k+\mathsf h^\vee(\stackrel\circ{\mathfrak g})} - \frac{\mathsf k\dim \stackrel\circ{\mathfrak h}}{\mathsf k+\mathsf h^\vee(\stackrel\circ{\mathfrak h})}

를 정의하면, 이는 비라소로 대수의 유니터리 표현을 이룬다.[11] 이를 '''공액류 구성'''(coset construction영어) 또는 '''고더드-켄트-올리브 구성'''(Goddard–Kent–Olive construction영어) 또는 '''GKO 구성'''(GKO construction영어)이라고 한다.

이를 통하여 비라소로 대수의 모든 c<1 유니터리 표현을 구현할 수 있다. 구체적으로, c = 1-6/(k+2)(k+3) 유니터리 표현을 구현하려면,

:\hat{\mathfrak g} = \widehat{\mathfrak{su}}(2)_k\times\widehat{\mathfrak{su}}(2)_1

:\hat{\mathfrak h} = \widehat{\mathfrak{su}}(2)_{k+1}

를 취하면 된다. 여기서 \stackrel\circ{\mathfrak h}=\mathfrak{su}(2)는 \stackrel\circ{\mathfrak g}=\mathfrak{su}(2)\oplus\mathfrak{su}(2)의 대각 성분이다. 이 경우

:\dim\mathfrak{su}(2) = 3

:\mathsf h^\vee(\mathfrak{su}(2)) = 2

이므로,

:\mathsf c=\frac{3k}{k+2}+\frac{3\times1}{1+2}-\frac{3(k+1)}{k+3}=1-\frac6{(k+2)(k+3)}

임을 계산할 수 있다.

아핀 리 대수의 바일 군은 0-모드 대수(루프 대수를 정의하는 데 사용되는 리 대수)의 바일 군과 코루트 격자의 반직접곱으로 표현될 수 있다.

아핀 리 대수의 대수적 문자의 바일 문자 공식은 바일-카츠 문자 공식으로 일반화된다.

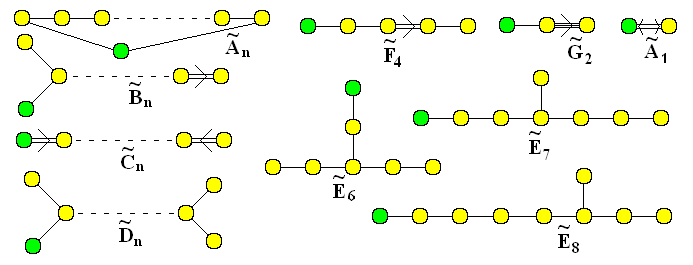
4. 분류

단순 아핀 리 대수는 딘킨 도표(Dynkin diagram)를 이용하여 분류할 수 있다. 딘킨 도표에서 하나의 꼭짓점을 제거하면 단순 리 대수의 딘킨 도표를 얻을 수 있다.

단순 아핀 리 대수 및 그 딘킨 도표는 아래 표와 같다. 표에서 "긴 실근의 동치류 수"는 근 \(\Delta\)에서 \(\delta\)를 더한 것을 무시한 동치류들 가운데, 긴 근 및 짧은 근들의 수이다. \(\tilde A_{2n}^{(2)}\)의 경우 근의 길이가 세 종류가 있으며, 이 경우 중간 길이 및 가장 짧은 길이의 근들의 수를 "짧은 근"에 표기하였다. 긴 근의 길이는 항상 \(\sqrt2\)로 규격화하였고, 짧은 근의 길이는 이에 비례하여 측정하였다.

딘킨 그림에서, 4중 화살표 (카르탕 행렬에서 \(A_{ij}A_{ji}=4\)인 경우)는 \(\xrightarrow4\) 및 \(\stackrel4\leftrightarrow\)로 표기하였다. 이 경우 \(A_{ij}=A_{ji}=-2\)인 경우는 \(\stackrel4\leftrightarrow\)이며, \(A_{ij}=-1,\;A_{ji}=-4\)인 경우는 \(\xrightarrow4\)이다.

기호[3]타 기호[12]타 기호[13]타 기호[4]바일 군 궤도 수긴 실근의
동치류 수		짧은 실근의
동치류 수		딘킨 도표콕서터 라벨[4]쌍대 콕서터 라벨[4][12]콕서터 수[3]쌍대 콕서터 수[3]
\(\tilde A_1\)\(A_1^u=A_1^t\)\(A_1\)\(A_1^{(1)}\)220\(\bullet\stackrel4\leftrightarrow\bullet\)\(1\stackrel4\leftrightarrow1\)2
\(\tilde A_n\) \((n\ge2)\)\(A_n^u=A_n^t\)\(A_n\)\(A_n^{(1)}\)1\(n(n+1)\)0\(\bullet<{\bullet-\cdots-\bullet\atop\bullet-\cdots-\bullet}>\bullet\)\(1<{1-\cdots-1\atop1-\cdots-1}>1\)\(n+1\)
\(\tilde B_n\)\(B_n^u\)\(B_n\)\(B_n^{(1)}\)2\(2n(n-1)\)\(2n\) (길이 \(1\))\(\bullet\Leftarrow\bullet-\cdots-\bullet<{\bullet\atop\bullet}\)\(2\Leftarrow2-\cdots-2<{1\atop1}\)\(1\Leftarrow2-\cdots-2<{1\atop1}\)\(2n\)\(2n-1\)
\(\tilde C_n\)\(C_n^u\)\(C_n\)\(C_n^{(1)}\)3\(2n\)\(2n(n-1)\) (길이 1)\(\bullet\Rightarrow\bullet-\bullet-\cdots-\bullet-\bullet\Leftarrow\bullet\)\(1\Rightarrow2-2-\cdots-2-2\Leftarrow1\)\(1\Rightarrow1-1-\cdots-1-1\Leftarrow1\)\(2n\)\(n+1\)
\(\tilde D_n\)\(D_n^u=D_n^t\)\(D_n\)\(D_n^{(1)}\)1\(2n(n-1)\)0\({\bullet\atop\bullet}>\bullet-\bullet-\cdots-\bullet<{\bullet\atop\bullet}\)\({1\atop1}>2-2-\cdots-2<{1\atop1}\)\(2n-2\)
\(\tilde E_6\)\(E_6^u=E_6^t\)\(E_6\)\(E_6^{(1)}\)1720\({\bullet-\bullet\atop\bullet-\bullet}>\bullet-\bullet-\bullet\)\({1-2\atop1-2}>3-2-1\)12
\(\tilde E_7\)\(E_7^u=E_7^t\)\(E_7\)\(E_7^{(1)}\)11260\({\bullet-\bullet-\bullet\atop\bullet-\bullet-\bullet}>\bullet-\bullet\)\({1-2-3\atop1-2-3}>4-2\)18
\(\tilde E_8\)\(E_8^u=E_8^t\)\(E_8\)\(E_8^{(1)}\)12400\({\bullet\atop{}}{-\atop{}}{\bullet\atop\bullet}>\bullet-\bullet-\bullet-\bullet-\bullet-\bullet\)\({2\atop{}}{-\atop{}}{4\atop3}>6-5-4-3-2-1\)30
\(\tilde F_4\)\(F_4^u\)\(F_4\)\(F_4^{(1)}\)22424 (길이 1)\(\bullet-\bullet-\bullet\Rightarrow\bullet-\bullet\)\(1-2-3\Rightarrow4-2\)\(1-2-3\Rightarrow2-1\)129
\(\tilde G_2\)\(G_2^u\)\(G_2\)\(G_2^{(1)}\)266 (길이 \(\sqrt{2/3}\))\(\bullet-\bullet\Rrightarrow\bullet\)\(1-2\Rrightarrow3\)\(1-2\Rrightarrow1\)64
\(\tilde A_{2n-1}^{(2)}\)\(C_n^t\)\(B_n^\vee\)\(C_n^{(2)}\)3\(2n\)\(2n(n-1)\) (길이 1)\(\bullet\Rightarrow\bullet-\cdots-\bullet<{\bullet\atop\bullet}\)\(1\Rightarrow2-\cdots-2<{1\atop1}\)\(2\Rightarrow2-\cdots-2<{1\atop1}\)\(2n-1\)\(2n\)
\(\tilde A_2^{(2)}\)\(BC_1^m\)\(BC_1\)\(\tilde B_1^{(2)}\)2\(2\)\(2\) (길이 \(1/\sqrt2\))\(\bullet\xrightarrow4\bullet\)\(1\xrightarrow42\)\(2\xrightarrow41\)3
\(\tilde A_{2n}^{(2)}\) \((n\ge2)\)\(BC_n^m\)\(BC_n\)\(\tilde B_n^{(2)}\)3\(2n\)\(2n(n-1)\) (길이 1)
\(2n\) (길이 \(1/\sqrt2\))		\(\bullet\Rightarrow\bullet-\bullet-\cdots-\bullet-\bullet\Rightarrow\bullet\)\(1\Rightarrow2-2-\cdots-2-2\Rightarrow2\)\(2\Rightarrow2-2-\cdots-2-2\Rightarrow1\)\(2n+1\)
\(\tilde D_4^{(3)}\)\(G_2^t\)\(G_2^\vee\)\(G_2^{(3)}\)266 (길이 \(\sqrt{2/3}\))\(\bullet-\bullet\Lleftarrow\bullet\)\(1-2\Lleftarrow1\)\(1-2\Lleftarrow3\)46
\(\tilde D_{n+1}^{(2)}\)\(B_n^t\)\(C_n^\vee\)\(B_n^{(2)}\)2\(2n(n-1)\)\(2n\) (길이 1)\(\bullet\Leftarrow\bullet-\bullet-\cdots-\bullet-\bullet\Rightarrow\bullet\)\(1\Leftarrow1-1-\cdots-1-1\Rightarrow1\)\(1\Leftarrow2-2-\cdots-2-2\Rightarrow1\)\(n+1\)\(2n\)
\(\tilde E_6^{(2)}\)\(F_4^t\)\(F_4^\vee\)\(F_4^{(2)}\)22424 (길이 1)\(\bullet-\bullet\Rightarrow\bullet-\bullet-\bullet\)\(1-2\Rightarrow3-2-1\)\(2-4\Rightarrow3-2-1\)912



아핀 리 대수의 카르탕 행렬은 딘킨 도표에서 하나의 꼭짓점을 제거하여 얻는 단순 리 대수의 카르탕 행렬 및 콕서터 라벨 · 쌍대 콕서터 라벨로 재구성할 수 있다.

\(n\ge2\)일 경우, \(\tilde A_n\)의 카르탕 행렬은 다음과 같은 \((n+1)\times(n+1)\) 대칭 정사각 행렬이다.

:\(\operatorname{Cartan}(\tilde A_n)=\begin{pmatrix}

2 & -1 & 0 & 0 & \cdots & 0 & -1 \\


  • 1 & 2 & -1 & 0 & \cdots & 0 & 0 \\

0 & -1 & 2 & -1 & \dots & 0 & 0 \\

0 & 0 & -1 & 2 & \cdots & 0 & 0 \\

\vdots & \vdots & \vdots & \vdots & \ddots & \vdots &\vdots \\

0 & 0 & 0 & 0 & \cdots & 2& -1\\

  • 1 & 0 & 0 & 0 & \cdots & -1 & 2

\end{pmatrix}\)

\(\tilde A_1\)의 카르탕 행렬은 다음과 같다.

:\(\operatorname{Cartan}(\tilde A_1)=\begin{pmatrix}2&-2\\-2&2\end{pmatrix}\)

\(\tilde A_n\)의 딘킨 도표는 \(n\ge2\)일 경우 \(n+1\)개의 꼭짓점을 갖는 순환 그래프이다.

\(n\ge2\)일 때, \(\tilde A_{2n}^{(2)}\)의 카르탕 행렬은 다음과 같은 \((n+1)\times(n+1)\) 비대칭 정사각 행렬이다.

:\(\operatorname{Cartan}(\tilde A_{2n}^{(2)})=\begin{pmatrix}

2 & -1 & 0 & \cdots & 0 & 0 & 0 \\

  • 2 & 2 & -1 & \cdots & 0 & 0 & 0 \\

0 & -1 & 2 & \dots & 0& 0 & 0 \\

\vdots & \vdots & \vdots & \ddots & \vdots& \vdots &\vdots \\

0 & 0 & 0 & \cdots & 2& -1 & 0\\

0 & 0 & 0 & \cdots & -1& 2& -1\\

0 & 0 & 0 & \cdots & 0 & -2 & 2

\end{pmatrix}\)

여기서 행·열 \(0,1,\dots,n\)의 순서는 다음과 같다.

:\(\alpha_0\Rightarrow\alpha_1-\cdots-\alpha_{n-1}\Rightarrow\alpha_n\)

\(\tilde A_2^{(2)}\)의 카르탕 행렬은 다음과 같다.

:\(\operatorname{Cartan}(\tilde A_2^{(2)})

=\begin{pmatrix}2&-1\\-4&2\end{pmatrix}

\)

여기서 행·열 0, 1의 순서는 다음과 같다.

:\(\alpha_0\xrightarrow4\alpha_1\)



\(\tilde G_2\)의 카르탕 행렬은 다음과 같다.

:\(\operatorname{Cartan}(\tilde G_2)=\begin{pmatrix}

2 & -1 & 0\\

  • 1 & 2&-1\\

0 & -3&2 \end{pmatrix}

\)

여기서 행·열 0, 1, 2의 순서는

:\(\alpha_0-\alpha_1\Rrightarrow\alpha_2\)

이다.

\(\tilde D_4^{(3)}\)의 카르탕 행렬은 다음과 같다.

:\(\operatorname{Cartan}(\tilde D_4^{(3)})=\begin{pmatrix}

2 & -1 & 0\\

  • 1 & 2&-3\\

0 & -1&2 \end{pmatrix}

\)

여기서 행·열 0, 1, 2의 순서는

:\(\alpha_0-\alpha_1\Lleftarrow\alpha_2\)

이다.

각 아핀 리 대수의 Dyn킨 다이어그램은 해당 단순 리 대수의 다이어그램과 허수 근을 추가하는 것에 해당하는 추가 노드로 구성된다. 각 단순 리 대수에 대해 리 대수의 외부 자기 동형 사상 그룹의 카디널리티와 동일한 수의 가능한 연결이 존재한다. 특히 이 그룹은 항상 항등원을 포함하며, 해당 아핀 리 대수는 '''untwisted''' 아핀 리 대수라고 불린다. 단순 대수가 내부 자기 동형 사상이 아닌 자기 동형 사상을 허용할 때, 다른 Dyn킨 다이어그램을 얻을 수 있으며 이는 '''twisted''' 아핀 리 대수에 해당한다.

아핀 리 대수를 위한 Dynkin diagram
확장된 (untwisted) 아핀 Dyn킨 다이어그램의 집합, 녹색으로 추가된 노드 포함


5. 예

\mathfrak g = \mathbb C가 1차원 아벨 리 대수라고 하자. 그렇다면, 그 로랑 다항식 대수

:\mathbb C[\mathsf z,\mathsf z^{-1}]

역시 아벨 리 대수이다. 이 경우, 중심 확대

:0 \to \mathbb C\mathsf k \to \hat{\mathfrak g} \to \mathbb C[\mathsf z,\mathsf z^{-1}] \to 0

에서

:[\mathsf z^m,\mathsf z^n] = \delta_{m+n,0} m\mathsf k

:[\mathsf k,\mathsf z^m] = 0

이 된다. 이 경우,

:\mathsf z^{-n} = \sqrt n\mathsf p_n\qquad(n>0)

:\mathsf z^n = \sqrt n\mathsf q_n\qquad(n>0)

:\mathsf k = \hbar

로 놓으면,

:[\mathsf q_m,\mathsf p_n] = \delta_{m,n}\hbar

가 되어, 이는 무한 차원 하이젠베르크 리 대수와 (\mathsf z^0으로 생성되는) 1차원 아벨 리 대수의 직합이 된다.[9] 특히, 이는 무한 차원 보손 포크 공간 \mathbb C[\mathsf x_1,\mathsf x_2,\dotsb] 위에 표준적으로 작용한다.[9]

이 경우, 스가와라 구성은 다음과 같다.[9]

:\mathsf L_n = - \frac12\sum_{m\in\mathbb Z} \mathsf z^{\min\{m,n-m\}} \mathsf z^{\max\{m,n-m\}}

:\mathsf c = 1

물리학적으로, 이는 자유 보손에 대한 2차원 등각 장론에 해당한다.

하이젠베르크 대수[2]는 생성자 a_n, n \in \mathbb{Z}에 의해 정의되며, 교환 관계

:[a_m, a_n] = m\delta_{m+n,0}c

를 만족하며, 아핀 리 대수 \hat \mathfrak u(1)로 실현될 수 있다.

6. 역사

빅토르 카츠와 로버트 무디(Robert Moody영어)가 (다른 카츠-무디 대수와 함께) 아핀 리 대수를 발견하였다. ‘아핀’이라는 이름은 그 바일 군이 근계에 아핀 변환으로 작용하기 때문이다.

스가와라 구성은 스가와라 히로타카( 菅原 寛孝|스가와라 히로타카일본어 )가 1968년에 발견하였다.[14] 공액 구성은 피터 고더드(Peter Goddard영어, 1945~) · 에이드리언 켄트(Adrian Kent영어) · 데이비드 올리브(David Olive영어, 1937~2012)가 1985년에 발견하였다.[15]

7. 응용

아핀 리 대수는 스가와라 구성에 따라 모든 아핀 리 대수의 보편 포락 대수가 비라소로 대수를 부분 대수로 갖는다. 이를 통해 아핀 리 대수는 WZW 모형 또는 코셋 모형과 같은 등각장론의 대칭 대수로 사용될 수 있다. 결과적으로 아핀 리 대수는 끈 이론의 세계면 묘사에도 나타난다.

아핀 리 대수는 이론 물리학(등각장론과 같은 WZW 모델, 코셋 모델, heterotic string의 세계면 등), 기하학, 수학의 다른 분야에서 자연스럽게 나타난다.

참조

[1] 서적 A Mathematical Introduction to Conformal Field Theory https://link.springe[...] Springer-Verlag 2008-09-11
[2] 서적 Conformal Field Theory 1997
[3] 서적 Infinite dimensional Lie algebras https://archive.org/[...] Cambridge University Press 1990
[4] 서적 Affine Lie algebras and quantum groups: an introduction with applications in conformal field theory http://www.cambridge[...] Cambridge University Press 1995-03
[5] 서적 Proceedings of the International Congress of Mathematicians, Berkeley, California, USA, 1986. Volume Ⅰ 1987
[6] 서적 Conformal field theory https://archive.org/[...] Springer-Verlag
[7] 서적 Conformal field theory and topology American Mathematical Society
[8] 서적 Loop groups Oxford University Press
[9] 간행물 Sugawara construction for higher genus Riemann surfaces 1998
[10] 간행물 Conformal field theory: a case study 1999-04-21
[11] 간행물 Unitary representations of the Virasoro and super-Virasoro algebras 1986
[12] 서적 Affine Lie algebras and affine root systems https://esc.fnwi.uva[...] 암스테르담 대학교 2012-04-20
[13] 서적 Affine Hecke algebras and orthogonal polynomials Cambridge University Press 2003
[14] 간행물 A field theory of currents 1968
[15] 간행물 Virasoro algebras and coset space models 1985


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com