마름모

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의 및 성질
3. 넓이
4. 쌍대성
5. 타일링
6. 3차원 도형과의 관계
참조

1. 개요

마름모는 네 변의 길이가 같은 사각형으로, 평행사변형의 특수한 형태이다. 대각선은 서로 수직으로 이등분하며, 대각선을 이용하여 넓이를 계산할 수 있다. 마름모는 평행사변형과 연의 성질을 모두 가지며, 모든 변에 내접하는 원을 갖는다. 또한, 마름모는 타일링에 사용될 수 있으며, 마름모 면을 가진 다양한 3차원 도형들이 존재한다. 한국 문화에서는 트럼프 다이아몬드, 야마구치구미 문장, 미쓰비시 그룹 로고 등에서 마름모 형태를 찾아볼 수 있다.

2. 정의 및 성질

마름모는 ῥόμβος|rhómbos^grc에서 유래되었으며, 이는 회전하는 것을 의미한다.^[3] 이 단어는 동사 ῥέμβω|rhémbō^grc(빙빙 돌다)에서 파생되었다.^[4] 이 단어는 유클리드와 아르키메데스가 사용했으며, 아르키메데스는 두 개의 직각 원뿔이 공통 밑면을 공유하는 이중뿔에 대해 "입체 마름모"라는 용어를 사용했다.^[5]

오늘날 우리가 ''마름모''라고 부르는 표면은 두 원뿔의 꼭짓점을 지나는 평면에서 이중뿔의 단면이다.

단순 (자기 교차하지 않는) 사각형은 다음 중 하나에 해당할 필요충분 조건일 때 마름모이다:^[6]^[7]

네 변의 길이가 같은 사각형 (정의에 의함)
대각선이 서로 수직이고 서로를 이등분하는 사각형
각 대각선이 두 개의 마주보는 내각을 이등분하는 사각형
평행 사변형에서 대각선이 내각을 이등분하는 경우
적어도 두 개의 연속된 변의 길이가 같은 평행 사변형
대각선이 서로 수직인 평행 사변형 (수직 직교 대각선 평행 사변형)
사각형 ''ABCD''가 평면 상의 점 ''P''를 가지고 있어 네 개의 삼각형 ''ABP'', ''BCP'', ''CDP'' 및 ''DAP''가 모두 합동인 경우^[8]
삼각형 ''ABC'', ''BCD'', ''CDA'' 및 ''DAB''의 내접원이 공통점을 갖는 사각형 ''ABCD''인 경우^[9]

모든 마름모는 마주보는 꼭짓점 쌍을 연결하는 두 개의 대각선과 두 쌍의 평행한 변을 갖는다. 합동 삼각형을 사용하여 마름모가 각 대각선에 대해 대칭임을 증명할 수 있다. 따라서 모든 마름모는 다음과 같은 성질을 갖는다.

마름모의 마주보는 각도는 크기가 같다.
마름모의 두 대각선은 수직이다. 즉, 마름모는 직교 사변형이다.
대각선은 마주보는 각도를 이등분한다.

첫 번째 성질은 모든 마름모가 평행사변형임을 의미한다. 따라서 마름모는 평행사변형의 모든 성질을 갖는다. 예를 들어, 마주보는 변은 평행하고, 인접한 각은 보각이며, 두 대각선은 서로를 이등분하며, 중점을 지나는 모든 선은 면적을 이등분하고, 변의 제곱의 합은 대각선의 제곱의 합과 같다(평행사변형 법칙). 따라서 공통 변을 ''a''로, 대각선을 ''p''와 ''q''로 표시하면 모든 마름모에서 다음과 같은 식이 성립한다.

:

\displaystyle 4a^2=p^2+q^2.

모든 평행사변형이 마름모인 것은 아니지만, 수직인 대각선을 가진 평행사변형(두 번째 성질)은 마름모이다. 일반적으로 수직인 대각선을 갖고 그 중 하나가 대칭선인 사각형은 연이다. 모든 마름모는 연이고, 연이자 평행사변형인 모든 사변형은 마름모이다.

마름모는 접선 사변형이다.^[10] 즉, 네 변 모두에 접하는 내접원을 갖는다.

마름모. 검은 점으로 표시된 각 각도는 직각이다. 높이 ''h''는 인접하지 않은 두 변 사이의 수직 거리이며, 이는 내접원의 지름과 같다. 길이 ''p''와 ''q''의 대각선은 빨간 점선 세그먼트이다.

마름모는 평행사변형의 특수한 형태이므로 다음의 성질을 모두 가진다.

2쌍의 대변은 서로 평행하고 길이는 같다.
2쌍의 대각의 크기도 서로 같다.
대각선이 각각의 중점에서 수직으로 만난다.

마름모는 선대칭 도형이며, 대칭축은 2개의 대각선이다. 또한 점대칭 도형이기도 하며, 대각선의 교점을 중심으로 180° 회전하면 원래의 도형과 겹쳐진다.

대각선이 직교하고, 인접한 변의 길이가 같은 쌍이 2개 있는 사각형은 일반적으로 연꼴이라고 불리며, 마주보는 변은 반드시 평행하지 않다. 마름모는 연꼴의 특수한 형태이다.

마름모를 대각선을 경계로 2개로 나누면 각각 합동인 이등변삼각형이 된다.

2. 1. 증명 (두 대각선은 서로 수직이다)

마름모는 마주보는 변의 길이가 같다. 두 대각선 AC와 BD의 교점을 I라고 하면, 마름모는 평행사변형이므로

\triangle IAB

와

\triangle IAD

에서

:

\overline{IB}=\overline{ID},\overline{AB}=\overline{AD}, \overline{IA}

는 공통

:

\therefore \triangle IAB \equiv \triangle IAD \therefore \angle AIB = \angle AID = 90^\circ

그러므로

\overline{AC} \perp \overline{BD}

이다.

2. 2. 대각선

마름모의 변의 길이 ''a''와 한 꼭지각 ''α''를 사용하여 대각선 ''p = AC''와 ''q = BD''의 길이를 다음과 같이 표현할 수 있다.

:

p=a\sqrt{2+2\cos{\alpha}}

:

q=a\sqrt{2-2\cos{\alpha}}.

이 공식들은 코사인 법칙의 직접적인 결과이다.

마름모는 대칭축이 2개의 대각선인 선대칭 도형이며, 대각선의 교점을 중심으로 180° 회전하면 원래의 도형과 겹쳐지는 점대칭 도형이기도 하다.

마름모를 대각선을 경계로 2개로 나누면 각각 합동인 이등변삼각형이 된다.

2. 3. 내접원

마름모는 항상 내접원이 있다.^[10] 마름모에 내접하는 원의 반지름(내접원)은 ''r''로 표기하며, 두 대각선 ''p''와 ''q''를 사용하여 다음과 같이 나타낼 수 있다.

:\frac{p \cdot q}{2\sqrt{p^2+q^2}}

또는 변의 길이 ''a''와 꼭지각 ''α'' 또는 ''β''를 사용하여 다음과 같이 나타낼 수 있다.

:\frac{a\sin\alpha}{2} = \frac{a\sin\beta}{2}

3. 넓이

마름모의 넓이 ''S''는 평행사변형의 넓이 공식 ''S'' = (밑변) × (높이)를 사용하여 구할 수도 있지만, 다음 식으로 계산하는 방법이 널리 알려져 있다.^[11]

: $S=\frac {AC\times BD}{2}$

여기서 AC 및 BD는 각각 마주보는 꼭짓점을 연결하는 대각선의 길이이다. 이 공식은 연꼴의 넓이에도 적용할 수 있다.^[11]

한 대각선의 길이가 $l$ , 다른 대각선의 길이가 $w$ 라 하면

:

S=\frac{1}{2} lw

한 변의 길이가 $a$ 이고, 그 끼인 각의 크기를 $\theta$ 라 하면

:

S=a^2 \sin \theta

모든 평행사변형과 마찬가지로, 마름모의 넓이 ''K''는 밑변과 높이(''h'')의 곱이다. 밑변은 단순히 변의 길이 ''a''이다.

:

K = a \cdot h .

넓이는 또한 변의 제곱과 임의의 각도의 사인 값을 곱한 값으로 표현할 수 있다.

:

K = a^2 \cdot \sin \alpha = a^2 \cdot \sin \beta ,

또는 높이와 꼭짓점 각도를 사용하여 표현할 수도 있다.

:

K=\frac{h^2}{\sin\alpha} ,

또는 대각선 ''p'', ''q''의 곱의 절반으로 표현할 수도 있다.

:

K = \frac{p \cdot q}{2} ,

또는 반둘레와 마름모에 내접원의 반지름 (내접원 반지름)의 곱으로 표현할 수도 있다.

:

K = 2a \cdot r .

평행사변형과 마찬가지로, 두 인접한 변을 이중 벡터를 형성하는 벡터로 간주하여, 넓이는 이중 벡터의 크기(두 벡터의 외적의 크기), 즉 두 벡터의 데카르트 좌표의 행렬식이다. ''K'' = ''x''₁''y''₂ – ''x''₂''y''₁.^[11]

4. 쌍대성

마름모의 쌍대 다각형은 직사각형이다.^[12]

마름모는 모든 변의 길이가 같지만, 직사각형은 모든 각의 크기가 같다.
마름모는 서로 마주보는 각의 크기가 같지만, 직사각형은 서로 마주보는 변의 길이가 같다.
마름모는 내접원을 가지지만, 직사각형은 외접원을 가진다.
마름모는 서로 마주보는 꼭짓점 각의 각 쌍을 지나는 대칭축을 가지지만, 직사각형은 서로 마주보는 변의 각 쌍을 지나는 대칭축을 가진다.
마름모의 대각선은 서로 수직으로 교차하지만, 직사각형의 대각선은 길이가 같다.
마름모의 변의 중점을 연결하여 만들어진 도형은 직사각형이며, 그 반대도 성립한다.

5. 타일링

5가지 2차원 격자 유형 중 하나는 마름모 격자이며, 중심 직사각형 격자라고도 한다.
마름모는 2차원 평면을 변과 변이 닿도록 타일링할 수 있으며, 60° 마름모를 포함하여 세 가지 다른 방식으로 주기적으로 타일링할 수 있다. 이는 마름모 타일링이다.

위상적 정사각형 타일링으로		30-60도 마름모 타일링으로

6. 3차원 도형과의 관계

마름모를 면으로 갖는 볼록 다면체에는 무한한 집합인 마름모 육면체가 포함되며, 이는 초입방체의 사영 외피로 볼 수 있다.

능면체(마름모 육면체라고도 함)는 3쌍의 평행한 면이 직사각형 대신 최대 3가지 유형의 마름모를 갖는다는 점을 제외하고 육면체(직사각형 평행육면체라고도 함)와 같은 3차원 도형이다.^[1]
마름모십이면체는 12개의 합동 마름모를 면으로 갖는 볼록 다면체이다.^[1]
마름모삼십면체는 30개의 황금 마름모(대각선이 황금비를 이루는 마름모)를 면으로 갖는 볼록 다면체이다.^[1]
큰 마름모삼십면체는 30개의 교차하는 마름모 면을 가진 비볼록 등면체 등각 다면체이다.^[1]
마름모육십면체는 마름모삼십면체의 별모양이다.^[1] 이는 정이십면체 대칭을 갖는 60개의 황금 마름모 면을 가진 비볼록 다면체이다.^[1]
마름모구십면체는 각 꼭짓점에서 3개, 5개 또는 6개의 마름모가 만나는 90개의 마름모 면으로 구성된 다면체이다.^[1] 60개의 넓은 마름모와 30개의 얇은 마름모가 있다.^[1]
마름모이십면체는 20개의 마름모 면으로 구성된 다면체로, 각 꼭짓점에서 3개, 4개 또는 5개가 만난다.^[1] 극축에 10개의 면이 있고 적도를 따라 10개의 면이 있다.^[1]

모든 마름모 면을 가진 다면체의 예
등면체		등면체 황금 마름모		2-등면체	3-등면체
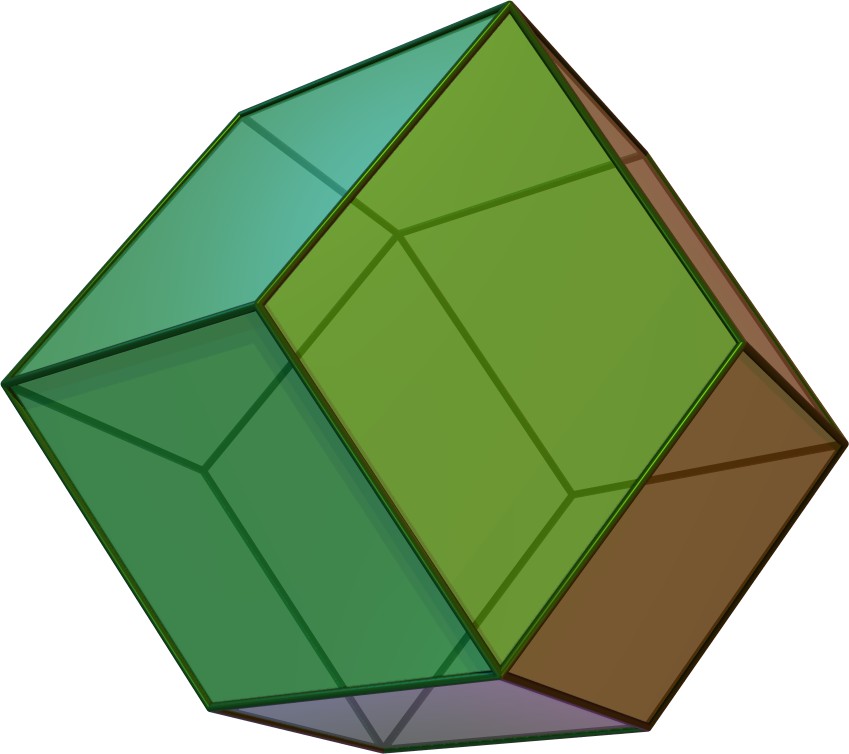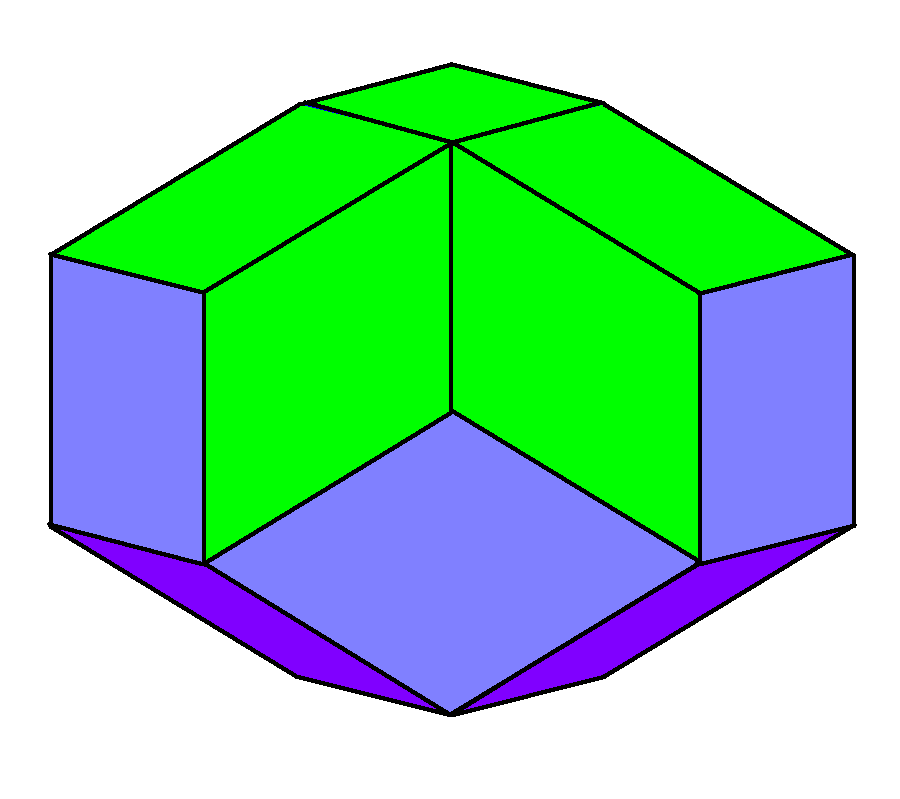삼각 사다리꼴 육면체	마름모십이면체	마름모삼십면체	마름모이십면체	마름모구십면체	능면체

참조

_[1] 서적 A Mathematical Space Odyssey: Solid Geometry in the 21st Century https://books.google[...] American Mathematical Soc. 2015-12-31
_[2] 간행물 The role and function of a hierarchical classification of quadrilaterals 1994-02
_[3] 웹사이트 ῥόμβος https://www.perseus.[...]
_[4] 웹사이트 ρέμβω https://www.perseus.[...]
_[5] 웹사이트 The Origin of Rhombus http://www.pballew.n[...] 2005-01-25
_[6] 서적 The Classification of Quadrilaterals. A Study of Definition https://books.google[...] Information Age Publishing 2008
_[7] 서적 Methods for Euclidean Geometry https://books.google[...] Mathematical Association of America 2010
_[8] 간행물 A Characterization of the Rhombus http://forumgeom.fau[...] 2016
_[9] 웹사이트 IMOmath, "26-th Brazilian Mathematical Olympiad 2004" https://imomath.com/[...] 2020-01-06
_[10] Mathworld Rhombus Rhombus
_[11] Youtube WildLinAlg episode 4 https://www.youtube.[...] Norman J Wildberger, Univ. of New South Wales 2010
_[12] 간행물 Equiangular cyclic and equilateral circumscribed polygons 2011-03

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com