몬테카를로 방법
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
몬테카를로 방법은 계산 이론, 수치 적분, 강화 학습, 통계학 등 다양한 분야에서 사용되는 계산 기법이다. 이 방법은 난수를 활용하여 문제를 해결하며, 특히 복잡한 시스템의 시뮬레이션이나 불확실성이 높은 문제에 유용하다. 몬테카를로 방법은 계산 복잡도 이론의 여러 클래스를 정의하는 데 사용되며, 수치 적분에서는 고차원 문제의 해결을 가능하게 한다. 또한, 게임 인공지능 분야에서는 몬테카를로 트리 탐색(MCTS)으로 발전하여 바둑과 같은 게임에서 인공지능의 성능을 향상시키는 데 기여했다. 이 외에도 물리학, 공학, 금융, 법률 등 다양한 분야에서 응용되고 있다.
더 읽어볼만한 페이지
- 계산물리학 - 다이너모 이론
다이너모 이론은 회전, 대류, 전기 전도성을 가진 유체가 자기장을 생성하고 유지하는 과정을 설명하며, 지구와 태양 같은 천체의 지속적인 자기장 존재를 설명하는 데 사용되고, 지구 외핵 액체 철의 대류와 코리올리 효과가 핵심적인 역할을 수행한다. - 계산물리학 - 분자동역학
분자동역학은 원자 및 분자의 움직임을 시뮬레이션하여 물질의 물리적 특성을 연구하는 계산 방법으로, 다양한 분야에서 활용되며 시뮬레이션 설계, 포텐셜 함수, 알고리즘, 소프트웨어 등 여러 요소에 의해 제약받는다. - 확률적 알고리즘 - 알고리즘 정보 이론
알고리즘 정보 이론은 콜모고로프 복잡성을 기반으로 객체의 정보량을 측정하는 척도를 제공하며, 최소 설명 길이 원리 등에 응용될 수 있다. - 확률적 알고리즘 - 몬테카를로 알고리즘
몬테카를로 알고리즘은 정확한 답을 보장하지 않는 확률적 알고리즘으로, 단측 또는 양측 오류를 가지며 반복 실행으로 오류를 줄일 수 있고, 라스베가스 알고리즘과 함께 랜덤 알고리즘의 주요 분류를 이루며 다양한 분야에 응용된다. - 몬테카를로 방법 - 메트로폴리스-헤이스팅스 알고리즘
메트로폴리스-헤이스팅스 알고리즘은 마르코프 연쇄 몬테카를로 방법으로, 확률 밀도 함수에 비례하는 함수를 알 때 원하는 확률 분포에서 난수열을 생성하며 통계 모델링, 데이터 분석 등에 응용된다. - 몬테카를로 방법 - 피셔-예이츠 셔플
피셔-예이츠 셔플은 유한 집합에서 임의의 순열을 생성하는 알고리즘으로, 피셔와 예이츠가 처음 소개한 후 더스텐펠트에 의해 컴퓨터에 최적화되었으며, 구현 시 편향 요인을 주의해야 한다.
| 몬테카를로 방법 | |
|---|---|
| 개요 | |
 | |
| 유형 | 확률적 알고리즘 |
| 풀이 영역 | 다양한 문제 영역 |
| 발견 시기 | 1940년대 |
| 상세 정보 | |
| 핵심 아이디어 | 무작위 표본 추출을 통한 근사 해법 |
| 활용 분야 | 수치 적분 최적화 시뮬레이션 금융 공학 물리학 화학 |
| 장점 | 비교적 간단한 구현 고차원 문제에 효과적 병렬 처리 용이 |
| 단점 | 정확도 보장 어려움 수렴 속도 느림 난수 생성 품질에 민감 |
| 역사 | |
| 어원 | 몬테카를로 시 (모나코 소재의 도박의 도시) |
| 개발 배경 | 맨해튼 계획 (핵무기 개발 프로젝트) |
| 주요 개발자 | 스타니스와프 울람 존 폰 노이만 니콜라스 메트로폴리스 |
| 작동 원리 | |
| 기본 개념 | 무작위 추출을 통해 원하는 값을 근사적으로 계산 |
| 예시 | 원주율 추정 (무작위 점 찍기 방식) |
| 수식 | (제공된 문서에 수식 이미지 파일명만 존재하므로, 수식 내용은 생략) |
| 응용 분야 | |
| 수학 | 수치 적분 (고차원 적분) 최적화 문제 |
| 물리학 | 통계 물리학 입자 물리 |
| 금융 공학 | 파생 상품 가격 결정 위험 관리 |
| 컴퓨터 과학 | 전역 조명 계산 (레이 트레이싱) 인공지능 |
| 변형 및 확장 | |
| 주요 기법 | MCMC (Markov Chain Monte Carlo) 깁스 샘플링 (Gibbs Sampling) 메트로폴리스-헤이스팅스 알고리즘 (Metropolis-Hastings Algorithm) 상호 작용 입자 방법 (Interacting Particle Method) 순차적 몬테카를로 방법 (Sequential Monte Carlo) |
| 관련 항목 | |
| 관련 알고리즘 | 준 몬테카를로 방법 (Quasi-Monte Carlo) 분산 감소 기법 (Variance Reduction Techniques) 병렬 몬테카를로 (Parallel Monte Carlo) |
| 관련 개념 | 난수 생성 (Random Number Generation) 표본 추출 (Sampling) 수치 해석 |
2. 계산 이론
계산 이론 분야에서 몬테카를로 방법은 오답할 확률의 상한이 주어지는 난수화 알고리즘 (랜덤 알고리즘)으로 정의된다. 소수 판별 문제에 대한 밀러-라빈 소수 판별법이 그 예이다. 밀러-라빈 소수 판별법은 주어진 숫자가 소수인 경우 확실하게 Yes라고 답하지만, 합성수인 경우에는 매우 낮은 확률로 No라고 답해야 할 것을 Yes라고 답하는 경우가 있다. 일반적으로 몬테카를로 방법은 독립적인 난수를 사용하여 반복하며, 실행 시간을 희생하면 오답할 확률을 얼마든지 작게 할 수 있다. 또한 몬테카를로 방법 중 임의의 입력에 대해 최대 시간 복잡도의 상한이 입력 크기의 다항식으로 주어지는 것을 효율적인 몬테카를로 방법이라고 한다.
몬테카를로 방법은 수치 적분에 유용하게 사용된다. 특히 함수가 많은 변수를 가질 때 발생하는 차원의 저주 문제를 해결하는 데 효과적이다.
이와 대조적으로 이론상 반드시 종료한다고 할 수는 없지만, 만약 답을 얻으면 반드시 정답인 난수화 알고리즘을 라스베이거스 알고리즘이라고 한다.
계산 복잡도 이론에서는 확률적 튜링 기계에 의한 모델링을 통해 몬테카를로 방법을 사용하여 해결할 수 있는 문제의 복잡도 클래스를 몇 가지 정의하고 있다. 대표적인 것으로는 '''RP''', '''BPP''', '''PP''' 등이 있다. 이러한 클래스와 '''P'''와 '''NP'''와의 관련성을 해명함으로써, 몬테카를로 방법과 같이 랜덤성을 포함하는 알고리즘으로 풀 수 있는 문제의 범위가 확대되고 있는지(P ≠ BPP 인지), 아니면 단순히 결정적 알고리즘으로 풀 수 있는 문제의 다항식 시간의 차수를 줄이고 있는 것인지(P=BPP 인지)는 계산 복잡도 이론의 주요 과제 중 하나이다. 현재, '''NP''' ⊂ '''PP''' , '''RP''' ⊆ '''NP'''임이 알려져 있지만 '''BPP'''와 '''NP''' 간의 관계는 알려져 있지 않다.
3. 수치 적분
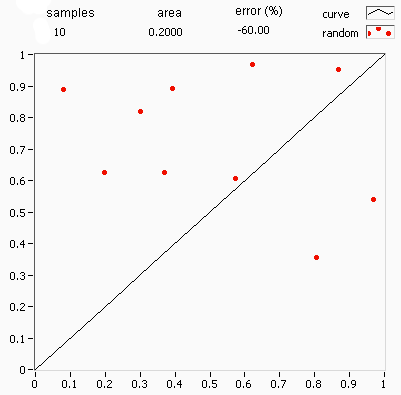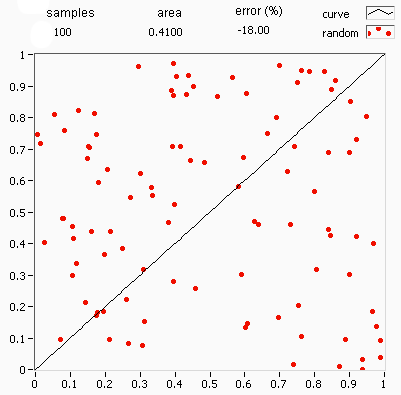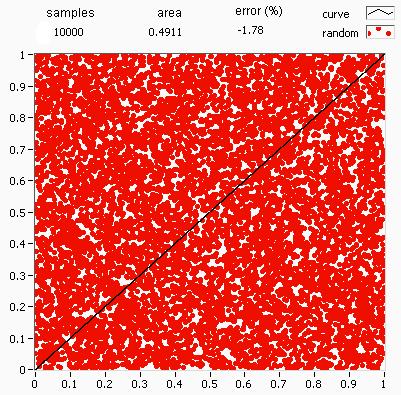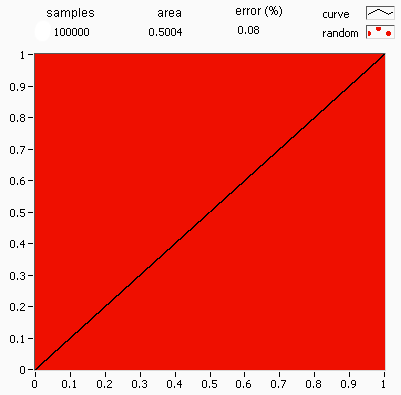
결정론적 수치 적분 알고리즘은 낮은 차원에서는 잘 작동하지만, 변수가 많아지면 계산량이 기하급수적으로 증가하고, 다차원 영역의 복잡한 경계 때문에 문제를 반복 적분으로 표현하기 어려워진다.
몬테카를로 방법은 이러한 문제를 해결하기 위해 무작위 표본 추출을 사용한다. 100차원 공간과 같이 함수가 합리적으로 잘 동작하는 문제에서 무작위로 점을 선택하고, 이 점들에서의 함수 값의 평균을 구해 적분값을 추정한다. 중심 극한 정리에 따르면 이 방법은 수렴을 보이며, 샘플링된 점의 수를 네 배로 늘리면 오차가 절반으로 줄어든다.
중요도 샘플링은 적분 함수가 큰 곳에서 더 자주 점을 무작위로 샘플링하는 방법으로, 몬테카를로 방법의 정확도를 높인다. 이를 위해서는 이미 적분을 알아야 하지만, 유사한 함수의 적분으로 근사하거나, 층별 샘플링, 재귀적 층별 샘플링, 적응형 우산 샘플링, VEGAS 알고리즘과 같은 적응형 알고리즘을 사용할 수 있다.
준 몬테카를로 방법은 Low-discrepancy sequence|초일양 분포열영어을 사용하여 영역을 더 잘 "채우고" 가장 중요한 점을 더 자주 샘플링하여 더 빠른 수렴을 얻을 수 있다. 이 방법은 Quasi-Monte Carlo method|준 몬테카를로 방법영어이라고 한다. 난수를 이용하는 것보다 수렴이 빨라지는 경우가 있지만, 순수하게 무작위적인 방법이 아니므로 정답을 얻을 가능성이 확률론적으로 낮아지는 경우가 있다.
초일양 분포열로는 다음과 같은 것들이 있다.
점을 샘플링하는 또 다른 방법은 체적에 대한 무작위 보행을 시뮬레이션하는 것이다. (Markov chain Monte Carlo|마르코프 연쇄 몬테카를로영어). 이러한 방법에는 메트로폴리스-헤이스팅스 알고리즘, 깁스 샘플링, 왕-란다우 알고리즘 및 순차적 몬테카를로 샘플러와 같은 상호 작용 유형 MCMC 방법론이 포함된다.[90]
''n''회 시뮬레이션을 수행하고 어떤 사건이 ''m''회 발생하면, 해당 사건이 발생할 확률은 ''m''/''n''으로 근사된다. 시행 횟수가 많을수록 더 정확한 근사값을 얻을 수 있다.
영역 ''R''의 면적 ''S''는, 영역 ''R''을 포함하는 면적 ''T''의 영역 내에서 무작위로 점을 찍고, 영역 ''R'' 안에 들어갈 확률 ''p''를 몬테카를로 방법으로 구하면, ''S'' = ''pT''로 근사할 수 있다.
''n'' 중적분
:
을 표본 크기 ''N''의 몬테카를로 방법으로 계산하려면, 0 이상 1 이하의 값을 갖는 ''n'' × ''N''개의 균일 난수
:
를 생성하여,
:
으로 하면, ''IN''이 적분값의 근사값이 된다. 균일 난수를 초균일 분포열로 바꾸면 준 몬테카를로 방법이 된다.
층화 추출법을 적용한 MISER 방법이나, 가중 샘플링을 수행하는 VEGAS 방법과 같은 개선된 알고리즘도 있다. MISER 방법은 적분 범위를 분할하고 각 영역에서 무작위 샘플링을 수행하며, 피적분 함수 값의 분산이 가장 큰 영역을 더 작은 영역으로 분할하여 추가 샘플링을 수행한다. VEGAS 방법은 피적분 함수 값이 큰 위치에 샘플링 점을 늘려 적분값에 기여가 큰 곳에 집중한다.
사다리꼴 공식, 심슨 공식, 이중 지수 함수형 수치 적분 공식 등도 있지만, 몬테카를로 방법은 다차원 문제에서 사용하기 쉽고 오차가 적다.
3. 1. 몬테카를로 적분 예제
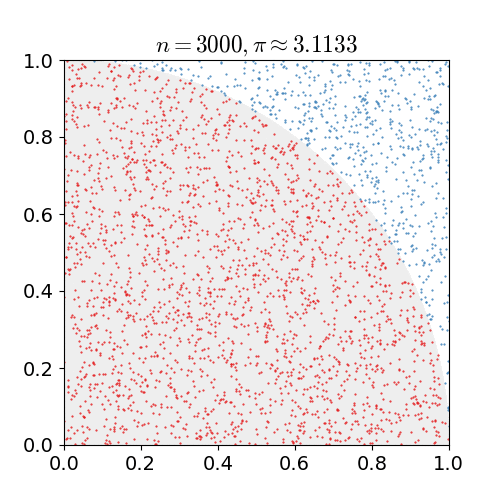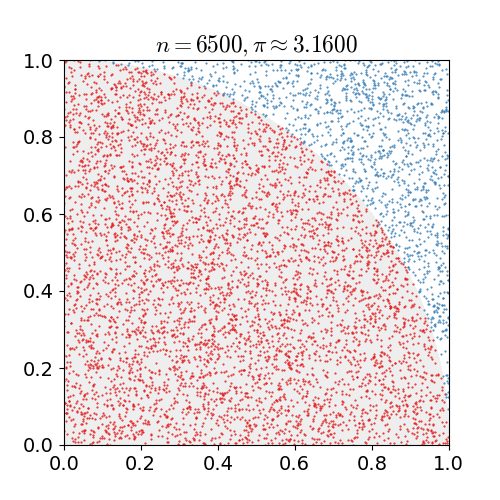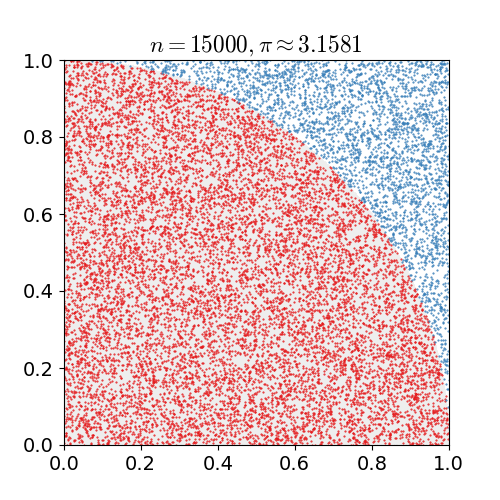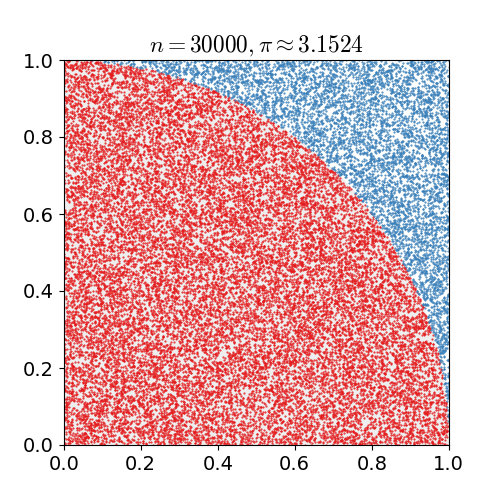

단위 정사각형에 내접하는 원의 사분원을 예로 들어보자. 두 면적의 비율이 이므로, 몬테카를로 방법을 사용하여 π의 값을 근사할 수 있다.
# 정사각형을 그리고, 그 안에 사분원을 내접시킨다.
# 정사각형 위에 주어진 수의 점들을 균등하게 뿌린다.
# 사분원 내부에 있는 점의 수를 센다. 즉, 원점으로부터의 거리가 1보다 작은 점의 수를 센다.
# 내부 점의 수와 총 표본 수의 비율은 두 면적의 비율인 의 추정치이다. 결과에 4를 곱하여 π를 추정한다.
이 과정에서 입력값의 영역은 사분원을 외접하는 정사각형이다. 정사각형 위에 곡물을 뿌려 무작위 입력값을 생성한 다음, 각 입력값에 대한 계산(사분원 내에 속하는지 여부 테스트)을 수행한다. 결과를 집계하면 최종 결과인 π의 근사값이 나온다.
여기에는 두 가지 중요한 고려 사항이 있다.
# 점들이 균등하게 분포되어 있지 않으면 근사값이 좋지 않다.
# 전체 정사각형에 무작위로 점이 몇 개만 배치되면 일반적으로 근사값이 좋지 않다. 평균적으로 더 많은 점을 배치할수록 근사값이 향상된다.
4. 강화 학습
기계 학습의 강화 학습에서 몬테카를로 방법은 경험을 통해 얻은 보상만을 바탕으로 상태 가치와 행동 가치를 추정하는 방법이다.[102]
5. 통계학
통계학에서 몬테카를로 실험의 기준은 사윌로스키에 의해 정립되었다.[68] 응용 통계학에서 몬테카를로 방법은 적어도 네 가지 목적으로 사용될 수 있다.
# 현실적인 데이터 조건에서 소표본에 대한 경쟁 통계량을 비교한다. 통계량의 제1종 오류와 검정력 특성은 고전적인 이론적 분포(예: 정규 분포, 코시 분포)에서 추출된 데이터에 대해 점근 조건(즉, 무한대 표본 크기 및 무한소 처리 효과)에서 계산할 수 있지만, 실제 데이터는 종종 이러한 분포를 갖지 않는다.[69]
# 가설 검정에 대한 구현을 제공하는데, 이는 순열 검정과 같은 정확한 검정(계산이 불가능한 경우가 많음)보다 효율적이며, 점근 분포에 대한 임계값보다 더 정확하다.
# 베이즈 추론에서 사후 분포로부터의 무작위 표본을 제공한다. 이 표본은 사후 분포의 모든 필수 특징을 근사하고 요약한다.
# 피셔 정보 행렬의 추정치를 형성하기 위해 평균화될 수 있는 음의 로그-우도 함수의 헤시안 행렬의 효율적인 무작위 추정치를 제공한다.[70][71]
몬테카를로 방법은 근사 무작위화와 순열 검정 사이의 타협점이기도 하다. 근사 무작위화 검정은 모든 순열의 지정된 부분 집합을 기반으로 한다(이는 어떤 순열이 고려되었는지에 대한 잠재적으로 엄청난 관리 작업이 필요하다). 몬테카를로 접근 방식은 지정된 수의 무작위로 추출된 순열을 기반으로 한다(순열이 두 번 이상 추출되는 경우 정밀도의 약간의 손실을 순열이 이미 선택되었는지 추적할 필요가 없는 효율성으로 교환한다).
통계학에서의 몬테카를로 방법의 하나로, 부트스트랩이 있다.
6. 난수(열)의 선택
몬테카를로 방법의 결과는 사용하는 난수의 품질에 크게 의존한다. 따라서 상황에 맞는 난수열을 선택하는 것이 중요하다.
- 의사 난수열: 의사 난수는 초기 상태에 따라 이후의 모든 수열이 결정되므로, 엄밀히 말해 "진정한 난수"는 아니다. 하지만 시뮬레이션에서는 재현 가능하다는 중요한 특징이 있다. 즉, 같은 초기 조건에서 동일한 결과를 얻을 수 있다.
- 물리 난수: 진정한 난수가 필요하거나, 의사 난수열 생성기의 초기 상태를 설정하기 위해 양질의 난수가 필요한 경우, 물리 현상을 이용하는 물리 난수(진성 난수)를 생성하는 하드웨어를 사용한다. 예를 들어, 다이오드의 PN 접합부에서 발생하는 열 잡음을 이용하거나, 방사성 원소를 사용할 수 있다.
- 초일양 분포열: 규칙성이 강한 수열로, 수치 적분에 사용된다.[103] 초일양 분포열을 사용하는 몬테카를로 방법을 준 몬테카를로 방법이라고 한다. 초일양 분포열은 '''저분산 수열''' 또는 '''준난수열'''[104]이라고도 불린다. 초일양 분포열을 수치 적분에 사용하면 정확도를 높일 수 있다.
7. 정밀도
몬테카를로 방법의 정밀도는 표본 크기에 따라 달라지며, 일반적으로 표본 크기가 커질수록 정밀도가 향상된다. 점이 균일하게 분포되지 않으면 근사치가 떨어지지만, 평균적으로 더 많은 점을 배치할수록 근사치가 개선된다.
원하는 신뢰 수준을 선택하고, z를 해당 신뢰 수준에 해당하는 ''z''-점수라고 할 때, ''s''2를 추정 분산("표본" 분산)이라고 하며, 다음 식으로 표현된다.
:[11][12]
''n'' ≤ ''k''이면, ''mk'' = m'';'' 충분한 표본 시뮬레이션이 수행되어 ''mk''가 ''μ''의 ''ε'' 이내에 있는지 확인되었다. 만약 ''n'' > ''k''이면, "처음부터" ''n''개의 시뮬레이션을 실행하거나, k개의 시뮬레이션이 이미 수행되었으므로 ''n'' – ''k''개의 시뮬레이션을 더 실행하고 그 결과를 표본 시뮬레이션의 결과에 추가할 수 있다.
개념적, 알고리즘적으로 단순함에도 불구하고, 몬테카를로 시뮬레이션과 관련된 계산 비용은 매우 높을 수 있다. 일반적으로 좋은 근사치를 얻기 위해 많은 표본이 필요하며, 단일 표본의 처리 시간이 길 경우 임의로 큰 총 실행 시간이 소요될 수 있다.[13] 이는 매우 복잡한 문제에서 심각한 제약이 되지만, 이 알고리즘의 병렬 처리 특성으로 인해 지역 프로세서, 클러스터, 클라우드 컴퓨팅, GPU, FPGA 등에서 병렬 컴퓨팅 전략을 통해 이러한 막대한 비용을 줄일 수 있다(아마도 실행 가능한 수준으로).[14][15][16][17]
확률론에 따르면 몬테카를로 방법에 의한 수치 적분의 정밀도는 샘플 사이즈 ''N''을 늘리면 대부분의 경우에 좋아진다. 샘플이 진정한 무작위 난수열인 경우, 몬테카를로 방법으로 얻을 수 있는 적분의 근사값의 참값으로부터의 오차는 다음과 같다.
:
샘플 사이즈 ''N''을 한없이 증대시키면 거의 확실히 0에 수렴한다(대수의 법칙). 이 수렴 속도에 관해서는 다음과 같다.
:
이는 Law of the iterated logarithm|반복 로그 법칙영어에 따른 것이다. 즉, 오차의 크기를 10분의 1배로 줄이기 위해서는 샘플 수 ''N''을 100배로 늘릴 필요가 있다.
이에 대해, 어떤 준 몬테카를로 방법에서는 적분 변수의 수를 ''n''이라고 할 때, 다음과 같다.
:
따라서 오차의 크기를 10분의 1배로 줄이기 위해서는 샘플 수 ''N''을 약 10배로 늘리는 것만으로 충분하다. 이것이 준 몬테카를로 방법을 사용하는 이점이다.[103] 단, 고차원 적분을 수행하는 경우에는 차원의 수 ''n''이 크므로 효과가 감소하여, 단순한 몬테카를로 방법이 더 좋은 결과를 제공하는 경우가 많다.
8. 응용 분야
몬테카를로 방법은 불확실성이 크거나 복잡한 시스템을 모델링하는 데 유용하며, 과학, 공학, 금융, 게임 등 다양한 분야에서 활용된다.
- 물리학: 전산 물리학, 물리 화학 등에서 열 차폐, 공기 역학 형태 설계, 방사선 재료 과학 등 다양한 분야에 응용된다.
- 공학: 민감도 분석 및 확률적 정량적 공정 설계 분석에 널리 사용된다.
- 금융 및 비즈니스: 금융 분야의 몬테카를로 방법은 사업 투자 분석, 프로젝트 관리, 옵션 가격 결정, 채무 불이행 위험 분석 등 다양한 분야에서 활용된다.
- 게임 인공지능: 몬테카를로 트리 탐색은 바둑과 같은 게임에서 최적의 수를 찾는 데 사용되는 기술이다.
- 기타: 전역 조명 계산, 미국 해안 경비대의 수색 및 구조 작전, 법률, 도서 출판 등 다양한 분야에 응용된다.
8. 1. 물리학
몬테카를로 방법은 전산 물리학, 물리 화학 및 관련 응용 분야에서 매우 중요하다. 복잡한 양자 색역학 계산에서 열 차폐 및 공기 역학 형태 설계, 방사선 선량 계산을 위한 방사선 수송 모델링에 이르기까지 다양한 응용 분야를 가지고 있다.[57][58][59] 통계 물리학에서 몬테카를로 분자 모델링은 전산 분자 역학의 대안이며, 몬테카를로 방법은 간단한 입자 및 고분자 시스템의 통계장 이론을 계산하는 데 사용된다.[33][60] 양자 몬테카를로 방법은 양자 시스템에 대한 다체 문제를 해결한다.[8][9][25] 방사선 재료 과학에서 이온 주입을 시뮬레이션하기 위한 이진 충돌 근사는 일반적으로 다음 충돌하는 원자를 선택하기 위해 몬테카를로 접근 방식에 기반한다.[61] 실험 입자 물리학에서 몬테카를로 방법은 검출기 설계, 동작 이해 및 실험 데이터와 이론 비교에 사용된다. 천체 물리학에서는 은하 진화[62]와 거친 행성 표면을 통과하는 마이크로파 방사선 전송 모델링과 같이 다양한 방식으로 사용된다.[63] 몬테카를로 방법은 또한 현대 일기 예보의 기초가 되는 앙상블 모델에도 사용된다.8. 2. 공학
몬테카를로 방법은 공학 분야에서 민감도 분석 및 확률적 정량적 공정 설계 분석에 널리 사용된다. 이는 일반적인 공정 시뮬레이션의 상호 작용적이고 공선적이며 비선형적인 동작에서 비롯된다. 예를 들면 다음과 같다.- 마이크로 전자 공학에서 몬테카를로 방법은 아날로그 신호 및 디지털 데이터 집적 회로의 상관 및 비상관 변화를 분석하는 데 사용된다.
- 지질 통계학 및 지질 금속학에서 몬테카를로 방법은 광물 처리 흐름도 설계를 뒷받침하고 정량적 위험 분석에 기여한다.[2]
- 유체 역학, 특히 희박 기체 역학에서 몬테카를로 방법은 직접 시뮬레이션 몬테카를로[64] 방법을 고효율 계산 알고리즘과 결합하여 유한한 누센 수 유체 흐름에 대한 볼츠만 방정식을 푸는 데 사용된다.[65]
- 자율 로봇에서 몬테카를로 국소화는 로봇의 위치를 결정할 수 있다. 이는 종종 칼만 필터 또는 입자 필터와 같은 확률적 필터에 적용되며, 이는 SLAM (동시적 위치 추정 및 지도 작성) 알고리즘의 핵심을 형성한다.
- 통신에서 무선 네트워크를 계획할 때, 설계는 주로 사용자 수, 위치 및 사용하려는 서비스에 따라 달라지는 다양한 시나리오에서 작동함을 입증해야 한다. 몬테카를로 방법은 일반적으로 이러한 사용자와 해당 상태를 생성하는 데 사용된다. 그런 다음 네트워크 성능을 평가하고, 결과가 만족스럽지 않으면 네트워크 설계는 최적화 프로세스를 거친다.
- 신뢰성 공학에서 몬테카를로 시뮬레이션은 구성 요소 수준의 응답을 바탕으로 시스템 수준의 응답을 계산하는 데 사용된다.
- 신호 처리 및 베이즈 추론에서 입자 필터 및 순차적 몬테카를로 기법은 상호 작용하는 경험적 측정을 사용하여 일부 시끄럽고 부분적인 관찰이 주어질 때 신호 프로세스의 사후 분포를 샘플링하고 계산하기 위한 평균장 입자 방법의 한 종류이다.[66]
8. 3. 금융 및 비즈니스
몬테카를로 시뮬레이션은 다양한 의사 결정 옵션의 결과에 영향을 미치는 위험과 불확실성을 평가하는 데 널리 사용된다. 비즈니스 위험 분석가는 몬테카를로 시뮬레이션을 통해 판매량, 상품 및 노동 가격, 이자율 및 환율과 같은 변수의 불확실성과 계약 취소 또는 세법 변경과 같은 특정 위험 사건의 전체 효과를 통합할 수 있다.[81]금융 분야의 몬테카를로 방법은 사업부 또는 기업 수준에서 프로젝트 투자 또는 기타 금융 평가를 분석하는 데 자주 사용된다. 각 작업에 대한 최악, 최상, 최빈값(most likely) 기간 추정치를 시뮬레이션하여 전체 프로젝트 결과를 파악하는 프로젝트 관리 일정 모델링에 활용할 수 있다.[81] 또한, 몬테카를로 방법은 옵션 가격 결정, 채무 불이행 위험 분석에도 사용된다.[82][83] 더불어, 의료 개입의 재정적 영향을 추정하는 데에도 사용될 수 있다.[84]
8. 4. 게임 인공지능
몬테카를로 방법은 게임에서 최적의 수를 찾는 데 유용한 몬테카를로 트리 탐색(MCTS) 기술로 발전했다. 가능한 수는 탐색 트리로 구성되며, 각 수의 장기적인 잠재력을 추정하기 위해 많은 무작위 시뮬레이션이 사용된다. 블랙 박스 시뮬레이터는 상대방의 수를 나타낸다.[72]몬테카를로 트리 탐색(MCTS) 방법은 다음 네 단계로 구성된다:[73]
1. 트리의 루트 노드에서 시작하여, 리프 노드에 도달할 때까지 최적의 자식 노드를 선택한다.
2. 리프 노드를 확장하고 그 자식 중 하나를 선택한다.
3. 해당 노드에서 시작하여 시뮬레이션된 게임을 진행한다.
4. 해당 시뮬레이션 게임의 결과를 사용하여 해당 노드와 상위 노드를 업데이트한다.
많은 시뮬레이션 게임을 거치면서, 수(move)를 나타내는 노드의 값은 올라가거나 내려가며, 이 노드가 좋은 수를 나타내는지 여부에 해당하는 결과를 얻게 된다.
몬테카를로 트리 탐색은 바둑,[74] 탠트릭스,[75] 배틀쉽,[76] 하바나,[77] 그리고 아리마와 같은 게임을 성공적으로 플레이하는 데 사용되었다.[78]
8. 5. 기타 응용 분야
몬테카를로 방법은 입력에 상당한 불확실성이 있고 많은 결합된 자유도를 가진 시스템의 현상을 시뮬레이션하는 데 특히 유용하며, 다음과 같은 분야에 응용된다.[13]- 경로 추적은 가능한 광선 경로의 무작위 표본을 추적하여 3D 장면을 렌더링한다. 주어진 픽셀을 반복적으로 샘플링하면 결국 샘플의 평균이 렌더링 방정식의 올바른 해로 수렴하여 현존하는 가장 물리적으로 정확한 3D 그래픽 렌더링 방법 중 하나가 된다.
- 전역 조명 계산에 사용되어, 비디오 게임, 건축, 디자인, 컴퓨터 생성 영화 및 영화 특수 효과에 적용되는 가상 3D 모델의 사실적인 이미지를 생성한다.
- 미국 해안 경비대는 수색 및 구조 작전 중 선박의 예상 위치를 계산하기 위해 컴퓨터 모델링 소프트웨어 SAROPS 내에서 몬테카를로 방법을 사용한다. 각 시뮬레이션은 제공된 변수를 기반으로 무작위로 분포된 최대 10,000개의 데이터 포인트를 생성할 수 있다.[79] 그런 다음 이러한 데이터의 외삽을 기반으로 수색 패턴이 생성되어 포괄 확률(POC) 및 탐지 확률(POD)을 최적화하며, 이 둘을 합하면 전체 성공 확률(POS)이 된다. 이는 확률 분포의 실제 적용으로, 인명과 자원을 모두 절약하면서 가장 신속하고 효율적인 구조 방법을 제공한다.[80]
- 위스콘신 주의 여성 청원인들이 괴롭힘 및 가정 폭력 신청에서 성공할 수 있도록 돕는 제안된 프로그램의 잠재적 가치를 평가하는 데 사용되었다. 이 프로그램은 여성들에게 더 나은 옹호를 제공하여 청원 성공을 돕고, 그 결과 강간 및 폭행의 위험을 줄이는 것을 목표로 했다. 그러나 금지 명령의 효과, 옹호 유무에 따른 청원인의 성공률 등 완벽하게 추정할 수 없는 많은 변수가 존재했다. 이 연구에서는 이러한 변수를 다양하게 변화시키는 실험을 진행하여 제안된 프로그램 전체의 성공 수준에 대한 전반적인 추정치를 도출했다.[85]
- 말레이시아의 도서 장르에 따른 도서 출판 수 시뮬레이션에도 사용되었다. 몬테카를로 시뮬레이션은 이전의 출판된 전국 도서 출판 데이터와 현지 시장의 도서 장르별 도서 가격을 활용했다. 몬테카를로 결과는 말레이시아인들이 어떤 종류의 도서를 좋아하는지 결정하는 데 사용되었으며, 말레이시아와 일본 간의 도서 출판을 비교하는 데 사용되었다.[86]
참조
[1]
논문
Why the Monte Carlo method is so important today
[2]
논문
Modeling Without Measurements
http://viewer.zmags.[...]
2009-10
[3]
논문
Equation of State Calculations by Fast Computing Machines
1953-06-01
[4]
논문
Monte Carlo sampling methods using Markov chains and their applications
1970-04-01
[5]
논문
The Multiple-Try Method and Local Optimization in Metropolis Sampling
2000-03-01
[6]
논문
Estimation via Markov Chain Monte Carlo
[7]
논문
Stationarity and Convergence of the Metropolis-Hastings Algorithm: Insights into Theoretical Aspects
[8]
서적
Nonlinear Markov processes
Cambridge University Press
[9]
서적
Mean field simulation for Monte Carlo integration
http://www.crcpress.[...]
Chapman & Hall/[[CRC Press]]
[10]
논문
Sequential Monte Carlo samplers
[11]
서적
Monte Carlo Theory, Methods and Examples
https://artowen.su.d[...]
Work in progress
2013
[12]
논문
Determining the number of Iterations for Monte Carlo Simulations of Weapon Effectiveness
https://apps.dtic.mi[...]
2004-04
[13]
서적
Explorations in Monte Carlo Methods
Springer
[14]
논문
On the parallelization approaches for Intel MIC architecture
[15]
논문
Uncertainty quantification through the Monte Carlo method in a cloud computing setting
[16]
논문
A GPU-based parallelized Monte-Carlo method for particle coagulation using an acceptance–rejection strategy
[17]
논문
Random number generators for large-scale parallel Monte Carlo simulations on FPGA
[18]
논문
Los Alamos Bets on ENIAC: Nuclear Monte Carlo Simulations, 1947-1948
https://ieeexplore.i[...]
2014
[19]
논문
Propagation of chaos for a class of non-linear parabolic equations
[20]
논문
A class of Markov processes associated with nonlinear parabolic equations
[21]
논문
Estimation of particle transmission by random sampling
https://dornsifecms.[...]
[22]
논문
Computing machinery and intelligence
[23]
논문
Esempi numerici di processi di evoluzione
[24]
논문
Symbiogenetic evolution processes realized by artificial methods
[25]
서적
Feynman–Kac formulae. Genealogical and interacting particle approximations
https://www.springer[...]
Springer
[26]
서적
Séminaire de Probabilités XXXIV
http://www.numdam.or[...]
Springer
[27]
논문
A Moran particle system approximation of Feynman–Kac formulae.
[28]
논문
Particle approximations of Lyapunov exponents connected to Schrödinger operators and Feynman–Kac semigroups
http://journals.camb[...]
2003
[29]
논문
Diffusion Monte Carlo Methods with a fixed number of walkers
http://qmcchem.ups-t[...]
2000
[30]
논문
Comment on Feynman–Kac Path-Integral Calculation of the Ground-State Energies of Atoms
1993
[31]
논문
Observations on the statistical iteration of matrices
1984
[32]
논문
Note on census-taking in Monte Carlo calculations
http://scienze-como.[...]
1948
[33]
논문
Monte-Carlo calculations of the average extension of macromolecular chains
1955
[34]
논문
Novel approach to nonlinear/non-Gaussian Bayesian state estimation
1993-04
[35]
논문
Monte carlo filter and smoother for non-Gaussian nonlinear state space models
[36]
논문
Non Linear Filtering: Interacting Particle Solution.
https://web.archive.[...]
1996
[37]
논문
Optimal Non-linear Filtering in GPS/INS Integration.
https://web.archive.[...]
1997-07
[38]
간행물
"Estimation and nonlinear optimal control: An unified framework for particle solutions"
LAAS-CNRS, Toulouse
1991-04
[39]
간행물
"Nonlinear and non Gaussian particle filters applied to inertial platform repositioning."
LAAS-CNRS, Toulouse
1991-09
[40]
간행물
"Estimation and nonlinear optimal control: Particle resolution in filtering and estimation: Experimental results"
1992-01
[41]
간행물
"Estimation and nonlinear optimal control: Particle resolution in filtering and estimation: Theoretical results"
1992-10
[42]
간행물
"Particle filters in radar signal processing: detection, estimation and air targets recognition"
LAAS-CNRS, Toulouse
1992-12
[43]
간행물
"Estimation and nonlinear optimal control: Particle resolution in filtering and estimation". Studies on: Filtering, optimal control, and maximum likelihood estimation.
1993-01
[44]
논문
Measure Valued Processes and Interacting Particle Systems. Application to Non Linear Filtering Problems
http://projecteuclid[...]
1998
[45]
논문
Convergence of a branching particle method to the solution of the Zakai
1998
[46]
논문
Nonlinear filtering and measure-valued processes
1997
[47]
논문
A particle approximation of the solution of the Kushner–Stratonovitch equation
1999
[48]
논문
Discrete filtering using branching and interacting particle systems
http://web.maths.uns[...]
1999
[49]
논문
On the stability of Measure Valued Processes with Applications to filtering
1999
[50]
논문
On the stability of interacting processes with applications to filtering and genetic algorithms
http://web.maths.uns[...]
2001
[51]
문서
1987
[52]
문서
2003
[53]
문서
2008
[54]
논문
An efficient sensitivity analysis method for modified geometry of Macpherson suspension based on Pearson Correlation Coefficient
[55]
문서
1992
[56]
논문
Radio-flaring Ultracool Dwarf Population Synthesis
2017-08-10
[57]
논문
GPU-based high-performance computing for radiation therapy
[58]
논문
Advances in kilovoltage x-ray beam dosimetry
2014-03
[59]
논문
Fifty years of Monte Carlo simulations for medical physics
[60]
문서
2009
[61]
논문
Tridyn — A TRIM simulation code including dynamic composition changes
1984-03-01
[62]
문서
1982
[63]
문서
1979
[64]
문서
Molecular Gas Dynamics
Clarendon, Oxford
1976
[65]
논문
A Scalar optimized parallel implementation of the DSMC technique
[66]
논문
Improvement of generalized finite difference method for stochastic subsurface flow modeling
2021-03-15
[67]
서적
Climate Change 2013 The Physical Science Basis
http://www.climatech[...]
Cambridge University Press
2013
[68]
논문
Simulating confidence for the Ellison-Glaeser Index
[69]
문서
2003
[70]
논문
Monte Carlo Computation of the Fisher Information Matrix in Nonstandard Settings
[71]
논문
Efficient Monte Carlo computation of Fisher information matrix using prior information
[72]
웹사이트
Monte-Carlo Tree Search: A New Framework for Game AI
http://sander.landof[...]
2017-10-28
[73]
웹사이트
Monte Carlo Tree Search - About
https://web.archive.[...]
2013-05-15
[74]
서적
Computers and Games
[75]
보고서
Monte-Carlo Tree Search in the game of Tantrix: Cosc490 Final Report
https://www.tantrix.[...]
[76]
웹사이트
Monte-Carlo Planning in Large POMDPs
https://web.archive.[...]
2017-10-28
[77]
서적
Computers and Games
[78]
웹사이트
Arimaa challenge – comparison study of MCTS versus alpha-beta methods
http://www.arimaa.co[...]
2017-10-28
[79]
웹사이트
How the Coast Guard Uses Analytics to Search for Those Lost at Sea
http://insights.dice[...]
2014-01-03
[80]
웹사이트
Search Modeling and Optimization in USCG's Search and Rescue Optimal Planning System (SAROPS)
http://www.ifremer.f[...]
2017-10-28
[81]
웹사이트
Project Risk Simulation (BETA)
https://risk.octigo.[...]
2024-05-21
[82]
서적
Numerical Methods in Finance
Springer Berlin Heidelberg
2012
[83]
서적
Handbook of Monte Carlo Methods
John Wiley & Sons
[84]
논문
A Monte Carlo simulation approach for estimating the health and economic impact of interventions provided at a student-run clinic
[85]
웹사이트
Increasing Access to Restraining Orders for Low Income Victims of Domestic Violence: A Cost-Benefit Analysis of the Proposed Domestic Abuse Grant Program
https://web.archive.[...]
State Bar of Wisconsin
2016-12-12
[86]
논문
Perbandingan Penerbitan dan Harga Buku Mengikut Genre di Malaysia dan Jepun Menggunakan Data Akses Terbuka dan Simulasi Monte Carlo
http://web.usm.my/km[...]
2021-10-29
[87]
문서
Press, Teukolsky, Vetterling, Flannery, 1996
[88]
논문
Adaptive umbrella sampling: Self-consistent determination of the non-Boltzmann bias
1986-12-31
[89]
논문
Probability Distributions for Complex Systems: Adaptive Umbrella Sampling of the Potential Energy
1997-12-31
[90]
논문
Sequential Monte Carlo samplers
[91]
문서
Spall, J. C. (2003), Introduction to Stochastic Search and Optimization: Estimation, Simulation, and Control, Wiley, Hoboken, NJ. http://www.jhuapl.edu/ISSO
[92]
문서
Mosegaard, Tarantola, 1995
[93]
문서
Tarantola, 2005
[94]
문서
McCracken, D. D., (1955) The Monte Carlo Method, Scientific American, 192(5), pp. 90-97
[95]
문서
Elishakoff, I., (2003) Notes on Philosophy of the Monte Carlo Method, International Applied Mechanics, 39(7), pp.753-762
[96]
문서
Grüne-Yanoff, T., & Weirich, P. (2010). The philosophy and epistemology of simulation: A review, Simulation & Gaming, 41(1), pp. 20-50
[97]
문서
van der Corput sequence
[98]
문서
Halton sequence
[99]
문서
Sobol sequence
[100]
문서
Niederreiter sequence
[101]
문서
Faure sequence
[102]
서적
Reinforcement Learning: An Introduction
http://incompleteide[...]
[103]
서적
C言語による最新アルゴリズム事典
技術評論社
[104]
문서
quasi-random sequence
[105]
논문
Why the Monte Carlo method is so important today
https://semanticscho[...]
[106]
논문
The beginning of the Monte Carlo method
http://library.lanl.[...]
[107]
논문
Modeling Without Measurements
http://viewer.zmags.[...]
2009-10
[108]
논문
Equation of State Calculations by Fast Computing Machines
https://semanticscho[...]
1953-06-01
[109]
논문
Monte Carlo sampling methods using Markov chains and their applications
https://semanticscho[...]
1970-04-01
[110]
논문
The Multiple-Try Method and Local Optimization in Metropolis Sampling
https://semanticscho[...]
2000-03-01
[111]
논문
Estimation via Markov Chain Monte Carlo
[112]
논문
Stationarity and Convergence of the Metropolis-Hastings Algorithm: Insights into Theoretical Aspects
[113]
서적
Nonlinear Markov processes
Cambridge Univ. Press
[114]
서적
Mean field simulation for Monte Carlo integration
http://www.crcpress.[...]
Chapman & Hall/CRC Press
[115]
서적
Mean field simulation for Monte Carlo integration
http://www.crcpress.[...]
Chapman & Hall/CRC Press
[116]
논문
Sequential Monte Carlo samplers
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com