이동평균

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

이동평균은 금융, 공학 등 다양한 분야에서 사용되는 데이터 분석 기법으로, 데이터의 추세를 파악하고 노이즈를 줄이는 데 활용된다. 이동평균에는 단순이동평균(SMA), 가중이동평균(WMA), 지수이동평균(EMA), 누적이동평균(CMA) 등 여러 종류가 있으며, 각기 다른 방식으로 데이터에 가중치를 부여하여 평균을 계산한다. 단순이동평균은 각 데이터에 동일한 가중치를 부여하고, 가중이동평균은 최근 데이터에 더 큰 가중치를 부여하며, 지수이동평균은 지수적으로 가중치를 감소시킨다. 누적이동평균은 데이터 스트림의 모든 데이터에 대한 평균을 계산한다. 이 외에도 수정 이동 평균(MMA), 삼각 이동 평균(TMA), 이동 중앙값 등의 변형된 이동평균 방법이 존재하며, 데이터의 특성과 분석 목적에 따라 적합한 이동평균 방법을 선택하여 사용한다.

더 읽어볼만한 페이지

기술적 분석 - 다우 이론
다우 이론은 시장의 움직임을 예측하기 위한 기술적 분석 방법론으로, 세 가지 움직임과 세 단계로 구성된 시장 추세, 주식 시장 평균의 상호 확인, 거래량에 의한 추세 확인 등을 핵심으로 하며 투자 전략 수립에 도움을 주지만 비판과 재평가도 존재한다.
기술적 분석 - 일목균형표
일목균형표는 시간 개념을 중요시하여 주식 시장의 변화 시점을 예측하는 기술적 분석 지표로, 여러 요소로 구성되어 시장 추세와 지지/저항 수준을 파악하고 현재와 미래의 시세 흐름 및 매수/매도 신호를 제공한다.
시계열 분석 - 공적분
공적분은 불안정한 시계열 변수들 간의 장기적인 안정 관계를 나타내는 개념으로, 개별 시계열이 불안정하더라도 특정 선형 결합이 안정적인 경우를 설명하며, 엥글-그레인저 2단계 방법, 요한센 검정 등으로 검정한다.
시계열 분석 - ARCH 모형
ARCH 모형은 시계열 데이터의 변동성 군집 현상을 설명하기 위해 개발된 통계적 모형이며, 과거 오차항의 제곱을 사용하여 조건부 변동성을 나타낸다.
통계 차트와 다이어그램 - 레이더 차트
레이더 차트는 여러 변수의 상대적 크기를 시각적으로 비교하는 차트로, 중심점에서 방사형으로 뻗어나가는 축을 사용하여 데이터 패턴 파악, 유사성 비교, 이상치 탐색 등에 활용되지만, 면적 왜곡 등의 단점도 존재하여 데이터 해석 시 주의가 필요하다.
통계 차트와 다이어그램 - 연표
연표는 시간 순서에 따라 사건, 현상, 변화 등을 시각적으로 표현하는 방식으로, 역사 기록에서 시작하여 표 형태로 발전했으며 다양한 분야에서 활용되고 여러 형태로 정보를 제시한다.

이동평균

2. 단순이동평균 (SMA)

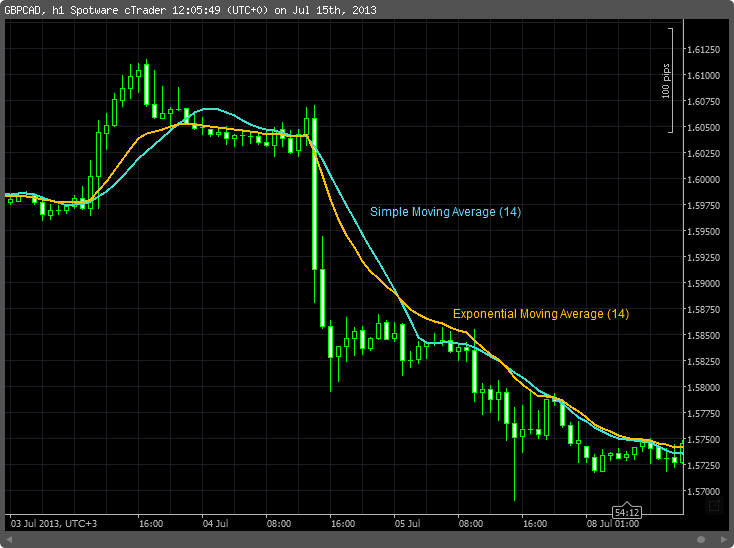
금융 분야에서 '''단순이동평균'''(Simple Moving Average, SMA)은 이전 n개 데이터의 비가중 평균이다. 과학 및 공학 분야에서는 일반적으로 중앙값 양쪽에 있는 동일한 수의 데이터에서 평균을 가져오며, 이로써 평균의 변동은 시간이 아닌 데이터의 변동과 일치하게 된다.

선택하는 기간은 단기, 중기 또는 장기 등 관심 있는 이동 유형에 따라 다르다. 금융 용어에서 이동평균 수준은 하락장에서의 지지선 또는 상승장에서의 저항선으로 해석될 수 있다.

2. 1. 단순이동평균의 계산

n일 동안의 단순이동평균은 최근 n일 동안의 종가를 모두 더한 후 n으로 나누어 계산한다. 예를 들어, 주식시장에서 n일 동안의 주가에 대한 단순이동평균은 이전 n일 동안의 종가의 평균이다. 그 가격이

p_M, p_{M-1}, \dots, p_{M-(n-1)}

일 경우 공식은 다음과 같다.^[13]

:

\begin{align}\overline{p}_\text{SM} &= \frac{p_M + p_{M-1} + \cdots + p_{M-(n-1)}}{n} \\&= \frac{1}{n} \sum_{i=0}^{n-1} p_{M-i}.\end{align}

연속적인 값을 계산할 때는 새로운 값을 더하고 가장 오래된 값을 빼는 방식으로 효율적인 계산이 가능하다. 다음 날의 단순 이동 평균을 구하려면, 전날 계산한 평균값에서 가장 오래된 종가를 뺀 값을 n으로 나누고, 새로운 종가를 더한 값을 n으로 나누어 더해주면 된다.^[14]

:

\overline{p}_\text{SM} = \overline{p}_{\text{SM},\text{prev}} + \frac{1}{n} (p_M - p_{M-n}).

2. 2. 단순이동평균의 특징과 한계

단순이동평균(SMA)은 계산이 간단하고 이해하기 쉽다는 장점이 있다. 주식시장에서 n일 동안의 주가에 대해 이전 n일의 종가 평균을 구하는 방식으로, 다음 공식으로 계산할 수 있다.

:

\overline{p}_\text{SM} = \frac{p_M + p_{M-1} + \cdots + p_{M-(n-1)}}{n} = \frac{1}{n} \sum_{i=0}^{n-1} p_{M-i}.

연속적인 값을 계산할 때는 새로운 값을 더하고 가장 오래된 값을 빼는 방식으로 계산을 단순화할 수 있다.

:

\overline{p}_\text{SM} = \overline{p}_{\text{SM},\text{prev}} + \frac{1}{n} (p_M - p_{M-n}).

하지만 단순이동평균은 몇 가지 한계점을 가지고 있다.

모든 데이터에 동일한 가중치를 부여하기 때문에, 최근의 추세를 반영하는 데 시간이 걸릴 수 있다.
단기적인 신호에 민감하게 반응하지 못하고, 때로는 실제 추세와 반대되는 신호를 생성할 수 있다.^[2] 예를 들어, 데이터의 저점 위치에 고점이 나타나는 예상치 못한 결과가 발생할 수 있다.
또한, 일부 빈번한 변동이 제대로 제거되지 않아 결과가 예상보다 부드럽지 않을 수 있다.

3. 가중이동평균 (WMA)

가중이동평균(WMA, Weighted Moving Average)은 최근 데이터에 더 큰 가중치를 부여하여 단순이동평균의 단점을 보완한 방법이다. 가중평균은 샘플 창의 다른 위치에 있는 데이터에 다른 가중치를 부여하기 위해 계수를 곱한 평균이다. 수학적으로 가중이동평균은 고정 가중 함수를 사용한 기준점의 합성곱이다. 금융 데이터의 기술적 분석에서는 가중치가 등차수열로 감소하는 방식을 주로 사용한다.^[25]

위 그림은 *n* = 15인 경우의 가중이동평균에서 가중치가 어떻게 변화하는지 보여준다. 가장 최근 데이터에 가장 큰 가중치가 부여되고, 오래된 데이터일수록 가중치가 점차 감소하여 0에 가까워진다. ''n''일 가중이동평균에서 최신 날짜의 가중치는 ''n'', 두 번째로 최근 날짜는 ''n-1''과 같이 1씩 감소하며, 가중치가 1이 될 때까지 이 과정이 반복된다.^[4]

3. 1. 가중이동평균의 계산

가중이동평균(WMA)은 각 데이터에 서로 다른 가중치를 부여하여 계산하는 평균값이다. 특히 금융 데이터의 기술적 분석에서 사용되는 가중이동평균은 가중치가 등차수열 형태로 감소하는 특징을 갖는다.^[25]

일반적으로 선형 가중이동평균(LWMA)이 사용되며, 최근 데이터에 가장 큰 가중치를 부여하고, 과거 데이터로 갈수록 가중치가 선형적으로 감소한다. 예를 들어, *n*일 가중이동평균에서 가장 최근 데이터의 가중치는 *n*, 그 전날은 *n*-1과 같이 감소하며, 가중치가 1이 될 때까지 줄어든다.^[4]

n*일 가중이동평균의 계산 공식은 다음과 같다.

:

\text{WMA}_{M} = { n p_{M} + (n-1) p_{M-1} + \cdots + 2 p_{(M-n+2)} + p_{(M-n+1)} \over n + (n-1) + \cdots + 2 + 1}

여기서 분모는 삼각수

n(n+1)\over2

로 계산할 수 있다.

위 그림은 가중치가 가장 최근 데이터에 대한 가장 높은 값에서 0까지 어떻게 감소하는지를 보여준다.

연속적인 값에 대한 WMA를 계산할 때,

\text{WMA}_{M+1}

과

\text{WMA}_{M}

의 분자 차이는

np_{M+1} - p_{M} - \dots - p_{M-n+1}

이다.

p_{M} + \dots + p_{M-n+1}

의 합을

\text{Total}_{M}

으로 표시하면 다음과 같이 나타낼 수 있다.

:

\text{Total}_{M+1} = \text{Total}_M + p_{M+1} - p_{M-n+1}

:

\text{Numerator}_{M+1} = \text{Numerator}_M + n p_{M+1} - \text{Total}_M

:

\text{WMA}_{M+1} = { \text{Numerator}_{M+1} \over n + (n-1) + \cdots + 2 + 1}

3. 2. 가중이동평균의 특징

가중이동평균(WMA)은 각 데이터에 서로 다른 가중치를 부여하여 평균을 계산하는 방식이다. 특히 선형 가중이동평균(LWMA)은 가중치를 선형적으로 감소시키는 기법을 말한다. 예를 들어, ''n''일간의 WMA에서는 가장 최근 데이터에 ''n''의 가중치를, 그 전날에는 ''n-1'', 이런 식으로 가중치를 1씩 줄여나가 1이 될 때까지 계산한다.^[25]^[4]

위 그림은 WMA에서 가중치가 어떻게 감소하는지를 보여준다. 가장 최근 데이터에 가장 높은 가중치가 부여되고, 오래된 데이터일수록 가중치가 점차 감소하여 0에 수렴한다.

WMA는 단순이동평균보다 최근 데이터에 더 큰 가중치를 주기 때문에 최근 추세를 더 잘 반영한다. 그러나 여전히 과거 데이터의 영향을 받기 때문에, 급격한 변화를 즉시 반영하지 못하는 한계가 있다.

4. 지수이동평균 (EMA)

'''지수이동평균'''(Exponential Moving Average^영어^[26]) 또는 '''지수가중이동평균'''(Exponentially Weighted Moving Average^영어)은 지수적으로 감소하는 가중치를 적용하는 필터다. 오래된 데이터에 대한 가중치는 기하 급수적으로 감소하지만 0이 되지는 않는다.

지수 이동 평균은 지수 가중 이동 평균이라고도 불리며, 가중치가 지수 함수적으로 감소하는 방식을 사용한다. 최근 데이터를 중시하면서도, 오래된 데이터를 완전히 버리지 않는 특징을 가지고 있다. 가중치의 감소 정도는 0과 1 사이의 값을 갖는 평활화 계수(α)로 결정되며, 이 값에 따라 과거 데이터의 영향력이 조절된다.

EMA는 '''지수 평활 평균'''(Exponential Average^영어)이라고도 불린다.^[5]

4. 1. 지수이동평균의 계산

지수이동평균(EMA)의 계산은 평활화 계수(α)를 사용하며, 재귀적으로 계산할 수 있다. α는 0과 1 사이의 값을 가지며, α가 클수록 최근 데이터에 더 큰 가중치가 부여된다.^[26]

:

S_t = \begin{cases}Y_1,                      & t = 1 \\\alpha \cdot Y_t + (1 - \alpha) \cdot S_{t-1}, & t > 1\end{cases}

''α'': 평활상수로, 0과 1 사이의 값을 가지며 가중치 감소 정도를 나타낸다. ''α'' 가 클수록 오래된 관측치가 더 빨리 감소한다.
''Y _t'': 기간 ''t'' 에서의 값이다.
''S _t'': 임의의 기간 ''t'' 에서의 지수이동평균 값이다.

일반적으로 α = 2 / (N + 1) 공식을 사용하여 N일 단순이동평균과 유사한 가중치를 갖는 EMA를 계산한다.

\alpha_{\mathrm{EMA}} = 2 / \left(N_{\mathrm{SMA}} + 1\right)

일 때 단순이동평균과 지수이동평균의 가중치가 같은 값을 갖기 때문이다.

''N''일간의 EMA라고 하는 경우의 ''N''은 단순히 계수 α를 나타낼 뿐이며, 실제 계산은 ''N''일간의 데이터만으로는 끝나지 않는다. 다만, 최근 ''N''일간의 데이터가 EMA에서 86%의 가중치를 갖는다.

99.9%의 가중치(정확도)로 계산하고 싶은 경우에는, 계산할 항목 수를

k={ \log (0.001)  \over \log (1-\alpha)}

로 하면 된다.

\log\,(1-\alpha)

는 ''N''이 증가함에 따라

-\alpha = {-2 \over {N+1}}

에 가까워지기 때문에, ''N''이 클 때는

k=3.45(N+1)

로 하면 거의 99.9%의 정확도가 된다.

4. 2. 지수이동평균의 특징

지수이동평균(EMA)은 지수가중이동평균(EWMA)이라고도 불리며, 최근 데이터에 더 많은 가중치를 두면서 오래된 데이터의 영향은 지수적으로 감소시키는 방식으로 계산된다. Exponential Moving Average^영어 (EMA)는 Exponentially Weighted Moving Average^영어 (EWMA) 또는 Exponentially Smoothed Moving Average^영어라고도 한다. 이러한 특징 덕분에 단순이동평균이나 가중이동평균에 비해 최근의 추세를 더 빠르게 반영할 수 있다.^[5]

오래된 데이터에 대한 가중치는 지수적으로 감소하지만, 완전히 0이 되지는 않는다. 즉, 과거 데이터도 어느 정도 영향을 미치지만, 그 영향력은 시간이 지날수록 점점 줄어든다.^[6]

EMA 계산에는 0과 1 사이의 값을 가지는 평활화 계수 α (알파)가 사용된다. α 값이 클수록 최근 데이터에 더 큰 가중치가 부여되고, 오래된 데이터의 영향은 더 빠르게 감소한다. α는

\alpha={2\over{N+1}}

와 같이 N일 동안의 기간으로 표현할 수 있다. 예를 들어 N=19라면 α=0.1이 된다.^[16]

EMA는 초기값 설정에 따라 값이 달라질 수 있다. 보통 첫 번째 EMA 값 (S₂)은 첫 번째 데이터 값 (Y₁)으로 설정하거나, 처음 몇 개의 데이터의 평균값으로 설정한다. α 값이 작을수록 초기값 설정이 중요하지만, α 값이 크면 초기값의 영향은 빠르게 줄어든다.^[16]

α 값에 따라서도 EMA의 추세 반영 속도가 달라진다. α 값이 크면 최근 데이터의 영향을 크게 받아 추세를 빠르게 반영하고, α 값이 작으면 과거 데이터의 영향을 더 많이 받아 추세 반영이 느려진다.^[16]

5. 누적이동평균 (CMA)

'''누적이동평균'''(Cumulative moving average, CMA)은 데이터가 순서대로 들어올 때, 현재까지의 모든 데이터의 평균을 계산하는 방식이다. 예를 들어, 투자자는 특정 주식에 대한 현재까지 모든 주식 거래의 평균 가격을 원할 수 있다.

새로운 거래가 발생할 때마다, 거래 시점의 평균 가격은 현재까지의 모든 거래에 대해 누적 평균을 사용하여 계산할 수 있다. 일반적으로 균등하게 가중된 ''N'' 값들의 시퀀스인 $x_1. \ldots, x_n$ 의 현재까지 평균은 다음과 같다.

: $\textit{CMA}_n = {{x_1 + \cdots + x_n} \over n}\,.$

새로운 값 $x_{n+1}$ 이 주어지면 다음 공식을 사용하여 누적 평균을 간단히 업데이트할 수 있다.

: $\textit{CA}_{n+1} = .$

따라서 현재 누적 평균은 이전 누적 평균에 ''n''을 곱한 값에 최신 데이터를 더한 값을 지금까지 받은 점의 수, 즉 ''n''+1로 나눈 값과 같다. 모든 데이터가 도착하면(), 누적 평균은 최종 평균과 같아진다. ^[23]

5. 1. 누적이동평균의 계산

새로운 데이터가 추가될 때마다 이전 누적이동평균과 새로운 데이터를 사용하여 업데이트한다.

이를 계산하는 가장 간단한 방법은 모든 데이터를 저장하고, 새 데이터가 들어올 때마다 지금까지의 모든 데이터의 합계를 계산하고 데이터 개수로 나누는 것이다. 그러나 이 방법은 데이터가 많아질수록 계산량이 많아진다.

좀 더 효율적인 방법은 다음과 같은 공식을 사용하여 누적 평균을 업데이트하는 것이다.

:

\textit{CA}_{n+1} = .

여기서,

$\textit{CA}_{n+1}$ 은 새로운 데이터 $x_{n+1}$ 이 추가된 후의 누적 평균이다.
$\textit{CA}_n$ 은 이전까지의 누적 평균이다.
$n$ 은 이전까지의 데이터 개수이다.

이 공식에 따르면, 새로운 누적 평균은 이전 누적 평균에 이전 데이터 개수를 곱한 값에 새로운 데이터를 더한 후, 전체 데이터 개수 (n+1)로 나누어 계산한다.

모든 데이터가 도착하면, 누적 평균은 최종 평균과 같아진다.^[23]

5. 2. 누적이동평균의 특징

누적이동평균(Cumulative moving average, CMA)은 데이터가 순차적으로 들어올 때, 현재 시점까지의 모든 데이터의 평균을 계산하는 방법이다. 투자자는 이 방법을 사용하여 특정 주식의 모든 거래에 대한 평균 가격을 구할 수 있다.^[23]

새로운 거래가 발생할 때마다, 현재까지의 모든 거래 가격을 더한 후 거래 횟수로 나누어 누적 평균을 계산한다. 이 값은 현재까지의 주식 평균 매수 단가를 나타낸다. 새로운 데이터(x_n+1)가 들어오면, 다음 공식을 사용하여 누적 평균을 업데이트할 수 있다.^[23]

: ''CA''_n+1 = ( (x_n+1 + n * ''CA''_n) / (n+1) )

이 공식은 새로운 데이터와 이전 누적 평균을 사용하여 현재 누적 평균을 쉽게 계산할 수 있게 해준다. 모든 데이터가 도착하면 (n = N), 누적 평균은 최종 평균과 같아진다. 이처럼 누적 평균을 사용하면 데이터의 전체적인 추세를 파악하는 데 유용하며, 투자자가 특정 주식의 평균 매수 단가를 쉽게 계산할 수 있다.^[23]

6. 수정 이동 평균 (MMA)

수정 이동 평균(Modified Moving Average; MMA)은 러닝 이동 평균(Running Moving Average, RMA), 평활 이동 평균(Smoothed Moving Average) 등으로도 불린다.

정의는 다음과 같다.

:MMA|MMA^영어 = {(N - 1) × MMA|MMA^영어 + 가격} / N

이는 α = 1 / N 으로 한 지수 이동 평균이다.

7. 삼각 이동 평균 (TMA)

삼각 이동 평균(TMA)은 단순 이동 평균을 두 번 적용한 것이다.^[1]

정의는 다음과 같다. ''w''는 (N+1)/2의 올림 값이다.

: $\text{TMA} = \text{SMA}(\text{SMA}(\text{가격}, w), w)$

가중치의 그래프는 이등변삼각형이 된다.^[1] ''w'' - 1일 전에 가장 큰 가중치가 적용된다.^[1]

8. 기타 이동 평균

연속 이동 평균은 주어진 함수 f에 대해 특정 구간에서의 적분값을 구간의 폭으로 나누어 계산하는 방식이다. 이를 통해 함수의 그래프를 부드럽게 만들 수 있다. 적분 구간의 폭(ε)이 클수록 더 부드러운 그래프를 얻는다.

주식 거래에서는 거래량에 따라 가중치를 부여하는 거래량 가중 방식이 사용되기도 한다. 계리 분야에서는 스펜서의 15점 이동 평균이 사용되는데, 이는 특정 가중 계수를 사용하여 2차 또는 3차 다항식 형태의 데이터를 변형시키지 않고 유지하는 특징을 갖는다.^[7]

금융 외 분야에서도 다양한 가중 이동 평균이 활용되며, 각 가중 함수(커널)는 고유한 특성을 지닌다. 공학과 과학 분야에서는 필터의 주파수 및 위상 응답을 통해 데이터에 적용되는 왜곡을 이해하는 것이 중요하다. 이동 평균은 데이터를 평활화하는 것 외에도 저역 통과 필터의 역할을 하므로, 사용되는 필터의 효과를 이해하고 적절한 필터를 선택해야 한다.

8. 1. 정현 가중 이동 평균 (SWMA)

가중 이동 평균에서 가중치 부여에 정현파(삼각함수)를 이용한다. 선형 가중 이동 평균에 가까운

\cos

를 이용하는 방법과 삼각 이동 평균에 가까운

\sin

을 이용하는 방법이 있다.

8. 2. 콜모고로프-주르벤코 필터 (KZ 필터)

단순 이동 평균을 여러 번 반복하여 적용하는 필터를 콜모고로프-주르벤코 필터(KZ 필터)라고 한다. 이 필터는 단순 이동 평균보다 주파수 특성이 양호하다.^[7] 반복 횟수를 충분히 늘리면, KZ 필터의 임펄스 응답은 가우스 함수에 점근한다.

9. 이동 중앙값

통계적 관점에서 볼 때, 시계열의 기본 추세를 추정하는 데 사용되는 이동 평균은 급격한 충격이나 기타 이상치와 같은 희귀한 사건에 취약하다. 추세에 대한 보다 강력한 추정치는 ''n''개의 시간 지점에 대한 '''단순 이동 중앙값'''이다.

: $\widetilde{p}_\text{SM} = \text{Median}( p_M, p_{M-1}, \ldots, p_{M-n+1} )$

여기서 중앙값은 괄호 안의 값을 정렬하고 가운데 값을 찾는 방식으로 구한다. ''n''의 값이 클수록 중앙값은 색인 가능한 스킵 리스트를 업데이트하여 효율적으로 계산할 수 있다.^[10]

추세에 대한 변동이 정규 분포를 따르면 이동 평균이 시계열의 기본 추세를 복구하는 데 최적이지만, 정규 분포는 추세에서 매우 큰 편차에 높은 확률을 두지 않으므로 이러한 편차가 추세 추정에 불균형적으로 큰 영향을 미친다. 변동이 라플라스 분포를 따른다고 가정하면 이동 중앙값이 통계적으로 최적임이 입증될 수 있다.^[11] 주어진 분산에 대해 라플라스 분포는 정규 분포보다 희귀한 사건에 더 높은 확률을 부여하므로, 이동 중앙값이 이동 평균보다 충격에 더 잘 견디는 이유를 설명한다.

위의 단순 이동 중앙값이 중앙에 위치하면 평활화는 이미지 신호 처리에 적용되는 중앙값 필터와 동일하다.

10. 이동평균 회귀모형

이동 평균 회귀 모형에서 관심 변수는 관찰되지 않은 독립적인 오차항의 가중 이동 평균으로 간주된다.^[1] 이동 평균의 가중치는 추정해야 할 매개변수이다.^[1]

이 두 개념은 이름 때문에 혼동되는 경우가 많지만, 유사점이 많음에도 불구하고 별개의 방법론을 나타내며 매우 다른 맥락에서 사용된다.^[1]

참조

_[1] 간행물 Hydrologic Variability of the Cosumnes River Floodplain http://www.waterboar[...] Booth et al., San Francisco Estuary and Watershed Science 2006
_[2] 서적 Statistical Analysis Holt International 1975
_[3] 문서 Savitzky–Golay filter
_[4] 웹사이트 Weighted Moving Averages: The Basics http://www.investope[...] Investopedia
_[5] 웹사이트 DEALING WITH MEASUREMENT NOISE - Averaging Filter http://lorien.ncl.ac[...] 2010-10-26
_[6] 웹사이트 NIST/SEMATECH e-Handbook of Statistical Methods: Single Exponential Smoothing http://www.itl.nist.[...] National Institute of Standards and Technology
_[7] 웹사이트 Spencer's 15-Point Moving Average — from Wolfram MathWorld http://mathworld.wol[...]
_[8] 문서 Moving averages https://robjhyndman.[...] 2009-11-08
_[9] 문서 Statistics 153 (Time Series) : Lecture Three https://www.stat.ber[...] 2012-01-24
_[10] 웹사이트 Efficient Running Median using an Indexable Skiplist « Python recipes « ActiveState Code http://code.activest[...]
_[11] 서적 Nonlinear Signal Processing: A Statistical Approach Wiley 2005
_[12] 웹사이트 基本用語集（い） https://www.stat.go.[...] 統計局 2024-06-22
_[13] 문서 수치계산
_[14] 웹사이트 Moving Averages page http://www.forexabod[...] ForexAbode.com
_[15] 서적 Statistical Analysis Holt International 1975
_[16] 웹사이트 NIST/SEMATECH e-Handbook of Statistical Methods: Single Exponential Smoothing http://www.itl.nist.[...] 미국립표준기술연구소
_[17] 웹사이트 NIST/SEMATECH e-Handbook of Statistical Methods: EWMA Control Charts http://www.itl.nist.[...] 미국립표준기술연구소
_[18] 문서 EMA 수식
_[19] 문서 분자 수식
_[20] 문서 극한 값
_[21] 문서 테일러 전개
_[22] 문서 log 값
_[23] 문서 CA 계산식
_[24] 간행물 Hydrologic Variability of the Cosumnes River Floodplain http://www.waterboar[...] Booth et al., San Francisco Estuary and Watershed Science 2006
_[25] 웹인용 Weighted Moving Averages: The Basics http://www.investope[...] Investopedia
_[26] 웹인용 Archived copy http://lorien.ncl.ac[...] 2010-10-26

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com