쥘리아 집합

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 기본적인 성질
4. 거동
5. 이차 함수의 예
- 5.1. 구체적인 예
6. 일반화
7. 쥘리아 집합 그리기
- 7.1. 역 반복 방법 (IIM)
- 7.2. 거리 추정 방법 (DEM/J)
8. 더 알아보기
참조

1. 개요

쥘리아 집합은 주어진 복소수 c에 대해 점화식 z_n+1 = z_n² + c를 따르는 수열이 발산하지 않는 복소수 z의 집합이다. 이는 만델브로 집합과 밀접한 관련이 있으며, 자기 유사성과 초기 조건에 대한 민감성을 특징으로 한다. 쥘리아 집합은 파투 집합의 여집합으로 정의되며, 다항식 함수의 경우 반복 합성 시 궤도가 무한대로 발산하지 않는 점들의 집합의 경계로 나타난다. 쥘리아 집합은 카오스적인 움직임을 보이며, 연결 집합 또는 칸토어 집합 형태를 가질 수 있다. 쥘리아 집합은 역 반복 방법(IIM) 또는 거리 추정 방법(DEM/J)을 사용하여 그릴 수 있다.

더 읽어볼만한 페이지

복소동역학 - 복잡계
복잡계는 카오스 이론, 복잡 적응계, 비선형 역학계 등을 포함하며 초기 조건 민감성, 자기 조직화, 창발성 등의 특징을 보이는, 개별 요소들의 단순한 합으로 설명할 수 없는 복잡한 현상을 연구하는 학문 분야이다.
복소동역학 - 망델브로 집합
망델브로 집합은 복소수 c에 대해 $z_{n+1} = z_n^2 + c$ 점화식(단, $z_0 = 0$ )으로 정의되는 수열이 발산하지 않는 c 값들의 프랙탈 집합이며, 쥘리아 집합과 관련 있고 자기 유사성을 띤다.
극한 집합 - 안정성 이론
안정성 이론은 미분 방정식과 동역학적 시스템의 해의 점근적 성질과 궤적을 다루며, 평형점, 주기 궤도의 안정성, 섭동과 선형화, 랴푸노프 함수 등을 사용하여 시스템의 안정성을 분석한다.
극한 집합 - 끌개
끌개는 시간의 흐름에 따라 접근하는 상태 공간의 부분 공간으로, 시스템의 장기적인 거동을 결정하며, 파라미터 변화에 따라 분기 현상을 겪고 카오스적인 비선형 신호 분석에 활용된다.
프랙탈 - 브라운 운동
브라운 운동은 액체나 기체 속 미세 입자가 매질 분자와 충돌하여 불규칙하게 움직이는 현상으로, 아인슈타인과 스몰루호프스키의 이론적 설명과 페랭의 실험적 검증을 통해 원자 존재 입증에 기여했으며, 확산/랑주뱅 방정식으로 모델링되어 다양한 분야에 응용된다.
프랙탈 - 프랙탈 우주론
프랙탈 우주론은 우주의 구조가 프랙탈 기하학적 특성을 갖는다는 이론이며, 관측 결과는 우주가 균질하다는 것을 보여주지만, 이론적 연구에서는 큰 규모나 미시적 규모에서 프랙탈 구조를 제안하기도 한다.

쥘리아 집합
개요
Julia 집합의 예시
유형	프랙탈
연구 분야	복소 동역학
정의 함수	z ↦ z^2 + c (가장 일반적인 형태) z ↦ z^n + c (일반화된 형태)
세부 정보
관련 개념	망델브로 집합 충전된 Julia 집합
성질	자기 유사성 복잡한 경계
차원	일반적으로 정수가 아닌 값 (프랙탈 차원)
역사
이름의 유래	가스통 쥘리아의 이름에서 유래
연구 시기	20세기 초
응용 분야
활용	카오스 이론 연구 컴퓨터 그래픽스 예술

2. 정의

쥘리아 집합은 주어진 복소수 c에 대하여 다음 점화식에 따라 정의된 수열이 발산하지 않는 성질을 갖는 복소수 z의 집합이다.

:z_n+1 = z_n² + c

이 점화식은 만델브로 집합의 것과 같지만, 만델브로 집합은 z₀=0+0i일 때 z를 발산하지 않게 하는 c의 집합이라는 점이 다르다. 즉, z와 c의 역할이 뒤바뀐 것이다.

쥘리아 집합은 만델브로 집합과 동일하게 자기유사성을 가지며, 가까운 두 점이 서로 다른 양상을 보이는 초기 조건의 민감성도 가진다.

2. 1. 정규족을 이용한 정의

리만 구(Riemann sphere)에서 자신으로 가는 비상수 메로모픽 함수(meromorphic function) f(z)|f(z)^영어에 대해, f(z)|f(z)^영어의 반복 합성에 대한 함수열이 정규족(normal family)이 되지 않는 점들의 집합을 쥘리아 집합 J(f)|J(f)^영어라고 정의한다. 정규족은 함수열이 국소적으로 균등 수렴하는 부분열을 갖는 성질을 의미하며, 이는 동등 연속(equicontinuous) 개념과 밀접하게 관련되어 있다. 파투 집합(Fatou set) F(f)|F(f)^영어는 J(f)|J(f)^영어의 여집합으로, 함수열이 정규족을 이루는 점들의 집합이다.

f|f^일본어를 리만 구 ''''''}}에서 자신으로의 정칙 함수 ''f'' : ''''''|''f'' : '''''' → ''''''}}라고 하자. 어떤 점 ''z'' ∈ ''''''}}에 f|f^일본어의 n|n^일본어회 반복 합성을 수행하여 얻은 값을 ''f'' ^''n''(''z'')|''f''^''n''(''z'')^일본어로 나타낸다. z|z^일본어에 반복 합성을 적용했을 때 정해지는

:

\{ f^{k}(z) \}^\infty_{k=0} = \{ z,\ f(z),\ f^{2}(z),\ \ldots \}

라는 점렬을 궤도 또는 전방 궤도라고 한다. 복소 역학계에서는 궤도의 점근적 거동 등, 반복 합성을 수행했을 때 나타나는 성질에 관심을 갖는다.

점 ''z'' ∈ ''''''}}의 어떤 근방 ''U''(''z'') ⊂ ''''''}} 위에서, 족 ''f'' ^''n''|''f''^''n''^일본어 이 정규족이 될 때, 이러한 점 전체의 집합을 '''파투 집합'''이라고 한다. f|f^일본어의 파투 집합은 ''F_f''|''F_f''^일본어나 ''F''(''f'')|''F''(''f'')^일본어 등으로 나타낸다.

'''쥘리아 집합'''은 파투 집합의 여집합으로 정의된다. f|f^일본어의 줄리아 집합을 ''J_f''|''J_f''^일본어나 ''J''(''f'')|''J''(''f'')^일본어 등으로 나타낸다. 즉,

:

J_f = \hat{\mathbf{C}} \setminus F_f

로 줄리아 집합이 정해진다. 이 정의는 추상적이지만, 정규족의 개념은 동등 연속성과 연결되어 있으며, 동등 연속성에 의해 복소 역학계의 거동을 잘 특징지을 수 있게 되어 있다.

일반적으로 유형 함수 족 ''F'' : ''D'' → ''''''}}가 D|D^일본어 위에서 정규족이기 위한 필요 충분 조건은 아스콜리-아르첼라의 정리에 의해 F|F^일본어가 D|D^일본어 위의 각 점에서 동등 연속이라는 것이다. 족 ''f_n''|''f_n''^일본어이 영역 D|D^일본어 위의 점 z|z^일본어에서 동등 연속이라는 것은, 임의의 ε > 0|ε > 0^일본어이 주어졌을 때 적절한 ''δ'' > 0|''δ'' > 0^일본어을 선택하면 ''d''(''z'', ''ω'') < δ|''d''(''z'', ''ω'') < δ^일본어를 만족하는 임의의 ω|ω^일본어와 임의의 n|n^일본어에 대해 ''d''(''f''_''n''(''z''), ''f''_''n''(''ω'')) < ε|''d''(''f''_''n''(''z''), ''f''_''n''(''ω'')) < ε^일본어가 되는 것을 말한다(여기서 d|d^일본어는 거리). 이러한 동등 연속성은 반복 합성으로 이루어진 함수 족에 있어서 가까운 초기값에 대한 함수의 값이 균일하게 가깝다는 것을 의미하며, 초기값에 대한 일종의 안정성을 나타낸다. 정규족의 개념은 어떤 점에서 출발하는 궤도가 안정적인지 여부를 표현하는 도구이며, 정규족의 개념에 의해 궤도가 안정적인 부분과 불안정한 부분을 영역을 분할한다.

위에서처럼 정규족의 개념을 사용하여 줄리아 집합을 정의함으로써, 복소 함수론의 기술적 도구를 사용하기 쉬워지고, 유리 함수나 유형 함수 등의 넓은 범위의 복소 함수까지 이론을 전개할 수 있다. 표준적으로 줄리아 집합은 정규족의 개념으로 정의된다.

2. 2. 다항식 함수에서의 정의

P^영어를 2차 이상의 복소 다항식이라 하자. 계수도 복소수이다. 우선, 복소 평면에서 자신으로의 다항식 함수 P^영어의 '''채워진 쥘리아 집합''' K^영어를 다음과 같이 정의한다.

:

K_P = \left \{ z \in \mathbf{C} \; | \; \lim_{n \rightarrow \infty} P^{n}(z) \nrightarrow \infty \right \}

채워진 쥘리아 집합이란, 궤도가 무한대로 가지 않는 점들의 집합이라고 할 수 있다.

'''쥘리아 집합'''은 채워진 쥘리아 집합의 경계로 정의된다. 즉, P^영어의 쥘리아 집합을 J^영어로 나타내면 다음과 같다.

:

J_P = \partial K_P

이 정의의 쥘리아 집합은 궤도가 무한대로 가지 않는 점들의 집합과 궤도가 무한대로 가는 점들의 집합의 경계가 된다.

반복하는 복소 함수가 다항식이라면, 이 정의의 쥘리아 집합과 위의 정규족을 사용한 정의의 쥘리아 집합은 동치이다.

2. 3. 쥘리아 집합의 표현

f(z)

를 리만 구에서 자신으로 가는 비상수 메로모픽 함수라고 하자. 이러한 함수

f(z)

는 정확히 비상수 복소수 유리 함수이며,

f(z) = p(z)/q(z)

와 같이 표현할 수 있다. 여기서

p(z)

와

q(z)

는 복소수 다항식이다.

\operatorname{J}(f)

는 다음 성질을 갖는다.^[3]^[4]

$\operatorname{J}(f)$ 는 최소한 세 점을 포함하는 가장 작은 닫힌 집합이며, ''f''에 대해 완전히 불변한다.
$\operatorname{J}(f)$ 는 반발 주기점들의 집합의 폐포이다.
최대 두 점을 제외한 모든 점 $\;z \in X\;$ 에 대해, 쥘리아 집합은 전체 역궤도 $\bigcup_n f^{-n}(z)$ 의 극한점들의 집합이다.
만약 ''f''가 전체 함수라면, $\operatorname{J}(f)$ 는 반복 하에서 무한대로 수렴하는 점들의 집합의 경계이다.
만약 ''f''가 다항식이면, $\operatorname{J}(f)$ 는 채워진 쥘리아 집합의 경계이다. 즉, ''f''의 반복 하에서 궤도가 제한된 상태로 유지되는 점들을 의미한다.

3. 기본적인 성질

쥘리아 집합은 공집합이 아닌 닫힌 집합이다.^[5] 또한, 고립점을 갖지 않는 완전 집합이다.^[5] 쥘리아 집합은 완전 불변이어서, 함수 f에 대한 상(image)과 역상(inverse image)이 모두 쥘리아 집합에 포함된다.^[5]

: $f^{-1}(\operatorname{J}(f)) = f(\operatorname{J}(f)) = \operatorname{J}(f).$

쥘리아 집합 가 복소 평면( ) 또는 리만 구( )와 일치하지 않으면, 내점을 갖지 않는다. 가 다항식 함수일 때는, 는 항상 내점을 갖지 않는다.

4. 거동

쥘리아 집합 위의 점들은 함수 f의 반복 합성에 의해 혼돈(카오스)적인 움직임을 보인다.^[3] 반발 주기점(repelling periodic point) 또는 유리적 중립 주기점(rationally indifferent periodic point)은 쥘리아 집합에 포함된다.^[4] 초월 정함수 또는 2차 이상의 유리 함수 f에 대해, f의 반발 주기점 전체 집합은 쥘리아 집합 J_f에서 조밀하다.^[4] 비표준적으로, f가 다항식 함수일 때에는, f의 반발 주기점 전체의 폐포를 쥘리아 집합으로 정의하기도 한다.

쥘리아 집합 J_f 위의 점은 f에 의해 카오스적으로 움직인다.^[3] 리만 구면 위의 부분 집합 E에서 E로의 연속 사상 f가 주기점의 조밀성, 위상적 추이성, 초기값 민감성을 가질 때, f는 E 위에서 (데바니의 의미로) 카오스적이라고 한다. 주기점의 조밀성은 f의 주기점이 E 위에 조밀하게 존재한다는 것이고, f의 반발 주기점 전체 집합이 J_f에서 조밀하므로 주기점의 조밀성도 성립한다. 위상적 추이성이란, 비어 있지 않은 임의의 부분 열린 집합 U, V ⊂ E에 대해, f^k(U) ∩ V ≠ ∅를 만족하는 k > 0이 존재한다는 것이다. 초기값 민감성이란, 어떤 δ > 0이 존재하고, 임의의 z ∈ E와 근방 N(z) ⊂ E에서 |f^k(z) - f^k(ω)| > δ를 만족하는 ω ∈ N(z)와 k > 0이 존재한다는 것이다.

f를 2차 이상의 유리 함수로 하면, f는 J_f 위에서 (데바니의 의미로) 카오스적이다. 즉, f의 카오스적 거동을 일으키는 집합이 f의 쥘리아 집합이라고 할 수 있다.

5. 이차 함수의 예

상수 $c$를 갖는 이차 함수

: $f_{c}(z) = z^2 +c$

는 간단하면서도 복잡한 쥘리아 집합을 생성한다. 이 함수의 쥘리아 집합 $J_f$는 $c$의 값에 따라 크게 달라진다. 예를 들어, 가시나무 가지, 펼쳐진 구름, 불꽃놀이의 잔불, 토끼, 용의 꼬리 등과 같은 다양한 모습으로 나타난다. $c = 0$에서는 쥘리아 집합은 단위 원이지만, $c = -0.12375 + 0.56508i$로 설정하면, 쥘리아 집합은 더 이상 매끄럽지 않고, 일부를 계속 확대해도 톱니 모양의 프랙탈 도형이 된다.^[3]

$f_c$는 좁은 범위의 형태로 제한되는 것처럼 보이지만, 임의의 2차 함수와 공액 관계에 있다. 따라서 $f_c$의 쥘리아 집합을 조사하면 2차 함수 전체의 쥘리아 집합의 성질을 알 수 있다.^[4] 또한, $f_c$는 복소 역학계에서 중요한 역할을 하는 임계점($\frac{df}{dz}(z_0) = 0$을 만족하는 $z_0$)이 원점 $0$에 있어 다루기 쉽다.^[5]

복소 평면 및 만델브로 집합의 상반부에, 대표적인 ''c''의 쥘리아 집합을 겹쳐 놓은 그림

쥘리아 집합 $J_f$는 크게 연결 집합 또는 칸토어 집합 중 하나가 된다. 임계점 $0$에서 시작하는 전방 궤도 $\{f^k(0)\}_{k \ge 1}$가 유계이면, 즉 $k \to \infty$일 때 $f^k(0) \nrightarrow \infty$이면, $J_f$는 연결 집합이다. $0$에서 시작하는 궤도가 무한대로 발산하면, 즉 $k \to \infty$일 때 $f^k(0) \to \infty$이면, $J_f$는 칸토어 집합이다.

상수 $c$를 변화시킬 때 복소 함수 $z \mapsto z^2 + c$의 쥘리아 집합. 그림의 흰색 부분이 쥘리아 집합이며, 흰색 부분과 녹색 부분을 합한 것이 채워진 쥘리아 집합

이들과 대응하여 쥘리아 집합의 전체 모습을 나타내는 것이 $f_c$의 상수 $c$의 집합에서 정의되는 만델브로 집합 $M_f \subset \mathbb{C}$이며, $c$가 $M_f$ 위에 있으면 $J_f$는 연결되고, $c$가 $M_f$에서 벗어나면 $J_f$는 완전 비연결이 된다.

5. 1. 구체적인 예

f(z) = z^{2}

인 경우, 쥘리아 집합은 단위 원이며, 이 집합에서 반복은 각도를 두 배로 하는 연산으로 주어진다. 파투 영역은 원의 내부와 외부 두 영역으로 나뉘며, 각각 0과 ∞를 향해 반복한다.

g(z) = z^{2} - 2

인 경우, 쥘리아 집합은 -2와 2 사이의 선분이다. 파투 영역은 하나이며, 선분에 없는 점들은 ∞를 향해 반복한다.^[1]

복소 함수 $z \mapsto z^2$ 의 쥘리아 집합은 단위 원이다. 단위 원 위의 점(녹색)은 반복해도 그 위에 계속 존재하며, 단위 원 밖의 점(빨간색과 파란색)은 단위 원에서 멀어져 무한대 또는 원점을 향한다.

가장 간단한 예로

P(z) = z^2

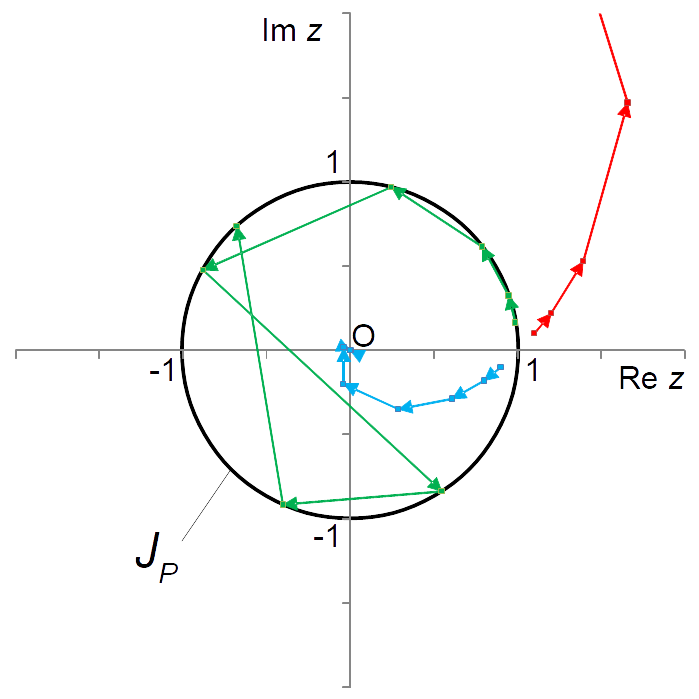
라는 복소 함수를 들 수 있다. 이 함수는 주어진

z

를 제곱하는 함수로, 도형적으로는 복소 평면상에서

z

의 절댓값을 제곱하고,

z

의 편각을 2배로 한다. 복소수를 극형식으로 나타내면

z = |z|e^{i\theta}

이므로, 이 경우

P

의

k

회 반복은 다음과 같다.

:

P^{k}(z) = \vert z \vert ^{2^k} e^{i (2^k \theta)}

따라서

|z| < 1

이면

k \to \infty

일 때

P^k(z) \to 0

이고,

|z| > 1

이면

k \to \infty

일 때

P^k(z) \to \infty

이다. 예를 들어 절댓값이

\sqrt{5}

인

z = 1 + 2i

에서 시작하면 다음과 같다.

$z = 1 + 2i$
$P(z) = -3 + 4i$
$P^2(z) = -7 - 24i$
$P^3(z) = -527 + 336i$
$P^4(z) = 164833 - 354144i$
...

이 값은

\infty

에 가까워진다. 한편, 절댓값이

\sqrt{0.34}

인

z = 0.5 + 0.3i

에서 시작하면 다음과 같다.

$z = 0.5 + 0.3i$
$P(z) = 0.16 + 0.3i$
$P^2(z) = -0.0644 + 0.096i$
$P^3(z) = -0.00507 - 0.01236i$
$P^4(z) = -0.00013 + 0.00013i$
...

이 값은 원점

0

에 가까워진다.

|z| = 1

, 즉

z

가 단위 원 위의 점일 때,

|P(z)| = 1

이므로

P

의 상도 단위 원 위의 점이다. 따라서

|z| = 1

이면 모든

k

에 대해

P^k(z)

는 단위 원 위에 머문다. 게다가 단위 원 위에는 주기점이 조밀하게 존재한다. 예를 들어

\theta = \frac{2\pi}{7}, \frac{4\pi}{7}, \frac{8\pi}{7}

과

\theta = \frac{6\pi}{7}, \frac{10\pi}{7}, \frac{12\pi}{7}

는 3주기점의 짝이다.

결론적으로

P(z) = z^2

의 채워진 쥘리아 집합

K_P

는 단위 원판

\{|z| \le 1\}

이고, 쥘리아 집합

J_P

는 그 경계인 단위 원

\{|z| = 1\}

이다. 또한 파투 집합

F_P

는

\{|z| < 1\} \cup \

6. 일반화

쥘리아 집합과 파투 집합의 정의는 초월 유사해석 함수나 아담 엡스타인의 '''유한형 맵'''과 같이 정의역을 포함하는 일부 함수의 경우에도 적용된다.^[3] 여러 복소 변수에서의 역학 연구에서도 쥘리아 집합이 정의된다.^[4]

7. 쥘리아 집합 그리기

쥘리아 집합은 복소 평면에서 특정 함수를 반복 적용했을 때 발산하지 않는 점들의 집합이다. 이 집합을 시각적으로 표현하는 방법, 즉 그리는 방법에 대해 설명한다.각 파투 영역(안정된 영역)에는 서로 수직으로 교차하는 두 종류의 선이 존재한다. 하나는 등전위선으로, 전위 함수 또는 실수 반복 횟수가 같은 점들을 연결한 선이다. 다른 하나는 필드선(외부 광선)으로, 반복을 통해 무한대로 발산하는 점들의 경로를 나타낸다.반복 횟수에 따라 파투 영역에 색을 칠하면, 반복 띠가 등전위선의 경로를 보여준다. 만약 반복이 무한대로 발산하는 경우(예:

z^2 + c

함수의 외부 파투 영역), x축 위 또는 아래의 반복 시퀀스에서 마지막 점에 따라 색을 다르게 하여 필드선의 경로를 쉽게 파악할 수 있다.

필드선은 흡인 파투 영역의 한 점에서 시작하여 여러 번 반복하면 유한 사이클 'C'로 수렴한다. 필드선은 'C'의 점에서 시작하고, 'C'의 점으로 반복되는 무한히 많은 점에서 시작한다. 그리고 이 선들은 비혼돈적인(유한 사이클을 생성하는) 점에서 쥘리아 집합에서 끝난다.

파투 영역에 색을 칠하기 위해, 작은 값 ε을 설정하고 반복 시퀀스

z_k

가

|z_k - z^*| < \epsilon

을 만족할 때 중지하도록 한다. 여기서

z^*

는 사이클 'C'의 한 점이다. 점 'z'에 숫자 'k'(또는 실수 반복 횟수)에 따라 색을 입힌다.

z^*

에서 특정 각도 'θ'로 방향을 정하면, 이 방향에서

z^*

에서 나오는 필드선은 숫자

z_k - z^*

의 인수 'ψ'가 다음 조건을 만족하는 점 'z'로 구성된다.

:

\psi - k\beta = \theta \mod \pi. \,

여기서 β는

f(f(\dots f(z)))

맵에서

z^*

근처의 회전 각도를 나타낸다. 필드선의 방향으로 반복 띠를 통과하면 반복 횟수 'k'는 1씩 증가하고, ψ는 β만큼 증가하므로,

\psi - k\beta \mod \pi

는 필드선을 따라 일정하게 유지된다.

필드선에 색을 칠하는 것은 필드선 쌍 사이의 공간에 색을 칠하는 것을 의미한다.

z^*

에서 나오는 여러 방향을 선택하고, 각 방향 주위에 두 방향을 더 선택한다. 한 쌍의 두 필드선이 쥘리아 집합의 같은 점에서 끝나지 않을 수 있으므로, 색칠된 필드선은 쥘리아 집합으로 가면서 갈라질 수 있다. 필드선의 중심선까지의 거리를 기준으로 색을 칠하고, 이 색을 일반적인 색과 섞을 수 있다.

색칠된 필드선(두 필드선 사이의 영역)은 반복 띠에 의해 나뉘며, 이 부분들은 단위 정사각형과 일대일 대응될 수 있다. 한 좌표는 경계 필드선 중 하나에서 (계산된) 거리이고, 다른 좌표는 경계 반복 띠의 내부에서 (계산된) 거리이다(이 숫자는 실수 반복 횟수의 소수 부분).

7. 1. 역 반복 방법 (IIM)

쥘리아 집합은 주어진 점들의 역상의 집합의 극한점으로 찾을 수 있다. 따라서 쥘리아 집합을 다음과 같은 방식으로 그릴 수 있다. 쥘리아 집합에 속하는 임의의 점 ''z'' (예: 척력적 주기점)에서 시작하여, 함수 ''f''의 고차 반복

f^n

아래에서 ''z''의 모든 역상을 계산한다.

하지만, 반복된 역상의 수가 기하급수적으로 증가하므로, 이는 계산적으로 실행하기 어렵다. 그러나 이는 반복 함수 시스템에 대한 "무작위 게임" 방법과 유사하게 조정할 수 있다. 즉, 각 단계에서 ''f''의 역상 중 하나를 무작위로 선택한다.

예를 들어, 2차 다항식 ''f_c''의 경우, 역방향 반복은 다음과 같이 설명된다.

:

z_{n-1} = \sqrt{z_n - c} .

각 단계에서 두 제곱근 중 하나가 무작위로 선택된다.

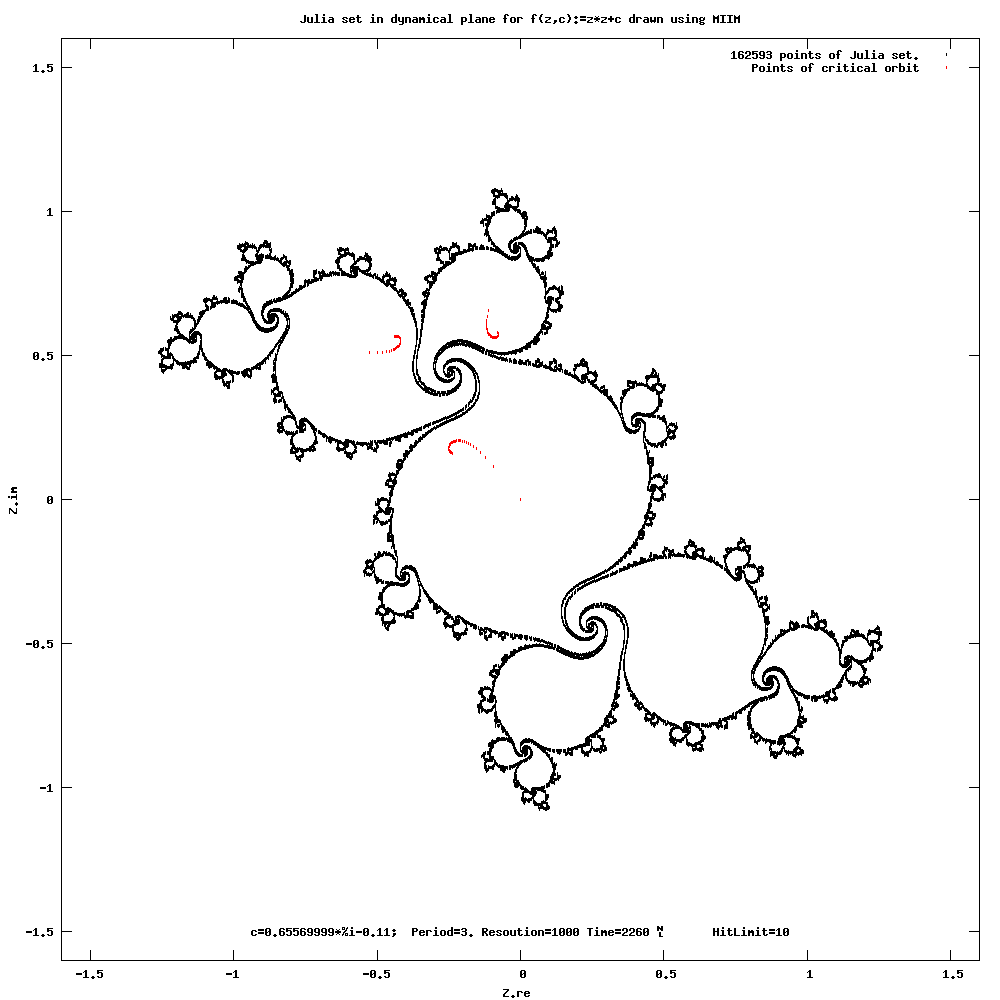
쥘리아 집합의 특정 부분은 역 쥘리아 알고리즘으로 접근하기 매우 어렵다.^[9] 이러한 이유로, 더 나은 이미지를 생성하기 위해 IIM/J (MIIM/J라고 불림)를 수정하거나 다른 방법을 사용해야 한다.

7. 2. 거리 추정 방법 (DEM/J)

쥘리아 집합의 거리 추정 방법(DEM/J)은 쥘리아 집합을 흑백으로 더 잘 그리기 위한 방법이다. 픽셀에서 집합까지의 거리를 추정하여, 집합에 가까운 픽셀에 색상을 지정하는 방식이다.

거리 추정 공식은 전위 함수 φ(z)의 공식에서 파생된다. φ(z)에 대한 등전위선이 가까울수록 숫자 |φ'(z)|는 커지고, 그 반대의 경우도 마찬가지이다. 따라서 함수 δ(z) = φ(z)/|φ'(z)|에 대한 등전위선은 대략 규칙적으로 배치되어야 한다. 이 공식으로 계산된 값은 z가 쥘리아 집합으로 수렴할수록 실제 거리에 수렴하는 것으로 증명되었다.^[9]

함수 f(z)가 유리수 함수, 즉 f(z) = p(z)/q(z) (p(z)와 q(z)는 복소수 다항식)라고 가정하면, φ(z)의 도함수를 계산해야 한다. z_k = f(f(⋯f(z)))) (k번 합성)이므로, z'_k는 f'(z_k)의 곱으로 계산된다. 이 수열은 z'₀ = 1에서 시작하여 z'_k+1 = f'(z_k)z'_k로 재귀적으로 계산할 수 있다.

반복이 ∞로 향할 때 (∞가 초흡인 고정점일 때), 다음 공식을 얻는다.

:δ(z) = φ(z)/|φ'(z)| = lim_k→∞ log|z_k||z_k|/|z'_k|.

점 z^*를 포함하고 차수가 r인 유한 흡인 사이클(초흡인이 아님)로 반복될 때는 다음 공식을 얻는다.

:δ(z) = φ(z)/|φ'(z)| = lim_k→∞ |z_kr - z^*|/|z'_kr|.

초흡인 사이클의 경우, 공식은 다음과 같다.

:δ(z) = lim_k→∞ log|z_kr - z^*|²/|z'_kr|.

반복이 멈출 때 이 숫자를 계산한다. 거리 추정은 사이클의 흡인력과 무관하며, 초월 함수(예: sin(z), tan(z))에도 적용 가능하다.

거리 함수는 경계를 그리는 것 외에도 3차원 프랙탈 풍경을 만드는 데 사용될 수 있다.

8. 더 알아보기

쥘리아 집합과 파투 집합의 정의는 정의역을 포함하는 일부 함수의 경우에도 쉽게 적용된다. 특히 초월 유사해석 함수와 아담 엡스타인의 '''유한형 맵'''이 대표적이다.^[4]

쥘리아 집합은 또한 여러 복소 변수에서의 역학 연구에서도 일반적으로 정의된다.^[4]

참조

_[1] 논문 Mémoire sur l'iteration des fonctions rationnelles Journal de Mathématiques Pures et Appliquées 1918
_[2] 논문 Sur les substitutions rationnelles Comptes Rendus de l'Académie des Sciences de Paris 1917
_[3] 서적 Iteration of Rational Functions
_[4] 서적 Iteration of Rational Functions
_[5] 서적 Iteration of Rational Functions
_[6] 간행물 Similarity between the Mandelbrot set and Julia Sets http://projecteuclid[...] Communications in Mathematical Physics 1990
_[7] 웹사이트 Renormalizing the Mandelbrot Escape https://linas.org/ar[...] Creative Commons 2023-11-05
_[8] 간행물 Etude dynamique des polynômes complexes 1984, 1985
_[9] 서적 The Beauty of Fractals Springer-Verlag 1986

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com