망델브로 집합

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 역사
4. 성질
5. 기하학
6. 일반화
7. 컴퓨터를 이용한 묘사
8. 대중 문화 속 망델브로 집합
참조

1. 개요

망델브로 집합은 복소수 수열의 발산 여부에 따라 정의되는 프랙탈의 일종이다. 20세기 초 복소 역학 연구에서 기원했으며, 브누아 망델브로가 시각화하여 널리 알려졌다. 망델브로 집합은 프랙탈 도형으로 나타나며, 자기 유사성, 하우스도르프 차원, 연결성 등의 성질을 갖는다. 쥘리아 집합과 밀접한 관계를 가지며, 일반화된 형태도 존재한다. 컴퓨터를 이용하여 묘사할 수 있으며, 다양한 알고리즘과 소프트웨어가 개발되어 있다. 대중 문화에서도 자주 언급되는 등 널리 알려진 프랙탈이다.

더 읽어볼만한 페이지

복소동역학 - 복잡계
복잡계는 카오스 이론, 복잡 적응계, 비선형 역학계 등을 포함하며 초기 조건 민감성, 자기 조직화, 창발성 등의 특징을 보이는, 개별 요소들의 단순한 합으로 설명할 수 없는 복잡한 현상을 연구하는 학문 분야이다.
복소동역학 - 쥘리아 집합
쥘리아 집합은 복소수 c에 대해 점화식 z_n+1 = z_n² + c를 반복할 때 발산하지 않는 복소수 z의 집합으로, 자기 유사성과 초기 조건에 민감한 특징을 가지며 파투 집합의 여집합으로 정의되어 복소 함수론과 복소 역학계 연구에서 중요한 역할을 한다.
프랙탈 - 브라운 운동
브라운 운동은 액체나 기체 속 미세 입자가 매질 분자와 충돌하여 불규칙하게 움직이는 현상으로, 아인슈타인과 스몰루호프스키의 이론적 설명과 페랭의 실험적 검증을 통해 원자 존재 입증에 기여했으며, 확산/랑주뱅 방정식으로 모델링되어 다양한 분야에 응용된다.
프랙탈 - 프랙탈 우주론
프랙탈 우주론은 우주의 구조가 프랙탈 기하학적 특성을 갖는다는 이론이며, 관측 결과는 우주가 균질하다는 것을 보여주지만, 이론적 연구에서는 큰 규모나 미시적 규모에서 프랙탈 구조를 제안하기도 한다.

망델브로 집합

2. 정의

망델브로 집합은 다음 점화식으로 정의되는 복소수 수열 {''z''_''n''}이 발산하지 않는 복소수 ''c''의 집합이다.^[54]

: $\begin{cases}z_{n+1} = z_n^2 + c \\z_0 = 0\end{cases}$

이때, 수열 {''z''_''n''}_{''n''∈'''N∪{0}'''} 은 ''n'' → ∞ 의 극한에서 무한대로 발산하지 않아야 한다.

복소수 ''c'' 를 복소 평면 상의 점으로 나타내면, 망델브로 집합은 프랙탈 도형으로 나타난다.

복소수를 사용하지 않고 실수부와 허수부로 나누어 표현할 수도 있다. ''z''_''n''을 (''x''_''n'', ''y''_''n'')로, ''c''를 (''a'', ''b'')로 치환하면 다음과 같다.

: $\begin{cases}x_{n+1} = x_n^2 - y_n^2 + a \\y_{n+1} = 2x_n y_n + b \\(x_0, y_0) = (0, 0)\end{cases}$

3. 역사

1978년 로버트 W. 브룩스와 피터 마텔스키가 처음으로 발표한 만델브로 집합 그림

망델브로 집합은 20세기 초 프랑스 수학자 피에르 파투와 가스통 줄리아의 복소 역학 연구에서 기원한다. 1978년 로버트 W. 브룩스와 피터 마텔스키가 클라인 군 연구의 일환으로 처음 정의하고 그렸다.^[3] 1980년 3월 1일, 뉴욕주 요크타운하이츠의 IBM 토마스 J. 왓슨 연구 센터에서 브누아 망델브로가 처음으로 이 집합을 시각화했다.^[4]

1980년, 망델브로는 이차 다항식의 매개변수 공간을 연구한 논문을 발표했다.^[5] 망델브로 집합에 대한 본격적인 수학적 연구는 아드리앙 두아디와 존 H. 허바드 (1985)의 연구로 시작되었으며,^[6] 이들은 망델브로 집합의 많은 기본적인 성질을 확립하고, 프랙탈 기하학에 대한 망델브로의 업적을 기려 이 집합의 이름을 명명했다.

하인츠-오토 파이겐과 페터 리히터는 사진, 서적(1986),^[7] 독일 괴테 인스티튜트의 국제 순회 전시회(1985)를 통해 망델브로 집합을 대중에게 알렸다.^[8]^[9]

1985년 8월 ''사이언티픽 아메리칸''의 표지에서는 망델브로 집합을 계산하는 알고리즘을 소개했다. 표지는 브레멘 대학교의 파이겐, 리히터, 자우페가 제작했다.^[10] 1980년대 중반, 개인용 컴퓨터가 발전하면서 망델브로 집합은 컴퓨터 그래픽 데모로 두각을 나타냈다.^[11]

4. 성질

망델브로 집합은 다음과 같은 성질을 갖는다.

콤팩트 집합: 망델브로 집합은 닫힌 집합이며, 원점을 중심으로 하는 반지름 2의 닫힌 원판에 포함되므로 콤팩트 집합이다. 이는 모든 $n\geq 0$ 에 대해 $|z_n|\leq 2$ 일 때 점 $c$ 가 망델브로 집합에 속하기 때문이다. 즉, $z_n$ 의 절댓값이 2 이하로 유지되어야 하며, 2를 초과하면 수열은 무한대로 발산한다.^[15]

연결 공간: 두아디와 허바드는 망델브로 집합이 연결 공간임을 증명했다. 이들은 망델브로 집합의 여집합과 닫힌 단위 원판의 여집합 사이에 등각 동형 사상을 구성하여 이를 보였다.^[17]

하우스도르프 차원: 망델브로 집합의 경계는 하우스도르프 차원이 2이다. 이는 시시쿠라 미츠히로의 결과이다.^[28]

자기 유사성: 망델브로 집합은 미시우레비치 점 근처에서 확대하면 자기 유사성을 보인다. 그러나 무작위로 작은 축척에서 약간 다른 작은 버전 자체를 찾을 수 있기 때문에 완벽한 자기 유사성은 아니고, 준 자기 유사성을 보인다.^[25]^[26]

쥘리아 집합과의 관계: 망델브로 집합은 쥘리아 집합의 일종의 "지도" 역할을 한다. 망델브로 집합 내부의 점에 대응하는 쥘리아 집합은 연결 공간인 반면, 바깥의 점들은 연결 공간이 아닌 쥘리아 집합에 대응한다.^[20]

실수 축과의 교집합: 망델브로 집합( $M$ )과 실수 축의 교집합은 구간 $\left[-2,\frac{1}{4}\right]$ 이다. 이 구간은 실수 로지스틱 맵 계열의 매개변수와 일대일 대응을 이룬다.^[16]

분기 궤적: 망델브로 집합의 경계는 이차 다항식 계열의 분기 궤적이다. 즉, 경계는 이차 사상 $z_n=z_{n-1}^2+c$ 의 역학이 $c$ 에 대한 민감한 의존성을 보이는 모든 매개변수 $c$ 의 집합이다.^[19]

음의 ''x'' 방향으로 이동하면서 둥근 특징을 확대하여 보여주는 자기 유사성을 보이는 망델브로 집합.

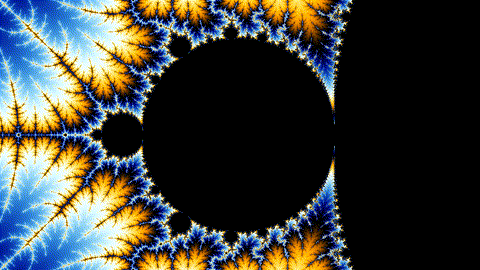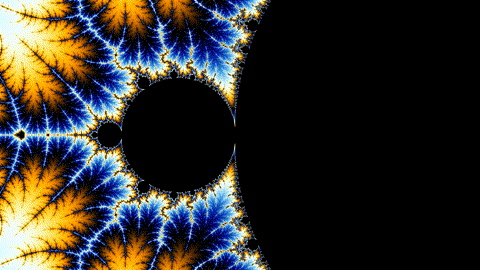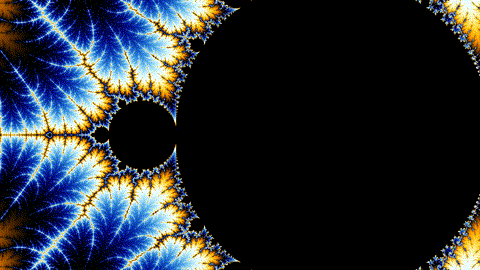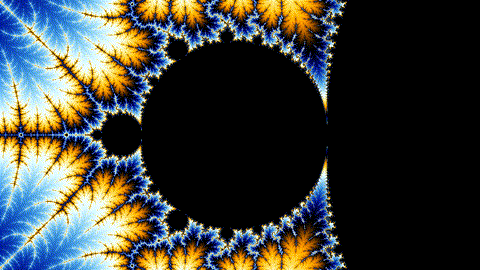
4. 1. 주요 구성 요소

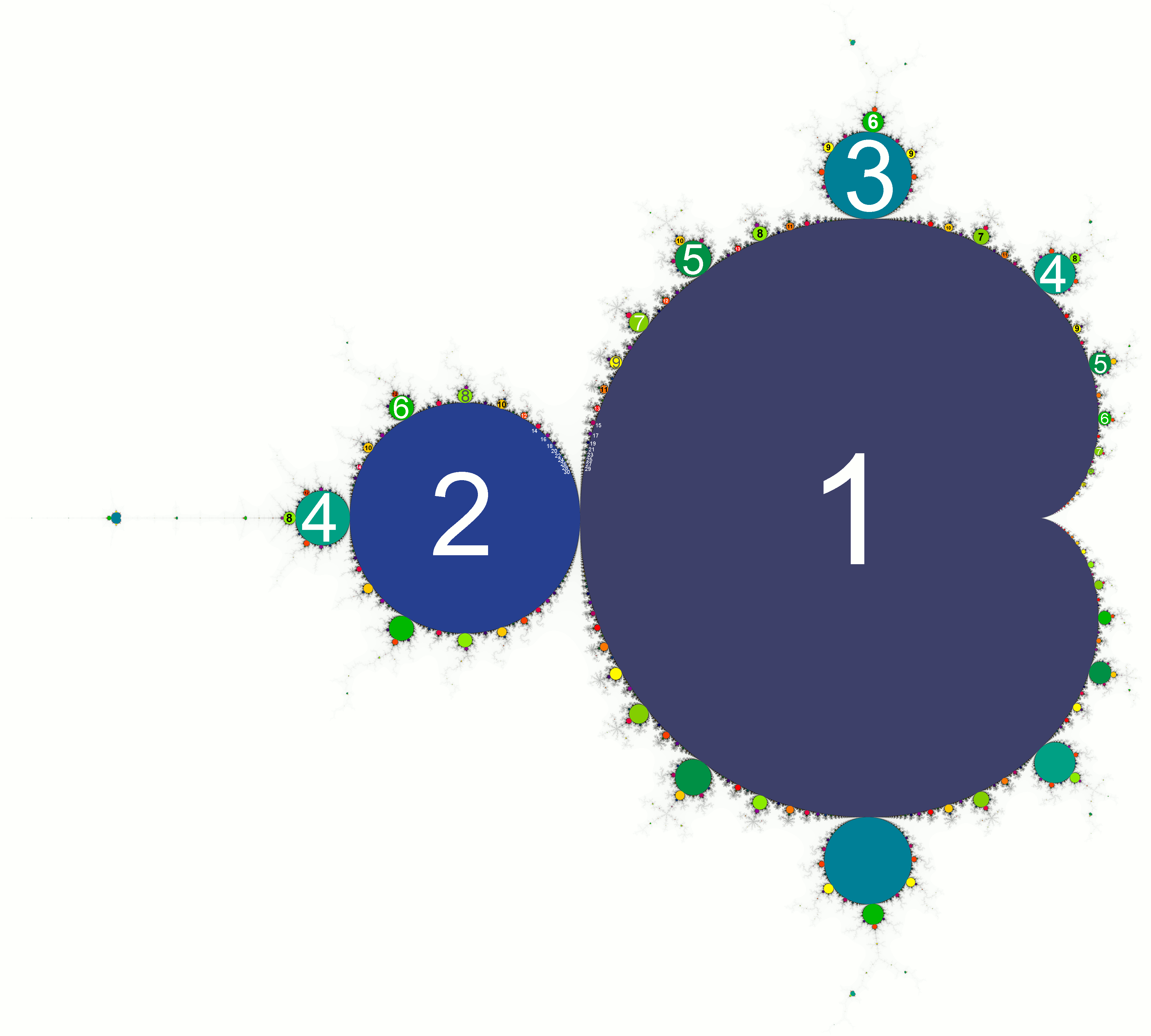
주 심장형은 주기 1 대륙으로, 다음 맵을 갖는 매개변수 c의 영역이다.

:

f_c(z) = z^2 + c

끌리는 고정점을 가지며, 다음과 같은 형태의 모든 매개변수로 구성된다.

:

c(\mu) := \frac\mu2\left(1-\frac\mu2\right)

열린 단위 원판의

\mu

에 대해.

주 심장형의 왼쪽에 부착된 원형 벌브는 ''주기 2 벌브''이다. 이 벌브는

f_c

가 주기 2의 끌리는 주기를 갖는

c

로 구성되며, −1을 중심으로 하는 반경 1/4의 채워진 원이다.

더 일반적으로, 모든 양의 정수

q>2

에 대해 주 심장형에 접하는

\phi(q)

개의 원형 벌브가 있는데, 이를 ''주기-q 벌브''라고 한다. (

\phi

는 오일러 파이 함수) 이는

f_c

가 주기

q

의 끌리는 주기를 갖는 매개변수

c

로 구성된다. 각 원시

q

차 단위원의 근

r=e^{2\pi i\frac{p}{q}}

(

0<\frac{p}{q}<1

)에 대해,

\frac{p}{q}

벌브라고 하는 하나의 주기-q 벌브가 있으며, 이는 다음 매개변수에서 주 심장형에 접한다.

:

c_{\frac{p}{q}} := c(r) = \frac{r}2\left(1-\frac{r}2\right),

이 벌브는 조합 회전수

\frac{p}{q}

를 갖는

q

-주기를 가진 매개변수를 포함한다. 더 정확하게는, 끌리는 주기를 포함하는

q

주기 파투 성분은 모두 공통점(

\alpha

-고정점)에서 접한다. 이러한 성분

U_0,\dots,U_{q-1}

을 반시계 방향으로 레이블링하면,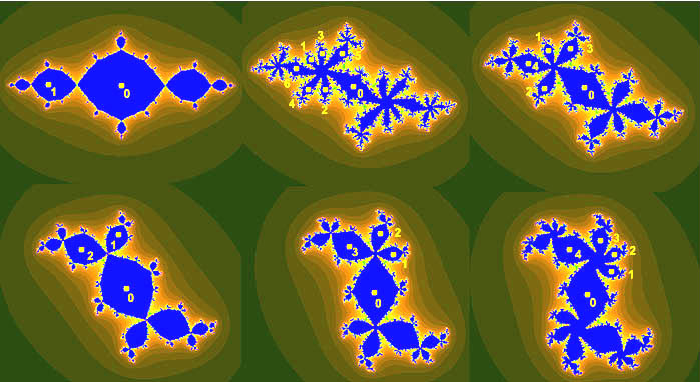

f_c

는 성분

U_j

를 성분

U_{j+p\,(\operatorname{mod} q)}

로 매핑한다.

1/2, 3/7, 2/5, 1/3, 1/4, 1/5 벌브의 매개변수에 대한 끌리는 주기 및 줄리아 집합

c_{\frac{p}{q}}

에서 발생하는 행동의 변화는 분기로 알려져 있다. 즉, 끌리는 고정점은 반발 주기-''q'' 주기와 "충돌"한다. 분기 매개변수를 통해

\tfrac{p}{q}

-벌브로 이동하면, 끌리는 고정점은 반발 고정점(

\alpha

-고정점)으로 바뀌고, 주기-''q'' 주기는 끌리는 주기가 된다.

맵

f_c

가 매력적인 주기적 사이클을 갖는 망델브로 집합의 내부 구성 요소는 ''쌍곡선 성분''이라고 불린다.^[20]

이들은

M

의 내부 영역이며

M

에서 조밀하다는 가설이 있다. ''쌍곡선성의 조밀성''으로 알려진 이 문제는 복소 동역학에서 가장 중요한 미해결 문제 중 하나이다.^[21]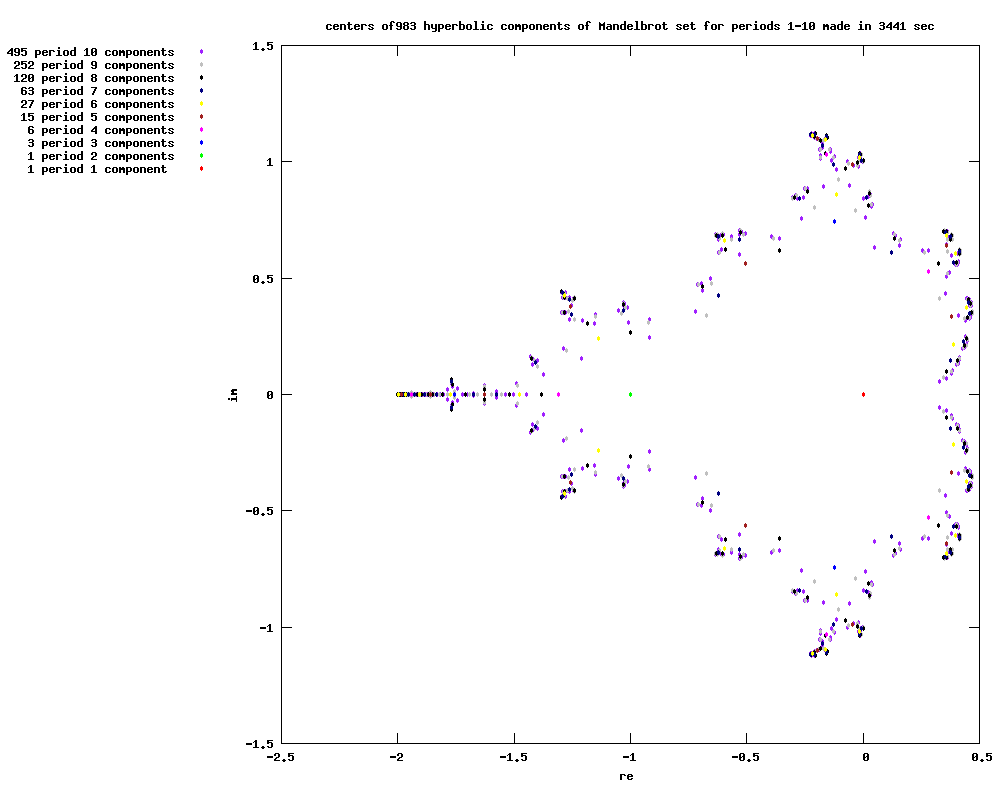

각 쌍곡선 성분은 ''중심''을 가지며, 이는

f_c(z)

의 내부 파투 영역이 초매력적인 사이클을 갖는 점 ''c''이다. 즉, 매력이 무한하다는 의미이며, 이는 사이클이 임계점 0을 포함하여 0이 몇 번의 반복 후에 다시 자신에게 반복된다는 것을 의미한다.

4. 2. 국소 연결성

장-크리스토프 요코즈는 유한하게 재정규화 가능한 매개변수, 즉 대략적으로 말해 유한한 수의 작은 망델브로 복사본에만 포함되는 매개변수에서 망델브로 집합의 국소 연결성을 확립했다.^[24] 그 이후로, 국소 연결성은 망델브로 집합의 다른 많은 점에서 증명되었지만, 전체 추측은 여전히 미해결 상태이다.

4. 3. 쥘리아 집합과의 관계

망델브로 집합은 쥘리아 집합의 일종의 "지도" 역할을 한다. 망델브로 집합이 그려지는 복소 평면의 각 점은 쥘리아 집합의 초기값과 일대일 대응이 되는데, 망델브로 집합 내부의 점에 대응하는 쥘리아 집합은 연결 공간인 반면, 바깥의 점들은 연결 공간이 아닌 쥘리아 집합에 대응하기 때문이다.^[20]

복소 평면에서 c의 값에 해당하는 줄리아 집합을 매칭하여 만든 모자이크. 만델브로 집합은 연결된 줄리아 집합의 맵이다.

만델브로 집합의 정의에 따라, 주어진 점에서 만델브로 집합의 기하학과 해당 쥘리아 집합의 구조 사이에는 밀접한 관계가 있다. 예를 들어, c의 값은 해당 줄리아 집합이 연결되어 있을 때에만 만델브로 집합에 속한다. 따라서, 만델브로 집합은 연결된 줄리아 집합의 맵으로 볼 수 있다.

이 원리는 만델브로 집합에 대한 거의 모든 심오한 결과에 활용된다. 예를 들어, 시시쿠라는 만델브로 집합 경계의 조밀한 매개변수 집합에 대해 줄리아 집합이 하우스도르프 차원 2를 갖는다는 것을 증명한 다음, 이 정보를 매개변수 평면으로 전달했다.^[28] 마찬가지로, 요코즈는 줄리아 집합의 국소 연결성을 먼저 증명한 다음, 해당 매개변수에서 만델브로 집합에 대해 이를 확립했다.^[24]

다음 점화식에서

:

\begin{cases}z_{n+1} = z_n^2 + c \\z_0 = 0\end{cases}

''z''₀ 을 0 이외의 복소수로 했을 경우, 만델브로 집합의 주위가 변형되어, 쥘리아 집합과 비슷한 프랙탈 형태의 곡선이 나타난다.

5. 기하학

망델브로 집합은 통계적인 자기 유사성을 지닌다. 콤팩트 집합이며, 닫힌 집합이고 원점을 중심으로 하는 반지름 2의 닫힌 원판에 포함된다.

z_{n} 반복이 수직 축에 플롯되면, 망델브로 집합은 주기-2^k 성분에서 분기되는 것을 볼 수 있다.

M

과 실수 축의 교집합은 구간

\left[-2,\frac{1}{4}\right]

이다. 이 구간을 따라 있는 매개변수는 실수 로지스틱 맵 계열의 매개변수와 일대일 대응을 이룬다.

두아디(Douady)와 허바드(Hubbard)는 망델브로 집합이 연결 공간임을 보였다. 만델브로(Mandelbrot)는 원래 망델브로 집합이 비연결될 것이라고 추측했으나, 추가 실험을 통해 연결되어야 한다고 생각을 바꾸었다.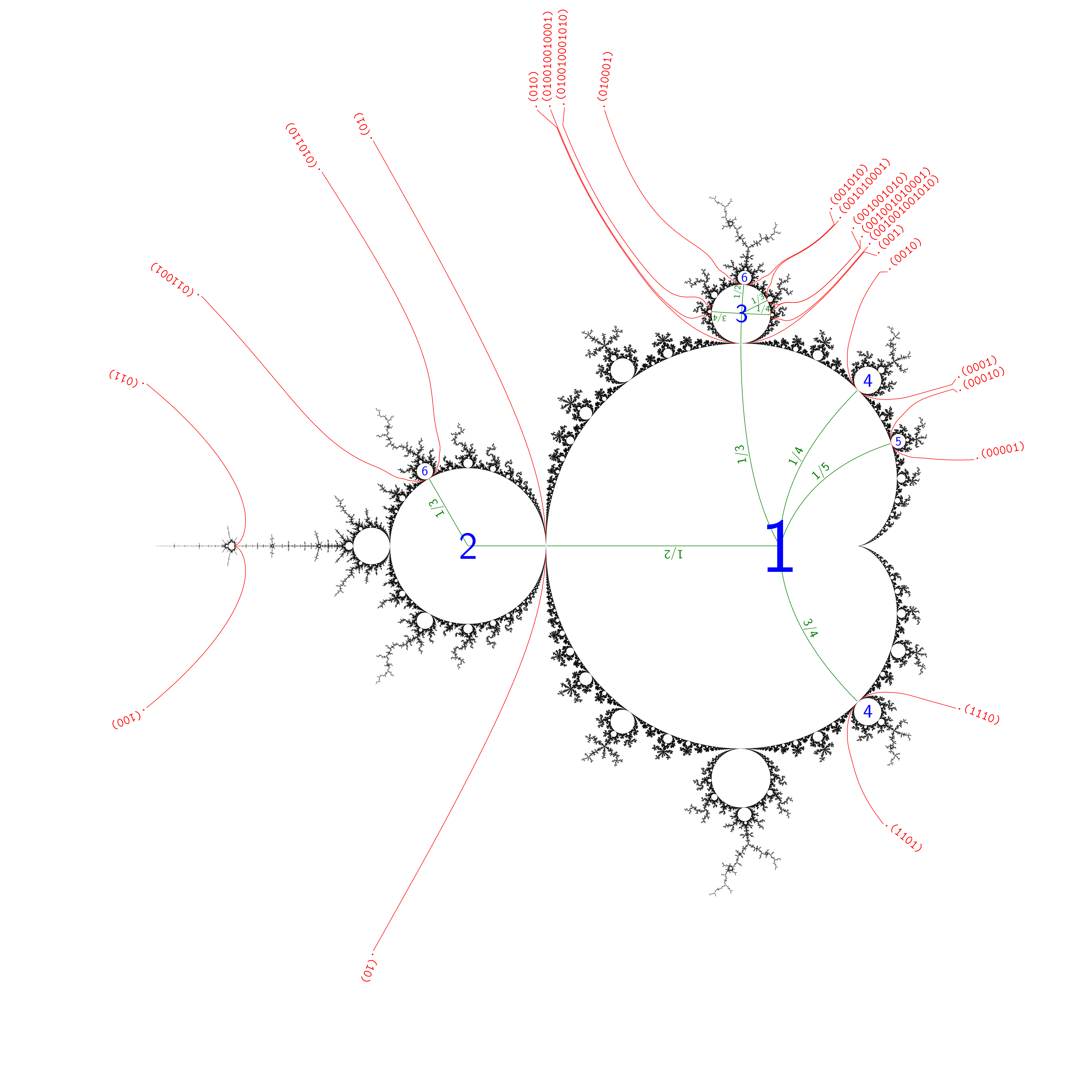

만델브로 집합의 연결성을 증명하는 과정에서 유도된 만델브로 집합의 여집합의 균일화에 대한 동적 공식은 만델브로 집합의 외부 광선을 생성한다.

만델브로 집합의 경계는 이차 다항식 계열의 분기 궤적이다. 즉, 만델브로 집합의 경계는 이차 사상

z_n=z_{n-1}^2+c

의 역학이

c

에 대한 민감한 의존성을 보이는 모든 매개변수

c

의 집합이며,

c

의 임의로 작은 변화에 따라 급격하게 변한다. 이는 대수 곡선의 수열, 즉 다항식 르미스케이트로 알려진 "만델브로 곡선"으로 구성될 수 있다.

모든 유리수

\tfrac{p}{q}

에 대해, ''p''와 ''q''가 서로소이면, 주기가 ''q''인 쌍곡선 성분이 메인 심장에서

\tfrac{2\pi p}{q}

에 해당하는 심장 가장자리의 내부 각도 지점에서 분기된다.^[29] 이 분기점에서 메인 심장과 연결된 부분은 '''''p''/''q''-가지'''''라고 불린다.

주기-''q'' 가지는 가지 맨 위에

q-1

개의 "안테나"를 갖는다. 주어진 구근의 주기는 이 안테나의 수를 세어 결정된다. 회전수 분자 ''p''는 가지에서 반시계 방향으로 각 안테나에 1부터

q-1

까지 번호를 매기고 가장 짧은 안테나가 어떤 것인지 찾아 결정한다.^[29]

1991년 데이비드 볼은 컴퓨터 실험을 통해,

z = -\tfrac{3}{4}+ i\varepsilon

(

-\tfrac{3}{4}

는 그 위치)에 대한 급수의 발산을 위해 필요한 반복 횟수를 계산했다.

\varepsilon

의 값에 필요한 반복 횟수를 곱하면 작은 ''

\varepsilon

''에 대해 더 나은

\pi

(원주율)의 근사값을 얻을 수 있다는 사실을 발견했다.^[30]

만델브로 집합은 여러 개의 구근이 직접 연결된 근본적인 심장 모양을 특징으로 한다.^[32] 기하학적 관점에서 특정 부분을 확대하면 경계 내의 위치와 관련된 구근에서 파생된 매개변수에 대한 해당 동적 거동에 대한 정보를 알 수 있다.^[33]

만델브로 집합 내의 주요 심장형에 부착된 구근 중 하나에서 파생된 매개변수

c

를 사용하는 2차 다항식

f_c(z) = z^2 + c

의 반복은 지정된 주기

q

와 회전수

p/q

를 갖는 매력적인 주기를 특징으로 하는 지도를 생성한다.^[33]^[34]

만델브로 집합 내의 구근은 매력적인 주기와 구조의 기하학적 특징으로 구별된다. 각 구근은 접합점에서 뻗어나와 그 주기를 나타내는 특정 수의 스포크를 표시하는 안테나로 특징지어진다. 예를 들어,

2/5

구근은 회전수가

2/5

인 매력적인 주기로 식별되며, 5개의 스포크가 뻗어나오는 접합점으로 구성된다.^[35]

메인 심장의 근점이

c=1/4

에서 첨점인 경우, 메인 심장은

0/1

-구근이다. 다른 구근의 근점은 이 구근이 메인 심장에 부착되는 지점이다.

0/1

과

1/2

-구근의 근점 사이에서 가장 큰 구근은

1/3

-구근이다.

1/3

은 이전 두 분수에서 파레이 합을 통해 얻어진다.

:

\frac{0}{1}

\oplus

\frac{1}{2}

=

\frac{1}{3}

마찬가지로,

1/3

과

1/2

-구근 사이에서 가장 큰 구근은

2/5

-구근이며, 파레이 합으로 주어진다.

:

\frac{1}{3}

\oplus

\frac{1}{2}

=

\frac{2}{5}

2/5

와

1/2

-구근 사이에서 가장 큰 구근은

3/7

-구근이고,

2/5

와

1/3

-구근 사이에서 가장 큰 구근은

3/8

-구근 등이다.^[33]^[37] 만델브로 집합 내의 구근 배열은 파레이 트리에 의해 지배되는 패턴을 따른다.^[35]

1/3

구근에서 시작하여

1/2

원을 향해 진행하면, 수열은 체계적으로 전개된다.

1/2

와

1/3

사이의 가장 큰 구근은

2/5

이고,

1/3

과

2/5

사이는

3/8

등이다.^[38] 만델브로 집합에서 순차적 스케일의 원형 구근 주기의 분모는 피보나치 수열에 부합한다.^[39]^[40] 피보나치 수열은 만델브로 집합의 특정 지점에서 나선형 팔의 수로 나타나며, 위쪽과 아래쪽 모두에서 나타난다.^[41]

만델브로 집합은 점화식

:

\begin{cases}z_{n+1} = z_n^2 + c \\z_0 = 0\end{cases}

으로 정의되는 복소수 수열 {''z''_''n''}이 ''n'' → ∞ 의 극한에서 무한대로 발산하지 않는다는 조건을 만족하는 복소수 ''c'' 전체가 만드는 집합이다.^[54]

복소수 ''c'' 를 복소 평면 상의 점으로 나타내면, 만델브로 집합은 프랙탈 도형으로 나타난다. 만델브로 집합의 대부분 면적은, 원점을 포함하는 심장형 곡선에 무수한 원이 외접하고, 그 원에 다시 무수한 작은 원이 외접하는 것을 무한히 반복하여 만들어지는 프랙탈 도형이다. 주위를 확대하면 이 프랙탈 도형과 유사한 "월경지"와 같은 도형이 무수히 보인다.

만델브로 집합 주위를 확대하면 반복해서 나타나는 "월경지"는 전체와 매우 유사하지만, 서로 다르다. 즉, 주변은 ''자기 유사성이 없는 프랙탈''의 일종이다.

만델브로 집합을 복소수를 사용하지 않고 다시 쓰려면, ''z''_''n'' 을 점 (''x''_''n'', ''y''_''n'') 에, ''c'' 를 점 (''a'', ''b'') 에 각각 치환하여,

:

\begin{cases}x_{n+1} = x_n^2 - y_n^2 + a \\y_{n+1} = 2x_n y_n + b\end{cases}

로 표현할수 있다.

6. 일반화

Multibrot 집합은 복소 평면에서 다음과 같은 단항 일변수 다항식 재귀식 군의 원소에 대해 발견되는 경계 집합이다.

: $z \mapsto z^d + c$ .

정수 ''d''에 대해, 이 집합들은 동일한 공식을 사용하여 구축된 쥘리아 집합에 대한 연결성 위치이다.

Multibrot 집합은 지수 ''d''의 값을 변경하여 얻는다. ''d''가 양의 정수일 때, 이 집합 각각의 중심 영역은 항상 $(d-1)$ 개의 첨점을 가진 외사상선이다. 음의 정수 지수를 가진 유사한 전개는 링 안쪽에 $(1-d)$ 개의 틈새가 생기며, 여기서 집합의 주요 중심 영역은 $(1-d)$ 개의 첨점을 가진 내사상선이다.

4차원 줄리아 집합은 3차원으로 투영되거나 단면으로 잘릴 수 있으며, 이 때문에 4차원 만델브로 집합도 가능하다.

3차원으로의 망델브로 집합의 완벽한 확장은 존재하지 않는다. 왜냐하면 반복할 수 있는 복소수의 3차원 유사체가 없기 때문이다. 복소수를 4차원으로 확장한 사원수가 있는데, 이는 망델브로 집합과 줄리아 집합을 4차원으로 완벽하게 확장한다.^[43] 그런 다음 이를 단면 또는 투영하여 3차원 구조로 만들 수 있다.

트리콘 프랙탈은 다음과 같은 반해석 계열의 연결성 궤적이다.

:

z \mapsto \bar{z}^2 + c

.

트리콘 (때로는 "만델바"라고도 함)은 밀너가 실수 3차 다항식의 매개변수 슬라이스를 연구하면서 발견했다.

버닝 쉽 프랙탈은 다음을 반복하여 얻을 수 있다.

:

z \mapsto (|\Re \left(z\right)|+i|\Im \left(z\right)|)^2 + c

.

7. 컴퓨터를 이용한 묘사

망델브로 집합을 실제로 그릴 때는 점화식에 따라 z_n을 계산하면서 수열이 발산하는지 여부를 검사한다. z_n의 절댓값이 2보다 크면 z_n은 발산하며, 이때의 c는 망델브로 집합에 속하지 않는다. 이때 2는 경계값 역할을 한다. 망델브로 집합 안에 속한 점은 z_n이 발산하지 않으므로 무한히 계산해도 끝나지 않는다. 따라서 적절한 n값 이후에 계산을 멈춰야 하며, 무한히 계산하지 않는 한 근사적인 집합만 얻을 수 있다.

수학적으로는 망델브로 집합 내부와 외부 두 가지만 의미가 있지만, 많은 프랙탈 생성 소프트웨어에서는 경계값을 처음 벗어난 z_n의 n값에 따라 집합 바깥 영역을 다르게 색칠한다. 예를 들어 발산 속도가 빠르면 어두운 녹색, 느릴수록 밝은 녹색으로 칠하면 c값이 망델브로 집합에 가까울수록 발산 속도가 늦다는 것을 시각적으로 알 수 있다.

망델브로 집합에 색을 입히는 방법에 따라 프랙탈 예술적인 그림을 만들 수 있다.
이탈 시간 알고리즘은 가장 널리 사용되는 알고리즘으로, 복소 평면 영역을 픽셀 단위로 나누어 각 픽셀에 대해 반복 계산을 수행한다. 계산 결과에 따라 픽셀의 색상을 결정한다.

각 점의 x, y 위치를 반복 계산의 초깃값으로 사용하고, 각 반복 결과를 다음 반복의 초깃값으로 사용한다. 값이 임계적인 "이탈" 조건에 도달하면 계산을 중지하고 픽셀을 그린다.

색상은 값이 이탈점에 얼마나 빨리 도달했는지를 나타낸다. 검은색은 반복 횟수 제한 전에 이탈하지 않는 값을, 밝은 색상은 이탈하는 점에 대해 사용한다.

의사 코드는 다음과 같다.

'''화면의 각''' 픽셀(Px, Py) '''에 대해'''

x0 := 픽셀의 x 좌표를 스케일링(만델브로 X 스케일(-2.00, 0.47) 내에 있도록 스케일링)
y0 := 픽셀의 y 좌표를 스케일링(만델브로 Y 스케일(-1.12, 1.12) 내에 있도록 스케일링)
x := 0.0
y := 0.0
iteration := 0
max_iteration := 1000
'''while''' (x² + y² ≤ 2² AND iteration < max_iteration) '''do'''
xtemp := x² - y² + x0
y := 2*x*y + y0
x := xtemp
iteration := iteration + 1

color := palette[iteration]
plot(Px, Py, color)

여기서 c, z, f_c의 관계는 다음과 같다.

z = x + iy
z² = x² + i2xy - y²
c = x₀ + iy₀

따라서 x와 y는 다음과 같이 계산된다.

x = x² - y² + x₀
y = 2xy + y₀

실행된 반복 횟수에 따라 색상을 할당하는 다양한 함수(선형, 지수 등)를 사용할 수 있다.

다음은 파이썬으로 구현한 코드 예시이다.

```python

import numpy as np

import matplotlib.pyplot as plt

# 매개변수 설정 (이 값들은 변경될 수 있습니다.)

xDomain, yDomain = np.linspace(-2,1.5,500), np.linspace(-2,2,500)

bound = 2

power = 2 # 임의의 양의 부동 소수점 값

max_iterations = 50 # 임의의 양의 정수 값

colormap = 'magma' # matplotlib 유효한 모든 컬러맵으로 설정

# 만델브로 집합을 나타내는 2차원 배열 계산

iterationArray = []

for y in yDomain:

row = []

for x in xDomain:

c = complex(x,y)

z = 0

for iterationNumber in range(max_iterations):

if(abs(z) >= bound):

row.append(iterationNumber)

break

else: z = z**power + c

else:

row.append(0)

iterationArray.append(row)

# 데이터 플로팅

ax = plt.axes()

# plt.rc('text', usetex = True) # LaTeX가 설치된 경우 tex 사용을 활성화하려면 이 줄의 주석을 해제합니다.

ax.set_aspect('equal')

graph = ax.pcolormesh(xDomain, yDomain, iterationArray, cmap = colormap)

plt.colorbar(graph)

plt.xlabel("실수 축")

plt.ylabel("허수 축")

plt.title('수식 $z_ = z^} + c$에 대한 만델브로 집합'.format(power))

plt.show()

```

`power` 변수 값을 수정하여 멀티브로 집합 이미지를 생성할 수 있다.

만델브로 집합은 방대한 계산 시간을 필요로 하므로 컴퓨터 벤치마크 테스트에 이용되기도 한다. 또한, 기하학적인 아름다움 때문에 감상을 위한 프로그램도 존재한다.

Fractint (대부분의 플랫폼 지원)
ChaosPro (Microsoft Windows용)
Xaos (실시간 발생 프로그램, Windows, Mac, Linux 등)

8. 대중 문화 속 망델브로 집합

망델브로 집합은 가장 인기 있는 프랙탈로 널리 알려져 있으며, 여러 대중 문화에서 언급되었다.

조나단 쿨턴의 노래 "Mandelbrot Set"은 프랙탈 자체와 그 이름을 딴 사람인 브누아 망델브로를 기리는 곡이다.
블루 맨 그룹의 1999년 데뷔 앨범 ''오디오''는 "Opening Mandelbrot", "Mandelgroove", "Klein Mandelbrot"라는 곡의 제목에서 망델브로 집합을 언급한다. 그들의 두 번째 앨범 ''The Complex''(2003)은 "Mandelbrot IV"라는 숨겨진 트랙으로 끝을 맺는다.
피어스 앤서니의 ''모드 시리즈'' 두 번째 책인 ''프랙탈 모드''는 집합의 완벽한 3차원 모델인 세계를 묘사한다.
아서 C. 클라크의 소설 ''그랜드 뱅크스의 유령''에는 망델브로 집합의 모양을 복제한 인공 호수가 등장한다.
브누아 망델브로와 그의 이름을 딴 집합은 2020년 11월 20일 구글 두들의 주제였다(고 브누아 망델브로의 96번째 생일).
미국의 록 밴드 Heart는 2004년 앨범 ''Jupiters Darling''의 표지에 망델브로 집합의 이미지를 사용했다.
영국의 블랙 메탈 밴드 Anaal Nathrakh는 Eschaton 앨범 커버 아트에 망델브로 집합과 유사한 이미지를 사용한다.
텔레비전 드라마 ''디르크 젠틀리의 전체론적 탐정 사무소''(2016)는 아만다 캐릭터의 환상과 관련하여 망델브로 집합을 두드러지게 보여준다. 두 번째 시즌에서 그녀의 재킷 뒤에는 프랙탈의 큰 이미지가 있다.
이언 스튜어트의 2001년 저서 ''플래터랜드''에는 프랙탈을 캐릭터와 독자에게 설명하는 데 도움을 주는 만델블롯이라는 캐릭터가 등장한다.
미완성된 앨런 무어의 1990년 만화 시리즈 ''빅 넘버스''는 프랙탈 기하학과 카오스 이론에 대한 망델브로의 연구를 이 작품의 구조를 뒷받침하는 데 사용했다. 무어는 한때 이 만화 시리즈의 이름을 ''The Mandelbrot Set''으로 지을 예정이었다.
만화 ''여름에 히카루가 죽었다''에서 요시키가 가짜 히카루의 몸속으로 손을 뻗을 때 망델브로 집합을 환각한다.

참조

_[1] 백과사전 Mandelbrot set https://web.archive.[...] Oxford University Press
_[2] 웹사이트 Mandelbrot set 2022-01-30
_[3] 서적 Riemann Surfaces and Related Topics: Proceedings of the 1978 Stony Brook Conference https://web.archive.[...] Princeton University Press 2019-07-01
_[4] 학술지 Biophilic Fractals and the Visual Journey of Organic Screen-savers http://sprott.physic[...] Society for Chaos Theory in Psychology & Life Sciences 2009-01-01
_[5] 학술지 Fractal aspects of the iteration of $z\mapsto\lambda z(1-z)$ for complex $\lambda, z$
_[6] 문서 Etude dynamique des polynômes complexes Prépublications mathémathiques d'Orsay 1984/1985
_[7] 서적 The Beauty of Fractals Springer-Verlag
_[8] 문서 Frontiers of Chaos
_[9] 서적 Chaos: Making a New Science Cardinal
_[10] 학술지 Exploring The Mandelbrot Set https://www.jstor.or[...] 1985-08
_[11] 잡지 Turbocharging Mandelbrot https://archive.org/[...] 2015-11-11
_[12] 학술지 One hundred years of complex dynamics 2016-01
_[13] 웹사이트 Mandelbrot Set https://mathworld.wo[...] 2024-01-24
_[14] 웹사이트 Mandelbrot Set Explorer: Mathematical Glossary http://math.bu.edu/D[...] 2007-10-07
_[15] 웹사이트 Escape Radius https://mrob.com/pub[...] 2024-01-17
_[16] 웹사이트 The Logistic Map is hiding in the Mandelbrot Set https://thatsmaths.c[...] 2024-02-18
_[17] 웹사이트 The Mandelbrot Set is Connected: a Topological Proof http://www.math.brow[...] 2001-08-08
_[18] 문서 The Mandelbrot set, theme and variations https://books.google[...] Cambridge University Press
_[19] 웹사이트 Mandelbrot Set Lemniscate https://mathworld.wo[...] 2023-07-17
_[20] 학위논문 The Mandelbrot set https://scholarworks[...] Theses Digitization Project
_[21] 논문 A survey on MLC, Rigidity and related topics
_[22] 서적 Exploring the Mandelbrot set. The Orsay Notes
_[23] 학위논문 Homeomorphisms on Edges of the Mandelbrot Set RWTH Aachen University
_[24] 서적 Topological methods in modern mathematics (Stony Brook, NY, 1991) Publish or Perish
_[25] 학술지 Similarity between the Mandelbrot set and Julia Sets http://projecteuclid[...]
_[26] 서적 Computers in Geometry and Topology https://books.google[...] Taylor & Francis
_[27] 학술지 On a Visualization of the Convergence of the Boundary of Generalized Mandelbrot Set to (n-1)-Sphere https://reader.digit[...] 2022-05-18
_[28] 학술지 The Hausdorff dimension of the boundary of the Mandelbrot set and Julia sets
_[29] Youtube Number Sequences in the Mandelbrot Set https://www.youtube.[...] The Mathemagicians' Guild 2020-06-04
_[30] 서적 The Computational Beauty of Nature MIT Press
_[31] 학술지 π in the Mandelbrot Set
_[32] 학술지 The Mandelbrot Set, the Farey Tree, and the Fibonacci Sequence http://dx.doi.org/10[...] 1999-04
_[33] 웹사이트 Illuminating the Mandelbrot set https://math.bu.edu/[...] 2019-01-07
_[34] 웹사이트 The Mandelbrot Set and the Farey Tree https://sites.math.w[...] 2016-05
_[35] 웹사이트 The Mandelbrot Set and the Farey Tree https://math.bu.edu/[...] 1997-12-29
_[36] 웹사이트 Iteration des Polynomials Quadratiques Complexes https://pi.math.corn[...] 1982
_[37] 웹사이트 The Mandelbrot Set Explorer Welcome Page http://math.bu.edu/D[...] 2024-02-17
_[38] 웹사이트 Maths Town https://www.patreon.[...] 2024-02-17
_[39] 논문 The Unexpected Fractal Signatures in Fibonacci Chains 2019-12
_[40] 웹사이트 7 The Fibonacci Sequence https://math.bu.edu/[...] 2024-02-17
_[41] 웹사이트 fibomandel angle 0.51 https://www.desmos.c[...] 2024-02-17
_[42] 웹사이트 Rudy Rucker's discussion of the CCM http://www.cs.sjsu.e[...]
_[43] 웹사이트 Expanding the Mandelbrot Set into Higher Dimensions https://archive.brid[...] 2021-09-15
_[44] 뉴스 This Trippy Music Video Is Made of 3D Fractals. https://gizmodo.com/[...] Ryan F. Mandelbaum 2018
_[45] 뉴스 what are Fractals? https://thewest.com.[...] Olga de Moeller 2018
_[46] 웹사이트 Mandelbrot Set http://www.jonathanc[...] 2015-01-15
_[47] 웹사이트 Blue Man Group – Audio Album Reviews, Songs & More https://www.allmusic[...] 2023-07-04
_[48] 서적 Fractal Mode https://books.google[...] HarperCollins
_[49] 서적 The Ghost From The Grand Banks https://books.google[...] Orion
_[50] 웹사이트 Google honors mathematician Benoit Mandelbrot with new Doodle https://www.upi.com/[...] 2020-12-30
_[51] 웹사이트 Hannah Marks "Amanda Brotzman" customized black leather jacket from Dirk Gently's Holistic Detective Agency https://www.icollect[...]
_[52] 논문 Book Review: ''Flatterland: Like Flatland, Only More So'' https://www.ams.org/[...] 2002-04
_[53] 웹사이트 The Great Alan Moore Reread: Big Numbers'' by Tim Callahan https://www.tor.com/[...] 2012-05-21
_[54] 웹사이트 만델브로 집합이란 https://azisava.saku[...] 2020-07-27
_[55] 논문 The Hausdorff dimension of the boundary of the Mandelbrot set and Julia sets

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com