맨위로가기

대칭 관계

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

대칭 관계는 집합 X 위의 이항 관계 R⊆X²에서 임의의 x, y∈X에 대해 (x, y)∈R이면 (y, x)∈R을 만족하는 관계를 의미한다. 크기 n의 유한 집합 위에는 총 2n(n+1)/2개의 대칭 관계가 존재한다. 동치 관계는 추이적이며 반사적인 대칭 관계의 예시이며, "같다"는 등식, "…와 결혼했다" 등의 관계 또한 대칭 관계에 해당한다. 비대칭 관계와 반대칭 관계와는 독립적인 관계이다.

광고

더 읽어볼만한 페이지

  • 집합론 - 퍼지 집합
    퍼지 집합은 각 원소가 0과 1 사이의 소속도를 가지며, 소속 함수를 통해 정의되고, 여집합, 합집합, 교집합 등의 연산을 수행하며, 퍼지 논리, 퍼지 수, 엔트로피 등의 개념과 L-퍼지 집합, 직관적 퍼지 집합 등으로 확장된다.
  • 집합론 - 무한 집합
    무한 집합은 유한 집합이 아니며, 자연수보다 큰 크기를 가지고 자신의 진부분집합과 일대일 대응을 가지며, 가산 무한 집합과 비가산 무한 집합으로 나뉜다.

2. 정의

집합 X 위의 이항 관계 R\subseteq X^2가 다음 조건을 만족시키면, '''대칭 관계'''라고 한다.


  • 임의의 x,y\in X에 대하여, 만약 (x,y)\in R라면, (y,x)\in R

3. 성질

크기 n인 유한 집합 위에는 총 2^{n(n+1)/2}개의 대칭 관계가 존재한다. 작은 n에 대하여, 이는 다음과 같다 (n=0,1,2,\dots).

:1, 2, 8, 64, 1024, …

대칭적이고 추이 관계는 항상 준반사 관계이다.

''n''개의 원소에 대한 대칭 관계의 수는 이진 행렬 표현에서 오른쪽 위 삼각형이 관계를 완전히 결정하고 임의로 주어질 수 있다는 점을 통해 구할 수 있다. 따라서 이진 위 삼각형 행렬의 수, 즉 2''n''(''n''+1)/2만큼의 대칭 관계가 존재한다.

3. 1. 반사 대칭 관계

집합 X 위의 반사 대칭 관계 R에 대하여, CR을 R의 극대 클릭들의 집합이라고 하자. 즉, CR은 다음 조건을 만족시키는 극대 부분 집합 C⊆X들로 구성된다.

  • 임의의 c, c'∈C에 대하여, (c, c')∈R


그렇다면, CR은 X의 덮개이며, 다음 두 성질을 만족시킨다.

  • (A) 임의의 C∈CR 및 F⊆CR에 대하여, 만약 C⊆∪F라면, ∩F⊆C이다.
  • (B) 임의의 S⊆X에 대하여, 만약 S가 CR의 원소의 부분 집합이 아니라면, CR의 원소의 부분 집합이 아닌 두 원소 집합 {s, t}⊆S가 존재한다.


반대로, 조건 (A)와 (B)를 만족시키는 X의 덮개 C가 주어졌을 때, X 위에 다음과 같은 이항 관계 RC를 정의하자.

:(x, y)∈RC ⇔ ∃C∈C: x, y∈C

그렇다면, RC는 반사 대칭 관계이다. R↦CR은 X 위의 반사 대칭 관계들의 집합과 조건 (A)와 (B)를 만족시키는 X의 덮개들의 집합 사이의 일대일 대응이며, 그 역함수는 C↦RC이다. 즉, 반사 대칭 관계의 개념은 위 두 조건을 만족시키는 덮개의 개념과 동치이다.[2]

4. 예

모든 동치 관계는 대칭 관계이다. 예를 들어 "같다"(등식)는 대칭 관계이지만, "보다 작다"는 대칭 관계가 아니다.[1]

순서체 K 위에서 |x-y|≤1과 같이 정의된 이항 관계는 반사 대칭 관계이다. 반면 0<|x-y|≤1과 같이 정의된 이항 관계는 대칭 관계이지만, 반사 관계는 아니다.

"…와 (대부분의 법적 체계에서) 결혼했다", "…의 완전한 생물학적 형제/자매이다" 등은 대칭 관계의 예시이다.[1]

4. 1. 수학에서의 예


  • "같다" (등식) (반면 "보다 작다"는 대칭적이지 않다)[1]
  • 부분 순서 집합의 원소에 대해 "…와 …는 비교 가능하다"[1]
  • "...와 ...는 홀수이다"[1]:
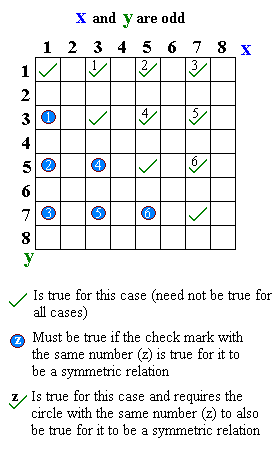
  • 「(A는 B와) 결혼했다」는 대칭 관계이지만, 「(A는 B보다) 작다」는 대칭 관계가 아니다.[1]
  • 「(A는 B와) 같다」(등식).[1]
  • 「A는 홀수이고, B도 홀수이다」[1]

4. 2. 수학 외의 예


  • "…와 (대부분의 법적 체계에서) 결혼했다"
  • "…의 완전한 생물학적 형제/자매이다"
  • "…의 동음이의어이다"
  • "…의 동료이다"
  • "…의 팀 동료이다"

5. 비대칭 관계 및 반대칭 관계와의 관계

대칭 관계와 반대칭 관계


정의에 따르면, 공집합이 아닌 관계는 대칭 관계이면서 동시에 비대칭 관계일 수 없다. (여기서 'a'가 'b'와 관련이 있다면, 'b'는 ('a'와) 같은 방식으로 관련될 수 없다.) 그러나 관계는 대칭적이지도 비대칭적이지도 않을 수 있는데, 이는 "이하" 및 "포식"의 경우에 해당한다.

대칭 관계와 반대칭 관계 (여기서 'a'가 'b'와 관련되고 'b'가 'a'와 관련될 수 있는 유일한 방법은 a = b인 경우)는 실제로 서로 독립적이다. 다음 예시들이 이를 보여준다.

수학적 예시
대칭대칭 아님
반대칭등호나누어떨어짐, 이하
반대칭 아님합동 (모듈러 산술에서)// (정수 나눗셈), 대부분의 비자명 순열



비수학적 예시
대칭대칭 아님
반대칭동일 인물임, 결혼함~의 복수형임
반대칭 아님~의 완전한 생물학적 형제임~를 포식함



; 동치 관계: 추이적이며 반사적인 대칭 관계

6. 성질


  • 대칭적이고 추이 관계는 항상 준반사 관계이다.
  • ''n''개의 원소에 대한 대칭 관계의 수는 2''n''(''n''+1)/2이다.[1]


다양한 유형의 ''n''-원소 이진 관계 수
원소이진 관계추이 관계반사 관계대칭 관계전순서부분 순서 집합강한 약한 순서전순서동치 관계
0111111111
1221211111
216134843322
3512171646429191365
465536399440961024355219752415
n2n22n(n−1)2n(n+1)/2∑|k=0부터 n까지영어 k!S(n, k)n!∑|k=0부터 n까지영어 S(n, k)


  • 제2종 스털링 수 ''S''(''n'', ''k'')는 크기가 ''n''인 집합을 ''k''개의 서로소 부분집합으로 나누는 경우의 수를 의미한다.
  • 동치 관계: 추이적이며 반사적인 대칭 관계

참조

[1] 웹사이트 MAD3105 1.2 https://www.math.fsu[...] Florida State University 2024-03-30
[2] 저널 On existence conditions for compatible tolerances 1976


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com