도이치–조사 알고리듬

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 문제 설명
3. 역사
4. 알고리듬
- 4.1. 작동 원리
5. 고전적 해와의 비교
6. 의의 및 영향
참조

1. 개요

도이치-조사 알고리듬은 주어진 함수가 상수 함수인지 균형 함수인지 판단하는 양자 알고리듬이다. 데이비드 도이치에 의해 처음 제안되었으며, 이후 개선되어 단 한 번의 함수 평가로 문제를 해결할 수 있게 되었다. 이 알고리듬은 양자 오라클을 사용하여 작동하며, 초기 상태에 아다마르 변환을 적용하고 오라클을 거쳐 다시 아다마르 변환을 수행하는 과정을 거친다. 최종 상태를 측정하여 함수가 상수인지 균형인지 판단하며, 고전적인 알고리듬보다 효율적으로 문제를 해결한다. 도이치-조사 알고리듬은 양자 컴퓨터가 고전 컴퓨터보다 특정 문제를 더 효율적으로 해결할 수 있음을 보여주는 초기 사례이며, 양자 컴퓨팅 발전에 중요한 영향을 미쳤다.

2. 문제 설명

도이치-조사 문제에서는 오라클이라고 알려진 블랙박스 양자 컴퓨터가 주어진다. 이 오라클은 다음 함수 $f$ 를 구현한다:

$f\colon\{0,1\}^n\rightarrow \{0,1\}$

이 함수는 $n$ 비트 이진수 값을 입력으로 받아, $0$ 또는 $1$ 을 출력한다. 함수 $f$ 는 다음 두 가지 종류 중 하나라는 약속이 있다.^[12]^[1]

상수 함수: 모든 입력에 대해 동일한 값( $0$ 또는 $1$ )을 출력한다.
균형 함수: 입력 정의역의 정확히 절반에 해당하는 입력에 대해서는 $1$ 을 출력하고, 나머지 절반에 대해서는 $0$ 을 출력한다.

도이치-조사 문제는 주어진 오라클을 사용하여 함수

f

가 상수 함수인지 아니면 균형 함수인지를 결정하는 것이다.

3. 역사

도이치-조사 알고리듬은 데이비드 도이치가 1985년에 발표한 초기 연구를 일반화한 것이다. 이 초기 연구는 입력값이 1비트인 불 함수 $f: \{0,1\} \rightarrow \{0,1\}$ 가 주어졌을 때, 이 함수가 상수 함수인지 아닌지를 판별하는 문제( $n=1$ 인 경우)에 대한 해법을 다루었다.^[13]^[5] 하지만 도이치가 처음 제안한 알고리듬은 결정론적이지 않았고, 절반의 확률로만 성공했다.

1992년, 도이치와 조사는 이 문제를 $n$ 비트 입력을 갖는 함수로 일반화하여 결정론적인 알고리듬을 개발했다. 다만 이 알고리듬은 함수를 두 번 평가해야 했다.

이후 클레브 등은 도이치-조사 알고리듬을 더욱 개선하여,^[14]^[2] 함수 $f$ 를 단 한 번만 호출하면서도 결정론적으로 답을 얻는 알고리듬을 만들었다. 그럼에도 불구하고 이 알고리듬은 도이치와 조사가 제시한 획기적인 접근 방식을 기리기 위해 여전히 '도이치-조사 알고리듬'이라고 불린다.^[9]^[2]

4. 알고리듬

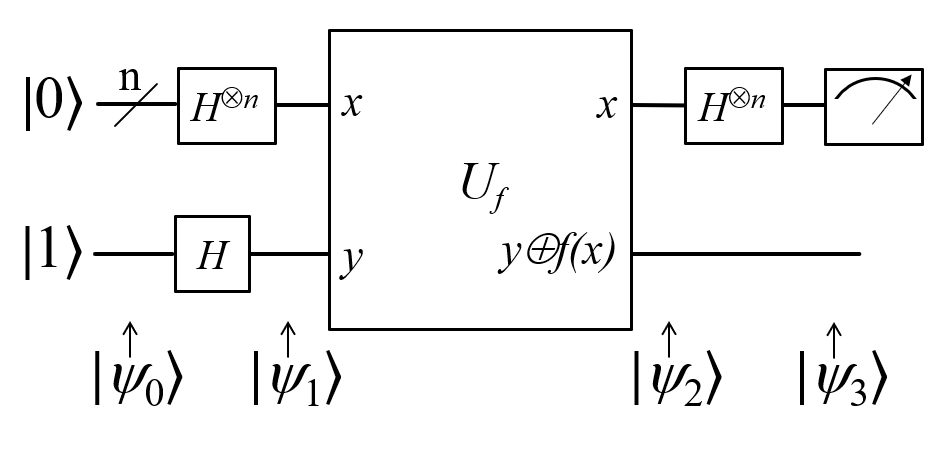
도이치-조사 알고리듬은 주어진 함수 $f(x)$ 가 상수 함수인지 아니면 입력값의 절반에 대해서는 0을, 나머지 절반에 대해서는 1을 출력하는 균형 함수(balanced function)인지를 양자 컴퓨터를 이용하여 효율적으로 판별하는 방법이다.^[1] 이 알고리듬은 양자 중첩과 양자 간섭 현상을 핵심 원리로 활용하여, 고전적인 방법으로는 여러 번 함수를 계산해야 알 수 있는 함수의 전역적 속성을 단 한 번의 계산으로 알아낼 수 있다는 특징을 가진다.

알고리듬의 실행을 위해서는 함수

f(x)

를 계산하는 특수한 양자 오라클이 필요하다. 이 오라클은 입력 상태

|x\rangle|y\rangle

를

|x\rangle|y\oplus f(x) \rangle

로 변환하는 연산을 수행하며, 이 과정에서 양자 상태의 양자 결어긋남을 일으키지 않아야 한다.

알고리듬은

n+1

개의 큐비트를 사용하여

|0\rangle^{\otimes n} |1\rangle

상태에서 시작한다. 먼저 모든 큐비트에 아다마르 변환을 적용하여 중첩 상태를 생성한다. 그 다음, 양자 오라클을 적용하여 함수

f(x)

의 정보를 큐비트 상태의 위상(phase)에 반영시킨다. 마지막으로 첫

n

개의 큐비트에 다시 아다마르 변환을 적용하고 이 큐비트들을 측정한다.

최종 측정 결과, 모든 큐비트가

0

인 상태, 즉

|0\rangle^{\otimes n}

가 측정되면 함수

f(x)

는 상수 함수임을 확신할 수 있다. 만약 그 외의 다른 상태가 측정된다면 함수

f(x)

는 균형 함수이다. 이러한 결과는 함수가 상수일 경우 특정 경로의 양자 상태들이 보강 간섭을 일으켜

|0\rangle^{\otimes n}

상태의 확률 진폭을 1로 만드는 반면, 함수가 균형 함수일 경우에는 상쇄 간섭이 일어나

|0\rangle^{\otimes n}

상태의 확률 진폭이 0이 되기 때문에 가능하다.

4. 1. 작동 원리

도이치-조사 알고리듬이 제대로 작동하기 위해서는 몇 가지 조건이 필요하다. 우선 함수

f(x)

값을 계산하는 오라클은 입력값

x

에 결어긋남을 일으키지 않는 양자 오라클이어야 한다. 또한, 계산 과정에서

x

의 복사본을 만들어서는 안 되는데, 이는 양자역학의 복제 불가능성 정리에 위배되기 때문이다.^[1]

알고리듬은 총

n+1

개의 큐비트를 사용하며, 초기 상태는

|0\rangle^{\otimes n} |1\rangle

이다. 이는 첫

n

개의 큐비트가 모두

|0\rangle

상태이고, 마지막 큐비트만

|1\rangle

상태임을 의미한다.

첫 단계로, 각 큐비트에 아다마르 변환(Hadamard gate)을 적용한다. 이 변환을 통해 큐비트들은 중첩 상태가 되며, 전체 시스템의 상태는 다음과 같이 표현된다.

:

\frac{1}{\sqrt{2^{n+1}}}\sum_{x=0}^{2^n-1} |x\rangle (|0\rangle - |1\rangle )

여기서

|x\rangle

는

n

개의 큐비트가 나타낼 수 있는

0

부터

2^n-1

까지의 모든 가능한 상태를 의미한다.

다음으로, 함수

f

를 구현한 양자 오라클을 시스템에 적용한다. 이 오라클은 입력 상태

|x\rangle|y\rangle

를

|x\rangle|y\oplus f(x) \rangle

로 변환한다. 여기서

\oplus

는 모듈로 2 덧셈(XOR 연산)을 의미한다. 오라클을 적용한 후의 상태는 다음과 같다.

:

\frac{1}{\sqrt{2^{n+1}}}\sum_{x=0}^{2^n-1} |x\rangle (|0\oplus f(x)\rangle - |1\oplus f(x)\rangle )

함수

f(x)

의 값은

0

또는

1

이다.

만약 $f(x)=0$ 이면, $|0\oplus 0\rangle - |1\oplus 0\rangle = |0\rangle - |1\rangle$ 이 된다.
만약 $f(x)=1$ 이면, $|0\oplus 1\rangle - |1\oplus 1\rangle = |1\rangle - |0\rangle = -(|0\rangle - |1\rangle)$ 이 된다.

따라서 위 상태는

(-1)^{f(x)}

라는 위상 인수를 사용하여 다음과 같이 간단하게 표현할 수 있다.

:

\frac{1}{\sqrt{2^{n+1}}}\sum_{x=0}^{2^n-1} (-1)^{f(x)} |x\rangle (|0\rangle - |1\rangle )

이 상태에서 마지막 큐비트

\frac

5. 고전적 해와의 비교

전통적인 결정론적 알고리즘의 경우,

n

이 비트 수일 때 최악의 경우에는 함수

f

를

2^{n-1} + 1

번 평가해야 한다. 예를 들어, 함수

f

가 상수 함수임을 증명하려면 가능한 모든 입력값의 절반 이상을 확인하여 출력이 모두 같은지 봐야 한다. 이는 함수가 균형 함수 또는 상수 함수 둘 중 하나임이 보장되기 때문이다. 가장 좋은 경우는 함수가 균형 함수이고 처음 확인한 두 입력값에 대한 출력이 다를 때 발생한다.

반면, 전통적인 확률적 알고리즘을 사용하면, 함수를 상수

k

번 계산하여 높은 확률로 정답을 얻을 수 있다. 이때 실패할 확률은

k \geq 1

에 대해

\epsilon \leq 1/2^{k}

이다. 하지만 오류 가능성을 완전히 없애고 항상 정확한 답을 얻으려면, 여전히

k=2^{n-1} + 1

번의 함수 평가가 필요하다.

이에 비해 도이치–조사 알고리듬은 함수

f

를 단 한 번만 평가하고도 항상 정확한 답을 얻는다는 점에서 고전적인 알고리듬들과 비교하여 큰 효율성을 보인다.

도이치–조사 문제는 이처럼 결정론적 고전 컴퓨터로는 많은 계산이 필요한 문제를 양자 컴퓨터가 오류 없이 효율적으로 풀 수 있음을 보여주기 위해 의도적으로 설계된 블랙 박스 문제이다.

6. 의의 및 영향

도이치-조자 문제는 양자 알고리듬으로는 쉽게 풀 수 있지만, 결정론적 고전 알고리즘으로는 풀기 어렵도록 의도적으로 설계된 문제이다. 이 문제는 결정론적 고전 컴퓨터로는 많은 쿼리가 필요한 블랙 박스 문제를 양자 컴퓨터가 오류 없이 효율적으로 풀 수 있다는 것을 보여주기 위해 고안되었다.

따라서 이 알고리듬은 양자 컴퓨터가 고전 컴퓨터보다 특정 문제를 훨씬 효율적으로 해결할 수 있음을 보여주는 초기 사례 중 하나로 평가받는다. 이는 양자 알고리듬의 잠재력을 제시하며 이후 양자 컴퓨팅 분야 발전에 중요한 계기가 되었다. 비록 이 알고리듬 자체의 직접적인 실용성은 제한적이지만, 양자 우월성 개념을 설명하는 중요한 이론적 도구로 여겨진다.

참조

_[1] 논문 Rapid solutions of problems by quantum computation
_[2] 논문 Quantum algorithms revisited
_[3] 서적 Proceedings 35th Annual Symposium on Foundations of Computer Science 1994-11
_[4] 논문 Efficient classical simulation of the Deutsch–Jozsa and Simon's algorithms
_[5] 논문 Quantum Theory, the Church-Turing Principle and the Universal Quantum Computer
_[6] 논문 Rapid Solution of Problems by Quantum Computation http://rspa.royalsoc[...] 1992-12-08
_[7] 논문 Quantum algorithms revisited http://www.royalsoci[...] 1998-01-08
_[8] 논문 Rapid solutions of problems by quantum computation
_[9] 논문 Quantum algorithms revisited
_[10] 논문 On the Power of Quantum Computation http://citeseer.ist.[...]
_[11] 논문 Efficient classical simulation of the Deutsch–Jozsa and Simon's algorithms
_[12] 논문 Rapid solutions of problems by quantum computation
_[13] 논문 Quantum Theory, the Church-Turing Principle and the Universal Quantum Computer
_[14] 논문 Quantum algorithms revisited

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com