인과 집합
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
인과 집합은 일반 상대성 이론과 양자 역학을 통합하려는 시도로, 시공간을 기본적으로 이산적인 구조로 간주하는 이론이다. 이 이론은 시공간 사건들의 집합과 그들 사이의 인과 관계를 부분 순서 집합으로 표현하며, '순서 + 숫자 = 기하학'이라는 원리를 따른다. 인과 집합은 반사적, 반대칭적, 추이적, 국소 유한 조건을 만족해야 하며, 측지선과 같은 기하학적 구조를 정의하고 차원을 추정하는 방법을 제공한다. 또한, 인과 집합을 연속적인 시공간에 충실하게 매장할 수 있는지 여부가 중요한 연구 과제이며, 흩뿌림과 같은 방법을 통해 인과 집합을 구성할 수 있다. 인과 집합의 동역학은 어떤 인과 집합이 물리적으로 실현 가능한 시공간에 해당하는지를 결정하는 규칙을 제공하며, 경로 적분과 순차적 성장 모델과 같은 접근 방식을 통해 연구되고 있다.
더 읽어볼만한 페이지
- 양자중력 - 중력자
중력자는 중력 상호작용을 매개하는 가상의 기본 입자로 여겨지지만, 양자화된 일반 상대성 이론의 문제로 인해 완전한 이론이 확립되지 않았으며, 중력파의 존재가 간접적으로 뒷받침하지만 직접적인 검출은 현재 불가능하고 질량에 대한 상한선이 제시되고 있으며 초대칭 파트너인 그라비티노의 존재가 예측된다. - 양자중력 - 양자 중력
양자 중력은 양자역학과 일반 상대성이론을 통합하여 중력이 강한 극한 조건에서 발생하는 이론적 모순을 해결하려는 시도로, 재규격화 불능성과 시공간 배경 의존성 차이 등의 난제 해결을 위해 끈 이론, 루프 양자 중력 등 다양한 접근 방식이 연구되고 있으며, 우주 마이크로파 배경 데이터 등을 이용한 실험적 검증이 시도되고 있다. - 이론물리학 - 시공간
시공간은 시간과 공간을 4차원 연속체로 통합한 개념으로, 아인슈타인의 상대성이론에 따라 상대적이며, 일반 상대성이론에서는 중력을 시공간의 곡률로 설명하고, 현대 물리학과 우주론 연구에 필수적이다. - 이론물리학 - 대응원리
대응 원리는 플랑크 상수가 0에 가까워지는 극한에서 양자역학이 고전역학으로 근사적으로 환원됨을 보이는 원리로서, 초기 양자역학 발전에 기여했으나 현대에는 유추적인 역할로 중요성이 감소하였지만, 고전역학과 양자역학의 수학적 대응 관계 연구를 통해 계승되고 있다. - 순서론 - 스콧 위상
스콧 위상은 부분 순서 집합 위에 정의되는 위상으로, 하향 집합과 directed set의 상한에 대해 닫혀있는 집합을 닫힌 집합으로 정의하며, 컴퓨터 과학, 특히 프로그램 의미론에서 연속 함수의 개념을 일반화하고 프로그램의 계산 과정을 모델링하는 데 사용된다. - 순서론 - 사전식 순서
사전식 순서는 정렬된 집합의 순서를 일반화하여 곱집합의 순서를 정의하는 데 사용되며, 단어 순서 정렬 방식과 유사하게 다양한 분야에 응용되는 수학적 개념이다.
2. 역사
상대성 이론이 정립된 후, 헤르만 바일과 헨드릭 로렌츠는 인과 관계를 중심으로 이론을 구성하려는 시도를 했다.[2] 알프레드 롭은 1914년과 1936년에 발표한 책에서 인과적 선행 관계를 공리적으로 정의했다.[1] 수마티 수르야, E. H. 크론하이머, 로저 펜로즈는 시공간의 인과 구조를 양자화하려는 초기 제안을 했다.[3]
'''인과 집합'''()은 다음 조건을 만족시키는 부분 순서 집합이다.
데이비드 말라멘트의 정리는 크리스토퍼 지먼,[5] 스티븐 호킹 등의 이전 연구를 확장한 것이다.[6][1] 이 정리에 따르면, 과거와 미래를 구분하는 두 시공간 사이에 인과 구조를 보존하는 전단사 맵이 존재하면, 그 맵은 등각 사상이다. 이때, 등각 인자는 시공간 영역의 부피와 관련이 있으며, 이 부피는 해당 영역의 점 수를 세어 구할 수 있다.
라파엘 소르킨은 "순서 + 숫자 = 기하학"이라는 슬로건을 제시하며 인과 집합 이론을 시작했고, 현재까지 이 프로그램을 주도하고 있다. 이 프로그램은 시공간이 근본적으로 이산적이면서도 지역적 로렌츠 불변성을 유지하는 이론을 제공한다.
3. 정의
는 이고 일 때 사용한다.
집합 는 시공간 사건의 집합을 나타내며, 순서 관계 는 사건 간의 인과 관계를 나타낸다. (유사한 개념은 로렌츠 다양체에서 인과 구조를 참조).
이 정의는 반사적 관례를 사용하지만, 순서 관계가 비반사적이고 비대칭적인 비반사적 관례를 선택할 수도 있다.
로렌츠 다양체의 인과 관계 (닫힌 인과 곡선이 없는)는 처음 세 가지 조건을 만족한다. 시공간의 이산성을 도입하는 것은 국소 유한 조건이다.
4. 기하
다양체 이론을 인과 집합에 그대로 적용하기는 어렵지만, 측지선이나 차원 등 일부 기하학적 구조는 적용 가능하다.[15] 이러한 정의는 인과 집합이 내포될 수 있는 배경 시공간에 의존하지 않고, 인과 집합 자체에만 의존해야 한다.[15]
4. 1. 측지선
사슬은 원소의 수열 에서 일 때 가 만족되는 것을 말하며, 이 사슬의 길이는 이다.'''측지선'''은 두 원소 가 고리로만 연결되는 사슬이며 다음 조건을 만족한다.
# 이고
# 사슬의 길이 은 와 를 잇는 모든 사슬에 대해 최대다.
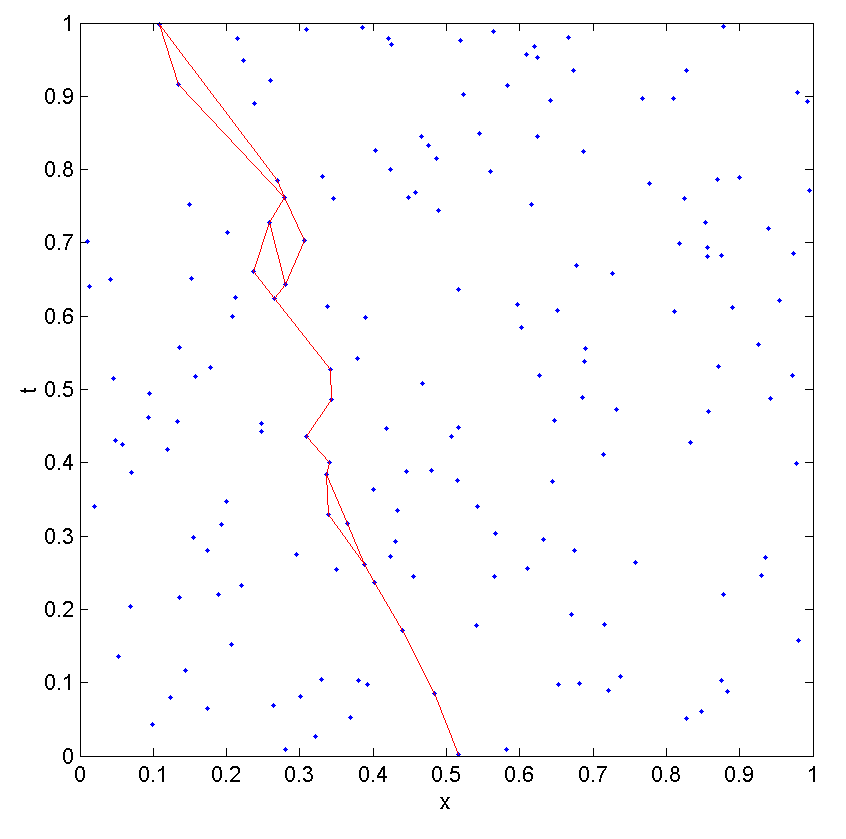
인과 집합에서 ''링크''는 이지만 를 만족하는 가 없는 두 원소 의 쌍이다.
''사슬''은 과 같은 원소의 수열이며, 여기서 에 대해 이다. 사슬의 길이는 이다. 사슬의 모든 이 링크를 형성하면, 사슬을 ''경로''라고 한다.
두 인과 집합 원소 간의 측지선은 순서 비교가 가능해야 하며, 인과적으로 연결되어야 한다. 두 원소 사이의 측지선은 다음 조건을 만족하는 링크로만 구성된 사슬이다.
# 그리고
# 사슬의 길이, 은 에서 까지의 모든 사슬 중에서 최대이다.
일반적으로 두 개의 비교 가능한 요소 사이에 둘 이상의 측지선이 있을 수 있다.
Myrheim[8][16]은 이러한 측지선의 길이가 두 시공간 점을 잇는 시간과 같은 측지선을 따라 고유 시간에 직접 비례해야 한다고 제안했다. 평탄한 시공간에 뿌려진 인과 집합을 사용하여 이 추측에 대한 테스트 결과 비례 관계가 성립하는 것으로 나타났으며, 곡선 시공간에서도 뿌려지는 경우에도 성립할 것으로 추정된다.
4. 2. 차원 추정
인과 집합의 차원을 추정하기 위한 다양한 방법들이 개발되었다. 이 방법들은 인과 집합을 사용하여 그에 대응하는 다양체의 차원을 추정하는 것을 목표로 한다. 지금까지 개발된 알고리즘은 인과 집합을 충실하게 임베딩할 수 있는 민코프스키 시공간의 차원을 찾는 것을 기반으로 한다.- '''Myrheim–Meyer 차원'''
이 방법은 차원 민코프스키 시공간에 뿌려진 길이의 체인 수를 추정한다. 인과 집합에서 길이의 체인 수를 계산하여 에 대한 추정을 할 수 있다.
- '''중점 스케일링 차원'''
이 방법은 민코프스키 시공간의 두 점 사이의 고유 시간과 그 사이의 시공간 간격 부피 사이의 관계를 이용한다. 두 점 와 사이의 최대 체인 길이(고유 시간 추정)를 계산하고, 인 요소 의 수(시공간 간격 부피 추정)를 계산하여 시공간의 차원을 계산한다.
이러한 추정기들은 차원 민코프스키 시공간에 고밀도로 뿌려진 인과 집합에 대해 올바른 차원을 제공해야 한다. 등각 평탄 시공간에 대한 테스트[9][17]는 이 두 가지 방법이 정확하다는 것을 보여주었다.
5. 연속체와의 비교
인과 집합 이론의 핵심 질문 중 하나는 인과 집합이 로렌츠 다양체에 충실하게 매장될 수 있는지 여부이다. 하우프트버뮤퉁(기본 추측)은 동일한 인과 집합이 대규모로 유사하지 않은 두 시공간에 충실하게 매장될 수 없다는 추측이다.[1]
인과 집합을 로렌츠 다양체에 임베딩할 때는, 인과 집합의 원소를 다양체의 점으로 매핑하고, 인과 집합의 순서 관계가 다양체의 인과적 순서와 일치해야 한다. 이때, 평균적으로 다양체의 영역에 매핑된 인과 집합 요소의 수가 해당 영역의 부피에 비례한다면, 이 임베딩은 "충실하다"고 한다. 이 경우 인과 집합을 '다양체 유사'하다고 간주할 수 있다.[1]
하지만, 두 시공간이 '대규모로 유사'한 시점을 결정하기 어렵기 때문에 이 추측을 정확하게 정의하기는 어렵다. 인과 집합이 주어졌을 때, 이것이 다양체와 유사한지 결정하는 것 또한 어려운 속성이다.[1]
5. 1. 흩뿌림(Sprinkling)
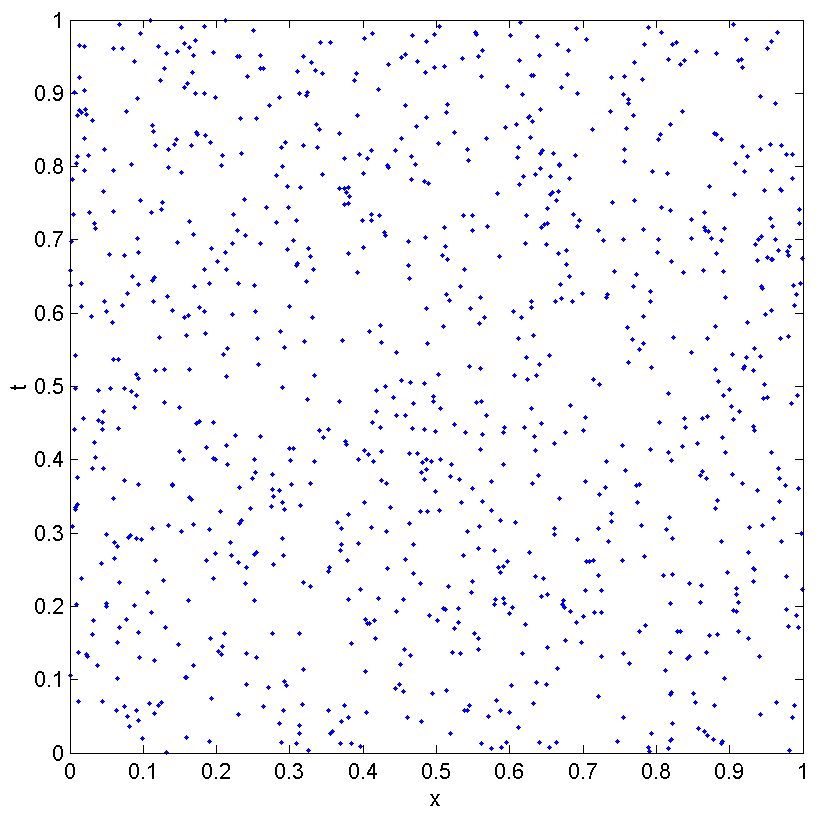
어떤 인과 집합을 어떤 다양체에 임베딩할 수 있는지를 결정하는 데 어려움이 있어, 반대 방향으로 접근할 수 있다. 로렌츠 다양체에 점을 흩뿌려 인과 집합을 만들 수 있다. 시공간 영역의 부피에 비례하여 점을 흩뿌리고, 다양체에서 인과 순서 관계를 사용하여 흩뿌려진 점들 간의 순서 관계를 유도함으로써 (구성에 의해) 다양체에 충실하게 임베딩될 수 있는 인과 집합을 생성할 수 있다.
로렌츠 불변성을 유지하기 위해 이러한 점의 흩뿌림은 푸아송 과정을 사용하여 무작위로 수행해야 한다. 따라서 부피 의 영역에 개의 점을 흩뿌릴 확률은 다음과 같다.
:
여기서 는 흩뿌리는 점의 밀도이다.
점을 정규 격자로 흩뿌리는 것은 점의 개수를 영역 부피에 비례하게 유지하지 못한다.
6. 동역학
인과 집합의 동역학은 어떤 인과 집합이 물리적으로 실현 가능한 시공간에 해당하는지를 결정하는 규칙을 제공한다. 현재 인과 집합 동역학을 개발하는 가장 주된 접근 방식은 양자역학의 경로 적분 공식, 즉 '역사의 합(sum-over-histories)'에 기반한다. 이 접근 방식은 인과 집합을 한 번에 하나의 요소씩 성장시키면서 인과 집합에 대한 합을 수행한다. 각 요소는 양자역학적 규칙에 따라 추가되며, 간섭은 큰 다양체와 같은 시공간이 기여를 지배하도록 보장한다.
현재 가장 좋은 동역학 모델은 각 요소가 확률에 따라 추가되는 고전적 모델이다. 이 모델은 데이비드 라이드아웃(David Rideout)과 라파엘 소킨에 의해 고전적 순차적 성장(CSG) 역학으로 알려져 있다.[10] 고전적 순차적 성장 모델은 새로운 요소를 하나씩 추가하여 인과 집합을 생성하며, 새로운 요소가 추가되는 방법에 대한 규칙이 지정되어 모델의 매개변수에 따라 서로 다른 인과 집합이 생성된다.
경로 적분 공식의 양자역학적 유사성을 통해 인과 집합에 대한 양자 역학을 개발하는 한 가지 접근 방식은 합-과-인과 집합 접근 방식에서 작용 원리를 적용하는 것이다. 소킨은 달랑베르 연산자에 대한 이산적 유사체를 제안했으며, 이를 사용하여 리치 곡률 스칼라와 그에 따라 인과 집합에 대한 베닌카사-도우커 작용을 정의할 수 있다.[11][12] 몬테카를로 방법 시뮬레이션은 베닌카사-도우커 작용을 사용하여 2차원에서 연속체 위상에 대한 증거를 제공했다.[13]
참조
[1]
논문
The causal set approach to quantum gravity
https://link.springe[...]
2019-09-27
[2]
서적
Hermann Weyl
https://plato.stanfo[...]
Metaphysics Research Lab, Stanford University
2024-11-18
[3]
논문
On the structure of causal spaces
https://www.cambridg[...]
1967
[4]
논문
The class of continuous timelike curves determines the topology of spacetime
https://hal.archives[...]
1977-07
[5]
간행물
Causality Implies the Lorentz Group
https://archive.toda[...]
J. Math. Phys.
1964
[6]
논문
A new topology for curved space–time which incorporates the causal, differential, and conformal structures
https://pubs.aip.org[...]
1976-02-01
[7]
논문
Structure of random discrete spacetime
1991-01-21
[8]
간행물
CERN preprint
http://doc.cern.ch//[...]
CERN
1978
[9]
논문
Manifold dimension of a causal set: Tests in conformally flat spacetimes
2003-01-30
[10]
논문
Classical sequential growth dynamics for causal sets
[11]
arXiv
Does Locality Fail at Intermediate Length-Scales
2007-03-20
[12]
논문
The Scalar Curvature of a Causal Set
2010-05
[13]
논문
Evidence for the continuum in 2D causal set quantum gravity
2012-07
[14]
간행물
The class of continuous timelike curves determines the topology of spacetime
http://link.aip.org/[...]
Journal of Mathematical Physics
1977-07
[15]
논문
Structure of random discrete spacetime
http://link.aps.org/[...]
1991
[16]
간행물
CERN preprint
http://doc.cern.ch//[...]
CERN
1978
[17]
논문
Manifold dimension of a causal set: Tests in conformally flat spacetimes
2003
[18]
논문
A classical sequential growth dynamics for causal sets
2000
[19]
논문
Structure of random discrete spacetime
http://link.aps.org/[...]
1991
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com

