맨위로가기

다변량 정규분포

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

다변량 정규 분포는 여러 변수의 결합된 확률 분포로, 각 변수가 정규 분포를 따르는 경우를 일반화한 것이다. k차원 확률 벡터 X가 평균 벡터 μ와 공분산 행렬 Σ를 가질 때, X ~ N(μ, Σ)로 표기하며, 모든 성분의 선형 결합이 정규 분포를 따른다는 특징을 갖는다. 다변량 정규 분포는 표준 정규 확률 벡터, 중심 정규 확률 벡터, 정규 확률 벡터로 정의될 수 있으며, 공분산 행렬이 양의 정부호 행렬인 경우 비퇴화, 그렇지 않은 경우 퇴화 분포로 분류된다.

다변량 정규 분포는 확률 밀도 함수, 누적 분포 함수, 여누적 분포 함수, 고차 모멘트, 조건부 분포, 주변 분포, 아핀 변환 등 다양한 성질을 가지며, 기하학적으로는 타원 형태를 띤다. 통계적 추론에서 다변량 정규 분포는 가우스 판별 분석, 모수 추정, 베이즈 추론, 다변량 정규성 검정 등에 활용되며, 분포로부터 값 추출(표본 추출)을 위한 계산 방법이 존재한다.

2. 정의

다변량 정규 분포는 여러 개의 확률 변수가 서로 상관관계를 가지면서 결합된 정규 분포를 이루는 경우를 의미한다.

임의의 확률 벡터 \mathbf{X} = (X_1,\ldots,X_k)^{\mathrm T}가 다변량 정규 분포를 갖는다는 것은 다음 조건들을 만족하는 것과 동등하다.


  • \mathbf{X}의 성분들의 모든 선형 결합 Y=a_1 X_1 + \cdots + a_k X_k가 정규 분포를 따른다. (단, \mathbf{a} \in \mathbb{R}^k는 임의의 상수 벡터이고, Y=\mathbf{a}^{\mathrm T}\mathbf{X}는 일변량 정규 분포이며, 분산이 0인 경우는 평균에 대한 점 질량이다.)
  • ''k''-벡터 \mathbf{\mu}와 대칭, 양의 준정부호 k \times k 행렬 \boldsymbol\Sigma가 존재하여 \mathbf{X}의 특성 함수가 다음과 같다.




\varphi_\mathbf{X}(\mathbf{u}) = \exp\Big( i\mathbf{u}^\mathrm{T}\boldsymbol\mu - \tfrac{1}{2} \mathbf{u}^\mathrm{T}\boldsymbol\Sigma \mathbf{u} \Big).



구형 정규 분포는 모든 직교 좌표계에서 성분이 독립적인 고유한 분포로 특징지을 수 있다.

2. 1. 표기법 및 매개변수

''k''차원 확률 벡터 \mathbf{X} = (X_1,\ldots,X_k)^{\mathrm T}의 다변량 정규 분포는 다음과 같은 표기법으로 나타낼 수 있다.

:

\mathbf{X}\ \sim\ \mathcal{N}(\boldsymbol\mu,\, \boldsymbol\Sigma)



또는 ''X''가 ''k''차원임을 명시적으로 나타내기 위해 다음과 같이 표기하기도 한다.

:

\mathbf{X}\ \sim\ \mathcal{N}_k(\boldsymbol\mu,\, \boldsymbol\Sigma)



여기서 ''k''차원 평균 벡터는 다음과 같다.

: \boldsymbol\mu = \operatorname{E}[\mathbf{X}] = ( \operatorname{E}[X_1], \operatorname{E}[X_2], \ldots, \operatorname{E}[X_k] ) ^ \mathrm{T}

k \times k 공분산 행렬은 다음과 같다.

: \Sigma_{i,j} = \operatorname{E} [(X_i - \mu_i)( X_j - \mu_j)] = \operatorname{Cov}[X_i, X_j]

(단, 1 \le i \le k이고 1 \le j \le k이다.)

공분산 행렬의 역행렬은 정밀도 행렬이라고 하며, \boldsymbol{Q}=\boldsymbol\Sigma^{-1}로 표기한다.

2. 2. 표준 정규 확률 벡터

실수 확률 벡터 \mathbf{X} = (X_1,\ldots,X_k)^{\mathrm T}의 모든 성분 X_i가 서로 독립이며 각각 평균 0, 분산 1인 정규 분포를 따르는 확률 변수이면, 즉 모든 i=1\ldots k에 대해 X_i \sim\ \mathcal{N}(0,1)이면 \mathbf{X}를 '''표준 정규 확률 벡터'''라고 한다.[1]

2. 3. 중심 정규 확률 벡터

실수 확률 벡터 \mathbf{X} = (X_1,\ldots,X_k)^{\mathrm T}는 결정론적 k \times \ell 행렬 \boldsymbol{A}가 존재하여 \boldsymbol{A} \mathbf{Z}가 \mathbf{X}와 동일한 분포를 가질 때 '''중심 정규 확률 벡터'''라고 불리며, 여기서 \mathbf{Z}는 \ell개의 성분을 가진 표준 정규 확률 벡터이다.[1]

2. 4. 정규 확률 벡터

실수 확률 벡터 \mathbf{X} = (X_1,\ldots,X_k)^{\mathrm T}는 표준 정규 확률 벡터인 \ell-벡터 \mathbf{Z}와 k-벡터 \mathbf{\mu}, 그리고 k \times \ell 행렬 \boldsymbol{A}가 존재하여 \mathbf{X}=\boldsymbol{A} \mathbf{Z} + \mathbf{\mu}를 만족하면 '''정규 확률 벡터'''라고 한다.[2][1] 공분산 행렬은 \boldsymbol\Sigma = \boldsymbol{A} \boldsymbol{A}^{\mathrm T}이다. 퇴화된 경우, 즉 공분산 행렬이 특이 행렬인 경우, 해당 분포는 밀도를 갖지 않는다. 이 경우는 통계학에서 자주 발생하며, 예를 들어 최소제곱법 회귀 분석에서 잔차 벡터의 분포에서 발생한다. X_i는 일반적으로 독립적이지 않으며, 독립적인 가우스 변수 \mathbf{Z}의 집합에 행렬 \boldsymbol{A}를 적용한 결과로 볼 수 있다.

2. 5. 동등한 정의

임의 벡터 \mathbf{X} = (X_1, \ldots, X_k)^\mathrm{T}가 다음 조건 중 하나를 만족하면 다변량 정규 분포를 갖는다.

  • 성분의 모든 선형 결합 Y=a_1 X_1 + \cdots + a_k X_k가 정규 분포를 따른다. 즉, 임의의 상수 벡터 \mathbf{a} \in \mathbb{R}^k에 대해, 임의 변수 Y=\mathbf{a}^{\mathrm T}\mathbf{X}는 일변량 정규 분포를 가지며, 분산이 0인 일변량 정규 분포는 평균에 대한 점 질량이다.
  • ''k''-벡터 \mathbf{\mu}와 대칭, 양의 준정부호 k \times k 행렬 \boldsymbol\Sigma가 존재하여 \mathbf{X}의 특성 함수는 다음과 같다.




\varphi_\mathbf{X}(\mathbf{u}) = \exp\Big( i\mathbf{u}^\mathrm{T}\boldsymbol\mu - \tfrac{1}{2} \mathbf{u}^\mathrm{T}\boldsymbol\Sigma \mathbf{u} \Big).



구형 정규 분포는 모든 직교 좌표계에서 성분이 독립적인 고유한 분포로 특징지을 수 있다.

3. 성질

다변량 정규 분포는 대칭 공분산 행렬 \boldsymbol\Sigma가 양의 정부호 행렬일 때 "비퇴화"라고 하며, 이 경우 확률 밀도 함수를 갖는다.[5]

:

f_{\mathbf X}(x_1,\ldots,x_k) = \frac{\exp\left(-\frac 1 2 \left({\mathbf x} - {\boldsymbol\mu}\right)^\mathrm{T}{\boldsymbol\Sigma}^{-1}\left({\mathbf x}-{\boldsymbol\mu}\right)\right)}{\sqrt{(2\pi)^k |\boldsymbol\Sigma|}}



여기서 {\mathbf x}는 실수 ''k''차원 열 벡터이고, |\boldsymbol\Sigma|\equiv \det\boldsymbol\Sigma는 \boldsymbol\Sigma의 행렬식이며, 일반화 분산이라고도 한다. 위의 방정식은 \boldsymbol\Sigma가 1 \times 1 행렬(즉, 단일 실수)인 경우 일변량 정규 분포의 방정식으로 축소된다.

각 등밀도 궤적(동일한 특정 밀도 값을 제공하는 ''k''차원 공간의 점들)은 타원 또는 더 높은 차원의 일반화이다. 따라서 다변량 정규 분포는 타원 분포의 특수한 경우이다.

\sqrt{({\mathbf x}-{\boldsymbol\mu})^\mathrm{T}{\boldsymbol\Sigma}^{-1}({\mathbf x}-{\boldsymbol\mu})}는 마할라노비스 거리로 알려져 있으며, 이는 테스트 점 {\mathbf x}에서 평균 {\boldsymbol\mu}까지의 거리를 나타낸다. k = 1인 경우, 분포는 일변량 정규 분포로 축소되고 마할라노비스 거리는 표준 점수의 절댓값으로 축소된다.

3. 1. 확률 밀도 함수

이변량 정규 결합 밀도


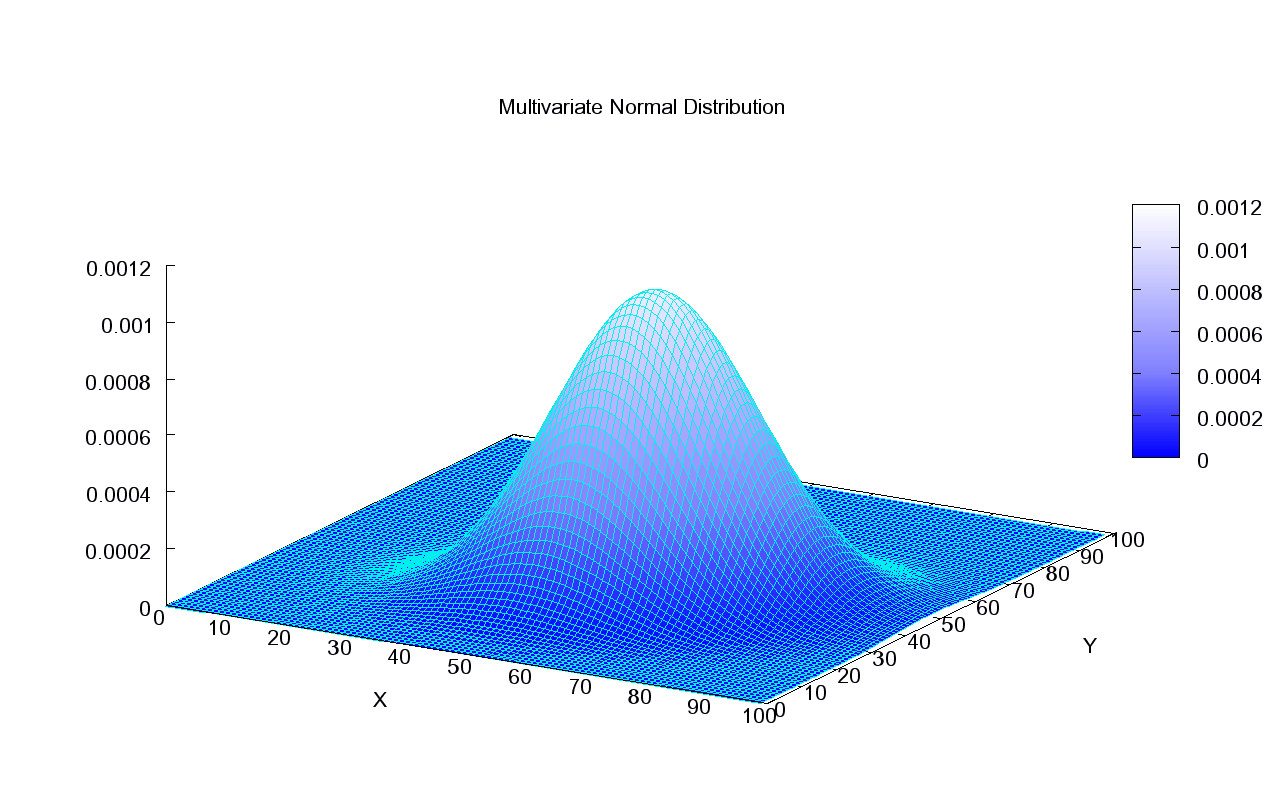
2차원 비특이 사례(k = \operatorname{rank}\left(\Sigma\right) = 2)에서, 벡터 \text{[XY]}\prime의 확률 밀도 함수는 다음과 같다.[37]

:

f(x,y) =

\frac{1}{2 \pi \sigma_X \sigma_Y \sqrt{1-\rho^2}}

\exp

\left( -\frac{1}{2\left[1 - \rho^2\right]}\left[

\left(\frac{x-\mu_X}{\sigma_X}\right)^2 -

2\rho\left(\frac{x - \mu_X}{\sigma_X}\right)\left(\frac{y - \mu_Y}{\sigma_Y}\right) +

\left(\frac{y - \mu_Y}{\sigma_Y}\right)^2

\right]

\right)



여기서 \rho는 X와 Y 간의 상관 관계이며, \sigma_X>0 및 \sigma_Y>0 이다. 이 경우,

:

\boldsymbol\mu = \begin{pmatrix} \mu_X \\ \mu_Y \end{pmatrix}, \quad

\boldsymbol\Sigma = \begin{pmatrix} \sigma_X^2 & \rho \sigma_X \sigma_Y \\

\rho \sigma_X \sigma_Y & \sigma_Y^2 \end{pmatrix}.



x,y-평면에 플롯된 이변량 등밀도 궤적은 타원이며, 이의 주축은 공분산 행렬 \boldsymbol\Sigma의 고유 벡터로 정의된다(타원의 장반경과 단반경은 정렬된 고유값의 제곱근과 같다).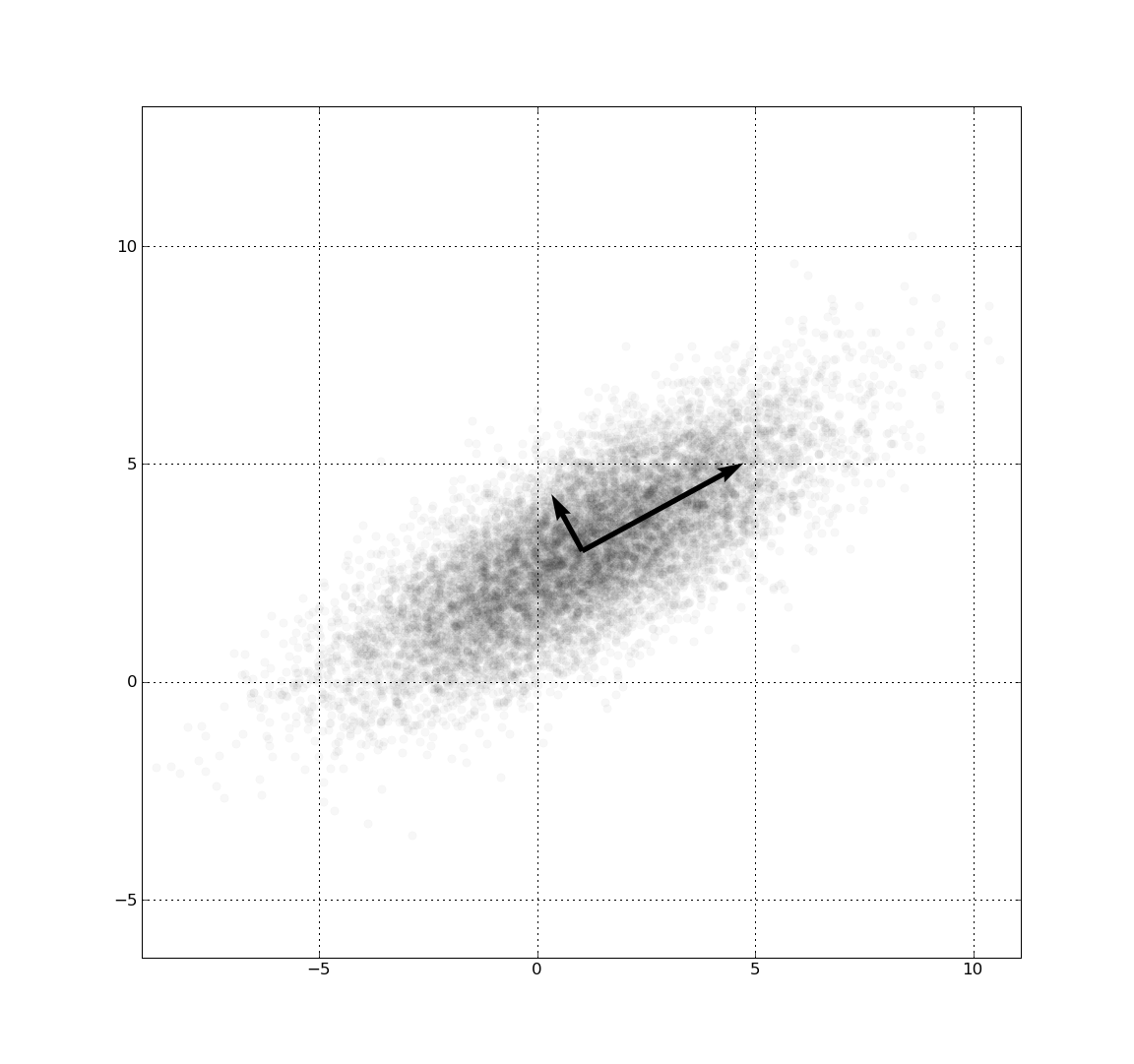

(1, 3)에 중심을 두고 대략 (0.878, 0.478) 방향으로 표준 편차 3과 직교 방향으로 1을 갖는 이변량 정규 분포


상관 관계 매개변수 \rho의 절댓값이 증가함에 따라 이러한 궤적은 다음 선을 향해 좁혀진다.[38]

:

y(x) = \sgn (\rho)\frac{\sigma_Y}{\sigma_X} (x - \mu _X) + \mu_Y.



이것은 \sgn(\rho) (여기서 sgn은 부호 함수)를 \rho로 대체한 이 표현식이 X의 주어진 값에 대한 Y의 최량 선형 불편 추정이기 때문이다.

3. 1. 1. 비퇴화인 경우

다변량 정규 분포는 대칭 공분산 행렬 \boldsymbol\Sigma가 양의 정부호 행렬일 때 "비퇴화"라고 한다. 이 경우 분포는 확률 밀도 함수를 갖는다.[46]

:f_{\mathbf X}(x_1,\ldots,x_k) = \frac{\exp\left(-\frac 1 2 ({\mathbf x}-{\boldsymbol\mu})^\mathrm{T}{\boldsymbol\Sigma}^{-1}({\mathbf x}-{\boldsymbol\mu})\right)}{\sqrt{(2\pi)^k|\boldsymbol\Sigma|}}

여기서 {\mathbf x}는 실수 ''k''차원 열 벡터이고, |\boldsymbol\Sigma|\equiv \det\boldsymbol\Sigma는 \boldsymbol\Sigma의 행렬식이다. 각 등밀도 궤적은 타원 또는 더 높은 차원의 일반화이다. 수량 \sqrt{({\mathbf x}-{\boldsymbol\mu})^\mathrm{T}{\boldsymbol\Sigma}^{-1}({\mathbf x}-{\boldsymbol\mu})}는 마할라노비스 거리로 알려져 있다.

3. 1. 2. 이변량인 경우

2차원 비특이 사례(k = \operatorname{rank}\left(\Sigma\right) = 2)에서, 벡터 \text{[XY]}\prime의 확률 밀도 함수는 다음과 같다.[48]

:

f(x,y) =

\frac{1}{2 \pi \sigma_X \sigma_Y \sqrt{1-\rho^2}}

\exp\left(

  • \frac{1}{2(1-\rho^2)}\left[

\frac{(x-\mu_X)^2}{\sigma_X^2} +

\frac{(y-\mu_Y)^2}{\sigma_Y^2} -

\frac{2\rho(x-\mu_X)(y-\mu_Y)}{\sigma_X \sigma_Y}

\right]

\right)



여기서 \rho는 X와 Y 간의 상관 관계이며, \sigma_X>0 및 \sigma_Y>0 이다. 이때,

:

\boldsymbol\mu = \begin{pmatrix} \mu_X \\ \mu_Y \end{pmatrix}, \quad

\boldsymbol\Sigma = \begin{pmatrix} \sigma_X^2 & \rho \sigma_X \sigma_Y \\

\rho \sigma_X \sigma_Y & \sigma_Y^2 \end{pmatrix}



2차원일 때는, 다변량 정규 분포가 되기 위한 동치 조건으로 언급한 첫 번째 조건은 약간 완화될 수 있다. 가산 무한 가지의 X와 Y의 선형 결합이 모두 정규 분포를 따른다면, 벡터 \text{[XY]}\prime는 이변량 정규 분포를 따른다.

두 변수의 경우의 등고선을 ''x,y'' 평면에 그리면 타원이 된다. 상관 계수 ''ρ''가 커질수록, 타원은 다음 직선:

:

y(x) = \sgn (\rho)\frac{\sigma_Y}{\sigma_X} (x - \mu _X) + \mu_Y.



의 방향으로 찌그러진다. 이 배경으로, 이 식의 \sgn (\rho) (부호 함수)를 \rho로 바꾼 것은, ''X''의 값이 주어졌을 때 ''Y''의 최량 선형 불편 예측량이 된다는 성질이 있다.[49]

3. 2. 누적 분포 함수

1차원에서의 누적 분포 함수(cdf) 개념은 직사각형 영역과 타원형 영역을 기반으로 다차원 경우로 두 가지 방식으로 확장될 수 있다.

첫 번째 방법은 랜덤 벡터 \mathbf{X}의 cdf F(\mathbf{x})를 \mathbf{X}의 모든 구성 요소가 벡터 \mathbf{x}의 해당 값보다 작거나 같을 확률로 정의하는 것이다.[8]

: F(\mathbf{x}) = \mathbb{P}(\mathbf{X}\leq \mathbf{x}), \quad \text{where } \mathbf{X} \sim \mathcal{N}(\boldsymbol\mu,\, \boldsymbol\Sigma).

F(\mathbf{x})에 대한 폐쇄적인 형태는 없지만, 이를 수치적으로 https://cran.r-project.org/package=TruncatedNormal 추정하는 여러 알고리즘이 있다.[8][9]

다른 방법은 cdf F(r)을 표본이 가우스 분포로부터의 마할라노비스 거리 r에 의해 결정되는 타원체 내에 속할 확률로 정의하는 것으로, 표준 편차의 직접적인 일반화이다.[10] 이 함수의 값을 계산하기 위해 폐쇄적인 해석 공식이 존재한다.[10]

3. 3. 여누적 분포 함수 (꼬리 분포)

여누적 분포 함수(ccdf) 또는 '''꼬리 분포'''는 \overline F(\mathbf{x}) = 1 - \mathbb P\left(\mathbf X\leq \mathbf x\right)로 정의된다. \mathbf{X} \sim \mathcal{N}(\boldsymbol\mu,\, \boldsymbol\Sigma)일 때, ccdf는 종속적인 가우스 변수들의 최댓값에 대한 확률로 표현될 수 있다.[11]

: \overline F(\mathbf{x}) = \mathbb P\left(\bigcup_i\{X_i\geq x_i\}\right) = \mathbb P\left(\max_i Y_i\geq 0\right),

\quad \text{where } \mathbf{Y} \sim \mathcal{N}\left(\boldsymbol\mu - \mathbf{x},\, \boldsymbol\Sigma\right).

ccdf를 계산하기 위한 간단한 닫힌 공식은 없지만, 종속적인 가우스 변수들의 최댓값은 몬테카를로 방법을 통해 정확하게 추정할 수 있다.[11][12]

3. 4. 고차 모멘트

'''x'''의 ''k''차 모멘트는 다음과 같다.

:\mu_{1,\ldots,N}(\mathbf{x})

\mathrel\stackrel{\mathrm{def}}{=} \mu _{r_1,\ldots,r_N}(\mathbf{x})

\mathrel\stackrel{\mathrm{def}}{=} \operatorname E\left[ \prod_{j=1}^N X_j^{r_j} \right]



여기서 이다.

''k''차 중심 모멘트는 다음과 같다.

# ''k''가 홀수이면 이다.

# ''k''가 짝수이고 이면,

:

\mu_{1,\dots,2\lambda}(\mathbf{x}-\boldsymbol\mu ) = \sum \left( \sigma_{ij} \sigma_{k\ell} \cdots \sigma_{XZ}\right)



여기서 합은 집합 \left\{ 1,\ldots,2\lambda \right\}를 ''λ'' (정렬되지 않은) 쌍으로 할당하는 모든 경우에 대해 계산된다. 즉, ''k''차 중심 모멘트의 경우, 공분산의 곱을 더한다 (예상 값 '''''μ'''''는 간결성을 위해 0으로 간주된다).

:\begin{align}

& \operatorname E[X_1 X_2 X_3 X_4 X_5 X_6] \\[8pt]

= {} & \operatorname E[X_1 X_2]\operatorname E[X_3 X_4]\operatorname E[X_5 X_6] + \operatorname E[X_1 X_2]\operatorname E[X_3 X_5]\operatorname E[X_4 X_6] + \operatorname E[X_1 X_2]\operatorname E[X_3 X_6] \operatorname E[X_4 X_5] \\[4pt]

& {} + \operatorname E[X_1 X_3]\operatorname E[X_2 X_4]\operatorname E[X_5 X_6] + \operatorname E[X_1 X_3]\operatorname E[X_2 X_5]\operatorname E[X_4 X_6] + \operatorname E[X_1 X_3]\operatorname E[X_2 X_6] \operatorname E[X_4 X_5] \\[4pt]

& {} + \operatorname E[X_1 X_4]\operatorname E[X_2 X_3]\operatorname E[X_5 X_6] + \operatorname E[X_1 X_4]\operatorname E[X_2 X_5]\operatorname E[X_3 X_6]+ \operatorname E[X_1 X_4]\operatorname E[X_2 X_6] \operatorname E[X_3 X_5] \\[4pt]

& {} + \operatorname E[X_1 X_5]\operatorname E[X_2 X_3]\operatorname E[X_4 X_6] + \operatorname E[X_1 X_5]\operatorname E[X_2 X_4]\operatorname E[X_3 X_6] + \operatorname E[X_1 X_5]\operatorname E[X_2 X_6] \operatorname E[X_3 X_4] \\[4pt]

& {} + \operatorname E[X_1 X_6]\operatorname E[X_2 X_3]\operatorname E[X_4 X_5] + \operatorname E[X_1 X_6]\operatorname E[X_2 X_4]\operatorname E[X_3 X_5] + \operatorname E[X_1 X_6]\operatorname E[X_2 X_5]\operatorname E[X_3 X_4].

\end{align}



이것은 합에서 개의 항 (위의 경우 15개)을 생성하며, 각 항은 ''λ'' (이 경우 3) 공분산의 곱이다. 4차 모멘트(4개의 변수)의 경우 3개의 항이 있다. 6차 모멘트의 경우 개의 항이 있으며, 8차 모멘트의 경우 개의 항이 있다.

그런 다음 공분산은 목록 [ 1, \ldots, 2\lambda]의 항을, ''r''1 개의 1, 다음 ''r''2 개의 2 등으로 구성된 목록의 해당 항으로 대체하여 결정된다. 이를 설명하기 위해 다음 4차 중심 모멘트 사례를 살펴보자.

:

\begin{align}

\operatorname E \left [ X_i^4 \right ] & = 3\sigma_{ii}^2 \\[4pt]

\operatorname E \left[ X_i^3 X_j \right ] & = 3\sigma_{ii} \sigma_{ij} \\[4pt]

\operatorname E \left[ X_i^2 X_j^2 \right ] & = \sigma_{ii}\sigma_{jj}+2 \sigma _{ij}^2 \\[4pt]

\operatorname E \left[ X_i^2 X_j X_k \right ] & = \sigma_{ii}\sigma _{jk}+2\sigma _{ij}\sigma_{ik} \\[4pt]

\operatorname E \left [ X_i X_j X_k X_n \right ] & = \sigma_{ij}\sigma _{kn} + \sigma _{ik} \sigma_{jn} + \sigma_{in} \sigma _{jk}.

\end{align}



여기서 \sigma_{ij}는 ''Xi''와 ''Xj''의 공분산이다. 위의 방법을 사용하면 먼저 ''k''개의 서로 다른 ''X'' 변수를 가진 ''k''차 모멘트의 일반적인 경우, E\left[ X_i X_j X_k X_n\right]을 찾은 다음 이에 따라 이를 단순화한다. 예를 들어, \operatorname E[ X_i^2 X_k X_n ]의 경우, 로 놓고 라는 사실을 사용한다.

3. 5. 결합 정규성

확률 변수 X와 Y가 정규 분포를 따르고 독립이면, 이들의 결합 분포는 결합 정규 분포이다. 즉, 쌍 (X, Y)는 2변량 정규 분포를 따른다. 하지만, 다변량 정규 분포를 따르는 확률 변수 벡터의 서로 다른 두 성분이 독립일 필요는 없다. 이들이 독립인 경우는 무상관( \rho = 0)인 경우로 제한된다.[13]

두 확률 변수 X와 Y가 모두 정규 분포를 따른다고 해서 쌍 (X, Y)가 결합 정규 분포를 갖는다는 것을 의미하지는 않는다. 예를 들어 X가 기댓값 0, 분산 1인 정규 분포를 따르고, |X| > c일 때 Y = X이고, |X| < c일 때 Y = -X인 경우를 생각할 수 있다. (여기서 c > 0이다.) 일반적으로, 이들은 혼합 모형으로 합산된다.[14]

일반적으로, 확률 변수는 상관관계가 없을 수 있지만 통계적으로 종속적일 수 있다. 그러나 확률 벡터가 다변량 정규 분포를 가지면 상관관계가 없는 두 개 이상의 구성 요소는 독립이다.[1]

3. 5. 1. 정규 분포와 독립성

X와 Y가 정규 분포를 따르고 독립이라면, (X,Y) 쌍은 다변량 정규 분포를 가져야 한다. 하지만, 다변량 정규 분포를 따르는 변수 쌍이 반드시 독립일 필요는 없다 (상관관계가 없는 경우, \rho = 0일 경우에만 독립이다).[13]

확률 변수 X와 Y가 정규 분포를 따르고 독립이라면, 이들의 결합 분포는 결합 정규 분포이다. 즉, 쌍 (X, Y)는 2변량 정규 분포를 따른다. 하지만, 다변량 정규 분포를 따르는 확률 변수 벡터의 서로 다른 두 성분이 독립일 필요는 없다. 이들이 독립인 경우는 무상관( \rho = 0)인 경우로 제한된다.[13]

일반적으로, 2개의 확률 변수가 무상관이어도 독립일 필요는 없다. 그러나 확률 변수 벡터가 다변량 정규 분포를 따르는 경우, 2개 이상의 성분이 서로 무상관이면, 그것들은 독립이다. 특히, 이것들이 쌍별 독립이면 독립이다.[13]

그러나, 2개의 확률 변수가 정규 분포를 따르고 무상관이라고 해서, 그것들이 독립인 것은 아니다.[13]

3. 5. 2. 두 정규 분포 확률 변수가 반드시 결합 이변량 정규 분포를 따르는 것은 아니다

두 확률 변수 X와 Y가 모두 정규 분포를 따른다고 해서 쌍 (X, Y)가 결합 정규 분포를 갖는다는 것을 의미하지는 않는다. 간단한 예로, X가 기댓값 0, 분산 1인 정규 분포를 따르고, |X| > c일 때 Y = X이고, |X| < c일 때 Y = -X인 경우를 생각할 수 있다. 여기서 c > 0이다. 두 개 이상의 확률 변수에 대해서도 유사한 반례가 존재한다. 일반적으로, 이들은 혼합 모형으로 합산된다.[14]

3. 5. 3. 상관관계와 독립성

일반적으로, 확률 변수는 상관관계가 없을 수 있지만 통계적으로 종속적일 수 있다. 그러나 확률 벡터가 다변량 정규 분포를 가지면 상관관계가 없는 두 개 이상의 구성 요소는 독립이다. 이는 쌍별 독립인 두 개 이상의 구성 요소가 독립임을 의미한다. 그러나 (개별적으로, 주변적으로) 정규 분포를 따르고 상관관계가 없는 두 개의 확률 변수가 독립적인 것은 아니다.[1]

X영어와 Y영어의 상관 계수가 0이 되도록 상수 c영어를 선택하면, 2개의 확률 변수가 정규 분포를 따르고 무상관이라고 해서, 그것들이 독립인 것은 아니다.[1]

3. 6. 조건부 분포

''N''차원 벡터 '''x'''가 다음과 같이 분할된다고 가정한다.

:

\mathbf{x}

=

\begin{bmatrix}

\mathbf{x}_1 \\

\mathbf{x}_2

\end{bmatrix}

\text{ 크기 }\begin{bmatrix} q \times 1 \\ (N-q) \times 1 \end{bmatrix}

이에 따라 평균 벡터 '''''μ'''''와 공분산 행렬 '''Σ'''가 다음과 같이 분할된다.

:

\boldsymbol\mu

=

\begin{bmatrix}

\boldsymbol\mu_1 \\

\boldsymbol\mu_2

\end{bmatrix}

\text{ 크기 }\begin{bmatrix} q \times 1 \\ (N-q) \times 1 \end{bmatrix}

:

\boldsymbol\Sigma

=

\begin{bmatrix}

\boldsymbol\Sigma_{11} & \boldsymbol\Sigma_{12} \\

\boldsymbol\Sigma_{21} & \boldsymbol\Sigma_{22}

\end{bmatrix}

\text{ 크기 }\begin{bmatrix} q \times q & q \times (N-q) \\ (N-q) \times q & (N-q) \times (N-q) \end{bmatrix}

이때 '''x'''2 = '''a'''라는 조건 하에서 '''x'''1의 조건부 분포는 다변량 정규분포를 따른다.[18] 즉, ('''x'''1  '''x'''2 '''a''') ~ ''N''('''''μ''''', '''Σ''')이며, 조건부 평균 '''''μ'''''과 조건부 공분산 행렬 '''Σ'''은 다음과 같다.

:

\bar{\boldsymbol\mu}

=

\boldsymbol\mu_1 + \boldsymbol\Sigma_{12} \boldsymbol\Sigma_{22}^{-1}

\left(

\mathbf{a} - \boldsymbol\mu_2

\right)



:

\overline{\boldsymbol\Sigma}

=

\boldsymbol\Sigma_{11} - \boldsymbol\Sigma_{12} \boldsymbol\Sigma_{22}^{-1} \boldsymbol\Sigma_{21}.

[19]

여기서 \boldsymbol\Sigma_{22}^{-1}은 \boldsymbol\Sigma_{22}의 일반화 역행렬이며, \overline{\boldsymbol\Sigma}은 '''Σ'''에서 '''Σ'''22의 슈어 보수이다. 이는 전체 공분산 행렬을 역전시키고, 조건에 맞는 변수에 해당하는 행과 열을 삭제한 후, 다시 역전시켜 조건부 공분산 행렬을 얻는 과정과 동일하다.

'''x'''2 = '''a'''라는 조건 하에서 새로운 분산은 '''a'''의 특정 값에 의존하지 않지만, 분산 값 자체는 변한다. 또한, 평균은 \boldsymbol\Sigma_{12} \boldsymbol\Sigma_{22}^{-1} \left(\mathbf{a} - \boldsymbol\mu_2 \right)만큼 이동한다. 만약 '''a'''의 값을 모르는 상황이라면, '''x'''1은 \mathcal{N}_q \left(\boldsymbol\mu_1, \boldsymbol\Sigma_{11} \right)의 분포를 갖게 된다.

흥미로운 사실은 랜덤 벡터 \mathbf{x}_2와 \mathbf{y}_1=\mathbf{x}_1-\boldsymbol\Sigma_{12}\boldsymbol\Sigma_{22}^{-1}\mathbf{x}_2가 서로 독립이라는 점이다.

행렬 '''Σ'''12'''Σ'''22−1은 회귀 분석에서 계수 행렬로 사용된다.

3. 6. 1. 이변량 조건부 기댓값

X_2가 주어졌을 때 X_1의 조건부 분포는 다음과 같다.[20]

:X_1\mid X_2=a \ \sim\ \mathcal{N}\left(\mu_1+\frac{\sigma_1}{\sigma_2}\rho( a - \mu_2),\, (1-\rho^2)\sigma_1^2\right)

여기서 \rho는 X_1과 X_2 사이의 상관 계수이다.

3. 7. 주변 분포

다변량 정규 확률 변수의 부분 집합에 대한 주변 분포를 얻으려면, 평균 벡터와 공분산 행렬에서 관련 없는 변수(주변화하려는 변수)를 삭제하기만 하면 된다. 이에 대한 증명은 다변량 정규 분포 및 선형 대수의 정의에서 따른다.[22]

'''예시'''

'''X''' = [''X''1, ''X''2, ''X''3]를 평균 벡터가 '''μ''' = [''μ''1, ''μ''2, ''μ''3]이고 공분산 행렬이 '''Σ'''인 다변량 정규 확률 변수라고 하자(다변량 정규 분포의 표준 매개변수화). 그러면 '''''X′''''' = [''X''1, ''X''3]의 결합 분포는 평균 벡터가 '''''μ′''''' = [''μ''1, ''μ''3]이고 공분산 행렬이 다음과 같은 다변량 정규 분포이다.

\boldsymbol\Sigma' =

\begin{bmatrix}

\boldsymbol\Sigma_{11} & \boldsymbol\Sigma_{13} \\

\boldsymbol\Sigma_{31} & \boldsymbol\Sigma_{33}

\end{bmatrix}


3. 8. 아핀 변환

'''Y''' = '''c''' + '''BX'''가 \mathbf{X}\ \sim \mathcal{N}(\boldsymbol\mu, \boldsymbol\Sigma)의 아핀 변환이고, 여기서 '''c'''는 M \times 1 상수 벡터이고 '''B'''는 M \times N 상수 행렬이라면, '''Y'''는 기댓값이 '''c''' + '''Bμ'''이고 분산이 '''BΣB'''T인 다변량 정규 분포를 갖는다. 즉, \mathbf{Y} \sim \mathcal{N} \left(\mathbf{c} + \mathbf{B} \boldsymbol\mu, \mathbf{B} \boldsymbol\Sigma \mathbf{B}^{\rm T}\right)이다.

특히, ''Xi''의 임의의 부분 집합은 또한 다변량 정규 분포를 갖는 주변 분포를 가진다. 예를 들어 부분 집합 (''X''1, ''X''2, ''X''4)T를 추출하려면, 다음과 같은 행렬 '''B'''를 사용한다.

:

\mathbf{B}

=

\begin{bmatrix}

1 & 0 & 0 & 0 & 0 & \ldots & 0 \\

0 & 1 & 0 & 0 & 0 & \ldots & 0 \\

0 & 0 & 0 & 1 & 0 & \ldots & 0

\end{bmatrix}



또 다른 결과는 '''Z''' = '''b''' · '''X'''의 분포인데, 여기서 '''b'''는 '''X'''와 같은 수의 요소를 가진 상수 벡터이고 점(·)은 내적을 나타내며, Z\sim\mathcal{N}\left(\mathbf{b}\cdot\boldsymbol\mu, \mathbf{b}^{\rm T}\boldsymbol\Sigma \mathbf{b}\right)를 갖는 일변량 가우시안 분포이다. 이 결과는 다음을 사용함으로써 얻을 수 있다.

:

\mathbf{B}=\begin{bmatrix}

b_1 & b_2 & \ldots & b_n

\end{bmatrix} = \mathbf{b}^{\rm T}.



'''Σ'''의 양의 정부호성은 내적의 분산이 반드시 양수가 되어야 함을 의미한다.

2'''X'''와 같은 '''X'''의 아핀 변환은 '''X'''의 두 개의 독립적인 실현 값의 합과는 동일하지 않다.

3. 9. 기하학적 해석

비특이 다변량 정규 분포의 등밀도 윤곽선은 평균을 중심으로 하는 타원(초구의 아핀 변환)이다.[23] 따라서 다변량 정규 분포는 타원 분포 클래스의 한 예시이다. 타원의 주축 방향은 공분산 행렬 \boldsymbol\Sigma의 고유 벡터에 의해 주어진다. 주축의 제곱 상대 길이는 해당 고유값에 의해 주어진다.

만약 \mathbf{X}\ \sim \mathcal{N}(\boldsymbol\mu, \boldsymbol\Sigma) 가 열이 단위 고유 벡터이고 \boldsymbol\Lambda 가 고유값의 대각 행렬인 고유값 분해라면, 다음을 얻는다.

::\mathbf{X}\ \sim \mathcal{N}(\boldsymbol\mu, \boldsymbol\Sigma) \iff \mathbf{X}\ \sim \boldsymbol\mu+\mathbf{U}\boldsymbol\Lambda^{1/2}\mathcal{N}(0, \mathbf{I}) \iff \mathbf{X}\ \sim \boldsymbol\mu+\mathbf{U}\mathcal{N}(0, \boldsymbol\Lambda).

또한 '''U'''는 회전 행렬로 선택할 수 있다. 분포 ''N''('''μ''', '''Σ''')는 효과적으로 '''Λ'''1/2에 의해 스케일링되고, '''U'''에 의해 회전하며, '''μ'''에 의해 변환된 ''N''(0, '''I''')이다.

기하학적으로 이것은 적어도 하나의 주축의 길이가 0이므로 모든 윤곽 타원이 무한히 얇고 ''n''차원 공간에서 부피가 0임을 의미한다. 이것은 퇴화 분포이다.

1차원에서 정규 분포의 표본을 구간 \mu\pm \sigma에서 찾을 확률은 약 68.27%이지만, 고차원에서는 표준 편차 타원 영역에서 표본을 찾을 확률이 더 낮다.[25]

차원확률
10.6827
20.3935
30.1987
40.0902
50.0374
60.0144
70.0052
80.0018
90.0006
100.0002


4. 통계적 추론

다변량 정규분포의 통계적 추론 방법은 다음과 같다.


  • 모수 추정: 공분산 행렬 추정에서 다변량 정규 분포의 최대 우도 추정 공분산 행렬 유도는 간단하다. ''n''개 관측치 표본으로부터 공분산 행렬의 최대우도(ML) 추정량은 표본 공분산 행렬을 사용하여 계산할 수 있으며, 이는 편향 추정량이다. 불편향 표본 공분산을 구하는 방법도 제시되어 있다. 피셔 정보 행렬을 통해 크라메르-라오 하한을 계산할 수 있다.
  • 베이즈 추론: 베이즈 통계학에서 평균 벡터의 켤레 사전 분포는 또 다른 다변량 정규 분포이며, 공분산 행렬의 켤레 사전 분포는 역-위샤트 분포이다. 주어진 관측치와 켤레 사전 분포를 이용하여 사후 분포를 계산할 수 있다.
  • 다변량 정규성 검정: 주어진 데이터 집합이 다변량 정규 분포와 유사한지 확인하는 방법이다. 귀무 가설은 데이터 집합이 정규 분포와 유사하다는 것이며, 충분히 작은 p값(''p''-값)은 비정규 데이터를 나타낸다. 다변량 정규성 검정에는 Cox-Small 검사, 래리 래프스키와 제롬 H. 프리드먼이 개발한 Friedman-Rafsky 검사의 Smith와 Jain의 변형, Mardia의 검정, BHEP 검정 등이 있다. Mardia의 검정은 왜도 및 첨도 척도의 다변량 확장에 기반하며, BHEP 검정은 경험적 특성 함수와 정규 분포의 이론적 특성 함수 간의 차이를 이용한다.

4. 1. 모수 추정

공분산 행렬 추정에서 다변량 정규 분포의 최대 우도 추정 공분산 행렬 유도는 간단하다. ''n''개 관측치 표본으로부터 공분산 행렬의 최대우도(ML) 추정량은 다음과 같다.

:\widehat{\boldsymbol\Sigma} = {1 \over n}\sum_{i=1}^n ({\mathbf x}_i-\overline{\mathbf x})({\mathbf x}_i-\overline{\mathbf x})^\mathrm{T}

이는 표본 공분산 행렬이며, 편향 추정량으로 그 기댓값은 다음과 같다.

:E\left[\widehat{\boldsymbol\Sigma}\right] = \frac{n-1}{n} \boldsymbol\Sigma.

불편향 표본 공분산은 다음과 같다.

:\widehat{\boldsymbol\Sigma} = \frac1{n-1}\sum_{i=1}^n (\mathbf{x}_i-\overline{\mathbf{x}})(\mathbf{x}_i-\overline{\mathbf{x}})^{\rm T}

= \frac1{n-1} \left[X'\left(I - \frac{1}{n} \cdot J\right) X\right] (행렬 형태; I는 K\times K 항등 행렬, J는 K \times K의 1로 이루어진 행렬; 괄호 안 항은 K \times K 중심화 행렬)

다변량 정규 분포 모수 추정을 위한 피셔 정보 행렬은 닫힌 형식 표현식을 가지며, 크라메르-라오 하한 계산 등에 사용될 수 있다. 자세한 내용은 피셔 정보를 참조.

4. 2. 베이즈 추론

베이즈 통계학에서 평균 벡터의 켤레 사전 분포는 또 다른 다변량 정규 분포이며, 공분산 행렬의 켤레 사전 분포는 역-위샤트 분포 \mathcal{W}^{-1}이다. ''n''개의 관측치 \mathbf{X} = \{\mathbf{x}_1,\dots,\mathbf{x}_n\} \sim \mathcal{N}(\boldsymbol\mu,\boldsymbol\Sigma)가 주어졌고, 켤레 사전 분포가 다음과 같이 할당되었다고 가정한다.

:p(\boldsymbol\mu,\boldsymbol\Sigma)=p(\boldsymbol\mu\mid\boldsymbol\Sigma})\ p(\boldsymbol\Sigma),

여기서

:p(\boldsymbol\mu\mid\boldsymbol\Sigma) \sim\mathcal{N}(\boldsymbol\mu_0,m^{-1}\boldsymbol\Sigma) ,

:p(\boldsymbol\Sigma) \sim \mathcal{W}^{-1}(\boldsymbol\Psi,n_0).

이다. 그렇다면[26]

:

\begin{array}{rcl}

p(\boldsymbol\mu\mid\boldsymbol\Sigma,\mathbf{X}) & \sim & \mathcal{N}\left(\frac{n\bar{\mathbf{x}} + m\boldsymbol\mu_0}{n+m},\frac{1}{n+m}\boldsymbol\Sigma\right),\\

p(\boldsymbol\Sigma\mid\mathbf{X}) & \sim & \mathcal{W}^{-1}\left(\boldsymbol\Psi+n\mathbf{S}+\frac{nm}{n+m}(\bar{\mathbf{x}}-\boldsymbol\mu_0)(\bar{\mathbf{x}}-\boldsymbol\mu_0)', n+n_0\right),

\end{array}



여기서

:

\begin{align}

\bar{\mathbf{x}} & = \frac{1}{n}\sum_{i=1}^{n} \mathbf{x}_i ,\\

\mathbf{S} & = \frac{1}{n}\sum_{i=1}^{n} (\mathbf{x}_i - \bar{\mathbf{x}})(\mathbf{x}_i - \bar{\mathbf{x}})' .

\end{align}


4. 3. 다변량 정규성 검정

다변량 정규성 검정은 주어진 데이터 집합이 다변량 정규 분포와 유사한지 확인하는 방법이다. 귀무 가설은 데이터 집합이 정규 분포와 유사하다는 것이므로, 충분히 작은 p값(''p''-값)은 비정규 데이터를 나타낸다. 다변량 정규성 검정에는 Cox-Small 검사[27]와 래리 래프스키와 제롬 H. 프리드먼이 개발한 Friedman-Rafsky 검사의 Smith와 Jain의 변형이 있다.[28][29]

'''Mardia의 검정'''[34]은 왜도 및 첨도 척도의 다변량 확장에 기반한다. ''k''차원 벡터의 표본 {'''x'''1, ..., '''x'''''n''}에 대해 다음을 계산한다.

:\begin{align}

& \widehat{\boldsymbol\Sigma} = {1 \over n} \sum_{j=1}^n \left(\mathbf{x}_j - \bar{\mathbf{x}}\right)\left(\mathbf{x}_j - \bar{\mathbf{x}}\right)^\mathrm{T} \\

& A = {1 \over 6n} \sum_{i=1}^n \sum_{j=1}^n \left[ (\mathbf{x}_i - \bar{\mathbf{x}})^\mathrm{T}\;\widehat{\boldsymbol\Sigma}^{-1} (\mathbf{x}_j - \bar{\mathbf{x}}) \right]^3 \\

& B = \sqrt{\frac{n}{8k(k+2)}}\left\)^\mathrm{T}\;\widehat{\boldsymbol\Sigma}^{-1} (\mathbf{x}_i - \bar{\mathbf{x}}) \right]^2 - k(k+2) \right\}

\end{align}

다변량 정규성의 귀무 가설 하에서 통계량 ''A''는 대략 \frac{1}{6}⋅''k''(''k'' + 1)(''k'' + 2) 자유도를 갖는 카이제곱 분포를 가지며, ''B''는 대략 표준 정규 분포 ''N''(0,1)을 갖는다.

Mardia의 첨도 통계량은 왜곡되어 있으며, 극한 정규 분포에 매우 느리게 수렴한다. 중간 크기의 표본 (50 \le n < 400)의 경우, 첨도 통계량의 점근 분포의 매개변수가 수정된다.[30] 작은 표본 검정(n<50)의 경우 경험적 임계값이 사용된다. 두 통계량에 대한 임계값 표는 Rencher[31]에 의해 ''k'' = 2, 3, 4에 대해 주어졌다.

Mardia의 검정은 아핀 불변이지만 일관성이 없다. 예를 들어, 다변량 왜도 검정은 대칭 비정규 대안에 대해 일관성이 없다.[32]

'''BHEP 검정'''[35]은 경험적 특성 함수와 정규 분포의 이론적 특성 함수 간의 차이의 노름을 계산한다. 노름의 계산은 가우시안 가중 함수 \mu_\beta(\mathbf{t}) = (2\pi\beta^2)^{-k/2} e^{-|\mathbf{t}|^2/(2\beta^2)}에 대한 제곱 적분 가능 함수의 L2(''μ'') 공간에서 수행된다. 검정 통계량은

:\begin{align}

T_\beta &= \int_{\mathbb{R}^k} \left| {1 \over n} \sum_{j=1}^n e^{i\mathbf{t}^\mathrm{T}\widehat{\boldsymbol\Sigma}^{-1/2}(\mathbf{x}_j - \bar{\mathbf{x})}} - e^{-|\mathbf{t}|^2/2} \right|^2 \; \boldsymbol\mu_\beta(\mathbf{t}) \, d\mathbf{t} \\

&= {1 \over n^2} \sum_{i,j=1}^n e^{-{\beta^2 \over 2}(\mathbf{x}_i-\mathbf{x}_j)^\mathrm{T}\widehat{\boldsymbol\Sigma}^{-1}(\mathbf{x}_i-\mathbf{x}_j)} - \frac{2}{n(1 + \beta^2)^{k/2}}\sum_{i=1}^n e^{ -\frac{\beta^2}{2(1+\beta^2)} (\mathbf{x}_i-\bar{\mathbf{x}})^\mathrm{T}\widehat{\boldsymbol\Sigma}^{-1}(\mathbf{x}_i-\bar{\mathbf{x}})} + \frac{1}{(1 + 2\beta^2)^{k/2}}

\end{align}

이 검정 통계량의 극한 분포는 카이제곱 확률 변수의 가중 합이다.[35]

이러한 검정 절차 및 기타 검정 절차에 대한 자세한 설문 조사가 제공된다.[36]

5. 계산 방법

다변량 정규분포에서 임의의 벡터 '''x'''를 표본 추출하는 방법은 다음과 같다.[40]

1. '''AA'''T = '''Σ''' 가 되도록 하는 임의의 실수 행렬 '''A'''를 찾는다. '''Σ'''가 양의 정부호일 때 일반적으로 촐레스키 분해가 사용되며, 두 경우 모두 적절한 행렬 '''A'''를 얻을 수 있도록 이 분해의 확장된 형태를 항상 사용할 수 있다(공분산 행렬이 양의 준정부호일 수 있으므로). 또 다른 방법은 '''Σ''' = '''UΛU'''−1의 스펙트럼 분해에서 얻은 행렬 '''A''' = '''UΛ'''1/2를 사용하는 것이다. 이론적으로 두 접근 방식 모두 적절한 행렬 '''A'''를 결정하는 데 똑같이 좋은 방법을 제공하지만 계산 시간에 차이가 있다.

2. '''z''' = (''z''1, ..., ''zN'')T를 구성 요소가 ''N''개의 통계적 독립 정규 분포 변량인 벡터로 한다(예를 들어, 박스-뮬러 변환을 사용하여 생성할 수 있음).

3. '''x'''를 '''μ''' + '''Az'''로 한다. 이는 아핀 변환 속성으로 인해 원하는 분포를 갖는다.[50]

5. 1. 분포로부터 값 추출 (표본 추출)

'''μ'''를 평균 벡터, '''Σ'''를 공분산 행렬로 갖는 ''N''차원 다변량 정규분포에서 임의의 벡터 '''x'''를 그리는(표본 추출) 방법은 다음과 같다.[40]

# '''AA'''T = '''Σ''' 가 되도록 하는 임의의 실수 행렬 '''A'''를 찾는다. '''Σ'''가 양의 정부호일 때 일반적으로 촐레스키 분해가 사용되며, 두 경우 모두 적절한 행렬 '''A'''를 얻을 수 있도록 이 분해의 확장된 형태를 항상 사용할 수 있다(공분산 행렬이 양의 준정부호일 수 있으므로). 또 다른 방법은 '''Σ''' = '''UΛU'''−1의 스펙트럼 분해에서 얻은 행렬 '''A''' = '''UΛ'''1/2를 사용하는 것이다. 전자의 접근 방식은 계산이 더 간단하지만 행렬 '''A'''는 임의 벡터의 요소 순서에 따라 변경되는 반면, 후자의 접근 방식은 간단한 재정렬과 관련된 행렬을 제공한다. 이론적으로 두 접근 방식 모두 적절한 행렬 '''A'''를 결정하는 데 똑같이 좋은 방법을 제공하지만 계산 시간에 차이가 있다.

# '''z''' = (''z''1, ..., ''zN'')T를 구성 요소가 ''N''개의 통계적 독립 정규 분포 변량인 벡터로 한다(예를 들어, 박스-뮬러 변환을 사용하여 생성할 수 있음).

# '''x'''를 '''μ''' + '''Az'''로 한다. 이는 아핀 변환 속성으로 인해 원하는 분포를 갖는다.[50]

참조

[1] 서적 A Foundation in Digital Communication Cambridge University Press
[2] 서적 An Intermediate Course in Probability Springer
[3] 논문 On a characterization of the normal distribution 1939
[4] 논문 Characterization of the p-generalized normal distribution 2009
[5] 웹사이트 Computer Vision: Models, Learning, and Inference http://www.computerv[...] 2012-06
[6] 논문 Multivariate outliers and decompositions of Mahalanobis distance
[7] 웹사이트 linear algebra - Mapping between affine coordinate function https://math.stackex[...] 2022-06-24
[8] 논문 The normal law under linear restrictions: simulation and estimation via minimax tilting 2016
[9] 서적 Computation of Multivariate Normal and t Probabilities https://www.springer[...] Springer 2009
[10] 문서 N-Dimensional Cumulative Function, And Other Useful Facts About Gaussians and Normal Densities https://upload.wikim[...] 2006
[11] 간행물 Tail distribution of the maximum of correlated Gaussian random variables IEEE 2015-12-06
[12] 간행물 Efficient simulation for tail probabilities of Gaussian random fields IEEE 2008-12-07
[13] arXiv Methods to integrate multinormals and compute classification measures 2020
[14] 웹사이트 Multiple Linear Regression : MLE and Its Distributional Results http://amath.colorad[...] 2010
[15] 논문 Entropy Expressions and Their Estimators for Multivariate Distributions 1989-05
[16] 논문 Derivations for Linear Algebra and Optimization https://stanford.edu[...]
[17] 서적 Information Theory, Inference and Learning Algorithms Cambridge University Press 2003-10-06
[18] 논문 Essential Aspects of Bayesian Data Imputation https://papers.ssrn.[...]
[19] 서적 Multivariate Statistics: a Vector Space Approach John Wiley and Sons
[20] 서적 Statistics for Petroleum Engineers and Geoscientists Elsevier
[21] 서적 Limited Dependent and Qualitative Variables in Econometrics Cambridge University Press
[22] 웹사이트 An algebraic computation of the marginal distribution is shown here http://fourier.eng.h[...]
[23] 웹사이트 The CMA Evolution Strategy: A Tutorial http://www.lri.fr/~h[...] 2012-01-07
[24] 웹사이트 The Hoyt Distribution (Documentation for R package 'shotGroups' version 0.6.2) http://finzi.psych.u[...]
[25] 논문 Confidence Analysis of Standard Deviational Ellipse and Its Extension into Higher Dimensional Euclidean Space 2015-03-13
[26] 논문 Introduction to Bayesian Data Imputation https://papers.ssrn.[...]
[27] 논문 Testing multivariate normality
[28] 논문 A test to determine the multivariate normality of a data set
[29] 논문 Multivariate Generalizations of the Wald–Wolfowitz and Smirnov Two-Sample Tests
[30] 문서 Rencher 1995
[31] 문서 Rencher 1995
[32] 논문 Limit distributions for measures of multivariate skewness and kurtosis based on projections
[33] 논문 Tolerance regions for a multivariate normal population http://www.ism.ac.jp[...]
[34] 논문 Measures of multivariate skewness and kurtosis with applications
[35] 논문 A consistent test for multivariate normality based on the empirical characteristic function
[36] 논문 Invariant tests for multivariate normality: a critical review
[37] 논문 On the determination of the bivariate normal distribution from distributions of linear combinations of the variables
[38] 웹사이트 Linear least mean-squared error estimation http://web.mit.edu/6[...] 2008-11-26
[39] 서적 Linear Statistical Inference and Its Applications Wiley
[40] 서적 Computational Statistics https://cds.cern.ch/[...] Springer
[41] 논문 The General Projected Normal Distribution of Arbitrary Dimension: Modeling and Bayesian Inference
[42] 서적 A Foundation in Digital Communication Cambridge University Press
[43] 서적 An Intermediate Course in Probability Springer
[44] 논문 On a characterization of the normal distribution 1939
[45] 논문 Characterization of the p-generalized normal distribution 2009
[46] 웹사이트 UIUC, Lecture 21. The Multivariate Normal Distribution http://www.math.uiuc[...]
[47] 웹사이트 周辺分布についての正式な証明は http://fourier.eng.h[...]
[48] 논문 On the determination of the bivariate normal distribution from distributions of linear combinations of the variables
[49] 웹사이트 Linear least mean-squared error estimation http://web.mit.edu/6[...]
[50] 서적 Computational Statistics http://cds.cern.ch/r[...] Springer


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com