매듭 (수학)
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
매듭(knot)은 원을 3차원 유클리드 공간 또는 3-구에 매장하는 것이다. 두 매듭은 앰비언트 아이소토피가 존재할 경우 동치로 정의된다. 매듭은 정칙 사영으로 표현될 수 있으며, 매듭의 정칙 투영 또는 매듭 다이어그램은 4가 평면 그래프로 나타낼 수 있다. 가장 단순한 매듭은 자명한 매듭이며, 세잎 매듭, 8자 매듭, 오엽 매듭 등이 있다. 순한 매듭과 야생 매듭으로 구분되며, 틀 매듭은 솔리드 토러스의 매립으로 확장된다. 매듭의 여집합 연구는 3차원 다양체 이론으로 이어진다. JSJ 분해와 서스턴의 쌍곡화 정리는 매듭 연구를 다양한 기하학적 다양체 연구로 축소시킨다. 그래프 이론과의 연관성을 통해 매듭의 특성을 분석하며, 링크리스 임베딩과 노트리스 임베딩을 갖는 그래프가 연구된다. 일반화된 매듭 개념은 다양체의 임베딩과 관련되며, 쇼플리스 정리, 알렉산더 정리 등이 매듭의 존재 여부를 설명한다.
더 읽어볼만한 페이지
- 매듭 이론 - 꼬임군 (위상수학)
꼬임군은 n개의 가닥 꼬기 연산을 연구하는 수학적 구조로, 꼬임들의 연결을 통해 군 연산을 수행하며 매듭 이론 등 다양한 분야에 응용된다. - 매듭 이론 - 천-사이먼스 이론
천-사이먼스 이론은 천싱선과 제임스 해리스 사이먼스가 정의한 3차 천-사이먼스 형식을 기반으로 3차원 다양체에서 정의되는 위상 양자장론으로, 양자장론, 매듭 이론, 끈 이론 등 다양한 분야와 연관되어 있으며 존스 다항식, 베스-추미노-위튼 모형, 분수 양자 홀 효과 설명 등에 활용된다.
| 매듭 (수학) | |
|---|---|
| 개요 | |
 | |
| 수학적 주제 | 매듭 이론 |
| 위상수학적 정의 | S¹의 E³ (또는 R³)으로의 임베딩 |
| 다른 정의 | S의 S로의 임베딩, 여기서 1=j = n − 2 |
| 매듭 종류 | |
| 기본 매듭 | 소수 매듭 |
| 가장 간단한 비자명 매듭 | 세잎매듭 (3₁) |
| 다음으로 간단한 매듭 | 8자 매듭 (4₁) |
| 7번 교차 매듭 예시 | 7₄ |
| 꼬임 매듭 | 세잎매듭 8자 매듭 |
| 다른 매듭 예시 | 프레첼 매듭 |
| 관련 개념 | |
| 연관된 개념 | 연결 고리 |
| 매듭 다이어그램 | 매듭의 평면 표현 |
2. 엄밀한 정의
매듭은 원 (''S''1영어)을 3차원 유클리드 공간 () 또는 3-구 ()(3-구는 콤팩트 공간이므로)에 매장하는 것이다.[1] 두 매듭은 이들 사이에 앰비언트 아이소토피가 존재할 경우 동치로 정의된다.
2. 1. 사영 표현
'''R'''3 (또는 '''S'''3)의 매듭은 '''R'''2 (또는 '''S'''2)에 투영될 수 있다. 이 투영은 거의 항상 '''정칙'''인데, 이는 매듭의 ''두 점''의 투영이며, 이 점들이 공선이 아닌 ''유한 개수''의 교차점을 제외하고는 모든 곳에서 단사임을 의미한다. 이 경우, 투영 측면을 선택하여 이러한 교차점에서 간단한 상하 정보를 기록하여 정칙 투영으로 매듭의 등위 클래스를 완전히 인코딩할 수 있다. 그래프 이론 용어로, 매듭의 정칙 투영 또는 매듭 다이어그램은 따라서 상하로 장식된 정점을 가진 사원 평면 그래프이다. 이 그래프의 지역 수정은 (평면의 주변 등위까지) 동일한 매듭의 다른 다이어그램으로 이동할 수 있으며, 이를 라이데마이스터 이동이라고 한다.3. 매듭의 종류
가장 단순한 매듭은 자명한 매듭으로, 3차원 공간에 포함된 둥근 원이다.[2] 일반적인 의미에서 자명한 매듭은 전혀 "매듭"이 아니다. 가장 단순한 비자명 매듭으로는 세잎 매듭, 8자 매듭, 오엽 매듭 등이 있다.[2]
여러 매듭이 함께 연결되거나 얽혀 있는 것을 고리라고 한다. 매듭은 단일 성분으로 이루어진 고리이다.
3. 1. 순한 매듭과 야생 매듭
다각형 매듭은 에서 상이 선분의 유한 집합의 합집합인 매듭이다.[3] 순한 매듭은 다각형 매듭과 동치인 매듭이다.[3] 순한 매듭이 아닌 매듭은 야생 매듭이라고 하며,[4] 병리적인 행동을 보일 수 있다.[4] 매듭 이론과 3-다양체 이론에서는 종종 "순한"이라는 형용사를 생략한다. 예를 들어, 매끄러운 매듭은 항상 순한 매듭이다.에서의 매듭이 꺾인선 매듭이란, 선분으로 이루어진 유한 집합의 합집합이 되는 것을 말한다. 꺾인선 매듭과 동치인 매듭은 순한 매듭이라고 한다. 그렇지 않은 매듭은 야생 매듭이라고 하며, 종종 병적인 거동을 보인다. 매듭 이론이나 3차원 다양체 이론에서는 종종 순한 매듭만을 다루며, 이를 단순히 매듭이라고 부른다. 예를 들어, (사상으로서) 매끄러운 매듭은 항상 순하다.
3. 2. 두꺼운 매듭 (Framed Knot)
'''틀 매듭'''은 고리매듭을 3차원 구()에 의 솔리드 토러스의 매립으로 확장한 것이다.매듭의 '''틀'''은 리본 의 이미지와 매듭의 연결수이다. 틀 매듭은 매립된 리본으로 볼 수 있으며 틀은 (부호가 있는) 꼬임의 수이다.[5] 이 정의는 '틀 고리'에 대한 유사한 정의로 일반화된다. 틀 고리는 솔리드 토러스로의 확장이 주변 동위가 된다면 '동치'라고 한다.
틀 고리 '''그림'''은 각 성분에 틀을 나타내기 위해 표시된 고리 그림이며, 경선과 선호된 경도에 대한 기울기를 나타내는 정수로 표시된다. 표시가 없는 고리 그림을 틀 고리를 나타내는 것으로 보는 표준적인 방법은 '흑판 틀'을 사용하는 것이다. 이 틀은 각 성분을 평면에 평평하게 놓인 리본으로 변환하여 얻어진다. 제1형 라이데마이스터 이동은 명백히 흑판 틀을 변경하지만(리본의 꼬임 수를 변경함) 다른 두 이동은 변경하지 않는다. 제1형 이동을 수정된 제1형 이동으로 대체하면 흑판 틀을 가진 고리 그림에 대해 라이데마이스터 정리와 유사한 결과가 나타난다. 흑판 틀을 가진 고리 그림은 (수정된) 제1, II, III형 이동의 시퀀스로 연결되는 경우에만 동치 틀 고리를 나타낸다.
주어진 매듭에 대해 무한히 많은 틀을 정의할 수 있다. 고정된 틀이 있는 매듭이 주어졌다고 가정해 보자. 리본을 자르고 매듭을 중심으로 2π의 정수 배수로 비틀어 잘린 부분에 다시 붙임으로써 기존 틀에서 새로운 틀을 얻을 수 있다. 이러한 방식으로, 매듭을 고정시킨 채 틀 매듭에 대한 동치 관계까지 이전 틀에서 새로운 틀을 얻을 수 있다.[6] 이 의미에서 틀은 벡터장이 매듭을 중심으로 수행하는 꼬임의 수와 관련이 있다. 벡터장이 매듭을 중심으로 몇 번 꼬이는지 알면, 미분 동위까지 벡터장을 결정할 수 있으며, 틀의 동치 클래스는 틀 정수라고 하는 이 정수에 의해 완전히 결정된다.
'''두꺼운 매듭'''은 채워진 토러스 의 로의 매립을 생각한 것이다.
'''비틀림 수'''는 두꺼운 매듭에 부수되는 띠 모양 영역 의 상의 꼬임수를 말한다. 두꺼운 매듭은 이 띠 모양 영역의 매립으로, 비틀림 수는 그 매듭에 더해진 (부호가 있는) 비틀림의 총수로 이해할 수 있다.[22] 두꺼운 꼬임의 비틀림 수 또한 마찬가지로 일반화하여 정의할 수 있다. 두꺼운 꼬임이 서로 동치라는 것은, 그것들을 채워진 토러스로 보았을 때 전체 동위라는 것을 말한다.
4. 매듭의 여집합
3차원 구(S³)에서 주어진 매듭의 매듭의 여집합은 매듭에 포함되지 않은 3차원 구의 모든 점을 의미한다. 고든-루에케 정리에 따르면, 최대 두 개의 매듭만이 위상 동형인 여집합을 가진다(원래 매듭과 거울 반사). 이는 매듭 연구를 여집합 연구, 더 나아가 3차원 다양체 이론으로 전환시켰다.[7]
5. JSJ 분해
JSJ 분해와 서스턴의 쌍곡화 정리는 3차원 구에서의 매듭 연구를 다양한 기하학적 다양체 연구로 축소시킨다. 이는 '접합' 또는 위성 연산을 통해서 이루어진다.[1] JSJ 분해는 매듭의 여집합을 세 개의 다양체의 합집합으로 나누는데, 예를 들어 두 개의 클로버 매듭의 여집합과 보로미안 고리의 여집합으로 나눌 수 있다.[1] 클로버 매듭의 여집합은 H|에이치영어2 × R|아르영어의 기하학을 가지며, 보로미안 고리의 여집합은 H|에이치영어3의 기하학을 가진다.[1]
6. 그래프 이론으로의 응용
매듭 이론은 그래프 이론과도 관련이 깊다. 매듭 다이어그램을 통해 평면 그래프를 정의하고, 이를 통해 매듭의 성질을 연구할 수 있다.
조르당 곡선 정리에 따라, 매듭 다이어그램에서 정의된 평면 그래프의 면들은 흑백으로 칠할 수 있다. 이때 무경계 면은 검은색이고, 경계 모서리를 공유하는 두 면은 반대 색상을 갖는다.
링크리스 임베딩은 그래프의 모든 두 사이클이 서로 얽혀있지 않은(언링크) 임베딩을 의미하며, 노트리스 임베딩은 그래프의 모든 단일 사이클이 풀려있는 매듭(언노트)으로 이루어진 임베딩을 의미한다. 페테르센 그래프군은 링크리스 임베딩을 갖는 그래프의 예시이며,[14] 완전 그래프 ''K''7는 노트리스 임베딩에 대한 최소 금지 그래프 중 하나로 알려져있다.[15]
6. 1. 중간 그래프 (Medial Graph)
매듭 다이어그램은 정점이 교차점이고 모서리가 연속적인 교차점 사이의 경로인 평면 그래프를 정의한다. 조르당 곡선 정리에 따라, 이 평면 그래프의 면은 흑백으로 칠할 수 있는데, 이때 무경계 면은 검은색이고 경계 모서리를 공유하는 두 면은 반대 색상을 갖는다.중간 그래프는 흰색 면이 정점, 교차점이 모서리가 되는 새로운 평면 그래프이다. 이 그래프의 각 모서리는 해당 교차점에서 어떤 가닥이 위/아래로 지나가는지에 따라 부호(+/-)를 붙일 수 있다. 일반적으로 왼쪽 모서리에는 + 부호를, 오른쪽 모서리에는 - 부호를 붙이거나, 왼쪽 모서리를 실선, 오른쪽 모서리를 점선으로 표시한다.
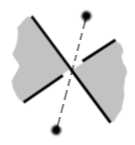
원래 매듭 다이어그램은 이 중간 그래프의 미디얼 그래프이며, 각 교차점의 유형은 해당 모서리의 부호에 의해 결정된다. 모든 모서리의 부호를 변경하면 매듭을 거울에 반사하는 것과 같다.
6. 2. 링크 없는 임베딩과 매듭 없는 임베딩
2차원에서는 오직 평면 그래프만이 교차 없이 유클리드 평면에 임베딩될 수 있지만, 3차원에서는 모든 무방향 그래프가 교차 없이 공간에 임베딩될 수 있다. 하지만, 평면 그래프의 공간적 유사성을 링크리스 임베딩과 노트리스 임베딩을 갖는 그래프들이 제공한다. 링크리스 임베딩은 그래프의 모든 두 사이클이 언링크되어 있는 임베딩이며, 노트리스 임베딩은 그래프의 모든 단일 사이클이 언노트되어 있는 임베딩이다. 링크리스 임베딩을 갖는 그래프는 본질적으로 얽혀 있는 일곱 개의 그래프 집합인 페테르센 그래프군(Petersen family)과 관련된 금지된 그래프 특성을 갖는다.[14]
7. 일반화
현대 수학에서 "매듭"이라는 용어는 임베딩과 관련된 더 일반적인 현상을 설명하는 데 사용되기도 한다. 다양체 M과 부분 다양체 N이 주어지면, N이 M에 동위인 임베딩이 존재하지 않을 경우, N이 M에서 매듭을 이룬다고 말한다. 전통적인 매듭은 N = S1이고 M = R3 또는 M = S3인 경우이다.[16][17]
쇼플리스 정리는 원이 2-구에서 매듭을 이루지 않는다고 말한다. 즉, 2-구 내의 모든 위상적 원은 기하학적 원과 동위이다.[18] 알렉산더 정리는 2-구가 3-구에서 매끄럽게 (또는 PL 또는 tame 위상적으로) 매듭을 이루지 않는다고 말한다.[19] tame 위상 범주에서, 모든 n에 대해 n-구는 n+1-구에서 매듭을 이루지 않는 것으로 알려져 있다. 이것은 모턴 브라운, 배리 매주어, 머스턴 모스의 정리이다.[20] 알렉산더 뿔 달린 구는 tame하지 않은 3-구 내의 매듭 2-구의 예이다.[21] 매끄러운 범주에서, n ≠ 3일 경우 n-구는 n+1-구에서 매듭을 이루지 않는 것으로 알려져 있다. n = 3인 경우는 4-구에 이국적인 매끄러운 구조가 존재하는가 하는 질문과 밀접하게 관련된 오래된 미해결 문제이다.
참조
[1]
간행물
2004
[1]
간행물
1994
[2]
간행물
1994
[2]
간행물
1993
[3]
간행물
1983
[4]
서적
Knot Theory
https://books.google[...]
Cambridge University Press
[5]
논문
An invariant of regular isotopy
http://www.math.uic.[...]
[6]
간행물
Framed Knots
[7]
간행물
1994
[8]
PhD
Harmonic knots
https://www.proquest[...]
University of Iowa
1995
[9]
서적
Ideal Knots
World Scientific
[10]
서적
The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots
American Mathematical Society
[11]
웹사이트
Entrelacs.net tutorial
http://www.entrelacs[...]
[12]
논문
On Knots I
https://zenodo.org/r[...]
1876–1877
[13]
논문
On Links (Abstract)
https://zenodo.org/r[...]
1876–1877
[14]
간행물
Graph Structure Theory: Proc. AMS–IMS–SIAM Joint Summer Research Conference on Graph Minors
http://people.math.g[...]
American Mathematical Society
[15]
논문
Spatial graphs and oriented matroids: the trefoil
[16]
서적
Knotted Surfaces and their Diagrams
American Mathematical Society
[17]
서적
Surface-Knots in 4-Space
Springer
[18]
서적
Topology
https://books.google[...]
Dover Publications
[19]
서적
Foliations and the geometry of 3-manifolds
https://books.google[...]
Oxford University Press
[20]
논문
On embeddings of spheres
[20]
논문
A proof of the generalized Schoenflies theorem
[20]
논문
A reduction of the Schoenflies extension problem
[21]
논문
An Example of a Simply Connected Surface Bounding a Region which is not Simply Connected
National Academy of Sciences
[22]
간행물
An invariant of regular isotopy
http://www.math.uic.[...]
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com