볼츠만 머신

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 구조
3. 학습
- 3.1. 훈련 과정
- 3.2. 문제점
4. 종류
- 4.1. 제한 볼츠만 머신 (Restricted Boltzmann Machine, RBM)
  - 4.1.1. 스파이크 앤 슬래브 RBM (Spike-and-slab RBM)
- 4.2. 딥 볼츠만 머신 (Deep Boltzmann Machine, DBM)
5. 역사
6. 수학적 배경
참조

1. 개요

볼츠만 머신은 셔링턴-키르크패트릭 모델과 호프필드 네트워크와 유사한 연결된 유닛들의 네트워크로, 전체 네트워크에 정의된 에너지(해밀토니안)를 갖는 확률적 모델이다. 유닛은 이진 결과를 생성하며, 가중치는 확률적이다. 볼츠만 머신은 훈련을 통해 데이터의 분포를 학습하고, 주어진 데이터를 근사하는 데 사용된다. 제한된 볼츠만 머신(RBM)과 딥 볼츠만 머신(DBM)과 같은 변형이 존재하며, 딥 러닝 분야에서 활용된다. 볼츠만 머신은 데이비드 셔링턴과 스콧 키르크패트릭의 스핀 글래스 모델을 기반으로 제프리 힌턴과 테리 세이노스키에 의해 개발되었으며, 2024년 존 홉필드와 제프리 힌턴은 볼츠만 머신과 같은 기계 학습에 대한 기여로 노벨 물리학상을 수상했다.

더 읽어볼만한 페이지

신경망 아키텍처 - 홉필드 네트워크
홉필드 네트워크는 상호 연결된 뉴런으로 구성된 순환 신경망으로, 모든 뉴런이 서로 연결되고 연결 가중치가 대칭적인 특징을 가지며, 연상 메모리로서 입력된 패턴을 가장 가까운 저장된 패턴으로 수렴시키는 방식으로 작동하여 최적화 문제 해결 및 패턴 인식 등에 응용된다.
신경망 아키텍처 - 알렉스넷
알렉스넷은 2012년 이미지 인식 대회에서 우승하며 딥 러닝과 CNN의 중요성을 알린 모델이며, GPU를 활용하여 학습 속도를 높이고 8개의 층으로 구성되어 컴퓨터 비전과 딥 러닝 연구 발전에 기여했다.
루트비히 볼츠만 - 볼츠만 상수
볼츠만 상수 k는 온도와 에너지를 연결하는 상수이며, 기체 상수와 아보가드로 상수의 비로 정의되고, SI 단위계에서 1.380649×10⁻²³ J/K의 값을 가지며, 거시 물리학과 미시 물리학을 연결하는 중요한 역할을 한다.
루트비히 볼츠만 - 볼츠만 분포
볼츠만 분포는 특정 상태의 확률이 해당 상태의 에너지와 계의 온도의 함수로 주어지는 확률 분포이며, 통계역학, 수학, 경제학 등 다양한 분야에서 활용된다.

볼츠만 머신

2. 구조

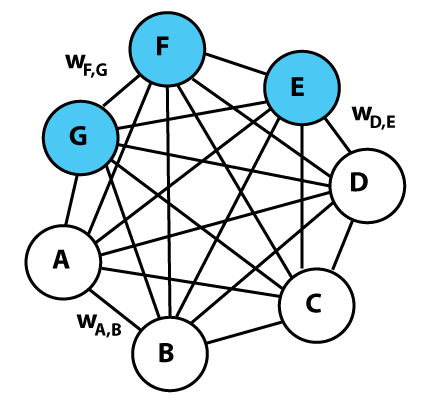
볼츠만 머신은 상호 연결된 유닛들의 네트워크로 구성되며, 각 유닛은 이진(0 또는 1) 상태를 가진다. 네트워크의 전체 에너지 $E$ 는 연결 강도와 유닛의 상태에 따라 결정된다.^[1]

가중치 레이블이 있는 볼츠만 머신의 그래픽 표현. — 가중치가 몇 개 라벨링된 볼츠만 머신의 그래픽 표현. 각 무방향 엣지는 종속성을 나타내며 가중치 $w_{ij}$ 로 가중치가 부여됩니다. 이 예에서는 3개의 숨겨진 유닛(파란색)과 4개의 보이는 유닛(흰색)이 있습니다. 이것은 제한된 볼츠만 머신이 아닙니다.

볼츠만 머신은 셔링턴-키르크패트릭 모델과 마찬가지로, 전체 네트워크에 대해 정의된 총 "에너지"(해밀토니안)를 가지는 유닛 네트워크이다. 유닛은 이진 결과를 생성하며, 볼츠만 머신 가중치는 확률적이다. 볼츠만 머신은 통계적 변동을 사용한 홉필드 네트워크의 일종으로 볼 수 있으며, 신경망 내부를 학습할 수 있는 최초의 신경망 중 하나이다. 하지만 연결 제한이 없는 볼츠만 머신은 기계 학습이나 추론에 실용적이지 않다고 알려져 있다. 그럼에도 불구하고, 볼츠만 머신은 국소성과 학습 알고리즘의 헤브의 법칙적 성질, 그리고 병렬 처리와 동적 역학의 단순한 물리적 프로세스와의 유사성 때문에 이론적으로 매력적이다. 볼츠만 머신은 확률 밀도 함수 자체를 계산하며, 사용되는 샘플링 함수(통계 역학에서의 볼츠만 분포, 즉 소프트맥스 함수)에서 이름을 따왔다.^[1]

2. 1. 기본 구조

볼츠만 머신은 상호 연결된 유닛들의 네트워크로 구성되며, 각 유닛은 0 또는 1 (활성 또는 비활성)의 이진 값을 가진다. 각 유닛의 값은 불규칙 과정에 의해 결정된다. 네트워크 전체의 에너지, 즉 "글로벌 에너지" (

E

)는 홉필드 네트워크와 유사하게 정의된다.

볼츠만 머신의 글로벌 에너지는 다음과 같다.^[1]

:

E = -(\sum_{i

$w_{ij}$ : 유닛 $i$ 와 유닛 $j$ 사이의 연결 강도
$s_i$ : 유닛 $i$ 의 상태 ( $s_i \in \{0,1\}$ )
$\theta_i$ : 유닛 $i$ 의 바이어스 ( $-\theta_i$ 는 유닛의 임계값)

연결에는 다음과 같은 두 가지 제약 조건이 적용된다.^[1]

$w_{ii}=0\qquad \forall i$ (자기 자신과의 연결은 없음)
$w_{ij}=w_{ji}\qquad \forall i,j$ (모든 연결은 대칭적임)

따라서 가중치는 대각선에 0이 있는 대칭 행렬

W=[w_{ij}]

로 표현된다.^[1]

유닛

i

가 0 또는 1의 값을 가질 때 발생하는 글로벌 에너지 차이

\Delta E_i

는 다음과 같다.^[1]

:

\Delta E_i = \sum_j w_{ij} \, s_j + \theta_i

이는 두 에너지 상태의 차이로 표현할 수 있다.^[1]

:

\Delta E_i = E_\text{i=off} - E_\text{i=on}

볼츠만 인자를 활용하여 각 상태의 확률을 계산하고, 이를 정리하면 유닛

i

가 1일 확률

p_\text{i=on}

은 다음과 같이 표현된다.^[1]

:

p_\text{i=on} = \frac{1}{1+\exp(-\frac{\Delta E_i}{T})} = \varsigma_1 \left(\frac{\Delta E_i}{T}\right)

여기서

T

는 시스템의 온도이며,

\varsigma_1

는 표준 시그모이드 함수이다. 이 관계는 볼츠만 머신에서 확률 계산의 기반이 된다.^[1]

2. 2. 유닛 상태 확률

단일 유닛

i

가 0(꺼짐) 또는 1(켜짐) 상태일 때의 전역 에너지 차이(

\Delta E_i

)는 다음과 같이 표현된다.^[1]

:

\Delta E_i = \sum_{j>i} w_{ij} \, s_j + \sum_{j

이는 두 상태의 에너지 차이로도 나타낼 수 있다.^[1]

:

\Delta E_i = E_\text{i=off} - E_\text{i=on}

각 상태의 에너지를 볼츠만 인자에 따른 상대 확률로 대체하고, 볼츠만 분포의 특성을 이용하면 다음과 같은 식이 유도된다.^[1]

:

\Delta E_{i}= -k_{B} T \ln(p_\text{i=off})

(-k_{B} T \ln(p_\text{i=on})),

여기서

k_{B}

는 볼츠만 상수이며, 인위적인 온도

T

개념에 흡수된다. 유닛이 켜짐 또는 꺼짐일 확률의 합이 1임을 고려하여 식을 정리하면,

i

번째 유닛이 켜질 확률은 다음과 같이 주어진다.^[1]

:

p_{i=\text{on}} = \frac{1}{1+\exp\Big(-\frac{\Delta E_{i}}{k_{B}T}\Big)},

여기서 스칼라

T

는 시스템의 온도를 의미한다. 이 관계는 볼츠만 머신의 변형에서 확률 표현식에 사용되는 로지스틱 함수의 기반이 된다.^[1]

2. 3. 평형 상태

이 네트워크는 반복적으로 유닛을 선택하고 상태를 재설정한다. 특정 온도에서 충분히 오래 실행하면, 네트워크의 전역 상태 확률은 볼츠만 분포에 따라 해당 전역 상태의 에너지에만 의존하며, 프로세스가 시작된 초기 상태에는 의존하지 않는다. 이는 전역 상태의 로그 확률이 에너지에 따라 선형적으로 변한다는 것을 의미한다. 이러한 관계는 기계가 "열 평형 상태"에 있을 때, 즉 전역 상태의 확률 분포가 수렴되었을 때 성립한다.

3. 학습

볼츠만 머신의 학습은 네트워크가 주어진 데이터의 분포를 잘 나타내도록 연결 강도를 조정하는 과정이다. 볼츠만 머신의 유닛은 '가시적(visible)' 유닛과 '은닉(hidden)' 유닛으로 나뉜다. 가시적 유닛은 환경으로부터 정보를 받는 유닛으로, 훈련 집합은 가시적 유닛 집합에 대한 이진 벡터 집합이다. 훈련 집합에 대한 분포는 $P^{+}(V)$ 로 표기한다.

볼츠만 머신이 열 평형에 도달하면 전역 상태에 대한 분포가 수렴한다. 이 분포는 은닉 유닛에 대해 주변 분포를 구하여 $P^{-}(V)$ 로 표기한다.

볼츠만 머신은 "실제" 분포 $P^{+}(V)$ 를 근사하기 위해 기계가 생성한 $P^{-}(V)$ 를 사용하며, 두 분포의 유사성은 쿨백-라이블러 발산 $G$ 로 측정한다. $G$ 는 가중치의 함수인데, 가중치는 상태의 에너지를 결정하고, 에너지는 볼츠만 분포에 의해 $P^{-}(v)$ 를 결정하기 때문이다. $G$ 에 대한 경사 하강법 알고리즘은 주어진 가중치 $w_{ij}$ 를 가중치에 대한 $G$ 의 편미분을 빼서 변경한다.

3. 1. 훈련 과정

볼츠만 머신 훈련은 두 단계로 번갈아 진행된다. 첫 번째는 가시적 유닛의 상태가 훈련 집합에서 샘플링된 이진 상태 벡터로 고정되는 "양성(positive)" 단계이다(

P^{+}

에 따라). 두 번째는 네트워크가 자유롭게 실행되는 "음성(negative)" 단계이다. 음성 단계에서는 입력 노드의 상태만 외부 데이터에 의해 결정되고, 출력 노드는 자유롭게 변화할 수 있다.^[2]

훈련의 목표는 기계가 생성한 분포

P^{-}(V)

를 사용하여 실제 분포

P^{+}(V)

를 근사하는 것이다. 두 분포의 유사성은 쿨백-라이블러 발산

G

를 사용하여 측정한다.

:

G = \sum_{v}{P^{+}(v)\ln\left({\frac{P^{+}(v)}{P^{-}(v)}}\right)}

G

는 가중치의 함수이므로, 경사 하강법 알고리즘을 사용하여

G

를 최소화할 수 있다. 주어진 가중치

w_{ij}

는 가중치에 대한

G

의 편미분을 빼서 변경한다.

w_{ij}

에 대한 기울기는 다음 방정식으로 주어진다.^[2]

:

\frac{\partial{G}}{\partial{w_{ij}}} = -\frac{1}{R}[p_{ij}^{+}-p_{ij}^{-}]

여기서,

$p_{ij}^{+}$ 는 양성 단계에서 평형 상태일 때 유닛 ''i''와 ''j''가 모두 켜져 있을 확률이다.
$p_{ij}^{-}$ 는 음성 단계에서 평형 상태일 때 유닛 ''i''와 ''j''가 모두 켜져 있을 확률이다.
$R$ 은 학습률을 나타낸다.

이 학습 규칙은 연결(생물학적 시냅스)이 연결된 두 뉴런 외에 다른 정보는 필요로 하지 않기 때문에 생물학적으로 타당하다고 볼 수 있다. 이는 역전파와 같은 다른 신경망 훈련 알고리즘보다 생물학적으로 더 현실적이다.

볼츠만 머신 훈련은 기대-최대화 알고리즘을 사용하지 않는다. 대신 쿨백-라이블러 발산을 최소화하여 데이터의 로그 우도를 최대화한다. 즉, 훈련 절차는 관측된 데이터의 로그 우도에 대한 경사 상승법을 수행한다.

바이어스 훈련은 다음 식을 따르며, 단일 노드 활동만 사용한다는 점에서 위 식과 차이가 있다.

:

\frac{\partial{G}}{\partial{\theta_{i}}} = -\frac{1}{R}[p_{i}^{+}-p_{i}^{-}]

3. 2. 문제점

이론적으로 볼츠만 머신은 매우 일반적인 계산 매체이다. 예를 들어, 사진에 대해 훈련되면 이론적으로 사진의 분포를 모델링하며, 그 모델을 사용하여 부분적인 사진을 완성할 수 있다.

불행하게도 볼츠만 머신은 심각한 실질적인 문제에 직면하는데, 즉 기계의 크기가 사소한 크기보다 커지면 제대로 학습을 멈추는 것처럼 보인다는 것이다. 이는 다음과 같은 중요한 영향 때문이다.

기계의 크기와 연결 강도의 크기에 따라 평형 통계를 수집하는 데 필요한 시간이 기하급수적으로 증가한다.
연결된 유닛의 활성화 확률이 0과 1 사이일 때 연결 강도는 더욱 가변적이어서 소위 분산 트랩으로 이어집니다. 궁극적인 결과는 노이즈로 인해 연결 강도가 활성도가 포화될 때까지 무작위 보행을 따른다는 것이다.

4. 종류

볼츠만 머신에는 여러 종류가 있지만, 그중에서도 학습 효율을 높이기 위해 특정 제약을 가한 형태들이 주로 사용된다.

제한 볼츠만 머신(RBM): 일반적인 볼츠만 머신은 학습이 어렵지만, RBM은 은닉 유닛과 가시 유닛 사이에만 연결을 허용하고 같은 층의 유닛끼리는 연결을 제한하여 학습 효율을 높였다. RBM을 여러 층으로 쌓아 딥 러닝 모델을 만들 수도 있다.^[6] 음성 인식 분야에 응용되기도 한다.^[7]
스파이크 앤 슬래브 RBM (''ss''RBM): 실수 값을 사용하는 딥 러닝 모델에 적용하기 위해 개발되었다. 이진 스파이크 변수와 실수 값 슬래브 변수를 조합하여 연속적인 값을 표현한다.^[12]
딥 볼츠만 머신(DBM): 여러 층의 은닉 유닛을 가진 무방향 그래프 모델이다. 상향식 및 하향식 추론을 모두 사용하여 입력 데이터의 특징을 더 잘 파악할 수 있다.^[9]^[10]^[11] 그러나 추론 및 학습 속도가 느려 성능과 기능에 제약이 있다.^[8]

4. 1. 제한 볼츠만 머신 (Restricted Boltzmann Machine, RBM)

제한된 볼츠만 머신의 그래픽 표현. 4개의 파란색 유닛은 은닉 유닛을 나타내고, 3개의 빨간색 유닛은 가시 상태를 나타냅니다.

일반적인 볼츠만 머신에서는 학습이 비실용적이지만, 은닉 유닛과 가시 유닛 간의 층 내 연결을 허용하지 않는 제한 볼츠만 머신(RBM)에서는 매우 효율적으로 학습할 수 있다. 즉, 가시 유닛끼리, 은닉 유닛끼리는 서로 연결되지 않는다. 하나의 RBM을 훈련시킨 후, 해당 은닉 유닛의 활동은 더 높은 수준의 RBM을 훈련하기 위한 데이터로 취급될 수 있다. 이러한 RBM 스태킹 방법은 여러 은닉 유닛 계층을 효율적으로 훈련할 수 있게 해주며, 딥 러닝의 일반적인 전략 중 하나이다. 새로운 계층이 추가될 때마다 생성 모델이 개선된다.

RBM은 이진 데이터뿐만 아니라 실수 값을 사용할 수 있도록 확장할 수 있다.^[6]

RBM의 실용적인 응용 사례 중 하나는 음성 인식 분야이다.^[7]

4. 1. 1. 스파이크 앤 슬래브 RBM (Spike-and-slab RBM)

스파이크 앤 슬래브 제한된 볼츠만 머신(''ss''RBM)은 가우시안 RBM과 같이 실수 값 입력을 사용한 딥 러닝의 필요성으로 인해 등장했으며, 이진 잠재 변수로 연속 값 입력을 모델링한다.^[12] 기본적인 제한된 볼츠만 머신 및 변형과 유사하게 스파이크 앤 슬래브 RBM은 이분 그래프이며, GRBM과 마찬가지로 가시적 유닛(입력)은 실수 값을 갖는다. 차이점은 각 숨겨진 유닛이 이진 스파이크 변수와 실수 값 슬래브 변수를 갖는 숨겨진 레이어에 있다는 것이다. 스파이크는 0에서 이산적인 확률 질량이고, 슬래브는 연속적인 영역에 대한 확률 밀도이며,^[13] 이들의 혼합은 사전 확률을 형성한다.^[14]

μ-ssRBM이라고 불리는 ssRBM의 확장은 에너지 함수에 추가적인 항을 사용하여 추가적인 모델링 능력을 제공한다. 이러한 항 중 하나는 관측치를 기준으로 슬래브 변수를 주변화하여 스파이크 변수의 조건부 확률 분포를 형성할 수 있게 한다.

4. 2. 딥 볼츠만 머신 (Deep Boltzmann Machine, DBM)

딥 볼츠만 머신(DBM)은 여러 층의 은닉 변수를 가진 이진 쌍별 마르코프 랜덤 필드(무방향) 확률적 그래프 모델의 일종이다. 이는 대칭적으로 결합된 확률적 이진 변수의 네트워크이다. 가시 유닛

\boldsymbol{\nu} \in \{0,1\}^D

과 은닉 유닛

\boldsymbol{h}^{(1)} \in \{0,1\}^{F_1}, \boldsymbol{h}^{(2)} \in \{0,1\}^{F_2}, \ldots, \boldsymbol{h}^{(L)} \in \{0,1\}^{F_L}

의 층으로 구성되며, 동일한 층의 유닛을 연결하는 연결 링크는 없다( RBM과 유사). DBM에서 벡터

\boldsymbol{\nu}

에 할당된 확률은 다음과 같다.

:

p(\boldsymbol{\nu}) = \frac{1}{Z}\sum_h e^{\sum_{ij}W_{ij}^{(1)}\nu_i h_j^{(1)} + \sum_{jl}W_{jl}^{(2)}h_j^{(1)}h_l^{(2)}+\sum_{lm}W_{lm}^{(3)}h_l^{(2)}h_m^{(3)}},

여기서

\boldsymbol{h} = \{\boldsymbol{h}^{(1)}, \boldsymbol{h}^{(2)}, \boldsymbol{h}^{(3)} \}

는 은닉 유닛 집합이고,

\theta = \{\boldsymbol{W}^{(1)}, \boldsymbol{W}^{(2)}, \boldsymbol{W}^{(3)} \}

는 가시-은닉 및 은닉-은닉 상호 작용을 나타내는 모델 매개변수이다.^[8] DBN에서는 상위 두 층만 제한된 볼츠만 머신(무방향 그래프 모델)을 형성하는 반면, 하위 층은 방향성 생성 모델을 형성한다. DBM에서는 모든 층이 대칭적이고 무방향이다.

DBM은 DBN과 마찬가지로, 제한된 라벨 데이터를 사용하여 대량의 라벨이 없는 감각 입력 데이터로 구축된 표현을 미세 조정하여, 객체 인식 또는 음성 인식과 같은 작업에서 입력에 대한 복잡하고 추상적인 내부 표현을 학습할 수 있다. 그러나 DBN 및 딥 합성곱 신경망과 달리, DBM은 상향식 및 하향식으로 추론 및 훈련 절차를 수행하여 입력 구조의 표현을 더 잘 드러낼 수 있도록 한다.^[9]^[10]^[11]

그러나 DBM의 느린 속도는 성능과 기능성을 제한한다. 정확한 최대 우도 학습이 다루기 어렵기 때문에, 근사 최대 우도 학습만 가능하다. 또 다른 옵션은 평균장 추론을 사용하여 데이터 종속 기댓값을 추정하고 마르코프 체인 몬테카를로 (MCMC)를 사용하여 기대 충분 통계를 근사하는 것이다.^[8] 각 테스트 입력에 대해 수행해야 하는 이 근사 추론은 DBM에서 단일 하향식 통과보다 약 25~50배 더 느리다. 이로 인해 대규모 데이터 세트에서 결합 최적화가 비실용적이게 되며, DBM의 사용이 특징 표현과 같은 작업으로 제한된다.

5. 역사

존 홉필드는 1982년 논문에서 통계 역학, 특히 1970년대에 개발된 데이비드 셔링턴과 스콧 키르크패트릭의 스핀 글래스 이론을 사용하여 연상 기억을 연구했다.^[15]^[16]

이러한 에너지 기반 모델을 인지 과학에 처음 적용한 것은 제프리 힌턴과 테리 세이노스키의 논문이다.^[17]^[18]^[19] 힌턴은 1995년 인터뷰에서 1983년 2월 또는 3월에 홉필드 네트워크에서 시뮬레이티드 어닐링에 대한 강연을 할 예정이었고, 강연을 위해 학습 알고리즘을 설계해야 했으며, 그 결과 볼츠만 머신 학습 알고리즘이 탄생했다고 말했다.^[20]

1984년 더글러스 호프스태터의 카피캣 프로젝트에서도 어닐링된 깁스 샘플링을 사용한 이징 모델 적용 아이디어가 사용되었다.^[21]^[22]

볼츠만 머신 공식은 통계 역학과의 명시적인 유추를 통해 물리학에서 차용한 "에너지"와 같은 용어를 사용하며, 이는 이 분야의 표준이 되었다. 폴 스몰렌스키의 "조화 이론"에서도 에너지 함수에서 부호를 변경하는 유사한 아이디어가 발견된다.^[23]

2024년, 홉필드와 힌턴은 볼츠만 머신과 같은 기계 학습에 대한 기본적인 기여로 노벨 물리학상을 수상했다.^[24] 볼츠만 머신은 통계적 변동을 사용한 홉필드 네트워크의 일종으로 간주할 수 있다.

6. 수학적 배경

볼츠만 머신은 셔링턴-키르크패트릭 모델과 마찬가지로 전체 네트워크에 대해 정의된 총 "에너지"(해밀토니안)를 가진 유닛 네트워크이다. 유닛은 이진 결과를 생성하며, 볼츠만 머신 가중치는 확률적이다. 볼츠만 머신의 전역 에너지 $E$ 는 호프필드 네트워크와 이징 모델과 동일한 형태를 갖는다.

: $E = -\left(\sum_{i$

여기서:

$w_{ij}$ 는 유닛 $j$ 와 유닛 $i$ 간의 연결 강도이다.
$s_i$ 는 유닛 $i$ 의 상태이며, $s_i \in \{0,1\}$ 이다.
$\theta_i$ 는 전역 에너지 함수에서 유닛 $i$ 의 바이어스이다. ( $-\theta_i$ 는 유닛의 활성화 임계값이다.)

일반적으로 가중치

w_{ij}

는 대각선에 0이 있는 대칭 행렬

W=[w_{ij}]

로 표시된다.

더 일반적인 수학적 환경에서 볼츠만 분포는 깁스 측도라고도 알려져 있다. 통계학과 기계 학습에서는 로그-선형 모형이라고 한다. 딥 러닝에서 볼츠만 분포는 볼츠만 머신과 같은 확률적 신경망의 표본 추출 분포에 사용된다.

참조

_[1] 논문 Solvable Model of a Spin-Glass
_[2] 학술지 A Learning Algorithm for Boltzmann Machines http://learning.cs.t[...]
_[3] 학술지 Boltzmann machine 2007-05-24
_[4] 서적 International Neural Network Conference Springer Netherlands 1990-01-01
_[5] 논문 On the Anatomy of MCMC-Based Maximum Likelihood Learning of Energy-Based Models https://ojs.aaai.org[...]
_[6] Youtube Recent Developments in Deep Learning https://www.youtube.[...] 2010-03-22
_[7] 학술지 Context-Dependent Pre-trained Deep Neural Networks for Large Vocabulary Speech Recognition http://research.micr[...]
_[8] 학술지 A better way to pretrain deep Boltzmann machines http://machinelearni[...] 2017-08-18
_[9] conference Efficient Learning of Deep Boltzmann Machines http://machinelearni[...] 2017-08-18
_[10] 웹사이트 Scaling Learning Algorithms towards AI http://www.iro.umont[...] 2007
_[11] conference Efficient Learning of Deep Boltzmann Machines http://machinelearni[...] 2017-08-18
_[12] 학술지 A Spike and Slab Restricted Boltzmann Machine http://machinelearni[...] 2019-08-25
_[13] conference Proceedings of the 28th International Conference on Machine Learning 2019-08-25
_[14] 학술지 Bayesian Variable Selection in Linear Regression 1988
_[15] 학술지 Solvable Model of a Spin-Glass 1975-12-29
_[16] 학술지 Neural networks and physical systems with emergent collective computational abilities "[s.n.]"
_[17] conference Analyzing Cooperative Computation http://digitalcollec[...] 2020-02-17
_[18] conference Optimal Perceptual Inference IEEE Computer Society 1983-06
_[19] 간행물 Massively parallel architectures for Al: NETL, Thistle, and Boltzmann machines. 1983
_[20] 서적 Talking Nets: An Oral History of Neural Networks 2000
_[21] 서적 The Copycat Project: An Experiment in Nondeterminism and Creative Analogies. Defense Technical Information Center 1984-01
_[22] 서적 Physics of cognitive processes World Scientific 1988
_[23] 문서 Information processing in dynamical systems: Foundations of harmony theory. 1986
_[24] 웹사이트 John Hopfield and Geoffrey Hinton share the 2024 Nobel Prize for Physics https://physicsworld[...] 2024-10-18
_[25] 웹사이트 A Learning Algorithm for Boltzmann Machines http://learning.cs.t[...] 1985

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com