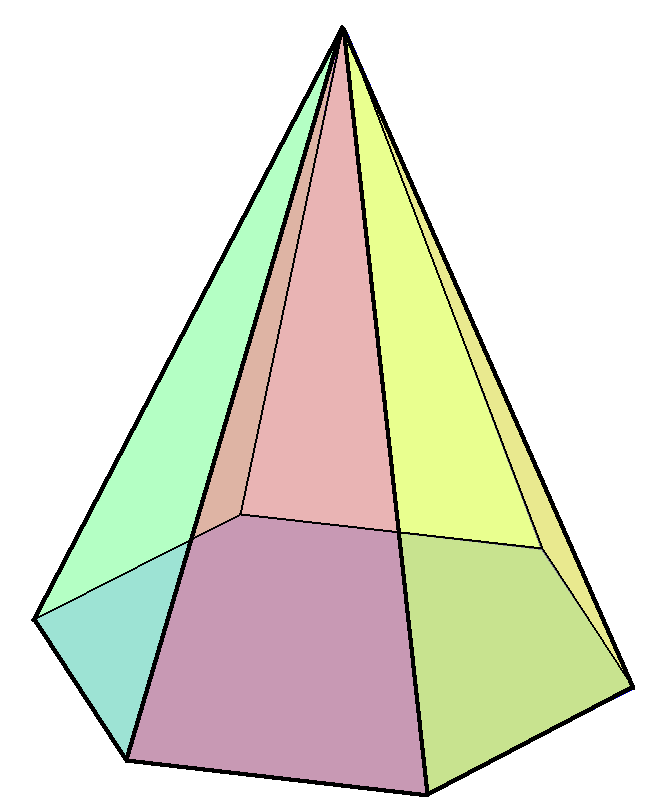
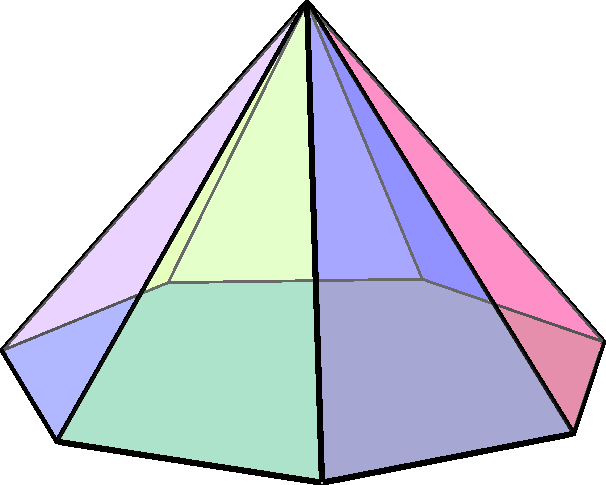
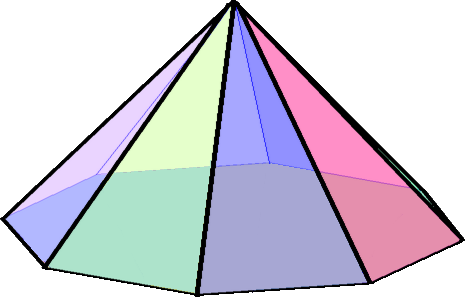
육각뿔

1. 개요

육각뿔은 7개의 꼭짓점, 12개의 모서리, 그리고 7개의 면으로 이루어진 다면체이다. 밑면은 육각형이며, 나머지 6개의 면은 삼각형이다. 육각뿔은 순환군 C6v의 뿔대칭을 가지며, 자기 쌍대 다면체로 쌍대 다면체가 육각뿔 자체이다. 정사면체는 삼각뿔이며, 사각뿔, 오각뿔 등과 함께 다양한 종류의 정각뿔이 존재한다.

더 읽어볼만한 페이지

• 각뿔과 쌍각뿔 - 비틀어 늘린 쌍각뿔
  비틀어 늘린 쌍각뿔은 n각 쌍뿔의 두 밑면 사이에 n각 엇각기둥을 추가하여 만들어지며, 밑면의 형태에 따라 종류가 나뉘고, 정삼각형으로만 이루어진 경우 델타다면체로 불린다.
• 각뿔과 쌍각뿔 - 오각뿔
  오각뿔은 밑면이 오각형이고 한 점에서 만나는 5개의 삼각형으로 이루어진 다면체로, 밑면이 정오각형이고 높이가 밑면 중심에 수직인 경우 정오각뿔이라고 하며, 존슨의 다면체 중 하나로 다양한 분야에 응용된다.
• 자기쌍대 다면체 - 오각뿔
  오각뿔은 밑면이 오각형이고 한 점에서 만나는 5개의 삼각형으로 이루어진 다면체로, 밑면이 정오각형이고 높이가 밑면 중심에 수직인 경우 정오각뿔이라고 하며, 존슨의 다면체 중 하나로 다양한 분야에 응용된다.
• 자기쌍대 다면체 - 늘린 사각뿔
  늘린 사각뿔은 정육면체에 정사각뿔을 붙여 만든 다면체로, 겉넓이와 부피는 각각 $(4+\sqrt{3})a^2$와 $a^3 + \frac{1}{3}a^2h$이며, C4v 대칭을 가지고, 공간 테셀레이션에 사용될 수 있다.
• 기둥형 다면체 - 직육면체
  직육면체는 6개의 직사각형 면으로 이루어진 볼록 다면체로, 모든 이면각이 직각이고 마주보는 면이 합동인 특징을 가지며, 정사각형 직육면체와 정육면체 같은 특수한 경우가 있고 부피, 표면적, 공간 대각선은 가로, 세로, 높이로 계산하며, 공간 감각과 기하학적 개념 이해에 중요한 역할을 한다.
• 기둥형 다면체 - 오각지붕
  오각지붕은 5개의 정삼각형, 5개의 정사각형, 1개의 정오각형, 1개의 정십각형으로 이루어진 존슨의 다면체이며, 회전 대칭을 갖고, 다양한 다면체를 구성하는 데 사용된다.