피에르시몽 드 라플라스 후작
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
피에르시몽 드 라플라스 후작은 1749년 프랑스에서 태어나 1827년 사망한 프랑스의 수학자, 물리학자, 천문학자, 통계학자이자 정치가이다. 그는 천체 역학, 라플라스 변환, 구면 조화 함수, 확률론 및 통계학 등 다양한 분야에서 업적을 남겼으며, 결정론에 대한 과학적 설명을 제시했다. 라플라스는 나폴레옹 시대에 내무부 장관을 역임했고, 부르봉 왕정 복고 후 후작 작위를 받았다. 그의 이름은 라플라스 변환, 라플라스 방정식, 라플라스의 악마 등 여러 용어에 남아 있으며, 그의 업적은 오늘날까지 다양한 분야에 영향을 미치고 있다.
더 읽어볼만한 페이지
- 피에르시몽 라플라스 - 라플라스 방정식
라플라스 방정식은 리만 다양체에서 라플라스-벨트라미 연산자의 2차 편미분 방정식이며, 조화 함수를 해로 갖고 유체 역학, 정전기학 등 다양한 분야에 응용된다. - 피에르시몽 라플라스 - 라플라스 연산자
라플라스 연산자는 준 리만 다양체 위의 매끄러운 벡터 다발에서 정의되는 2차 미분 연산자로, 물리학과 수학에서 정의에 차이가 있을 수 있으며, 기울기, 음악 동형, 발산의 합성, 콤팩트 리만 다양체 위의 함수에 대한 고윳값, 합동 변환과의 가환성, 확산 이론 등 다양한 특징과 응용을 가진다. - 프랑스의 내무장관 - 니콜라 사르코지
니콜라 사르코지는 헝가리 출신 아버지와 그리스계 유대인 어머니 사이에서 태어나 프랑스 제23대 대통령(2007년-2012년)을 역임한 정치인으로, 재임 중 경제 및 이민 정책, 리비아 군사 개입 등으로 논란을 빚었으며 퇴임 후 부패 혐의로 유죄 판결을 받았다. - 프랑스의 내무장관 - 쥘 뒤포르
쥘 뒤포르는 프랑스 제3공화국 초기에 총리를 지낸 변호사이자 정치인으로, 웅변과 법률 지식을 바탕으로 정계에 입문하여 여러 장관직을 거쳐 온건 공화파로서 활동하며 정치적 안정과 배심원 제도 법 통과 등의 업적을 남겼다.
| 피에르시몽 드 라플라스 후작 - [인물]에 관한 문서 | |
|---|---|
| 기본 정보 | |
 | |
| 출생일 | 1749년 3월 23일 |
| 출생지 | 프랑스 왕국 노르망디 보몽-앙-오주 |
| 사망일 | 1827년 3월 5일 |
| 사망지 | 프랑스 왕국 파리 |
| 분야 | 천문학 및 수학 |
| 직장 | 에콜 밀리테르 (1769–1776) |
| 모교 | 캉 대학교 |
| 지도 교수 | 장 르 롱 달랑베르 |
| 학문적 조언자 | 크리스토프 가드블레 피에르 르 카누 |
| 주요 제자 | 시메옹 드니 푸아송 나폴레옹 보나파르트 |
| 알려진 업적 | 천체역학 연구 블랙홀 존재 예측 베이즈 추론 베이즈 확률 라플라스 방정식 라플라시안 라플라스 변환 역 라플라스 변환 라플라스 분포 라플라스의 악마 영-라플라스 방정식 라플라스 수 라플라스 한계 라플라스 불변량 라플라스 원리 라플라스의 불충분 이유의 원리 라플라스 방법 라플라스 힘 라플라스 필터 라플라스 함수 라플라스 행렬 라플라스 운동 라플라스 평면 라플라스 압력 라플라스 공명 라플라스의 구면 조화 함수 라플라스 평활화 라플라스 전개 라플라스 전개 라플라스-베이즈 추정량 라플라스-스틸체스 변환 라플라스-룽게-렌츠 벡터 |
 | |
| 정치 경력 | |
| 직책 | 내무부 장관 |
| 임기 시작 | 1799년 11월 12일 |
| 임기 종료 | 1799년 12월 25일 |
| 총리 | 나폴레옹 보나파르트 (제1통령으로서) |
| 이전 | 니콜라 마리 키네트 |
| 이후 | 뤼시앵 보나파르트 |
| 이름 | |
| 프랑스어 | 피에르 시몽 라플라스 |
| 학문적 정보 | |
| 저명한 학생 | 시메옹 드니 푸아송 나폴레옹 |
| 기타 | |
| 왕립 학회 회원 | code: NA5191 title: Laplace; Pierre Simon (1749 - 1827); Marquis de Laplace accessdate: 2012-03-28 |
2. 생애
라플라스는 1827년 3월 5일 알레산드로 볼타가 사망한 같은 날, 파리에서 사망했다.[8] 그의 뇌는 주치의인 프랑수아 마장디(François Magendie프랑스어)에 의해 적출되어 오랫동안 보관되었으며, 결국 영국을 순회하는 해부학 박물관에 전시되었다. 뇌의 크기는 평균보다 작았다고 한다.[8] 라플라스는 파리의 페르 라셰즈 묘지에 묻혔지만, 1888년 유해는 오르벡의 생 쥘리앵 드 마이요에 있는 가족 소유지로 옮겨져 재매장되었다.[85] 묘는 프랑스 노르망디 생 쥘리앵 드 마이요 마을을 내려다보는 언덕에 위치해 있다.
2. 1. 유년 시절
라플라스는 1749년 노르망디 보몽앙오주(Beaumont-en-Auge프랑스어)에서 태어났다.[139] 그의 아버지는 피에르 라플라스(Pierre Laplace프랑스어)였고, 어머니는 마리안 소숑(Marie-Anne Sochon프랑스어)이었다. 라플라스 가족은 농업에 종사했다.[8][9] 그의 종조부인 매트르 올리버 드 라플라스는 왕실 외과의사라는 직함을 가지고 있었다.[9]라플라스 가족 저택이 1925년에 화재로 손실되면서 라플라스의 생애에 대한 기록이 상당수 소실되어, 라플라스의 유년에 대해서는 자료가 적다.[8][139] 칼 피어슨[8][139] 은 라플라스 가족이 부유한 농경 집안이었다고 주장한다.

라플라스는 베네딕토회 수도원에서 운영하는 마을의 학교에 다녔다. 16세에, 아버지의 뜻에 따라 신학을 공부하기 위해 캉 대학교에 보내졌다.[10] 대학교에서 그는 수학에 대한 열정을 불러일으킨 크리스토프 가블레드와 피에르 르 카누의 지도를 받았다. 라플라스는 성직자의 소명이 없음을 깨닫고 전문 수학자가 되기로 결심했다. 그는 장 르 롱 달랑베르에게 소개장을 받아 파리로 떠났다.[10][11]
2. 2. 학창 시절
라플라스는 1765년에 캉 대학교에 입학하였다.[139] 처음에 라플라스는 로마 가톨릭 교회 신학을 공부하려 하였으나, 곧 수학으로 관심을 돌렸다.[139] 대학교에서 그는 수학에 대한 열정을 불러일으킨 두 명의 열정적인 수학 교사인 크리스토프 가블레드와 피에르 르 카누의 지도를 받았다.[10] 여기서 라플라스의 수학자로서의 뛰어난 재능이 빠르게 인정되었고, 그는 캉에 있는 동안 'Sur le Calcul integral aux differences infiniment petites et aux differences finies'라는 논문을 썼다. 이것은 라플라스와 조제프루이 라그랑주 사이의 첫 번째 서신을 제공했다.[10] 이때 그는 성직자의 소명이 없음을 깨닫고 전문 수학자가 되기로 결심했다. 라플라스는 신학을 졸업하지 않고 르 카누로부터 당시 과학계에서 최고 권위자였던 장 르 롱 달랑베르에게 소개장을 받아 파리로 떠났다.[10][11]2. 3. 성년 시절
라플라스는 1769년에 장 르 롱 달랑베르를 찾아 파리로 상경했다.[139] 달랑베르는 라플라스를 귀찮게 여겨 두꺼운 수학책을 주고 다 읽으면 오라고 했으나, 며칠 뒤 라플라스가 돌아와 책 내용에 대해 답하자 그를 인정하게 되었다.[139]1771년부터 달랑베르의 소개로 파리 군관학교에서 교편을 잡았다. 1773년 프랑스 과학 아카데미 회원이 되었다. 1788년 5월 15일, 39세의 나이로 18세의 마리 샤를로트 드 쿠르티 드 로망주(Marie-Charlotte de Courty de Romanges프랑스어)와 결혼하여 아들 사를에밀 라플라스(Charles-Émile Laplace프랑스어)와 딸 소피쉬잔(Sophie-Suzanne프랑스어)을 두었다.
2. 4. 나폴레옹 집권기
나폴레옹 보나파르트는 1799년 11월 9일에 브뤼메르 18일 쿠데타로 권력을 잡은 뒤, 라플라스를 내무부 장관으로 임명하였다.[6] 그러나 이 임명은 6주 만에 끝나고 뤼시앵 보나파르트가 그 자리를 받았다.[6] 볼에 따르면, 라플라스는 나폴레옹이 집권하자 그에게 내무부 장관직을 얻고자 찾아갔다고 한다.[140]나폴레옹은 자서전에서 라플라스를 해고한 이유를 다음과 같이 적었다. "일류의 기하학자였던 라플라스는 평균 이하의 행정가임을 오래지 않아 드러냈다. 그의 첫 번째 공직 활동에서 우리는 우리의 실수를 깨달았다. 라플라스는 어떤 문제도 올바른 각도에서 고려하지 않았고, 모든 곳에서 미묘함을 찾았으며, 문제만 생각했고, 마침내 "무한소"의 정신을 행정에 적용했다."[13][141] 그러나 그라탄-기네스는 이러한 발언을 "편향적"이라고 묘사하며, 라플라스가 "나폴레옹이 권력을 공고히 하는 동안 임시 허수아비, 자리 지키는 사람으로 임명되었음"에는 의심의 여지가 없어 보인다고 하였다.[76]
라플라스가 내무부에서 해고됐지만, 나폴레옹과 라플라스는 서로 친밀한 관계를 유지하고자 했다.[140] 나폴레옹은 1799년 12월 24일에 그를 상원의원에 추대했으며,[140] 1806년에는 백작 작위를 수여하였다.[140] 라플라스는 《천체 역학》(Mécanique céleste프랑스어) 제3권을 나폴레옹에게 헌정하였으나, 부르봉 왕정 복고 이후에 출판된 것에는 이것이 삭제되어 있다.[140]
볼은 라플라스와 나폴레옹 간의 유명한 일화를 소개한다. 라플라스가 나폴레옹에게 자신의 저작을 진상했을 때, 나폴레옹은 책에 신에 대한 언급이 없음을 지적하며 "라플라스 경, 사람들이 말하길, 당신이 우주에 대해 방대한 책을 썼으면서도, 창조주에 관한 이야기를 한 마디도 쓰지 않았다고 하오."라고 질문했다. 라플라스는 "제게는 그 가설이 필요 없었나이다."라고 답했다. 나폴레옹은 이 대답을 조제프루이 라그랑주에게 전했고, 라그랑주는 "아, 이건 멋진 가설이다. 그것 하나만으로 많은 것이 설명되지 않는가."라고 반응했다.[140]
2. 5. 부르봉 왕정 복고 이후
1814년 나폴레옹 보나파르트의 세력이 쇠퇴하고 있다는 신호를 감지한 라플라스는 재빨리 부르봉 왕가의 쪽으로 돌아섰다.[6] 부르봉 왕정복고 이후 판매된 책에서는 유럽의 평화 중재자에 대한 헌신을 표명한 각주가 삭제되었다.[6] 1817년에 라플라스는 부르봉 왕정복고와 함께 후작으로 승격되었다.[6][13]로저 한은 라플라스를 기회주의자이자 변절자로 묘사하는 것에 반박하며, 그도 나폴레옹의 러시아 원정 실패 이후 심각한 우려를 표했다고 지적한다. 라플라스 부부는 황제와 함께 동부 전선에 있던 아들 에밀의 안전을 걱정했고, 이 시점에서 라플라스의 충성심은 약해지기 시작했다.[77]
라플라스는 1827년 파리에서 사망하였다.[8] 그의 뇌는 주치의인 프랑수아 마장디(François Magendie프랑스어)에 의해 적출되어 오랫동안 보관되었으며, 결국 영국을 순회하는 해부학 박물관에 전시되었다. 뇌의 크기는 평균보다 작았다고 한다.[8]
3. 주요 업적
천문학을 포함한 역학 등의 자연 과학을 발전시켰으며, 그 성과는 응용적인 공학에서도 많이 이용되고 있다. 라플라스의 이름에 관련된 용어는 많으며, 라플라시안, 라플라스 방정식 외에 "칸트-라플라스의 성운설" 등이 있다.
==== 천체 역학 ====
라플라스는 저서 《천체 역학》(Mécanique céleste프랑스어, 총 5권)에서 고전역학에서 뉴턴이 택했던 방식인 기하학적 접근방식에 대한 번역을 실어, 당시 물리학을 집대성하고 확장했다.[24] 《천체 역학》에서는 강체 또는 유체의 운동에서부터, 지구의 모양, 조석이론까지 논하고 있으며, 이 문제들은 미분방정식을 푸는 것이지만, 새로운 방법을 제시하여 발전시킨 것이 많다. 특히 오차평가 등은 그가 썼던 확률론의 응용이기도 하다. 그는 성운 가설을 다시 진술하고 발전시켰는데, 이는 블랙홀과 중력 붕괴에 대한 최초의 이론적 예측이다.[24]
1687년 아이작 뉴턴 경은 자신의 저서인 ''자연철학의 수학적 원리''를 출판하여, 케플러의 법칙을 유도해냈는데, 이 법칙은 운동 법칙과 만유인력의 법칙으로부터 행성의 운동을 설명한다. 그러나 뉴턴은 사적으로 미적분학적 방법을 개발했음에도 불구하고, 출판된 모든 저작에서 복잡한 기하학적 추론을 사용했는데, 이는 행성 간의 상호작용에 따른 보다 미묘한 고차 효과를 설명하기에는 적합하지 않았다. 뉴턴 자신은 수학적 해법의 가능성에 대해 의문을 품었으며, 심지어 태양계의 안정을 보장하기 위해서는 주기적인 기적이 필요하다고 결론 내리기도 했다.[24] 신의 개입에 대한 가설을 없애는 것은 라플라스의 과학적 생애의 주요 활동이 될 것이다.
관측 천문학에서 제기된 한 가지 문제는 목성의 궤도가 수축하고 토성의 궤도가 팽창하는 것처럼 보이는 겉보기 불안정성이었다. 이 문제는 1748년 레온하르트 오일러와 1763년 조제프루이 라그랑주가 해결하려 했지만, 성공하지 못했다.[26] 1776년, 라플라스는 자신의 논문을 발표했는데, 여기서 그는 처음으로 추정되는 광 에테르의 영향이나 순간적으로 작용하지 않는 중력의 법칙 가능성을 탐구했다. 그는 궁극적으로 뉴턴의 중력에 대한 지적 투자를 재개했다.[27] 오일러와 라그랑주는 운동 방정식에서 작은 항들을 무시함으로써 실용적인 근사를 했다. 라플라스는 그 항들이 작더라도 적분하면 시간이 지남에 따라 중요해질 수 있다는 점에 주목했다. 라플라스는 이 분석을 고차 항, 즉 세제곱까지 확장했다. 이보다 더 정확한 분석을 사용하여, 라플라스는 두 행성과 태양은 상호 평형 상태에 있어야 한다고 결론 내렸고, 이를 통해 태양계의 안정성에 대한 연구를 시작했다.[28]
라플라스는 1784년, 1785년, 1786년에 행성 불균등에 관한 논문을 세 부분으로 발표했다. 이 논문은 주로 현재 "목성-토성 대부등(great Jupiter–Saturn inequality)"으로 알려진 섭동의 식별과 설명에 관한 것이었다. 라플라스는 이 행성들의 움직임을 연구하고 예측하는 데 있어 오랫동안 해결되지 않던 문제를 해결했다. 그는 일반적인 고찰을 통해 먼저 두 행성의 상호 작용이 궤도의 이심률과 경사각에 큰 변화를 일으킬 수 없음을 보였다. 그러나 더욱 중요한 것은 목성과 토성의 평균 운동이 거의 공약성을 띠기 때문에 목성-토성 계에서 특이한 현상이 발생한다는 것을 보여주었다.[6][57]
라플라스는 에마누엘 스베덴보리에 의해 처음 제안되고 이마누엘 칸트에 의해 확장된 성운 가설을 발전시켰다.[58] 라플라스가 설명한 가설에 따르면, 태양계는 발광 가스의 구형 덩어리가 질량 중심을 관통하는 축을 중심으로 회전하면서 진화했다. 이 덩어리가 냉각되면서 수축했고, 잇따른 고리들이 외부 가장자리에서 떨어져 나왔다. 이 고리들은 차례로 냉각되어 마침내 행성으로 응축되었고, 태양은 여전히 남아있는 중심핵을 나타냈다. 이 관점에서 라플라스는 더 먼 행성이 태양에 더 가까운 행성보다 더 오래되었을 것이라고 예측했다.[13][58]
태양계에 대한 라플라스의 분석적 논의는 5권으로 출판된 그의 ''천체역학''에 나와 있다. 1799년에 출판된 첫 두 권에는 행성의 운동을 계산하고, 그 모양을 결정하며, 조석 문제를 해결하는 방법이 포함되어 있다.[6] 1802년과 1805년에 출판된 세 번째와 네 번째 권에는 이러한 방법의 적용과 여러 천문 표가 포함되어 있다. 1825년에 출판된 다섯 번째 권은 주로 역사적이지만, 라플라스의 최신 연구 결과를 부록으로 제공한다.
==== 라플라스 변환 ====
레온하르트 오일러, 조제프루이 라그랑주의 뒤를 이어 1744년경 라플라스는 다음과 같은 형태의 미분방정식의 해를 찾는 연구를 시작했다.[142][74]
: z = \int X(x) e^{ax} \, dx\text{ and }z = \int X(x) x^a \, dx.
1785년, 라플라스는 위 식을 이용한 라플라스 변환을 개발하여 미분 방정식을 대수 방정식으로 변환한 뒤, 대수 방정식의 해를 구하고 이를 다시 역변환하여 미분 방정식의 해를 얻는 방법을 제시했다.[142] 이 방식은 공학 수학 분야에서 널리 응용되고 있다.[143]
라플라스 변환은 시간(t)의 함수를 복소 주파수로 해석되는 복소 변수(s)의 함수로 변환하는 적분 연산자 형태를 갖는다.
라플라스는 라플라스 방정식이라는 편미분 방정식을 고찰하여, 여러 개의 미지수를 갖는 편미분 방정식을 하나의 미지수 방정식으로 대체하는 라플라스 변환의 길을 열었다.[134] 이 수학적 기법은 이후 올리버 헤비사이드에 의해 회로 방정식을 푸는 기법으로 응용되었으며, 1950년대에는 고전 제어 이론의 이론 구축에 기여하여 PID 제어로 발전했다.
라플라스 변환은 천문학을 포함한 역학 등의 자연 과학 발전에 기여했으며, 공학 분야에서도 널리 이용되고 있다.
==== 구면 조화 함수 ====
아드리앵마리 르장드르는 1783년 파리 아카데미에 보낸 논문에서 연관 르장드르 함수를 발표했다.[140][13] 라플라스는 이를 3차원으로 확장하여 '''구면 조화 함수'''를 정의하고, 스칼라 퍼텐셜 개념을 발전시켰다.[13]
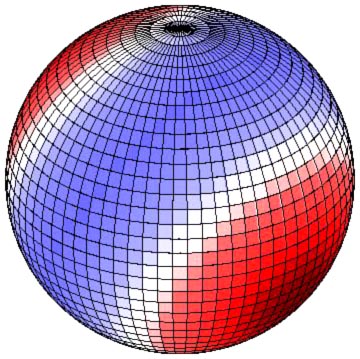
두 점 사이의 거리를 극좌표로 나타내고, 이를 테일러 급수로 전개하면 르장드르 연관 함수를 얻는다. 라플라스는 이 결과를 3차원으로 확장하여 구면 조화 함수를 정의했다.[140] 구면 조화 함수를 이용하면 제곱 적분 가능한 모든 3차원 공 모양 평면 위의 함수를 표현할 수 있다.[140]
라플라스는 미적분학을 퍼텐셜 함수에 적용하여 라플라스 방정식()을 유도하고, 중력 이론을 발전시켰다.[140][13] 구면좌표계에서 라플라스 방정식을 변수분리법으로 풀면 각도 부분의 해는 구면 조화 함수의 합으로 나타낼 수 있다.[140]
구면 고조화 함수는 라플라스 방정식의 실용적인 해법에 매우 중요하며, 천문학을 포함한 역학 등의 자연 과학에 응용된다.[13][56] 라플라시안, 라플라스 방정식, "칸트-라플라스의 성운설" 등이 라플라스의 이름과 관련된 용어이다.
==== 확률론 및 통계학 ====
라플라스는 1812년에 통계학의 많은 기본 결과를 제시한 《확률의 해석적 이론》(Théorie analytique des probabilités)을 발간했다.[70] 이 책의 전반부는 확률 방법과 문제를, 후반부는 통계적 방법과 응용을 다루었다. 비록 라플라스의 증명은 현대적 기준에 비해 엄밀하지 않고, 베이즈주의와 비베이즈주의적 관점을 자유롭게 넘나들어 일부 연구를 따라가기 어렵게 만들지만, 그의 결론은 대부분 타당하다.[70]
라플라스는 《확률에 대한 철학적 에세이》(1814)에서 귀납적 추론에 기반한 수학적 시스템, 즉 오늘날 베이즈 확률을 제시했다. 그는 확률을 "선호되는 사건"과 전체 가능한 사건의 비율로 정의하고, 독립적인 사건의 경우 모든 사건이 발생할 확률은 각 확률을 곱한 값이라고 설명했다. 또한, 두 사건 ''A''와 ''B''가 서로 의존할 때 복합 사건의 확률은 ''A''의 확률에 ''A''가 주어졌을 때 ''B''가 발생할 확률을 곱한 값이며, ''B''가 발생했을 때 ''A''가 발생할 확률은 ''A''와 ''B''가 발생할 확률을 ''B''의 확률로 나눈 값이라고 정의했다.[23] 이는 베이즈 정리와 같다.
라플라스는 연속 규칙을 통해 다음 시도가 성공할 확률을 추정하는 공식을 도출했다.
:\Pr(\text{다음 결과는 성공}) = \frac{s+1}{n+2}
여기서 ''s''는 이전에 관찰된 성공 횟수이고 ''n''은 관찰된 전체 시도 횟수이다. 이 공식은 사건 공간을 알고 있지만 샘플 수가 적은 경우 사건의 확률을 추정하는 데 사용된다.
라플라스는 1779년에 유리한 경우의 수를 전체 가능한 경우의 수에 대한 비율을 추정하는 방법을 제시했다. 이는 어떤 함수의 연속적인 값을 다른 변수에 관하여 다른 함수의 전개식에서 계수로 취급하는 것으로, 후자를 전자의 확률 생성 함수라고 불렀다.[6] 라플라스는 보간법을 사용하여 이러한 계수를 생성 함수에서 결정하고, 유한 차분 방정식의 해를 구하여 계수로부터 생성 함수를 찾는 역 문제를 해결했다.[13]
1810년과 1811년에 발표된 논문에서 라플라스는 특성 함수를 개발하고 최초의 일반적인 중심 극한 정리를 증명했다.[70] 그는 중심 극한 정리가 최소제곱법에 대한 베이즈주의적 정당성을 제공한다는 것을 보였다. 즉, 최소제곱 추정치는 사후 분포로 간주되는 우도 함수를 최대화할 뿐만 아니라, 기대 사후 오차를 최소화한다.[70] 또한, 선형 회귀 문제에서 선형 계수의 선형 불편 추정치에 집중하여, 관측 횟수가 많을 경우 이 추정치가 근사적으로 정규 분포를 따르며, 최소제곱법이 "최고"의 선형 추정치를 제공한다고 주장했다.[70]
베이즈 정리는 라플라스에 의해 체계화 되었으며, 따라서 베이즈보다 라플라스에 기인한다는 견해도 있다.
==== 기타 업적 ====
라플라스는 순수 및 응용 수학 분야에서 다양한 업적을 남겼다. 1772년에는 알렉상드르-테오필 방데르몽드와 함께 행렬식의 일반 이론을 논의했고,[13] 홀수 차수의 모든 방정식은 최소한 하나의 실수 인수를 가져야 한다는 것을 증명했다.[13] 또한 적분을 근사하는 라플라스 방법을 제시하고, 2차 선형 편미분 방정식의 해를 연구했다.[13] 그는 혼합 차분 방정식과 관련된 어려운 문제를 처음으로 고려했으며, 1차 및 2차 유한 차분 방정식의 해는 항상 연분수 형태로 얻을 수 있음을 증명했다.[6][13]
확률 이론에서 라플라스는 드 무아브르-라플라스 정리를 통해 이항 분포를 정규 분포로 근사했고,[13] 몇 가지 일반적인 정적분을 평가했으며,[13] 라그랑주 역전 정리의 일반적인 증명을 제시했다.[13]
라플라스는 토머스 영의 연구를 바탕으로 모세관 현상과 영-라플라스 방정식 이론을 발전시켰다. 1816년에는 공기 중의 소리의 속도가 비열비에 따라 달라진다는 점을 처음으로 지적했다. 이는 뉴턴의 이론이 제시한 값보다 더 정확했는데, 공기의 단열 압축을 고려했기 때문이다.[13] 라플라스는 1782년부터 1784년까지 라부아지에와 함께 다양한 물체의 비열을 연구했다.[13]
국제도량형위원회 위원으로서 라플라스는 미터법 제정에 기여했다. 그는 지구의 북극점에서 적도까지의 자오선 호 길이를 정밀하게 측량하여, 그 1000만 분의 1을 1미터의 기준으로 삼을 것을 제창했다. 이는 1983년[135]까지 이어진 "1미터의 정의"의 기초가 되었다.[136]
라플라스는 프랑스 혁명의 혼란 속에서도 살아남아 정치가로도 활동했다. 1799년 나폴레옹 보나파르트의 통령 정부에서 잠시 내무 장관을 역임했고, 원로원 의원이 되었다. 프랑스 왕정복고 후에는 루이 18세 아래에서 귀족원 의원이 되었다.
3. 1. 천체 역학
라플라스는 저서 《천체 역학》(Mécanique céleste프랑스어, 총 5권)에서 고전역학에서 뉴턴이 택했던 방식인 기하학적 접근방식에 대한 번역을 실어, 당시 물리학을 집대성하고 확장했다.[24] 《천체 역학》에서는 강체 또는 유체의 운동에서부터, 지구의 모양, 조석이론까지 논하고 있으며, 이 문제들은 미분방정식을 푸는 것이지만, 새로운 방법을 제시하여 발전시킨 것이 많다. 특히 오차평가 등은 그가 썼던 확률론의 응용이기도 하다. 그는 성운 가설을 다시 진술하고 발전시켰는데, 이는 블랙홀과 중력 붕괴에 대한 최초의 이론적 예측이다.[24]1687년 아이작 뉴턴 경은 자신의 저서인 ''자연철학의 수학적 원리''를 출판하여, 케플러의 법칙을 유도해냈는데, 이 법칙은 운동 법칙과 만유인력의 법칙으로부터 행성의 운동을 설명한다. 그러나 뉴턴은 사적으로 미적분학적 방법을 개발했음에도 불구하고, 출판된 모든 저작에서 복잡한 기하학적 추론을 사용했는데, 이는 행성 간의 상호작용에 따른 보다 미묘한 고차 효과를 설명하기에는 적합하지 않았다. 뉴턴 자신은 수학적 해법의 가능성에 대해 의문을 품었으며, 심지어 태양계의 안정을 보장하기 위해서는 주기적인 기적이 필요하다고 결론 내리기도 했다. 신의 개입에 대한 가설을 없애는 것은 라플라스의 과학적 생애의 주요 활동이 될 것이다.[24]
관측 천문학에서 제기된 한 가지 문제는 목성의 궤도가 수축하고 토성의 궤도가 팽창하는 것처럼 보이는 겉보기 불안정성이었다. 이 문제는 1748년 레온하르트 오일러와 1763년 조제프루이 라그랑주가 해결하려 했지만, 성공하지 못했다.[26] 1776년, 라플라스는 자신의 논문을 발표했는데, 여기서 그는 처음으로 추정되는 광 에테르의 영향이나 순간적으로 작용하지 않는 중력의 법칙 가능성을 탐구했다. 그는 궁극적으로 뉴턴의 중력에 대한 지적 투자를 재개했다.[27] 오일러와 라그랑주는 운동 방정식에서 작은 항들을 무시함으로써 실용적인 근사를 했다. 라플라스는 그 항들이 작더라도 적분하면 시간이 지남에 따라 중요해질 수 있다는 점에 주목했다. 라플라스는 이 분석을 고차 항, 즉 세제곱까지 확장했다. 이보다 더 정확한 분석을 사용하여, 라플라스는 두 행성과 태양은 상호 평형 상태에 있어야 한다고 결론 내렸고, 이를 통해 태양계의 안정성에 대한 연구를 시작했다.[28]
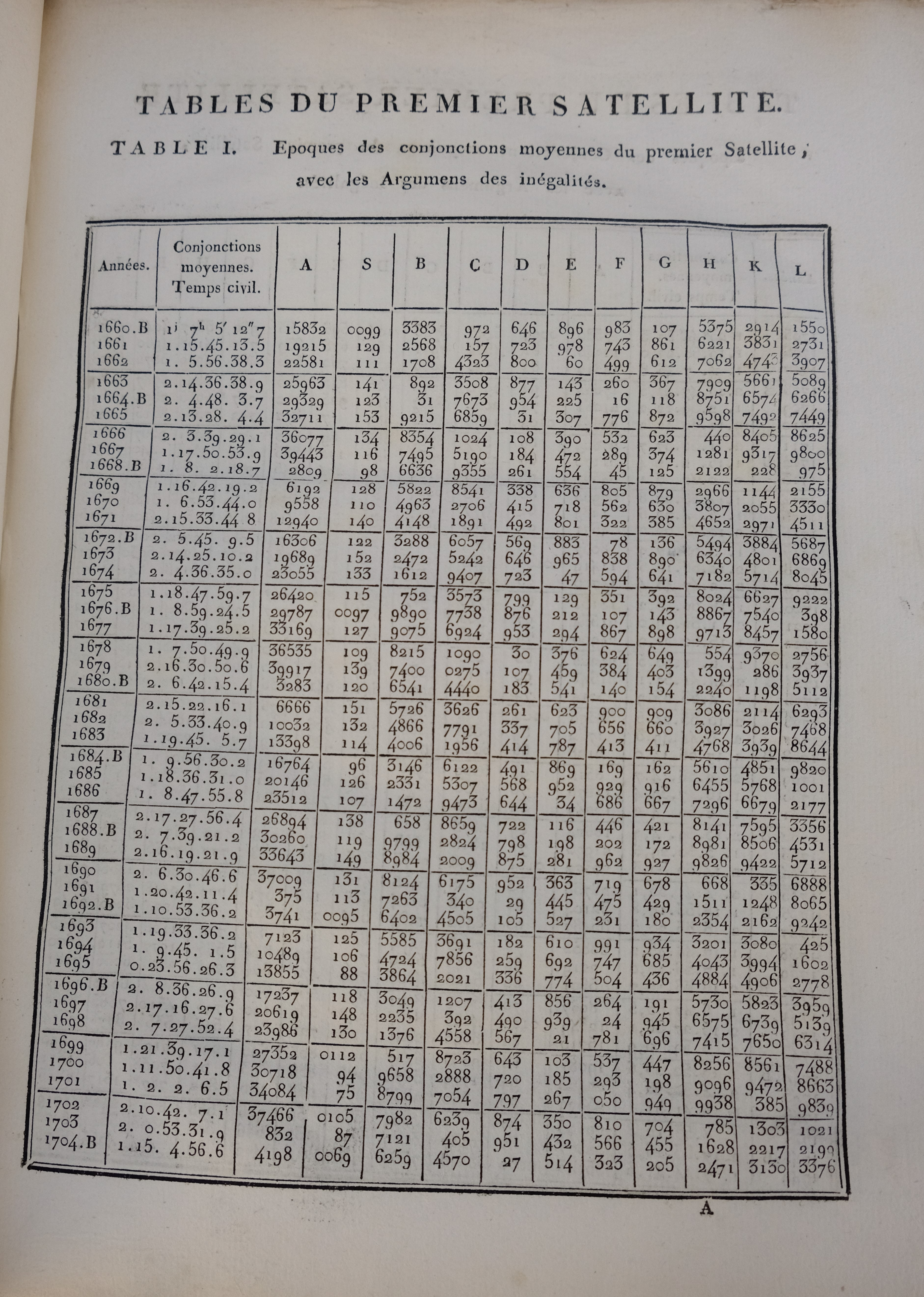
|left|thumb|248x248px|1817년 들랑브르의 "''목성의 위성의 식 테이블''" 복사본 표지. 이 표지에는 라플라스의 기여가 언급되어 있다.]]
|thumb|253x253px|1817년 들랑브르의 "''목성의 위성의 식 테이블''"에 수록된 표 - 이 계산은 라플라스의 이전 발견의 영향을 받았다.]]
라플라스는 1784년, 1785년, 1786년에 행성 불균등에 관한 논문을 세 부분으로 발표했다. 이 논문은 주로 현재 "목성-토성 대부등(great Jupiter–Saturn inequality)"으로 알려진 섭동의 식별과 설명에 관한 것이었다. 라플라스는 이 행성들의 움직임을 연구하고 예측하는 데 있어 오랫동안 해결되지 않던 문제를 해결했다. 그는 일반적인 고찰을 통해 먼저 두 행성의 상호 작용이 궤도의 이심률과 경사각에 큰 변화를 일으킬 수 없음을 보였다. 그러나 더욱 중요한 것은 목성과 토성의 평균 운동이 거의 공약성을 띠기 때문에 목성-토성 계에서 특이한 현상이 발생한다는 것을 보여주었다.[6][57]
라플라스는 에마누엘 스베덴보리에 의해 처음 제안되고 이마누엘 칸트에 의해 확장된 성운 가설을 발전시켰다.[58] 라플라스가 설명한 가설에 따르면, 태양계는 발광 가스의 구형 덩어리가 질량 중심을 관통하는 축을 중심으로 회전하면서 진화했다. 이 덩어리가 냉각되면서 수축했고, 잇따른 고리들이 외부 가장자리에서 떨어져 나왔다. 이 고리들은 차례로 냉각되어 마침내 행성으로 응축되었고, 태양은 여전히 남아있는 중심핵을 나타냈다. 이 관점에서 라플라스는 더 먼 행성이 태양에 더 가까운 행성보다 더 오래되었을 것이라고 예측했다.[13][58]
태양계에 대한 라플라스의 분석적 논의는 5권으로 출판된 그의 ''천체역학''에 나와 있다. 1799년에 출판된 첫 두 권에는 행성의 운동을 계산하고, 그 모양을 결정하며, 조석 문제를 해결하는 방법이 포함되어 있다.[6] 1802년과 1805년에 출판된 세 번째와 네 번째 권에는 이러한 방법의 적용과 여러 천문 표가 포함되어 있다. 1825년에 출판된 다섯 번째 권은 주로 역사적이지만, 라플라스의 최신 연구 결과를 부록으로 제공한다.
|alt=Exposition du Système du Monde (1799)의 첫 페이지|thumb|150x150px|''천체계의 해설'' (1799)의 첫 페이지]]
3. 2. 라플라스 변환
레온하르트 오일러, 조제프루이 라그랑주의 뒤를 이어 1744년경 라플라스는 다음과 같은 형태의 미분방정식의 해를 찾는 연구를 시작했다.[142][74]:
1785년, 라플라스는 위 식을 이용한 라플라스 변환을 개발하여 미분 방정식을 대수 방정식으로 변환한 뒤, 대수 방정식의 해를 구하고 이를 다시 역변환하여 미분 방정식의 해를 얻는 방법을 제시했다.[142] 이 방식은 공학 수학 분야에서 널리 응용되고 있다.[143]
라플라스 변환은 시간()의 함수를 복소 주파수로 해석되는 복소 변수()의 함수로 변환하는 적분 연산자 형태를 갖는다.
라플라스는 라플라스 방정식이라는 편미분 방정식을 고찰하여, 여러 개의 미지수를 갖는 편미분 방정식을 하나의 미지수 방정식으로 대체하는 라플라스 변환의 길을 열었다.[134] 이 수학적 기법은 이후 올리버 헤비사이드에 의해 회로 방정식을 푸는 기법으로 응용되었으며, 1950년대에는 고전 제어 이론의 이론 구축에 기여하여 PID 제어로 발전했다.
라플라스 변환은 천문학을 포함한 역학 등의 자연 과학 발전에 기여했으며, 공학 분야에서도 널리 이용되고 있다.
3. 3. 구면 조화 함수
아드리앵마리 르장드르는 1783년 파리 아카데미에 보낸 논문에서 연관 르장드르 함수를 발표했다.[140][13] 라플라스는 이를 3차원으로 확장하여 '''구면 조화 함수'''를 정의하고, 스칼라 퍼텐셜 개념을 발전시켰다.[13]두 점 사이의 거리를 극좌표로 나타내고, 이를 테일러 급수로 전개하면 르장드르 연관 함수를 얻는다. 라플라스는 이 결과를 3차원으로 확장하여 구면 조화 함수를 정의했다.[140] 구면 조화 함수를 이용하면 제곱 적분 가능한 모든 3차원 공 모양 평면 위의 함수를 표현할 수 있다.[140]
라플라스는 미적분학을 퍼텐셜 함수에 적용하여 라플라스 방정식()을 유도하고, 중력 이론을 발전시켰다.[140][13] 구면좌표계에서 라플라스 방정식을 변수분리법으로 풀면 각도 부분의 해는 구면 조화 함수의 합으로 나타낼 수 있다.[140]
구면 고조화 함수는 라플라스 방정식의 실용적인 해법에 매우 중요하며, 천문학을 포함한 역학 등의 자연 과학에 응용된다.[13][56] 라플라시안, 라플라스 방정식, "칸트-라플라스의 성운설" 등이 라플라스의 이름과 관련된 용어이다.
3. 4. 확률론 및 통계학
라플라스는 1812년에 통계학의 많은 기본 결과를 제시한 《확률의 해석적 이론》(Théorie analytique des probabilités)을 발간했다.[70] 이 책의 전반부는 확률 방법과 문제를, 후반부는 통계적 방법과 응용을 다루었다. 비록 라플라스의 증명은 현대적 기준에 비해 엄밀하지 않고, 베이즈주의와 비베이즈주의적 관점을 자유롭게 넘나들어 일부 연구를 따라가기 어렵게 만들지만, 그의 결론은 대부분 타당하다.[70]라플라스는 《확률에 대한 철학적 에세이》(1814)에서 귀납적 추론에 기반한 수학적 시스템, 즉 오늘날 베이즈 확률을 제시했다. 그는 확률을 "선호되는 사건"과 전체 가능한 사건의 비율로 정의하고, 독립적인 사건의 경우 모든 사건이 발생할 확률은 각 확률을 곱한 값이라고 설명했다. 또한, 두 사건 ''A''와 ''B''가 서로 의존할 때 복합 사건의 확률은 ''A''의 확률에 ''A''가 주어졌을 때 ''B''가 발생할 확률을 곱한 값이며, ''B''가 발생했을 때 ''A''가 발생할 확률은 ''A''와 ''B''가 발생할 확률을 ''B''의 확률로 나눈 값이라고 정의했다.[23] 이는 베이즈 정리와 같다.
라플라스는 연속 규칙을 통해 다음 시도가 성공할 확률을 추정하는 공식을 도출했다.
:
여기서 ''s''는 이전에 관찰된 성공 횟수이고 ''n''은 관찰된 전체 시도 횟수이다. 이 공식은 사건 공간을 알고 있지만 샘플 수가 적은 경우 사건의 확률을 추정하는 데 사용된다.
라플라스는 1779년에 유리한 경우의 수를 전체 가능한 경우의 수에 대한 비율을 추정하는 방법을 제시했다. 이는 어떤 함수의 연속적인 값을 다른 변수에 관하여 다른 함수의 전개식에서 계수로 취급하는 것으로, 후자를 전자의 확률 생성 함수라고 불렀다.[6] 라플라스는 보간법을 사용하여 이러한 계수를 생성 함수에서 결정하고, 유한 차분 방정식의 해를 구하여 계수로부터 생성 함수를 찾는 역 문제를 해결했다.[13]
1810년과 1811년에 발표된 논문에서 라플라스는 특성 함수를 개발하고 최초의 일반적인 중심 극한 정리를 증명했다.[70] 그는 중심 극한 정리가 최소제곱법에 대한 베이즈주의적 정당성을 제공한다는 것을 보였다. 즉, 최소제곱 추정치는 사후 분포로 간주되는 우도 함수를 최대화할 뿐만 아니라, 기대 사후 오차를 최소화한다.[70] 또한, 선형 회귀 문제에서 선형 계수의 선형 불편 추정치에 집중하여, 관측 횟수가 많을 경우 이 추정치가 근사적으로 정규 분포를 따르며, 최소제곱법이 "최고"의 선형 추정치를 제공한다고 주장했다.[70]
베이즈 정리는 라플라스에 의해 체계화 되었으며, 따라서 베이즈보다 라플라스에 기인한다는 견해도 있다.
3. 5. 기타 업적
라플라스는 순수 및 응용 수학 분야에서 다양한 업적을 남겼다. 1772년에는 알렉상드르-테오필 방데르몽드와 함께 행렬식의 일반 이론을 논의했고,[13] 홀수 차수의 모든 방정식은 최소한 하나의 실수 인수를 가져야 한다는 것을 증명했다.[13] 또한 적분을 근사하는 라플라스 방법을 제시하고, 2차 선형 편미분 방정식의 해를 연구했다.[13] 그는 혼합 차분 방정식과 관련된 어려운 문제를 처음으로 고려했으며, 1차 및 2차 유한 차분 방정식의 해는 항상 연분수 형태로 얻을 수 있음을 증명했다.[6][13]확률 이론에서 라플라스는 드 무아브르-라플라스 정리를 통해 이항 분포를 정규 분포로 근사했고,[13] 몇 가지 일반적인 정적분을 평가했으며,[13] 라그랑주 역전 정리의 일반적인 증명을 제시했다.[13]
라플라스는 토머스 영의 연구를 바탕으로 모세관 현상과 영-라플라스 방정식 이론을 발전시켰다. 1816년에는 공기 중의 소리의 속도가 비열비에 따라 달라진다는 점을 처음으로 지적했다. 이는 뉴턴의 이론이 제시한 값보다 더 정확했는데, 공기의 단열 압축을 고려했기 때문이다.[13] 라플라스는 1782년부터 1784년까지 라부아지에와 함께 다양한 물체의 비열을 연구했다.[13]
국제도량형위원회 위원으로서 라플라스는 미터법 제정에 기여했다. 그는 지구의 북극점에서 적도까지의 자오선 호 길이를 정밀하게 측량하여, 그 1000만 분의 1을 1미터의 기준으로 삼을 것을 제창했다. 이는 1983년[135]까지 이어진 "1미터의 정의"의 기초가 되었다.[136]
라플라스는 프랑스 혁명의 혼란 속에서도 살아남아 정치가로도 활동했다. 1799년 나폴레옹 보나파르트의 통령 정부에서 잠시 내무 장관을 역임했고, 원로원 의원이 되었다. 프랑스 왕정복고 후에는 루이 18세 아래에서 귀족원 의원이 되었다.
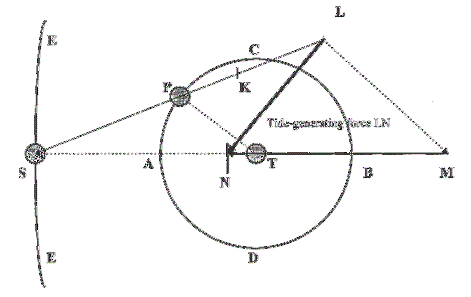
4. 조석 이론
뉴턴은 조석력을 설명하여 조석을 설명했고, 베르누이는 조석 포텐셜에 대한 지구 해수의 정적 반응에 대한 설명을 제공했다.[30] 그러나 1775년 라플라스가 개발한 ''조석의 동역학 이론''은 조석력에 대한 해양의 실제 반응을 설명한다.[31] 라플라스의 해양 조석 이론은 마찰, 공명, 그리고 해양 분지의 고유 주기를 고려했다. 이 이론은 세계 해양 분지에서 거대한 양극성 흐름 시스템을 예측했으며, 실제로 관찰되는 해양 조석을 설명한다.[32][33]
태양과 달의 중력 기울기에 기반하지만 지구 자전, 대륙의 영향 및 기타 중요한 효과를 무시하는 평형 이론으로는 실제 해양 조석을 설명할 수 없었다.[34][35][36][32][37][38][39][40][41] 측정 결과가 이론을 뒷받침함에 따라, 조석이 심해 능선 및 해산 열과 어떻게 상호 작용하여 심해에서 표면으로 영양분을 운반하는 심해 와류를 발생시키는지 등 많은 현상에 대한 설명이 가능해졌다.[42] 평형 조석 이론은 조석파의 높이를 0.5미터 미만으로 계산하지만, 동역학 이론은 조석이 최대 15미터까지 되는 이유를 설명한다.[43] 위성 관측은 동역학 이론의 정확성을 확인하며, 현재 전 세계 조석은 수 센티미터 이내로 측정된다.[44][45] CHAMP 위성의 측정 결과는 TOPEX 데이터를 기반으로 한 모델과 밀접하게 일치한다.[46][47][48] 전 세계 조석의 정확한 모델은 연구에 필수적인데, 이는 조석으로 인한 변동을 제거해야 중력과 해수면 변화를 계산할 수 있기 때문이다.[49]
1776년 라플라스는 조류 흐름을 바트로픽 2차원 시트 흐름으로 설명하는 편미분 방정식의 단일 집합을 공식화했다.[50] 전향력이 도입되었으며 중력에 의한 측면 힘도 작용했다. 라플라스는 유체 역학 방정식을 단순화하여 이러한 방정식을 얻었다. 그러나 이 방정식은 라그랑주 방정식을 통해 에너지 적분으로부터 유도될 수도 있다.
평균 두께 ''D''의 유체 시트에서 수직 조석 상승 ''ζ''와 수평 속도 성분 ''u'' 및 ''v''(각각 위도 ''φ'' 및 경도 ''λ'' 방향)는 '''라플라스 조석 방정식'''을 만족한다.[50]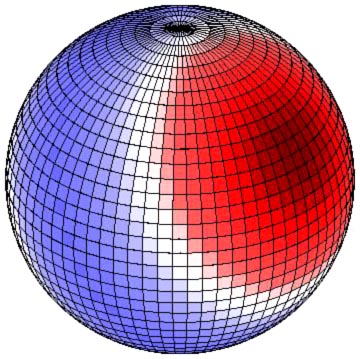
윌리엄 톰슨(켈빈 경)은 컬을 사용하여 라플라스의 운동량 항을 다시 작성하여 와도에 대한 방정식을 찾았다. 특정 조건에서 이는 와도의 보존으로 다시 작성될 수 있다.
4. 1. 조석의 동역학 이론
뉴턴은 조석력을 설명하여 조석을 설명했고, 베르누이는 조석 포텐셜에 대한 지구 해수의 정적 반응에 대한 설명을 제공했다.[30] 그러나 1775년 라플라스가 개발한 ''조석의 동역학 이론''은 조석력에 대한 해양의 실제 반응을 설명한다.[31] 라플라스의 해양 조석 이론은 마찰, 공명, 그리고 해양 분지의 고유 주기를 고려했다. 이 이론은 세계 해양 분지에서 거대한 양극성 흐름 시스템을 예측했으며, 실제로 관찰되는 해양 조석을 설명한다.[32][33]태양과 달의 중력 기울기에 기반하지만 지구 자전, 대륙의 영향 및 기타 중요한 효과를 무시하는 평형 이론으로는 실제 해양 조석을 설명할 수 없었다.[34][35][36][32][37][38][39][40][41] 측정 결과가 이론을 뒷받침함에 따라, 조석이 심해 능선 및 해산 열과 어떻게 상호 작용하여 심해에서 표면으로 영양분을 운반하는 심해 와류를 발생시키는지 등 많은 현상에 대한 설명이 가능해졌다.[42] 평형 조석 이론은 조석파의 높이를 0.5미터 미만으로 계산하지만, 동역학 이론은 조석이 최대 15미터까지 되는 이유를 설명한다.[43] 위성 관측은 동역학 이론의 정확성을 확인하며, 현재 전 세계 조석은 수 센티미터 이내로 측정된다.[44][45] CHAMP 위성의 측정 결과는 TOPEX 데이터를 기반으로 한 모델과 밀접하게 일치한다.[46][47][48] 전 세계 조석의 정확한 모델은 연구에 필수적인데, 이는 조석으로 인한 변동을 제거해야 중력과 해수면 변화를 계산할 수 있기 때문이다.[49]
4. 2. 라플라스 조석 방정식
1776년 라플라스는 조류 흐름을 바트로픽 2차원 시트 흐름으로 설명하는 편미분 방정식의 단일 집합을 공식화했다.[50] 전향력이 도입되었으며 중력에 의한 측면 힘도 작용했다. 라플라스는 유체 역학 방정식을 단순화하여 이러한 방정식을 얻었다. 그러나 이 방정식은 라그랑주 방정식을 통해 에너지 적분으로부터 유도될 수도 있다.평균 두께 ''D''의 유체 시트에서 수직 조석 상승 ''ζ''와 수평 속도 성분 ''u'' 및 ''v''(각각 위도 ''φ'' 및 경도 ''λ'' 방향)는 '''라플라스 조석 방정식'''을 만족한다.[50]
윌리엄 톰슨(켈빈 경)은 컬을 사용하여 라플라스의 운동량 항을 다시 작성하여 와도에 대한 방정식을 찾았다. 특정 조건에서 이는 와도의 보존으로 다시 작성될 수 있다.
5. 결정론
라플라스는 인과적 결정론에 대한 최초의 과학적 설명을 발표했다.[91] 그는 우주의 현재 상태를 과거의 결과이자 미래의 원인으로 보았다. 특정 순간에 자연을 움직이는 모든 힘과 자연을 구성하는 모든 항목의 위치를 알고, 이 데이터를 분석할 수 있는 지성이 있다면, 우주의 가장 큰 물체와 가장 작은 원자의 움직임을 단일 공식으로 포괄할 수 있다고 주장했다. 이러한 지성에게는 불확실한 것이 없으며, 미래는 과거와 마찬가지로 현재가 될 것이라고 보았다.[71]
이 지성은 종종 '라플라스의 악마'라고 불리며, 때로는 '라플라스의 슈퍼맨'이라고도 불린다. 라플라스 자신은 "악마"라는 단어를 사용하지 않았고, 이는 후대에 추가된 표현이다. 그는 단순히 "지성"이라고 언급했다.[71]
라플라스는 결정론자였으며, 앞으로 일어날 모든 현상은 지금까지 일어난 일에 기인하며 완전히 결정되어 있다고 생각했다. 특정 시점의 우주 모든 입자[137]의 운동 상태를 알 수 있다면, 앞으로 일어날 모든 현상을 미리 계산할 수 있다는 것이다. 라플라스의 결정론은 "모든 사상의 원인과 결과는 인과율에 지배받기 때문에 미래는 유일하게 결정된다"라고 하는 "인과적 결정론"에 속하며, 결정론 중에서도 "강한" 부류에 속한다. "라플라스의 악마"는 "어떤 순간의 모든 물질의 역학적 상태를 알 수 있고, 또한 그 데이터를 분석할 수 있는 능력의 지성"이며[138], "결정론적으로 정해진 미래를 완전히 내다볼 수 있는 자"라는 사고상의 개념적인 존재이다.
하지만, 철학적 맥락에서 이러한 인과적 결정론의 개념은 라플라스 이전에도 널리 퍼져 있었으며, 모페르튀의 '예언에 관하여'(1756년)에서도 찾아볼 수 있다.[72] 또한, 예수회 과학자 로제 조제프 보스코비치는 1758년 저서 ''자연 철학 이론''에서 라플라스와 매우 유사한 과학적 결정론 버전을 제안했다.[73]
6. 정치 및 사회 활동
피에르시몽 드 라플라스는 프랑스 혁명기의 혼란 속에서도 살아남아 정치 활동을 이어갔다.[81] 그는 1799년 나폴레옹 보나파르트의 통령 정부에서 잠시 내무 장관으로 등용되었으며,[81] 이후 호헌원로원 의원이 되었다.[81] 프랑스 왕정복고 후에는 루이 18세에 의해 귀족원 의원으로 임명되었다.[81]
라플라스는 1814년 ''철학적 시론'' 제2판에서 정치와 통치에 대한 견해를 밝혔다. 그는 "사회를 낳고 보존하는 것은 이성, 정의, 그리고 인간성의 영원한 원칙을 실천하는 것"이라고 강조하며, 이 원칙에서 벗어나는 것을 경계했다.[78][79] 또한, "정복욕에 취한 강대국"의 팽창은 "자연적인 한계"에 의해 제어되며, 이 한계를 넘어서는 국가는 결국 쇠퇴할 것이라고 주장하며 나폴레옹의 행동을 비판했다.[80][81]
그는 혁명적 변화보다는 점진적 변화를 선호했다. "자연 과학에서 유용했던 관찰과 계산에 기반한 방법을 정치 및 도덕 과학에 적용하자"라고 제안하며, "과거의 경험을 통해 기존 제도의 단점을 알고 있지만, 변화가 일으킬 수 있는 질병의 정도는 알지 못한다"고 지적했다. 따라서 확률 이론에 따라 급격한 변화를 피해야 한다고 주장했다.[82] 그는 과학적 발견을 통해 드러난 자연의 안정성이 인간 종을 보존하는 최적의 모델이라고 믿었다.[81]
라플라스는 보르다 투표 방식을 옹호하며, 대수의 법칙을 적용하여 후보자 순위 결정의 정당성을 입증했다. 이 투표 방식은 과학 아카데미의 새로운 회원 선출에 사용되었다.[83][84] 또한 국제도량형위원회 위원으로서 미터법 제정에 기여했는데, 지구의 북극점에서 적도까지 자오선 호 길이의 1000만 분의 1을 1미터로 정의하는 기준을 제안했다.[136] 이는 1983년까지 이어진 "1미터의 정의"의 기초가 되었다.[135]
7. 종교적 견해
라플라스는 가톨릭 신자로 성장했지만, 성인이 되면서 유신론적 입장을 취한 것으로 보인다.[6] 그러나 그의 동시대인 중 일부는 그를 무신론자로 여겼고,[94] 최근의 많은 학자들은 그를 불가지론자로 묘사한다.[114][115][116]
라플라스는 나폴레옹과의 일화에서 "나는 그 가설이 필요 없었다"라고 말한 것으로 유명하다.[13] 하지만 이 일화는 외전일 가능성이 있으며, 실제로 일어났더라도 라플라스가 정확히 어떤 의도로 말했는지는 불분명하다.[13] 에르베 페이는 라플라스가 신의 존재 자체가 아니라, 특정한 시점에서의 신의 개입을 가설로 취급한 것이라고 주장했다.[87][88] 스티븐 호킹은 라플라스가 신이 존재하지 않는다고 주장한 것이 아니라, 과학 법칙을 깨는 신의 개입을 부정했을 뿐이라고 설명했다.[91] 윌리엄 허셜의 기록에 따르면, 라플라스는 자연적인 원인들이 천체 시스템의 구성과 보존을 설명할 수 있다고 믿었으며, 이는 나폴레옹의 반박을 받았다.[92]
장 에티엔 구에타르는 라플라스의 신 존재 부정에 놀랐다고 언급했으며, 그의 무신론이 철저한 유물론에 기반한 것으로 보인다고 말했다.[95] 그러나 장바티스트 뒤마는 라플라스가 유물론자들에게 그럴듯한 주장을 제공했지만, 그들의 신념을 공유하지는 않았다고 기록했다.[96][97] 라플라스는 자신의 저술에서 신의 존재를 부인한 적이 없으며,[98] 그의 사적인 편지에는 무신론과 일치하지 않는 표현이 나타난다.[6] 예를 들어, 그는 아들에게 보낸 편지에서 신에게 기도를 드린다고 언급했다.[88][99]
라플라스는 뉴턴이 태양계의 질서를 유지하기 위해 신의 개입이 필요하다고 주장한 것을 비판하며, 행성의 배열이 운동 법칙에 의해 완전히 설명될 수 있다고 주장했다.[101][102][103] 그는 뉴턴이 신의 능력에 대해 매우 좁은 생각을 가지고 있다고 비판한 라이프니츠의 견해에 동의했다.[104][105] 라플라스는 기독교의 기적적인 사실을 부정하고,[106] 성변화 교리가 이성, 경험, 자연 법칙, 그리고 신에 대한 숭고한 생각에 위배된다고 주장했다.[107] 그는 또한 신학에서 확률을 사용하는 것을 조롱했다.[108]
노년에도 라플라스는 신의 문제에 대해 호기심을 가졌으며,[109] 장프레데리크 테오도르 모리스와 자주 기독교에 대해 논의했다.[110] 그는 모리스에게 기독교가 문명화에 긍정적인 영향을 미쳤다고 칭찬했지만, 자연 법칙의 불변성이 초자연적인 사건을 허용하지 않는다는 자신의 확신을 굳게 지켰다.[109] 라플라스는 죽기 직전 시메옹 드니 푸아송에게 세속적인 추구의 헛됨을 암시하는 말을 남겼다.[111][112] 그는 외방전교회 신부로부터 종부성사를 받았다.[97][112] 그러나 그의 전기 작가 로저 한은 라플라스가 가톨릭적인 최후를 맞이했다는 것을 믿을 수 없다고 하며, 그가 마지막 순간까지 회의론자로 남았다고 주장한다.[113]
한편, 라플라스는 교황 칼릭스토 3세가 핼리 혜성을 파문했다는 이야기를 과장한 것으로 알려져 있다.[118] 그러나 이는 사실과 다르며, 라플라스는 교황이 혜성을 "축출"하라고 명령했다고 언급했을 뿐이다.[119] 파문에 대한 이야기는 프랑수아 아라고에 의해 처음 언급되었다.[119][120][121]
8. 유산 및 영향
라플라스의 업적은 수학, 물리학, 천문학, 통계학 등 다양한 분야에 큰 영향을 미쳤다. 그의 이름은 라플라스 변환, 라플라스 방정식, 라플라스의 악마 등 여러 용어에 남아 있다. 1809년 네덜란드 왕립 연구소의 통신 회원이었다.[122] 1822년에는 미국 예술 과학 아카데미의 외국 명예 회원이었다.[123]
소행성 4628 라플라스는 라플라스의 이름을 따서 명명되었다.[124] 달의 유라 산맥의 지맥은 라플라스 곶으로 알려져 있다. 그의 이름은 에펠탑에 새겨진 72개의 이름 중 하나이다. 유럽 우주국의 유로파-목성 시스템 미션의 잠정적인 작업명은 "라플라스" 우주 탐사선이다. 아르쾨이의 RER B에 있는 기차역과 러시아 로스토프나도누 근처 베르흐네테메르니츠키의 거리도 그의 이름을 따서 명명되었다. 전기 전자 기술자 협회(IEEE) 신호 처리 학회의 초기 경력 기술 성취상은 그의 이름을 기려 명명되었다.[125]
참조
[1]
서적
The Large Scale Structure of Space-Time
Cambridge University Press
[2]
웹사이트
Happy Birthday, Pierre-Simon Laplace
https://www.comsol.c[...]
2024-12-04
[3]
서적
The History of Statistics: The Measurement of Uncertainty before 1900
Harvard University Press
[4]
논문
Michell, Laplace and the Origin of the Black Hole Concept
https://www.sciengin[...]
2009
[5]
논문
Laplace and the Speed of Sound
https://www.journals[...]
1964
[6]
백과사전
Laplace, Pierre Simon
[7]
논문
Pierre Simon Laplace, 1749–1827: A Determined Scientist (Book review)
[8]
간행물
Laplace, being Extracts from Lectures delivered by Karl Pearson
1929-12
[9]
서적
A Short Account of the History of Mathematics
[10]
웹사이트
Laplace
http://www-history.m[...]
2007-08-25
[11]
논문
Laplace
https://www.jstor.or[...]
1949
[12]
서적
[13]
서적
[14]
웹사이트
The Chemical Revolution of Antoine-Laurent Lavoisier International Historic Chemical Landmark
https://www.acs.org/[...]
1999-06-08
[15]
논문
Antoine Laurent Lavoisier, Pierre Simon, Marquis de Laplace, Henry Guerlac
1983-06
[16]
서적
[17]
웹사이트
Effects of the Scientific Community on Laplace
https://sites.google[...]
2018-01-10
[18]
서적
[19]
서적
[20]
서적
[21]
서적
[22]
서적
[23]
서적
[24]
서적
[25]
서적
Celestial Mechanics: The waltz of the planets
Springer
[26]
서적
[27]
서적
[28]
서적
[29]
웹사이트
Laplace
http://www-history.m[...]
University of St. Andrews
[30]
웹사이트
Short notes on the Dynamical theory of Laplace
http://www.preservea[...]
2011-11-20
[31]
웹사이트
Tide Dynamics
http://faculty.washi[...]
2005
[32]
웹사이트
Higher Education
http://www.pearsonhi[...]
[33]
웹사이트
An Astronomer's View on the Current College-Level Textbook Descriptions of Tides
http://ocean.kisti.r[...]
Korean Earth Science Society
2009-09
[34]
웹사이트
Tidal theory
http://www.sanho.co.[...]
[35]
웹사이트
Dynamic theory for tides
http://www.oberlin.e[...]
Oberlin.edu
[36]
웹사이트
Dynamic Theory of Tides
http://ffden-2.phys.[...]
[37]
웹사이트
Dynamic Tides – In contrast to "static" theory, the dynamic theory of tides recognizes that water covers only three-quarters o
http://web.vims.edu/[...]
Web.vims.edu
2012-06-02
[38]
웹사이트
The Dynamic Theory of Tides
http://www.coa.edu/s[...]
Coa.edu
2012-06-02
[39]
웹사이트
Welcome to nginx!
https://beacon.salem[...]
2022-02-03
[40]
웹사이트
Tides – building, river, sea, depth, oceans, effects, important, largest, system, wave, effect, marine, Pacific
http://www.waterency[...]
Waterencyclopedia.com
2010-06-27
[41]
웹사이트
TIDES
http://ocean.tamu.ed[...]
Ocean.tamu.edu
2012-06-02
[42]
웹사이트
Tides
http://www.seafriend[...]
Seafriends.org.nz
2012-06-02
[43]
웹사이트
The Cause & Nature of Tides
http://www.linz.govt[...]
[44]
웹사이트
Scientific Visualization Studio TOPEX/Poseidon images
http://svs.gsfc.nasa[...]
Svs.gsfc.nasa.gov
2012-06-02
[45]
웹사이트
TOPEX/Poseidon Western Hemisphere: Tide Height Model : NASA/Goddard Space Flight Center Scientific Visualization Studio : Free Download & Streaming : Internet Archive
https://archive.org/[...]
2000-06-15
[46]
웹사이트
TOPEX/Poseidon Flat Earth Tide Height Model
http://svs.gsfc.nasa[...]
2015-09-18
[47]
웹사이트
http://www.geomag.us[...]
2023-11-00
[48]
웹사이트
OSU Tidal Data Inversion
http://volkov.oce.or[...]
Volkov.oce.orst.edu
2012-06-02
[49]
웹사이트
Dynamic and residual ocean tide analysis for improved GRACE de-aliasing (DAROTA)
http://www.dgfi.tum.[...]
[50]
웹사이트
The Laplace Tidal Equations and Atmospheric Tides
http://kiwi.atmos.co[...]
2017-10-28
[51]
서적
Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences
https://books.google[...]
Johns Hopkins University Press
2003
[52]
서적
A Short Account of the History of Mathematics
http://www.maths.tcd[...]
1908
[53]
서적
An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism
Nottingham
1828
[54]
서적
Mathematical thought from ancient to modern times
https://archive.org/[...]
Oxford University Press
1972
[55]
논문
General principles of the motion of fluids
[56]
서적
A Treatise on Electricity and Magnetism
http://www.aproged.p[...]
1881
[57]
서적
Laplace: Eulogy
https://books.google[...]
Smithsonian Institution
1874
[58]
백과사전
Solar system: origin of the solar system
Encyclopædia Britannica
2001
[59]
논문
The Rise and Fall of Laplacian Physics
https://www.jstor.or[...]
1974
[60]
서적
A History of Optics from Greek Antiquity to the Nineteenth Century
https://books.google[...]
OUP Oxford
2012-01-26
[61]
서적
A history of the theories of aether & electricity
Dover Publications
1989
[62]
서적
Allgemeine geographische Ephemeriden herausgegeben von F. von Zach
Cambridge University Press
1973
[63]
논문
Michell, Laplace and the origin of the Black Hole Concept
http://www.narit.or.[...]
2009
[64]
문서
See Israel (1987), sec. 7.2.
[65]
문서
Gribbin, 299
[66]
문서
Fourier (1829).
[67]
문서
Crosland (1967), p. 1
[68]
웹사이트
Laplace, Pierre-Simon Marquis de – Encyclopedia of Mathematics
https://encyclopedia[...]
2021-06-18
[69]
서적
A Philosophical Essay on Probabilities
John Wiley & Sons
1902
[70]
문서
Stigler, 1975
[71]
서적
A Philosophical Essay
New York
1902
[72]
논문
On the origins and foundations of Laplacian determinism
https://pubmed.ncbi.[...]
2021-02-05
[73]
서적
Ludwig Boltzmann, The Man Who Trusted Atoms
https://archive.org/[...]
Oxford University Press
1998
[74]
서적
(Gillispie (1997))
[75]
서적
2006
[76]
서적
2005
[77]
서적
2005
[78]
서적
A Philosophical Essay
New York
1902
[79]
서적
2005
[80]
서적
A Philosophical Essay
New York
1902
[81]
서적
2005
[82]
서적
A Philosophical Essay
New York
1902
[83]
서적
The Theory of Committees and Elections
Springer Science & Business Media
1987
[84]
서적
Analytical Theory of Democracy. Vols. 1 and 2
Springer
2020
[85]
서적
1997
[86]
서적
Mémoires du docteur F. Antommarchi, ou les derniers momens de Napoléon
https://books.google[...]
Barrois L'Ainé
1825
[87]
서적
Sur l'origine du monde: théories cosmogoniques des anciens et des modernes
Gauthier-Villars
1884
[88]
논문
Les hypothèses cosmogoniques (suite)
http://www.persee.fr[...]
1898
[89]
간행물
Laplace: Eulogy before the French Academy
1874
[90]
서적
A History of Mathematics
American Mathematical Society
1999
[91]
웹사이트
Does God Play Dice?
https://www.hawking.[...]
1999
[92]
서적
The Herschel Chronicle
Cambridge University Press
2013
[93]
뉴스
The Hypothetical Atheist
http://www.commentar[...]
2007-06-18
[94]
서적
Talks of Napoleon at St. Helena with General Baron Gourgaud
A.C. McClurg & Co.
1903
[95]
서적
2005
[96]
서적
Discours et éloges académiques
Gauthier-Villars
1885
[97]
서적
Christianity and the Leaders of Modern Science: A Contribution to the History of Culture in the Nineteenth Century
http://www.ebooksrea[...]
B. Herder
1911
[98]
서적
1981
[99]
서적
Œuvres de Laplace
Gauthier-Villars
1878
[100]
서적
Revolutionaries of the Cosmos: The Astrophysicists
Cambridge University Press
2006
[101]
서적
Principia
1713
[102]
서적
Exposition du système du monde
https://archive.org/[...]
Brussels
1827
[103]
서적
Exposition
1827
[104]
서적
The Leibniz–Clarke Correspondence
Manchester University Press
1956
[105]
서적
The Leibniz–Clarke Correspondence
Manchester University Press
1956
[106]
서적
(제목 없음)
2005
[107]
서적
(제목 없음)
2005
[108]
서적
Pascal
2004
[109]
서적
(제목 없음)
2005
[110]
서적
(제목 없음)
2005
[111]
서적
A budget of paradoxes
Longmans, Green, and co
1872
[112]
서적
(제목 없음)
2005
[113]
서적
Pierre Simon Laplace, 1749–1827: A Determined Scientist
Harvard University Press
2005
[114]
서적
Pierre Simon Laplace, 1749–1827: A Determined Scientist
Harvard University Press
2005
[115]
서적
Mathematics and the Search for Knowledge
Oxford University Press
1986
[116]
서적
Mathematics and the Imagination
Courier Dover Publications
2001
[117]
서적
Comet Lore
Schilling Press, New York
1910
[118]
저널
The Legend of 1P/Halley 1456
[119]
백과사전
Pierre-Simon Laplace
가톨릭 백과사전
[120]
백과사전
Bartolomeo Platina
가톨릭 백과사전
[121]
저널
An Historical Examination of the Connection of Calixtus III with Halley's Comet
http://adsabs.harvar[...]
1910-04
[122]
웹사이트
P.S. de Laplace (1749–1827)
http://www.dwc.knaw.[...]
Royal Netherlands Academy of Arts and Sciences
2015-07-19
[123]
웹사이트
Book of Members, 1780–2010: Chapter L
http://www.amacad.or[...]
American Academy of Arts and Sciences
2014-07-28
[124]
서적
Dictionary of Minor Planet Names
Springer-Verlag
2003
[125]
웹사이트
Awards & Submit Award Nomination
https://signalproces[...]
2016-01-03
[126]
서적
A Philosophical Essay on Probability
1902
[127]
서적
A Philosophical Essay on Probability
1902
[128]
저널
Essai philosophique sur les probabilités
https://books.google[...]
1814
[129]
서적
Des Indes à la planète Mars: étude sur un cas de somnambulisme avec glossolalie
https://books.google[...]
Slatkine
1899
[129]
서적
From India to the Planet Mars: A Study of a Case of Somnambulism
https://books.google[...]
Cosimo, Inc.
2007
[130]
서적
A Philosophical Essay on Probability
1902
[131]
서적
The System of the World
1830
[132]
웹사이트
Laplace's theories of cognitive illusions, heuristics, and biases∗
http://www.stat.colu[...]
unpublished
2021-01-17
[133]
웹사이트
Laplace; Pierre Simon (1749 - 1827); Marquis de Laplace
2012-03-28
[134]
웹사이트
工業の暁文庫「天体力学」
https://www.kanazawa[...]
金沢工業大学
2022-02-13
[135]
문서
미터#정의의 변천
[136]
문서
(제목 없음)
[137]
문서
(제목 없음)
[138]
서적
確率の解析的理論
1812
[139]
저널
Laplace, being Extracts from Lectures delivered by Karl Pearson
https://archive.org/[...]
1929-12
[140]
서적
A Short Account of the History of Mathematics
https://archive.org/[...]
1908
[141]
서적
Mémoires de Sainte Hélène
[142]
서적
Pierre Simon Laplace 1749–1827: A Life in Exact Science
https://archive.org/[...]
Princeton University Press
[143]
저널
The development of the Laplace transform
1981
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com