회로 이론
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
회로 이론은 발전기에서 부하 부품을 거쳐 다시 발전기로 전류가 흐르는 회로를 정의하고, 회로의 정의, 분류, 전원 종류, 회로 해석 방법 등을 다룬다. 회로는 능동 소자의 유무에 따라 능동 회로와 수동 회로로, 선형성에 따라 선형 회로와 비선형 회로로 분류된다. 회로 해석에는 키르히호프의 법칙, 옴의 법칙, 테브난의 정리, 노턴의 정리, 중첩의 원리 등이 활용되며, 등가 회로, 전달 함수, 비선형 회로, 시간 가변 회로, 벡터 회로 이론 등 다양한 개념과 기법이 존재한다.
더 읽어볼만한 페이지
- 회로 이론 - 전압
전압은 두 지점 사이의 전위차로서 단위 전하당 에너지 차이를 나타내며, 정전기학에서는 단위 전하를 이동시키는 데 필요한 일, 회로 이론에서는 노드 간 전위차로 정의되고, 직류 및 교류 전압으로 구분되며, 다양한 방식으로 발생하여 여러 분야에 응용된다. - 회로 이론 - 키르히호프의 전기회로 법칙
키르히호프의 전기회로 법칙은 전기 회로 해석에 사용되는 전류 법칙(KCL)과 전압 법칙(KVL)을 총칭하며, 각각 전하 보존 법칙과 에너지 보존 법칙에 기반하여 회로망 분석에 중요한 역할을 한다. - 전자공학 - 전자전
전자전은 적의 전투 능력을 저하시키기 위해 전자기 에너지를 사용하는 군사 작전이며, 전자 공격, 전자 보호, 전자 지원의 세 가지 영역으로 나뉘어 통신 방해, 레이더 교란, 스텔스 기술 등을 포함한다. - 전자공학 - 옴의 법칙
옴의 법칙은 1827년 게오르크 옴이 발표한, 전압(V)은 전류(I)와 저항(R)의 곱(V=IR)으로 표현되는, 전압, 전류, 저항 간의 관계를 나타내는 기본 법칙이다.
| 회로 이론 | |
|---|---|
| 개요 | |
| 분야 | 전기 회로 |
| 설명 | 전기 네트워크 내의 전압과 전류를 결정하는 데 사용되는 방법 |
| 관련 학문 | 회로 이론 네트워크 이론 |
| 해석 방법 | |
| 기본 법칙 | 옴의 법칙 키르히호프의 회로 법칙 |
| 노드 해석 (마디 해석) | 회로의 각 마디에서의 전압을 구하는 방법 |
| 메시 해석 (망 전류법) | 회로의 각 망에 흐르는 전류를 구하는 방법 |
| 중첩의 원리 | 여러 전원이 있는 회로에서 각 전원에 의한 영향을 개별적으로 계산하여 합산하는 방법 |
| 테브난의 정리 | 복잡한 회로를 전압원과 저항의 직렬 연결로 등가화하는 방법 |
| 노턴의 정리 | 복잡한 회로를 전류원과 저항의 병렬 연결로 등가화하는 방법 |
| 밀만의 정리 | 여러 전압원 또는 전류원이 있는 회로를 하나의 등가 전압원 또는 전류원으로 변환하는 방법 |
| Y-Δ 변환 (Π-T 변환) | Y 또는 Δ 형태로 연결된 저항 네트워크를 등가적인 Δ 또는 Y 네트워크로 변환하는 방법 |
| 소스 변환 | 전압원을 전류원으로, 또는 전류원을 전압원으로 변환하는 방법 |
| 주요 개념 | |
| 회로 요소 | 저항 커패시터 인덕터 전압원 전류원 |
| 임피던스 | 교류 회로에서 전압과 전류의 비율 |
| 어드미턴스 | 임피던스의 역수 |
| 위상 | 교류 신호의 시간적인 위치 |
| 주파수 | 교류 신호의 반복 횟수 |
| 전달 함수 | 입력 신호에 대한 출력 신호의 비율 |
| 보드 선도 | 주파수에 따른 전달 함수의 크기와 위상을 나타내는 그래프 |
| 안정성 | 회로가 정상적으로 동작하는지 여부 |
| 응용 분야 | |
| 전기 회로 설계 | 다양한 전기 회로의 동작을 분석하고 설계하는 데 사용 |
| 전자 회로 설계 | 트랜지스터, 다이오드, 연산 증폭기 등의 전자 부품을 포함하는 회로 분석 및 설계 |
| 전력 시스템 | 전력망의 안정성을 분석하고 제어하는 데 사용 |
| 통신 시스템 | 신호 전송 회로의 성능을 분석하고 최적화하는 데 사용 |
| 제어 시스템 | 제어 회로의 동작을 분석하고 설계하는 데 사용 |
| 관련 이론 | |
| 선형 회로 | 회로 요소의 특성이 선형적인 회로 |
| 비선형 회로 | 회로 요소의 특성이 비선형적인 회로 |
| 시불변 시스템 | 시간에 따라 회로 특성이 변하지 않는 회로 |
| 선형 시불변 시스템 | 선형 회로이면서 시불변 시스템인 회로 |
| 기타 | |
| 관련 도구 | 회로 시뮬레이터 (SPICE, LTspice 등) 계산기 오실로스코프 함수 발생기 멀티미터 |
2. 회로의 정의 및 구성 요소
| 용어 | 설명 |
|---|---|
| 부품 | 전류가 흘러 들어가거나 나올 수 있는 두 개 이상의 단자를 가진 장치이다. |
| 노드 | 두 개 이상의 부품 단자가 연결된 지점을 말한다. 실제적으로 저항이 0인 도체는 분석을 위해 노드로 간주될 수 있다. |
| 분기 | 두 노드를 연결하는 부품 또는 부품들의 집합이다. |
| 메시 | 네트워크 내에서, 내부에 다른 루프를 포함하지 않으면서 완전한 루프를 형성하는 분기들의 그룹이다. |
| 포트 | 한쪽 단자로 들어가는 전류가 다른 쪽 단자로 나가는 전류와 동일한 한 쌍의 단자를 의미한다. |
| 회로 | 발전기의 한 단자에서 시작하여 부하 부품들을 거쳐 다른 단자로 전류가 다시 흘러 들어가는 경로를 말한다. 이런 의미에서 회로는 분석하기 쉬운 1-포트 네트워크이다. 만약 다른 회로와의 연결이 있다면, 이는 더 복잡한 네트워크를 형성하며 최소 두 개 이상의 포트가 필요하다. 종종 회로와 네트워크라는 용어는 혼용되지만, 일부 분석가들은 네트워크를 이상적인 부품으로 구성된 이론적 모델을 지칭하는 데 사용하기도 한다.[1] |
| 전달 함수 | 두 포트 사이의 전류 및/또는 전압 관계를 나타내는 함수이다. 주로 입력 포트와 출력 포트 사이의 관계를 설명하며, 이득이나 감쇠로 표현된다. |
| 부품 전달 함수 | 두 개의 단자를 가진 부품(즉, 1-포트 부품)의 경우, 전류와 전압을 각각 입력과 출력으로 간주하여 전달 함수를 정의할 수 있다. 이 전달 함수는 임피던스 또는 어드미턴스의 단위를 가진다 (전압과 전류 중 어느 것을 입력으로 볼지는 편의에 따라 결정된다). 세 개 이상의 단자를 가진 부품은 실제로는 두 개 이상의 포트를 가지며, 이 경우 전달 함수는 단일 임피던스로 표현하기 어렵다. 일반적인 접근 방식은 전달 함수를 매개변수 행렬로 나타내는 것이다. 이 매개변수들은 임피던스일 수도 있지만, 다른 여러 방식(2-포트 네트워크)도 사용된다. |
회로는 구성 요소의 종류나 특성에 따라 여러 방식으로 분류할 수 있다. 주요 분류 기준은 다음과 같다.
3. 회로의 분류
3. 1. 능동/수동 소자 유무에 따른 분류
3. 2. 선형성(Linearity)에 따른 분류
4. 전원의 종류
회로 이론에서 사용되는 전원은 크게 독립 전원(Independent Source)과 종속 전원(Dependent Source)으로 나눌 수 있다.
4. 1. 독립 전원 (Independent Source)
이상적인 독립 전원은 정해진 규칙에 따라 전압이나 전류를 일정하게 유지하는 전원이다. 이는 회로 내 다른 소자들의 영향을 받지 않는다는 특징을 가진다. 대표적인 예로는 직류(DC) 전원이나 교류(AC) 전원 중 사인파 형태를 가지는 전원 등이 있다.4. 2. 종속 전원 (Dependent Source)
종속 전원(Dependent Source)은 회로의 다른 부분에 있는 전압이나 전류 값에 따라 자신의 출력 전압이나 전류 값이 결정되는 전원이다. 즉, 회로 내 다른 요소의 상태에 의존하여 동작하는 전압원 또는 전류원을 의미한다.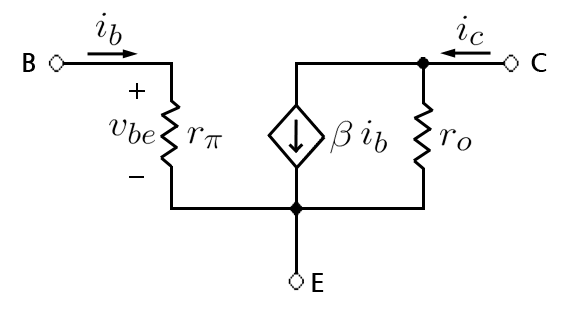
(그림 1)은 접합형 트랜지스터(BJT)의 저주파수 hybrid-pi 모델을 보여주는 예시이다. 이 모델에서 컬렉터(collector)에 흐르는 전류 는 베이스(base)에 흐르는 전류 에 의해 제어된다. 이처럼 회로의 다른 부분(베이스 전류 )에 의해 그 값이 결정되는 전류원()을 종속 전류원이라고 한다.
종속 전원은 제어하는 변수(전압 또는 전류)와 출력되는 변수(전압 또는 전류)의 조합에 따라 다음과 같이 네 가지 종류로 나눌 수 있다.
| 종류 | 설명 | 수식 |
|---|---|---|
| 전압 제어 전압원 (VCVS, Voltage-Controlled Voltage Source) | 특정 위치의 전압 에 의해 제어되는 전압원 | |
| 전압 제어 전류원 (VCCS, Voltage-Controlled Current Source) | 특정 위치의 전압 에 의해 제어되는 전류원 | |
| 전류 제어 전류원 (CCCS, Current-Controlled Current Source) | 특정 위치의 전류 에 의해 제어되는 전류원 | |
| 전류 제어 전압원 (CCVS, Current-Controlled Voltage Source) | 특정 위치의 전류 에 의해 제어되는 전압원 |
접합형 트랜지스터(BJT)는 전류 제어 전류원(CCCS)의 대표적인 예시이다. BJT를 모델링할 때, 베이스 전류()와 컬렉터 전류()의 관계를 CCCS 형태로 표현한다. 제어 신호가 전류라는 것은 입력이 전류 기준이라는 의미이다. 회로는 옴의 법칙을 만족해야 하므로, 입력 전류는 입력 임피던스에 따라 입력 전압을 결정하게 된다. 입력단에서는 전압과 전류가 함께 존재하지만, 제어의 관점에서 보면 입력 전류()에 따라서만 출력 전류()가 선형적인 배수() 또는 특정 공식에 따라 결정된다는 의미이다. (그림 1)의 BJT 모델에서, 컬렉터 전류 는 베이스 전류 의 배만큼 흐르게 된다 (). 즉, 를 기준으로 출력 전류 가 결정되어 공식으로 표현할 수 있다. 물론 이때 베이스 전압 는 베이스 입력 저항 (또는 )에 의해 로 결정될 것이다.
4. 3. 전원, 부하, 싱크 (Source, Load and Sink)
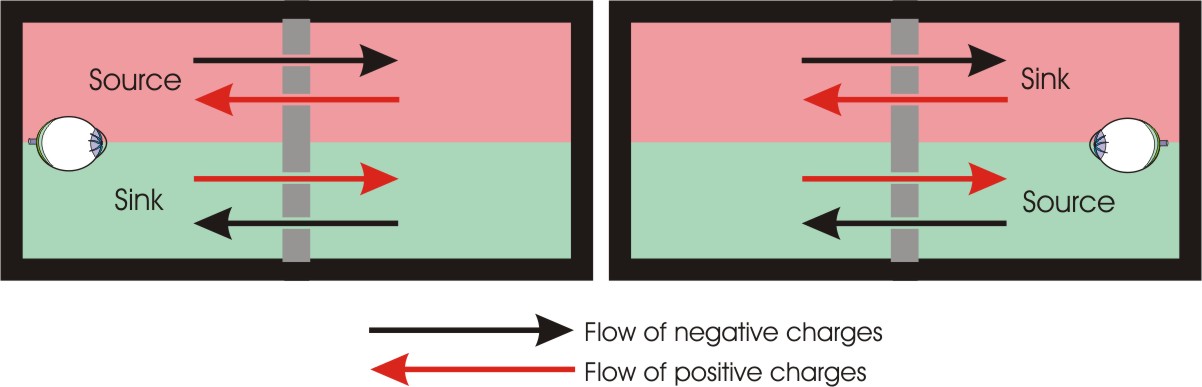
소스(Source)는 전원에서 전류가 흘러 나오는 것을 의미한다. 대표적인 예로 축전지가 있다. 회로 입장에서 보면 축전지에서는 전류가 흘러나온다. 하지만 소스인지 싱크(Sink)인지는 관점에 따라 결정된다. 예를 들어, 특정 회로(원본 소스에 언급된 그림 1은 제공되지 않음)에서 콜렉터(C) 단자를 기준으로 보면, 전류를 소모하는 역할을 하므로 전류 싱크가 될 수 있다.
소스는 목적 회로에 전력을 공급하는 개념이며, 목적 회로 입장에서는 전력을 받아 사용하는 것이다. 반대로 싱크는 목적 대상에서 전력을 만들어 싱크 쪽으로 흘려보내는 개념이다. 즉, 관찰 대상인 목적 회로에서 전력을 만들어 공급해야 하는 상황을 의미하며, 이는 보통 목적 회로 내 어딘가에 다른 소스가 존재함을 뜻한다 (에너지 보존법칙). 예를 들어, BJT의 이미터 공통 회로에서는 콜렉터 쪽에 외부 전원 소스가 연결되어 전력을 공급한다.

TTL(Transistor-Transistor Logic) 회로에서도 소스와 싱크 개념을 볼 수 있다. (그림 3)은 간단한 NAND 게이트의 출력 부분을 보여준다. NAND 게이트는 입력 A와 B가 모두 1일 때만 출력 Q가 0이 된다. 논리 0 상태는 전압이 근처를 유지해야 하므로, 출력 쪽 BJT(그림 3의 오른쪽 아래 BJT)가 포화 상태가 된다. 이때 출력 단자 Q에서 보면, 이 BJT는 전류 싱크로 작동한다. 즉, 를 유지하기 위해 출력 저항(그림 3의 오른쪽 저항)을 통해 흐르는 전류와 다음 게이트 입력 상태에 따라 흘러 들어오는 전류를 모두 출력 BJT가 흡수하는 것이다. 이러한 동작을 정확히 해석하기 위해서는 BJT를 하이브리드- 모델로 변환해야 한다.
회로를 해석할 때 소스냐 싱크냐는 본질적으로 부호의 문제이다. 해석 기준에 따라 전류 또는 전압의 방향을 정하고, 그에 맞춰 + 또는 - 기호를 적용하면 된다.
5. 회로 이론 및 해석
회로 이론 및 해석을 위해 사용되는 기본적인 용어들은 다음과 같다.
| 용어 | 설명 |
|---|---|
| 부품 | 전류가 흘러 들어가거나 나올 수 있는 두 개 이상의 단자를 가진 장치. |
| 노드 | 두 개 이상의 부품의 단자가 연결된 지점. 실질적으로 0의 저항을 가진 도체는 분석 목적으로 노드로 간주된다. |
| 분기(Branch) | 두 노드를 연결하는 부품(들). |
| 메시 | 내부에 다른 루프가 없는 완전한 루프를 형성하도록 연결된 네트워크 내의 분기 그룹. |
| 포트 | 한쪽으로 들어가는 전류가 다른 쪽으로 나가는 전류와 동일한 두 개의 단자. |
| 회로 | 발전기의 한 단자에서 부하 부품을 거쳐 다른 단자로 다시 흐르는 전류. 이러한 의미에서 회로는 1-포트 네트워크이며 분석하기 쉬운 경우이다. 다른 회로에 연결이 있으면 복잡한 네트워크가 형성되고 최소한 두 개의 포트가 존재해야 한다. 종종 "회로"와 "네트워크"는 상호 교환적으로 사용되지만, 많은 분석가들은 "네트워크"를 이상적인 부품으로 구성된 이상적인 모델을 의미하는 데 사용한다.[1] |
회로 분석에서는 다음과 같은 개념도 중요하다.
- '''전달 함수''': 두 포트 사이의 전류 및/또는 전압 관계. 가장 흔하게, 입력 포트와 출력 포트에 대해 논의되며, 전달 함수는 이득 또는 감쇠로 설명된다.
- '''부품 전달 함수''': 두 단자 부품(즉, 1-포트 부품)의 경우, 전류와 전압이 입력 및 출력으로 간주되며, 전달 함수는 임피던스 또는 어드미턴스 단위를 갖는다(전압 또는 전류 중 어느 것을 입력으로 간주하는지는 주로 편의에 따라 임의로 결정된다). 세 개(또는 그 이상)의 단자 부품은 실제로 두 개(또는 그 이상)의 포트를 가지며, 전달 함수는 단일 임피던스로 표현될 수 없다. 일반적인 접근 방식은 전달 함수를 매개변수 행렬로 표현하는 것이다. 이러한 매개변수는 임피던스일 수 있지만, 다른 많은 접근 방식이 있다(2-포트 네트워크 참조).
5. 1. 기본 법칙
- 키르히호프의 전류법칙 (Kirchhoff's current law): 특정 노드에 들어오는 전류의 합은 0이다. 이는 에너지 보존 법칙과 연관된다.
- 키르히호프의 전압법칙 (Kirchhoff's voltage law): 폐쇄 루프의 전압 총합은 0이다.
- 옴의 법칙 (Ohm's law): 저항 양단의 전압은 저항값과 전류의 곱과 같다.
- 노턴의 정리 (Norton's theorem): 전압원, 전류원 및 저항으로 이루어진 선형 회로망은 이상적인 하나의 전류원과 병렬로 연결된 하나의 저항으로 변환할 수 있다.
- 테브난의 정리 (Thévenin's theorem): 전압원, 전류원 및 저항으로 이루어진 선형 회로망은 하나의 전압원과 직렬로 연결된 하나의 저항으로 변환할 수 있다.
- 중첩 원리 (Superposition principle): 선형 회로망에서 모든 전원이 함께 작동할 때의 해석 결과는, 각 전원이 개별적으로 작동할 때의 해석 결과를 모두 합한 것과 같다. 회로를 해석할 때, 하나의 전원만 남기고 나머지 전원은 0으로 만들어(전압원은 단락, 전류원은 개방) 해석한다. 이렇게 각 전원에 대해 얻은 결과들을 합하면 모든 전원이 동작할 때의 최종 결과를 얻을 수 있다.
전압 분배직렬로 연결된 n개의 임피던스를 고려해 보자. 임피던스 에 걸리는 전압 는 다음과 같다.
:
노드 해석회로 이론에서 노드 해석은 노드 전압의 개념을 사용하며, 노드 전압을 미지 변수로 간주한다. 모든 노드에 대해, 선택된 기준 노드를 제외하고, 노드 전압은 해당 노드에서 기준 노드까지의 전압 강하로 정의된다. 따라서, N개의 노드가 있는 회로에는 N-1개의 노드 전압이 존재한다.
원칙적으로, 노드 해석은 키르히호프의 전류 법칙 (KCL)을 N-1개의 노드에 적용하여 N-1개의 독립 방정식을 얻는다. KCL로 생성된 방정식은 노드 안팎으로 흐르는 전류에 관한 것이므로, 이러한 전류의 값이 알려져 있지 않다면, 미지 변수(노드 전압)로 표현해야 한다. 저항 및 커패시터와 같은 일부 소자의 경우, 소자 전류를 노드 전압으로 나타내는 것은 매우 쉽다.
독립 전압원이 있는 회로와 같이 이것이 어려운 경우, 수퍼노드(supernode)와 같은 특수한 방법이 사용된다.
# 회로의 모든 '''노드'''에 레이블을 붙인다. 임의의 노드를 기준 노드로 선택한다.
# 나머지 모든 노드에서 기준 노드로 가는 전압 변수를 정의한다. 이 전압 변수는 기준 노드를 기준으로 전압 상승으로 정의되어야 한다.
# 기준 노드를 제외한 모든 노드에 대해 KCL 방정식을 작성한다.
# 결과 방정식 시스템을 푼다.
망 해석메시 (Mesh)는 내부 루프를 포함하지 않는 루프를 의미한다.
# 회로의 "창문"(독립적인 폐루프) 개수를 센다. 각 창문에 메시 전류를 할당한다.
# 전류가 알려지지 않은 모든 메시에 대해 키르히호프의 전압 법칙 (KVL) 방정식을 작성한다.
# 결과 방정식을 푼다.
5. 2. 회로망 방정식 설정 방법
주어진 회로망에 대한 방정식을 설정하는 방법에는 다음 세 가지가 있다[8]。- 가지 전류법
- 폐로 전류법 (망목 전류법, 임피던스법)
- 절점 전위법 (어드미턴스법)
각 방법은 미지수로 두는 것이 다르다. 절점 수가 n개, 가지 수가 b개, 기본 폐로의 수가 l개인 회로망에서 필요한 방정식의 수는 다음과 같다[8]。
- 가지 전류법: (n-1) + l = b 개
- 폐로 전류법: l = b - n + 1 개
- 절점 전위법: n - 1 개
5. 3. 회로 해석 기법
회로를 해석하는 데 사용되는 기본적인 법칙과 정리는 다음과 같다.- 키르히호프의 전류 법칙 (Kirchhoff's current law, KCL): 특정 노드에 들어오거나 나가는 전류의 대수 합은 0이다. 이는 전하량 보존 법칙과 관련이 있다.
- 키르히호프의 전압 법칙 (Kirchhoff's voltage law, KVL): 임의의 닫힌 회로 루프를 따라 전압 상승과 강하의 대수 합은 0이다. 이는 에너지 보존 법칙과 관련이 있다.
- 옴의 법칙 (Ohm's law): 저항 양단의 전압은 저항값과 저항을 통해 흐르는 전류의 곱과 같다. ()
- 노턴의 정리 (Norton's theorem): 전압원, 전류원 및 저항으로 구성된 선형 회로망은 등가적으로 하나의 이상적인 전류원과 병렬로 연결된 하나의 저항으로 변환할 수 있다.
- 테브난의 정리 (Thévenin's theorem): 전압원, 전류원 및 저항으로 구성된 선형 회로망은 등가적으로 하나의 이상적인 전압원과 직렬로 연결된 하나의 저항으로 변환할 수 있다.
- 중첩 원리 (Superposition principle): 선형 회로망에서 여러 독립 전원이 있을 때, 특정 소자에 흐르는 전류나 걸리는 전압은 각 독립 전원이 개별적으로 작용할 때의 전류 또는 전압의 합과 같다. 해석 시, 하나의 전원만 남기고 나머지 전압원은 단락(short)시키고 전류원은 개방(open)하여 계산한 후, 각 결과를 합산한다.
주요 해석 기법=== 노드 해석법 ===
노드 해석은 회로의 각 노드 전압을 미지 변수로 사용하여 회로를 해석하는 방법이다. 기준 노드를 하나 정하고, 나머지 노드들에 대해 기준 노드 대비 전압을 정의한다. N개의 노드가 있는 회로에는 N-1개의 노드 전압이 존재한다.
노드 해석은 기본적으로 키르히호프의 전류 법칙(KCL)을 기준 노드를 제외한 모든 노드(N-1개)에 적용하여 N-1개의 독립적인 방정식을 세우는 방식으로 진행된다. 각 노드에 연결된 소자를 통해 흐르는 전류를 노드 전압으로 표현하여 방정식을 완성한다. 만약 회로 내에 독립 전압원이 존재하면, 수퍼노드(supernode) 개념을 도입하여 해석하기도 한다.
노드 해석 절차는 다음과 같다.
# 회로의 모든 '''노드'''를 식별하고 표시한다. 임의의 노드를 기준 노드(보통 접지)로 선택한다.
# 기준 노드를 제외한 나머지 모든 노드에 대해, 기준 노드로부터 해당 노드까지의 전압 변수(노드 전압)를 정의한다.
# 기준 노드를 제외한 모든 노드에 대해 KCL 방정식을 작성한다. 이때 각 전류는 노드 전압과 소자 값(저항, 커패시턴스 등)으로 표현한다.
# 얻어진 연립 방정식을 풀어 각 노드 전압을 구한다.
=== 메시 해석법 ===
메시 해석은 회로 내의 독립적인 폐쇄 루프, 즉 메시(mesh)에 가상의 메시 전류를 설정하고, 각 메시에 키르히호프의 전압 법칙(KVL)을 적용하여 회로를 해석하는 방법이다. 메시는 내부에 다른 루프를 포함하지 않는 가장 작은 루프를 의미한다.
메시 해석 절차는 다음과 같다.
# 회로에서 독립적인 메시(내부 루프를 포함하지 않는 루프)의 수를 파악한다. 각 메시에 시계 방향 또는 반시계 방향으로 메시 전류를 할당한다.
# 전류 값이 이미 알려진 메시(예: 전류원이 포함된 메시)를 제외한 모든 메시에 대해 KVL 방정식을 작성한다. 이때 각 소자에 걸리는 전압은 메시 전류와 소자 값으로 표현한다.
# 얻어진 연립 방정식을 풀어 각 메시 전류를 구한다.
=== 중첩 정리 ===
중첩 정리는 선형 회로에서 여러 개의 독립 전원이 있을 때, 각 전원의 영향을 개별적으로 계산하여 합산하는 방법이다. 하나의 전원만 고려할 때, 다른 전압원은 단락시키고 전류원은 개방시킨다. 이렇게 각 전원에 대해 개별적으로 계산된 특정 지점의 전류 또는 전압 값을 모두 더하면, 모든 전원이 함께 동작할 때의 실제 전류 또는 전압 값을 얻을 수 있다.
이 방법은 회로 소자가 선형적(전압과 전류 관계가 비례)이라는 가정 하에 성립한다. 따라서 다이오드나 트랜지스터와 같은 비선형 소자가 포함된 회로에는 적용할 수 없다.[2] 또한, 전력 계산에는 중첩 원리를 직접 적용할 수 없다. 전력은 전압이나 전류의 제곱에 비례하므로(), 각 전원에 의한 전력을 단순히 합산하면 실제 총 전력과 달라진다. 총 전력을 구하려면 중첩 원리를 이용해 총 전압과 총 전류를 먼저 구한 뒤, 이 값들을 이용하여 전력을 계산해야 한다.
해석 방법의 선택어떤 해석 방법을 사용할지는 회로의 특성과 구하고자 하는 값에 따라 달라질 수 있으며, 분석가의 선호도에 따라 선택되기도 한다.[3] 회로가 단순하거나 특정 부분의 전압 또는 전류만 필요하다면, 복잡한 체계적 방법 대신 간단한 등가 회로 변환 등을 통해 답을 얻을 수도 있다. 주요 해석 기법의 특징은 다음과 같다.
| 기법 | 주요 원리 | 미지수 | 적용 제약 | 장점 | 단점 |
|---|---|---|---|---|---|
| 노드 해석 | 키르히호프의 전류 법칙 (KCL) | 노드 전압 (노드 수 - 1) | 없음 | 모든 회로에 적용 가능, 체계적 | 전압원이 많으면 수퍼노드 등 추가 개념 필요 |
| 메시 해석 | 키르히호프의 전압 법칙 (KVL) | 메시 전류 (메시 수) | 평면 회로에만 적용 가능[3] | 전류 계산에 유용, 체계적 | 비평면 회로 적용 불가, 전류원이 있으면 복잡해질 수 있음 |
| 중첩 | 각 전원의 개별 효과 합산 | - | 선형 회로에만 적용 가능, 전력 계산 직접 불가[2] | 개념적으로 단순 | 회로가 복잡하거나 전원이 많으면 계산량 증가 |
- 유효 매질 근사: 매우 많은 저항 소자가 무작위로 연결된 고밀도 회로의 경우, 개별 소자에 대한 정확한 해를 구하기 어려울 때 사용된다. 회로의 전체적인 그래프 구조와 기하학적 특성을 이용하여 등가적인 저항이나 전류 분포를 모델링한다.[4]
어떤 회로망이 주어졌을 때, 그 회로망에 대한 방정식을 설정하는 방법에는 크게 세 가지 접근법이 있다.[8]
# 가지 전류법: 각 가지(branch)에 흐르는 전류를 미지수로 설정한다. 필요한 방정식의 수는 가지 수(b)와 같다.
# 폐로 전류법 (망목 전류법, 임피던스법): 메시 해석과 유사하며, 독립적인 폐회로에 흐르는 전류를 미지수로 설정한다. 필요한 방정식의 수는 독립 루프의 수(l = b - n + 1)와 같다. (n: 노드 수)
# 절점 전위법 (노드 해석법, 어드미턴스법): 노드 해석과 같으며, 각 노드의 전위를 미지수로 설정한다. 필요한 방정식의 수는 (n - 1)이다.[8]
6. 등가 회로 (Equivalent Circuits)
회로 분석에서 유용한 절차 중 하나는 부품 수를 줄여 네트워크를 단순화하는 것이다. 이는 물리적 부품을 동일한 효과를 갖는 다른 가상 부품으로 대체하여 수행할 수 있다.
두 회로가 한 쌍의 단자에 대해 단자 간의 전압과 단자를 통과하는 전류가 다른 네트워크의 단자에서 전압 및 전류와 동일한 관계를 갖는 경우 '''등가'''라고 한다.
구체적으로 1포트 네트워크의 경우, 단자 ab와 xy에 대해 회로 1과 회로 2가 등가라는 것은, V1의 모든 값에 대해 V2=V1일 때 I2=I1임을 의미한다.
포트가 두 개 이상인 경우, 모든 해당 포트 쌍 간의 전류와 전압이 동일한 관계를 가져야 한다. 예를 들어, 스타(Y) 및 델타(Δ) 네트워크는 효과적으로 3포트 네트워크이며, 이들 간의 등가 변환은 회로 분석에 유용하게 사용된다.
회로를 단순화하는 구체적인 방법으로는 임피던스의 직렬 및 병렬 연결, Y-Δ 변환, 전원 변환 등이 있다. 이러한 기법들은 회로를 더 다루기 쉬운 형태로 만들어 분석을 용이하게 한다.
이러한 등가 회로 개념과 분석 원리는 저항기, 이상적인 전류원, 이상적인 전압원만 포함하는 저항 회로나 직류 회로뿐만 아니라, AC 회로의 페이저 분석에도 동일하게 적용된다. 회로 분석의 목표는 결국 회로에 존재하는 전압과 전류를 구하는 것이다.
6. 1. 임피던스(Impedance)의 직/병렬 연결
회로를 분석할 때, 여러 개의 임피던스를 하나의 등가 임피던스로 대체하여 회로를 단순화하는 경우가 많다. 임피던스는 직렬 또는 병렬로 연결될 수 있으며, 각 연결 방식에 따라 전체 등가 임피던스를 계산하는 방법이 다르다.직렬 연결여러 개의 임피던스가 직렬로 연결된 경우, 전체 등가 임피던스 는 각 임피던스의 합과 같다.
직렬로 연결된 임피던스들에는 동일한 전류가 흐른다. 각 임피던스에 걸리는 전압은 전압 분배 법칙에 따라 나뉜다. 임피던스 에 걸리는 전압 는 다음과 같이 계산할 수 있다.
여기서 는 직렬 회로 전체에 걸리는 전압이고, 는 회로에 흐르는 전류이다.
병렬 연결여러 개의 임피던스가 병렬로 연결된 경우, 전체 등가 임피던스 의 역수는 각 임피던스의 역수(어드미턴스)의 합과 같다.
특히 두 개의 임피던스 과 가 병렬로 연결된 경우, 등가 임피던스는 다음과 같이 간단하게 표현할 수 있다.
병렬로 연결된 임피던스들에는 동일한 전압이 걸린다. 전체 전류는 전류 분배 법칙에 따라 각 임피던스로 나뉘어 흐른다. 어드미턴스 를 사용하여 임피던스 (어드미턴스 )를 통과하는 전류 를 계산하면 다음과 같다.
여기서 는 병렬 회로 전체에 흐르는 전류이고, 는 회로 양단에 걸리는 전압이다.
두 개의 임피던스 과 가 병렬로 연결된 경우, 각 임피던스를 흐르는 전류는 다음과 같이 계산할 수도 있다.
6. 2. Y-Δ 변환 (Y-Δ Transformation)
두 개 이상의 단자를 가진 임피던스 네트워크는 단일 임피던스 등가 회로로 간단히 축소할 수 없다. n개의 단자를 가진 네트워크는 기껏해야 n개의 임피던스로 축소될 수 있으며, 최악의 경우 개의 임피던스가 필요할 수 있다. 특히 3단자 네트워크의 경우, 세 개의 임피던스는 3개의 노드를 가진 델타(Δ) 네트워크 또는 4개의 노드를 가진 스타(Y) 네트워크로 표현될 수 있다. 이 두 네트워크는 서로 등가이며, 그들 사이의 변환 공식은 아래와 같다. 임의의 노드 수를 가진 일반적인 네트워크는 단순히 직렬 및 병렬 조합만으로는 최소 임피던스 수로 축소할 수 없는 경우가 많다. 이런 경우 Y-Δ 변환 및 Δ-Y 변환을 함께 사용해야 한다. 일부 복잡한 네트워크에서는 Y-Δ 변환을 스타-다각형 변환으로 확장하는 것이 필요할 수도 있다.
두 네트워크가 등가이기 위해서는, 어떤 단자 쌍 사이의 임피던스라도 두 네트워크 모두에서 동일해야 한다. 이를 통해 세 개의 연립 방정식을 얻을 수 있다. 아래 방정식은 저항으로 표현되었지만, 일반적인 임피던스를 사용하는 경우에도 동일하게 적용된다.
=== Δ에서 Y로 변환 ===
=== Y에서 Δ로 변환 ===
=== 일반적인 네트워크 노드 제거 ===
스타-델타 변환과 직렬 저항 변환은 일반적인 저항 네트워크 노드 제거 알고리즘의 특별한 경우로 볼 수 있다. N개의 저항 으로 노드 에 연결된 공통 노드는, 나머지 N개 노드를 서로 연결하는 개의 저항으로 대체될 수 있다. 임의의 두 노드 x, y 사이의 저항은 다음과 같이 주어진다.
- 스타-델타 변환 (): 이 경우 위 공식은 Y에서 Δ로 변환하는 공식과 동일하게 축소된다.
- 직렬 저항 변환 (): 두 저항이 직렬로 연결된 경우와 동일하다.
- 매달린 저항 제거 (): 하나의 저항만 연결된 경우, 이므로 해당 노드와 저항은 제거된다.
6. 3. 전원 변환 (Source Transformation)

회로 분석에서 회로를 더 간단하게 만들기 위해 부품 수를 줄이는 것은 유용한 방법이다. 이는 실제 부품을 동일한 효과를 내는 가상의 부품으로 바꾸는 방식으로 이루어진다. 예를 들어, 내부 임피던스를 가진 전원(비이상적인 전원)은 이상적인 전압원과 직렬 임피던스 또는 이상적인 전류원과 병렬 임피던스로 표현될 수 있다. 이 두 형태는 서로 등가이며 변환이 가능하다. 이를 전원 변환이라고 한다.
두 회로가 한 쌍의 단자(예: 단자 ab)에 대해 서로 등가라는 것은, 한 회로의 단자 사이 전압과 단자를 통과하는 전류의 관계가 다른 회로의 단자 전압 및 전류 관계와 동일하다는 것을 의미한다. 즉, 어떤 전압 에 대해 전류 이 흐를 때, 등가 회로에서도 같은 전압 에 대해 동일한 전류 이 흐른다면 두 회로는 등가이다. 이는 1포트 네트워크에 대한 정의이다.
내부 저항 R을 가진 전압원 와 내부 저항 R을 가진 전류원 사이의 변환 관계는 다음과 같다. 두 회로가 단자 ab에 대해 등가라면, 단자에 걸리는 전압 와 흐르는 전류 는 두 회로 모두에서 동일해야 한다. 따라서 다음 관계가 성립한다.
: 또는
이러한 전원 변환은 노턴의 정리와 테브난의 정리와 밀접한 관련이 있다.
- 노턴의 정리는 임의의 2단자 선형 회로망을 이상적인 전류원과 병렬 임피던스로 변환할 수 있음을 보여준다.
- 테브난의 정리는 임의의 2단자 선형 회로망을 이상적인 전압원과 직렬 임피던스로 변환할 수 있음을 보여준다.
전원 변환은 이러한 정리를 활용하여 회로를 더 간단한 형태로 바꾸어 분석을 용이하게 하는 데 사용된다.
7. 전달 함수 (Transfer Function)
전달 함수는 회로망의 입력과 출력 사이의 관계를 나타내는 중요한 개념이다. 단순히 저항만으로 구성된 회로망에서는 전달 함수가 실수 또는 실수로 계산되는 수식으로 표현된다. 이는 저항성 회로망이 여러 개의 대수 방정식을 함께 푸는 시스템으로 표현되기 때문이다.
하지만 인덕터나 캐패시터를 포함하는 일반적인 선형 회로망은 여러 개의 선형 미분 방정식 시스템으로 표현된다. 회로망 분석에서는 이러한 미분 방정식을 직접 다루기보다 라플라스 변환을 먼저 적용하는 것이 일반적이다. 변환된 결과는 라플라스 파라미터 's' (일반적으로 복소수)를 사용하여 표현하는데, 이를 s-영역(s-domain)에서 작업한다고 말한다. 반면, 미분 방정식을 직접 사용하는 것은 시간에 따라 변하는 값을 다루므로 시간 영역(t-domain) 또는 t-영역에서 작업한다고 한다. 라플라스 변환은 이 두 영역 사이를 변환하는 수학적인 도구이다.
이러한 접근 방식은 제어 이론에서 표준적으로 사용되며, 예를 들어 피드백이 있는 증폭기 시스템의 안정성을 판단하는 데 유용하다.
두 개의 단자를 가진 소자, 또는 더 일반적으로 비선형 소자의 경우, 구성 방정식은 소자에 입력되는 전류와 그 결과로 나타나는 전압 사이의 관계를 설명한다. 이때 전달 함수 Z(s)는 임피던스 단위를 가지며, 단위는 옴(Ω)이다. 전기 회로에서 흔히 사용되는 세 가지 수동 소자(저항, 인덕터, 캐패시터)의 전달 함수(임피던스)는 s-영역에서 다음과 같이 표현된다.
| 소자 | 전달 함수 Z(s) |
|---|---|
| 저항 (Resistor) | |
| 인덕터 (Inductor) | |
| 캐패시터 (Capacitor) |
회로에 정상 상태의 교류(AC) 신호만 가해지는 경우, s를 ''jω'' (여기서 j는 허수 단위, ω는 각주파수)로 대체하면 교류 회로 이론에서 더 익숙한 형태의 임피던스 값을 얻을 수 있다.
| 소자 | 전달 함수 Z(jω) |
|---|---|
| 저항 | |
| 인덕터 | |
| 캐패시터 |
마지막으로, 정상 상태의 직류(DC) 신호만 가해지는 경우, s를 0으로 대체하면 직류 회로 이론이 적용된다. 이때 인덕터는 단락(short circuit) 상태처럼 동작하고(임피던스 0), 캐패시터는 개방(open circuit) 상태처럼 동작한다(임피던스 무한대).
| 소자 | 전달 함수 Z (DC) |
|---|---|
| 저항 | |
| 인덕터 | (단락) |
| 캐패시터 | (개방) |
일반적으로 제어 이론에서는 전달 함수를 기호 H(s)로 표시한다. 전자 공학에서는 주로 입력 전압에 대한 출력 전압의 비율로 정의하며, 기호 A(s) 또는 (주로 정현파 응답을 분석하므로) ''A''(''jω'')로 표시한다.
여기서 ''A''는 문맥에 따라 감쇠(attenuation) 또는 증폭(amplification)을 의미한다. 일반적으로 ''A''(''jω'')는 네트워크의 임피던스와 개별 전달 함수 분석을 통해 유도될 수 있는 ''jω''에 대한 복소 함수이다. 때로는 이득의 크기만 중요하고 위상각은 중요하지 않을 수 있는데, 이 경우 전달 함수에서 복소수 부분을 제외하고 다음과 같이 크기만 나타낼 수 있다.
=== 2포트 회로 ===
2포트 회로(Two-port network) 개념은 회로 분석에서 블랙 박스 접근 방식을 사용할 때 유용하다. 2포트 회로의 동작은 내부 구조를 몰라도 더 큰 회로 내에서 완전히 특성화될 수 있다. 하지만 이를 위해서는 위에서 설명한 ''A''(''jω'') 이상의 정보가 필요하다. 2포트 회로를 완전히 특성화하려면 4개의 파라미터가 필요하다. 예를 들어, 순방향 전달 함수, 입력 임피던스, 역방향 전달 함수(출력에 전압이 가해질 때 입력에 나타나는 전압), 출력 임피던스가 될 수 있다. 이 외에도 다양한 파라미터 조합이 있으며, 네 개의 파라미터를 모두 임피던스로 표현하는 방식도 있다. 일반적으로 이 네 파라미터는 행렬로 표현된다.
이 행렬은 대표 요소로 또는 간단히 로 축약하여 나타낼 수 있다.
이러한 개념은 2개 이상의 포트를 가진 네트워크로 확장될 수 있지만, 실제로는 많은 경우 포트가 순수한 입력 또는 순수한 출력으로 간주되기 때문에 잘 사용되지 않는다. 역방향 전달 함수를 무시할 수 있다면, 다중 포트 네트워크는 여러 개의 2포트 네트워크로 분해될 수 있다.
네트워크가 개별적인 소자들로 구성된 경우, 2포트 네트워크 분석은 필수적이지 않으며, 개별 소자의 전달 함수를 사용하여 분석할 수도 있다. 그러나 네트워크가 분산 소자 모델(Distributed-element model)을 포함하는 경우, 예를 들어 전송선로(Transmission line)와 같이 개별 소자가 명확히 구분되지 않는 경우에는 개별 소자 분석이 불가능하다. 이런 경우 가장 일반적인 접근 방식은 해당 부분을 2포트 네트워크로 모델링하고 2포트 파라미터를 사용하여 특성화하는 것이다. 고주파 트랜지스터의 베이스 영역을 통과하는 전하 운반자를 모델링하는 것도 이 기술의 예시인데, 베이스 영역은 집중 정수 회로(Lumped element model)가 아닌 분산된 저항과 커패시턴스로 모델링해야 한다.
=== 이미지 임피던스 ===
전송선로나 특정 유형의 필터 설계에서는 이미지 임피던스(Image impedance) 방법을 사용하여 전달 파라미터를 결정하기도 한다. 이 방법은 동일한 네트워크가 무한히 길게 연결된 체인의 동작을 고려한다. 이 무한 체인에 대한 입력 및 출력 임피던스, 순방향 및 역방향 전달 함수를 계산한다. 이론적으로 얻어진 값들은 실제 유한한 길이의 체인에서는 정확히 구현될 수 없지만, 체인이 충분히 길다면 실제 동작에 대한 매우 좋은 근사치를 제공한다.
8. 시뮬레이션 기반 회로 분석
전자 회로 시뮬레이션 참조.
대부분의 회로 분석 방법은 메모리 소자가 없는 정적 회로의 전압과 전류 값을 계산하는 데 효과적이지만, 복잡한 동적 회로 분석에는 어려움이 따른다. 일반적으로 동적 회로의 동작을 설명하는 방정식은 미분-대수 방정식 시스템(DAE) 형태로 나타난다. DAE는 풀기 어려우며, 이를 해결하는 방법은 아직 완전히 이해되거나 개발되지 않았다(2010년 기준). 또한 DAE 해의 존재성과 유일성을 보장하는 일반적인 정리도 없다.[5]
특별한 경우, 동적 회로 방정식이 상미분 방정식(ODE) 형태가 되면, 19세기 후반부터 발전해 온 수치 해석 방법을 이용해 비교적 쉽게 풀 수 있다. ODE 해법을 DAE에 적용하는 전략 중 하나인 '직접 이산화'는 회로 시뮬레이션에서 선호되는 방식이다.
시간 영역에서 회로를 분석하는 시뮬레이션 기반 방법은 회로를 초기값 문제(IVP)로 설정하여 푼다. 즉, 커패시터 전압이나 인덕터 전류 같은 메모리 소자의 초기값(t0)이 주어지면, 특정 시간 구간(t0 ≤ t ≤ tf) 동안의 회로 동작을 분석한다. t0부터 tf까지 연속적인 모든 시간에 대한 해를 구하는 것은 불가능하므로, 이 시간 구간을 유한개의 '시간 지점'으로 나누어(이산화) 각 지점에서의 해를 구한다. 이 시간 지점들 사이의 간격을 '시간 단계'(time step)라고 하며, 고정된 크기일 수도 있고 적응형 단계 크기 조절 기법을 사용할 수도 있다.
초기값 문제(IVP)를 풀 때, tn+1 시점의 해는 이미 알고 있는 tn 시점의 해를 바탕으로 계산한다. 이 과정에서 시간적 이산화 기법을 사용하여 미분항을 차분(difference) 형태로 근사한다. 예를 들어 후진 오일러 방법에서는 도함수를 x'(tn+1) ≈ (xn+1 - xn) / hn+1 와 같이 근사한다. 여기서 hn+1은 시간 단계(tn+1 - tn)이다.
회로의 모든 소자가 선형이거나 미리 선형화되었다면, 결과 방정식은 선형 방정식 시스템이 되며 수치 선형 대수 기법으로 풀 수 있다. 회로에 비선형 소자가 포함된 경우, 비선형 방정식 시스템이 되며 뉴턴-랩슨 방법과 같은 근 찾기 알고리즘을 포함한 비선형 수치 해석 방법을 사용해 푼다.
시뮬레이션 기반 분석은 라플라스 변환을 이용한 방법보다 훨씬 적용 범위가 넓다. 라플라스 변환은 주로 선형 시불변(LTI) 시스템에서 전달 함수를 구하는 데 사용되며, 복잡하거나 비선형적인 회로에는 적용하기 어렵다. 또한 라플라스 변환 기반 방법은 임의의 입력 신호를 다루는 데 제약이 있을 수 있다.
9. 비선형 회로 (Non-linear Networks)
대부분의 실제 전자 회로 설계는 비선형 소자를 포함하기 때문에 비선형적이다. 특히 반도체 소자는 거의 예외 없이 비선형 특성을 가지는데, 이상적인 반도체 p-n 접합의 전달 특성은 다음의 비선형적인 관계로 표현된다.
:
여기서 ''i''와 ''v''는 순간 전류와 전압, ''Io''는 소자 구조에 따라 달라지는 역방향 누설 전류, ''VT''는 온도에 비례하는 열 전압(실온 약 25mV)이다.
이 외에도 다양한 방식으로 회로망에 비선형성이 나타날 수 있다. 비선형 소자가 존재하면 선형 중첩과 같은 선형 회로 분석 기법들을 사용할 수 없게 된다. 따라서 회로의 종류와 분석 목적에 따라 비선형성을 다루는 여러 접근 방식이 필요하다.
비선형 회로 분석에서는 해의 유일성과 안정성 문제가 중요하다. 선형 소자로만 구성된 회로는 주어진 경계 조건에 대해 항상 단 하나의 고유한 해를 가지지만, 비선형 회로는 그렇지 않을 수 있다. 예를 들어, 일정한 전류가 흐르는 선형 저항의 전압은 하나로 정해지지만, 비선형 터널 다이오드는 특정 전류 값에 대해 최대 세 개의 다른 전압 해를 가질 수 있다. 즉, 해가 유일하지 않을 수 있으며, 경우에 따라서는 해가 아예 존재하지 않을 수도 있다. 또한, 특정 해가 존재하더라도 안정적이지 않아 작은 외부 자극에도 상태가 쉽게 변할 수 있다. 모든 조건에서 절대적으로 안정적인 회로망은 각 조건에 대해 단 하나의 해만 가져야 함을 보일 수 있다.[6]
비선형 회로를 해석하는 방법에는 여러 가지가 있으며, 대표적인 접근 방식은 다음과 같다. 상세한 내용은 하위 섹션에서 다룬다.
- 스위칭 소자 분석
- 분리 분석 기법 (그래픽 방법, 소신호 모델, 구간 선형 모델 포함)
9. 1. 비선형 소자의 구성 방정식 (Constitutive Equations)
다이오드 방정식은 일반적인 형태의 소자 구성 방정식의 예시이다.:
이것은 비선형 저항으로 생각할 수 있다. 이에 상응하는 비선형 인덕터와 커패시터의 구성 방정식은 각각 다음과 같다.
:
:
여기서 ''f''는 임의의 함수이고, ''φ''는 저장된 자기 선속이며, ''q''는 저장된 전하이다.
9. 2. 비선형 회로 해석 방법
스위칭 소자는 비선형성을 이용하여 두 개의 반대 상태를 만드는 소자이다. 예를 들어, 디지털 회로의 CMOS 소자는 출력 단자가 양(+) 또는 음(-)의 전원 레일에 연결되며, 스위칭되는 과도 기간을 제외하고는 중간 상태를 거의 나타내지 않는다. 이러한 소자는 비선형성이 극단적으로 설계되어 분석이 용이하다. 이런 종류의 네트워크는 두 상태("켜짐"/"꺼짐", "양"/"음" 등)를 부울 대수의 상수 "0"과 "1"에 할당하여 분석할 수 있다.이 분석에서는 소자의 실제 상태와 부울 값에 할당된 공칭 상태 간의 약간의 차이나 과도 현상은 무시된다. 예를 들어, 부울 "1"이 +5V 상태에 할당되었을 때, 소자 출력이 +4.5V여도 분석가는 이를 부울 "1"로 간주한다. 소자 제조업체는 일반적으로 데이터 시트에 '정의되지 않음'(결과를 예측할 수 없음)으로 간주되는 값의 범위를 명시한다.
과도 현상이 분석가에게 완전히 무관한 것은 아니다. 최대 스위칭 속도는 한 상태에서 다른 상태로 전환되는 속도에 의해 결정된다. 다행히 많은 소자에서 대부분의 전환은 소자 전달 함수의 선형적인 부분에서 발생하므로, 선형 회로 분석을 적용하여 근사적인 해답을 얻을 수 있다.
수학적으로는 두 개 이상의 상태를 가진 부울 대수를 만들 수도 있다. 전자공학에서는 이런 대수가 많이 사용되지는 않지만, 3상태 소자는 흔히 사용된다.
=== 분리 분석 기법 ===
이 기법은 회로의 동작이 본질적으로 선형이어야 하지만, 구현에 사용된 소자가 비선형적인 경우에 사용된다. 트랜지스터 증폭기가 대표적인 예이다. 분석을 두 부분으로 나누는 것이 핵심이다.
1. 직류 바이어스 분석: 비선형적인 방법을 사용하여 회로의 정지 동작점을 설정한다.
2. 미소 신호 분석: 회로의 미소 신호 특성을 선형 회로 분석을 사용하여 분석한다.
==== 그래픽 방법 ====
많은 회로 설계에서 직류 바이어스는 저항(또는 저항 네트워크)을 통해 비선형 소자에 공급된다. 저항은 선형 소자이므로, 비선형 소자의 전달 함수 그래프에서 정지 동작점을 비교적 쉽게 결정할 수 있다. 방법은 다음과 같다.
- 선형 회로망 분석을 통해 저항 네트워크와 이를 구동하는 전원에 대한 출력 전달 함수(출력 전압 대 출력 전류)를 계산한다. 이는 직선 형태(부하선)가 된다.
- 이 부하선을 비선형 소자의 전달 함수 그래프 위에 겹쳐 그린다.
- 두 선이 교차하는 지점이 바로 정지 동작점이다.
가장 쉬운 실용적인 방법 중 하나는 선형 회로망의 개방 회로 전압과 단락 회로 전류를 계산하여 비선형 소자의 전달 함수 그래프에 표시하는 것이다. 이 두 점을 연결하는 직선이 바로 회로망의 전달 함수(부하선)이다.
실제 회로 설계에서는 설명된 과정과 반대 방향으로 진행하는 경우가 많다. 즉, 제조업체의 데이터 시트에 제공된 비선형 소자의 그래프에서 원하는 동작점을 먼저 선택한 다음, 이를 달성하기 위한 선형 소자(저항 등)의 값을 계산한다.
이 방법은 바이어스가 다이오드와 같이 자체적으로 비선형인 다른 소자를 통해 공급되는 경우에도 사용할 수 있다. 하지만 이 경우 회로망 전달 함수 플롯이 더 이상 직선이 아니므로 작업이 더 복잡해진다.
==== 소신호 모델 ====
이 방법은 네트워크의 입력 및 출력 신호 변화량이 비선형 소자 전달 함수의 실질적으로 선형적인 부분 내에 있거나, 전달 함수의 곡선을 선형으로 간주할 수 있을 만큼 충분히 작을 때 사용된다. 이 조건 하에서 비선형 소자는 등가 선형 회로로 표현될 수 있다. 이 등가 회로는 가상적이며 소신호 변화에 대해서만 유효하다는 점에 유의해야 한다. 소자의 직류 바이어스에는 적용되지 않는다.
단순한 2단자 소자의 경우, 소신호 등가 회로는 두 가지 요소로 구성될 수 있다.
- 동작점에서의 전압-전류(v/i) 곡선 기울기와 같은 값을 가지며 곡선에 접하는 저항(동적 저항)
- 이 접선이 일반적으로 원점을 통과하지 않으므로 필요한 전원(전압원 또는 전류원)
단자가 더 많으면 더 복잡한 등가 회로가 필요하다.
트랜지스터 제조업체에서 소신호 등가 회로를 명시하는 데 널리 사용하는 형식은 h-파라미터이다. 이는 2포트 네트워크 파라미터의 일종으로, [z] 파라미터처럼 4개의 파라미터로 구성된 행렬이지만, [h] 파라미터는 임피던스, 어드미턴스, 전류 이득, 전압 이득이 혼합된 형태이다. 이 모델에서는 3개의 단자를 가진 트랜지스터를 하나의 단자가 두 포트에 공통인 2포트 네트워크로 간주한다. h-파라미터는 어떤 단자를 공통으로 선택하느냐에 따라 상당히 달라진다. 트랜지스터에서 가장 중요한 파라미터는 일반적으로 공통 이미터 구성에서의 순방향 전류 이득인 h21이며, 데이터 시트에서는 hfe로 표기된다.
2포트 파라미터를 이용한 소신호 등가 회로는 종속 전원 개념으로 이어진다. 즉, 전압원 또는 전류원의 값이 회로 내 다른 곳의 전압이나 전류에 선형적으로 의존하는 것이다. 예를 들어, [z] 파라미터 모델은 아래 그림과 같이 종속 전압원을 포함한다.
2포트 파라미터 등가 회로에는 항상 종속 전원이 존재한다. 이는 [h] 파라미터뿐만 아니라 [z] 파라미터 및 다른 모든 종류의 파라미터 모델에도 해당된다. 이러한 종속성은 더 큰 선형 네트워크를 분석하고 방정식을 세울 때 반드시 유지되어야 한다.
==== 구간 선형 방법 ====
이 방법에서는 비선형 소자의 전달 함수를 여러 영역으로 나눈다. 각 영역은 직선으로 근사된다. 따라서 전달 함수는 특정 지점까지 선형이다가 불연속점을 만나고, 그 지점을 지나면 다른 기울기를 가진 선형 함수가 된다.
이 방법의 잘 알려진 응용 예는 pn 접합 다이오드의 전달 함수 근사이다. 이상적인 다이오드의 전달 함수는 지수 함수 형태이지만, 실제 네트워크 분석에서는 구간 선형 근사가 더 자주 사용된다.
- 역방향 전압에서는 다이오드 전류가 매우 작은 역포화 전류(-Io)로 빠르게 감소하므로, 대부분의 경우 이를 무시하고 개방 회로로 간주한다.
- 순방향 전압이 특정 값(전이점 또는 문턱 전압)에 도달할 때까지는 여전히 개방 회로로 본다. 다이오드는 지수 곡선의 '무릎(knee)' 지점(문턱 전압)까지 개방 회로로 모델링된다.
- 전압이 전이점을 넘어서면, 다이오드는 반도체 재료의 벌크 저항과 같은 일정 저항으로 모델링된다.
전이점 전압은 일반적으로 실리콘 소자의 경우 0.7V, 게르마늄 소자의 경우 0.3V로 간주된다. 스위칭 응용에서는 더 간단하게 순방향 전압에서는 단락 회로, 역방향 전압에서는 개방 회로로 모델링하기도 한다.
약 0.7V의 일정한 전압 강하를 갖는 순방향 바이어스된 pn 접합 모델은 증폭기 설계에서 트랜지스터 베이스-이미터 접합 전압에 대한 근사로도 매우 널리 사용된다.
구간 선형 방법은 신호가 특정 경계 내에 머무르는 경우에만 선형 회로 분석 기법을 적용할 수 있다는 점에서 소신호 모델과 유사하다. 신호가 불연속점을 넘어서면 모델은 더 이상 유효하지 않다. 하지만 이 모델은 신호와 DC 바이어스에 동일하게 적용될 수 있다는 장점이 있다. 따라서 신호와 바이어스를 동일한 연산으로 분석하고 선형적으로 중첩할 수 있다.
10. 시간 가변 회로 (Time-Varying Components)
선형 회로를 분석할 때는 보통 회로를 구성하는 부품들의 값이 변하지 않는다고 가정한다. 하지만 스위프 발진기, 전압 제어 증폭기, 가변 이퀄라이저와 같은 일부 회로에서는 부품 값이 시간에 따라 변한다. 많은 경우 이러한 부품 값의 변화는 주기적으로 일어난다. 예를 들어, 주기적인 신호가 가해진 비선형 부품은 주기적으로 값이 변하는 "선형" 부품처럼 생각할 수 있다. 시드니 달링턴은 이렇게 주기적으로 시간이 변하는 회로를 분석하는 방법을 발표했다. 그는 선형 회로 분석에 사용되는 로널드 M. 포스터와 빌헬름 카우어의 정규형과 유사한 정규 회로 형식을 개발했다.[7]
11. 벡터 회로 이론 (Vector Circuit Theory)
스핀트로닉스와 같이 새롭게 발전하는 회로에서는 기존의 스칼라량 기반 회로 이론을 벡터 전류 개념으로 일반화할 필요성이 있다. 일반화된 회로 이론에서는 회로 변수가 스칼라 전류와 x, y, z 각 방향의 벡터 스핀 전류를 포함하여 총 네 가지 요소로 구성된다. 전압과 전류는 각각 벡터량으로 취급되며, 이들 사이의 관계는 4x4 크기의 스핀 컨덕턴스 행렬을 통해 설명된다.
참조
[1]
논문
Summary of the history of circuit theory
1962-05
[2]
서적
Circuit Analysis and Feedback Amplifier Theory
CRC Press
2005
[3]
서적
Electric Circuits
https://books.google[...]
Pearson Prentice Hall
[4]
논문
Current distribution in conducting nanowire networks
[5]
서적
Circuit Simulation
John Wiley & Sons
2010
[6]
간행물
Nonlinear circuits
Academic Press
2005
[7]
특허
Synthesis of two-port networks having periodically time-varying elements
1966-08-09
[8]
문서
伊佐(2010) p.131
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com