그래프 그리기

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 교차수 부등식
4. 예
5. 역사
6. 그래프 표현 방법
7. 품질 측정 기준
8. 레이아웃 방법
9. 응용 분야
참조

1. 개요

그래프 그리기는 다중 그래프를 특정 조건에 따라 평면이나 곡면에 표현하는 방법을 의미한다. 그래프의 교차수, 면적, 대칭성, 모서리 단순화 등 다양한 품질 측정 기준을 통해 그래프의 미학과 사용성을 평가하며, 힘 기반 레이아웃, 스펙트럼 레이아웃, 직교 레이아웃 등 다양한 레이아웃 방법이 존재한다. 그래프 그리기는 소셜 네트워크, 생물 정보학, 소프트웨어 공학 등 다양한 분야에서 활용되며, 특히 소셜 네트워크 분석, 데이터 시각화, 전자 설계 자동화 등에서 중요한 역할을 한다.

더 읽어볼만한 페이지

그래프 그리기 - 덴드로그램
덴드로그램은 데이터 분석에서 데이터 포인트 간 계층적 관계를 시각적으로 표현하는 나무 형태의 다이어그램으로, 군집 분석에서 클러스터 간 유사성을 나타내기 위해 활용되며 다양한 분야에 응용된다.
그래프 그리기 - 상태도 (오토마타 이론)
상태도는 유한 오토마타 이론에서 시스템의 상태와 전이를 시각적으로 표현하는 유향 그래프이며, 무어 머신, 밀리 머신, 하렐 상태도 등 다양한 형태로 활용된다.
그래프 이론 - 다이어그램
다이어그램은 2차원 기하학적 기호를 사용하여 정보를 시각적으로 표현하는 기술로, 과학, 공학, IT, 비즈니스 등 다양한 분야에서 활용되며 정보를 간략하게 나타내고 시각적 사고를 돕는다.
그래프 이론 - 쾨니히스베르크의 다리 문제
쾨니히스베르크의 다리 문제는 프레겔 강에 놓인 7개의 다리를 한 번씩만 건너 출발점으로 되돌아올 수 있는지 묻는 문제로, 오일러에 의해 그래프 이론적으로 분석되어 해결되었으며 그래프 이론의 탄생에 기여했다.

그래프 그리기

2. 정의

2차원 다양체 $\Sigma$ 와 다중 그래프 $\Gamma$ 가 주어졌을 때, $\Gamma$ 의 $\Sigma$ 속의 '그리기'는 여러 조건을 만족시키는 함수 $f\colon\Gamma\to X$ 로 표현된다. 특히, 유한 그래프의 그리기는 유한 개의 꼭짓점을 갖는다.

2. 1. 그래프 그리기

2차원 다양체

\Sigma

와 다중 그래프

\Gamma

가 주어졌을 때,

\Gamma

의

\Sigma

속의 '''그리기'''는 다음 조건들을 모두 만족시키는 함수

f\colon\Gamma\to X

이다.

$\Gamma$ 에 CW 복합체 위상을 주었을 때, $f$ 는 연속 함수이다.
임의의 $x\in X$ 에 대하여, $|f^{-1}(x)| \le 2$ 이다.
변의 교차점은 꼭짓점이 아니다. 즉, $\{x\in X\colon |f^{-1}(x)| = 2\} \cap f(\operatorname V(\Gamma)) = \varnothing$ 이다.
임의의 두 변의 교차점은 유한 개이다. 즉, 임의의 두 변 $e,f\in\operatorname E(\Gamma)$ 에 대하여, $\{(s,t) \colon f(s) = f(t),\; s \in t, t\in t\}$ 는 유한 집합이다. ( $e\ne f$ 일 필요는 없다. 즉, 변은 스스로와 유한 번 교차할 수 있다.)
임의의 교차점 $x\in X$ 에 대하여, $f\restriction U=\iota_V\circ \tilde f\circ \iota_U$ 가 되는, 다음과 같은 $U,V,\iota_U,\iota_V$ 가 존재한다.
$U\subseteq\Gamma$ 는 열린집합이다.
$V\subseteq X$ 는 열린집합이다.
$\iota_V\colon \mathbb D^2\to X$ 는 열린 원판에서 $V$ 로 가는 위상 동형이다.
$\iota_U\colon (-1,1)\sqcup (-1,1)\to U$ 는 두 열린구간의 분리합집합에서 $U$ 로 가는 위상 동형이다.
여기서 $\tilde f\colon(-1,1)\sqcup (-1,1)\to\mathbb D^2$ 는 다음과 같다.
$(-1,1)\sqcup (-1,1)\cong(-1,1)\times\{\mathsf x,\mathsf y\}$ 라면, $f(t,\mathsf x)=(0,t)$ 이며 $f(t,\mathsf y)=(t,0)$ 이다.

특히, 유한 그래프의 그리기는 유한 개의 꼭짓점을 갖는다.

다중 그래프

\Gamma

의 그리기

f\colon X\to\Gamma

의 '''교차수'''는 기수

|\{x\in X\colon |f^{-1}(x)| = 2\}|

이다. 다중 그래프

\Gamma

의 '''교차수'''는 평면

\mathbb R^2

속의 그리기의 교차수의 최솟값이며, 이를

\operatorname{cr}(\Gamma)

로 표기한다. 보다 일반적으로, 곡면

\Sigma

속의 그리기의 교차수의 최솟값을

\operatorname{cr}_\Sigma(\Gamma)

로 표기한다.

교차수가 0인 그래프 그리기를 '''그래프 매장'''(graph embedding^영어)이라고 한다. 다중 그래프

\Gamma

의 '''종수'''(genus^영어)는

\Gamma

가 매장을 갖는 연결 콤팩트 2차원 유향 다양체

(\mathbb T^2)^{\#g}

의 최소 종수

g\in\mathbb N

이다.

:

\operatorname{genus}(\Gamma) = \min \left\{g\in\mathbb N \colon \operatorname{cr}_{(\mathbb T^2)^{\#g}}(\Gamma) = 0\right\}

2. 2. 교차수

다중 그래프

\Gamma

의 그리기

f\colon X\to\Gamma

의 '''교차수'''는

|\{x\in X\colon |f^{-1}(x)| = 2\}|

이다. 즉, 그래프를 평면에 그릴 때 변들이 서로 교차하는 횟수이다. 다중 그래프

\Gamma

의 '''교차수'''는 평면

\mathbb R^2

속의 그리기의 교차수의 최솟값이며,

\operatorname{cr}(\Gamma)

로 표기한다. 보다 일반적으로, 곡면

\Sigma

속의 그리기의 교차수의 최솟값은

\operatorname{cr}_\Sigma(\Gamma)

로 표기한다.

2. 3. 그래프 매장

교차수가 0인 그래프 그리기를 '''그래프 매장'''(graph embedding^영어)이라고 한다. 그래프 매장은 그래프의 위상적 성질을 보존하는 중요한 개념이다.

2. 4. 종수

다중 그래프

\Gamma

의 '''종수'''(種數, genus^영어)는

\Gamma

가 매장을 갖는 연결 콤팩트 2차원 유향 다양체

(\mathbb T^2)^{\#g}

의 최소 종수

g\in\mathbb N

이다.

:

\operatorname{genus}(\Gamma) = \min \left\{g\in\mathbb N \colon \operatorname{cr}_{(\mathbb T^2)^{\#g}}(\Gamma) = 0\right\}

3. 교차수 부등식

임의의 유한 그래프 $\Gamma$에 대하여 다음이 성립한다.

$|\operatorname E(\Gamma)| > 7|\operatorname V(\Gamma)|$라면, $29 \operatorname{cr}(\Gamma) |\operatorname V(\Gamma)|^2 \ge |\operatorname E(\Gamma)|^3$이다.^[38]
$|\operatorname E(\Gamma)| > 4 |\operatorname V(\Gamma)|$라면, $64 \operatorname{cr}(\Gamma) |\operatorname V(\Gamma)|^2 \ge |\operatorname E(\Gamma)|^3$이다.

4. 예

평면 그래프의 교차수와 종수는 정의에 따라 $\operatorname{cr}(\Gamma)=\operatorname{genus}(\Gamma)=0$ 이다.

완전 그래프, 완전 이분 그래프, 일반화 페테르센 그래프 등의 교차수와 종수에 대한 구체적인 예시는 하위 섹션에서 확인할 수 있다.

4. 1. 완전 그래프

완전 그래프의 교차수는 아직 완전히 알려지지 않았다. 다만, 다음과 같은 부등식이 알려져 있다.

:

\operatorname{cr}(K_n) \le \frac14 \left\lfloor \frac n2\right\rfloor \left\lfloor \frac{n-1}2\right\rfloor \left\lfloor \frac {n-2}2\right\rfloor \left\lfloor \frac {n-3}2\right\rfloor

이 부등식은

n\le 12

에 대하여 등식이라는 것이 알려져 있다. 이 부등식이

n>12

인 경우에 대하여 역시 등식이 된다고 추측되지만, 이는 미해결 난제이다.

유한 완전 그래프의 종수는 다음과 같다.

:

\operatorname{genus}(K_n) = \begin{cases}\left\lceil (n-3)(n-4)/12 \right\rceil & n \ge 3\\0 & n \le 4\end{cases}

4. 2. 완전 이분 그래프

완전 이분 그래프의 교차수는 아직 완전히 알려지지 않았다. 다만, 다음과 같은 상계가 알려져 있다.

:

\operatorname{cr}(K_{m,n}) \le \left\lfloor \frac m2\right\rfloor \left\lfloor \frac {m-1}2\right\rfloor\left\lfloor \frac n2\right\rfloor \left\lfloor \frac{n-1}2\right\rfloor

이 부등식이 등식이 되는 충분 조건은 다음과 같다.

$\min\{m,n\} \le 6$ 일 때^[26]
$7 = \min\{m,n\} \le \max\{ m,n \} \le 9$ 일 때^[27]

'''자란키에비치 추측'''(Zarankiewicz conjecture^영어)에 따르면, 이 부등식이 항상 등식이 된다고 추측되지만, 이는 미해결 난제이다.

유한 완전 이분 그래프의 종수는 다음과 같다.

:

\operatorname{genus}(K_{m,n}) =\begin{cases}\left\lceil (m-2)(n-2)/4 \right\rceil & \min\{m,n\} \ge2 \\0 & \min\{m,n\} \le 2\end{cases}

4. 3. 일반화 페테르센 그래프

각기둥 그래프

\operatorname{GPG}(n,1)

은 평면 그래프이므로 교차수와 종수가 0이다.

\operatorname{GPG}(6,2)

역시 평면 그래프이다.

페테르센 그래프

\operatorname{GPG}(5,2)

의 교차수는 2이다. 일반화 페테르센 그래프

\operatorname{GPG}(8,3)

의 교차수는 4이며, 그 종수는 1이다. 데자르그 그래프

\operatorname{GPG}(10,3)

의 교차수는 6이다. 나우루 그래프

\operatorname{GPG}(12,5)

의 교차수는 8이다. 특히, 이 두 그래프는 모두 평면 그래프가 아니다.

$\operatorname{GPG}(8,3)$ 의, 원환면 $\mathbb T^2$ 속의 매장. 따라서, $\operatorname{GPG}(8,3)$ 의 종수는 1이다.

5. 역사

그래프 그리기의 역사에서 중요한 문제 중 하나는 완전 이분 그래프의 교차수를 계산하는 문제였다. 이 문제는 1944년 투란 팔이 최초로 제시하였다.^[30]^[31] 투란은 제2차 세계 대전 기간 동안 헝가리에서 유대인 강제 노역을 하면서 겪은 경험을 바탕으로 이 문제를 고안했다. 벽돌 공장에서 벽돌을 운반하는 트롤리가 철로 교차점에서 자주 탈선하는 문제를 해결하기 위해, 교차점의 수를 최소화하는 방법을 고민하게 된 것이다.^[32]

투란에게서 이 문제를 들은 카지미에시 자란키에비치(Kazimierz Zarankiewicz^pl, 1902~1959)^[33]와 카지미에시 우르바니크(Kazimierz Urbanik^pl, 1930~2005)^[34]는 1950년대 초에 이 문제에 대한 해를 제시하는 논문을 발표했다. 그러나 이들의 증명에는 오류가 있었고, 실제로는 교차수의 상계만을 증명한 것으로 밝혀졌다.^[35]

교차수 부등식은 1980년대 초에 어이터이 미클로시(Ajtai Miklós^hu, 1946~) · 바츨라프 흐바탈(Václav Chvátal^cs, 1946~) · 몬로 몬티 뉴본(Monroe Monty Newborn^영어, 1938~) · 세메레디 엔드레^[36]와 프랭크 톰슨 레이턴(Frank Thomson Leighton^영어, 1956~)^[37]이 최초로 증명하였으며, 이후 다른 수학자들이 그 상수를 개선하였다.^[38]

하나니-텃 정리는 1934년에 하임 하나니(חַיִּים חַנַנִי^he, Chaim Chojnacki|하임 호이나츠키^pl, 1912~1991)가 증명하였으나, 논문에 매우 간접적으로 언급하였다.^[28] 1970년에 윌리엄 토머스 텃이 이 정리를 다시 언급하였다.^[29]

6. 그래프 표현 방법

그래프는 정점을 원, 사각형 또는 텍스트 레이블로 나타내고 간선을 선분, 폴리라인 또는 유클리드 평면의 곡선으로 표현하는 노드-링크 다이어그램으로 자주 그려진다.^[3] 이러한 방식은 13세기 박식가인 라이몬 룰의 이름으로 출판된 Pseudo-Lull의 14-16세기 작품에서 기원을 찾을 수 있다. Pseudo-Lull은 형이상학적 개념 집합 간의 모든 쌍별 조합을 분석하기 위해 완전 그래프에 대해 이러한 유형의 다이어그램을 사용했다.

유향 그래프에서 방향성을 나타내는 그래픽 표현으로 화살표가 일반적으로 사용된다.^[2] 그러나 사용자 연구에 따르면 테이퍼링과 같은 다른 표현 방법이 이 정보를 더 효과적으로 제공하는 것으로 나타났다.^[4] 상향 평면 그리기에서는 모든 간선이 더 낮은 정점에서 더 높은 정점으로 향하도록 하는 규칙을 사용하므로 화살표가 필요하지 않다.

노드-링크 다이어그램에 대한 대체 표현 방법은 다음과 같다.

정점이 평면의 분리된 영역으로 표시되고 간선이 영역 간의 인접성으로 표시되는 원 채우기
정점이 비분리 기하학적 객체로 표시되고 간선이 교차점으로 표시되는 교차 표현
정점이 평면의 영역으로 표시되고 간선이 서로에 대한 탁 트인 시야를 가진 영역으로 표시되는 가시성 표현
간선이 수학적 열차 선로 내의 부드러운 곡선으로 표시되는 합류형 그림
노드가 수평선으로 표시되고 간선이 수직선으로 표시되는 패브릭^[5]
그래프의 인접 행렬의 시각화

6. 1. 노드-링크 다이어그램

그래프는 정점을 원, 사각형 또는 텍스트 레이블로 나타내고 간선을 선분, 폴리라인 또는 유클리드 평면의 곡선으로 표현하는 노드-링크 다이어그램으로 자주 그려진다.^[3] 노드-링크 다이어그램은 13세기 박식가인 라이몬 룰의 이름으로 출판된 Pseudo-Lull의 14-16세기 작품으로 거슬러 올라간다. Pseudo-Lull은 형이상학적 개념 집합 간의 모든 쌍별 조합을 분석하기 위해 이러한 유형의 다이어그램을 완전 그래프에 대해 그렸다.

유향 그래프의 경우, 화살표는 그들의 방향성을 보여주기 위해 일반적으로 사용되는 그래픽 표현이다.^[2] 그러나 사용자 연구에 따르면 테이퍼링과 같은 다른 표현이 이 정보를 더 효과적으로 제공하는 것으로 나타났다.^[4] 상향 평면 그리기는 모든 간선이 더 낮은 정점에서 더 높은 정점으로 향하도록 하는 규칙을 사용하므로 화살표가 필요하지 않다.

6. 2. 유향 그래프 표현

유향 그래프에서 방향성을 나타내는 그래픽 표현으로 화살표가 일반적으로 사용된다.^[2] 그러나 사용자 연구에 따르면 테이퍼링과 같은 다른 표현 방법이 이 정보를 더 효과적으로 제공하는 것으로 나타났다.^[4] 상향 평면 그리기에서는 모든 간선이 더 낮은 정점에서 더 높은 정점으로 향하도록 하는 규칙을 사용하므로 화살표가 필요하지 않다.

6. 3. 대체 표현 방법

그래프는 정점을 원, 사각형 또는 텍스트 레이블로 나타내고 간선을 선분, 폴리라인 또는 유클리드 평면의 곡선으로 표현하는 노드-링크 다이어그램으로 자주 그려진다.^[3] 노드-링크 다이어그램은 13세기 박식가인 라이몬 룰의 이름으로 출판된 Pseudo-Lull의 14-16세기 작품으로 거슬러 올라간다.

유향 그래프의 경우, 화살표는 방향성을 보여주기 위해 일반적으로 사용되는 그래픽 표현이다.^[2] 그러나 사용자 연구에 따르면 테이퍼링과 같은 다른 표현이 이 정보를 더 효과적으로 제공하는 것으로 나타났다.^[4] 상향 평면 그리기는 모든 간선이 더 낮은 정점에서 더 높은 정점으로 향하도록 하는 규칙을 사용하므로 화살표가 필요하지 않다.

노드-링크 다이어그램에 대한 대체 표현은 다음과 같다.

정점이 평면의 분리된 영역으로 표시되고 간선이 영역 간의 인접성으로 표시되는 원 채우기
정점이 비분리 기하학적 객체로 표시되고 간선이 교차점으로 표시되는 교차 표현
정점이 평면의 영역으로 표시되고 간선이 서로에 대한 탁 트인 시야를 가진 영역으로 표시되는 가시성 표현
간선이 수학적 열차 선로 내의 부드러운 곡선으로 표시되는 합류형 그림
노드가 수평선으로 표시되고 간선이 수직선으로 표시되는 패브릭^[5]
그래프의 인접 행렬의 시각화

7. 품질 측정 기준

그래프 그리기에는 미학과 사용성을 평가하는 객관적인 수단을 찾기 위해 다양한 품질 측정 기준이 정의되어 왔다.^[6] 이러한 기준은 동일한 그래프에 대한 다양한 레이아웃 방법을 선택하는 데 도움을 줄 뿐만 아니라, 일부 레이아웃 방법은 이러한 기준을 직접 최적화하기도 한다.

교차수: 그림에서 서로 교차하는 모서리 쌍의 개수이다. 평면 그래프의 경우 교차수를 최소화하는 것이 중요하다.
면적: 두 꼭짓점 사이의 가장 가까운 거리에 상대적인, 가장 작은 경계 상자의 크기이다. 면적이 작은 그림은 특징을 더 크게 표시할 수 있어 가독성이 좋다. 경계 상자의 종횡비도 중요하다.
대칭 표시: 주어진 그래프 내에서 그래프 자기 동형 사상 그룹을 찾고, 가능한 한 많은 대칭을 표시하는 그림을 찾는 문제이다.
모서리 단순화: 눈으로 쉽게 따라갈 수 있도록 모서리의 모양은 가능한 한 단순해야 한다. 굴곡 최소화를 통해 모서리의 복잡성을 줄일 수 있다.
모서리 길이 균일화: 모서리의 총 길이와 최대 길이를 최소화하고, 균일한 길이를 유지하는 것이 좋다.
각도 분해능: 그래프 그림에서 가장 날카로운 각도의 측정치이다. 차수가 높은 꼭짓점이 있으면 각도 분해능이 작아질 수밖에 없다.
기울기 수: 직선 세그먼트 모서리가 있는 그림에 필요한 구별되는 모서리 기울기의 최소 개수이다(교차 허용). 3차 그래프는 기울기 수가 최대 4이지만, 차수가 5인 그래프는 무제한 기울기 수를 가질 수 있다. 차수가 4인 그래프의 기울기 수가 제한적인지 여부는 아직 풀리지 않은 문제이다.^[6]

7. 1. 교차수 최소화

그래프 그림에서 교차수는 서로 교차하는 모서리 쌍의 개수이다. 그래프가 평면 그래프인 경우, 모서리가 교차하지 않도록 그리는 것이 보기에 좋다. 이러한 그림은 그래프 임베딩을 나타낸다.^[7] 그러나 비평면 그래프는 여러 응용 분야에서 자주 나타나므로, 그래프 그리기 알고리즘은 일반적으로 모서리 교차를 허용해야 한다.^[7]

7. 2. 면적 최소화

그림의 면적은 두 꼭짓점 사이의 가장 가까운 거리에 상대적인, 가장 작은 경계 상자의 크기이다. 면적이 작은 그림이 면적이 큰 그림보다 일반적으로 선호되는데, 그림의 특징을 더 큰 크기로 표시할 수 있고 따라서 더 읽기 쉽기 때문이다. 경계 상자의 종횡비도 중요할 수 있다.^[6]

7. 3. 대칭성 표시

대칭 표시는 주어진 그래프 내에서 그래프 자기 동형 사상 그룹을 찾고, 가능한 한 많은 대칭을 표시하는 그림을 찾는 문제이다. 일부 레이아웃 방법은 자동으로 대칭 그림으로 이어지며, 다른 일부 그리기 방법은 입력 그래프에서 대칭을 찾아 그림을 구성하는 것으로 시작한다.^[8]

7. 4. 모서리 단순화

폴리라인 그림에서 모서리의 복잡성은 굴곡 최소화에 의해 측정될 수 있으며, 많은 방법이 총 굴곡이 적거나 모서리당 굴곡이 적은 그림을 제공하는 것을 목표로 한다. 마찬가지로 스플라인 곡선의 경우 모서리의 복잡성은 모서리의 제어점 수로 측정될 수 있다.^[6]

7. 5. 모서리 길이 균일화

눈으로 쉽게 따라갈 수 있도록 모서리의 모양이 가능한 한 단순해야 한다. 폴리라인 그림에서 모서리의 복잡성은 굴곡 최소화에 의해 측정될 수 있으며, 많은 방법은 총 굴곡이 적거나 모서리당 굴곡이 적은 그림을 제공하는 것을 목표로 한다. 마찬가지로 스플라인 곡선의 경우 모서리의 복잡성은 모서리의 제어점 수로 측정될 수 있다.^[6]

몇 가지 일반적으로 사용되는 품질 측정 기준은 모서리의 길이에 관한 것이다. 모서리의 총 길이와 임의의 모서리의 최대 길이를 최소화하는 것이 일반적으로 바람직하다. 또한 모서리의 길이가 매우 다양한 것보다 균일한 것이 더 나을 수 있다.

7. 6. 각도 분해능 최대화

각도 분해능은 그래프 그림에서 가장 날카로운 각도를 측정한 값이다. 그래프에 높은 차수를 가진 꼭짓점이 있으면, 각도 분해능이 작아질 수밖에 없지만, 각도 분해능은 차수의 함수로 하한을 설정할 수 있다.

7. 7. 기울기 수 최소화

3차 그래프는 기울기 수가 최대 4이지만, 차수가 5인 그래프는 무제한 기울기 수를 가질 수 있다. 차수가 4인 그래프의 기울기 수가 제한적인지 여부는 아직 풀리지 않은 문제이다.^[6]

8. 레이아웃 방법

그래프를 자동으로 배치하는 다양한 알고리즘은 다음과 같다.

힘 기반 레이아웃: 스프링이나 분자 역학 시스템과 같은 물리적 은유를 기반으로 힘을 계산하여 정점의 위치를 조정한다. 인접한 정점 사이에는 인력을, 모든 정점 쌍 사이에는 척력을 적용하여 균형 잡힌 레이아웃을 만든다.^[9]

스펙트럼 레이아웃: 그래프의 인접 행렬에서 파생된 라플라시안 행렬의 고유 벡터를 좌표로 사용한다.^[10]

직교 레이아웃: VLSI나 PCB 레이아웃 문제에 주로 사용되었던 방식으로, 가장자리를 가로 또는 세로로 그려 좌표 축과 평행하게 배치한다.^[11]

트리 레이아웃: 트리 구조에 적합하며, 각 노드의 자식들을 노드 주변의 원 위에 배치한다. 이때 원의 반지름은 하위 레벨로 갈수록 작아져 겹치지 않도록 한다.^[12]

계층적 그래프 그리기 (Sugiyama 스타일): 방향 비순환 그래프나 소프트웨어 시스템의 모듈 간 종속성 그래프와 같이 거의 순환이 없는 그래프에 적합하다. Coffman–Graham 알고리즘을 사용하여 노드를 수평 계층으로 배열하고, 가장자리가 아래로 향하도록 한다.^[13]

아크 다이어그램: 1960년대부터 사용된 방식으로,^[14] 정점을 선 위에 배치하고 가장자리를 선 위나 아래의 반원 또는 부드러운 곡선으로 그린다.

원형 레이아웃: 정점을 원 위에 배치하고, 가장자리는 원의 현이나 호로 그린다. 정점 순서를 신중하게 선택하여 교차를 줄이고 인접 정점을 가깝게 배치한다.^[15]

지배 드로잉: 한 정점이 다른 정점에서 도달 가능한 경우에만 위쪽, 오른쪽, 또는 두 방향 모두에 배치하여 도달 가능성 관계를 시각적으로 표현한다.^[16]

8. 1. 힘 기반 레이아웃

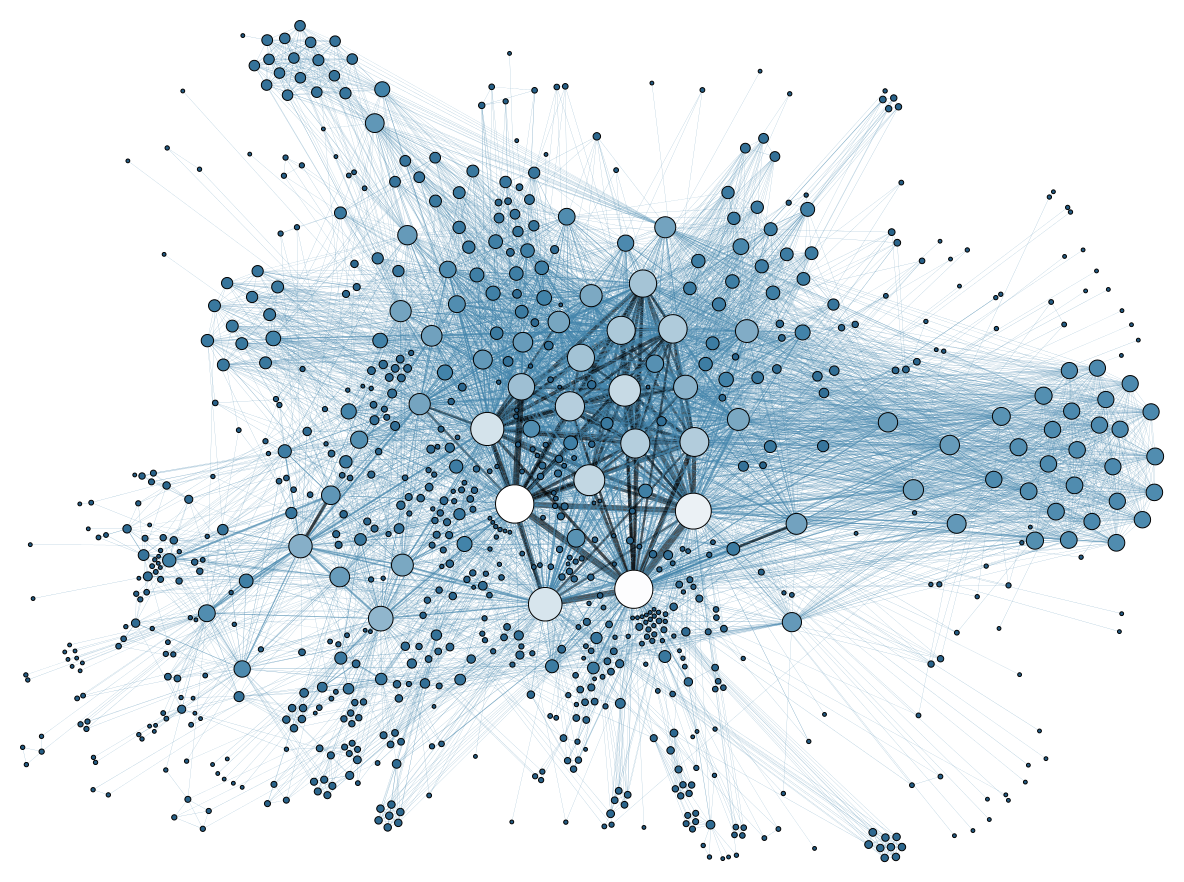
힘 기반 레이아웃 시스템에서, 그래프 그리기 소프트웨어는 스프링 또는 분자 역학 시스템과 관련된 물리적 은유에 기반한 일련의 힘에 따라 정점을 지속적으로 이동시켜 초기 정점 배치를 수정한다. 일반적으로 이러한 시스템은 인접한 정점 사이의 인력과 모든 정점 쌍 간의 척력을 결합하여, 가장자리 길이가 작으면서 정점이 잘 분리된 레이아웃을 찾는다. 이러한 시스템은 에너지 함수의 경사 하강법 기반 최소화를 수행하거나, 힘을 움직이는 정점의 속도 또는 가속도로 직접 변환할 수 있다.^[9]

8. 2. 스펙트럼 레이아웃

스펙트럼 레이아웃은 그래프의 인접 행렬에서 파생된 라플라시안 등 행렬의 고유 벡터를 좌표로 사용하는 방법이다.^[10]

8. 3. 직교 레이아웃

직교 레이아웃 방법은 그래프의 가장자리가 레이아웃의 좌표 축과 평행하게 가로 또는 세로로 그려지도록 하는 방식이다. 이 방법은 원래 VLSI 및 PCB 레이아웃 문제를 위해 설계되었지만, 그래프 그리기에도 적용된다.^[11]

일반적으로 직교 레이아웃은 다음과 같은 다단계 접근 방식을 따른다.^[11]

1. 입력 그래프를 평면화한다. (필요하다면 정점에서 교차점을 대체)

2. 평면화된 그래프의 위상적 임베딩을 찾는다.

3. 굴곡을 최소화하도록 가장자리 방향을 선택한다.

4. 위에서 결정된 방향과 일관되게 정점을 배치한다.

5. 레이아웃 압축 단계에서 그림의 면적을 줄인다.

8. 4. 트리 레이아웃

트리 레이아웃 알고리즘은 트리와 같은 형태를 보여주며, 트리에 적합하다. 종종 "풍선 레이아웃"이라고 하는 기술에서 트리의 각 노드의 자식은 노드를 둘러싸는 원 위에 그려지며, 이러한 원의 반지름은 트리에서 더 낮은 레벨에서 감소하여 이러한 원이 겹치지 않는다.^[12]

8. 5. 계층적 그래프 그리기 (Sugiyama 스타일)

계층적 그래프 그리기(Sugiyama 스타일 그리기라고도 함)는 방향 비순환 그래프 또는 소프트웨어 시스템의 모듈이나 함수 간의 종속성 그래프와 같이 거의 비순환적인 그래프에 가장 적합하다. 이러한 방법에서 그래프의 노드는 Coffman–Graham 알고리즘과 같은 방법을 사용하여 수평 계층으로 배열되어 대부분의 가장자리가 한 계층에서 다음 계층으로 아래로 향하도록 한다. 이 단계 후, 각 계층 내의 노드는 교차를 최소화하도록 정렬된다.^[13]

8. 6. 아크 다이어그램

아크 다이어그램은 1960년대부터 시작된 레이아웃 스타일로,^[14] 정점을 선 위에 배치하고, 가장자리를 선 위 또는 아래의 반원이나 여러 반원을 연결한 부드러운 곡선으로 그리는 방식이다.

8. 7. 원형 레이아웃

원형 레이아웃 방법은 그래프의 정점을 원 위에 배치하고, 교차를 줄이고 인접한 정점을 서로 가깝게 배치하기 위해 원 주위의 정점 순서를 신중하게 선택한다. 가장자리는 원의 현 또는 원 안이나 밖의 호로 그릴 수 있다. 경우에 따라 여러 개의 원을 사용할 수 있다.^[15]

8. 8. 지배 드로잉

지배 드로잉은 한 정점이 다른 정점에서 도달 가능한 경우에만 다른 정점보다 위쪽, 오른쪽, 또는 그 두 방향 모두에 배치하는 방식이다. 이러한 방식으로 레이아웃 스타일은 그래프의 도달 가능성 관계를 시각적으로 명확하게 만든다.^[16]

9. 응용 분야

그래프 및 그래프 그리기는 다양한 분야에서 활용된다.

분야	설명
소셜 네트워크 분석	소시오그램은 소셜 네트워크 분석 소프트웨어에서 자주 제공되는 소셜 네트워크 그림이다.^[17]
부분 순서	하세 다이어그램은 부분 순서에 특화된 그래프 그리기 유형이다.^[18]
대수 기하학	데생 도팡은 대수 기하학에 사용되는 그래프 그리기 유형이다.
유한 상태 기계	상태도는 유한 상태 기계의 그래픽 표현이다.
컴퓨터 네트워크	컴퓨터 네트워크 다이어그램은 컴퓨터 네트워크의 노드와 연결을 묘사한다.
알고리즘 및 제어 흐름	순서도 및 드라콘 차트는 노드가 알고리즘의 단계를 나타내고, 에지가 단계 간의 제어 흐름을 나타내는 그림이다.
정보 시스템	데이터 흐름도는 노드가 정보 시스템의 구성 요소를 나타내고 에지가 한 구성 요소에서 다른 구성 요소로의 정보 이동을 나타내는 그림이다.
생물 정보학	계통수, 단백질-단백질 상호 작용 네트워크 및 대사 경로를 포함한다.

전자 설계 자동화(EDA)의 배치 및 라우팅 단계는 그래프 그리기와 여러 면에서 유사하며, 분산 컴퓨팅에서의 탐욕적 임베딩 문제도 마찬가지이다. 그래프 그리기 문헌에는 EDA 문헌에서 빌려온 여러 결과가 포함되어 있다. 그러나 EDA에서는 미세 면적 최소화와 신호 길이가 미적 요소보다 더 중요하며, EDA의 라우팅 문제는 각 네트워크에 두 개 이상의 터미널을 가질 수 있는 반면, 그래프 그리기의 유사한 문제는 일반적으로 각 에지에 대해 쌍으로 된 정점만 포함한다는 차이점이 있다.

9. 1. 소셜 네트워크 분석

소시오그램은 소셜 네트워크 분석 소프트웨어에서 자주 제공되는 소셜 네트워크 그림이다.^[17] 소셜 네트워크 분석은 개인 또는 조직 간의 관계를 그래프 형태로 나타내어 분석하는 기법이다.

싸이월드의 일촌 관계, 페이스북의 친구 관계, 트위터의 팔로우 관계 등 한국의 소셜 네트워크 서비스(SNS)를 그래프로 표현할 수 있다. 이러한 그래프를 통해 사용자 간의 연결 구조, 영향력 있는 사용자, 정보 확산 경로 등을 파악할 수 있다.

9. 2. 생물 정보학

생물 정보학에서는 계통수, 단백질-단백질 상호 작용 네트워크, 대사 경로를 표현하는 데 그래프 그리기가 사용된다.^[18]

9. 3. 소프트웨어 공학

소시오그램: 소셜 네트워크 분석 소프트웨어에서 자주 제공되는 소셜 네트워크 그림^[17]
하세 다이어그램: 부분 순서에 특화된 그래프 그리기 유형^[18]
데생 도팡: 대수 기하학에 사용되는 그래프 그리기 유형
상태도: 유한 상태 기계의 그래픽 표현
컴퓨터 네트워크 다이어그램: 컴퓨터 네트워크의 노드와 연결을 묘사
순서도 및 드라콘 차트: 노드가 알고리즘의 단계를 나타내고, 에지가 단계 간의 제어 흐름을 나타내는 그림
데이터 흐름도: 노드가 정보 시스템의 구성 요소를 나타내고 에지가 한 구성 요소에서 다른 구성 요소로의 정보 이동을 나타내는 그림
생물 정보학에는 계통수, 단백질-단백질 상호 작용 네트워크 및 대사 경로가 포함된다.

또한, 전자 설계 자동화(EDA)의 배치 및 라우팅 단계는 그래프 그리기와 여러 면에서 유사하며, 분산 컴퓨팅에서의 탐욕적 임베딩 문제도 마찬가지이다. 그래프 그리기 문헌에는 EDA 문헌에서 빌려온 여러 결과가 포함되어 있다. 그러나 이러한 문제들은 여러 중요한 면에서 다르기도 하다. 예를 들어 EDA에서는 미세 면적 최소화와 신호 길이가 미적 요소보다 더 중요하며, EDA의 라우팅 문제는 각 네트워크에 두 개 이상의 터미널을 가질 수 있는 반면, 그래프 그리기의 유사한 문제는 일반적으로 각 에지에 대해 쌍으로 된 정점만 포함한다.

9. 4. 데이터 시각화

그래프 및 그래프 그리기는 여러 분야에서 활용된다.

소시오그램: 소셜 네트워크 분석 소프트웨어에서 자주 제공되는 소셜 네트워크 그림^[17]
하세 다이어그램: 부분 순서에 특화된 그래프 그리기 유형^[18]
데생 도팡: 대수 기하학에 사용되는 그래프 그리기 유형
상태도: 유한 상태 기계의 그래픽 표현
컴퓨터 네트워크 다이어그램: 컴퓨터 네트워크의 노드와 연결을 묘사
순서도 및 드라콘 차트: 노드가 알고리즘의 단계를 나타내고, 에지가 단계 간의 제어 흐름을 나타내는 그림
데이터 흐름도: 노드가 정보 시스템의 구성 요소를 나타내고 에지가 한 구성 요소에서 다른 구성 요소로의 정보 이동을 나타내는 그림
생물 정보학에는 계통수, 단백질-단백질 상호 작용 네트워크 및 대사 경로가 포함된다.

전자 설계 자동화(EDA)의 배치 및 라우팅 단계는 그래프 그리기와 유사하며, 분산 컴퓨팅에서의 탐욕적 임베딩 문제도 마찬가지이다. 그래프 그리기 문헌에는 EDA 문헌에서 빌려온 여러 결과가 포함되어 있다. 그러나 EDA에서는 미세 면적 최소화와 신호 길이가 미적 요소보다 더 중요하며, EDA의 라우팅 문제는 각 네트워크에 두 개 이상의 터미널을 가질 수 있는 반면, 그래프 그리기의 유사한 문제는 일반적으로 각 에지에 대해 쌍으로 된 정점만 포함한다는 차이점이 있다.

9. 5. 기타 응용 분야

그래프 및 그래프 그리기는 다른 여러 응용 분야에서도 활용된다.

소시오그램: 소셜 네트워크 분석 소프트웨어에서 자주 제공되는 소셜 네트워크의 그림이다.^[17]
하세 다이어그램: 부분 순서에 특화된 그래프 그리기 유형이다.^[18]
데생 도팡: 대수 기하학에 사용되는 그래프 그리기 유형이다.
상태도: 유한 상태 기계의 그래픽 표현이다.
컴퓨터 네트워크 다이어그램: 컴퓨터 네트워크의 노드와 연결을 묘사한다.
순서도 및 드라콘 차트: 노드가 알고리즘의 단계를 나타내고, 에지가 단계 간의 제어 흐름을 나타내는 그림이다.
데이터 흐름도: 노드가 정보 시스템의 구성 요소를 나타내고 에지가 한 구성 요소에서 다른 구성 요소로의 정보 이동을 나타내는 그림이다.
생물 정보학에는 계통수, 단백질-단백질 상호 작용 네트워크 및 대사 경로가 포함된다.

또한, 배치 및 라우팅 단계의 전자 설계 자동화(EDA)는 그래프 그리기와 여러 면에서 유사하며, 분산 컴퓨팅에서의 탐욕적 임베딩 문제도 마찬가지이다. 그래프 그리기 문헌에는 EDA 문헌에서 빌려온 여러 결과가 포함되어 있다. 그러나 이러한 문제들은 여러 중요한 면에서 다르기도 하다. 예를 들어 EDA에서는 미세 면적 최소화와 신호 길이가 미적 요소보다 더 중요하며, EDA의 라우팅 문제는 각 네트워크에 두 개 이상의 터미널을 가질 수 있는 반면, 그래프 그리기의 유사한 문제는 일반적으로 각 에지에 대해 쌍으로 된 정점만 포함한다.

참조

_[1] 간행물
_[2] 간행물
_[3] 간행물
_[4] 간행물
_[5] 간행물
_[6] 간행물
_[7] 간행물
_[8] 간행물
_[9] 간행물
_[10] 간행물
_[11] 간행물
_[12] 간행물
_[13] 간행물
_[14] 간행물
_[15] 간행물
_[16] 간행물
_[17] 간행물
_[18] 간행물
_[19] 간행물 "Graphviz and Dynagraph – Static and Dynamic Graph Drawing Tools"
_[20] 웹사이트 Introduction to graph drawing http://reference.wol[...] 2024-03-21
_[21] 간행물
_[22] 간행물 "Tulip – A Huge Graph Visualization Framework"
_[23] 간행물 "yFiles – Visualization and Automatic Layout of Graphs"
_[24] 간행물
_[25] 저널 The graph crossing number and its variants: a survey http://www.combinato[...] 2014-05-15
_[26] 저널 The crossing number of ''K''_5,''n''
_[27] 저널 Cyclic-order graphs and Zarankiewicz's crossing-number conjecture 1993-12
_[28] 저널 Über wesentlich unplättbare Kurven im dreidimensionalen Raume http://pldml.icm.edu[...] 1934
_[29] 저널 Toward a theory of crossing numbers
_[30] 저널 The early history of the brick factory problem 2010-06
_[31] 서적 Graph theory: favorite conjectures and open problems 1 2016
_[32] 저널 A note of welcome https://archive.org/[...] 1977
_[33] 저널 On a problem of P. Turan concerning graphs http://pldml.icm.edu[...] 1954
_[34] 저널 Solution du problème posé par P. Turán http://matwbn.icm.ed[...] 1953-01-02
_[35] 서적 Proof techniques in graph theory. Proceedings of the Second Ann Arbor Graph Theory Conference 1968 Academic Press 1969
_[36] 서적 Theory and practice of combinatorics. A collection of articles honoring Anton Kotzig on the occasion of his sixtieth birthday North-Holland 1982
_[37] 서적 Complexity issues in VLSI. Optimal layouts for the shuffle-exchange graph and other networks https://mitpress.mit[...] Massachusetts Institute of Technology Press 1983
_[38] 저널 On topological graphs with at most four crossings per edge 2013

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com