코쥘 접속

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 성질
4. 분류
5. 역사
6. 예시
참조

1. 개요

코쥘 접속은 매끄러운 다양체 위의 매끄러운 벡터 다발에서 정의되는 개념으로, 벡터 다발의 단면, 에레스만 접속, 또는 미분 형식에 작용하는 연산자를 통해 정의될 수 있다. 단면 위의 작용을 통한 정의는 곱 규칙을 만족하는 실수 선형 변환으로, 국소 좌표계에서 크리스토펠 기호를 사용하여 표현된다. 에레스만 접속을 통한 정의는 에레스만 접속이 특정 조건을 만족하는 경우 코쥘 접속으로 정의되며, 미분 형식 위의 작용을 통한 정의는 공변 외미분을 사용하여 정의된다. 코쥘 초접속은 코쥘 접속의 일반화된 개념으로, 초벡터 공간에 대해 정의된다. 코쥘 접속은 당김, 곡률, 평행 운송 등의 성질을 가지며, 평탄 코쥘 접속은 곡률이 0인 경우를 의미한다. 코쥘 접속의 개념은 아핀 접속에서 유래되었으며, 1950년 장루이 코쥘에 의해 현대적인 정의가 제시되었다. 코쥘 접속은 벡터 다발의 접속 공간을 형성하며, 레비-치비타 접속, 스핀 접속 등이 코쥘 접속의 예시에 해당한다.

더 읽어볼만한 페이지

접속 (수학) - 비틀림 텐서
비틀림 텐서는 매끄러운 다양체와 코쥘 접속에 대해 정의되며, 접속의 비대칭성을 나타내는 (1,2)차 텐서장이다.
접속 (수학) - 스핀 접속
스핀 접속은 매끄러운 다양체에서 필바인과 코쥘 접속을 사용하여 정의되며, 스피너 다발의 접속 성분을 구성하고 일반화된 텐서에 대한 공변 미분을 정의하며, 비틀림이 없는 경우 카르탕의 구조 방정식을 통해 비틀림과 곡률을 설명하는 데 사용된다.
벡터 다발 - 법다발
법다발은 다양체 $M$에 매장된 다양체 $N$의 접다발을 $M$의 접다발로 확장한 몫다발로, 리만 다양체에서는 법선 공간들의 모임으로 정의되며 여법선 다발과 관련이 깊다.
벡터 다발 - 접다발
접다발은 매끄러운 다양체 위의 각 점에 접하는 벡터 공간들을 모아놓은 공간으로, 국소 좌표계를 사용하여 정의되며, 사영 사상을 통해 매끄러운 벡터 다발을 이루고, 다양체의 미분 구조 연구에 중요한 역할을 한다.

코쥘 접속
개요
정의	벡터 다발에서의 평행 이동 개념
관련 항목	미분 기하학, 다양체론, 접속
표기법
변수	mvar: "0" (문맥에 따라 의미가 달라짐) mvar: X (다양체) mvar: P (X 위의 벡터 다발의 점) mvar: X (P에서의 X의 접공간) mvar: Q (X 위의 벡터 다발의 또 다른 점) mvar: X (Q에서의 X의 접공간)
영어 명칭	Koszul connection (코쥘 접속)

2. 정의

매끄러운 다양체 $M$ 위의 매끄러운 벡터 다발 $\pi\colon E\twoheadrightarrow M$ 이 주어졌을 때, 코쥘 접속은 다음과 같이 다양하게 정의될 수 있다.

벡터 다발의 매끄러운 단면 위에 작용하는 작용소
벡터 다발의 선형 구조와 호환되는 에레스만 접속
벡터 값 미분 형식 위에 작용하는 작용소

M

위의 '''아핀 접속'''(affine接續, affine connection^영어)은 그 접다발

\mathrm TM

위의 코쥘 접속이다. 아핀 접속을 갖춘 매끄러운 다양체를 '''아핀 다양체'''(affine多樣體, affine manifold^영어)라고 한다.

2. 1. 단면 위의 작용을 통한 정의

매끄러운 다양체

M

위의 매끄러운 벡터 다발

\pi\colon E\twoheadrightarrow M

이 주어졌을 때,

E

의 매끄러운 단면들의 실수 벡터 공간을

\Gamma^\infty(E)

라고 한다.

E

위의 코쥘 접속은 벡터 다발의 매끄러운 단면 위에 작용하는 작용소로 정의될 수 있다.^[90]

E

위의 (코쥘) 접속 또는 공변 미분(共變微分, covariant derivative^영어)

:

\nabla\colon\Gamma^\infty(E)\to\Gamma^\infty(\mathrm T^*M\otimes_{\mathbb R}E)

은 다음과 같은 곱 규칙을 만족시키는 실수 선형 변환이다.^[90]

:

\nabla(fs)=f\nabla s+\mathrm df\otimes s\qquad\forall f\in \mathcal C^\infty(M,\mathbb R),\;s\in\Gamma^\infty(E)

여기서

T^*M

은

M

의 공변접다발이며,

\mathrm df\in\Gamma^\infty(\mathrm T^*M)=\Omega^1(M)

은

f

의 외미분으로 얻은 1차 미분 형식이다.

이는

E\to\mathrm T^*M\otimes E

1차 미분 연산자를 이룬다.

임의의 벡터장

X\in\Gamma^\infty(\mathrm TM)

에 대하여,

:

\nabla_X\colon\Gamma^\infty(E)\to\Gamma^\infty(E)

:

\nabla_X\colon s\mapsto \langle X,\nabla s\rangle

를 정의할 수 있다. 이를

E

의 단면의

X

방향의 공변 미분이라고 한다.^[90]

\nabla

는 1차 미분 연산자이므로, 국소 좌표계에서 다음과 같은 꼴로 전개할 수 있다.

:

(\nabla_Xs)^a=X^i\left(\partial_is^a+\Gamma_{ib}^as^b\right)

여기서

i,j,\dotsc

는 접다발의 첨자이며

a,b,\dotsc

는

E

의 첨자이다. 코쥘 접속을 정의하는 성분

\Gamma_{ib}^a

을 크리스토펠 기호라고 한다.

2. 2. 에레스만 접속을 통한 정의

매끄러운 다양체

M

위의 매끄러운 벡터 다발

\pi\colon E\twoheadrightarrow M

이 주어졌다고 하자.

E

의 매끄러운 단면들의 실수 벡터 공간은

\Gamma^\infty(E)

로 표기한다.

E

위의 에레스만 접속

H\subseteq\mathrm TE

가 다음 두 조건을 만족시키면, '''코쥘 접속'''이라고 한다.

$H_{\lambda e}=\left(\mathrm T(\cdot\lambda)\right)(H_e)$
$\left(\mathrm T(+)\right)(H\times_MH)=H$

여기서

H\times_MH\subseteq E\times_ME

이고,

\lambda

는 임의의 실수이다.

에레스만 접속을 통한 정의와 단면 위의 작용을 통한 정의 사이의 관계는 다음과 같다.

1.

\operatorname{proj}_{\mathrm VE}\colon \mathrm TE\to\mathrm VE=\pi^*E

를

H

를 사용한, 수직 벡터 다발

\mathrm VE

위로의 사영이라고 하자 (즉,

H=\ker\operatorname{proj}_{\mathrm VE}

).

2. 임의의 단면

s\in\Gamma^\infty(E)

에 대하여, 미분

\mathrm Ts\colon\mathrm TM\to\mathrm TE

를 생각하자.

3.

\nabla\colon\mathrm TM\to s^*\mathrm VE=E

와

\nabla s=\operatorname{proj}_H\circ\mathrm Ts

를 정의하자.

그러면, 이는 적절한 곱 규칙을 만족시켜, 단면 위의 작용을 통한 정의에 해당한다.

2. 3. 미분 형식 위의 작용을 통한 정의

E

위의 '''코쥘 접속''' 또는 '''공변 미분'''(共變微分, covariant derivative^영어)은 다음 조건을 만족하는 실수 선형 변환이다.

:

\nabla\colon\Gamma^\infty(E)\to\Gamma^\infty(\mathrm T^*M\otimes_{\mathbb R}E)

:

\nabla(fs)=f\nabla s+\mathrm df\otimes s\qquad\forall f\in \mathcal C^\infty(M,\mathbb R),\;s\in\Gamma^\infty(E)

여기서

T^*M

은

M

의 공변접다발이며,

\mathrm df\in\Gamma^\infty(\mathrm T^*M)=\Omega^1(M)

은

f

의 외미분으로 얻은 1차 미분 형식이다. 이는

E\to\mathrm T^*M\otimes E

1차 미분 연산자를 이룬다.

매끄러운 다양체

M

위의 매끄러운 벡터 다발

E

위의 '''공변 외미분'''(共變外微分, covariant exterior derivative^영어)은 다음 곱 규칙을 만족시키는 실수 선형 변환이다.

:

\mathrm d^\nabla\colon\Omega^\bullet(M;E)\to\Omega^{\bullet+1}(M;E)

:

\mathrm d^\nabla(\alpha\wedge\omega)=\mathrm d\alpha\wedge\omega+(-)^p\alpha\wedge\mathrm d^\nabla\omega\qquad\forall\alpha\in\Omega^p(M),\;\omega\in\Omega(M;E)

(여기서

\Omega(M;E)

는

E

값 미분 형식의 공간이다.) 이러한 연산자를 공변 외미분이라고 한다.

임의의 공변 외미분

\mathrm d^\nabla\colon\Omega^\bullet(M;E)\to\Omega^{\bullet+1}(M;E)

가 주어졌을 때,

\Omega^0(M;E)=\Gamma^\infty(E)

이므로,

:

\mathrm d^\nabla|_{\Gamma^\infty(E)}\colon\Gamma^\infty(M;E)\to\Omega^1(M;E)=\Gamma^\infty(\mathrm T^*M\otimes_{\mathbb R}E)

는 단면 위에 적절한 곱 규칙을 만족시킨다. 반대로, 단면 위의 작용소

\nabla\colon\Gamma^\infty(E)\to\Gamma^\infty(\mathrm T^*M\otimes_{\mathbb R}E)

가 주어졌을 때, 미분 형식에 대한 곱 규칙을 만족시키게 유일하게 확장할 수 있다.

일반적 외미분과 달리, 공변 외미분은 일반적으로

\mathrm d^\nabla\circ\mathrm d^\nabla=0

을 만족시키지 못한다.^[90]

2. 4. 코쥘 초접속

매끄러운 다양체

M

위의 두 매끄러운 벡터 다발

E^\pm\twoheadrightarrow M

이 주어졌을 때,

E=E^+\oplus E^-

위의 '''코쥘 초접속'''(Koszul初接續, Koszul superconnection^영어)은

\mathbb Z/2

-등급 벡터 공간(초벡터 공간)에 대한 코쥘 접속의 일반화 개념이다.^[91]

코쥘 초접속은 단면 위의 작용과 미분 형식 위의 작용을 통해 정의될 수 있다.

=== 단면 위의 작용 ===

E

위의 코쥘 초접속은 다음 조건을 만족시키는 선형 변환이다.

:

\nabla^\pm\colon\Gamma^\infty(E^\pm)\to\bigoplus_{n=0}^\infty\Omega^{2n}(M;E^\mp)\oplus\bigoplus_{n=0}^\infty\Omega^{2n+1}(M;E^\pm)

:

\nabla^\pm(fs)=f\nabla s+(\mathrm d f)\otimes s\qquad\forall f\in\mathcal C^\infty(M;\mathbb R),\;s\in\Gamma^\infty(E^\pm)

=== 미분 형식 위의 작용 ===

E^\pm

값 미분 형식들의 공간

\Omega^\bullet(M;E^\pm)

으로부터, 다음을 정의할 수 있다.

:

\Omega^{\pm,k}(M;E)=\begin{cases}\Omega^k(M;E^\pm)&k\mid 2\\\Omega^k(M;E^\mp)&k\nmid2\end{cases}

:

\Omega^\pm(M;E)=\bigoplus_{k\in\mathbb N}\Omega^{\pm,k}(M;E)

즉, 아래 표에서, 흰색 바탕은

\Omega^+(M;E)

에, 회색 바탕은

\Omega^-(M;E)

에 속한다.

$\Omega^0(M;E^+)=\Gamma^\infty(E^+)$	$\Omega^1(M;E^+)$	$\Omega^2(M;E^+)$	$\Omega^3(M;E^+)$	$\Omega^4(M;E^+)$
$\Omega^0(M;E^-)=\Gamma^\infty(E^-)$	$\Omega^1(M;E^-)$	$\Omega^2(M;E^-)$	$\Omega^3(M;E^-)$	$\Omega^4(M;E^-)$

$E^\pm$ 위의 코쥘 초접속

: $\mathrm d^\nabla\colon\Omega^\pm(M;E)\to\Omega^\mp(M;E)$

은 다음과 같은 곱 규칙을 만족시키는 실수 선형 변환이다.^[91]

: $\mathrm d^\nabla(\alpha\wedge\omega)=(\mathrm d\alpha)\wedge\omega+(-)^p\alpha\wedge\mathrm d^\nabla\theta\qquad\forall\alpha\in\Omega^p(M),\;\omega\in\Omega(M;E)$

=== 코쥘 초접속의 구성 요소 ===

매끄러운 다양체 $M$ 위의 두 매끄러운 벡터 다발 $E^\pm\twoheadrightarrow M$ 위의 코쥘 초접속은 다음과 같은 데이터로 주어진다.^[91]

$E^\pm$ 위의 코쥘 접속 $\nabla_{E^\pm}$ (1등급 성분)
음이 아닌 짝수 $i\in2\mathbb N=\{0,2,4,\dotsc\}$ 에 대하여, 벡터 값 미분 형식 $T^i\in\Omega^i(M;E^+\otimes(E^-)^*\oplus E^-\otimes(E^+)^*)$
3 이상의 홀수 $i\in\{3,5,7,\dotsc\}$ 에 대하여, 벡터 값 미분 형식 $T^i\in\Omega^i(M;E^+\otimes(E^+)^*\oplus E^-\otimes(E^-)^*)$

이 데이터는

\Gamma^\infty(M;E^\pm)

및

\Omega(M;E)

위에 다음과 같이 작용한다.

:

\mathrm d^\nabla(\alpha\otimes s^\pm)=\nabla_{E^\pm}s^\pm\wedge\alpha+\sum_{i\in\mathbb N\setminus\{1\}}T^i(s)\qquad\forall s^\pm\in\Gamma^\infty(E^\pm)

:

\mathrm d^\nabla(\alpha\otimes s^\pm)=\nabla_{E^\pm}s^\pm\wedge\alpha+\sum_{i\in\mathbb N\setminus\{1\}}T^i(s)\wedge\alpha\qquad\forall s^\pm\in\Gamma^\infty(E^\pm),\;\alpha\in\Omega^p(M)

이러한 성분들은 초접속의 "크리스토펠 기호"에 해당한다.

3. 성질

벡터 다발 $E$ 위의 에레스만 접속이 특정 조건들을 만족하면 '''코쥘 접속'''이라고 불린다. 코쥘 접속은 에레스만 접속의 특수한 경우로, 평행 운송, 곡률 등의 성질을 갖는다.

코쥘 접속의 주요 성질은 다음과 같다:

당김(Pullback): 매끄러운 함수를 통해 한 다양체 위의 벡터 다발과 코쥘 접속을 다른 다양체 위로 "당겨올" 수 있다. 이 당겨진 접속은 원래 접속과 관련된 특정 조건을 만족한다.
곡률(Curvature): 코쥘 접속은 곡률 개념을 정의할 수 있게 해준다. 곡률은 벡터장을 따라 평행 운송을 했을 때 발생하는 변화를 측정하는 텐서이다. 곡률이 0인 코쥘 접속을 평탄 코쥘 접속이라고 한다.
평행 운송(Parallel Transport): 코쥘 접속은 벡터 다발의 단면을 곡선을 따라 "평행하게" 이동시키는 방법을 제공한다. 이는 벡터 공간들을 서로 연결하는 방법으로 이해할 수 있으며, 평행 운송을 통해 접속의 공변 도함수를 복구할 수 있다.

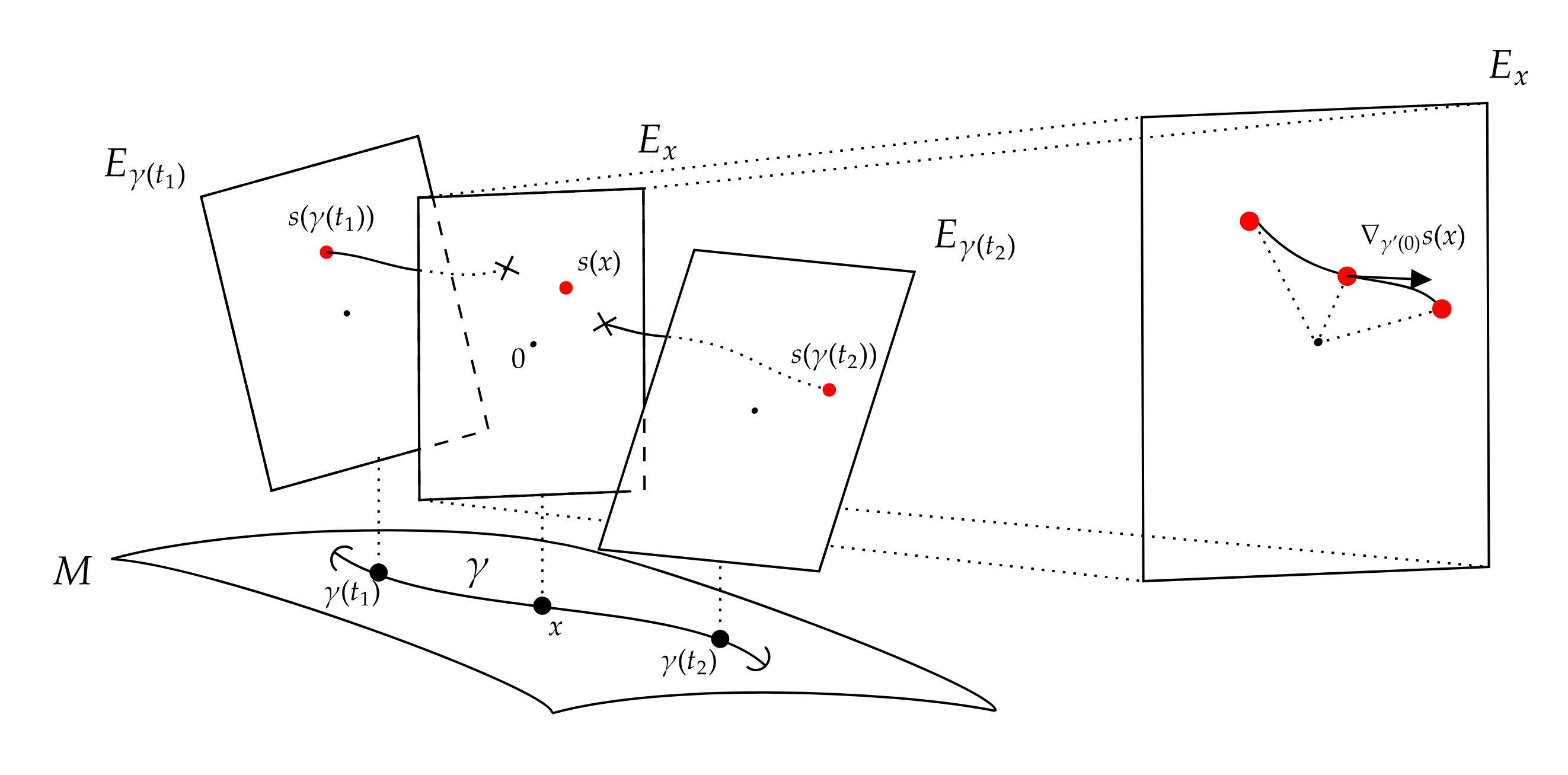
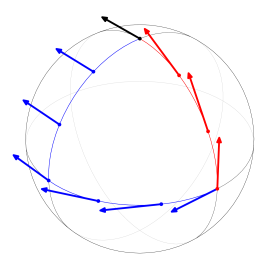
구면 상의 평행 이동. 측지선(대원)으로 둘러싸인 삼각형 상에서 벡터를 한 바퀴 평행 이동하면, 원래대로 돌아왔을 때 원래의 벡터로 돌아오지 않는다.

유클리드 공간과 달리, 어떤 곡선을 따라 평행 이동했는지에 따라 평행 이동의 결과가 달라진다. 예를 들어 곡선

P(t)

를 따른 평행 이동을

\varphi_{a,b}(v)

, 곡선

Q(t)

를 따른 평행 이동을

\psi_{a',b'}(v)

라고 할 때,

P(a)=Q(a')

이고

P(b)=Q(b')

이더라도

\varphi_{a,b}(v)=\psi_{a',b'}(v)

가 된다는 보장은 없다. 이러한 현상을 '''홀로노미'''라고 한다.^[41]

3. 1. 당김

두 매끄러운 다양체

M

과

N

사이의 매끄러운 함수

f\colon M\to N

가 주어졌다고 하자.

N

위의 매끄러운 벡터 다발

E\twoheadrightarrow N

와

E

위의 코쥘 접속

\nabla

가 주어지면,

f

를 통해

M

위의 당김 다발

f^*E

를 정의할 수 있다.

이 위에 당김 접속

:

f^*\nabla\colon\Gamma^\infty(f^*E)\to\Gamma^\infty(T^*M\otimes f^*E)

은 다음 조건을 만족시키는 유일한 코쥘 접속이다.^[35]

:

f^*\nabla_X\colon f^*s\mapsto f^*(\nabla_{f_*X}s)\qquad\forall s\in\Gamma^\infty(E),\;X\in\Gamma^\infty(TM)

여기서

f_*X=df(X)\in\Gamma^\infty(TN)

는

X\in\Gamma^\infty(TM)

의

N

으로의 밂(pushforward^영어)이다.

만약

N

위에 두 매끄러운 벡터 다발

E^\pm\twoheadrightarrow N

이 주어졌을 때,

E^\pm

위의 코쥘 초접속을 당김 다발

f^*E^\pm

위로 당길 수 있다.

M

위의 미분 가능한 벡터 번들

\pi : E \to M

의 접속

\nabla

와 미분 다양체

N

에서

M

으로의 미분 가능한 사상

f : N \to M

에 대해,

f

에 의한

E

의 당김

:

\pi' : f^*(E) \to N

을 생각할 수 있다.

N

,

M

의 국소 좌표

y : V \subset N \to \mathbb{R}^u

,

x : U \subset M \to \mathbb{R}^m

에서

V \subset f^{-1}(U)

가 되는 것을 선택하고,

U

위의

E

의 기저

e_1,\ldots,e_n

을 선택하여 접속

\nabla

를 접속 형식을 사용하여

:

\nabla^U s = (ds^i  + s^j \omega^i{}_j) \otimes e_i

와 같이 성분 표시한다.

f^*(E)

의 접속

f^*(\nabla)

를 그

V

로의 제한

f^*(\nabla)^V

가

:

f^*(\nabla)^Vs = (ds^i + s^j f^*(\omega^i{}_j))e_i

가 되도록 정의하고,

\nabla

의

f

에 의한 '''당김'''(pull back^영어),

f

에 의해

f^*(E)

에 '''유도된 접속'''(induced connection^영어)이라고 한다.^[35] 접속 계수를 사용하면,

:

f^*(\nabla)^V_Y s = (Y^k{\partial s^i \over \partial y^k}  + Y^ks^j {\partial x^{\ell} \over \partial y^k} \Gamma^{i}_{\ell j}) e_i

이다.

N

이 선분인 경우, 사상

P : (0,1) \to M

은

M

위의 곡선으로 간주할 수 있다. 곡선

P(t)

를 따른 단면

s

에 대해,

:

{\nabla s\over dt} := f_*\left(f^*(\nabla)_{\tfrac{d}{dt}}f^*(s)\right)

을 생각할 수 있다.

\tfrac{\nabla}{dt}s

를 접속

\nabla

에 의해 정해지는 '''곡선

P(t)

를 따른 단면

s

의 공변 미분'''이라고 한다. 성분으로 쓰면

:

{\nabla s\over dt}= \left({d s^i\over dt}+ {dx^k\over dt}s^j\Gamma_{kj}^i\right)e_i

가 되므로, 레비-치비타 접속의 경우 곡선

P(t)

를 따른 단면

s

의 공변 미분의 개념의 일반화가 됨을 알 수 있다.

3. 2. 곡률

매끄러운 벡터 다발

E\twoheadrightarrow M

위의 코쥘 접속

\nabla

에 대하여, 다음 조건을 만족시키는 텐서장

F^\nabla\in\Omega^2(M;\operatorname{End}E)

가 유일하게 존재한다.

:

F^\nabla(X,Y)\colon s\mapsto\nabla_X\nabla_Ys-\nabla_Y\nabla_Xs-\nabla_{[X,Y]}s\qquad\forall X,Y\in\Gamma^\infty(\mathrm TM),\;s\in\Gamma^\infty(E)

이를

\nabla

의 '''곡률'''(曲率, curvature^영어)이라고 하며, 이는

\operatorname{End}E\cong E\otimes E^*

값의 2차 미분 형식이다.^[90] 여기서

[X,Y]

는 벡터장의 리 미분이다. 이는 일반적 올다발 위의 에레스만 접속의 곡률의 특수한 경우이다.

곡률이 0인 코쥘 접속을 '''평탄 코쥘 접속'''(平坦Koszul接續, flat Koszul connection^영어)이라고 한다.

아핀 접속의 곡률은 '''리만 곡률'''이라고 하며, 이는 (3,1)-텐서장으로 여길 수 있다. 또한, 아핀 접속

\nabla

의 경우, 곡률과 더불어 '''비틀림'''을 정의할 수 있다. 비틀림

T^\nabla\in\Omega^2(M;\mathrm TM)

은 다음과 같다.

:

T^\nabla(X,Y)=\nabla_XY-\nabla_YX-[X,Y]

(여기서

\Omega^2(M;\mathrm TM)

은 접다발 값 2차 미분 형식의 공간이다.) 비틀림은 (2,1)-텐서장으로 여길 수 있다.

마찬가지로, 매끄러운 다양체

M

위의 두 매끄러운 벡터 다발

E^\pm

위의 코쥘 초접속

\nabla

가 주어졌을 때,

:

\mathrm d^\nabla\circ\mathrm d^\nabla\colon\Omega^\pm(M;E)\to\Omega^\pm(M;E)

는 항상 다음과 같은 꼴이다.^[91]

:

\mathrm d^\nabla\circ\mathrm d^\nabla\in\Omega(M;\operatorname{End}(E))

이를 초접속의 '''곡률'''이라고 한다.^[91] 곡률이 0인 코쥘 초접속을 '''평탄 코쥘 초접속'''(平坦Koszul超接續, flat Koszul superconnection^영어)이라고 한다.

E\to M

위의 접속

\nabla

의 '''곡률'''은 자기 사상 다발

\operatorname{End}(E) = E^* \otimes E

값을 갖는

M

위의 2-형식

F_{\nabla}

이다. 즉,

:

F_\nabla \in \Omega^2(\mathrm{End}(E)) = \Gamma(\Lambda^2T^*M \otimes \mathrm{End}(E)).

이것은 다음 식으로 정의된다.

:

F_\nabla(X,Y)(s) = \nabla_X\nabla_Y s- \nabla_Y\nabla_X s- \nabla_{[X,Y]}s

여기서

X

와

Y

는

M

위의 접선 벡터장이고

s

는

E

의 단면이다.

앞에서 언급했듯이, 공변 외미분

d_{\nabla}

는

E

값 형식을 연산할 때 제곱하면 0이 될 필요는 없다. 그러나 연산자

d_{\nabla}^2

는 엄밀히 텐서적이다(즉,

C^{\infty}(M)

-선형). 이것은 그것이

\operatorname{End}(E)

값을 갖는 2-형식에서 유도된다는 것을 의미한다. 이 2-형식은 위에 주어진 곡률 형식과 정확히 일치한다.

E

값 형식

\sigma

에 대해 다음이 성립한다.

:

(d_\nabla)^2\sigma = F_\nabla\wedge\sigma.

'''평탄 접속'''은 곡률 형식이 항등적으로 0인 접속이다.

곡률 형식은 '''카르탄 구조 방정식'''이라고 불리는 국소적 표현을 갖는다. 만약

\nabla

가

E

에 대한 어떤 자명화 열린 부분 집합

U\subset M

에서 국소적 형식

A

를 갖는다면,

U

에서 다음이 성립한다.

:

F_{\nabla} = dA + A \wedge A

Bianchi 항등식의 두 번째 (미분) 버전은 임의의 벡터 다발 위의 접속에 대해 성립한다. 벡터 다발

E\to M

위의 접속

\nabla

는

\operatorname{End}(E)

위에 자기 사상 접속을 유도한다는 것을 상기하자. 이 자기 사상 접속은 자체적으로 외대 공변 미분을 가지며, 이를 모호하게

d_{\nabla}

라고 부른다. 곡률은 전역적으로 정의된

\operatorname{End}(E)

값의 2-형식이므로, 외대 공변 미분을 적용할 수 있다. '''Bianchi 항등식'''은 다음과 같이 나타낸다.

:

d_{\nabla} F_{\nabla} = 0

3. 3. 평행 운송

코쥘 접속은 에레스만 접속의 특수한 경우이므로, '''평행 운송'''(parallel transport^영어)을 정의할 수 있다.

매끄러운 벡터 다발

E\twoheadrightarrow M

와 그 위의 코쥘 접속

\nabla

,

E

의 매끄러운 단면

s\in\Gamma^\infty(E)

, 그리고 매끄러운 곡선

\gamma\colon [0,1]\to M

이 주어졌다고 하자.

만약 모든

t\in[0,1]

에 대해

:

\nabla_{\dot\gamma(t)}\sigma=0

이 성립하면,

E

를 '''평행 단면'''(平行斷面, parallel section^영어)이라고 한다. 이는 단면의 당김

\gamma^*s\in\Gamma^\infty(\gamma^*E)

의, 당겨진 접속

\gamma^*\nabla

에 대한 공변 미분이 0이라는 것과 같다.

이때,

s(\gamma(1))\in E_{\gamma(1)}

를

s(\gamma(0))\in E_{\gamma(0)}

의, 곡선

\gamma

를 따른 '''평행 운송'''이라고 한다. 평행 운송은 선형 변환

:

\tau_\gamma\colon E_{\gamma(0)}\to E_{\gamma(1)}

으로 생각할 수 있으며, 이는 벡터 공간의 동형을 이룬다. 이처럼 코쥘 접속은

E

의 각 올공간들을 (주어진 경로에 따라) "이어붙이는" 역할을 한다.

마찬가지로, 코쥘 초접속 역시 일종의 평행 운송을 정의한다.^[92]

\nabla

를 상의 미분 가능한 벡터 다발

\pi~:~E \to M

의 접속으로 하고,

P(t)

를 상의 구간별로 매끄러운 곡선으로 하며, 를

P(t)

상의 의 단면으로 한다. 즉 각

P(t)

에 대해

s_{P(t)}\in E

가 정의될 수 있고,

t \mapsto s_{P(t)}

가 미분 가능하며, 게다가

\pi(s_{P(t)})=P(t)

가 임의의 에 대해 성립한다고 한다.

P(t)

를 따른 단면

s

,

s'

이 모두

P(t)

를 따라 평행하고, 시각

t=a

일 때

s_{P(a)}=s'_{P(a)}

이면, 다른 시각

t=b

에서도

s_{P(b)}=s'_{P(b)}

임을 보일 수 있다. 따라서 사상

:

\varphi_{a,b}~:~v=s_{P(a)}\in E_{P(a)} \mapsto s_{P(b)}\in E_{P(b)}

는 단면

s

의 선택에 관계없이 잘 정의(well-defined)된다.

유클리드 공간의 경우와 달리, '''어떤 곡선을 따라 평행 이동했는지에 따라 평행 이동의 결과가 다르다'''. 즉 곡선

P(t)

를 따른 평행 이동을

\varphi_{a,b}(v)

, 곡선

Q(t)

를 따른 평행 이동을

\psi_{a',b'}(v)

라고 할 때,

P(a)=Q(a')

,

P(b)=Q(b')

이라 하더라도

\varphi_{a,b}(v)=\psi_{a',b'}(v)

라는 보장은 없다. 이러한 현상을 '''홀로노미'''(holonomy)라고 한다.^[41]

\varphi_{a,b}

는

E_{P(a)}

에서

E_{P(b)}

로의 사상으로 간주할 수 있는데, 이 사상은 선형 동형 사상이다. 따라서 평행 이동에 의해, (접속이나 계량이 정의되지 않은) 다양체 에서는 원래 무관해야 할

E_{P(a)}

와

E_{P(b)}

가 연결(connect)되어,

E_{P(a)}

의 원소와

E_{P(b)}

의 원소를 비교할 수 있게 된다.

에 리만 계량 가 정의되어 있을 때는 임의의

v,v'\in E_{P(a)}

에 대해

:

g(v,v')=g(\varphi_{a,b}(v),\varphi_{a,b}(v'))

가 성립한다.

곡선

P(t)

상에 정의된 의 단면

e_1(t),\ldots,e_n(t)

로, 각 시각 에 대해

e_1(t),\ldots,e_n(t)

가 의 기저의 기저가 되며,

e_1(t),\ldots,e_n(t)

가

P(t)

를 따라 평행인 것을

P(t)

를 따른 '''수평 프레임'''(horizontal frame)이라고 한다.

지금까지 공변미분의 개념을 사용하여 평행 이동의 개념을 정의해 왔지만, 반대로 평행 이동의 개념을 사용하여 공변미분을 특징지을 수 있다.

다양체 위의 곡선

P(t)

와 의 벡터 번들의

P(t)

에 따른 절단

s(t)\in E_{P(t)}

를 생각할 때,

P(t)

에 따른 평행 이동을

\varphi_{a,t}

라고 하면,

:

{\nabla s\over dt}(a)

= \left.{d \over dt}\varphi_{a,t}{}^{-1}(s(t))\right|_{t=a}

가 성립한다.^[43]

여기서

{d \over dt}\varphi_{a,t}{}^{-1}(s(t))

는 벡터 공간

E_{P(a)}

에서의 미분

{d \over dt}\varphi_{a,t}{}^{-1}(s(t))=\lim_{t\to a}\tfrac{\varphi_{a,t}{}^{-1}(s(t))-s(a)}{t}

이다. 또한,

\varphi_{a,t}{}^{-1}(s(t))

는 에 관계없이

E_{P(a)}

에 속하므로,

E_{P(a)}

위의 차나 극한을 생각할 수 있다.

위의 내용을 통해 공변미분의 성분 표시에 의미를 부여할 수 있다.

즉,

:

\left.{\nabla s\over dt}\right|_{t=a}={d s^i\over dt}(a)e_i(x(a)) + s^i(a)\omega_i{}^j\left(\tfrac{dx}{dt}(a)\right)e_j(x(a))

의 첫 번째 항과 두 번째 항은 각각,

s=s^ie_i

를 라이프니츠 규칙에 따라 미분했을 때의 쪽의 미분, 쪽의 미분에 대응한다고 해석할 수 있다.

4. 분류

매끄러운 벡터 다발 $E\twoheadrightarrow M$ 위의 두 코쥘 접속 $\nabla^1$ , $\nabla^2$ 이 주어졌을 때, 그 차이 $\nabla^1-\nabla^2$ 는 매끄러운 다발 사상을 이룬다. 즉, 다음이 성립한다.

: $\nabla^1-\nabla^2\in=\Omega^1\left(M;\operatorname{End}(E)\right)=\Omega^1(M;E\otimes E^*)$

이에 따라, $E$ 위의 코쥘 접속들의 모듈라이 공간은 $\Omega^1(M;\operatorname{End}(E))$ 의 꼴을 갖는 아핀 공간이다.^[90]

다시 말해, $E$ 에 대한 접속 공간은 $\Omega^1(\operatorname{End}(E))$ 에 대한 아핀 공간이다.

마찬가지로, 두 매끄러운 벡터 다발 $E^\pm\twoheadrightarrow M$ 위의 두 코쥘 초접속의 경우에도, 그 차이는 다음과 같다.

: $\nabla^1-\nabla^2\in\Omega^-(M;\operatorname{End}(E))=\bigoplus_{i=0}^\infty\Omega^{2i}\left(M;E^+\otimes(E^-)^*\oplus E^-\otimes(E^+)^*\right)\oplus\bigoplus_{i=0}^\infty\Omega^{2i+1}\left(M;E^+\otimes(E^+)^*\oplus E^-\otimes(E^-)^*\right)$

따라서 $E$ 위의 코쥘 초접속들의 모듈라이 공간은 $\Omega^-(M;\operatorname{End}(E))$ 의 꼴을 갖는 아핀 공간이다.^[91]

5. 역사

엘리 카르탕은 1920년대 초 카르탕 접속 이론의 일부로 아핀 접속의 개념을 체계적으로 개발했다. 이와 동시에 헤르만 바일은 일반 상대성 이론의 수학적 기초를 위해 접속 이론을 개발했다. '접속'이라는 용어 역시 카르탕이 도입했다.^[93]

1950년 장루이 코쥘은 접다발 위의 아핀 접속 개념을 일반화하여, 임의의 벡터 다발 위 코쥘 접속의 현대적 정의를 제시했다.^[93]

1985년 대니얼 퀼런은 천 특성류를 연구하기 위해 초접속 개념을 도입했다.^[94]

6. 예시

코쥘 접속은 다양한 예시를 갖는다.

매끄러운 다양체의 접다발 위에는 '''아핀 접속'''이 주어질 수 있다. 아핀 접속을 갖춘 매끄러운 다양체를 '''아핀 다양체'''라고 한다.
유사 리만 기하학에서, 레비-치비타 접속은 접속 1-형식 $A$ 대신에 크리스토펠 기호 $\Gamma_{ij}^{\ \ k}$ 로 표현되는 경우가 많다.
다발 계량을 가지는 벡터 다발의 경우, 계량 접속은 다발 계량과 호환되는 접속으로 정의된다.
양-밀스 접속은 양-밀스 방정식의 운동을 만족하는 특수한 계량 접속이다.
리만 접속은 리만 다양체의 접다발에 대한 계량 접속이다.
외미분은 $E=M \times \R$ (''M'' 위의 자명한 선형 다발)에 대한 평탄한 접속이다.
전이 함수가 모두 상수인 평탄한 벡터 다발에는 임의의 자명화에서 외미분으로 주어지는 정규적인 평탄 접속이 존재한다.
$\pi: \R^2\times \R \to \R$ 에 대한 접속은 다음과 같은 연산자로 설명될 수 있다.

::

\nabla = d + \begin{bmatrix} f_{11}(x) & f_{12}(x) \\ f_{21}(x) & f_{22}(x) \end{bmatrix}dx

:

d

는 벡터 값을 갖는 매끄러운 함수에 대해 평가된 외미분이며,

f_{ij}(x)

는 매끄럽다. 단면

a \in \Gamma(\pi)

는 다음과 같은 맵으로 식별될 수 있다.

::

\begin{cases} \R \to \R^2 \\ x \mapsto (a_1(x),a_2(x)) \end{cases}

:그러면

::

\nabla(a)= \nabla \begin{bmatrix} a_1(x) \\ a_2(x) \end{bmatrix} = \begin{bmatrix} \frac{da_1(x)}{dx} + f_{11}(x)a_1(x) + f_{12}(x)a_2(x) \\ \frac{da_2(x)}{dx} + f_{21}(x)a_1(x) + f_{22}(x)a_2(x)\end{bmatrix}dx

다양체 위의 두 벡터 다발

E_1

와

E_2

가 있고, 각각의 벡터 다발에 접속

\nabla^1

와

\nabla^2

가 정의되어 있다고 하자. 그러면

E_1 \oplus E_2

와

E_1 \otimes E_2

위에도 다음과 같이 접속을 정의할 수 있다.^[37]

접속	정의
$(\nabla^1\oplus \nabla^2)$	$(\nabla^1\oplus \nabla^2)_X (s_1,s_2):=(\nabla^1_Xs_1,\nabla^2_Xs_2)$ for $X \in TM$ 、 $(s_1,s_2) \in \Gamma(E_1 \oplus E_2)$
$(\nabla^1 \otimes \nabla^2)$	$(\nabla^1 \otimes \nabla^2)_X s_1\otimes s_2:=\nabla^1_Xs_1 \otimes s_2 + s_1 \otimes \nabla^2_X s_2$ for $X \in TM$ 、 $s_1 \otimes s_2 \in \Gamma(E_1 \otimes E_2)$

6. 1. 자명한 벡터 다발 위의 접속

매끄러운 다양체

M

위에 자명한 벡터 다발

E=M\times\mathbb R^k\twoheadrightarrow M

이 주어졌다고 하자.

\mathbb R^k

의 기저를

\{e_1,\dots,e_k\}

라고 하면,

E

의 단면은 매끄러운 함수로 생각할 수 있다.

:

\Gamma^\infty(E)\cong\mathcal C^\infty(M,\mathbb R^n)

이 경우,

E

위의 모든 코쥘 접속은 다음과 같은 꼴이다.

:

\nabla\colon s\mapsto ds+\omega(s)

여기서

\omega\in\Omega^1(M)\otimes_{\mathbb R}\operatorname{End}(\mathbb R^n)

는 1차 미분 형식의

n\times n

정사각 행렬이며,

ds=\sum_ie_id\langle e_i,s_i\rangle\in\Gamma^\infty(\mathrm T^*\!M\otimes E)

는

s\colon M\to\mathbb R^n

의 각 벡터 성분에 대한 외미분이다. 이 때,

:

(\omega)^i{}_j=\langle e_j,\nabla e_j\rangle

를

\nabla

의 '''접속 형식'''(connection form^영어)이라고 한다. 접속 형식이 0이면, 코쥘 접속은 평탄 코쥘 접속을 이룬다.

일반적으로, 임의의 벡터 다발의 경우 (비표준적으로) 국소적 자명화를 잡아 위와 같이 접속 형식을 정의할 수 있다. 이는 선택한 국소적 자명화에 의존하며, 일반적으로 대역적으로 정의될 수 없다.

E

가 랭크

k

인 벡터 다발

E\to M

이고,

U

가

E

가 자명해지는

M

의 열린 부분 집합이라고 하자.

U

에서

E

는 국소 프레임을 갖는다.

:

\mathbf{e} = (e_1, \dots, e_k);\quad e_i: U \to \left.E\right|_U.

프레임

\mathbf{e}

가 모든

x\in U

에 대해 섬유

E_x

의 기저를 정의하므로, 임의의 국소 단면

s:U\to \left.E\right|_U

을 프레임으로 전개할 수 있다.

:

s = \sum_{i=1}^k s^i e_i

여기서

s^1, \dots, s^k: U \to \mathbb{R}

는 매끄러운 함수들이다.

E

위의 접속

\nabla

가 주어지면, 접속의 곱 규칙을 사용하여 단면의 국소 프레임으로

U

에서

\nabla

를 표현할 수 있다. 임의의 기저 단면

e_i

에 대해,

\nabla(e_i)\in \Omega^1(U) \otimes \Gamma(U,E)

는 국소 프레임

\mathbf{e}

로 다음과 같이 전개될 수 있다.

:

\nabla (e_i) = \sum_{j=1}^k A_i^{\ j} \otimes e_j,

여기서

A_i^{\ j}\in \Omega^1(U);\, j=1,\dots,k

는 국소 1-형식들이다. 이 형식들은 다음과 같이 1-형식의 행렬로 표현할 수 있다.

:

A = \begin{pmatrix} A_1^{\ 1} & \cdots & A_k^{\ 1} \\ \vdots & \ddots & \vdots \\ A_1^{\ k} & \cdots & A_k^{\ k} \end{pmatrix}\in \Omega^1(U, \operatorname{End}(\left.E\right|_U))

이를

U

에서

\nabla

의 국소 접속 형식이라고 한다.

\nabla

의 임의의 단면

s: U \to \left.E\right|_U

에 대한 작용은 곱 규칙을 사용하여

A

로 계산할 수 있다.

:

\nabla(s) = \sum_{j=1}^k \left(ds^j + \sum_{i=1}^k A_i^{\ j} s^i\right) \otimes e_j.

만약 국소 단면

s

가 국소 프레임

\mathbf{e}

를 기저로 사용하여 열 벡터로 쓰여진다면,

:

s = \begin{pmatrix} s^1 \\ \vdots \\ s^k\end{pmatrix},

행렬 곱셈을 사용하여

:

\nabla(s) = ds + As

로 쓸 수 있다. 여기서

ds

는 열 벡터

s

의 각 성분에 외미분

d

를 적용한 것이다. 종종 국소적으로

\left.\nabla\right|_U = d+A

라고 쓰며, 접속은 자명화에서 접속 1-형식에 의해 국소적으로 완전히 결정된다.

접속 집합의 아핀적 성질에 따르면, 임의의 접속은 자기사상 값 1-형식에 의해 다른 접속과 다르다. 접속 1-형식

A

는

\left.E\right|_U

위의 접속

\left.\nabla\right|_U

가

\left.E\right|_U

위의 자명한 접속

d

와 다른 정도를 나타내는 자기사상 값 1-형식이다.

6. 2. 레비치비타 접속

준 리만 다양체

(M,g)

위에는 리만 계량으로부터 레비치비타 접속이라는 아핀 접속을 표준적으로 정의할 수 있다. 레비-치비타 접속은 비틀림 텐서가 없는 접다발에 대한 계량 호환 접속으로, 특수한 리만 접속이다. 이는 임의의 리만 접속이 주어졌을 때, 비틀림이 없는 동등한 접속을 항상 하나만 찾을 수 있다는 점에서 유일하다. 여기서 '동등'하다는 것은 곡률 텐서는 다를 수 있지만 동일한 계량과 호환된다는 것을 의미한다. 평행이동을 참조하라. 리만 접속과 해당 레비-치비타 접속의 차이는 대비틀림 텐서에 의해 주어진다.^[6]^[7]

(M,g)

의 레비-치비타 접속

\nabla_XY

는 다음 성질들을 만족하는 유일한 접속이다.^[8]^[9]^[10]

성질
$\nabla_{X}s$ 는 $X$ 에 대해 $C^{\infty}(M)$ -선형
$\nabla_{X}s$ 는 $s$ 에 대해 $\mathbb{R}$ -선형
$\nabla_X(fY) = X(f)Y + f\nabla_X Y$
$\nabla_XY-\nabla_YX=[X,Y]$
$Z(g(X,Y))=g(\nabla_ZX,Y)+g(X,\nabla_Z Y)$ (리만 기하학의 기본 정리)

여기서 $X$ , $Y$ , $Z$ 는 $M$ 위의 임의의 미분 가능한 벡터장이며, $f$ 는 $M$ 위에 정의된 임의의 실수값 $C^{\infty}$ 급 함수이고, $[X,Y]$ 는 리 괄호이다.

국소 좌표 $(x^1,\ldots,x^m)$ 를 사용하여 레비치비타 접속을 표현하면 다음과 같다.

: $\nabla_X Y=\left(X^j{\partial Y^i \over \partial x^j} + X^jY^k \Gamma^i_{jk}\right){\partial \over \partial x^i}$

여기서 $\Gamma^i_{jk} = \frac{1}{2} g^{i\ell} \left({\partial g_{k\ell}\over \partial x^j}+ {\partial g_{\ell j}\over \partial x^k}$

{\partial g_{jk}\over \partial x^{\ell}} \right) 이며, $\Gamma^i{}_{jk}$ 를 국소 좌표 $(x^1,\ldots,x^m)$ 에 대한 '''크리스토펠 기호'''라고 한다.

6. 3. 스핀 접속

리만 계량을 갖춘 스핀 다양체

(M,g)

위의 스피너 다발

SM

위에는, 리만 계량으로 유도되는 표준적인 코쥘 (초)접속인 '''스핀 접속'''이 존재한다.

참조

_[1] 문서 Tu
_[2] 문서 Tu
_[3] 문서 Tu
_[4] 문서 Tu
_[4] 문서 Tu
_[5] 문서 Tu
_[6] 문서 Andrews
_[7] 문서 Tu
_[8] 문서 Andrews
_[8] 문서 Andrews
_[9] 문서 新井
_[10] 문서 Tu
_[11] 간행물 自己移入的Koszul多元環に対する有限条件(Fg) (有限群のコホモロジー論とその周辺) https://hdl.handle.n[...] 京都大学数理解析研究所 2018-04
_[12] 웹사이트 Koszul duality for factorization algebras and extended topological field theories http://marine.shinsh[...] 2023-10-19
_[13] 웹사이트 ２０２０年度幾何学 B アインシュタイン計量の幾何学 -リーマン幾何学入門とアインシュタイン計量の幾何学への応用- https://www.f.waseda[...] 2023-10-19
_[14] 문서 Spivak
_[15] 웹사이트 Lecture 5: Connections on principal and vector bundles https://empg.maths.e[...] 2023-01-12
_[16] 문서 森田
_[17] 문서 Tu
_[18] 문서 小林
_[19] 문서 Wendl3
_[20] 문서 Kolar
_[21] 문서 Koszul
_[22] 문서 Kobayashi-Nomizu-1
_[23] 웹사이트 Linear connection https://encyclopedia[...] 2023-10-17
_[24] 문서 Tu
_[25] 문서 小林
_[26] 문서 小林
_[27] 문서 Tu
_[28] 문서 Andrews
_[29] 문서 Tu
_[30] 문서 Tu
_[31] 문서 Wendl4
_[32] 문서 Tu
_[33] 문서 Tu
_[34] 문서 Wendl4
_[35] 문서 小林
_[36] 문서 Wang
_[37] 문서 小林
_[38] 서적 情報幾何学の基礎: 情報の内的構造を捉える新たな地平共立出版 2021-05-31
_[39] 문서 Wendl3
_[40] 문서 Tu
_[41] 문서 Tu
_[42] 문서 Tu
_[43] 문서 Spivak
_[44] 문서 小林
_[45] 문서 小林
_[46] 문서 Tu
_[47] 문서 Kobayashi-Nomizu-1
_[48] 문서 Tu
_[49] 문서 Tu
_[50] 문서 Tu
_[51] 문서 小林
_[52] 문서 Tu
_[53] 문서 Berger
_[54] 문서 Tu
_[55] 문서 小林
_[56] 문서 Tu
_[57] 문서 Spivak
_[58] 문서 Kobayashi-Nomizu-1
_[59] 문서 레ヴィ・チヴィタ接続#新井
_[60] 문서 레ヴィ・チヴィタ接続#Lee
_[61] 문서 레ヴィ・チヴィタ接続#佐々木
_[62] 문서 레ヴィ・チヴィタ接続#新井
_[63] 문서 Tu
_[64] 문서 小林
_[65] 문서 Tu
_[66] 문서 小林
_[67] 문서 新井
_[68] 문서 Tu
_[69] 문서 Tu
_[70] 문서 Wendl5
_[71] 문서 Kobayashi-Nomizu-1
_[72] 문서 小林
_[73] 문서 Tu
_[74] 문서 新井
_[75] 문서 Tu
_[76] 문서 Kobayashi-Nomizu-1
_[77] 문서 Tu
_[78] 문서 Viaclovsky
_[79] 문서 Tu
_[80] 문서 Tu
_[81] 문서 Lee
_[82] 문서 Tu
_[83] 문서 Tu
_[84] 문서 Carmo
_[85] 문서 Carmo
_[86] 문서 Prasolov
_[87] 문서 Rani
_[88] 문서 小林
_[89] 문서
_[90] 서적 Lectures on differential geometry World Scientific 1999-11
_[91] 서적 Heat kernels and Dirac operators http://www.springer.[...] Springer-Verlag 1992
_[92] 저널 Superconnections and parallel transport 2007
_[93] 저널 Homologie et cohomologie des algebres de Lie
_[94] 저널 Superconnections and the Chern character 1985

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com