태음태양력
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
태음태양력은 음력과 양력의 특징을 모두 가진 역법으로, 간지 순환법, 시간, 월령, 절기 등을 기준으로 한다. 간지를 활용하여 연, 월, 일을 기록하고, 하루를 12지(地支)에 대응하는 시간으로 나누어 사용한다. 월령은 달의 위상을 기준으로 날짜를 세며, 절기는 태양의 위치에 따라 1년을 24개로 구분한다. 태음태양력은 1년의 길이가 일정하지 않다는 단점이 있으며, 윤달을 두어 절기와 월령의 불일치를 보정한다. 한국, 중국, 일본 등 동아시아 문화권에서 널리 사용되었으며, 현재는 태양력을 주로 사용하지만, 명절과 같은 전통적인 행사에는 음력을 기준으로 한다.
더 읽어볼만한 페이지
- 태음태양력 - 중국력
중국력은 태음태양력으로 달의 움직임과 태양의 운행을 고려하여 1년의 달 배열을 정하고, 계절 변화를 파악하며, 설날 등 주요 명절 날짜 결정, 천체 현상 예측 등에 활용되어 왔으며, 다양한 역법으로 발전해 현재는 그레고리력과 함께 중국 문화와 삶에 중요한 역할을 한다. - 태음태양력 - 히브리력
히브리력은 유대교에서 사용되는 태음태양력으로, 음력 주기에 윤달을 더해 태양년과 일치시키며, 유대교 절기와 축제일을 결정하고, 힐렐 2세에 의해 확립되어 안노 문디 기원법으로 연도를 계산한다. - 표시 이름과 문서 제목이 같은 위키공용분류 - 라우토카
라우토카는 피지 비치레부섬 서부에 위치한 피지에서 두 번째로 큰 도시이자 서부 지방의 행정 중심지로, 사탕수수 산업이 발달하여 "설탕 도시"로 알려져 있으며, 인도에서 온 계약 노동자들의 거주와 미 해군 기지 건설의 역사를 가지고 있고, 피지 산업 생산의 상당 부분을 담당하는 주요 기관들이 위치해 있다. - 표시 이름과 문서 제목이 같은 위키공용분류 - 코코넛
코코넛은 코코넛 야자나무의 열매로 식용 및 유지로 사용되며, 조리되지 않은 과육은 100g당 354kcal의 열량을 내는 다양한 영양 성분으로 구성되어 있고, 코코넛 파우더의 식이섬유는 대부분 불용성 식이섬유인 셀룰로오스이며, 태국 일부 지역에서는 코코넛 수확에 훈련된 원숭이를 이용하는 동물 학대 문제가 있다. - 한국어 위키백과의 링크가 위키데이터와 같은 위키공용분류 - 라우토카
라우토카는 피지 비치레부섬 서부에 위치한 피지에서 두 번째로 큰 도시이자 서부 지방의 행정 중심지로, 사탕수수 산업이 발달하여 "설탕 도시"로 알려져 있으며, 인도에서 온 계약 노동자들의 거주와 미 해군 기지 건설의 역사를 가지고 있고, 피지 산업 생산의 상당 부분을 담당하는 주요 기관들이 위치해 있다. - 한국어 위키백과의 링크가 위키데이터와 같은 위키공용분류 - 코코넛
코코넛은 코코넛 야자나무의 열매로 식용 및 유지로 사용되며, 조리되지 않은 과육은 100g당 354kcal의 열량을 내는 다양한 영양 성분으로 구성되어 있고, 코코넛 파우더의 식이섬유는 대부분 불용성 식이섬유인 셀룰로오스이며, 태국 일부 지역에서는 코코넛 수확에 훈련된 원숭이를 이용하는 동물 학대 문제가 있다.
| 태음태양력 | |
|---|---|
| 개요 | |
| 이름 | 태음태양력 |
| 다른 이름 | 월력 음양력 이슬람력 (특정 문화권) |
| 정의 | |
| 유형 | 태음력과 태양력의 요소를 결합한 역법 |
| 설명 | 달의 삭망월을 기준으로 한 달을 정하고, 지구의 태양 주위를 도는 황도를 기준으로 한 해를 정함. 계절의 변화를 반영하기 위해 윤달 또는 윤년을 추가함. |
| 역사 및 문화 | |
| 기원 | 고대 문명 (메소포타미아, 중국 등) |
| 사용 문화권 | 동아시아 (중국, 한국, 일본, 베트남) 유대교 기타 문화권 |
| 관련 명절 | 설날 추석 단오 기타 음력 기반 명절 |
| 특징 | |
| 달력 구성 | 한 달: 삭망월 (약 29.5일) 일 년: 12개월 또는 13개월 (윤달 존재 시) |
| 윤달 | 태양년과의 차이를 보정하기 위해 추가되는 달 |
| 장점 | 달의 위상 변화와 계절 변화를 동시에 반영 전통적인 농경 생활과 밀접한 관련 |
| 단점 | 태양력에 비해 날짜 계산이 복잡함 윤달 때문에 해마다 길이가 달라짐 |
| 동아시아 태음태양력 | |
| 명칭 | 중국: 農曆 (nónglì, 농리) 한국: 태음태양력 일본: 旧暦 (kyūreki, 구력) 베트남: Âm dương lịch (음양력) |
| 특징 | 24절기를 사용하여 계절 구분 간지를 사용하여 연도 및 날짜 표시 각 나라별 약간의 차이 존재 |
| 유대력 | |
| 특징 | 종교적인 절기와 행사 날짜 결정에 사용 19년을 주기로 7번의 윤달 추가 니산월을 기준으로 시작 |
| 기타 태음태양력 | |
| 사례 | 티베트력 힌두력 기타 지역의 전통 역법 |
2. 간지순환법
육십갑자 주기 기반의 간지 시스템은 천간과 지지의 주기를 수학적으로 반복하여 사용한다. 천문학적 관측과 함께 연, 월, 일의 정의, 측정, 예측이 개선되었다. 특히 지구에서 본 태양 주기와 음력 주기를 수학적으로 연관시키려는 노력에 중점을 두었지만, 이는 어느 정도의 수치 근사치가 필요했다.[25][26][27]
간지는 연(年), 월(月), 일(日)을 표기하는데 사용되었다.
2. 1. 세차(歲次)
연(年)에 붙이는 간지를 세차(歲次) 또는 태세(太歲)라고 한다.[25] 예를 들어, 2022년은 임인년(壬寅年)이다. 한국 등에서는 태음력 체계에서 연대를 나타낼 때 '병자년, 정축년'과 같이 간지로 표기하는 간지기년법(干支紀年法)을 사용한다.[26] 간지기년법은 동한 건무 30년(AD 54)부터 사용하기 시작했다.[27]무령왕릉 표지석에는 백제 무령왕의 사망일을 “계묘년 5월 병술 삭 7일 임진”이라고 표기하여 세차(계묘년)를 기록했다.[28] 또한, 1911년에 있었던 혁명은 신해혁명(辛亥革命), 1592년에 발생한 조선과 일본 간의 전쟁은 임진왜란(壬辰倭亂)처럼 세차의 간지를 활용하여 역사적 사건을 명명하고 기록하기도 한다.
같은 간지가 돌아오는 데 걸리는 기간은 60년이며, 이를 회갑이라고 한다.
2. 2. 월건(月建)과 일진(日辰)
월건(月建)은 월(月)에 붙이는 간지이다.[27] 월건은 지지(地支)를 고정하고 천간(天干)만 순환하는 방식을 사용하는데, 이를 간지기월법(干支記月法)이라고 한다. 정월의 지지는 인(寅)으로 고정되어 있고, 2월은 묘(卯), 3월은 진(辰)이 되는 식이다. 즉, 정월부터 12월까지 순서대로 인(寅)부터 축(丑)까지 배속된다. 천간은 순환하기 때문에 5년마다 반복된다. 예를 들어 2022년 음력 1월은 임인(壬寅)월이지만, 2023년 음력 1월은 갑인(甲寅)월이 된다.일진(日辰)은 일(日)에 붙이는 간지이다. 간지로 일을 기록한 것은 노음공 3년(기원전 722년) 2월부터이다.[29] 이 간지기일법(干支記日法)은 약 2,700여 년 동안 중단 없이 기록되었기 때문에, 세계에서 가장 긴 체계적인 기일법이다.
2. 3. 생활 속의 영향
"일진(日辰)이 사납다"라는 표현이나, 축문의 시작을 "유세차(維歲次)..."로 하는 관습은 사주 체계가 언어생활에 영향을 준 사례이다.[30] 간지(干支)는 10간과 12지를 합쳐 두 글자로 나타내므로 사주는 여덟 글자로 나타낸다. 이를 사주팔자(四柱八字)라고 하며 간단히 팔자라고도 한다.[30] 태양태음력을 사용하는 문화권에서는 태어난 시각이 그 사람의 운세에 영향을 준다는 믿음이 있어, 사람의 타고난 운수나 분수를 팔자라고 부른다. 한국어에는 "팔자가 세다"거나 "팔자를 고쳤다"는 표현이 있다.[30]3. 시간과 하루
태음태양력은 하루를 12개로 나누어 12지에 대응시켰다. 예를 들어 자시, 축시, 인시, 묘시, 진시, 사시, 오시, 미시, 신시, 유시, 술시, 해시가 있다. 오늘날의 24시간 체계와 비교하면 자정은 자시(子時)가 되고, 정오는 오시(午時)가 된다.
| 12지 | 자(子) | 축(丑) | 인(寅) | 묘(卯) | 진(辰) | 사(巳) | 오(午) | 미(未) | 신(申) | 유(酉) | 술(戌) | 해(亥) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 24시간 | 23 ~ 1 | 1 ~ 3 | 3 ~ 5 | 5 ~ 7 | 7 ~ 9 | 9 ~ 11 | 11 ~ 13 | 13 ~ 15 | 15 ~ 17 | 17 ~ 19 | 19 ~ 21 | 21 ~ 23 |
시간 측정에는 앙부일구와 같은 해시계나 자격루와 같은 물시계가 사용되었다.[31] 해시계는 태양이 남중할 때를 정오로 측정하는 진태양시를 사용했다. 따라서 오늘날의 표준시간인 평균태양시와는 계절에 따라 차이가 발생한다. 평균태양시와 진태양시의 차이를 균시차라고 하는데, 균시차가 나타나는 이유는 지구 자전축이 황도에 비해 약 23.5˚ 정도 기울어져 있고, 지구 공전 궤도가 타원이기 때문이다.[32]
4. 월령
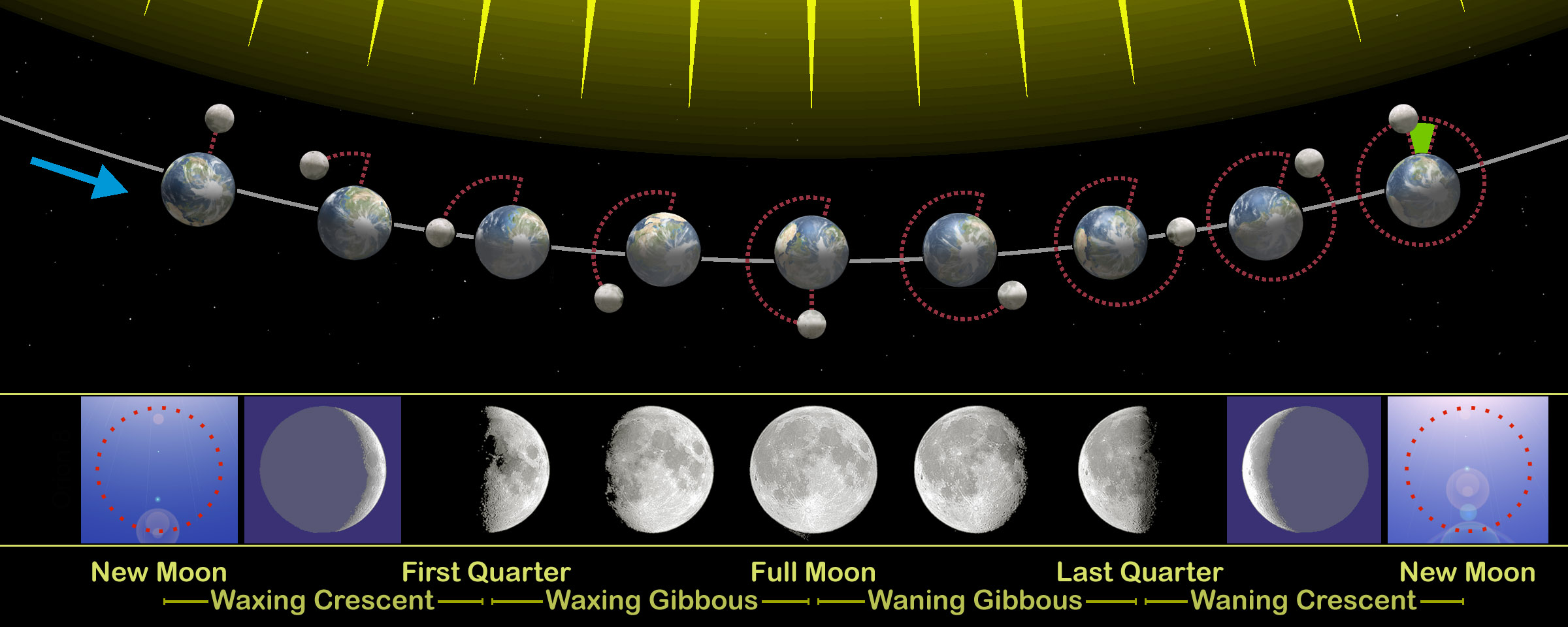
월령은 음력 초하룻날부터 헤아리는 날짜를 의미한다.[37] 해와 달의 황경이 같아지는 음력 초하룻날을 삭(朔)이라 하며, 보름달에서 다시 보름달이 되는 삭망월 주기는 29.5306일이다. 이는 달의 실제 공전주기인 27.322일보다 조금 더 긴데, 달이 지구 주위를 공전하는 동안 지구 역시 태양의 주위를 공전하고 있어서 달이 다시 보름이 되려면 조금 더 돌아야 하기 때문이다. 달의 위치는 황경을 기준으로 정하는데, 황경 0˚ 즉 태양과 달의 위치가 같을 때를 삭(朔) 즉 초하루로 하고 90˚일 때를 상현, 180˚일 때를 망(望) 즉 보름, 270˚일 때를 하현이라 한다.[36]
태음태양력의 월령은 큰 달은 30일, 작은 달은 29일이다. 큰 달과 작은 달은 번갈아 반복되는데 이는 삭망월 주기를 29.5일로 산정한 것이다. 한나라 시기에 제작된 태초력에서는 삭망주기를 일, 즉 29.530864일로 계산하여 비교적 정확하게 정립하였다.[38] 한 해에는 열두 달이 있으며, 숫자로 1월, 2월, ... 12월과 같이 나타내지만, 1월은 정월, 11월은 동짓달, 12월은 섣달이라고 부르기도 한다.
정월대보름과 추석과 같은 명절은 월령과 관련이 깊다. 정월대보름은 한국에서 오곡밥을 지어 먹고 부럼을 먹으며 무병장수를 비는 중요한 명절이다.[39] 추석 역시 한국에서 추수감사절과 같은 의미를 지니는 중요한 명절이다.[42] 태음태양력의 명절은 다음과 같다.
| 이름 | 날짜 |
|---|---|
| 설날 | 1월 1일 |
| 정월대보름 | 1월 15일 |
| 영등날 | 2월 1일 |
| 삼짇날 | 3월 3일 |
| 초파일 | 4월 8일 |
| 단오 | 5월 5일 |
| 유두 | 6월 15일 |
| 칠석 | 7월 7일 |
| 백중 | 7월 15일 |
| 추석 | 8월 15일 |
| 중양절 | 9월 9일 |
| 섣달 그믐 | 12월 그믐 |
5. 절기
태음태양력에서 태양의 위치는 역법 계산의 중요한 요소이다. 절기는 태양의 위치에 따라 24개로 나뉘는데, 입춘을 기준으로 홀수 절기는 '중', 짝수 절기는 '절'로 구분한다. 절기는 황경을 15˚ 간격으로 나누어 설정하며, 춘분을 0˚로 한다. 태양이 황경 0˚에 다다르는 날을 춘분입기일이라 하며, 우수 전까지의 기간 역시 춘분이라고 한다.[43]
| 황경 | 절기 | 황경 | 절기 |
|---|---|---|---|
| 315° | 입춘 | 135° | 입추 |
| 330° | 우수 | 150° | 처서 |
| 345° | 경칩 | 165° | 백로 |
| 0° | 춘분 | 180° | 추분 |
| 15° | 청명 | 195° | 한로 |
| 30° | 곡우 | 210° | 상강 |
| 45° | 입하 | 225° | 입동 |
| 60° | 소만 | 240° | 소설 |
| 75° | 망종 | 255° | 대설 |
| 90° | 하지 | 270° | 동지 |
| 105° | 소서 | 285° | 소한 |
| 120° | 대서 | 300° | 대한 |
황도를 기준으로 태양의 운행을 계산하면 24절기가 돌아오는 주기는 태양력과 같이 365.242199일이 된다. 한나라 시기 태초력은 이 주기를 365.25016일로 계산했다.[38] 태양력에서는 절기가 항상 비슷한 날짜에 돌아오지만, 태음태양력은 달의 삭망만을 따르므로 절기 날짜는 일정하지 않다.
절기 산정 방법으로는 1 주기를 평균하여 15.218425일씩 더하는 평기법이 오랫동안 쓰였다. 그러나 지구 공전궤도는 타원이므로 근일점에서는 절기가 빠르게, 원일점에서는 느리게 변한다. 청나라 시기 시헌력은 이러한 차이를 감안하여 절기 사이 길이를 조정했다.[24]
농사와 같이 계절 변화와 관련된 일에는 날짜보다 절기가 중요했다. 절기 기준 세시 풍습에는 한식, 망종, 삼복 등이 있다.
6. 윤달과 1년
태음태양력에서 윤달은 태음력과 태양력의 오차를 보정하기 위해 추가되는 달이다. 천자문에는 "윤여성세(閏餘成歲)"라는 구절이 있는데, 이는 윤달을 사용하여 절기와 월령을 맞춘다는 뜻이다.[44]
태음력은 달의 삭망월 주기를 기준으로 1년을 354일 (큰 달 6개월 + 작은 달 6개월)로 계산하는데, 이는 태양력의 1년보다 11일 정도 짧다. 이러한 오차가 누적되면 3년이 채 지나지 않아 한 달 이상의 차이가 발생하므로, 절기와 월령을 맞추기 위해 윤달을 추가해야 한다.
윤달을 정하는 방법으로는 무중치윤법(無中置閏法)이 사용된다. 무중치윤법은 24절기 중 중기(中氣)가 없는 달을 윤달로 삼는 방법이다.[44] 보통 19년에 7번의 윤달이 추가되는데, 이렇게 19년마다 태음태양력과 태양력이 일치되는 주기를 메톤 주기라고 한다.[45]
태음태양력의 1년은 평년에는 354일, 윤년에는 383~384일이다. 이처럼 1년의 길이가 일정하지 않다는 점은 태음태양력의 가장 큰 단점으로 꼽힌다.[46]
한국, 중국, 베트남은 같은 원리의 태음태양력을 사용하지만, 기준 자오선이 다르기 때문에 설날이 다른 날이 될 수 있다. 1914년부터 2099년까지 200년 동안 한국과 중국의 설날이 하루 차이 나는 경우는 15번이다.[47]
7. 각국의 태음태양력
중국, 불교, 버마, 아시리아, 히브리, 자이나교, 쿠르드 뿐만 아니라 전통적인 네팔력, 힌두, 일본, 한국, 몽골, 티베트, 베트남 (동아시아 중국 문화권) 달력과 고대 헬레니즘, 콜리니, 바빌론력은 모두 태음태양력이다.[1] 이슬람 이전 남아라비아의 일부 달력도 태음태양력을 따랐다.
일본에서는 아스카 시대의 원가력 이래, 중국 왕조가 제정한 달력(중국력, 일본에서는 '''한력'''이라고도 칭함)을 그대로 도입하여 와력으로 사용했다. 조간 4년(862년)에 선명력으로 개력한 이후, 약 800년이 넘도록 선명력을 계속 사용한 결과, 에도 시대 초에는 태양의 운행 예측에 약 2일의 오차가 발생했다.[12]
1685년 10월, 시부카와 하루미의 의견에 의해 일본 독자적인 태음태양력(수시력 기반)인 조쿄력으로 개력이 실현되었다(반력은 그 다음 해). 이후, 조쿄력(조쿄 2년 - 호레키 4년), 호레키력(호레키 5년 - 간세이 10년), 간세이력(간세이 10년 - 덴포 14년), 덴포력(덴포 15년〈고카 원년〉 - 메이지 5년)과 독자적인 태음태양력의 사용이 계속되었다. 메이지 5년 11월, 정부로부터 태음태양력에서 태양력으로 전환한다는 취지의 태정관 포고가 발령되어, 같은 해 12월 2일(덴포력의 날짜) 다음 날을 그레고리력에 따라 메이지 6년(1873년) 1월 1일로 함으로써, 그 역사가 막을 내렸다.
7. 1. 한국
삼국시대 이후 한국에서 쓰인 역은 모두 태음태양력이다. 거의 대부분 중국에서 사용되는 역법을 채택하였다. 1896년 (고종 33년)부터 태양력의 한 종류인 그레고리력을 채택하여 현재까지 사용하고 있다. 이로 인해 음력 사용은 공적 분야에서 단절되었으나, 민간에서는 개인의 생일이나 단오 등 여러 민간 행사에 여전히 음력을 사용하고 있다. 또한 정부에서도 설날, 추석, 석가탄신일 같은 전통 명절에 따른 법정공휴일 만큼은 음력을 기초로 하여 지정하고 있다.[25]| 시대 | 사용 역법 |
|---|---|
| 신라 | 인덕력 |
| 고구려 | 인덕력 |
| 백제 | 원가력 |
| 신라 | 대연력, 선명력 |
| 고려 | 선명력, 충선왕 때 수시력 채택 |
| 고려는 십정력, 칠요력, 견행력, 둔갑력, 태일력 등 독자적인 역법을 만들기도 하였으나, 실제로 쓰였는지는 확인되지 않는다. | |
| 공민왕 19년(1370년)에 수시력의 이름을 바꾼 대통력 채택 | |
| 조선 | 《칠정산내편》에 의해 수시력을 수정하여 사용 |
| 1653년(조선 효종 4년)에 서양식 계산법을 사용한 시헌력 채택 | |
| 갑오개혁의 일환으로 1896년부터 태양력의 한 종류인 그레고리력 채택 | |
| 대한제국 | 그레고리력을 사용하였고 현재까지 이어지고 있다. |
7. 2. 그 밖의 지역
중국력은 중국의 전통 역법으로, 한국, 일본 등 주변 국가의 역법에 큰 영향을 주었다.[1] 바빌로니아력은 고대 바빌로니아에서 사용되었으며, 메톤 주기를 활용하여 윤달을 배치하였다.[5] 힌두력은 인도에서 사용되는 역법으로, 항성년을 기준으로 한다.[1]그 외에도 불교력, 유대력, 일본력 등이 태음태양력에 속한다.
8. 미래
달과 지구 사이의 만유인력 때문에 발생하는 조석력은 지구의 자전 속도를 늦추는 힘으로 작용하며,[48] 달은 매년 3cm 정도씩 지구에서 멀어지고 있다.[49] 이는 매우 미미한 양이긴 하지만 달의 자전 주기가 점차 길어진다는 것을 뜻한다. 따라서 삭망월 주기도 길어지게 되고 태음태양력 역시 수정되게 될 것이다. 이러한 현상이 수만 년 이상 계속되어 삭망월 주기가 30일이 되면 큰 달과 작은 달의 구분 없이 태음태양력의 평년은 360일이 되고 윤달은 6년에 한 번꼴로 돌아오게 된다.
참조
[1]
간행물
TAʾRĪKH
[2]
논문
Considering Chengzhou ("Completion of Zhou") and Wangcheng ("City of the King")
http://www.kaogu.cn/[...]
2023-09-20
[3]
서적
Explanatory Supplement to the Astronomical Almanac
University Science Books
2013
[4]
서적
Explanatory Supplement to the Astronomical Almanac
https://archive.org/[...]
[5]
웹사이트
The Babylonian Calendar
https://webspace.sci[...]
Utrecht University
2021-07
[6]
서적
Primitive Time-Reckoning: A Study in the Origins and First Development of the Art of Counting Time among the Primitive and Early Culture Peoples
C. W. K. Gleerup
1920
[7]
서적
Musqueam Reference Grammar
UBC Press
[8]
문서
서역이야기
[9]
사전
세계대백과사전
평범사
[10]
서적
尚書 : 虞書 : 堯典
https://ctext.org/sh[...]
中國哲學書電子化計劃
[11]
서적
暦の歴史
[12]
서적
暦
[13]
웹사이트
国立天文台、質問3-4「旧暦」ってなに?
https://www.nao.ac.j[...]
국립천문대
[14]
문서
[15]
서적
暦
[16]
문서
[17]
웹사이트
季節はずれの赤穂浪士の討ち入り
http://blog.livedoor[...]
[18]
서적
お言葉ですが…(9) 芭蕉のガールフレンド
文春文庫
[19]
서적
역사용어 바로쓰기
역사비평사
[20]
웹사이트
'[네이버 지식백과] 새로운 달력, 그레고리력 도입! (초등학생을 위한 과학사)'
https://terms.naver.[...]
[21]
서적
일년이 열두 달이 된 이야기
문학동네
[22]
웹사이트
설(tet)
http://www.vietinfo.[...]
Vietnam Information
[23]
서적
달력과 권력
부키
[24]
논문
10간과 12지의 최소공배수는 60
http://kofst.or.kr/k[...]
한국과학기술단체총연합회
[25]
서적
옛날에도 일요일이 있었나요?
책이있는마을
[26]
웹사이트
'[네이버 지식백과] 역법 [曆法] (한국민족문화대백과, 한국학중앙연구원)'
https://terms.naver.[...]
[27]
서적
아주 쉽고도 재미있는 과학이야기
청담문학사
[28]
서적
일상생활의 기상학
시그마프레스
[29]
서적
아주 쉽고도 재미있는 과학이야기
청담문학사
[30]
사전
표준국어대사전 - 팔자
[31]
서적
째깍째깍 시계의 역사
비룡소
[32]
웹사이트
태양의 팔자걸음
http://astro.kasi.re[...]
천문우주지식정보
[33]
서적
기본 천문학(제5판)
시그마프레스
[34]
서적
한국과학사의 새로운 이해
연세대학교출판부
[35]
서적
한국과학사의 새로운 이해
연세대학교출판부
[36]
서적
기본 천문학(제5판)
시그마프레스
2008
[37]
문서
표준국어대사전 - 월령1
[38]
문서
글로벌 세계 대백과, 삼통력
[39]
서적
한국세시풍속사전(봄편)
국립민속박물관
2005
[40]
웹인용
元宵节的历史
https://web.archive.[...]
2014-02-08
[41]
웹사이트
小正月とは? - 岩手県政策地域部NPO・文化国際課『いわての正月・小正月』
http://www.bunka.pre[...]
[42]
서적
이것이 베트남이다
와이미디어
2007
[43]
서적
일상생활의 기상학
시그마프레스
2000
[44]
서적
일상생활의 기상학
시그마프레스
2000
[45]
서적
달력과 권력
부키
2001
[46]
서적
재미있는 과학이야기
서해문집
1998
[47]
뉴스
2006년 설날 날짜..."휴대전화를 믿지 마세요"
https://news.v.daum.[...]
노컷뉴스
2005-12-10
[48]
서적
지구에 관한 작은 책
시그마프레스
2006
[49]
서적
기본 천문학(제5판)
시그마프레스
2008
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
