단순 무작위 추출법
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
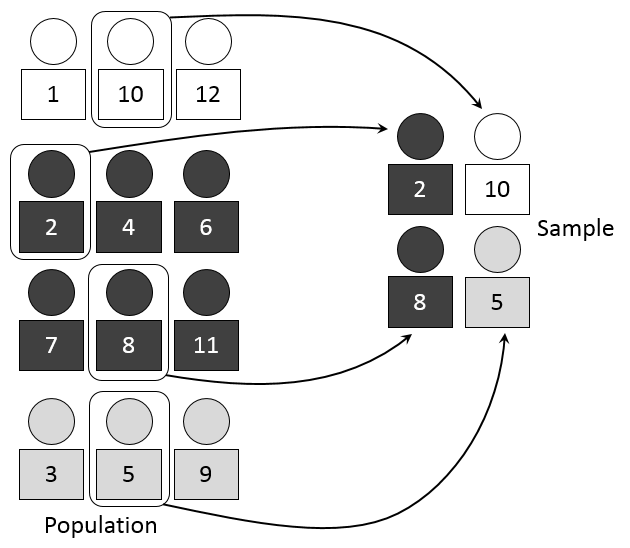
단순 무작위 추출법은 모집단에서 각 개체가 동일한 확률로 선택되는 확률적 표본 추출 방법이다. 모든 부분 집합이 표본으로 선택될 확률이 동일하며, 복원 추출과 비복원 추출 방식이 모두 사용된다. 장점으로는 방법의 단순성과 분류 오류가 적다는 점이 있으며, 모집단에 대한 사전 지식이 적을 때 유용하다. 단점은 모든 개체의 확인 및 표시가 필요하여 비용이 많이 들고, 지리적으로 분산된 개체 조사에 어려움이 있으며, 모집단 내 이질성이 존재할 경우 층화 추출법보다 효율성이 낮다는 것이다. 통계 조사에서 표본 오차를 추정하고 모집단의 특성을 추론하는 데 활용되며, 계통 추출법, 층화 추출법 등 다른 무작위 추출법과 비교된다. 한국의 통계 조사에서는 표본 추출 틀을 기반으로 난수표나 컴퓨터를 활용하여 표본을 추출한다.
더 읽어볼만한 페이지
- 표집 - 표본조사
표본조사는 모집단의 일부인 표본을 추출하여 전체 모집단의 특성을 추정하는 통계적 방법으로, 시간과 비용을 절약하면서 비교적 정확한 결과를 얻을 수 있도록 다양한 표본 추출 방법과 오차 최소화, 가중치 조정 등의 과정을 포함한다. - 표집 - 가위바위보
가위바위보는 두 명 이상이 주먹, 가위, 보 세 가지 손 모양으로 승패를 가리는 놀이로, 간단한 규칙과 직관성으로 널리 알려져 있으며 중국 또는 일본에서 유래되었다는 설이 있다. - 평가 방법 - 양적 연구
양적 연구는 사회 현상이나 자연 현상을 수치화하여 과학적 방법과 통계 분석 등을 통해 가설을 검증하고 인과 관계를 규명하는 연구 방법론이다. - 평가 방법 - 사례 연구
사례 연구는 소수 사례에 대한 심층 연구로 현상에 대한 풍부한 이해를 제공하는 질적 연구 방법으로, 다양한 연구 설계와 사례 선택 전략을 활용하여 이론 생성 및 검증 등에 유용하지만 일반화의 어려움과 선택 편향의 위험이 존재하며 교육 분야에서 교수법으로 활용된다.
2. 단순 무작위 추출의 개념 및 원리
단순 무작위 추출(단순 랜덤 추출, 단순 임의 추출)은 모집단의 모든 개체가 표본으로 선택될 확률이 동일한 추출 방법이다.probability sampling영어
예를 들어, ''N''명의 대학생 중 ''X'' (''N''보다 작음)명에게 농구 경기 티켓을 제공할 때, 공정한 방법으로 단순 무작위 추출을 사용할 수 있다. 모든 학생에게 0부터 ''N''-1까지 번호를 부여하고, 전자적 또는 난수표를 이용하여 무작위로 숫자를 생성한다. 처음 ''X''개의 숫자에 해당하는 학생들이 티켓을 받게 된다.
단순 무작위 추출은 의도적인 절차 없이 요소를 추출하는 것이 특징이다. 모든 요소는 동일한 확률로 추출된다. 예를 들어, 학급 청소 당번을 뽑을 때, "출석부에서 제비뽑기로 무작위 추출"하는 것은 단순 무작위 추출이지만, "선생님이 마음에 드는 학생을 임명"하는 것은 유의 추출이다. 단순 무작위 추출은 객관적인 공정성을 보장하며, "골판지로 만든 룰렛"이나 "인쇄 실패 용지 뒷면으로 만든 추첨함" 등 도구를 쉽게 만들 수 있어 널리 사용된다.
하지만 "무작위 추출"이라고 해도 객관적인 무작위성이 보장되지 않는 경우가 있다. 예를 들어, "출석부에서 우연히 눈에 띄는 학생을 청소 당번으로 임명"하는 것은 선생님이 특정 학생을 편애할 가능성을 배제할 수 없으므로 무작위 추출이 아니다.
통계 조사에서도 단순 무작위 추출이 사용된다. "나무젓가락으로 만든 추첨기"처럼 정밀도가 낮은 난수 발생기를 사용하면, "청소 당번 뽑기"와 같은 경우에는 큰 문제가 되지 않을 수 있지만, 통계 조사에서는 표본 오차의 원인이 되므로 문제가 된다. 따라서 통계 조사에서는 유의 추출이 아닌, 반드시 무작위 추출을 사용해야 한다.
공업 제품의 "샘플 검사"에서도 무작위성이 낮으면 불량품 비율을 정확하게 파악하기 어렵다. 따라서 비용이 들더라도 무작위성을 확보하는 것이 중요하다. 특히, 창고 안쪽에 쌓인 제품을 검사하는 것은 어렵기 때문에, 제품 전체를 무작위로 추출하기 위한 노력이 필요하다.
카드 게임과 같은 테이블 게임에서도 무작위 추출은 중요하다. 게임에서 무작위 추출처럼 보이면서 원하는 패를 뽑는 "부정 행위" 기술이 있지만, 이는 절대로 해서는 안 된다.
추측 통계학을 창시한 R.A. 피셔는 분산 분석법 등 다양한 통계 기법 개발에 무작위 추출을 이론적 전제로 사용했다.
2. 1. 정의
단순 무작위 추출법(또는 단순 랜덤 추출법, 단순 임의 추출법)은 모집단에서 개체를 뽑을 때 각각의 개체가 모두 동등한 확률로 뽑히는 확률적 표본 추출(probability sampling) 또는 무작위 표본 추출(random sampling)에 포함되는 하나의 추출법이다. 단순 무작위 추출은 모든 가능한 표본이 동일한 확률로 선택되도록 한다. 예를 들어 n개의 추출단위로 얻을 수 있는 모든 부분집합이 표본으로 선택될 확률이 같도록 한다.[3] 복원추출법에서는 크기가 N인 모집단에서 n개의 추출단위로 구성된 가능한 표본의 가짓수 에서 각각의 부분집합이 표본으로 선택될 확률이 으로 모두 같다.단순 무작위 추출법에는 한 번 뽑힌 요소를 다시 모집단으로 복원하여 표본을 뽑는 복원추출법과 한 번 뽑히면 모집단으로 다시 보내지 않는 비복원추출법이 모두 사용된다. 복원추출법은 비복원추출법에 비해 좀 더 빈번히 사용되며, 모집단의 크기가 비교적 작을 때 적합하다. 모집단의 크기가 크고 표본의 크기가 작을 때에는 같은 요소를 뽑을 확률이 적어지기 때문에 복원추출법과 비복원추출법 간의 차이 또한 적다.
무작위표본추출법 중에 가장 기본적인 유형이지만 실제로 순수한 의미에서의 단순 무작위 추출법은 거의 쓰이지 않는다. 단순 무작위 추출법의 원리는 동일한 수의 항목을 가진 모든 집합이 선택될 확률이 동일하다는 것이다. 작은 모집단과 큰 모집단에서 종종 이러한 추출은 일반적으로 "'''비복원 추출'''", 즉, 모집단의 어떤 구성원도 두 번 이상 선택하는 것을 의도적으로 피한다. 단순 무작위 추출은 대신 복원 추출로 수행될 수 있지만, 이는 덜 일반적이며 일반적으로 단순 무작위 추출 '''복원 추출'''로 더 자세히 설명된다.
비복원 추출로 수행된 추출은 더 이상 독립적이지 않지만 여전히 교환 가능성을 만족하므로, 수학적 통계의 대부분의 결과는 여전히 유효하다. 또한, 큰 모집단에서 작은 표본의 경우, 동일한 개체를 두 번 선택할 확률이 낮기 때문에 비복원 추출은 복원 추출과 거의 동일하다.
개인의 편향되지 않은 무작위 선택은 많은 표본이 추출될 경우 평균 표본이 모집단을 정확하게 나타내도록 하는 데 중요하다. 그러나 이는 특정 표본이 모집단의 완벽한 표현임을 보장하지 않는다. 단순 무작위 추출은 표본을 기반으로 전체 모집단에 대한 외부 타당한 결론을 도출할 수 있게 할 뿐이다.[4]
개념적으로 단순 무작위 추출은 확률적 추출 기법 중 가장 간단하다. 이는 완전한 추출틀을 필요로 하며, 이는 대규모 모집단에 대해 구성할 수 없거나 실현 가능하지 않을 수 있다. 완전한 틀이 사용 가능하더라도, 모집단의 단위에 대한 다른 유용한 정보를 사용할 수 있는 경우 더 효율적인 접근 방식이 가능하다.
단순 무작위 추출의 장점은 분류 오류가 없고, 틀 외에 모집단에 대한 최소한의 사전 지식만 필요하다는 것이다. 또한 단순성은 이러한 방식으로 수집된 데이터를 비교적 쉽게 해석할 수 있게 한다. 이러한 이유로 단순 무작위 추출은 모집단에 대한 정보가 많지 않고 데이터 수집을 무작위로 분산된 항목에서 효율적으로 수행할 수 있거나, 추출 비용이 효율성보다 단순성이 덜 중요하게 만드는 데 충분히 작을 때 가장 적합하다. 이러한 조건이 충족되지 않으면, 층화 추출 또는 군집 추출이 더 나은 선택일 수 있다.
1000명의 학생이 있는 학교를 예시로 들어보자. 연구자가 그중 100명을 추가 연구를 위해 선택하려 한다면, 모든 학생의 이름을 바구니에 넣고 100개의 이름을 꺼낼 수 있다. 이때, 모든 사람이 선택될 동등한 기회를 가지며, 표본 크기(''n'')와 모집단(''N'')을 알고 있으므로 주어진 사람이 선택될 확률(''P'')도 쉽게 계산할 수 있다.
- 어떤 사람이라도 한 번만 선택될 수 있는 경우 (선택 후 선택 풀에서 제거):
:
- 선택된 사람이 선택 풀로 반환되는 경우 (두 번 이상 선택될 수 있음):
:
이는 학교의 모든 학생이 어떤 경우든 이 방법을 사용하여 선택될 확률이 대략 10분의 1임을 의미한다. 또한 100명의 학생 어떤 조합도 선택될 확률이 동일하다.

단순 무작위 추출이란, 모집단의 모든 요소를 대상으로 무작위 추출하는 방법이다. 무작위 추출의 가장 기본적인 방법으로, 가장 단순한 방법이다. 단순 무작위 추출법은 "추출 틀"의 정보만 있으면 수행할 수 있으며, 추출 틀의 크기가 작은 경우에는 이 기법을 사용하는 것이 가장 쉽다. 그러나, 추출 틀이 큰 경우에는 매우 수고와 시간이 들기 때문에, "층화"나 "다단계 추출"을 하는 것이 더 쉽다. 계통 추출과는 달리, 인접한 요소끼리 선택되거나, 3개 이상 연속된 요소가 선택될 가능성이 있다.
2. 2. 복원 추출과 비복원 추출
단순 무작위 추출법에는 한 번 뽑힌 요소를 다시 모집단에 넣어 표본을 뽑는 복원 추출법과, 한 번 뽑힌 요소는 모집단에서 제외하는 비복원 추출법이 있다. 복원 추출법은 모집단 크기가 비교적 작을 때 적합하며, 비복원 추출법보다 더 빈번히 사용된다. 모집단 크기가 크고 표본 크기가 작을 때는 같은 요소를 뽑을 확률이 적어지기 때문에 복원 추출법과 비복원 추출법 간의 차이가 적다.[3]작은 모집단에서는 주로 '''비복원 추출'''을 사용하는데, 이는 모집단의 어떤 구성원도 두 번 이상 선택하지 않도록 의도적으로 피하는 방법이다. 반면 단순 무작위 추출은 복원 추출로 수행될 수도 있지만 덜 일반적이며, 이 경우 단순 무작위 추출 '''복원 추출'''로 더 자세히 설명된다.
비복원 추출은 독립적이지 않지만, 교환 가능성을 만족하여 수학적 통계의 대부분 결과가 여전히 유효하다. 큰 모집단에서 작은 표본을 추출할 때는 동일한 개체를 두 번 선택할 확률이 낮아 비복원 추출과 복원 추출이 거의 동일하다.[3]
예를 들어, 1000명의 학생이 있는 학교에서 100명을 선택하는 경우, 어떤 방법을 사용하든 학교의 모든 학생은 대략 10분의 1의 확률로 선택된다. 확률은 다음과 같이 계산할 수 있다.
- 비복원 추출 (한 번만 선택):
:
- 복원 추출 (두 번 이상 선택 가능):
:
무작위 추출을 반복할 때, 이미 추출된 요소를 모집단에서 제외하는 "비복원 추출"과, 요소를 제외하지 않고 다시 모집단에 넣는 "복원 추출"이 있다.
예를 들어, 반 학생 중 청소 당번을 뽑을 때 "복원 추출"을 하면 같은 사람이 여러 번 선택될 수 있어 불합리하므로, "비복원 추출"이 바람직하다. 그러나 주사위처럼 "비복원 추출"이 어려운 경우가 있다. 모집단이 매우 크고 추출되는 요소 수가 매우 적으면, 같은 사람이 여러 번 뽑힐 가능성은 매우 작으므로 "복원 추출"이 종종 사용된다.
3. 단순 무작위 추출의 장단점
단순 무작위 추출법은 방법이 단순하고 분류 오차가 미세하며, 상대적으로 자료를 분석하기 쉽다는 장점이 있다. 예를 들어, 통계 분석을 할 때 단순 무작위 추출법으로 구해진 표본을 이용하여 표본 평균의 신뢰구간을 정할 수 있다. 또한 모집단에 대한 사전 지식이 필요하지 않아 모집단 정보가 매우 적을 때 유용하게 쓰일 수 있다.
그러나 단순 무작위 추출법은 이론적으로는 가장 단순한 표본 추출법이지만, 모든 개체가 추출 이전에 확인되고 표시되어야 하기 때문에 비용이 많이 들고 실현 가능성이 적다는 단점이 있다. 각 개체가 뽑힐 확률이 동일하므로, 표본에 속한 개체가 지리적으로 넓게 분산될 수 있으며, 이 경우 각 개체를 조사하는 데 더 큰 비용이 들 수 있다.[16] 또한 모집단 안에 집단 간 이질성이 존재할 경우, 층화 추출법에 비해 모집단의 속성을 잘 반영하지 못하는 단점도 있다.
모집단 구성원이 "파란색", "빨간색", "검은색"과 같이 세 가지 종류로 나뉜다면, 주어진 크기의 표본에서 빨간색 요소의 수는 표본에 따라 달라지며, 이는 분포를 연구할 수 있는 확률 변수가 된다. 이 분포는 전체 모집단에서 빨간색과 검은색 요소의 수에 따라 달라진다. 단순 무작위 추출을 ''복원 추출''로 수행하는 경우, 그 분포는 ''이항 분포''가 된다. 단순 무작위 추출을 ''비복원 추출''로 수행하는 경우에는 ''초기하 분포''를 얻게 된다.[6]
3. 1. 장점
단순 무작위 추출법은 방법이 단순하고 이해하기 쉬우며, 분류 오차(classification error)가 적다는 장점이 있다.[3] 모집단에 대한 사전 정보가 필요하지 않고, 통계 분석이 용이하다는 점도 장점이다.[3] 이러한 이유로, 모집단에 대한 정보가 많지 않거나, 무작위로 분산된 항목에서 효율적으로 데이터를 수집할 수 있는 경우, 또는 추출 비용보다 단순성이 더 중요한 경우에 단순 무작위 추출법이 가장 적합하다.3. 2. 단점
단순 무작위 추출법은 이론적으로 가장 단순한 표본 추출법이지만, 모든 개체를 추출하기 전에 확인하고 표시해야 하므로 비용이 많이 들고 실현 가능성이 적다는 문제점이 있다.[16] 모집단 전체 목록(표본추출틀)이 필요하며, 이는 대규모 모집단에서는 구성하기 어렵거나 불가능할 수 있다.표본에 속한 개체가 지리적으로 넓게 분산되어 있을 수 있는데, 이 경우 각 개체를 조사하는 데 더 큰 비용이 들 수 있다.[16] 예를 들어, 주민 의식 조사 등에서 같은 세대의 사람은 비슷한 의견을 가질 가능성이 높으므로, 같은 세대에서 여러 명이 추출될 가능성이 있는 것은 단점이 될 수 있다.
모집단 안에 집단 간의 이질성이 존재할 경우, 층화 추출법에 비해 모집단의 속성을 잘 반영하지 못한다는 단점이 있다.[16] 즉, 모집단 내 이질성이 존재하면 대표성이 떨어질 수 있으며, 이 경우 층화 추출법이 더 효과적일 수 있다.
추출 틀이 큰 경우에는 단순 무작위 추출법보다 "층화"나 "다단계 추출"을 하는 것이 더 쉬울 수 있다.
4. 다른 추출법과의 관계
단순 무작위 표본 추출은 크기가 n인 모든 부분 집합이 표본으로 선택될 확률이 같다는 특징을 가진다. 이는 계통 추출법, 층화 추출법 등 다른 무작위 표본 추출 방법과는 구별된다.[5]
예를 들어, 100명의 학생들 중 10명의 표본을 구할 때, 단순 무작위 추출은 난수표를 사용하거나 제비뽑기를 이용하여 무작위로 10명을 뽑는다.
- '''계통 추출법과의 비교'''
계통 추출법은 100명의 학생들에게 001에서 100까지의 번호를 매기고 무작위로 숫자를 뽑는다. 만약 그 숫자가 013이라면, 표본은 003, 013, 023, 033, 043, 053, 063, 073, 083, 093번 학생이 된다. 이 경우, {001, 002, 003, 004, 005, 006, 007, 008, 009, 010}과 같은 부분집합이 뽑힐 확률은 0이 되므로 단순 무작위 추출과 다르다.
- '''층화 추출법과의 비교'''
층화 추출법은 모집단을 동질적인 집단으로 나누어 각 층의 비율에 따라 표본을 구한다. 예를 들어, 100명의 학생을 60명의 남학생과 40명의 여학생으로 나누어 남학생 중 6명, 여학생 중 4명을 무작위로 고를 수 있다. 이 경우, 10명이 모두 남학생이거나 모두 여학생인 표본은 나올 수 없다는 점에서 단순 무작위 표본 추출과 다르다.[3][4]
4. 1. 동일 확률 표본 추출 (EPSEM)
단순 무작위 추출은 항상 동일 확률 표본 추출(EPSEM)이 되지만, 모든 EPSEM 표본이 단순 무작위 추출(SRS)인 것은 아니다.[5] 예를 들어, 교사가 5줄 6열로 학생들을 앉힌 후 무작위로 5명을 뽑으려고 할 때, 6개 열 중 하나를 무작위로 선택할 수 있다. 이것은 EPSEM 표본이 되지만, 한 열로 구성된 부분 집합만 선택할 수 있으므로 5명으로 구성된 모든 부분 집합이 동일한 확률로 뽑히는 것은 아니다. 다단계 표본 추출의 경우처럼 최종 표본이 EPSEM이면서 SRS가 아닌 경우도 있다.[5] 계통 표본 추출은 각 개별 단위가 포함될 확률이 동일한 표본을 생성하지만, 서로 다른 단위 집합은 선택될 확률이 다르다.EPSEM인 표본은 '''자기 가중'''이며, 이는 각 표본의 선택 확률의 역수가 같다는 것을 의미한다.
4. 2. 계통 추출법 (Systematic Sampling)과의 비교
단순 무작위 표본 추출은 크기가 n인 모든 부분 집합이 표본으로 선택될 확률이 같다는 특징을 가진다. 이는 계통 추출법, 층화 추출법 등 다른 무작위 표본 추출 방법과 구별되는 점이다.예를 들어 100명의 학생 중 10명을 무작위로 뽑는 경우, 단순 무작위 추출은 난수표나 제비뽑기를 사용한다. 반면 계통 추출법은 100명에게 001부터 100까지 번호를 매기고 무작위로 숫자를 뽑아(예: 013) 해당 번호와 10 간격의 번호(003, 013, 023, ..., 093)를 표본으로 선택한다. 이 경우 {001, 002, ..., 010}과 같은 부분집합은 뽑힐 확률이 0이 된다.
1000명의 학생 중 100명을 선택하는 경우, 단순 무작위 추출에서는 모든 학생이 선택될 확률이 동일하며, 어떤 100명의 조합도 선택될 확률이 같다.

계통 추출(Systematic Sampling)은 무작위 추출에 체계적인 패턴이 도입된 경우이다. 예를 들어, 학생들에게 0001부터 1000까지 번호가 붙어 있고, 임의의 시작점(예: 0533)을 선택한 후 10번째 이름을 선택하여 100개의 표본을 얻는 방식이다. (0993에 도달하면 0003부터 다시 시작) 이는 첫 번째 단위를 선택하면 나머지가 결정되므로 군집 추출과 유사하지만, 단순 무작위 추출은 아니다. 예를 들어 {3, 13, 23, ..., 993}은 선택 확률이 1/10이지만, {1, 2, 3, ..., 100}은 선택될 수 없다.
등간격 추출법이라고도 불리는 계통 추출법은 추출 틀의 "처음부터 ''m'' 번째" 요소를 시작점으로 하여, "''n'' 개씩 건너뛰며" 요소를 표본 추출하는 방법이다. (''m'', ''n''은 임의의 수) 먼저 추출 단위의 총수를 추출 수로 나누어 추출 간격을 구한다. 예를 들어 12명 중 4명을 뽑는다면, 3명마다 추출한다. 시작점은 처음 3명 중에서 무작위로 결정하며, 이를 "시작 난수"라고 한다. 시작 난수를 작위적으로 선택하면 무작위 추출이 아니지만, 무작위로 선택하면 모든 요소가 같은 확률로 선택되는 무작위 추출이 된다.
추출 단위 총수를 추출 수로 나눈 경우 나머지가 생기면(예: 13명 중 4명), 13번째 이후에도 있다는 가정 하에 동일한 추출을 계속하여 모든 학생이 같은 확률로 추출되도록 한다.
계통 추출은 인접한 요소가 추출되지 않는다는 특징이 있다. 또한, 난수 발생기를 사용할 수 없는 상황에서도 수작업으로 수행할 수 있다. 예를 들어 1200명 중 400명을 뽑을 때, 1부터 3까지 적힌 룰렛을 만들어 시작 난수를 결정하면 나머지는 계통적으로 선택된다.
하지만 표본 추출 틀에 규칙성이 있으면(예: "3의 배수일 때 바보가 나열된 명부"에서 3개씩 건너뛰는 경우) 무작위 추출이 되지 않는다는 단점이 있다.
4. 3. 층화 추출법 (Stratified Sampling)과의 비교
단순 무작위 추출법은 모집단을 층으로 나누지 않고 무작위로 표본을 추출하는 방식이다. 반면, 층화 추출법은 모집단을 성격이 비슷한 여러 개의 층(예: 남, 녀)으로 나누고, 각 층에서 정해진 비율에 따라 무작위로 표본을 추출하는 방법이다.[3] 예를 들어, 100명의 학생(남학생 60명, 여학생 40명) 중 10명의 표본을 추출할 때, 층화 추출법은 남학생 6명과 여학생 4명을 무작위로 선정하여, 전체 모집단의 성비와 유사한 표본을 구성한다. 이렇게 하면 단순 무작위 추출에서는 불가능한, '10명 모두 남학생' 또는 '10명 모두 여학생'과 같은 극단적인 표본 구성을 방지할 수 있다.[4]요약하면, 단순 무작위 추출은 전체에서 무작위로 뽑는 것이고, 층화 추출은 그룹별로 나눠서 비율에 맞춰 뽑는 것이다. 층화 추출은 여론 조사에서 특별시, 광역시, 도(道), 시, 구, 군 등으로 나누어 표본 추출하는 방식으로 활용된다. 이는 모집단을 층별로 나누는 것이 단순 무작위 추출보다 쉽고, 각 지역별 여론도 파악할 수 있다는 장점 때문이다. 하지만, 층화 추출을 위해서는 모집단을 층으로 나눌 수 있는 추가 정보(예: 각 층의 비율)가 필요하다는 단점이 있다.
5. 단순 무작위 추출의 절차 및 방법
'''단순 무작위 추출법'''(또는 단순 랜덤 추출법, 단순 임의 추출법)은 모집단에서 개체를 뽑을 때 각각의 개체가 모두 동등한 확률로 뽑히는 추출법이다. 단순 무작위 추출법에서는 n개의 추출단위로 얻을 수 있는 모든 부분집합이 표본으로 선택될 확률이 같다. 복원 추출법에서는 크기가 N인 모집단에서 n개의 추출 단위로 구성된 가능한 표본의 가짓수 에서 각각의 부분집합이 표본으로 선택될 확률이 으로 모두 같도록 하는 추출법이다.[15]
단순 무작위 추출법에는 한 번 뽑힌 요소를 다시 모집단으로 복원하는 복원 추출법과 한 번 뽑히면 모집단으로 다시 보내지 않는 비복원 추출법이 모두 사용된다. 모집단의 크기가 비교적 작을 때에는 복원 추출법이 적합하며, 모집단의 크기가 크고 표본의 크기가 작을 때에는 복원 추출법과 비복원 추출법 간의 차이가 적다.
단순 무작위 추출의 원리는 동일한 수의 항목을 가진 모든 집합이 선택될 확률이 동일하다는 것이다. 예를 들어 ''N''명의 대학생 중 ''X'' (< ''N'')명에게 농구 경기 티켓을 제공할 때, 모든 사람에게 0부터 ''N''-1까지의 번호를 부여하고, 전자적으로 또는 난수표에서 난수를 생성한다. 0부터 ''N''-1까지의 범위를 벗어나거나 이전에 선택된 숫자는 무시하고, 처음 ''X''개의 숫자에 해당하는 학생들이 티켓을 받게 된다.
작은 모집단에서는 주로 '''비복원 추출'''을 사용하는데, 이는 모집단의 어떤 구성원도 두 번 이상 선택하지 않도록 한다. 비복원 추출은 독립적이지는 않지만 교환 가능성을 만족시켜 수학적 통계의 대부분의 결과가 여전히 유효하다. 큰 모집단에서 작은 표본을 추출할 때는 동일한 개체를 두 번 선택할 확률이 낮아 비복원 추출과 복원 추출이 거의 동일하다. 설문 조사 방법론에서는 비복원 단순 무작위 추출을 다른 추출 방식의 상대적 효율성을 계산하는 기준으로 간주한다.[3]
단순 무작위 추출은 개념적으로 확률적 추출 기법 중 가장 간단하며, 완전한 추출틀을 필요로 한다. 하지만 대규모 모집단에서는 완전한 추출틀을 구성하기 어렵거나 불가능할 수 있다. 장점은 분류 오류가 없고, 모집단에 대한 사전 지식이 거의 필요하지 않다는 것이다. 하지만 모집단에 대한 정보가 많지 않거나, 데이터 수집을 무작위로 분산된 항목에서 효율적으로 수행할 수 있거나, 추출 비용이 효율성보다 단순성이 덜 중요하게 만드는 데 충분히 작을 때 가장 적합하다. 이러한 조건이 충족되지 않으면, 층화 추출 또는 군집 추출이 더 나은 선택일 수 있다.[4]
5. 1. 난수표 이용 방법
난수표를 이용한 단순 무작위 추출법은 다음과 같다.# 모집단의 모든 개체에 같은 자릿수의 일련번호를 부여한다.
# 난수표에서 무작위로 시작점을 정하고, 그 시작점부터 개체에 부여된 번호와 같은 자릿수만큼의 숫자를 읽는다.
# 원하는 표본 크기만큼 반복해서 같은 자릿수의 숫자를 고른다. 이때 반복된 숫자나 일련번호 범위를 벗어나는 숫자는 제외한다.
# 뽑힌 숫자에 해당하는 일련번호를 가진 개체를 표본으로 정한다.[15]
예를 들어, 300명의 학생이 있는 고등학교에서 50명의 학생을 뽑아 급식 제도에 대한 찬반 의견을 조사할 때 난수표를 이용할 수 있다. 먼저 300명의 학생에게 001부터 300까지의 번호를 매긴다. তারপর 난수표에서 무작위로 시작점을 정하고 세 자리씩 숫자를 읽는다. 300을 초과하거나 000인 숫자는 제외하고, 총 50개의 서로 다른 숫자를 뽑는다. 뽑힌 숫자에 해당하는 번호의 학생들이 표본이 된다.
5. 2. 기타 방법
단순 무작위 추출법을 실제로 구현할 때는 제비뽑기, 샘플링 카드, 컴퓨터 난수 발생 프로그램을 이용하는 방법 등이 있다. [7][8]예를 들어, 트럼프 카드나 추첨기를 사용하여 무작위로 카드나 공을 뽑는 방식으로 진행할 수 있다. 트럼프 카드는 셔플을 통해, 추첨기는 회전(가라가라)을 통해 무작위성을 확보한다.

통계 조사와 같이 사람을 대상으로 무작위 추출을 할 때는, 조사 대상 집단(모집단)의 모든 구성원을 목록화하여 일련번호를 부여한 표본 추출 틀을 만든다. 그 후, 난수 발생기를 사용하여 무작위로 숫자를 생성하고, 해당 숫자에 해당하는 구성원을 표본으로 선택한다.
컴퓨터, 주사위 등 무작위로 요소를 배열하거나 난수를 생성하는 장치를 '''난수 생성기'''(랜더마이저)라고 부른다. 카드나 공을 사람이 직접 섞어 추출하기도 하지만, 표본 추출 틀을 사용하고 주사위나 룰렛 등의 난수 생성기로 생성된 숫자를 기반으로 추출하는 경우도 많다.
TRPG나 보드 게임에서는 플레이어나 다음 행동을 무작위로 결정하기 위해 '다면 주사위'라는 특수한 주사위를 사용하기도 한다. 동전 던지기도 간단한 난수 생성기이지만, '0'(앞면)과 '1'(뒷면)만 생성할 수 있어 표본 조사나 추출 검사에는 일반적으로 사용되지 않는다. 현대에는 100엔 숍이나 취미 숍에서 다양한 종류의 난수 생성기(주사위, 룰렛 등)를 쉽게 구할 수 있다.
추첨기나 자동 마작 테이블과 같이 난수 생성기가 무작위 추출의 모든 과정을 한 번에 처리하는 경우도 있다.
6. 통계 조사에서의 활용 (한국 사례 중심)
통계 조사는 모집단 전체를 조사하는 전수 조사와 일부 표본을 조사하는 표본 조사로 나뉜다. 무작위 추출은 표본 조사의 기본이며, 표본 오차를 추정하고 모집단의 특성을 추론하는 데 사용된다.[3]
표본 조사에서는 모집단을 대표하는 표본을 추출하기 위해 무작위 추출이 사용된다. 무작위 추출은 의도적인 절차 없이 집단의 모든 요소가 같은 확률로 추출되도록 하는 방법이다. 예를 들어, 반 청소 당번을 뽑을 때 출석부에서 제비뽑기로 무작위 추출하는 것은 객관적인 공정성을 담보한다.
통계 조사에서 무작위 추출은 표본 오차의 원인이 될 수 있는 낮은 무작위성을 방지하고, 정확한 통계 조사를 가능하게 한다. 따라서 통계 조사에서는 유의 추출이 아닌, 반드시 무작위 추출이 사용된다.[4] 무작위 추출법을 사용한 표본 조사에서 발생하는 오차(표본 오차)의 범위는 확률론에 근거하여 통계학적으로 계산할 수 있지만, 유의 추출법을 사용한 표본 조사에서 발생하는 오차의 범위는 확률론적으로 계산할 수 없고 불명확하다. 인터넷 모니터에 의한 시장 조사는 간편하지만, 샘플 자체에 편향이 발생하여 객관적인 신뢰성을 확보하기 어렵다. 따라서 여론 조사 등 객관적인 신뢰성이 중시되는 통계 조사에서는 무작위 추출법이 사용된다.
추측 통계학을 창시한 R.A. 피셔는 분산 분석법을 완성했으며, 차이 검증 등에도 무작위 추출이 이론적 전제가 된 다양한 수법이 사용된다.
6. 1. 통계 조사에서의 무작위 추출 기법
통계 조사에서 무작위 추출은 모집단 전체를 조사하는 전수 조사 대신, 일부 표본을 추출하여 모집단의 특성을 추정하는 표본 조사의 핵심 기법이다. 무작위 추출은 객관적인 공정성을 확보하고, 표본 오차를 줄여 정확한 통계 결과를 얻기 위해 사용된다.단순 무작위 추출법은 모집단의 모든 요소에 동일한 확률을 부여하여 표본을 추출하는 가장 기본적인 방법이다.[3] 예를 들어, 농구 경기 티켓을 얻고 싶은 ''N''명의 대학생 중 ''X''명(''X'' < ''N'')을 뽑는 경우, 모든 학생에게 번호를 부여하고 난수를 생성하여 당첨자를 결정한다. 이 방법은 모집단에 대한 사전 정보가 거의 필요 없고, 데이터 해석이 쉽다는 장점이 있다. 하지만 모집단이 크면 추출틀 구성이 어렵고, 인접한 요소가 함께 선택될 가능성이 있어 표본의 대표성이 떨어질 수 있다.[4]
계통 추출법(등간격 추출법)은 추출 틀에서 일정한 간격으로 표본을 추출하는 방법이다. 예를 들어, 12명의 학생 중 4명을 뽑는 경우, 3명 간격으로 추출한다. 시작점은 무작위로 결정하여 모든 요소가 선택될 확률을 동일하게 유지한다. 이 방법은 난수 생성기 없이도 쉽게 수행할 수 있지만, 추출 틀에 규칙성이 있으면 무작위성이 훼손될 수 있다.
층화 추출법은 모집단을 여러 개의 층(그룹)으로 나누고, 각 층에서 단순 무작위 추출을 수행하는 방법이다. 예를 들어, 여론 조사에서 지역별, 성별, 연령별 등으로 층을 나누어 표본을 추출한다. 이 방법은 각 층의 분포가 크게 다를 때 효과적이며, 모집단 전체를 대표하는 표본을 얻을 수 있다.
확률 비례 추출법은 각 층의 크기에 비례하여 표본 수를 배분하는 층화 추출법의 일종이다. 예를 들어, 남학생과 여학생의 비율에 맞춰 표본 수를 결정한다.
다단계 추출법은 모집단을 여러 단계로 나누어 표본을 추출하는 방법이다. 예를 들어, 전국 고등학생 500명을 추출하는 경우, 시/도 → 시/군/구 → 학교 → 학생 순으로 단계를 거쳐 표본을 추출한다.
집락 추출법 (Cluster Sampling)은 모집단을 집락(클러스터)으로 나누고, 특정 집락을 무작위로 선택하여 전수 조사하는 방법이다. 예를 들어, 시내 고등학생을 학교별로 나누고, 몇 개의 학교를 무작위로 선택하여 해당 학교 학생 전체를 조사한다.

현실에서는 여러 무작위 추출법을 조합하거나, 무작위 추출과 전수 조사를 함께 사용하기도 한다. 어떤 방법을 사용하든, 모든 요소가 추출될 확률이 동일해야 무작위 추출이라고 할 수 있다.
6. 2. 표본 추출 틀 (Sampling Frame)
무작위 추출을 하려면 모집단을 대표하는 요소가 기술된 "리스트", 즉 "표본 추출 틀"이 필요하다. 학교에서는 명부를, 일본의 여론 조사에서는 지방 자치 단체가 제작한 주민 기본 대장 등을 표본 추출 틀로 사용할 수 있다.[16] 표본 추출 틀이 없는 경우에는 모집단의 요소를 직접 목록으로 만들어야 한다. 현대에는 컴퓨터로 전화번호 표본 추출 틀을 생성하는 RDD법(Random Digit Dialing) 등의 방법이 활용된다.표본 추출 틀에서 요소를 무작위로 추출하기 위해서는 먼저 모든 요소에 일련 번호를 부여하고, 추출할 번호를 난수로 결정한다. 과거에는 난수표나 난수 주사위를 사용했지만, 현대에는 주로 컴퓨터의 의사 난수를 사용한다.
6. 3. 한국의 여론 조사 사례
RDD(Random Digit Dialing) 방식은 컴퓨터를 이용하여 무작위로 전화번호를 생성하여 여론 조사를 하는 방법이다. 이 방식은 휴대전화의 경우 시외 국번을 사용할 수 없다는 제약이 있다.[13] 따라서 컴퓨터로 만든 수억 개의 전화번호 목록에서 단순 무작위 추출을 할 수밖에 없다.[14]한편, 층화 추출법은 모집단을 미리 몇 개의 그룹(층)으로 나누고, 각 그룹에서 단순 무작위 추출을 하는 방식이다. 예를 들어, 여론 조사에서는 도도부현별, 자치체별 등으로 나누어 표본을 추출한다. 이 방법은 층화(그룹화)를 통해 단순 무작위 추출보다 더 쉽게 조사를 수행할 수 있고, 지역별 여론을 파악할 수 있다는 장점이 있다. 그러나 층화 추출을 위해서는 '추출 틀' 정보 외에 '층화'를 위한 추가 정보가 필요하다는 단점이 있다.
일본의 경우, 도쿄도(인구 약 1300만 명)와 돗토리현(인구 약 60만 명)처럼 인구 편차가 큰 도도부현으로 구성되어 있기 때문에, 단순 무작위 추출을 하면 인구가 적은 지역 주민은 표본으로 추출되지 않을 수 있다. 하지만 도도부현별로 층화하면 이러한 문제를 해결할 수 있다. 모든 일본 국민이 표본으로 추출될 확률이 동일하다면, 도도부현별로 나누어 표본을 추출해도 무작위 추출이라고 할 수 있다.
7. 비판 및 한계 (한국 사회의 관점)
단순 무작위 추출법은 이론적으로 간단하지만, 한국 사회의 현실적인 제약으로 인해 여러 한계에 직면한다.
- 표본 추출 틀의 한계: 모든 개체가 추출되기 전에 확인되고 표시되어야 하므로, 완벽한 표본 추출 틀을 확보하는 것은 어렵다. 예를 들어, 유권자 명부에는 이사 등으로 인한 누락이나 착오가 있을 수 있으며, 개인 정보 보호 문제로 인해 특정 집단의 정보를 얻기 어려울 수 있다.[16]
- 응답률 저하: 조사 참여율이 낮아지면 표본의 대표성에 문제가 발생할 수 있다. 특히 젊은 층이나 특정 정치 성향을 가진 집단에서 이러한 현상이 두드러질 수 있다. 예를 들어, 더불어민주당 지지층은 상대적으로 조사에 적극적으로 참여하는 경향이 있어 과대 대표될 가능성이 있다.
- 온라인 조사의 편향: 인터넷 사용 환경이나 설문 참여 의향에 따라 편향이 발생할 수 있다. 온라인 조사는 더불어민주당 지지층과 같이 특정 집단이 과대 대표될 가능성이 있다.
- 비용 문제: 모든 개체가 추출 이전에 확인되어야 하고 표시되어야 하기 때문에 비용이 많이 들고 실현 가능성이 적다. 특히, 표본에 속하는 개체가 지리적으로 넓게 분산되어 있는 경우, 각 개체를 조사하는 데 더 큰 비용이 들 수 있다.[16]
8. 결론 및 제언
단순 무작위 추출은 객관적이고 공정한 통계 조사를 위한 핵심적인 방법이지만, 완벽하게 구현하기는 어렵다. 정밀도가 낮은 추첨기를 사용하면 무작위성이 낮은 추출이 될 수 있으며, 이는 표본 오차의 원인이 된다.[1] 학술적 조사에서는 유의 추출이나 무작위성이 낮은 무작위 추출은 정확한 통계 조사를 할 수 없게 만든다.[1] 따라서, 통계 조사에서는 반드시 무작위 추출을 사용해야 하며, 인력으로 조사를 수행하는 데 드는 비용과 노력을 고려하면서도 무작위성을 높이기 위한 다양한 방법이 연구되고 있다.[1]
공업 제품의 샘플 검사에서도 무작위성이 낮으면 불량품 비율을 정확하게 파악할 수 없어, 회사의 신뢰도에 문제가 생길 수 있다.[1] 특히, 창고나 안쪽에 쌓인 제품을 검사하기 어려워 완전한 무작위 추출을 하지 않는 경우가 있으므로, 제품 전체의 무작위 추출을 쉽게 할 수 있도록 연구가 필요하다.[1]
카드 게임 등의 아날로그 게임에서도 무작위 추출은 중요하지만, 부정 행위의 가능성이 있으므로 주의해야 한다.[1]
단순 무작위 추출법은 모집단의 모든 요소를 대상으로 무작위 추출하는 가장 기본적인 방법이다.[1] 추출 틀의 정보만 있으면 수행할 수 있어 편리하지만, 추출 틀이 큰 경우에는 층화나 다단계 추출을 하는 것이 더 효율적일 수 있다.[1]
참조
[1]
서적
The Practice of Statistics, 3rd Ed.
Freeman
[2]
서적
Sampling
John Wiley & Sons
2012
[3]
서적
Sampling techniques
Wiley
1977
[4]
서적
Statistics for spatial data
John Wiley & Sons, Inc
2015
[5]
간행물
Achieving equal probability of selection under various random sampling strategies
1995
[6]
서적
Basic probability theory
Dover Publications
2008
[7]
서적
Sampling Algorithms - Springer
2006-01-01
[8]
논문
Scalable Simple Random Sampling and Stratified Sampling
http://jmlr.org/proc[...]
2013
[9]
논문
Development of Sampling Plans by Using Sequential (Item by Item) Selection Techniques and Digital Computers
1962-06-01
[10]
논문
List Sequential Sampling with Equal or Unequal Probabilities without Replacement
1977-01-01
[11]
논문
Random Sampling with a Reservoir
1985-03-01
[12]
논문
Faster methods for random sampling
1984-07-01
[13]
문서
そもそも、[[携帯電話]]で[[市外局番]]が使えたならば、それは、'''携帯'''電話でなくなってしまう。
[14]
문서
よって、Random Digit Dialing方式を用いる場合には、[[固定電話]]回線の契約数が[[携帯電話]]回線の契約数よりも下回ったとしても、Random Digit Dialing方式による層化無作為抽出方式の場合には、[[携帯電話]]回線は対象外となってしまう。
[15]
서적
일반통계학
영지문화사
2006
[16]
서적
Sampling of populations methods and application 4th edition
2011
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
