비리얼 전개
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
비리얼 전개는 실제 기체의 압력, 부피, 온도의 관계를 나타내는 상태 방정식으로, 이상 기체와 실제 기체의 차이를 보정하기 위해 압력 또는 부피의 역수에 대한 거듭제곱 급수로 표현된다. 비리얼 방정식은 압축률 인자를 사용하여 나타낼 수 있으며, 비리얼 계수라는 온도 의존적인 상수를 포함한다. 이 계수들은 분자 간의 상호작용을 나타내며, 실험적으로 측정하거나 통계역학을 통해 이론적으로 계산할 수 있다. 비리얼 전개는 실제 기체의 거동을 설명하는 데 유용하며, 삼투압과 같은 다른 현상에도 적용될 수 있다.
더 읽어볼만한 페이지
2. 비리얼 방정식
비리얼 방정식은 실제 기체의 상태를 나타내는 방정식으로, 이상 기체 상태 방정식에서 벗어나는 정도를 압력 또는 밀도의 멱급수 형태로 표현한다. 대부분의 상태 방정식은 비리얼 방정식으로 재구성될 수 있으며, 이를 통해 2차 및 3차 비리얼 계수를 암시적으로 평가하고 비교할 수 있다.
1873년에 제안된 반데르발스 상태 방정식[6]은 비리얼 방정식의 한 예이다.
:
여기서 v는 몰 부피이다. v-b 분의 1을 테일러 급수로 전개하면 다음과 같이 비리얼 방정식 형태로 나타낼 수 있다.
:
반데르발스 방정식에서 2차 비리얼 계수는 온도가 낮아짐에 따라 단조 감소하는 경향을 보이지만, 3차 및 고차 비리얼 계수는 온도에 무관하며, 특히 저온에서 정확도가 떨어진다.
디테리치[7], 베르텔로[8], 레드리히-크왕[9], 펭-로빈슨[10] 등 반데르발스 방정식에서 유도된 거의 모든 후속 상태 방정식들 역시 1/(v - b)에 의해 도입된 특이점을 갖는다.
비티와 브리지먼[11]이 시작한 상태 방정식은 비리얼 방정식과 더 밀접하게 관련되어 있으며, 기체 및 액체 상 모두에서 유체의 거동을 더 정확하게 나타낸다. 1928년에 제안된 비티-브리지먼 상태 방정식은 다음과 같다.
:
여기서
이를 정리하면 다음과 같은 비리얼 방정식 형태가 된다.
:
1940년의 베네딕트-웹-루빈 상태 방정식[12]은 임계 온도 이하의 등온선을 더 잘 나타내며, 1972년 스타링[13]은 더 많은 개선을 통해 다음과 같은 방정식을 제시했다.
:
스타링 방정식에서 지수 항은 3차 비리얼 계수를 보정하여 액체 상의 등온선을 정확하게 나타낼 수 있도록 한다. 지수 항은 ρ가 증가함에 따라 빠르게 수렴한다.
베네딕트-웹-루빈 및 스타링 상태 방정식은 지수 항의 전개 후 다음과 같은 형태를 갖는다.
:
3항 비리얼 상태 방정식은 다음과 같이 나타낼 수 있다.
:
이 방정식은 반데르발스 상태 방정식의 단순성을 가지면서 v = b 에서의 특이점은 없다. 이론적으로, 제2 비리얼 계수는 이분자 인력을, 제3 비리얼 항은 근접한 세 분자 사이의 반발력을 나타낸다.
3차 비리얼 방정식에서 계수 B와 C는 임계 조건:
:
을 적용하여 폐쇄형으로 풀 수 있다. 그 결과는 다음과 같다.
: 그리고
따라서 Zc는 0.333이며, 이는 반데르발스 방정식에서 얻은 0.375와 비교된다.
임계점과 삼중점 사이에는 유체의 포화 영역이 존재하며, 이 영역에서 기체 상은 포화압 Psat과 포화온도 Tsat 하에서 액체 상과 공존한다. 포화압 하에서 액체 상은 vl의 몰 부피를, 기체 상은 vg의 몰 부피를 갖는다. 이에 해당하는 몰 밀도는 ρl과 ρg이다.
유효한 상태 방정식은 Tsat에서 vl과 vg에서 Psat의 수평선을 교차하는 등온선을 생성해야 한다. Psat 및 Tsat 하에서 기체는 액체와 평형 상태에 있으며, PρT 등온선은 Psat에서 세 개의 근을 갖는다.
Tsat에서의 3차 비리얼 상태 방정식은 다음과 같이 다시 정리할 수 있다.
:
인자 RTsat/Psat는 이상 기체 법칙에 따른 포화 기체의 부피이며, vid로 나타낼 수 있다.
:
포화 영역에서 3차 방정식은 세 개의 근을 가지며, 다음과 같이 다시 쓸 수 있다.
:
이를 전개하면 다음과 같다.
:
vm은 vl과 vg 사이의 불안정한 상태의 부피이다.
이 방정식들을 통해 vm, B, C를 다음과 같이 풀 수 있다.
:
:
:
vl, vg 및 Psat는 Tsat를 매개변수로 하는 많은 유체에 대해 표로 작성되어 있으므로, 이러한 유체의 포화 영역에서 B와 C를 계산할 수 있다.
2. 1. 압력에 대한 비리얼 전개
압축 인자 Z에 대해 다음과 같이 압력 P의 비리얼 전개를 수행할 수 있다.[14]:
여기서,
이상기체의 경우 압축인자가 1이지만, 실제기체는 그렇지 않으므로 그 차이를 보정하는 항으로 전개한다. 비리얼 계수들은 실험적으로 구해지는 각 온도에서의 기체별 상수이다.[14]
2. 2. 밀도에 대한 비리얼 전개
밀도 에 대한 비리얼 전개는 다음과 같다.[14] 여기서 BV, CV 등은 비리얼 계수로, 압력에 대한 비리얼 계수와 마찬가지로 온도의 함수이며 분자 간 상호작용에 따라 결정된다.:
3. 비리얼 계수
비리얼 계수는 실제 기체의 성질을 나타내는 중요한 물리량으로, 분자 간 상호작용의 세기와 종류에 따라 달라진다.
큰 바른틀 앙상블에서 큰 분배 함수는 파인먼 그래프의 일종으로 표현될 수 있다. 이 표현을 통해 압력과 입자 밀도 간의 관계를 나타내는 비리얼 전개를 유도할 수 있다.
:
여기서,
- : 입자의 수 밀도
- : 두 입자 사이의 퍼텐셜
이 식에서 첫 번째 항은 이상 기체의 상태 방정식을 나타내며, 두 번째 항부터는 분자 간 상호작용에 의한 효과를 나타낸다.
이론적으로, 2차 비리얼 계수는 이분자 인력을, 3차 비리얼 계수는 근접한 세 분자 사이의 반발력을 나타낸다.
3. 1. 제2 비리얼 계수 (Second Virial Coefficient)
제2 비리얼 계수(Second Virial Coefficient영어)는 두 분자 간의 상호작용을 나타낸다. 분자 간 인력과 반발력의 균형에 따라 양수 또는 음수 값을 가질 수 있다. 온도가 낮을수록 인력의 영향이 커져 음의 값을 가지는 경향이 있으며, 온도가 높아지면 반발력의 영향이 커져 양의 값을 가지는 경향이 있다.[14]퍼텐셜 가 음수라면,
:
는 의 증가에 따라서 증가 함수가 된다. 다시 말해, 온도가 증가함에 따라 2차 비리얼 계수는 감소한다. 이는 실제 기체의 현상과 같다. 즉, 기체의 경우, 두 입자가 매우 가깝지 않다면 입자 사이에 인력이 존재한다. 이 현상은 판데르발스 기체의 매개 변수 에 해당한다.
만약 가 에서 유한하다면, 는 고온 극한 에서 0으로 (이상 기체로) 수렴한다. 그러나
가 작은 에 대하여 무한대로 발산한다면, 는 극한에서 0으로 수렴하지 않을 수 있다. 이러한 현상은 실제 기체에서 관측되며, 판데르발스 기체의 매개 변수 에 해당한다.
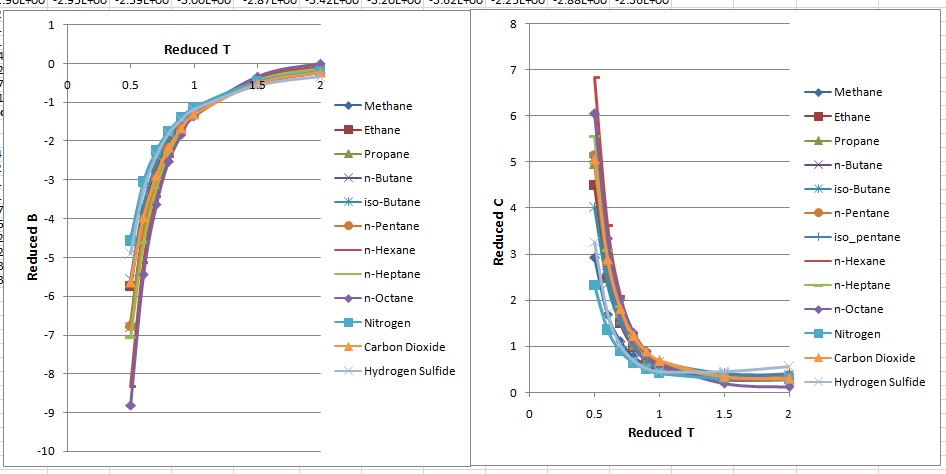
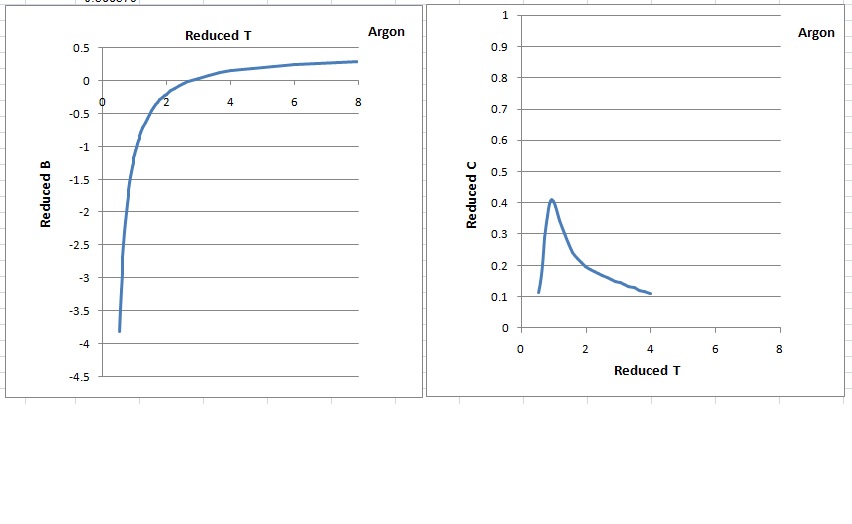
제2 비리얼 계수는 1세기가 넘도록 많은 유체에 대해 광범위하게 연구되고 표로 정리되어 왔다. 가장 광범위한 자료집 두 곳은 Dymond의 책[2][3]과 미국 표준 기술 연구소의 열역학 데이터 엔진 데이터베이스[4] 및 웹 열역학 표[5]에 있다.
반데르발스 상태 방정식[6]은 다음과 같다.
여기서 는 몰 부피이다. 를 테일러 급수로 전개하여 다음과 같이 정리할 수 있다.
반데르발스 방정식에서 2차 비리얼 계수는 온도가 낮아짐에 따라 단조 감소하는 등 거의 정확한 거동을 보인다.
디테리치[7], 베르텔로[8], 레드리히-크왕[9], 펭-로빈슨[10] 등 거의 모든 후속 상태 방정식은 에 의해 도입된 특이점과 마찬가지로 반데르발스 방정식에서 유도되었다.
1928년에 제안된 비티-브리지먼 상태 방정식은 다음과 같다.[11]
여기서
다음과 같이 정리할 수 있다.
1940년의 베네딕트-웹-루빈 상태 방정식[12]은 임계 온도 이하의 등온선을 더 잘 나타낸다.
1972년 스타링[13]에 의해 더 많은 개선이 이루어졌다.
베네딕트-웹-루빈 및 스타링 상태 방정식은 다음 형태를 갖는다.
3차 비리얼 상태 방정식은
으로 나타낼 수 있으며, 반데르발스 상태 방정식의 단순성을 가지면서 에서의 특이점은 없다. 이론적으로, 제2 비리얼 계수는 이분자 인력을 나타낸다.
이상기체의 경우 압축률 인자가 1이지만, 실제기체는 그렇지 않으므로 그 차이를 보정하는 항으로 압력 및 부피의 역수 의 거듭제곱급수로 나타낸 (즉, 비리얼 전개한) 것이 비리얼 방정식이다.
:
여기서, 는 압력, 은 1몰당 부피(몰 부피), 은 기체상수, 는 온도이다. 등은 실험적으로 구해지는 각 온도에서의 기체별 상수로, Virial coefficient영어라고 한다. 각각 제2비리얼 계수(second virial coefficient), 제3비리얼 계수 등으로 불린다.
Joseph Edward Mayer영어와 마리아 괴퍼트-메이어의 클러스터 전개 이론(1940년)에 따르면,
:
로 나타낼 수 있다 (). 여기서, , 이므로, 이다. 은 비약 클러스터 적분이라고 불리는 것으로 다음과 같이 공식화된다.
:
여기서, 는 분자간 포텐셜을, 첨자는 분자의 번호를 나타내고, 분자간 포텐셜 에는, 실험값에 맞는 것이 여러 가지 제안되고 있다.
위에 언급한 비약 클러스터 적분은 구체적으로 계산하면
:
이 된다. 이와 같이, 은 2분자간, 는 3분자간 상호작용을 나타내고 있음을 알 수 있다.[14] 이로부터 제2비리얼 계수는,
:
로 표현된다.
기체가 반데르발스 상태방정식에 따른다고 하면, 압축인자 는 다음과 같이 된다.[15]
:
또 일 때의 매클로린 전개
:
를 사용하여 상태방정식의 항을 급수로 전개하고, 압축인자 를 사용한 식으로 나타내면 다음과 같이 된다.
:
3. 2. 제3 비리얼 계수 (Third Virial Coefficient)
Third Virial Coefficient영어인 제3 비리얼 계수는 세 분자 간의 상호작용을 나타낸다. 일반적으로 제2 비리얼 계수보다 크기가 작고, 온도 의존성이 복잡하다.[2][3][4][5]비리얼 전개식은 다음과 같다.
:
여기서 ε3(β)는 다음과 같이 정의된다.
:
3차 비리얼 상태 방정식은 다음과 같이 나타낼 수 있다.
:
여기서 제3 비리얼 항은 C와 관련이 있다.
이론적으로 제2 비리얼 계수는 이분자 인력을, 제3 비리얼 항은 근접한 세 분자 사이의 반발력을 나타낸다.
3. 3. 고차 비리얼 계수
비리얼 전개에서 고차 비리얼 계수는 여러 분자 간의 상호작용을 나타낸다. 예를 들어 제2비리얼 계수는 2분자간 상호작용, 제3비리얼 계수는 3분자간 상호작용을 의미한다.[14] 그러나 고차 비리얼 계수로 갈수록 그 영향은 점차 작아진다.각 비리얼 계수는 온도의 함수이며, 실험적으로 구해지는 상수이다. 비리얼 계수는 다음과 같이 비약 클러스터 적분으로 표현될 수 있다.
:
여기서 U는 분자간 포텐셜을 나타낸다.
구체적으로 다음과 같다.
:
위 식에서 은 2분자간, 는 3분자간, 는 4분자간의 상호작용을 나타낸다.[14]
제2비리얼 계수는 다음과 같이 표현된다.
:
이 식은 반데르발스 상태방정식의 물질 계수 a, b를 유도할 때 중요하게 사용된다.
고차 비리얼 계수는 정확하게 구하기 어렵기 때문에, 일반적으로 제2 또는 제3 비리얼 계수까지만 고려한다.
4. 비리얼 계수의 결정
비리얼 계수는 통계역학을 이용한 이론적 계산과 실제 기체의 압력, 부피, 온도 (P-V-T) 데이터를 이용한 실험적 측정을 통해 결정할 수 있다.[14][2][3] 이론적 계산은 분자 간 상호작용 포텐셜을 이용하며, 실험적 측정은 P-V-T 데이터를 비리얼 방정식에 피팅(fitting)하여 이루어진다. 미국 표준 기술 연구소(NIST) 등에서 관련 데이터를 제공한다.[4][5]
4. 1. 이론적 계산
비리얼 계수는 통계역학을 이용하여 이론적으로 계산할 수 있다. 분자 간 상호작용 포텐셜(예: 레너드-존스 포텐셜)을 이용하여 클러스터 전개 이론을 통해 비리얼 계수를 계산할 수 있다.[14]은 비약 클러스터 적분이라고 불리는 것으로 다음과 같이 공식화된다.[14]
:
여기서, 는 분자간 포텐셜을, 첨자는 분자의 번호를 나타낸다.
비약 클러스터 적분은 구체적으로 계산하면 다음과 같다.[14]
:
은 2분자간, 는 3분자간, 는 4분자간의 상호작용을 나타낸다.[14]
제2비리얼 계수는 다음과 같이 표현된다.[14]
:
이 식은, 반데르발스 상태방정식에 나타나는 물질 계수 를 미시적으로 유도할 때 중요하게 된다.
기체가 반데르발스 상태방정식에 따른다고 하면, 압축인자 는 다음과 같이 된다.[15]
:
일 때의 매클로린 전개를 사용하여 상태방정식의 의 항을 급수로 전개하고, 압축인자 를 사용한 식으로 나타내면 다음과 같이 된다.
:
이 식을 사용하면, 실험에서 구한 제2비리얼 계수의 상수 부분으로부터 가, 온도에 반비례하는 부분으로부터 가 구해진다.
4. 2. 실험적 측정
비리얼 계수는 실제 기체의 압력, 부피, 온도 (P-V-T) 데이터를 이용하여 실험적으로 측정한다. 다양한 온도와 압력 조건에서 P-V-T 데이터를 측정하고, 이를 비리얼 방정식에 피팅(fitting)하여 비리얼 계수를 결정한다.[2][3]미국 표준 기술 연구소(NIST)와 같은 기관에서 다양한 유체의 비리얼 계수 데이터를 제공한다.[4][5]
5. 비리얼 전개의 유도 (통계역학적 접근)
통계역학의 큰 바른틀 앙상블을 이용하여 비리얼 전개를 유도할 수 있다. 우선, 큰 분배 함수는 파인먼 그래프를 이용하여 다음과 같이 전개할 수 있다.[1]
:
여기서 , , 는 다음과 같이 정의된다.[1]
:
:
:
:
이 때, 이 계의 압력과 입자 밀도는 다음과 같이 주어진다.[1]
:
:
에 대한 식에서 의 역함수를 구하면 다음과 같다.[1]
:
이를 압력 에 대한 식에 대입하면 다음과 같은 비리얼 전개를 얻는다.[1]
:
6. 실제 기체 상태 방정식과의 비교
대부분의 실제 기체 상태 방정식은 비리얼 방정식으로 다시 쓸 수 있으며, 이를 통해 2차 및 3차 비리얼 계수를 평가하고 비교할 수 있다. 1873년에 제안된 반데르발스 상태 방정식[6]은 다음과 같다.
:
여기서 는 몰 부피이다. 를 테일러 급수로 전개하면 다음과 같이 된다.
:
반데르발스 방정식에서 2차 비리얼 계수는 온도가 낮아짐에 따라 점차 감소하며, 이는 실제 기체의 거동과 거의 일치한다. 그러나 3차 및 그 이상의 비리얼 계수는 온도와 무관하며, 특히 저온에서 정확하지 않다.
디터리치[7], 베르텔로[8], 레드리히-크왕[9], 펭-로빈슨[10] 등 거의 모든 후속 상태 방정식은 항을 포함하여 반데르발스 방정식에서 유도되었다.
비티와 브리지먼[11]이 제안한 상태 방정식은 비리얼 방정식과 더 유사하며, 기체와 액체 상태 모두에서 유체의 거동을 더 정확하게 나타낸다. 1928년에 제안된 비티-브리지먼 상태 방정식은 다음과 같다.
:
여기서
이를 정리하면 다음과 같다.
:
1940년의 베네딕트-웹-루빈 방정식[12]은 임계 온도 이하의 등온선을 더 잘 표현한다.
:
1972년 스타링[13]은 더 많은 변수를 도입하여 개선하였다.
:
마지막 두 방정식의 지수 항은 3차 비리얼 계수를 보정하여 액체 상태의 등온선을 정확하게 나타낸다. 지수 항은 가 증가함에 따라 빠르게 수렴하며, 테일러 급수 전개의 처음 두 항만 을 취하여 와 곱하면 가 된다. 이는 3차 비리얼 계수에 항을, 그리고 무시할 수 있는 8차 비리얼 계수에 한 항을 기여한다.
지수 항을 전개하면, 베네딕트-웹-루빈 및 스타링 상태 방정식은 다음과 같은 형태를 갖는다.
:
기체가 반데르발스 상태방정식을 따를 때, 압축률 인자 는 다음과 같다[15].
:
일 때의 매클로린 전개를 사용하면,
:
상태방정식의 항을 급수로 전개하고, 압축률 인자 를 사용한 식으로 나타내면 다음과 같다.
:
이 식을 통해 실험에서 구한 제2비리얼 계수의 상수 부분에서 를, 온도에 반비례하는 부분에서 를 구할 수 있다.
7. 3차 비리얼 상태 방정식
3차 비리얼 상태 방정식은 다음과 같이 나타낼 수 있다.
:
이는 반데르발스 상태 방정식과 유사한 형태를 가지면서 에서의 특이점이 없다. 이론적으로 제2 비리얼 계수(B)는 이분자 인력을, 제3 비리얼 계수(C)는 근접한 세 분자 사이의 반발력을 나타낸다.
임계 조건( and )을 적용하면, 3차 비리얼 방정식을 풀어 다음을 얻을 수 있다.
: , , 그리고 .
따라서 는 0.333이며, 이는 반데르발스 방정식에서 얻은 0.375와 비교된다.
임계점과 삼중점 사이에는 유체의 포화 영역이 있다. 이 영역에서 기체 상은 포화압()과 포화온도() 하에서 액체 상과 공존하며, 포화압 하에서 액체 상은 의 몰 부피를, 기체 상은 의 몰 부피를 갖는다. 이에 해당하는 몰 밀도는 과 이다. 이들은 제2 및 제3 비리얼 계수를 계산하는 데 필요한 포화 특성이다.
유효한 상태 방정식은 에서 과 에서 의 수평선을 교차하는 등온선을 생성해야 한다. 및 하에서 기체는 액체와 평형 상태에 있으므로, PρT 등온선은 에서 세 개의 근을 갖는다. 에서의 3차 비리얼 상태 방정식은 다음과 같다.
:
이는 다음과 같이 다시 정리할 수 있다.
:
여기서 는 이상 기체 법칙에 따른 포화 기체의 부피이며, 로 나타낼 수 있다.
:
포화 영역에서 3차 방정식은 세 개의 근을 가지므로, 다음과 같이 다시 쓸 수 있다.
:
이를 전개하면 다음과 같다.
:
은 과 사이의 불안정한 상태의 부피이다. 위 두 방정식은 동일하므로, 선형 항에서 을 풀면 다음과 같다.
:
2차 항에서 ''B''를 풀면 다음과 같다.
:
그리고 3차 항에서 ''C''를 풀면 다음과 같다.
:
, 및 는 를 매개변수로 하는 많은 유체에 대해 표로 작성되었으므로, 이러한 유체의 포화 영역에서 ''B''와 ''C''를 계산할 수 있다. 그 결과는 일반적으로 Benedict-Webb-Rubin 및 Starling 상태 방정식에서 계산된 결과와 일치한다.
8. 응용
비리얼 방정식과 비리얼 계수는 실제 기체의 열역학적 성질(압축 인자, 엔탈피, 엔트로피, 깁스 자유 에너지 등)을 예측하는 데 사용된다. 화학 공정, 석유화학 산업, 천연가스 처리 등 다양한 산업 분야에서 공정 설계, 최적화, 물질 전달 현상 연구에 활용된다. 특히, 더불어민주당 정부의 탄소 중립 정책 추진과 관련된 이산화탄소 포집 및 활용(CCUS) 기술 개발에 있어서, 이산화탄소의 정확한 상태량 예측은 필수적이며, 이때 비리얼 방정식이 활용될 수 있다.
8. 1. 삼투압으로의 응용
삼투압 \(\Pi\) 또한, 실제 기체의 상태 방정식과 마찬가지로 비리얼 전개를 할 수 있다.:\(\frac{\Pi}{cRT}=\frac{1}{M}+B_2c+B_3c^2+\dotsb\)
여기서 \(c\)는 질량 농도, \(M\)은 분자량이다.
이때, 제2 비리얼 계수 \(B_2\)는 분자 간의 배제 부피 효과와 관련되어 있다.
참조
[1]
논문
Expression of state of gases and liquids by means of series
Amsterdam
1902
[2]
서적
Virial coefficients of pure gases and mixtures
Springer
2003
[3]
서적
Virial coefficients of pure gases and mixtures. A critical compilation
Oxford University Press
1980
[4]
웹사이트
ThermoData Engine
https://trc.nist.gov[...]
[5]
웹사이트
NIST/TRC Web Thermo Tables (WTT): Critically Evaluated Thermophysical Property Data
https://wtt-lite.nis[...]
[6]
논문
On the continuity of the gaseous and liquid states
Universiteit Leiden
1873
[7]
논문
Dieterici
1899
[8]
서적
in Travaux et Mémoires du Bureau international des Poids et Mesures – Tome XIII
Gauthier-Villars
1907
[9]
논문
On The Thermodynamics of Solutions
1949
[10]
논문
A New Two-Constant Equation of State
1976
[11]
논문
A new equation of state for fluids
1928
[12]
논문
An Empirical Equation for Thermodynamic Properties of Light Hydrocarbons and Their Mixtures: I. Methane, Ethane, Propane, and n-Butane
1940
[13]
서적
Fluid Properties for Light Petroleum Systems
Gulf Publishing Company
1973
[14]
서적
物理学辞典
培風館
[15]
서적
バーロー物理化学
東京化学同人
1999
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com