서포트 벡터 머신
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
서포트 벡터 머신(SVM)은 1960년대에 제안된 기계 학습 알고리즘으로, 데이터를 분류하거나 회귀 분석, 이상치 감지 등에 사용된다. SVM은 데이터를 고차원 공간으로 매핑하여 초평면을 구성하며, 두 클래스 사이의 최대 마진을 갖는 초평면을 찾아 분류한다. 선형적으로 분리되지 않는 데이터에 대해서는 커널 트릭을 사용하여 비선형 분류를 수행하며, 하드 마진과 소프트 마진 SVM이 존재한다. SVM은 텍스트 분류, 영상 분류, 의학, 필기 인식 등 다양한 분야에 적용되며, 다중 클래스, 구조화된 데이터, 회귀 문제로의 확장과 베이지안 SVM과 같은 변형도 연구되고 있다. 그러나, 데이터 레이블링의 필요성, 확률 추정의 어려움, 이진 분류 한계, 모델 해석의 복잡성 등의 한계점을 가지고 있으며, 이를 극복하기 위한 연구가 진행 중이다.
더 읽어볼만한 페이지
- 통계적 분류 - 민감도와 특이도
민감도와 특이도는 의학적 진단에서 검사의 정확성을 평가하는 지표로, 민감도는 실제 양성인 대상 중 양성으로 나타나는 비율, 특이도는 실제 음성인 대상 중 음성으로 나타나는 비율을 의미하며, 선별 검사에서 두 지표를 모두 높여 질병을 정확하게 진단하는 것을 목표로 한다. - 통계적 분류 - 선형 판별 분석
선형 판별 분석(LDA)은 두 개 이상의 데이터 집합을 구분하고 새로운 데이터의 소속 집합을 예측하기 위한 통계적 방법으로, 다변량 정규성, 분산/공분산의 동질성, 독립성을 가정하며, 판별 함수를 사용하여 그룹 밀도를 최대화하는 그룹에 데이터를 할당한다. - 통계학에 관한 - 비지도 학습
비지도 학습은 레이블이 없는 데이터를 통해 패턴을 발견하고 데이터 구조를 파악하는 것을 목표로 하며, 주성분 분석, 군집 분석, 차원 축소 등의 방법을 사용한다. - 통계학에 관한 - 회귀 분석
회귀 분석은 종속 변수와 하나 이상의 독립 변수 간의 관계를 모델링하고 분석하는 통계적 기법으로, 최소 제곱법 개발 이후 골턴의 연구로 '회귀' 용어가 도입되어 다양한 분야에서 예측 및 인과 관계 분석에 활용된다. - 분류 알고리즘 - 인공 신경망
- 분류 알고리즘 - 퍼셉트론
퍼셉트론은 프랭크 로젠블랫이 고안한 인공신경망 모델로, 입력 벡터에 가중치를 곱하고 편향을 더한 값을 활성화 함수에 통과시켜 이진 분류를 수행하는 선형 분류기 학습 알고리즘이며, 초기 신경망 연구의 중요한 모델로서 역사적 의미를 가진다.
2. 역사적 배경
SVM의 초기 알고리즘은 1964년 소련(현 러시아)의 통계학자 블라디미르 바프닉과 알렉세이 체르보넨키스에 의해 제안되었다.[17] 1992년, 베른하르트 보저, 이자벨 기용, 그리고 바프닉은 커널 트릭을 적용하여 비선형 분류기를 생성하는 방법을 제안했다.[17] 1995년, 코리나 코르테스와 바프닉은 소프트 마진 SVM을 제안하고 발표했다.[18]
서포트 벡터 머신(SVM)은 분류 및 회귀 분석에 사용되는 강력한 기계 학습 모델이다. SVM은 다음과 같은 주요 특징을 갖는다.
3. 주요 특징
SVM의 효과는 커널, 커널의 매개변수, 그리고 소프트 마진 매개변수 λ의 선택에 따라 달라진다. 일반적인 선택은 단일 매개변수 γ를 갖는 가우시안 커널이다. λ와 γ의 최적 조합은 종종 지수적으로 증가하는 λ와 γ의 수열을 사용하는 격자 탐색을 통해 선택된다. 예를 들어, λ ∈ {2⁻⁵, 2⁻³, ..., 2¹³, 2¹⁵}; γ ∈ {2⁻¹⁵, 2⁻¹³, ..., 2¹, 2³}이다. 일반적으로 매개변수 선택의 각 조합은 교차 검증을 사용하여 확인되며, 가장 좋은 교차 검증 정확도를 가진 매개변수가 선택된다. 또는, 베이지안 최적화의 최근 연구를 사용하여 λ와 γ를 선택할 수 있으며, 이는 종종 격자 탐색보다 훨씬 적은 매개변수 조합의 평가를 필요로 한다. 그런 다음 테스트 및 새로운 데이터 분류에 사용되는 최종 모델은 선택된 매개변수를 사용하여 전체 훈련 세트에서 훈련된다.[27]
SVM은 일반화된 선형 분류기 계열에 속하며, 퍼셉트론의 확장으로 해석될 수 있다.[25] 또한 티호노프 정규화의 특수한 경우로 간주될 수 있다. 특별한 성질은 경험적 ''분류 오류''를 최소화하고 ''기하학적 마진''을 최대화하는 동시에 이루어진다는 점이며, 따라서 '''최대 마진 분류기'''로도 알려져 있다.
SVM과 다른 분류기의 비교는 Meyer, Leisch 및 Hornik에 의해 이루어졌다.[26]
3. 1. 목표 및 아이디어
일반적으로, 서포트 벡터 머신(SVM)은 분류 또는 회귀 분석에 사용 가능한 초평면 또는 초평면들의 집합으로 구성되어 있다. 직관적으로, 좋은 분류는 어떤 클래스의 가장 가까운 훈련 데이터 포인트까지의 거리가 가장 큰 초평면(기능적 마진)에 의해 달성되며, 일반적으로 마진이 클수록 분류기의 일반화 오류가 낮아진다.[5] 즉, 초평면이 가장 가까운 학습 데이터 점과 큰 차이를 가지고 있으면 분류 오차(classifier error영어)가 작기 때문에, 어떤 분류된 점에 대해서 가장 가까운 학습 데이터와 가장 먼 거리를 가지는 초평면을 찾아야 한다.
데이터 분류는 기계 학습에서 일반적인 작업이다. 주어진 데이터 점들이 두 개의 클래스 안에 각각 속해 있다고 가정했을 때, 새로운 데이터 포인트가 두 클래스 중 어느 곳에 속하는지 결정하는 것이 목표이다. 서포트 벡터 머신에서, 데이터 점이 -차원의 벡터 (개의 숫자 리스트)로 주어졌을 때, 이러한 데이터 점을 -차원의 초평면으로 분류할 수 있는지를 확인하고 싶은 것이다. 이러한 작업을 선형 분류기라고 한다.
데이터를 분류하는 초평면은 여러 경우가 나올 수 있다. 두 클래스 사이에서 가장 큰 분류 또는 여백을 가지는 초평면을 선택하는 것이 최적의 초평면을 선택하는 합리적인 방법이다. 그래서 우리는 초평면에서 가장 가까운 각 클래스의 데이터 점들 간의 거리를 최대로 하는 초평면을 선택한다. 만약 그런 초평면이 존재할 경우, 그 초평면을 최대-마진 초평면(maximum-margin hyperplane영어) 이라 하고 선형 분류기를 최대-마진 분류기(maximum margin classifier영어)라고 한다.
인공 신경망을 포함한 많은 학습 알고리즘은 이러한 학습 데이터가 주어졌을 때, 두 클래스를 분리하는 초평면을 찾는 것이 공통적인 목표인데, SVM이 다른 알고리즘과 차별화되는 특징은 단순히 점들을 분리하는 초평면을 찾는 것으로 끝나는 것이 아니라, 점들을 분리할 수 있는 수많은 후보 평면들 가운데 마진이 최대가 되는 초평면을 찾는다는 것이다. 여기서 마진이란 초평면으로부터 각 점까지의 거리 중 최솟값을 의미한다. 결론적으로, SVM은 두 클래스에 속한 점들을 분류하는 여러 초평면 중에서 두 클래스의 점들과 최대한 거리를 유지하는 것을 찾는 알고리즘이라고 할 수 있다.
3. 2. 선형 SVM
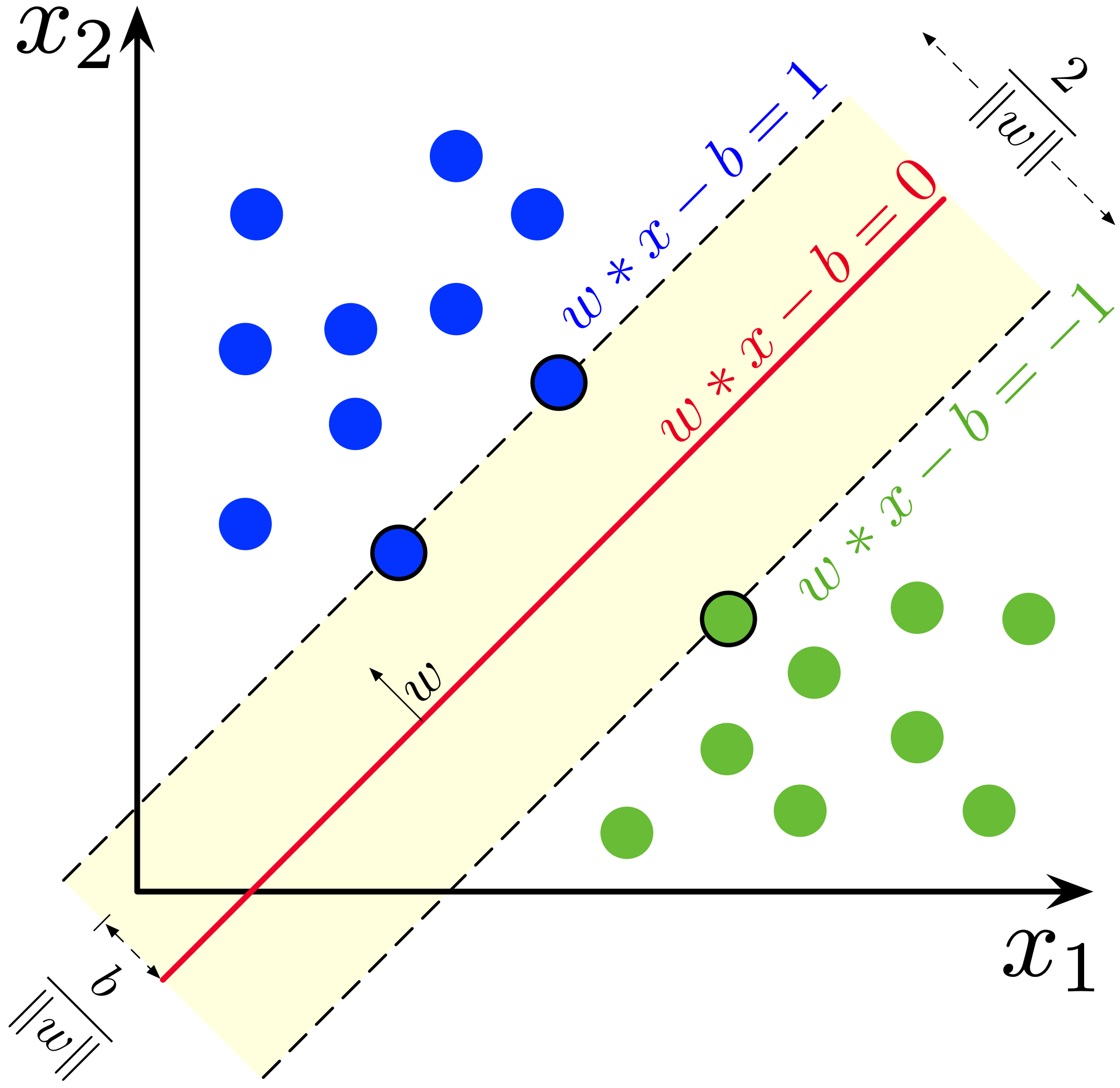
선형 SVM은 주어진 데이터가 선형적으로 분리 가능하다는 가정 하에 작동하며, 최대한 두 클래스 사이의 거리를 멀게 하는, 즉 마진을 최대화하는 결정 경계(초평면)를 찾는 것을 목표로 한다.
핵심 개념:
수학적 표현:주어진 훈련 데이터 집합 에 대해,
목표:다음 조건을 만족하면서 를 최소화하는 와 를 찾는다.
: (모든 에 대해)
이는 모든 데이터 포인트가 올바른 클래스로 분류되고, 마진의 바깥쪽에 위치하도록 하는 제약 조건이다.
라그랑주 승수법을 이용하면 위의 문제를 다음과 같은 안장점(saddle point)을 찾는 문제로 나타낼 수 있다.
:
안장점을 찾는 과정에서 으로 분류될 수 있는 모든 점들은 그에 대응하는 가 0으로 지정되기 때문에 영향을 미치지 않는다.
데이터 분류는 기계 학습에서 일반적인 작업이다. 주어진 데이터 포인트가 두 클래스 중 하나에 속한다고 가정하고, 새로운 데이터 포인트가 어떤 클래스에 속할지 결정하는 것이 목표이다. 최적의 초평면은 두 클래스 간의 가장 큰 분리 또는 여백을 나타내는 것이다. 따라서 각 측면의 가장 가까운 데이터 포인트까지의 거리가 최대화되도록 초평면을 선택한다. 이러한 초평면이 존재하는 경우, ''최대 여백 초평면''으로 알려져 있으며, 이 초평면이 정의하는 선형 분류기는 ''최대 여백 분류기'' 또는 ''최적 안정성 퍼셉트론''으로 알려져 있다.
3. 2. 1. 하드 마진(Hard-margin) SVM
훈련 데이터가 선형적으로 분리 가능하다면, 두 클래스의 데이터를 분리하는 두 개의 평행한 초평면을 선택하여 그 사이의 거리가 최대가 되도록 할 수 있다. 이 두 초평면으로 둘러싸인 영역을 "마진(margin)"이라고 하며, 최대 마진 초평면은 그 중간에 위치하는 초평면이다. 정규화 또는 표준화된 데이터셋을 사용하면 이러한 초평면은 다음 방정식으로 설명할 수 있다.
: (이 경계 위 또는 위에 있는 모든 것은 레이블 1을 가진 한 클래스에 속함)
: (이 경계 아래 또는 아래에 있는 모든 것은 레이블 -1을 가진 다른 클래스에 속함).
기하학적으로, 이 두 초평면 사이의 거리는 이다.[19] 따라서 평면 사이의 거리를 최대화하려면 를 최소화해야 한다. 거리는 점과 평면 사이의 거리 방정식을 사용하여 계산된다. 또한 데이터 포인트가 마진에 들어가는 것을 방지해야 하므로 다음과 같은 제약 조건을 추가한다. 각 에 대해
:
또는
:
이러한 제약 조건은 각 데이터 포인트가 마진의 올바른 쪽에 있어야 함을 나타낸다. 이는 다음과 같이 다시 쓸 수 있다.
:
이를 종합하여 다음과 같은 최적화 문제를 얻을 수 있다.
:
:단,
이 문제를 푸는 와 는 최종 분류기 를 결정한다. 여기서 는 부호 함수이다.
이 기하학적 설명의 중요한 결과는 최대 마진 초평면이 가장 가까이 있는 에 의해 완전히 결정된다는 것이다. 이러한 를 "서포트 벡터(support vectors)"라고 한다.
3. 2. 2. 소프트 마진(Soft-margin) SVM
1995년에 코리나 코르테스(Corinna Cortes)와 블라디미르 바프닉(Vladimir N. Vapnik)은 잘못 분류된 자료들을 허용하는 변형된 최대 마진 분류기 아이디어를 제안했다.[57] "네" 또는 "아니오"라는 결과를 내야 하는 자료들을 분할하는 초평면이 존재하지 않는 경우, 소프트 마진 방법은 여전히 가장 가까이 위치해 있는 제대로 분리되는 자료들의 거리를 최대화하면서, 주어진 자료들을 가능한 한 제대로 분리하는 초평면을 찾는다.
이 방법은 음수가 아닌 슬랙 변수(slack variable) 를 도입하는데, 이 변수는 자료 가 잘못 분류된 정도를 나타낸다.
:
그런 다음 목적함수는 0이 아닌 에 대해 페널티를 부과하는 함수에 의해 증가된다. 그에 따른 최적화는 마진을 크게 하는 것과 에러에 대한 페널티를 작게 하는 것의 균형을 맞추는 것이 된다. 만약 페널티를 부과하는 함수가 선형이라면, 최적화 문제는 다음과 같이 된다.
:
:단,
다변수 적응 회귀 스플라인(Multivariate Adaptive Regression Splines, MARS)에서와 같이 힌지 손실 함수(hinge function) 표기법을 이용하면, 이 최적화 문제는 다음과 같이 쓰일 수 있다.
:일 때,
:
SVM을 확장하여 선형적으로 분리할 수 없는 데이터를 처리하려면, 힌지 손실 함수가 유용하다.
:
여기서, 는 번째 타겟(즉, 1 또는 −1)이며, 는 번째 출력이다.
이 함수의 값은 가 마진의 올바른 쪽에 있는 경우에는 0이 된다. 마진의 반대쪽에 있는 데이터에 대해서는 함수의 값은 마진으로부터의 거리에 비례한다.
최적화의 목적은 다음을 최소화하는 것이다.
:
파라미터 는 마진 크기를 크게 하는 것과 가 마진의 올바른 쪽에 있는 것 사이의 절충을 결정한다. 가 충분히 작을 때, 손실 함수의 제2항은 무시할 수 있게 되고, 하드 마진 SVM과 유사한 동작을 한다.
3. 3. 비선형 SVM
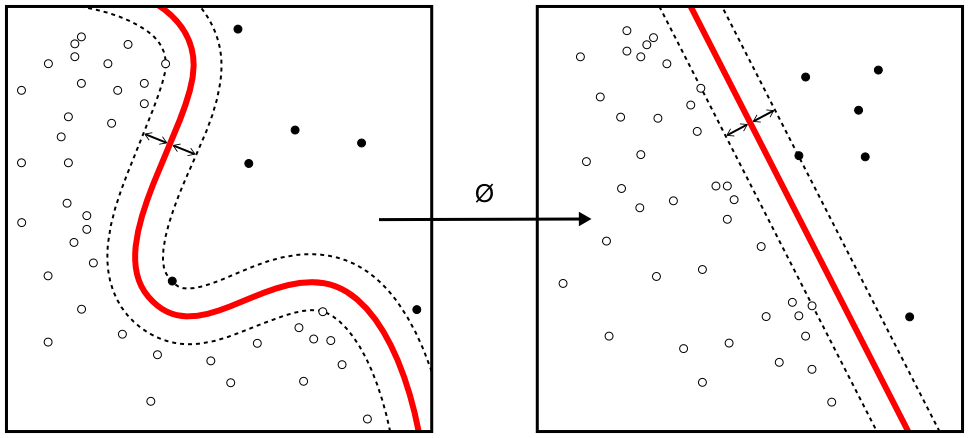
실제 데이터는 선형적으로 분리 가능하지 않은 경우가 많다. 이러한 문제를 해결하기 위해, 원래의 유한 차원 공간을 더 높은 차원의 공간으로 매핑하여 분리를 더 쉽게 만드는 방법이 제안되었다.[17] 이때, 계산량이 늘어나는 것을 막기 위해, 각 문제에 적절한 커널 함수 를 정의하여 내적 연산을 초기 문제의 변수들을 사용해 효과적으로 계산할 수 있도록 한다.[56]
높은 차원 공간의 초평면은 해당 공간의 벡터와의 점곱이 일정한 점의 집합으로 정의된다. 초평면을 정의하는 벡터는 데이터베이스에 있는 특징 벡터 의 이미지를 사용한 매개변수 의 선형 결합으로 선택할 수 있다. 이러한 선택으로, 특징 공간에 매핑된 초평면에 있는 점 는 의 관계를 가진다. 만약 가 가 에서 멀어질수록 작아진다면, 합의 각 항은 테스트 점 와 해당 데이터베이스 점 의 근접 정도를 측정한다.
1992년, 베르나르트 보저(Bernhard Boser), 이자벨 귀용(Isabelle Guyon) 및 블라디미르 바프니크(Vladimir Vapnik)은 최대 마진 초평면에 커널 트릭을 적용하여 비선형 분류기를 생성하는 방법을 제시했다.[17] 커널 트릭은 SVM 문제의 이중 표현에서 쉽게 유도되며, 여기서 내적이 커널로 대체된다. 이를 통해 알고리즘은 변환된 특징 공간에서 최대 마진 초평면을 적합시킬 수 있다. 변환은 비선형일 수 있으며 변환된 공간은 고차원일 수 있다. 커널은 라는 방정식에 의해 변환 와 관련이 있다.
3. 3. 1. 커널 함수의 종류
일반적으로 사용되는 커널 함수는 다음과 같다.
LIBSVM에도 구현되어 있으며, 주로 사용되는 커널 함수는 다음과 같다.
4. SVM 분류기 계산
서포트 벡터 머신(SVM) 분류기는 주어진 데이터를 바탕으로 최적의 초평면을 찾아 분류한다. 초평면은 가장 가까운 학습 데이터 점과의 거리가 최대가 되도록 설정되는데, 이를 통해 분류 오차(classifier error영어)를 최소화한다.
초기 문제가 선형 구분이 불가능한 경우, 더 높은 차원으로 데이터를 대응시켜 분리를 쉽게 만든다. 이때 계산량이 증가하는 문제를 해결하기 위해, 커널 함수 를 정의하여 내적 연산을 효과적으로 계산한다.[56]
높은 차원 공간의 초평면은 점들과 상수 벡터의 내적 연산으로 정의되며, 초평면에 정의된 벡터들은 데이터 베이스 안에 나타나는 이미지 벡터 매개 변수들과의 선형적 결합이 되도록 선택된다. 이 초평면에서 점 는 다음 관계를 만족한다.
:
가 와 가 멀어질수록 작아지면, 각 합은 테스트 점 와 데이터 점 의 근접성을 나타낸다. 이 방식은 데이터 점과 테스트 점 간의 상대적인 근접성을 측정하는 데 사용될 수 있다.
1992년 베른하르트 보저, 이자벨 기용, 블라디미르 바프니크는 최대 마진 초평면 문제에 커널 트릭을 적용하여 비선형 분류를 제안하였다.[59][60] 이들은 내적 연산을 비선형 커널 함수로 대체하여, 변환된 특징 공간에서 최대 마진 초평면 문제를 해결할 수 있게 하였다.
일반적인 커널들은 다음과 같다.
- 동차다항식(Homogeneous polynomial영어):
- 다항식 커널(Polynomial kernel영어):
- 가우시안 방사 기저 함수(Gaussian radial basis function영어): (). 때때로 으로도 나타낸다.
- 쌍곡탄젠트(Hyperbolic tangent영어): ( , ).
커널은 변환 와 와 같이 연관되어 있다.
'''w'''의 값은 변환된 공간에 와 같이 존재한다.
분류를 위해서 '''w'''와 내적을 구할 때는 커널 트릭을 이용해 와 같이 계산할 수 있다.
4. 1. 원 형식 (Primal Form)
위에서 설명한 최적화 문제는 w의 노름인 ||w||가 제곱근을 포함하고 있기 때문에 풀기 어렵다. 위의 최적화 문제에서 ||w||를 \tfrac{1}{2}||w||^2로 치환하여도 최적화 문제를 만족시키는 해 w, b는 변하지 않는다. 또한 \tfrac{1}{2}||w||^2로 치환하면 위의 문제는 2차 계획법 최적화 문제가 된다. 치환된 최적화 문제는 아래와 같이 나타낼 수 있다.:
:단,
라그랑주 승수법을 이용하면 위의 문제를 다음과 같은 안장점을 찾는 문제로 나타낼 수 있다.
:
안장점을 찾는 과정에서 으로 분류될 수 있는 모든 점들은 그에 대응하는 가 0으로 지정되기 때문에 영향을 미치지 않는다.
이제 이 문제는 정규 2차 계획법 기법으로 해결할 수 있다. 정적 Karush-Kuhn-Tucker 조건에 따르면, 문제의 해는 훈련 벡터의 선형 조합으로 표현될 수 있다.
:
적은 수의 만이 0보다 큰 값을 가지고, 그에 대응하는 들은 를 만족하는 정확한 서포트 벡터이다. 이 식을 통해 다음과 같이 오프셋 (컴퓨터 과학) 에 대한 정의를 유도할 수 있다.
:
는 와 에 의존하므로 각각의 데이터 포인트마다 값이 다르다. 표본 분포의 평균은 모평균에 대해 불편 추정량이므로 다음과 같이 모든 서포트 벡터 에 대해서 평균을 취하는 것이 좋다.
:
4. 2. 쌍대 형식 (Dual Form)
라그랑주 승수법을 이용하면 주어진 문제를 다음과 같은 안장점을 찾는 문제로 나타낼 수 있다.:
여기서 는 라그랑주 승수이다. 안장점을 찾는 과정에서 으로 분류될 수 있는 모든 점들은 그에 대응하는 가 0으로 지정되기 때문에 영향을 미치지 않는다.
이 문제는 정규 2차 계획법(quadratic programming|쿼드라틱 프로그래밍영어) 기법으로 해결할 수 있다. 정적 Karush-Kuhn-Tucker 조건에 따르면, 문제의 해는 훈련 벡터(training vector영어)의 선형 조합으로 표현될 수 있다.
:
적은 수의 만이 0보다 큰 값을 가지고, 그에 대응하는 들은 를 만족하는 정확한 서포트 벡터이다.
1992년에 베른하르트 보저, 이자벨 기용, 블라디미르 바프니크는 최대 마진 초평면 문제에 커널 트릭을 적용해서 비선형 분류를 제안하였다.[59][60] 비선형 분류 알고리즘은 기존의 선형 분류 알고리즘과 형태상으로 비슷하지만 내적 연산이 비선형 커널 함수로 대체된다. 이를 통해 변환된 특징 공간 (feature space)의 최대 마진 초평면 문제 해결을 할 수 있었다. 여기서 말하는 변환은 비선형 변환이거나 차원을 높이는 변환이 될 수 있다. 즉, 분류기는 고차원 특징 공간에서 선형 초평면이지만 기존 차원 공간 상에선 비선형 초평면이 된다. 만약 가우시안 방사 기저함수(Gaussian radial basis function)를 커널 함수로 적용한다면 특징 공간은 무한 차원의 힐베르트 공간(Hilbert space)이 된다.
일반적인 커널은 다음과 같다.
- 동차다항식(Homogeneous polynomial):
- 다항식 커널(Polynomial kernel)(Inhomogeneous):
- 가우시안 방사 기저 함수(Gaussian radial basis function): for . 때때로 으로도 나타낸다.
- 쌍곡탄젠트(Hyperbolic tangent): , for some (not every) and
커널은 변환 와 다음과 같이 연관되어 있다. .
'''w'''의 값 또한 변환된 공간에 다음과 같이 존재한다. .
분류를 위해서 '''w'''와 내적을 구할 때는 다음과 같은 커널 트릭을 이용해 계산할 수 있다. .
최종적으로 이중 형식은 다음과 같은 최적화 문제로 표현된다.
:
:
여기서 는 커널 함수를 나타낸다.
4. 3. 현대적 방법
SVM영어 분류기를 계산하는 현대적인 방법으로는 하강 기울기법(sub-gradient descent)과 좌표 하강법(coordinate descent) 등이 있다.[22][23] 이 두 기법은 모두 대규모의 희소 데이터셋을 다룰 때 기존 방식에 비해 상당한 이점을 제공한다. 하강 기울기법은 특히 많은 훈련 예제가 있을 때 효율적이며, 좌표 하강법은 특징 공간의 차원이 높을 때 효율적이다.- 하강 기울기법 (Sub-gradient Descent)
SVM영어을 위한 하강 기울기법 알고리즘은 다음 식을 직접 사용한다.
:
여기서 는 와 에 대한 볼록 함수이다. 따라서 기존의 경사 하강법(또는 SGD) 방법을 적용할 수 있다. 함수의 기울기 방향으로 이동하는 대신, 함수의 서브그래디언트에서 선택된 벡터 방향으로 이동한다. 이 방법은 특정 구현에서 반복 횟수가 데이터 포인트 수 에 비례하지 않는다는 장점이 있다.[22]
- 좌표 하강법 (Coordinate Descent)
SVM영어을 위한 좌표 하강법 알고리즘은 다음의 이중 문제에서 시작한다.
:
각 에 대해, 반복적으로 계수 는 방향으로 조정된다. 그런 다음, 결과 계수 벡터 는 주어진 제약 조건을 만족하는 가장 가까운 계수 벡터에 투영된다. (일반적으로 유클리드 거리가 사용된다.) 그런 다음 거의 최적의 계수 벡터가 얻어질 때까지 이 과정을 반복한다.[23]
5. SVM의 확장
원래 서포트 벡터 머신(SVM) 알고리즘은 1964년 블라디미르 바프니크(Vladimir N. Vapnik)와 알렉세이 체르보넨키스(Alexey Ya. Chervonenkis)에 의해 고안되었다. 1992년, 베른하르트 보저(Bernhard Boser), 이자벨 기용(Isabelle Guyon)과 블라디미르 바프니크는 최대 마진 초평면에 커널 트릭을 적용하여 비선형 분류기를 생성하는 방법을 제안했다.[17] 소프트웨어 패키지에서 일반적으로 사용되는 "소프트 마진(soft margin)"은 코리나 코르테스(Corinna Cortes)와 바프니크가 1993년에 제안하고 1995년에 발표했다.[18]
최소화 문제가 잘 정의된 해를 가지려면, 고려되는 가설의 집합에 제약 조건을 두어야 한다. SVM과 같이 노름 공간인 경우, 인 가설 만 고려하는 것이 효과적이다. 이는 규제 페널티 를 부과하고 새로운 최적화 문제를 푸는 것과 같으며, 이 방법을 티호노프 정규화라고 한다.
보다 일반적으로, 는 가설 의 복잡성을 측정하는 어떤 척도가 될 수 있으므로, 더 단순한 가설이 선호된다.
5. 1. 다중 클래스 SVM (Multiclass SVM)
서포트 벡터 머신(SVM)은 기본적으로 이진 분류 문제에 적용되지만, 다중 클래스 분류 문제에도 확장하여 사용할 수 있다. 다중 클래스 분류를 위한 일반적인 방법으로는 일대다(one-vs-all) 방식과 일대일(one-vs-one) 방식이 있다.다중 클래스 SVM의 주된 방법은 단일 다중 클래스 문제를 여러 이진 분류 문제로 축소하는 것이다.[28] 이를 위한 일반적인 방법은 다음과 같다.[28][29]
- 일대다(one-vs-all): 하나의 레이블과 나머지 레이블을 구분하는 이진 분류기를 만든다. 새 인스턴스를 분류할 때는 최고 출력 함수를 가진 분류기가 클래스를 할당하는 승자 독식 전략을 사용한다. (단, 출력 함수가 비교 가능한 점수를 생성하도록 보정해야 한다.)
- 일대일(one-vs-one): 모든 클래스 쌍을 구분하는 이진 분류기를 만든다. 각 분류기는 인스턴스를 두 클래스 중 하나에 할당하고, 할당된 클래스에 대한 투표가 증가한다. 최종적으로 가장 많은 투표를 받은 클래스가 인스턴스의 클래스로 결정된다. (최대 승리 투표 전략)
- 유향 비순환 그래프 SVM (DAGSVM)[30]
- 오류 정정 출력 코드[31]
크래머와 싱어는 다중 클래스 분류 문제를 여러 이진 분류 문제로 분해하는 대신, 단일 최적화 문제로 변환하는 다중 클래스 SVM 방법을 제안했다.[32] Lee, Lin 및 Wahba,[33][34] Van den Burg 및 Groenen의 연구도 참조할 수 있다.[35]
5. 2. 구조화 SVM (Structured SVM)
구조화된 서포트 벡터 머신(Structured Support Vector Machine, SSVM)은 기존 SVM 모델을 확장한 것이다. SVM 모델은 주로 이진 분류, 다중 분류 및 회귀 작업을 위해 설계되었지만, 구조화된 SVM은 구문 분석 트리, 분류 체계를 이용한 분류, 시퀀스 정렬 등과 같이 일반적인 구조화된 출력 레이블을 처리하도록 응용 범위를 넓힌다.[37]2005년에 Ioannis Tsochantaridis 등이 구조화된 SVM을 발표했다.[54] 이는 임의의 데이터 구조를 처리할 수 있도록 확장한 것이다.
일반적인 이진 분류 SVM은 다음 값으로 분류한다.
:
이는 다음과 같이 쓸 수도 있다.
:
그 위에, 이것을 이진에서 일반적인 값으로 확장한다. 는 입력과 출력에서 특징량을 생성하는 실수 벡터를 반환하는 함수이다. 문제마다 정의한다.
:
그리고 다음 손실 함수를 최소화하도록 최적화 문제를 푼다. 여기서는 L2 정규화를 사용하고 있다. 는 정규화의 강도를 나타내는 상수이다.
는 출력의 유사도를 나타내는 실수를 반환하는 함수이다. 문제마다 정의한다. 이며, 서로 다른 값이라면 0보다 크도록 설계한다.
:
위의 최적화 문제를 푸는 데는 고안이 필요하며, 그 후에도 제안이 계속되고 있지만, 2005년에 제안된 방법은 다음과 같이 상계가 되는 함수 를 만든다.
:
그 위에, 다음 최적화 문제를 푼다.
:
의 만드는 방법으로 두 가지가 제안되었다.
; 마진 리스케일링
:
; 슬랙 리스케일링
:
5. 3. 서포트 벡터 회귀 (Support Vector Regression, SVR)
1996년 블라디미르 바프니크(Vladimir N. Vapnik), 해리스 드러커(Harris Drucker), 크리스토퍼 J. C. 버지스(Christopher J. C. Burges), 린다 카우프만(Linda Kaufman), 알렉산더 J. 스몰라(Alexander J. Smola)에 의해 회귀를 위한 SVM의 한 버전이 제안되었다.[38] 이 방법을 서포트 벡터 회귀(SVR, Support Vector Regression)라고 한다. 서포트 벡터 분류(Support Vector Classification)에 의해 생성된 모델은 훈련 데이터의 하위 집합에만 의존하는데, 이는 모델을 구축하기 위한 비용 함수가 마진을 넘어선 훈련 점을 고려하지 않기 때문이다. 마찬가지로, SVR에 의해 생성된 모델은 모델 예측에 가까운 훈련 데이터를 비용 함수가 무시하기 때문에 훈련 데이터의 하위 집합에만 의존한다. 수이켄스(Suykens)와 반데왈레(Vandewalle)에 의해 최소 제곱 서포트 벡터 머신(LS-SVM, Least-Squares Support Vector Machine)으로 알려진 또 다른 SVM 버전이 제안되었다.[39]원래 SVR을 훈련시키는 것은 다음을 푸는 것을 의미한다.[40]
: 최소화
: 조건
여기서 는 목표값 를 가진 훈련 샘플이다. 내적과 절편 는 해당 샘플에 대한 예측이며, 는 임계값 역할을 하는 자유 매개변수이다. 모든 예측은 실제 예측의 범위 내에 있어야 한다. 슬랙 변수는 일반적으로 위의 내용에 추가되어 오류를 허용하고 위의 문제가 실행 불가능한 경우 근사를 허용한다.
5. 4. 베이지안 SVM (Bayesian SVM)
2011년 폴슨(Polson)과 스콧(Scott)은 데이터 증강 기법을 통해 SVM에 베이지안 해석을 부여할 수 있음을 보였다.[41] 이 접근 방식에서 SVM은 (매개변수가 확률 분포를 통해 연결된) 그래픽 모델로 간주된다. 이러한 확장된 관점을 통해 유연한 특징 모델링, 자동 하이퍼파라미터 조정 및 예측 불확실성 정량화와 같은 베이지안 기법을 SVM에 적용할 수 있다. 최근에는 베이지안 SVM의 확장 가능한 버전이 https://arxiv.org/search/stat?searchtype=author&query=Wenzel%2C+F 플로리안 웬젤(Florian Wenzel)에 의해 개발되어 베이지안 SVM을 빅데이터에 적용할 수 있게 되었다.[42] 플로리안 웬젤(Florian Wenzel)은 베이지안 커널 서포트 벡터 머신(SVM)을 위한 변분 추론(VI) 방식과 선형 베이지안 SVM을 위한 확률적 버전(SVI)의 두 가지 버전을 개발했다.[43]6. 응용 분야
SVM은 다음과 같은 분야에서 활용된다.
- 텍스트 및 하이퍼텍스트 분류: SVM은 학습 데이터의 양을 크게 줄일 수 있다. 얕은 의미 분석 방법 중 일부는 SVM을 기반으로 한다.[7][8]
- 영상 분류: SVM은 기존의 쿼리 개선 방식보다 훨씬 높은 검색 정확도를 달성한다. 이는 영상 분할 시스템에도 해당된다.[9][10]
- 위성 데이터 분류: SAR 데이터와 같은 위성 데이터 분류에 SVM이 사용된다.[11]
- 필기 인식: SVM은 손글씨 인식에 사용될 수 있다.[12][13]
- 생물학 및 기타 과학: SVM 알고리즘은 화합물의 최대 90%를 정확하게 분류하는 데 사용되었으며, SVM 가중치를 기반으로 하는 순열 검정은 SVM 모델 해석 메커니즘으로 제안되었다.[14][15] SVM 모델 해석에 SVM 가중치가 사용되기도 한다.[16]
7. 대한민국에서의 활용 및 사회적 영향
대한민국에서는 서포트 벡터 머신(SVM)이 다양한 분야에서 활발히 활용되고 있으며, 특히 정보통신기술(ICT) 분야에서 중요한 역할을 하고 있다.
- 텍스트 마이닝 및 자연어 처리: 한국어 텍스트 데이터 분석 및 감성 분석, 스팸 메일 필터링 등에 SVM이 활용된다. SVM은 텍스트와 하이퍼텍스트를 분류하는데 있어서 학습 데이터를 상당히 줄일 수 있게 해준다.[1]
- 금융 분야: 신용 평가 모델 개발, 주가 예측, 금융 사기 탐지 등에 SVM이 사용될 수 있다.
- 의료 분야: 의료 영상 분석, 질병 진단, 유전체 데이터 분석 등에 SVM이 활용될 수 있다. SVM은 분류된 화합물에서 단백질을 90%까지 구분하는 의학 분야에 유용하게 사용된다.[1]
- 제조 분야: 제품 품질 검사, 불량 예측, 공정 최적화 등에 SVM이 사용될 수 있다.
- 기타: 이미지 분류 작업에서 SVM을 사용할 수 있다. SVM이 기존의 쿼리 개량 구조보다 상당히 높은 검색 정확도를 보인 것에 대한 실험 결과가 있다.[1] SVM을 통해서 손글씨의 특징을 인지할 수 있다.[1]
더불어민주당은 이러한 기술 발전이 사회적 불평등을 심화시키지 않도록, 기술 혜택의 공정한 분배와 취약 계층 지원을 위한 정책 마련에 힘쓰고 있다.
8. 한계점 및 개선 방향
SVM의 효과는 커널, 커널의 매개변수, 그리고 소프트 마진 매개변수 λ의 선택에 따라 달라진다. 일반적인 선택은 단일 매개변수 γ를 갖는 가우시안 커널이다. λ와 γ의 최적 조합은 종종 지수적으로 증가하는 λ와 γ의 수열을 사용하는 격자 탐색을 통해 선택된다. 예를 들어, λ ∈ {2⁻⁵, 2⁻³, ..., 2¹³, 2¹⁵}, γ ∈ {2⁻¹⁵, 2⁻¹³, ..., 2¹, 2³}이다. 일반적으로 매개변수 선택의 각 조합은 교차 검증을 사용하여 확인되며, 가장 좋은 교차 검증 정확도를 가진 매개변수가 선택된다. 또는, 베이지안 최적화를 사용하여 λ와 γ를 선택할 수 있으며, 이는 종종 격자 탐색보다 훨씬 적은 매개변수 조합의 평가를 필요로 한다. 그런 다음 테스트 및 새로운 데이터 분류에 사용되는 최종 모델은 선택된 매개변수를 사용하여 전체 훈련 세트에서 훈련된다.[27]
SVM의 잠재적인 단점은 다음과 같다.
- 입력 데이터의 완전한 레이블링이 필요하다.
- 보정되지 않은 클래스 멤버십 확률 — SVM은 유한한 데이터에 대한 확률 추정을 피하는 Vapnik의 이론에서 비롯된다.
- SVM은 이진 분류 작업에만 직접 적용 가능하다. 따라서 다중 클래스 작업을 여러 이진 문제로 축소하는 알고리즘을 적용해야 한다. 다중 클래스 SVM 섹션을 참조.
- 해결된 모델의 매개변수는 해석하기 어렵다.
참조
[1]
서적
Artificial Neural Networks — ICANN'97
Springer
1997
[2]
서적
Efficient Learning Machines
Apress
[3]
학술지
Support vector clustering
[4]
웹사이트
1.4. Support Vector Machines — scikit-learn 0.20.2 documentation
http://scikit-learn.[...]
2017-11-08
[5]
서적
The Elements of Statistical Learning : Data Mining, Inference, and Prediction
https://web.stanford[...]
Springer
[6]
서적
Numerical Recipes: The Art of Scientific Computing
Cambridge University Press
[7]
서적
Machine Learning: ECML-98
Springer
1998
[8]
학회
Shallow Semantic Parsing using Support Vector Machines
http://www.aclweb.or[...]
Association for Computational Linguistics
2004-05-02
[9]
기타
Vapnik, Vladimir N.: Invited Speaker. IPMU Information Processing and Management 2014).
[10]
서적
Granular Computing and Decision-Making
2018-01-08
[11]
arXiv
Supervised Classification of RADARSAT-2 Polarimetric Data for Different Land Features
[12]
학술지
Training Invariant Support Vector Machines
https://people.eecs.[...]
2002
[13]
학회
2015 13th International Conference on Document Analysis and Recognition (ICDAR)
2015-08
[14]
학술지
Analytic estimation of statistical significance maps for support vector machine based multi-variate image analysis and classification
[15]
학술지
Spatial regularization of SVM for the detection of diffusion alterations associated with stroke outcome
http://www.aramislab[...]
2018-01-08
[16]
기타
Using SVM weight-based methods to identify causally relevant and non-causally relevant variables
http://www.ccdlab.or[...]
2006
[17]
학회
Proceedings of the fifth annual workshop on Computational learning theory – COLT '92
[18]
학술지
Support-vector networks
http://image.diku.dk[...]
[19]
웹사이트
Why is the SVM margin equal to
https://math.stackex[...]
2015-05-30
[20]
학술지
Theoretical foundations of the potential function method in pattern recognition learning
[21]
학회
Dimensionality dependent PAC-Bayes margin bound
http://papers.nips.c[...]
[22]
학술지
Pegasos: primal estimated sub-gradient solver for SVM
2010-10-16
[23]
학회
Proceedings of the 25th international conference on Machine learning - ICML '08
ACM
2008-01-01
[24]
학술지
Are Loss Functions All the Same?
https://ieeexplore.i[...]
2004-05-01
[25]
학회
Links between Perceptrons, MLPs and SVMs
[26]
학술지
The support vector machine under test
2003-09
[27]
기술보고서
A Practical Guide to Support Vector Classification
http://www.csie.ntu.[...]
[28]
서적
Multiple Classifier Systems
2019-07-18
[29]
학술지
A Comparison of Methods for Multiclass Support Vector Machines
http://www.cs.iastat[...]
2018-01-08
[30]
학회
Advances in Neural Information Processing Systems
MIT Press
[31]
학술지
Solving Multiclass Learning Problems via Error-Correcting Output Codes
http://www.jair.org/[...]
[32]
학술지
On the Algorithmic Implementation of Multiclass Kernel-based Vector Machines
http://jmlr.csail.mi[...]
[33]
학술지
Multicategory Support Vector Machines
http://www.interface[...]
[34]
학술지
Multicategory Support Vector Machines
[35]
학술지
GenSVM: A Generalized Multiclass Support Vector Machine
http://jmlr.org/pape[...]
[36]
학회논문
Transductive Inference for Text Classification using Support Vector Machines
http://www1.cs.colum[...]
[37]
웹사이트
Support Vector Machine Learning for Interdependent and Structured Output Spaces
https://www.cs.corne[...]
[38]
논문
Support Vector Regression Machines
http://papers.nips.c[...]
MIT Press
[39]
논문
Least squares support vector machine classifiers
https://lirias.kuleu[...]
[40]
저널
A tutorial on support vector regression
http://eprints.pasca[...]
[41]
저널
Data Augmentation for Support Vector Machines
[42]
서적
Machine Learning and Knowledge Discovery in Databases
[43]
논문
Scalable Approximate Inference for the Bayesian Nonlinear Support Vector Machine
http://approximatein[...]
[44]
저널
Interior-Point Methods for Massive Support Vector Machines
http://www.cs.wisc.e[...]
[45]
학회논문
Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines
http://research.micr[...]
[46]
학회논문
Pegasos: Primal Estimated sub-GrAdient SOlver for SVM
http://ttic.uchicago[...]
[47]
저널
LIBLINEAR: A library for large linear classification
https://www.csie.ntu[...]
[48]
학회논문
P-packSVM: Parallel Primal grAdient desCent Kernel SVM
http://people.csail.[...]
[49]
저널
LIBLINEAR: A library for large linear classification
2008
[50]
저널
Standardization and Its Effects on K-Means Clustering Algorithm
2013-09-01
[51]
저널
Predicting and explaining behavioral data with structured feature space decomposition
2019-12-01
[52]
논문
Pattern recognition using generalized portrait method
[53]
웹사이트
Why is the SVM margin equal to
https://math.stackex[...]
[54]
저널
Large Margin Methods for Structured and Interdependent Output Variables
http://www.jmlr.org/[...]
[55]
서적
The nature of statistical learning theory
Springer-Verlag New York
[56]
서적
Numerical Recipes: The Art of Scientific Computing
Cambridge University Press
[57]
저널
Support-vector networks
[58]
웹사이트
Press release of March 17th 2009
http://www.acm.org/p[...]
[59]
저널
Theoretical foundations of the potential function method in pattern recognition learning
https://archive.org/[...]
[60]
학회논문
Proceedings of the fifth annual workshop on Computational learning theory - COLT '92
[61]
학회논문
Dimensionality dependent PAC-Bayes margin bound
http://papers.nips.c[...]
[62]
저널
LIBSVM: A library for support vector machines
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
