자이페르트 곡면

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 성질
4. 예시
5. 역사
참조

1. 개요

자이페르트 곡면은 3차원 공간에 놓인 매듭 또는 연환을 경계로 갖는 2차원 유향 다양체이다. 모든 연환은 자이페르트 곡면을 가지며, 이는 유일하지 않다. 자이페르트 곡면은 자이페르트 알고리즘을 통해 구체적으로 구성할 수 있으며, 자이페르트 행렬과 알렉산더 다항식, 매듭의 부호와 같은 불변량을 계산하는 데 사용된다. 자이페르트 곡면의 종수는 매듭 불변량으로, 매듭의 종류를 구별하는 데 활용된다.

더 읽어볼만한 페이지

매듭 이론 - 꼬임군 (위상수학)
꼬임군은 n개의 가닥 꼬기 연산을 연구하는 수학적 구조로, 꼬임들의 연결을 통해 군 연산을 수행하며 매듭 이론 등 다양한 분야에 응용된다.
매듭 이론 - 천-사이먼스 이론
천-사이먼스 이론은 천싱선과 제임스 해리스 사이먼스가 정의한 3차 천-사이먼스 형식을 기반으로 3차원 다양체에서 정의되는 위상 양자장론으로, 양자장론, 매듭 이론, 끈 이론 등 다양한 분야와 연관되어 있으며 존스 다항식, 베스-추미노-위튼 모형, 분수 양자 홀 효과 설명 등에 활용된다.
곡면 - 뫼비우스의 띠
"상상력" 한가 아닌 답변을 바랍니다.
곡면 - 가우스의 빼어난 정리
가우스의 빼어난 정리는 곡면의 가우스 곡률이 외부 공간이 아닌 곡면 자체의 리만 계량만으로 결정된다는 정리로, 곡면의 변형 시 가우스 곡률이 보존됨을 의미하며, 지도 제작의 불가능성 증명과 고차원 리만 다양체 일반화에 응용되어 미분기하학과 일반 상대성 이론의 기초가 된다.

자이페르트 곡면

2. 정의

차분한(tame^영어) 유향 연환 $L \subsetneq \mathbb S^3$ 의 '''자이페르트 곡면'''은 $\partial\Sigma = L$ 인 $\mathbb S^3$ 속의 2차원 유향 연결 경계다양체 $\Sigma \subsetneq \mathbb S^3$ 이다.

3. 성질

연환은 자이페르트 곡면을 갖지만, 이는 유일하지 않다.^[3]

자이페르트 곡면의 1차 호몰로지 군은 자유 아벨 군이며, 다음과 같이 표현된다.

: $\operatorname H_1(\Sigma) \cong \mathbb Z^{2g}$

여기서 $g$ 는 자이페르트 곡면의 종수이다.

교차 형식이 다음과 같은 형태를 가지는 기저가 존재한다.

: $Q = \begin{pmatrix}0&-1\\1&0\end{pmatrix}\oplus \dotsb \oplus \begin{pmatrix}0&-1\\1&0\end{pmatrix}$

: $a_1,a_2,\dotsc,a_{2g}\in \operatorname H_1(\Sigma)$

이 기저를 이용하여 자이페르트 행렬(Seifert matrix^영어) $V$ 를 정의할 수 있다. 자이페르트 행렬은 $2g \times 2g$ 크기의 정사각 행렬이며, 각 성분은 정수이다. $(i, j)$ 번째 성분은 $a_i$ 와 $a_j$ 의 연환수이다.^[4]

자이페르트 행렬 $V$ 는 다음을 만족한다.

: $V - V^\top = Q$

여기서 $V^\top$ 는 $V$ 의 전치 행렬이다.

알렉산더 다항식은 자이페르트 행렬을 이용하여 다음과 같이 계산할 수 있다.

: $A_L(t) = \det (V - tV^\top)$

연환의 종수 $g(L)$ 은 알렉산더 다항식의 차수와 관련이 있으며, 다음 부등식을 만족한다.

: $g(L) \ge \left\lceil\frac12\deg A_L\right\rceil$

자이페르트 행렬의 대칭 행렬 $V + V^\top$ 의 부호수는 연환의 불변량이며, 이를 연환의 부호수(signature of a link/knot)라고 한다.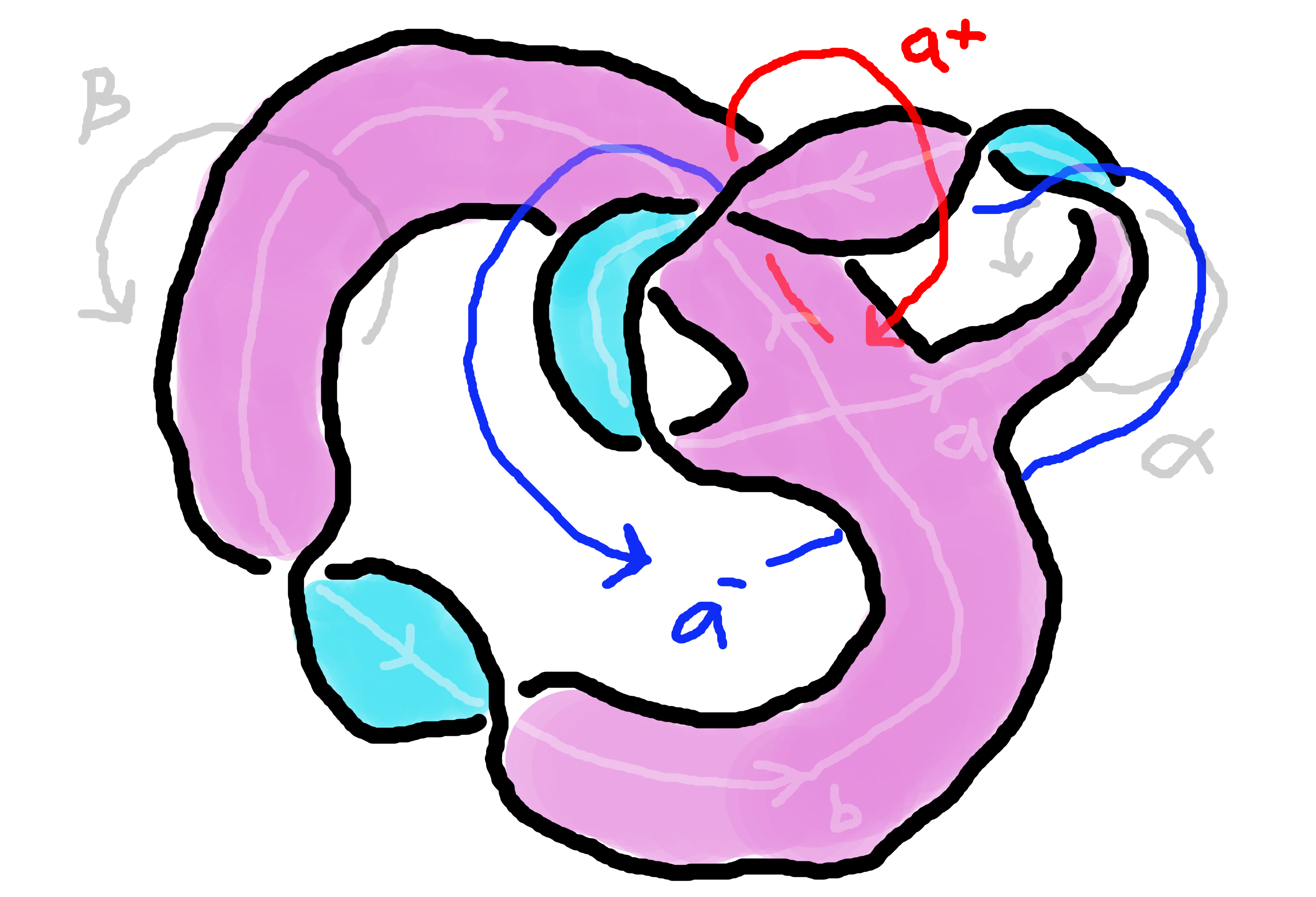

매듭의 자이페르트 곡면에 대한 호몰로지 생성기 ''a''의 양의 방향 및 음의 방향으로의 (동위인) 푸시 오프(pushoff) 예시

자이페르트 알고리즘으로 구성된 자이페르트 곡면은

m

개의 구멍을 가지며, 종수는 다음과 같다.

:

g = \frac{2 + d - f - m}{2}

(

m

: 연결 성분 개수,

d

: 교차점 개수,

f

: 자이페르트 원 개수)

주어진 연환의 자이페르트 곡면 중 최소 종수를 연환의 '''종수'''라고 한다. 매듭 ''K''의 '''종수'''는 ''K''에 대한 자이페르트 곡면의 최소 종수 ''g''로 정의되는 매듭 불변량이다.

임의의 두 유향 매듭

K

,

K'

에 대하여, 다음이 성립한다.

:

g(K) + g(K') = g(K \# K')

즉, 매듭의 연결합은 종수를 보존한다.

예를 들어:

매듭 없음은, 정의상, 원반의 경계이므로, 종수가 0이다. 또한, 매듭 없음은 종수가 0인 유일한 매듭이다.
클로버 매듭은 8자 매듭과 마찬가지로 종수가 1이다.
(''p'',''q'')-토러스 매듭의 종수는 (''p'' − 1)(''q'' − 1)/2이다.
매듭의 알렉산더 다항식의 차수는 종수의 두 배에 대한 하한이다.

3. 1. 존재와 유일성

모든 연환은 자이페르트 곡면을 갖는다. 그러나 이는 유일하지 않다.^[3]

연환의 자이페르트 곡면은 다음과 같은 알고리즘으로 구성된다. 우선, 연환

L

이

m

개의 연결 성분을 갖는다고 하자.

L

의 임의의 그림(평면으로의 투영)이 주어졌다고 하고, 이 그림이

d

개의 교차점을 갖는다고 하자. 그렇다면, 다음과 같이 그림에서 교차점들을 해소할 수 있다.

-|]]|]] ⇒ --|]]

교차점을 모두 해소하면 연환의 그림은 서로 교차하지 않는 원들로 구성되는데,

f

개의 원들이 있다고 하자.

그렇다면, 다음과 같은 자이페르트 곡면을 구성할 수 있다.

1. 연환면의 그림의 해소의 각 원 안에 원판을 붙인다. 즉,

f

개의 원판이 존재한다.

2. 연환면에서, 해소된 각 교차점에 대응하는 띠를 이어붙인다. 이 경우, 아래 그림과 같이 띠를 뒤틀어 이어붙이며, 띠를 뒤트는 방향은 해소되기 이전의 교차점의 방향을 따른다.

-|]]

이 경우, 교차점의 해소에서 방향을 보존해야 한다. (방향을 보존하지 않으면, 비가향 다양체를 얻을 수 있다.) 즉, 다음과 같은 꼴의 해소는 불가능하다.

- ⇒ ⩆

어떤 매듭이든 항상 연관된 자이페르트 곡면이 존재한다는 것은 정리이다. 이 정리는 1930년 프랑클(Frankl)과 폰트랴긴에 의해 처음 발표되었다.^[3] 1934년 헤르베르트 자이페르트에 의해 다른 증명이 발표되었으며, 이는 현재 자이페르트 알고리즘이라고 불리는 것에 의존한다. 이 알고리즘은 문제의 매듭 또는 링크의 투영이 주어지면 자이페르트 곡면

S

를 생성한다.

링크가 ''m''개의 구성 요소(매듭의 경우 ''m''=1)를 가지고, 다이어그램이 ''d''개의 교차점을 가지며, 교차점을 해결하면(매듭의 방향을 유지) ''f''개의 원이 생성된다고 가정해 보자. 그러면 곡면

S

는 ''f''개의 서로소인 디스크에 ''d''개의 밴드를 부착하여 구성된다. 호몰로지 군

H_1(S)

는 2''g''개의 생성자에 대한 자유 아벨 군이며, 여기서

:

g = \frac{1}{2}(2 + d - f - m)

는

S

의 종수이다.

H_1(S)

에 대한 교차 형식 ''Q''는 왜대칭 행렬이며, 2''g''개의 사이클

a_1, a_2, \ldots, a_{2g}

의 기저가 있고

Q = (Q(a_i, a_j))

는 행렬의 ''g''개의 복사본의 직접 합과 같다.

:

\begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}

2''g'' × 2''g'' 정수 '''자이페르트 행렬'''

:

V = (v(i, j))

에서

v(i, j)

는 유클리드 3차원 공간 (또는 3-구에서)의 ''a''_''i''와

S

의 양의 방향으로의 ''a''_''j''의 "푸시 오프(pushoff)" 사이의 연결수이다. 더 정확하게 말하면, 자이페르트 곡면은 양면성을 가지므로, 즉

S

의 임베딩을

S \times [-1, 1]

의 임베딩으로 확장할 수 있다는 것을 기억하면,

S

의 내부에 있는 호몰로지 생성기인 어떤 대표 루프

x

가 주어졌을 때, 양의 푸시 오프는

x \times \{1\}

이고 음의 푸시 오프는

x \times \{-1\}

이다.^[4]

이를 통해 다음과 같은 관계를 얻는다.

:

V - V^* = Q,

여기서 ''V''^∗ = (''v''(''j'', ''i''))는 전치 행렬이다.

V - V^* = Q

를 만족하는 모든 정수 2''g'' × 2''g'' 행렬

V

는 종수 ''g'' 자이페르트 곡면을 가진 매듭의 자이페르트 행렬로 나타난다.

알렉산더 다항식은

A(t) = \det\left(V - tV^*\right)

에 의해 자이페르트 행렬로부터 계산되며, 이는 미지수

t

에 대한 최대 2''g''차의 다항식이다. 알렉산더 다항식은 자이페르트 곡면

S

의 선택에 의존하지 않으며 매듭 또는 링크의 불변량이다.

매듭의 부호는 대칭 자이페르트 행렬

V + V^\mathrm{T}

의 부호이다. 이 또한 매듭 또는 링크의 불변량이다.

임의의 유향 꼬임 그림에 대해, 다음을 통해 꼬임의 자이페르트 곡면을 구성할 수 있다.

'''단계 1'''

: 주어진 유향 꼬임 그림에 대해 '''평활화'''(smoothing)라고 불리는 연산을 수행한다. 즉, 유향 꼬임 그림의 교차점은 반드시 아래 그림 1 또는 그림 2와 같으므로, 이를 그림 3과 같이 치환한다. 평활화를 통해 그림의 모든 교차점이 제거되고, 그림에는 (방향이 지정된) 유한 개의 원주가 남는다. 이러한 원주를 '''자이페르트 원주''' 또는 '''자이페르트 주'''라고 한다.

'''단계 2'''

: 각 자이페르트 원주에 대해, 그 원주를 경계로 갖는 원판을 덧댄다. 단, 원래의 투영 그림에 따라 어떤 자이페르트 원주의 내부에 다른 자이페르트 원주가 들어있는 경우가 있다. 이러한 경우에는, 안쪽 원주를 바깥쪽 원주보다 약간 위로 들어올린 다음 원판을 덧댄다. 이와 같이 하여 자이페르트 원주의 개수와 동일한, 서로 교차하지 않는 원판이 만들어진다.

'''단계 3'''

: 마지막으로, 단계 1의 평활화로 제거한 각 교차점에서, 양쪽의 원판을 180° 비튼 띠로 연결시킨다. 이때 띠의 비틀림은, 단계 1에서 평활화하기 전의 교차점의 상하와, 비틀린 띠의 경계(양쪽)의 상하가 일치하도록 한다.

이상으로, 주어진 유향 꼬임을 경계로 갖는 곡면을 구성할 수 있었다. 이 방법을 '''자이페르트의 알고리즘'''이라고 한다. 자이페르트의 알고리즘으로 구성된 곡면은 방향을 지정할 수 있으므로, 자이페르트 곡면이다. 단계 2에서 원판을 붙일 때, 자이페르트 원주가 시계 방향으로 방향지정되어 있으면 원판의 윗면을 앞면, 아랫면을 뒷면으로 하고, 원주가 반시계 방향일 때는 윗면을 뒷면, 아랫면을 앞면으로 정해두면, 평활화할 때 교차점 양쪽 원주의 방향이 반대인 것으로부터, 180° 비틀린 띠로 연결했을 때 한쪽 원판의 앞면이 다른 쪽 원판의 앞면에, 뒷면은 뒷면에 연결되어 있음을 알 수 있다.

3. 2. 자이페르트 알고리즘

연환의 자이페르트 곡면은 자이페르트 알고리즘으로 구체적으로 구성할 수 있다. 자이페르트 알고리즘은 다음과 같은 단계로 구성된다.

우선, 연환

L

이

m

개의 연결 성분을 갖는다고 하고,

L

의 임의의 그림(평면으로의 투영)이 주어졌다고 가정한다. 이 그림이

d

개의 교차점을 갖는다고 하면, 다음과 같이 교차점들을 해소할 수 있다.

-|]]|]] ⇒ --|]]

교차점을 모두 해소하면 연환의 그림은 서로 교차하지 않는 원들로 구성되는데, 이 원들의 개수를

f

개라고 한다.

이러한 정보를 바탕으로 다음과 같은 자이페르트 곡면을 구성할 수 있다.

# 연환면의 그림의 해소의 각 원 안에 원판을 붙인다. 즉,

f

개의 원판이 존재한다.

# 연환면에서, 해소된 각 교차점에 대응하는 띠를 이어붙인다. 이 경우, 아래 그림과 같이 띠를 뒤틀어 이어붙이며, 띠를 뒤트는 방향은 해소되기 이전의 교차점의 방향을 따른다.

#:--|]]

이때, 교차점의 해소에서 방향을 보존해야 한다. 방향을 보존하지 않으면 비가향 다양체를 얻을 수 있다. 즉, 다음과 같은 꼴의 해소는 불가능하다.

:-- ⇒ ⩆

어떤 매듭(knot)이든 항상 연관된 자이페르트 곡면이 존재한다는 것은 정리이다. 이 정리는 1930년 프랑클(Frankl)과 폰트랴긴에 의해 처음 발표되었다.^[3] 1934년 헤르베르트 자이페르트에 의해 다른 증명이 발표되었으며, 이는 현재 자이페르트 알고리즘이라고 불리는 것에 의존한다. 이 알고리즘은 문제의 매듭 또는 링크의 투영이 주어지면 자이페르트 곡면

S

를 생성한다.

자세한 자이페르트 알고리즘의 단계는 다음과 같다.

'''단계 1'''

: 주어진 유향 꼬임 그림에 대해 '''평활화'''(smoothing)라고 불리는 연산을 수행한다. 즉, 유향 꼬임 그림의 교차점은 반드시 아래 그림 1 또는 그림 2와 같으므로, 이를 그림 3과 같이 치환한다. 평활화를 통해 그림의 모든 교차점이 제거되고, 그림에는 (방향이 지정된) 유한 개의 원주가 남는다. 이러한 원주를 '''자이페르트 원주''' 또는 '''자이페르트 주'''라고 한다.

'''단계 2'''

: 각 자이페르트 원주에 대해, 그 원주를 경계로 갖는 원판을 덧댄다. 단, 원래의 투영 그림에 따라 어떤 자이페르트 원주의 내부에 다른 자이페르트 원주가 들어있는 경우가 있다. 이러한 경우에는, 안쪽 원주를 바깥쪽 원주보다 약간 위로 들어올린 다음 원판을 덧댄다. 이와 같이 하여 자이페르트 원주의 개수와 동일한, 서로 교차하지 않는 원판이 만들어진다.

'''단계 3'''

: 마지막으로, 단계 1의 평활화로 제거한 각 교차점에서, 양쪽의 원판을 180° 비튼 띠로 연결시킨다. 이때 띠의 비틀림은, 단계 1에서 평활화하기 전의 교차점의 상하와, 비틀린 띠의 경계(양쪽)의 상하가 일치하도록 한다.

이상을 통해 주어진 유향 꼬임을 경계로 갖는 곡면을 구성할 수 있다. 이 방법을 '''자이페르트의 알고리즘'''이라고 한다. 자이페르트의 알고리즘으로 구성된 곡면은 방향을 지정할 수 있으므로, 자이페르트 곡면이다.

3. 3. 종수 (Genus)

자이페르트 알고리즘으로 구성된 자이페르트 곡면은

m

개의 구멍을 가지며, 종수는 다음과 같다.

:

g = \frac{2 + d - f - m}{2}

(

m

: 연결 성분 개수,

d

: 교차점 개수,

f

: 자이페르트 원 개수)

주어진 연환의 자이페르트 곡면 중 최소 종수를 연환의 '''종수'''라고 한다. 매듭 ''K''의 '''종수'''는 ''K''에 대한 자이페르트 곡면의 최소 종수 ''g''로 정의되는 매듭 불변량이다.

임의의 두 유향 매듭

K

,

K'

에 대하여, 다음이 성립한다.

:

g(K) + g(K') = g(K \# K')

즉, 매듭의 연결합은 종수를 보존한다.

예를 들어:

매듭 없음은, 정의상, 원반의 경계이므로, 종수가 0이다. 또한, 매듭 없음은 종수가 0인 유일한 매듭이다.
클로버 매듭은 8자 매듭과 마찬가지로 종수가 1이다.
(''p'',''q'')-토러스 매듭의 종수는 (''p'' − 1)(''q'' − 1)/2이다.
매듭의 알렉산더 다항식의 차수는 종수의 두 배에 대한 하한이다.

종수의 기본적인 성질은 매듭 합에 대해 가산적이라는 것이다.

:

g(K_1 \mathbin{\#} K_2) = g(K_1) + g(K_2)

일반적으로 매듭의 종수를 계산하는 것은 어렵고, 자이페르트 알고리즘은 일반적으로 최소 종수의 자이페르트 곡면을 생성하지 않는다. 이러한 이유로 다른 관련 불변량이 유용할 때가 있는데, 매듭의 '''정규 종수'''

g_c

는 자이페르트 알고리즘으로 구성할 수 있는 모든 자이페르트 곡면의 최소 종수이며, '''자유 종수'''

g_f

는

S^3

에서 그 여집합이 핸들바디인 모든 자이페르트 곡면의 최소 종수이다. (자이페르트 알고리즘에 의해 생성된 자이페르트 곡면의 여집합은 항상 핸들바디이다.) 모든 매듭에 대해 부등식

g \leq g_f \leq g_c

가 분명히 성립하므로, 특히 이러한 불변량은 종수에 대한 상한을 설정한다.^[5]

매듭 종수는 이안 에이골, 조엘 하스 및 윌리엄 서스턴의 연구에 의해 NP-완전이다.^[6]

매듭 ''K''의 최소 자이페르트 곡면은, ''K''의 '''자이페르트 곡면''' 중에서 그 종수가 최소인 것을 말한다(이는 일반적으로 유일하지 않다). ''K''의 최소 자이페르트 곡면의 종수로 매듭 ''K''의 종수로 한다.

합성 매듭의 종수는, 그 인자 매듭의 종수의 합과 같다는 것을 슈베르트가 증명했다.

3. 4. 자이페르트 행렬

자이페르트 곡면

\Sigma

의 1차 호몰로지 군은 자유 아벨 군이며, 다음과 같이 표현된다.

:

\operatorname H_1(\Sigma) \cong \mathbb Z^{2g}

여기서

g

는 자이페르트 곡면의 종수이다.

이때, 교차 형식이 다음과 같은 형태를 가지는 기저가 존재한다.

:

Q = \begin{pmatrix}0&-1\\1&0\end{pmatrix}\oplus \dotsb \oplus \begin{pmatrix}0&-1\\1&0\end{pmatrix}

:

a_1,a_2,\dotsc,a_{2g}\in \operatorname H_1(\Sigma)

이 기저를 이용하여 자이페르트 행렬(Seifert行列, Seifert matrix^영어)

V

를 정의할 수 있다. 자이페르트 행렬은

2g \times 2g

크기의 정사각 행렬이며, 각 성분은 정수이다.

(i, j)

번째 성분은

a_i

와

a_j

의 연환수이다.^[4]

자이페르트 행렬

V

는 다음을 만족한다.

:

V - V^\top = Q

여기서

V^\top

는

V

의 전치 행렬이다.

알렉산더 다항식은 자이페르트 행렬을 이용하여 다음과 같이 계산할 수 있다.

:

A_L(t) = \det (V - tV^\top)

연환의 종수

g(L)

은 알렉산더 다항식의 차수와 관련이 있으며, 다음 부등식을 만족한다.

:

g(L) \ge \left\lceil\frac12\deg A_L\right\rceil

자이페르트 행렬의 대칭 행렬

V + V^\top

의 부호수는 연환의 불변량이며, 이를 연환의 부호수(signature of a link/knot)라고 한다.

4. 예시

호프 올림매듭의 자이페르트 곡면. 뫼비우스의 띠가 아닌 환대이며, 두 번의 반 회전을 가지고 있어 가향 곡면이다.

표준적인 뫼비우스의 띠는 경계로 자르지 않은 매듭을 갖지만, 가향 곡면이 아니므로 자르지 않은 매듭의 자이페르트 곡면이 아니다.^[1]

클로버 매듭의 일반적인 최소 교차 투영의 "체커보드" 채색은 세 번의 반 회전을 가진 뫼비우스의 띠를 제공한다. 그러나 이는 가향 곡면이 아니므로 자이페르트 곡면이 아니다. 이 다이어그램에 자이페르트 알고리즘을 적용하면 종수 ''g'' = 1인 구멍 뚫린 토러스가 만들어진다.

4. 1. 자명한 매듭과 연환

자명한 매듭은 원판이 자이페르트 곡면이므로 종수가 0이다.

k

개의 연결 성분을 갖는 자명한 연환의 자이페르트 곡면은

k

개의 구멍을 뚫은 구이며, 종수는 0이다. 종수가 0인 매듭은 자명한 매듭 밖에 없다. (그러나 종수가 0이지만 자명하지 않은 연환은 존재한다.)^[5]

4. 2. 세잎매듭 (Trefoil Knot)

클로버 매듭은 종수가 1이다.^[5] 클로버 매듭에 자이페르트 알고리즘을 적용하면 종수 ''g'' = 1인 구멍 뚫린 토러스를 얻는다.^[5]

4. 3. 8자 매듭 (Figure-Eight Knot)

8자 매듭(4¹번 매듭)의 종수는 1이다.^[5] 클로버 매듭도 8자 매듭과 마찬가지로 종수가 1이다.

4. 4. 원환면 매듭 (Torus Knot)

(p,q)

-원환면 매듭의 종수는

(p-1)(q-1)/2

이다. 예를 들어, (2,1)-원환면 매듭인 세잎매듭의 종수는 1이다.

4. 5. 호프 연환 (Hopf Link)

호프 연환의 종수는 0이며, 두 개의 원판을 연결한 모양(환대)의 자이페르트 곡면을 갖는다. 이는 두 개의 구멍이 뚫린 구(즉, 두 개의 원판의 연결합과 미분 동형)이다.

표준적인 뫼비우스의 띠는 경계로 자르지 않은 매듭을 갖지만, 가향 곡면이 아니므로 자르지 않은 매듭의 자이페르트 곡면이 아니다.^[1]

5. 역사

헤르베르트 자이페르트가 1934년에 자이페르트 곡면과 자이페르트 알고리즘을 도입하였다.^[9] 1930년 프랑클(Frankl)과 폰트랴긴이 처음으로 모든 매듭이 연관된 자이페르트 곡면을 갖는다는 정리를 발표하였다.^[3]

참조

_[1] 논문 Über das Geschlecht von Knoten
_[2] 논문 Visualization of Seifert Surfaces
_[3] 논문 Ein Knotensatz mit Anwendung auf die Dimensionstheorie
_[4] 서적 Knots and Links
_[5] 간행물 Bounding canonical genus bounds volume 1998-09-24
_[6] 서적 Proceedings of the thiry-fourth annual ACM symposium on Theory of computing Association for Computing Machinery 2002-05-19
_[7] 간행물 Seifert surfaces in the 4-ball 2022-05-30
_[8] 웹사이트 Special Surfaces Remain Distinct in Four Dimensions https://www.quantama[...] 2022-06-16
_[9] 저널 Über das Geschlecht von Knoten

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com