리만 합

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

리만 합은 주어진 구간에서 정의된 함수의 적분을 근사하는 데 사용되는 방법으로, 함수의 값을 구간의 분할에 따른 특정 점에서의 값과 각 분할의 길이를 곱하여 합산하는 것이다. 리만 합은 좌측, 우측, 중간, 상한, 하한 리만 합 등 다양한 유형으로 나뉘며, 분할점 선택에 따라 계산 방식이 달라진다. 리만 합은 수치 적분의 기본 방법 중 하나이며, 분할을 세분화할수록 실제 적분값에 가까워진다. 리만 합은 1차원 뿐만 아니라 2차원, 3차원, n차원으로 일반화될 수 있으며, 측도를 사용하여 일반적인 형태로 표현할 수 있다.

더 읽어볼만한 페이지

베른하르트 리만 - 리만 사상 정리
리만 사상 정리는 복소해석학에서 단일 연결 열린 진부분집합 사이의 각도를 보존하는 정칙함수, 즉 등각 사상의 존재를 보장하는 중요한 정리이다.
베른하르트 리만 - 리만-로흐 정리
리만-로흐 정리는 콤팩트 리만 곡면에서 인자의 차수, 유리형 함수 공간의 차원, 곡면의 종수 사이의 관계를 나타내는 정리로서, 유리형 함수를 구성하는 문제에 대한 해답을 제시하며 다양한 분야에서 중요한 역할을 한다.
적분학 - 미적분학
미적분학은 미분과 적분이라는 두 연산을 중심으로 하는 수학 분야로, 여러 고대 문명에서 기원하여 뉴턴과 라이프니츠에 의해 체계화되었고, 함수의 변화율과 면적을 계산하며, 다양한 분야에 응용된다.
적분학 - 절대 수렴
절대 수렴은 급수의 각 항에 절댓값을 취한 급수가 수렴하는 경우를 의미하며, 실수 또는 복소수 급수에서 절대 수렴하면 원래 급수도 수렴하고, 바나흐 공간에서는 절대 수렴하는 급수가 수렴한다.

리만 합
리만 합
일반적인 리만 합의 그림
분야	실해석학
유형	합
발명가	베른하르트 리만

2. 정의

실수의 부분집합 ''D''에서 정의되는 함수 ''f'': ''D'' → '''R'''를 생각하자. 그리고 ''I''=[''a'', ''b'']인 닫힌구간이 ''D'' 안에 들어있다고 하자. 점들의 유한 집합 {''x''₀, ''x''₁, ''x''₂, ... ''x''_''n''}은 ''a'' = ''x''₀ < ''x''₁ < ''x''₂ ... < ''x''_''n'' = ''b''이고 ''I''안에 들어있는 다음의 분할(partition|패리티션^영어)을 생성한다.

:''P'' = {[''x''₀, ''x''₁), [''x''₁, ''x''₂), ... [''x''_''n''-1, ''x''_''n'']}

만약 ''P''가 ''I''의 ''n'' 개의 원소들을 가지는 분할이라면, ''I'' 상에서 분할 ''P''를 가지는 ''f''의 '''리만 합'''은 다음과 같이 정의된다.

: $S = \sum_{i=1}^{n} f(y_i)(x_{i}-x_{i-1})$

여기서 ''x''_''i''-1 ≤ ''y''_''i'' ≤ ''x''_''i''이며, 구간 내에서 ''y''_''i''의 선택은 임의적이다.^[1] 모든 ''i''에 대하여 ''y''_''i'' = ''x''_''i''라면 ''S''는 '''오른쪽 리만 합''', ''y''_''i'' = ''x''_''i''-1라면 '''왼쪽 리만 합''', ''y''_''i'' = (''x''_''i''+''x''_i-1)/2라면 '''가운데 리만 합'''으로 각각 불린다. 왼쪽 리만 합과 오른쪽 리만 합의 평균을 취한 것은 ''사다리꼴 합''(Trapezoidal sum|사다리꼴 합^영어)과 같다.

다음 식을 보자.

: $S = \sum_{i=1}^{n} v_i(x_{i}-x_{i-1})$

여기서, ''v''_''i''는 [''x''_''i''-1, ''x''_''i'']에서 ''f''의 최소 상한이다. 그러면 ''S''는 '''위쪽 리만 합'''으로 정의될 수 있다. 이와 비슷하게, ''v''_''i''가 [''x''_''i''-1, ''x''_''i'']에서 ''f''의 최대 하한이라면 ''S''는 '''아래쪽 리만 합'''이다.

주어진 분할(''x''_''i''-1과 ''x''_''i'' 사이에서 임의로 선택한 ''y''_''i'')을 가지는 어떠한 리만 합도 위쪽 리만 합과 아래쪽 리만 합 사이에 들어있게 된다. 어떤 함수가 분할을 더 작게 쪼개면 쪼갤수록 아래쪽 리만 합과 위쪽 리만 합이 점점 가까워진다면 이 함수는 ''리만 적분 가능''으로 정의된다. 이 사실은 수치 적분에 사용된다.

3. 리만 합의 유형

리만 합은 $x_i^*$ 의 선택에 따라 다양한 유형으로 나뉜다.^[1]

모든 ''i''에 대해 $x_i^*=x_{i-1}$ 이면, '''좌측 규칙'''^[2]^[3]이며, '''좌측 리만 합'''을 제공한다.
모든 ''i''에 대해 $x_i^* = x_i$ 이면, '''우측 규칙'''^[2]^[3]이며, '''우측 리만 합'''을 제공한다.
모든 ''i''에 대해 $x_i^* = (x_i + x_{i - 1})/2$ 이면, '''중점 규칙'''^[2]^[3]이며, '''중간 리만 합'''을 제공한다.
$f(x_i^*) = \sup f([x_{i - 1}, x_i])$ (즉, $[x_{i - 1}, x_i]$ 에서 ''f''의 상한)이면, '''상한 규칙'''이며, '''상 다르부 합'''을 제공한다.
$f(x_i^*) = \inf f([x_{i - 1}, x_i])$ (즉, $[x_{i - 1}, x_i]$ 에서 ''f''의 하한)이면, '''하한 규칙'''이며, '''하 다르부 합'''을 제공한다.
좌측 및 우측 리만 합의 평균을 구하는 것은 '''사다리꼴 공식'''이며 '''사다리꼴 합'''을 제공한다.

이러한 모든 리만 합산 방법은 수치 적분을 수행하는 가장 기본적인 방법 중 하나이다. 주어진 분할에 대한 모든 리만 합(즉,

x_{i - 1}

과

x_i

사이의

x_i^*

의 모든 선택)은 하 다르부 합과 상 다르부 합 사이에 포함된다.

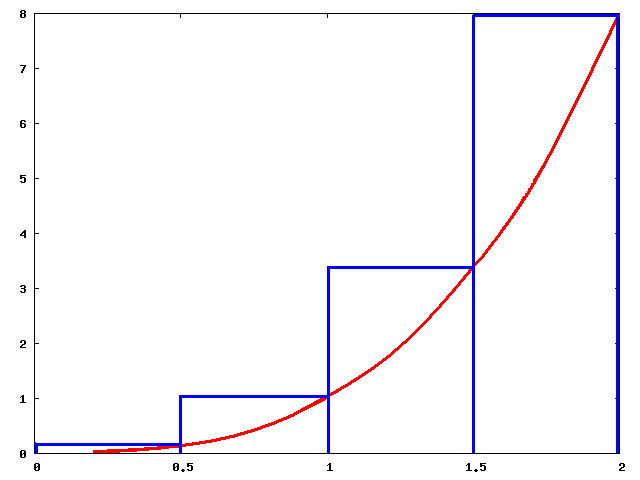
3. 1. 좌측 리만 합

왼쪽 리만 합은 분할한 각 구간의 왼쪽 끝점을 함숫값(높이)으로 이용하여 계산한다. 그러면 밑변 ''Q''와 높이 ''f''(''a''+''iQ'')를 가지는 여러 개의 사각형이 생긴다. 이것을 ''i''=0, 1, ..., ''n''−1 동안 반복하여 더하면 결과 면적은 다음과 같다.

:

Q\left[f(a) + f(a + Q) + f(a + 2Q)+\dots+f(b - Q)\right].\,

이 구간에서 ''f''가 단조 감소인 경우 왼쪽 리만 합은 실제 값보다 크게 예측한 것이 되고, 단조 증가라면 실제보다 작게 예측한 것이 된다.^[2]^[3]

모든 ''i''에 대해

x_i^*=x_{i-1}

이면, 이 방법은 '''좌측 규칙'''이며, '''좌측 리만 합'''을 제공한다.

예를 들어,

[1, 2]

에서

f(x)=x^2

일 때 등차수열

x_k = 1 + \frac{k}{n} \;  (k=0, 1, 2, \dots, n)

을 사용하면, 좌 리만 합은 다음과 같다.

:

\sum_{k=1}^{n} x_{k-1} ^ 2 \Delta x_k=\sum_{k=1}^{n} \left ( 1 + \frac{k-1}{n} \right )^2 \frac{1}{n}=\frac{7}{3}-\frac{3}{2 n}+ \frac{1}{6 n^2}

^[11]

등비수열

x_k = 2 ^{\frac{k}{n}} \; (k=0, 1, 2, \dots, n)

를 사용하면, 좌 리만 합은 다음과 같다.

:

\sum_{k=1}^{n} x_{k-1} ^ 2 \Delta x_k=\sum_{k=1}^{n}\left( 2 ^{\frac{k-1}{n}} \right)^2\, ( 2^\frac{k}{n} - 2^\frac{k-1}{n} )=\frac{7}{ 2^{\frac{2}{n}} + 2 ^{\frac{1}{n}} + 1 }

f(x)=x^2

는

[1, 2]

에서 단조 증가 함수이므로, 등차수열이든 등비수열이든 관계없이 좌 리만 합은 다른 리만 합보다 작다.

[1, 2]

에서

f(x)=\frac{1}{x}

일 때, 등비수열

x_k = 2 ^{\frac{k}{n}} \; (k=0, 1, 2, \dots, n)

을 취하면, 왼쪽 리만 합은 다음과 같다.

:

\sum_{k=1}^{n}\frac{1}{x_{k-1}} \Delta x_k=\sum_{k=1}^{n} \frac{1}{2 ^{\frac{k-1}{n}}}\, ( 2^\frac{k}{n} - 2^\frac{k-1}{n} )=n\left( 2 ^{ \frac{1}{n}} - 1 \right)

^[12]

f(x)=\frac{1}{x}

는

[1, 2]

에서 단조 감소 함수이므로, 왼쪽 리만 합은 다른 리만 합보다 크다.

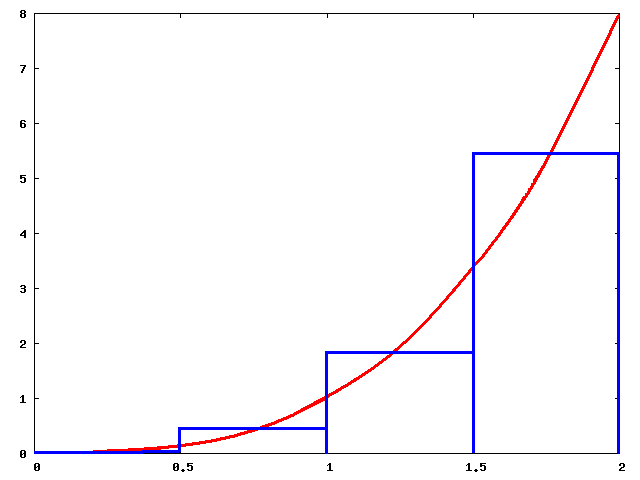
3. 2. 우측 리만 합

모든 ''i''에 대해

x_i^* = x_i

인 경우, 즉 각 부분 구간의 오른쪽 끝점을 선택하는 경우이다.^[2]^[3] 이 방법은 '''우측 리만 합'''을 제공한다.

예를 들어, 함수 f(x) = x² 를 구간 [1, 2]에서 등차수열

x_k = 1 + \frac{k}{n} \;  (k=0, 1, 2, \dots, n)

을 사용하여 우측 리만 합을 구하면 다음과 같다.

:

\sum_{k=1}^{n}  x_k ^ 2 \Delta x_k=\sum_{k=1}^{n} \left ( 1 + \frac{k}{n} \right )^2 \frac{1}{n}=\frac{7}{3}+\frac{3}{2 n}+ \frac{1}{6 n^2}

같은 함수와 구간에 대해 등비수열

x_k = 2 ^{\frac{k}{n}} \; (k=0, 1, 2, \dots, n)

을 사용하면 우측 리만 합은 다음과 같다.

:

\sum_{k=1}^{n}  x_k ^ 2 \Delta x_k=\sum_{k=1}^n\left( 2 ^{\frac{k}{n}} \right)^2\, ( 2^\frac{k}{n} - 2^\frac{k-1}{n} )=\frac{7}{ 2^{ - \frac{2}{n}} + 2 ^{ - \frac{1}{n}} + 1 }

f(x)=x^2

는 [1, 2]에서 단조 증가 함수이므로, 우측 리만 합은 좌측 리만 합보다 크거나 같다.

반대로, 함수 f(x) = 1/x 를 구간 [1,2]에서 등비수열

x_k = 2 ^{\frac{k}{n}} \; (k=0, 1, 2, \dots, n)

을 사용하여 우측 리만 합을 구하면 다음과 같다.

:

\sum_{k=1}^{n}\frac{1}{x_k} \Delta x_k=\sum_{k=1}^n \frac{1}{2 ^{\frac{k}{n}}}\, ( 2^\frac{k}{n} - 2^\frac{k-1}{n} )=n\left( 1 - 2 ^{ - \frac{1}{n}} \right)

f(x)=\frac{1}{x}

는 [1, 2]에서 단조 감소 함수이므로, 우측 리만 합은 좌측 리만 합보다 작거나 같다.

왼쪽 리만 합과 반대로, 오른쪽 리만 합은 단조 증가 함수 ''f''의 리만 합을 크게 예측하고, 단조 감소 함수 ''f''의 리만 합을 작게 예측한다.

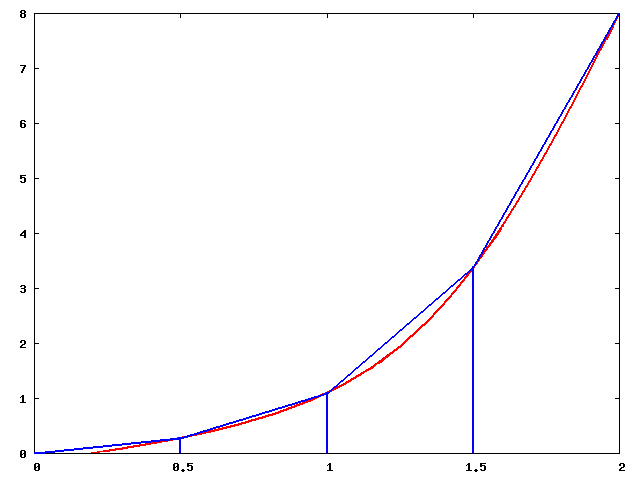
3. 3. 중간 리만 합

이 경우에는 각 부분 구간의 중간점에서 ''f''의 값을 구한다. 따라서 첫 번째 구간은 ''f''(''a'' + ''Q''/2)의 값을, 두 번째 구간은 ''f''(''a'' + 3''Q''/2)를 가진다. 이를 반복하여 마지막 구간에 다다르면 ''f''(''b''-''Q''/2)이 된다. 이것을 모두 합하면,

:

Q\left[f(a + Q/2) + f(a + 3Q/2)+\dots+f(b-Q/2)\right].

임을 알 수 있다.

이 식의 오차는

:

\left \vert \int_{a}^{b} f(x) - A_{mid} \right \vert \le \frac{M_2(b-a)^3}{(24n^2)},

가 된다. 여기서

M_2

는 이 구간에서

f^{\prime\prime}(x)

의 절댓값의 최댓값이다.

모든 ''i''에 대해

x_i^* = (x_i + x_{i - 1})/2

이면, 이 방법은 '''중점 규칙'''^[2]^[3]이며, '''중간 리만 합'''을 제공한다.

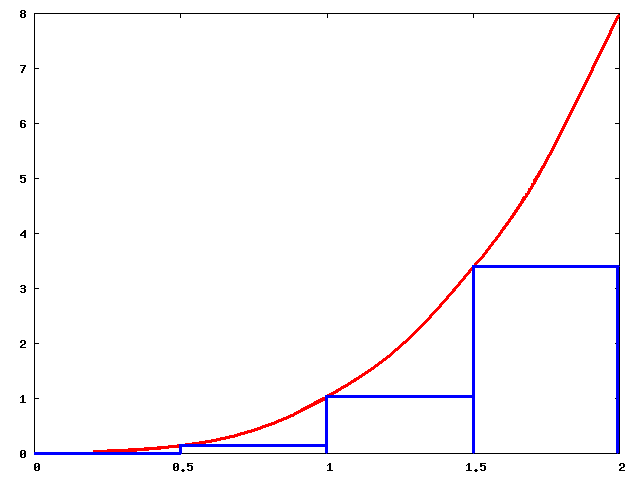
3. 4. 상한 리만 합 (상 다르부 합)

함수 ''f''가 실수의 부분집합 ''D''에서 정의되고, ''I''=[''a'', ''b'']]인 닫힌구간이 ''D'' 안에 있다고 가정하자. ''a'' = ''x''₀ < ''x''₁ < ''x''₂ ... < ''x''_''n'' = ''b''를 만족하는 점들의 유한 집합 {''x''₀, ''x''₁, ''x''₂, ... ''x''_''n''}은 ''I''의 분할 ''P'' = {[''x''₀, ''x''₁), [''x''₁, ''x''₂), ... [''x''_''n''-1, ''x''_''n'']}를 생성한다.

만약 다음 식을 가지고 있다고 하자.

:

S = \sum_{i=1}^{n} v_i(x_{i}-x_{i-1})

여기서 ''v''_''i''가 [''x''_''i''-1, ''x''_''i'']에서 ''f''의 최소 상한이면, ''S''는 '''상한 리만 합'''(상 다르부 합)으로 정의된다.

f(x_i^*) = \sup f([x_{i - 1}, x_i])

(즉,

[x_{i - 1}, x_i]

에서 ''f''의 상한)이면, 이 방법은 '''상한 규칙'''이며, '''상한 리만 합''' 또는 '''상 다르부 합'''을 제공한다.^[2]^[3]

3. 5. 하한 리만 합 (하 다르부 합)

f(x_i^*) = \inf f([x_{i - 1}, x_i])

(즉,

[x_{i - 1}, x_i]

에서 ''f''의 하한)이면, 이 방법은 '''하한 규칙'''이며, '''하한 리만 합''' 또는 '''하 다르부 합'''을 제공한다.^[2]^[3]

3. 6. 사다리꼴 합

0,2 구간에서 4개의 부분 구간을 가지는 ''x''³의 사다리꼴 리만 합

사다리꼴 공식은 각 구간의 왼쪽 끝점과 오른쪽 끝점의 평균값을 이용하여 적분을 근사한다. 이는 좌측 리만 합과 우측 리만 합의 평균으로 계산된다.^[2]^[3] 각 사다리꼴의 넓이인

A=h(b_1+b_2)/2

(평행한 두 변은 ''b''₁, ''b''₂, 높이가 ''h'')을 더하면, 다음과 같은 식을 얻는다.

:

\frac{1}{2}Q\left[f(a) + 2f(a+Q) + 2f(a+2Q) + 2f(a+3Q)+\dots+f(b)\right].

이 적분 근사식의 오차는 다음과 같다.

:

\left \vert \int_{a}^{b} f(x) - A_{trap} \right \vert \le \frac{M_2(b-a)^3}{(12n^2)},

여기서

M_2

는 이 구간에서

f^{\prime\prime}(x)

의 절댓값의 최댓값이다.

사다리꼴 합은 수치 적분을 수행하는 방법 중 하나이며, 심슨 공식 및 뉴턴-코츠 공식과 같이 더 복잡한 방법으로 적분을 근사할 수 있다.

4. 리만 합산 방법

리만 합을 계산하는 방법에는 여러 가지가 있다. 대표적으로 좌측, 우측, 중점, 사다리꼴 합이 있다. 여기서는 각 구간의 크기가 동일한 경우를 예로 들어 설명한다. 구간 \[''a'', ''b'']를 ''n''개의 동일한 구간으로 나누면, 각 구간의 길이는 ''Q''=(''b''-''a'')/''n''이다. 따라서 각 분할점은 다음과 같다.

: ''a'', ''a''+''Q'', ''a''+2''Q'', ..., ''a''+(''n''−2)''Q'', ''a''+(''n''−1)''Q'','' b''.

$x_i^*$ 를 어떻게 선택하느냐에 따라 다양한 유형의 리만 합을 얻을 수 있다.

모든 ''i''에 대해 $x_i^*=x_{i-1}$ 이면, '''좌측 규칙'''^[2]^[3]이며, '''좌측 리만 합'''을 얻는다.
모든 ''i''에 대해 $x_i^* = x_i$ 이면, '''우측 규칙'''^[2]^[3]이며, '''우측 리만 합'''을 얻는다.
모든 ''i''에 대해 $x_i^* = (x_i + x_{i - 1})/2$ 이면, '''중점 규칙'''^[2]^[3]이며, '''중간 리만 합'''을 얻는다.
$f(x_i^*) = \sup f([x_{i - 1}, x_i])$ (즉, $[x_{i - 1}, x_i]$ 에서 $f$ 의 상한)이면, '''상한 규칙'''이며, '''상한 리만 합''' 또는 '''상 다르부 합'''을 얻는다.
$f(x_i^*) = \inf f([x_{i - 1}, x_i])$ (즉, $[x_{i - 1}, x_i]$ 에서 ''f''의 하한)이면, '''하한 규칙'''이며, '''하한 리만 합''' 또는 '''하 다르부 합'''을 얻는다.

이러한 리만 합산 방법은 수치 적분의 가장 기본적인 방법 중 하나이다. 분할이 더 세밀해질수록 모든 리만 합이 수렴하면 함수는 리만 적분 가능하다고 할 수 있다.

리만 합에서 파생된 것은 아니지만, 좌측 및 우측 리만 합의 평균을 구하면 '''사다리꼴 공식'''을 이용한 '''사다리꼴 합'''이 된다. 이는 가중 평균을 사용하여 적분을 근사하는 방법 중 가장 간단한 방법 중 하나이다. 더 복잡한 방법으로는 심슨 공식 및 뉴턴-코츠 공식이 있다.

주어진 분할에 대한 모든 리만 합은 상 다르부 합과 하 다르부 합 사이에 포함된다. 이는 다르부 적분의 기초가 되며, 다르부 적분은 리만 적분과 같다.

일반적으로 리만 합을 계산할 때는 같은 크기의 부분 구간을 사용하는 것이 편리하다. 구간 [a, b]를

n

개의 부분 구간으로 나누면 각 구간의 길이는 다음과 같다.

:

\Delta x = \frac{b-a}{n}.

이때 분할점은 다음과 같다.

:

a, \; a + \Delta x, \; a + 2 \Delta x, \; \ldots, \; a + (n-2) \Delta x, \; a + (n - 1)\Delta x, \; b.

4. 1. 좌측 규칙

왼쪽 리만 합은 각 부분 구간의 왼쪽 끝점에서 함수의 값으로 근사한다. 즉, 밑변이

\Delta x

이고 높이가

f(a + i\Delta x)

인 여러 개의 직사각형을 만들고,

i = 0, 1, \dots, n-1

에 대해 이 직사각형들의 면적을 합하여 근사값을 구한다. 결과 면적은 다음과 같다.

:

S_\mathrm{left} = \Delta x \left[f(a) + f(a + \Delta x) + f(a + 2 \Delta x) + \dots + f(b - \Delta x)\right].

함수 ''f''가 이 구간에서 단조 감소 함수이면 좌측 리만 합은 실제 값보다 크게 예측되고, 단조 증가 함수이면 실제 값보다 작게 예측된다.

이 공식의 오차는 다음과 같이 표현할 수 있다.

:

\left\vert\int_{a}^{b} f(x)\, dx - S_\mathrm{left}\right\vert \le \frac{M_1 (b - a)^2}{2n},

여기서

M_1

은 구간에서

f^{\prime}(x)

의 절댓값의 최댓값이다.

예를 들어,

[1, 2]

에서

f(x)=x^2

일 때, 등차수열

x_k = 1 + \frac{k}{n} \;  (k=0, 1, 2, \dots, n)

을 사용하면 좌 리만 합은 다음과 같다.^[11]

:

\sum_{k=1}^{n} x_{k-1} ^ 2 \Delta x_k=\sum_{k=1}^{n} \left ( 1 + \frac{k-1}{n} \right )^2 \frac{1}{n}=\frac{7}{3}-\frac{3}{2 n}+ \frac{1}{6 n^2}

등비수열

x_k = 2 ^{\frac{k}{n}} \; (k=0, 1, 2, \dots, n)

를 사용하면, 좌 리만 합은 다음과 같다.

:

\sum_{k=1}^{n} x_{k-1} ^ 2 \Delta x_k=\sum_{k=1}^{n}\left( 2 ^{\frac{k-1}{n}} \right)^2\, ( 2^\frac{k}{n} - 2^\frac{k-1}{n} )=\frac{7}{ 2^{\frac{2}{n}} + 2 ^{\frac{1}{n}} + 1 }

[1, 2]

에서

f(x)=\frac{1}{x}

일 때, 등비수열

x_k = 2 ^{\frac{k}{n}} \; (k=0, 1, 2, \dots, n)

을 취하면, 왼쪽 리만 합은 다음과 같다.^[12]

:

\sum_{k=1}^{n}\frac{1}{x_{k-1}} \Delta x_k=\sum_{k=1}^{n} \frac{1}{2 ^{\frac{k-1}{n}}}\, ( 2^\frac{k}{n} - 2^\frac{k-1}{n} )=n\left( 2 ^ \frac{1}{n}} - 1 \right)

4. 2. 우측 규칙

우측 규칙은 각 부분 구간의 오른쪽 끝점에서 함수 값으로 근사한다. 밑변이 이고 높이가 인 여러 개의 직사각형을 만들고, 에 대해 이 과정을 반복하여 결과 영역을 합하면 다음을 얻는다.

:

함수 ''f''가 단조 감소 함수이면 우측 리만 합은 과소 평가가 되고, 단조 증가 함수이면 과대 평가가 된다.

이 공식의 오차는 다음과 같다.

:

여기서 은 구간에서 의 절댓값의 최댓값이다.^[11]

4. 3. 중점 규칙

중점 규칙은 함수를 부분 구간의 중점에서의 값으로 근사하는 방법이다. 첫 번째 부분 구간에 대해 f|에프^영어(''a'' + Δ''x''/2), 다음 부분 구간에 대해 f|에프^영어(''a'' + 3Δ''x''/2), 그리고 마지막 부분 구간 f|에프^영어(''b'' − Δ''x''/2)까지 계속하여 값을 구한다. 결과 영역을 모두 합하면 다음과 같다.

:

이 공식의 오차는 다음과 같이 나타낼 수 있다.

:

여기서 는 구간에서 의 절댓값의 최댓값이다. 이 오차는 사다리꼴 합 오차의 절반이며, 따라서 중점 리만 합이 리만 합에 대한 가장 정확한 근사 방법이다.^[1] 예를 들어, 구간 [1, 2]에서 f(x)|에프(엑스)^영어 = x^2|엑스 제곱^영어일 때,^[2]

4. 4. 일반화된 중점 규칙

일반화된 중점 규칙 공식은 향상된 중점 적분이라고도 하며, 다음과 같이 주어진다.^[1]

:

\int_0^1 f(x)\,dx = 2\sum_{m=1}^M {\sum_{n=0}^\infty {\frac{1}\left({2n+1}\right)!}}}}\,\,,

여기서

f^{(2n)}

은 짝수 도함수를 나타낸다.^[1]

구간

(a,b)

에서 정의된 함수

g(t)

의 경우, 적분은 다음과 같다.^[1]

:

\int_a^b g(t) \, dt = \int_0^{b-a} g(\tau+a) \, d\tau= (b-a) \int_0^1 g((b-a)x+a) \, dx.

따라서,

f(x) = (b-a) \, g((b-a)x+a)

라고 가정하여 이 일반화된 중점 적분 공식을 적용할 수 있다. 이 공식은 피적분 함수

f(x)

가 고도로 진동하는 함수일 때 수치 적분에 특히 효율적이다.^[1]

4. 5. 사다리꼴 규칙

각 구간의 왼쪽 끝점과 오른쪽 끝점의 평균값을 이용하여 구한다. 각 사다리꼴의 넓이인 A|A^영어 = h(b₁ + b₂)/2 (평행한 두 변은 ''b''₁, ''b''₂, 높이가 ''h'')을 더하면 다음과 같다.

: 1/2Q [f(a) + 2f(a+Q) + 2f(a+2Q) + 2f(a+3Q) + ... + f(b)]

이 적분 근사식의 오차는 다음과 같다.

: | int|∫^영어_a^b f(x)dx - A_trap | ≤ M₂(b-a)³ / (12n²)

여기서 M₂는 이 구간에서 f''(x)의 절댓값의 최댓값이다.

함수에 대한 사다리꼴 합으로 얻은 근사값은 해당 함수의 좌측 합과 우측 합의 평균과 같다.

5. 적분과의 관계

1차원 리만 합의 경우, 부분 구간의 최대 크기가 0으로 수렴하면(즉, 부분 구간의 노름의 극한이 0으로 감에 따라), 일부 함수는 모든 리만 합이 동일한 값으로 수렴한다. 이 극한값은 존재할 경우, 해당 구간에서 함수의 정적분으로 정의된다.

: $\int_a^b f(x)\, dx = \lim_{\|\Delta x\| \rightarrow 0} \sum_{i = 1}^{n} f(x_i^*)\, \Delta x_i.$

유한 크기의 구간의 경우, 부분 구간의 최대 크기가 0으로 수렴하면 부분 구간의 수가 무한대로 증가함을 의미한다. 유한 분할의 경우, 리만 합은 항상 극한값에 대한 근사이며, 분할이 미세해질수록 이 근사는 더 정확해진다.

여기서 빨간색 함수는 매끄러운 함수라고 가정하므로, 부분 구간의 수가 무한대로 갈 때 세 리만 합 모두 동일한 값으로 수렴한다.

6. 리만 합의 예시

예를 들어, 구간 [0, 2]에서 곡선 아래 영역은 리만 방법에 의해 절차적으로 계산될 수 있다.

구간 [0, 2]는 먼저 각각 $\tfrac{2}{n}$ 의 폭을 갖는 n개의 부분 구간으로 나뉜다. 이들은 리만 직사각형(이하 "상자")의 폭이다. 오른쪽 리만 합을 사용할 것이므로, 상자의 x 좌표 시퀀스는 $x_1, x_2, \ldots, x_n$ 이 된다. 따라서 상자 높이 시퀀스는 $x_1^2, x_2^2, \ldots, x_n^2$ 이 된다. $x_i = \tfrac{2i}{n}$ 이고 $x_n = 2$ 라는 것은 중요한 사실이다.

각 상자의 면적은 $\tfrac{2}{n} \times x_i^2$ 이 되므로, ''n''번째 오른쪽 리만 합은 다음과 같다.

$\begin{align}S &= \frac{2}{n} \left(\frac{2}{n}\right)^2 + \dots + \frac{2}{n} \left(\frac{2i}{n}\right)^2 + \dots + \frac{2}{n} \left(\frac{2n}{n}\right)^2\\[1ex]&= \frac{8}{n^3} \left(1 + \dots + i^2 + \dots + n^2\right)\\[1ex]&= \frac{8}{n^3} \left(\frac{n(n + 1)(2n + 1)}{6}\right)\\[1ex]&= \frac{8}{n^3} \left(\frac{2n^3 + 3n^2 + n}{6}\right)\\[1ex]&= \frac{8}{3} + \frac{4}{n} + \frac{4}{3n^2}.\end{align}$

만약 극한을 ''n'' → ∞로 본다면, 상자의 수가 증가함에 따라 근사값이 곡선 아래 영역의 실제 값에 접근한다고 결론을 내릴 수 있다. 따라서,

$\lim_{n \to \infty} S = \lim_{n \to \infty}\left(\frac{8}{3} + \frac{4}{n} + \frac{4}{3n^2}\right) = \frac{8}{3}.$

이 방법은 좀 더 기계적인 방식으로 계산된 정적분과 일치한다.

$\int_0^2 x^2\, dx = \frac{8}{3}.$

함수가 구간에서 연속적이고 단조 증가하므로, 오른쪽 리만 합은 적분을 가장 많이 과대 평가한다(반면 왼쪽 리만 합은 적분을 가장 많이 과소 평가할 것이다).

$f(x)=x^2$ 이고 구간이 [1, 2]인 경우, 등차수열 $x_k = 1 + \frac{k}{n} \; (k=0, 1, 2, \dots, n)$ 을 사용하면 좌 리만 합과 우 리만 합은 각각 다음과 같다.^[11]

: $\sum_{k=1}^{n} x_{k-1} ^ 2 \Delta x_k=\sum_{k=1}^{n} \left ( 1 + \frac{k-1}{n} \right )^2 \frac{1}{n}=\frac{7}{3}-\frac{3}{2 n}+ \frac{1}{6 n^2}$

: $\sum_{k=1}^{n} x_k ^ 2 \Delta x_k=\sum_{k=1}^{n} \left ( 1 + \frac{k}{n} \right )^2 \frac{1}{n}=\frac{7}{3}+\frac{3}{2 n}+ \frac{1}{6 n^2}$

등비수열 $x_k = 2 ^{\frac{k}{n}} \; (k=0, 1, 2, \dots, n)$ 을 사용하면, 좌 리만 합과 우 리만 합은 각각 다음과 같다.

: $\sum_{k=1}^{n} x_{k-1} ^ 2 \Delta x_k=\sum_{k=1}^{n}\left( 2 ^{\frac{k-1}{n}} \right)^2\, ( 2^\frac{k}{n} - 2^\frac{k-1}{n} )=\frac{7}{ 2^{\frac{2}{n}} + 2 ^{\frac{1}{n}} + 1 }$

: $\sum_{k=1}^{n} x_k ^ 2 \Delta x_k=\sum_{k=1}^n\left( 2 ^{\frac{k}{n}} \right)^2\, ( 2^\frac{k}{n} - 2^\frac{k-1}{n} )=\frac{7}{ 2^{ - \frac{2}{n}} + 2 ^{ - \frac{1}{n}} + 1 }$

$f(x)=x^2$ 는 [1, 2]에서 단조 증가 함수이므로, 등차수열이든 등비수열이든 관계없이 좌 리만 합과 우 리만 합 사이에는 다음의 관계가 성립한다.

: $\sum_{k=1}^{n} x_{k-1} ^ 2 \Delta x_k\leq\sum_{k=1}^{n} \xi_k ^ 2 \Delta x_k\leq\sum_{k=1}^{n} x_k ^ 2 \Delta x_k$

연속 함수의 좌 리만 합과 우 리만 합은 $n \to \infty$ 의 극한에서 수렴하므로, 다음을 얻을 수 있다.

: $\int _ 1 ^ 2 x ^ 2 d x=\lim_{n \to \infty} \sum_{k=1}^{n} \xi_k ^ 2 \Delta x_k=\frac{7}{3}$

$f(x)=\frac{1}{x}$ 이고 구간이 [1,2]인 경우, 등비수열 $x_k = 2 ^{\frac{k}{n}} \; (k=0, 1, 2, \dots, n)$ 을 취하면, 왼쪽 리만 합과 오른쪽 리만 합은 각각 다음과 같다.^[12]

: $\sum_{k=1}^{n}\frac{1}{x_{k-1}} \Delta x_k=\sum_{k=1}^{n} \frac{1}{2 ^{\frac{k-1}{n}}}\, ( 2^\frac{k}{n} - 2^\frac{k-1}{n} )=n\left( 2 ^{ \frac{1}{n}} - 1 \right)$

: $\sum_{k=1}^{n}\frac{1}{x_k} \Delta x_k=\sum_{k=1}^n \frac{1}{2 ^{\frac{k}{n}}}\, ( 2^\frac{k}{n} - 2^\frac{k-1}{n} )=n\left( 1 - 2 ^{ - \frac{1}{n}} \right)$

$f(x)=\frac{1}{x}$ 는 [1, 2]에서 단조 감소 함수이므로, 왼쪽 리만 합과 오른쪽 리만 합 사이에는 다음의 관계가 성립한다.

: $\sum_{k=1}^{n}\frac{1}{x_{k-1}} \Delta x_k\geq\sum_{k=1}^{n}\frac{1}{\xi_k} \Delta x_k\geq\sum_{k=1}^{n}\frac{1}{x_k} \Delta x_k$

연속 함수의 왼쪽 리만 합과 오른쪽 리만 합은 $n \to \infty$ 의 극한에서 수렴하므로, 다음을 얻을 수 있다.

: $\int _ 1 ^ 2 \frac{1}{x} d x=\lim_{n \to \infty}n\left( 2 ^ \frac{1}{n} - 1 \right)=\lim_{n \to \infty}n\left( 1 - 2 ^{ - \frac{1}{n}} \right)$

7. 고차원 리만 합

리만 합은 1차원 이상으로 일반화될 수 있다. 기본적인 아이디어는 정의역을 여러 조각으로 "나누고", 각 조각의 "크기"에 해당 조각에서 함수의 값을 곱한 다음, 이 모든 곱을 더하는 것이다.^[4]

1차원 이상에서 정의역을 분할하는 방법에 대한 기술적인 세부 사항은 1차원의 경우보다 훨씬 더 복잡해지며, 정의역의 기하학적 모양과 관련된 측면을 포함한다.^[4]

7. 1. 2차원

영역

A

는 여러 개의 2차원 셀

A_i

로 나눌 수 있으며,

A = \bigcup_i A_i

이다. 각 셀은

\Delta A_i

로 표시되는 "면적"을 갖는 것으로 해석될 수 있다.^[5] 2차원 리만 합은 다음과 같다.

:

S = \sum_{i = 1}^n f(x_i^*, y_i^*)\, \Delta A_i,

여기서

(x_i^*, y_i^*) \in A_i

이다.

7. 2. 3차원

3차원 공간에서 영역

V

는 여러 개의 3차원 세포

V_i

로 분할되며,

V = \bigcup_i V_i

를 만족한다. 각 세포는

\Delta V_i

로 표시되는 "부피"를 갖는 것으로 해석될 수 있다.^[6] 3차원 리만 합은 다음과 같다.

:

S = \sum_{i = 1}^n f(x_i^*, y_i^*, z_i^*)\, \Delta V_i,

여기서

(x_i^*, y_i^*, z_i^*) \in V_i

이다.

7. 3. n차원

''n''차원 리만 합은 다음과 같다.

: S = Σᵢ f(Pᵢ*)ΔVᵢ

여기서 Pᵢ* ∈ Vᵢ이며, 이는 ''n''차원 부피 ΔVᵢ를 가진 ''n''차원 셀 Vᵢ 내의 점이다.

8. 일반화

일반적으로 리만 합은 다음과 같이 쓸 수 있다.

: ''S'' = Σ_''i'' ''f''(''P''_''i''^*)''μ''(''V''_''i'')

여기서 ''P''_''i''^*는 집합 ''V''_''i''에 포함된 임의의 점을 나타내고, ''μ''는 기저 집합에 대한 측도이다. 대략적으로, 측도는 집합의 "크기"를 나타내는 함수이며, 이 경우 집합 ''V''_''i''의 크기를 나타낸다. 1차원에서는 종종 길이로, 2차원에서는 면적으로, 3차원에서는 부피 등으로 해석할 수 있다.

참조

_[1] 서적 Calculus Wiley
_[2] 서적 Calculus Wiley
_[3] 서적 Calculus from Graphical, Numerical, and Symbolic Points of View
_[4] 서적 Calculus with Analytic Geometry https://archive.org/[...] Prindle, Weber & Schmidt
_[5] 서적 Calculus from Graphical, Numerical, and Symbolic Points of View
_[6] 서적 Calculus with Analytic Geometry https://archive.org/[...] Prindle, Weber & Schmidt
_[7] 서적 リーマン論文集
_[8] 서적 積分の歴史 - アルキメデスからコーシー, リーマンまで - 現代数学社
_[9] 서적 微積分の歩んだ道森北出版
_[10] 서적 数学辞典岩波
_[11] 서적 微分と積分 - その思想と方法 - 日本評論社
_[12] 서적 微分と積分 - その思想と方法 - 日本評論社

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com