브라마굽타 공식

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 공식
3. 증명
- 3.1. 삼각법을 이용한 증명
- 3.2. 헤론의 공식을 이용한 증명
4. 특수한 경우
- 4.1. 헤론의 공식
- 4.2. 이중중심 사각형의 넓이
5. 일반화
- 5.1. 브레치나이더 공식
6. 역사
참조

1. 개요

브라마굽타 공식은 7세기경 인도의 수학자 브라마굽타가 제시한, 원에 내접하는 사각형의 넓이를 구하는 공식이다. 사각형의 네 변의 길이를 a, b, c, d, 반둘레를 s로 할 때, 공식은 S = √((s-a)(s-b)(s-c)(s-d))로 표현된다. 이 공식은 헤론의 공식을 삼각형에 적용한 것과 유사하며, 브레슈나이더 공식으로 일반화되어 원에 내접하지 않는 사각형에도 적용할 수 있다. 특수한 경우로 헤론의 공식과 이중중심 사각형의 넓이 공식이 있으며, 쿨리지 공식과 브레치나이더 공식으로 일반화될 수 있다.

2. 공식

내접 사각형 $ABCD$ 의 네 변의 길이를 $AB=a$ , $BC=b$ , $CD=c$ , $DA=d$ 라고 하고, 반둘레를 $s=\frac{a+b+c+d}2$ 라고 할 때, '''브라마굽타 공식'''에 따르면, 이 사각형의 넓이는 다음과 같다.

: $S=\sqrt{(s-a)(s-b)(s-c)(s-d)}$

이 공식은 헤론의 공식을 삼각형의 면적으로 일반화한 것이다. 삼각형은 길이가 0인 변이 하나 있는 사각형으로 간주할 수 있다. 이러한 관점에서, $d$ 가 0에 가까워짐에 따라, 원내접 사각형은 원내접 삼각형(외접원)으로 수렴하고, 브라마굽타 공식은 헤론의 공식으로 단순화된다.

반둘레를 사용하지 않는 경우, 브라마굽타 공식은 다음과 같이 표현할수 있다.

: $K=\frac{1}{4}\sqrt{(-a+b+c+d)(a-b+c+d)(a+b-c+d)(a+b+c-d)}.$

또한 브라마 굽타 공식을 일반화 하여 원에 내접하지 않는 사각형의 면적을 구하는 공식인 브레슈나이더 공식이 있다. 사각형 ABCD의 대각의 합, 예를 들어 ∠ABC + ∠CDA의 절반을 ''t''라고 하면

: $S=\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cos^2 t}$

가 성립한다. 만약, 사각형 ABCD가 원에 내접한다면, 대각의 합은 180°가 되므로 ''t'' = 90°이고 cos ''t'' = 0이 되므로, 브라마굽타 공식이 얻어진다.

3. 증명

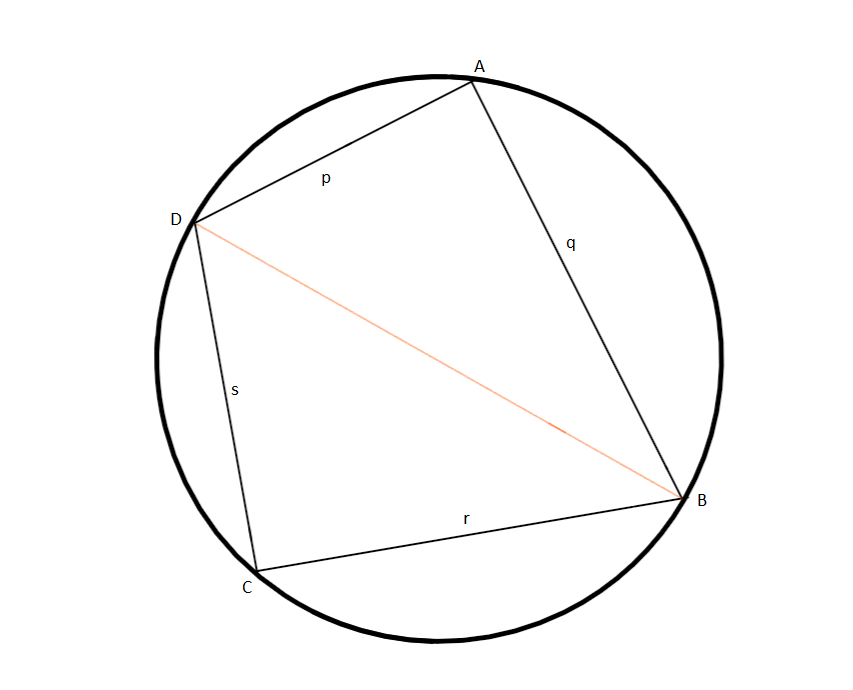
사변형 ABCD가 원 O에 내접한다고 가정하고, 꼭짓점을 A, B, C, D로,

:AB = ''a'', BC = ''b'', CD = ''c'', DA = ''d''

라고 한다. ∠ABC = ''t'' 라고 하면, 내접 사각형의 정리에 따라 ∠CDA = 180° − ''t'' 가 된다. 여기서 삼각형 면적 공식에 의해

:△ABC = (1/2) ''ab'' sin''t''

:△CDA = (1/2) ''cd'' sin(180° − ''t'') = (1/2)''cd'' sin''t''

따라서

:사각형 ABCD의 면적 = △ABC + △CDA

:= (1/2) ''ab'' sin ''t'' + (1/2) ''cd'' sin ''t''

:= (1/2)(''ab'' + ''cd'') sin ''t'' … (1)

또한, 코사인 법칙에 따르면

:AC² = ''a''² + ''b''² − 2''ab'' cos ''t''

:AC² = ''c''² + ''d''² − 2''cd'' cos(180° − ''t'') = ''c''² + ''d''² + 2''cd'' cos ''t''

이 두 식으로부터 cos ''t'' 를 구하면

:

\cos t=\frac{a^2 +b^2 -c^2 -d^2}{2(ab+cd)}

가 되므로

:(''ab'' + ''cd'')(1 − cos''t'') = 2(''s'' − ''a'')(''s'' − ''b'')

:(''ab'' + ''cd'')(1 + cos''t'') = 2(''s'' − ''c'')(''s'' − ''d'')

:변변 곱하여, (''ab'' + ''cd'')² sin²''t'' = 4(''s'' − ''a'')(''s'' − ''b'')(''s'' − ''c'')(''s'' − ''d'')

따라서 (1)에 의해 사각형 ABCD의 면적은

:

\frac{1}{2}(ab+cd)\sin t = \sqrt{(s-a)(s-b)(s-c)(s-d)}

가 된다.

일반화된 브레치나이더 공식 또한 유사하게 코사인 법칙을 사용하여 증명할 수 있다.

3. 1. 삼각법을 이용한 증명

내접 사각형의 두 대각은 서로 보각이라는 성질에 의하여, ∠B + ∠D = 180°이다. 삼각형 ABC와 ACD에 코사인 법칙을 적용하면 각각 AC² = a² + b² - 2ab cos B와 AC² = c² + d² - 2cd cos D = c² + d² + 2cd cos B를 얻으며, 이를 연립하면 2(ab + cd) cos B = a² + b² - c² - d²를 얻는다. 사각형 ABCD의 넓이는 삼각형 ABC와 ACD의 넓이의 합이므로, S = (1/2)ab sin B + (1/2)cd sin D = (1/2)(ab + cd) sin B이다. 따라서 16S² = 4(ab + cd)² sin²B = 4(ab + cd)² - 4(ab + cd)² cos²B = (2ab + 2cd)² - (a² + b² - c² - d²)² = (2ab + 2cd - a² - b² + c² + d²)(2ab + 2cd + a² + b² - c² - d²) = ((c + d)² - (a - b)²)((a + b)² - (c - d)²) = (c + d - a + b)(c + d + a - b)(a + b - c + d)(a + b + c - d) = 2(s - a) · 2(s - b) · 2(s - c) · 2(s - d) = 16(s - a)(s - b)(s - c)(s - d) 가 성립한다.

코사인 법칙과 삼각함수 공식을 이용한 다른 증명에서는, 볼록한 원내접 사각형의 넓이 K는 △ADB와 △BDC의 넓이의 합과 같으므로, K = (1/2)pq sin A + (1/2)rs sin C. □ABCD는 원내접 사각형이므로 ∠DAB = 180° - ∠DCB이다. 따라서 sin A = sin C 이므로, K = (1/2)pq sin A + (1/2)rs sin A 이고, K² = (1/4)(pq + rs)² sin² A, 4K² = (pq + rs)²(1 - cos² A) = (pq + rs)² - ((pq + rs)cos A)²이다. △ADB와 △BDC에서 코사인 법칙을 사용하면, p² + q² - 2pq cos A = r² + s² - 2rs cos C. cos C = -cos A를 대입하고 재정렬하면 (pq + rs) cos A = (1/2)(p² + q² - r² - s²). 이것을 넓이의 방정식에 대입하여 정리하면, 16K² = 4(pq + rs)² - (p² + q² - r² - s²)², 이후 우변을 인수분해 및 재정렬, 그리고 반둘레 S = (p + q + r + s)/2 를 도입하여 정리하면, 16K² = 16(S - p)(S - q)(S - r)(S - s). 제곱근을 취하면 K = √((S - p)(S - q)(S - r)(S - s))를 얻는다.

3. 2. 헤론의 공식을 이용한 증명

삼각 함수를 사용하지 않는 증명 방법은 헤론의 공식을 두 번 활용하여 유사한 삼각형에 적용하는 것이다.^[1] 사변형 ABCD가 원 O에 내접한다고 가정하고, 꼭짓점을 A, B, C, D로, AB = ''a'', BC = ''b'', CD = ''c'', DA = ''d''라고 한다. ∠ABC = ''t'' 라고 하면, 내접 사각형의 정리에 따라 ∠CDA = 180° − ''t'' 가 된다. 여기서 삼각형 면적 공식에 의해 △ABC = (1/2) ''ab'' sin''t''이고, △CDA = (1/2) ''cd'' sin(180° − ''t'') = (1/2)''cd'' sin''t''이다. 따라서 사각형 ABCD의 면적은 (1/2)(''ab'' + ''cd'') sin ''t'' … (1)이다.

코사인 법칙에 따르면, AC² = ''a''² + ''b''² − 2''ab'' cos ''t'' = ''c''² + ''d''² − 2''cd'' cos(180° − ''t'') = ''c''² + ''d''² + 2''cd'' cos ''t''이다. 이 두 식으로부터 cos ''t'' 를 구하면,

:

\cos t=\frac{a^2 +b^2 -c^2 -d^2}{2(ab+cd)}

가 되므로 (''ab'' + ''cd'')(1 − cos''t'') = 2(''s'' − ''a'')(''s'' − ''b''), (''ab'' + ''cd'')(1 + cos''t'') = 2(''s'' − ''c'')(''s'' − ''d'') 이고, 변변 곱하여, (''ab'' + ''cd'')² sin²''t'' = 4(''s'' − ''a'')(''s'' − ''b'')(''s'' − ''c'')(''s'' − ''d'')를 얻는다. 따라서 (1)에 의해 사각형 ABCD의 면적은

:

\frac{1}{2}(ab+cd)\sin t = \sqrt{(s-a)(s-b)(s-c)(s-d)}

가 된다.

일반화된 브레히나이더 공식 또한 유사하게 코사인 법칙을 사용하여 증명할 수 있다.

4. 특수한 경우

헤론의 공식은 브라마굽타 공식의 특수한 경우이다. 브라마굽타 정리에서 두 꼭짓점 C와 D가 같다고 하면, 사각형 ABCD는 삼각형 ABC가 되고, d=0, s=1/2(a+b+c)가 되어, 삼각형 ABC의 넓이는

:

가 된다. 헤론의 공식은 d=0일 때 삼각형의 넓이에 대한 특수한 경우이다.

브라마굽타 공식의 일반적인 형태와 확장된 형태의 관계는 코사인 법칙이 피타고라스 정리를 확장하는 방식과 유사하다. 말레이 등은 원에 있는 일반적인 다각형의 넓이에 대한 더욱 복잡한 폐쇄형 공식이 존재한다고 설명했다.^[3]

4. 1. 헤론의 공식

헤론의 공식은 브라마굽타 공식의 특수한 경우이다. 브라마굽타 정리에서 두 꼭짓점 C와 D가 같다고 하면, 사각형 ABCD는 삼각형 ABC가 되고, d=0, s=1/2(a+b+c)가 되어, 삼각형 ABC의 넓이는

:

S=\sqrt{s(s-a)(s-b)(s-c)}

가 된다. 헤론의 공식은 d=0일 때 삼각형의 넓이에 대한 특수한 경우이다.

브라마굽타 공식의 일반적인 형태와 확장된 형태의 관계는 코사인 법칙이 피타고라스 정리를 확장하는 방식과 유사하다. 말레이 등은 원에 있는 일반적인 다각형의 넓이에 대한 더욱 복잡한 폐쇄형 공식이 존재한다고 설명했다.^[3]

4. 2. 이중중심 사각형의 넓이

이중중심 사각형, 즉 외접원과 내접원을 모두 갖는 사각형

ABCD

의 네 변의 길이를

AB=a

,

BC=b

,

CD=c

,

DA=d

라고 할 때, 이 사각형의 넓이

S

는 다음과 같다.

:

S=\sqrt{abcd}

이는 이중중심 사각형이 내접 사각형이므로 브라마굽타 공식이 성립하고, 또한 외접 사각형이므로

:

a+c=b+d=s

이기 때문이다.

5. 일반화

비원형 사변형의 경우, 브라마굽타 공식은 사변형의 두 대각의 크기를 고려하여 확장할 수 있다.

: $K=\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cos^2\theta}$

여기서 θ는 두 대각의 합의 절반이다. (어떤 대각 쌍을 선택하든 상관없다. 다른 두 각을 취하면, 그들의 합의 절반은 180° − θ이다. cos(180° − θ) −cos θ이므로, cos²(180° − θ) cos² θ이다.) 이 더 일반적인 공식은 브레슈나이더 공식으로 알려져 있다.

원내접 사각형의 (그리고 궁극적으로 원주각의) 속성은 사변형의 대각의 합이 180°가 된다는 것이다. 결과적으로, 원내접 사각형의 경우, θ는 90°이며, 따라서

: $abcd\cos^2\theta=abcd\cos^2 \left(90^\circ\right)=abcd\cdot0=0,$

가 브라마굽타 공식의 기본 형태를 제공한다. 후자의 방정식에서 원내접 사각형의 면적은 주어진 변의 길이를 가진 모든 사변형에 대해 가능한 최대 면적임을 알 수 있다.

쿨리지에 의해 증명된 관련 공식은 일반 볼록 사변형의 면적을 제공한다. 그것은 다음과 같다.^[2]

: $K=\sqrt{(s-a)(s-b)(s-c)(s-d)-\textstyle{1\over4}(ac+bd+pq)(ac+bd-pq)}$

여기서 ''p''와 ''q''는 사변형의 대각선의 길이이다. 원내접 사각형에서, 프톨레마이오스 정리에 따르면 ''pq'' ''ac'' + ''bd''이며, 쿨리지의 공식은 브라마굽타 공식으로 축소된다.

'''브레치나이더 공식'''(Bretschneider^de公式, Bretschneider's formula^영어)은 브라마굽타 공식을 원에 내접하지 않을 수 있는 임의의 사각형에까지 일반화한다.^[2] 임의의 사각형 $ABCD$ 의 네 변의 길이를 $AB=a$ , $BC=b$ , $CD=c$ , $DA=d$ 라고 하고, 반둘레를 $s$ , 넓이를 $S$ 라고 할 경우 다음이 성립한다.

: $S=\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cos^2\frac{A+C}2}$

원내접 사각형에서는 $A+C=180^\circ$ 이므로

: $\cos\frac{A+C}2=0$

이다. 즉, 브라마굽타 공식은 브레치나이더 공식의 특수한 경우이다.

쿨리지에 의해 증명된 일반 볼록 사변형의 면적을 제공하는 공식은 다음과 같다.^[2]

: $K=\sqrt{(s-a)(s-b)(s-c)(s-d)-\textstyle{1\over4}(ac+bd+pq)(ac+bd-pq)}$

여기서 $p$ 와 $q$ 는 사변형의 대각선의 길이이다. 원내접 사각형에서, 프톨레마이오스 정리에 따르면 $pq = ac + bd$ 이며, 쿨리지의 공식은 브라마굽타 공식으로 축소된다.

5. 1. 브레치나이더 공식

'''브레치나이더 공식'''(Bretschneider^de公式, Bretschneider's formula^영어)은 브라마굽타 공식을 원에 내접하지 않을 수 있는 임의의 사각형에까지 일반화한다.^[2] 임의의 사각형

ABCD

의 네 변의 길이를

AB=a

,

BC=b

,

CD=c

,

DA=d

라고 하고, 반둘레를

s

, 넓이를

S

라고 할 경우 다음이 성립한다.

:

S=\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cos^2\frac{A+C}2}

원내접 사각형에서는

A+C=180^\circ

이므로

:

\cos\frac{A+C}2=0

이다. 즉, 브라마굽타 공식은 브레치나이더 공식의 특수한 경우이다.

쿨리지에 의해 증명된 일반 볼록 사변형의 면적을 제공하는 공식은 다음과 같다.^[2]

:

K=\sqrt{(s-a)(s-b)(s-c)(s-d)-\textstyle{1\over4}(ac+bd+pq)(ac+bd-pq)}

여기서

p

와

q

는 사변형의 대각선의 길이이다. 원내접 사각형에서, 프톨레마이오스 정리에 따르면

pq = ac + bd

이며, 쿨리지의 공식은 브라마굽타 공식으로 축소된다.

6. 역사

인도의 수학자 브라마굽타가 7세기경에 제시하였다.^[4] 그러나 그는 이에 대한 증명을 제시하지는 않았으며, 사각형이 원에 내접해야 한다고 명시하지도 않았다.^[5]

참조

_[1] 간행물 A highway from Heron to Brahmagupta Forum Geometricorum 2012
_[2] 간행물 A Historically Interesting Formula for the Area of a Quadrilateral American Mathematical Monthly 1939
_[3] 논문 On the areas of cyclic and semicyclic polygons 2005
_[4] 서적 Geometry Revisited Mathematical Association of America 1967
_[5] 서적 Mathematical Thoughts from Ancient to Modern Times. Volume 1 Oxford University Press 1972

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com