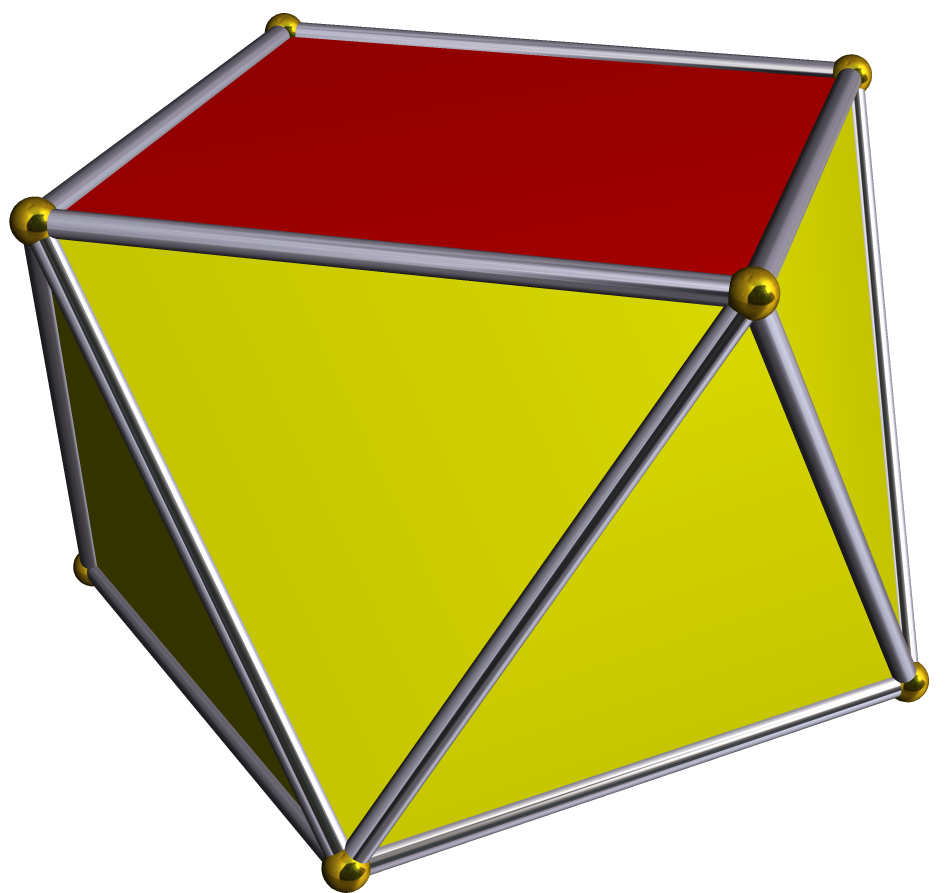
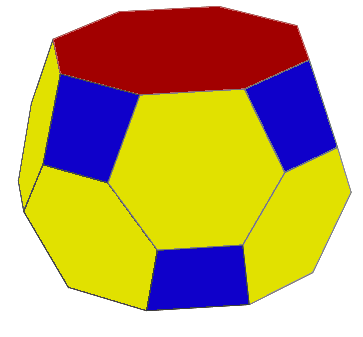
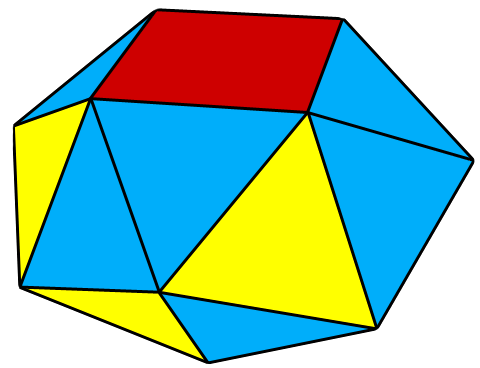
엇사각기둥
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
엇사각기둥은 8개의 점을 구 표면에 배치했을 때 나타나는 사각 반각기둥 형태를 의미하며, 분자 구조 및 건축, 위상적으로 동일한 다면체, 파생 다면체 등 다양한 맥락에서 언급된다. 분자 구조에서는 VSEPR 이론에 따라 팔황 분자와 같은 특정 분자들이 엇사각기둥 구조를 가지며, 건축에서는 원 월드 트레이드 센터와 같이 엇사각기둥 형태를 차용한 사례가 있다. 엇사각기둥은 꼬인 각기둥, 엇각 사각반각기둥과 같은 위상적으로 동일한 다면체와 관련 있으며, 존슨의 다면체와 같은 파생 다면체를 생성하는 데 활용된다.
더 읽어볼만한 페이지
2. 구면 상의 점 분포
8개의 점을 구 표면에 분포시킬 때, 그들 사이의 거리를 최대화하면 정육면체가 아닌 사각 반각기둥 형태가 된다. 점을 분포시키는 방법으로는 톰슨 문제처럼 점 사이 거리의 모든 역수의 합을 최소화하거나, 각 점의 가장 가까운 점까지의 거리를 최대화하거나, 점 사이 거리의 제곱의 모든 역수의 합을 최소화하는 방법 등이 있다.
VSEPR 이론에 따르면, 중심 원자를 둘러싼 8쌍의 전자는 점들 사이의 거리를 최대화하는 원리에 기반하여 사각 반각기둥 구조를 선호한다.[2] 옥타플루오로제논(VI) 이온 (XeF82-)은 이러한 구조를 갖는 대표적인 분자이지만, 이상적인 형태에서 약간 왜곡되어 있다.[2] 팔황(S8) 분자는 8개의 황 원자가 사각 반각기둥의 꼭짓점을 차지하는 구조를 갖는다. 리간드 간의 큰 반발력을 유발하기 때문에 PaF83- 이온과 같이 입방체 모양을 갖는 이온은 드물다.[3]
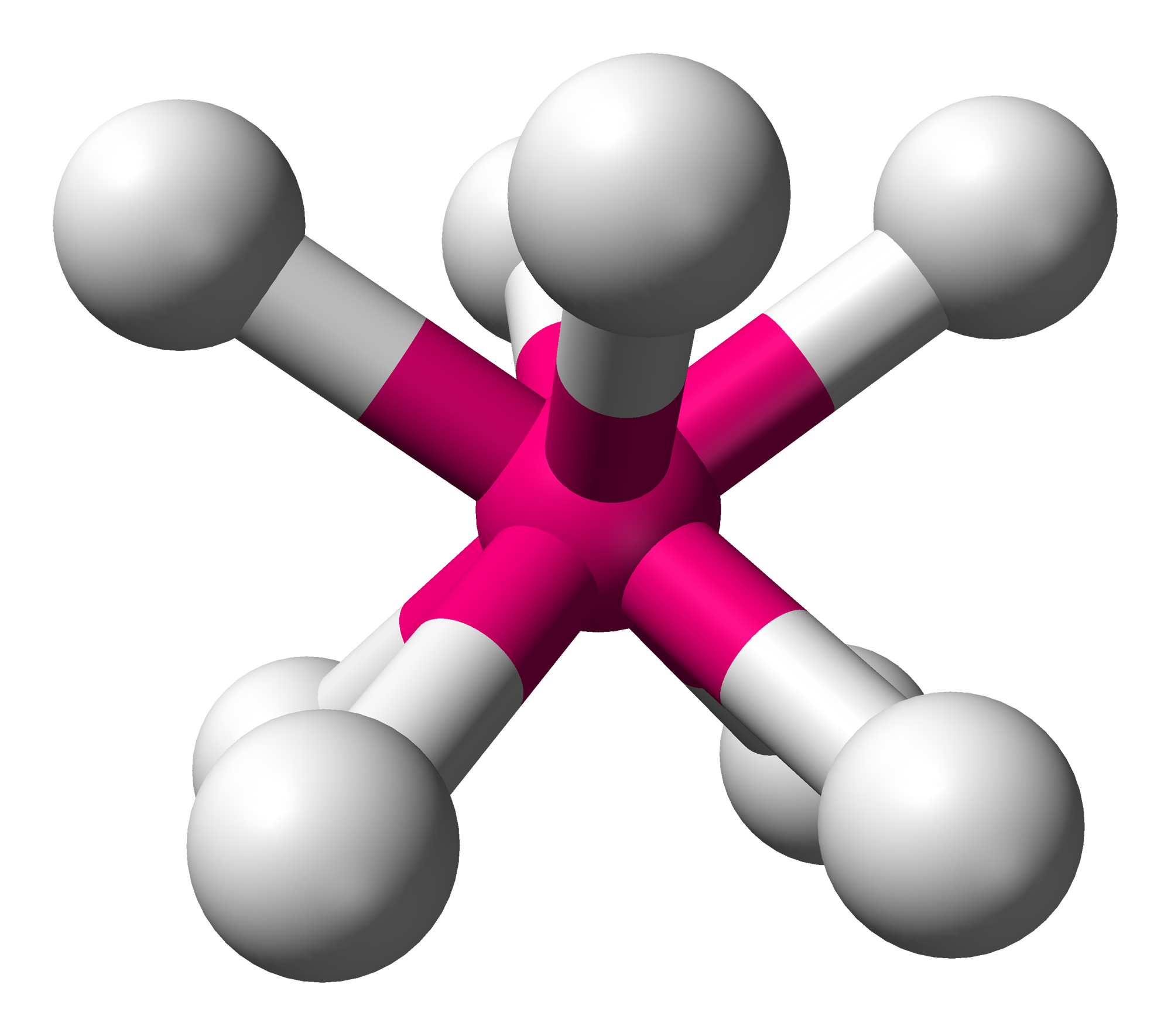

3. 분자 구조
4. 건축
원 월드 트레이드 센터 (구 세계 무역 센터가 2001년 9월 11일에 파괴된 부지에 위치)의 주요 건축 블록은 매우 높고 좁아지는 사각 엇각기둥의 형태를 하고 있다. 좁아지는 형태 때문에 진정한 엇각기둥은 아니다. 꼭대기 사각형은 밑면 사각형의 절반 면적을 가지고 있다.
5. 위상적으로 동일한 다면체
5. 1. 꼬인 각기둥
꼬인 각기둥은 동일한 꼭짓점 배열을 가지고 (시계 방향 또는 반시계 방향으로) 만들 수 있다. 이것은 측면을 따라 4개의 사면체가 깎여나간 볼록 형태로 볼 수 있다. 그러나 이렇게 된 후에는 새로운 꼭짓점을 추가하지 않고는 사면체로 삼각분할할 수 없다. 이것은 균일한 해의 대칭의 절반을 갖는다: D4 차수 4.[4][5]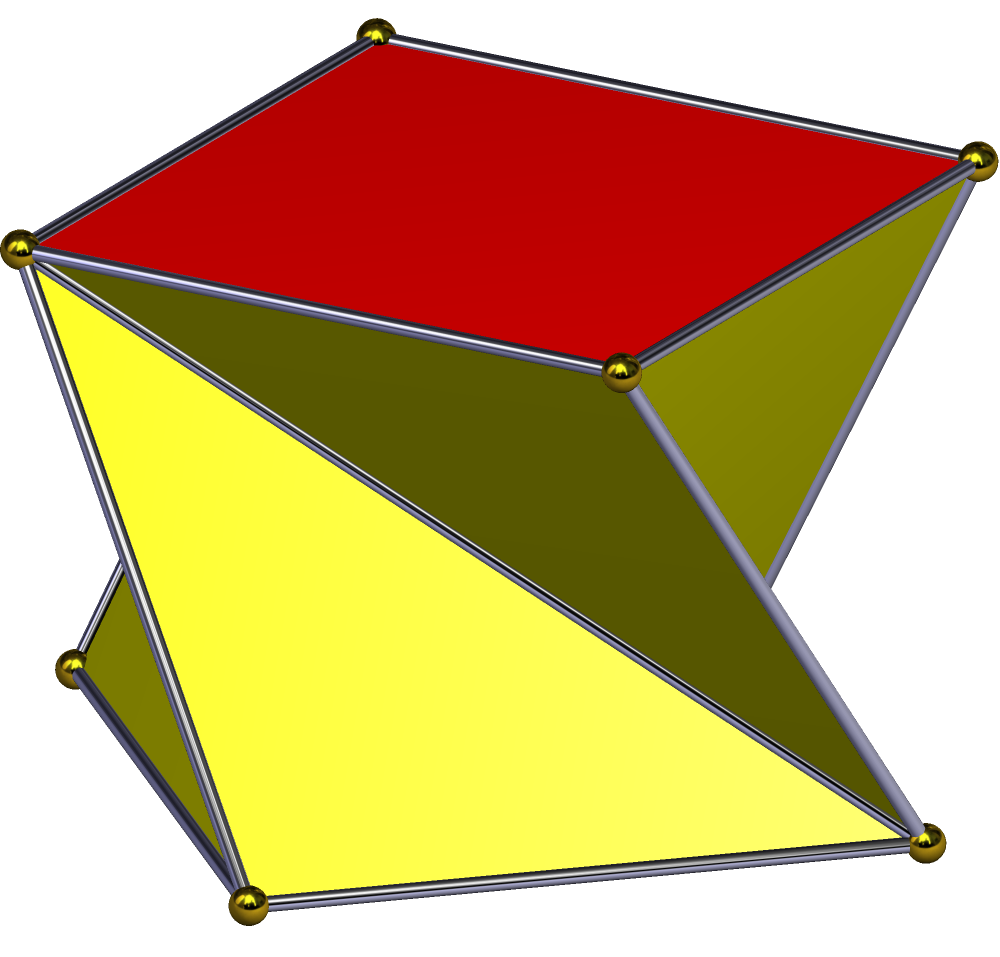
5. 2. 엇각 사각반각기둥
엇각 사각반각기둥은 별 다면체로, 사각반각기둥과 꼭짓점 배치는 같지만 위상적으로 사각기둥과 동일하다. 엇각 사각반각기둥은 모서리가 이등변삼각형이므로 균일하게 만들 수 없다. 꼭짓점 배치는 3.3/2.3.4이며, 삼각형 하나가 후진적이다. 엇각 사각반각기둥의 대칭성은 d4d (8차)이다.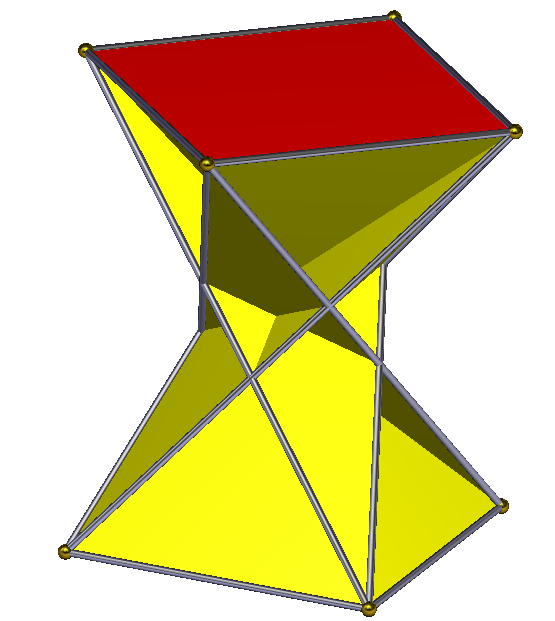
6. 관련 다면체
6. 1. 파생 다면체
자이로연장 정사각뿔(J10), 자이로연장 정사각쌍뿔(J17), 엇각뿔꼴 이면체(J84), 엇각 정사각 반각기둥(J85), 쐐기왕관(J86), 큰쐐기왕관(J88) 등은 엇사각기둥에서 파생된 존슨의 다면체이다. 자이로 연장 정사각뿔은 정사각뿔을, 자이로 연장 정사각쌍뿔은 정사각 반각기둥의 두 정사각형을 정사각뿔으로 대체하여 만들 수 있다. 엇각뿔꼴 이면체는 정사각 반각기둥의 두 정사각형을 정삼각형 쌍으로 대체하여, 엇각 정사각 반각기둥은 정사각 반각기둥의 중간에 정삼각형 사슬을 삽입하여 만들 수 있다.엇사각기둥은 절단 및 교대하여 엇각 반각기둥을 형성할 수 있다.
참조
[1]
서적
Inorganic Chemistry
Academic Press, Italy
[2]
논문
Antiprismatic Coordination about Xenon: the Structure of Nitrosonium Octafluoroxenate(VI)
1971-09
[3]
서적
[4]
서적
Geometry handbook
2003
[5]
웹사이트
Pictures of Twisted Prisms
http://www.korthalsa[...]
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com