전기 용량

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 개념
3. 정의
4. 자기 전기 용량
5. 상호 전기용량
- 5.1. 전기 용량 행렬
6. 축전기에 저장된 에너지
7. 축전기와 변위 전류
8. 축전기/인덕터 상보성
9. 축전기의 종류와 응용
10. 엘라스턴스
11. 정전 용량의 합성
- 11.1. 정전 용량의 병렬 연결
- 11.2. 정전 용량의 직렬 연결
참조

1. 개요

전기 용량은 물체에 전하가 축적되는 정도를 나타내는 물리량이다. 이는 단위 전압당 저장 또는 방출되는 전하의 양으로 정의되며, 기호 C로 표시하고, 국제단위계에서는 패럿(F)을 사용한다. 전기 용량은 축전기에서 중요한 개념으로, 축전기는 전기를 저장하는 장치이며, 두 도체 사이에 유전체를 두어 전기 용량을 증가시킨다. 전기 용량은 도체의 기하학적 구조와 유전체의 유전율에 따라 결정되며, 직렬 또는 병렬 연결을 통해 합성 전기 용량을 계산할 수 있다. 또한, 전기 용량의 역수는 엘라스턴스라고 하며, 축전기에 저장된 에너지는 전기 용량과 전압의 제곱에 비례한다.

더 읽어볼만한 페이지

전기 용량 - 전기적 탄성
전기적 탄성은 축전기 전기 용량의 역수로, 축전기 회로, 네트워크 이론, 마이크로파 공학 등에서 활용되며, 임피던스 유사성과 같은 역학적 유추에 사용되는 중요한 개념이다.
전기 - 전기장
전기장은 공간의 각 지점에서 단위 전하가 받는 힘으로 정의되는 벡터장으로, 전하 또는 시간에 따라 변하는 자기장에 의해 발생하며, 전기력선으로 표현되고 맥스웰 방정식으로 기술되는 전자기장의 한 요소이다.
전기 - 전압
전압은 두 지점 사이의 전위차로서 단위 전하당 에너지 차이를 나타내며, 정전기학에서는 단위 전하를 이동시키는 데 필요한 일, 회로 이론에서는 노드 간 전위차로 정의되고, 직류 및 교류 전압으로 구분되며, 다양한 방식으로 발생하여 여러 분야에 응용된다.
물리학 개념 - 절연체
절연체는 전기 전도성을 막아 전기의 흐름을 제어하고 안전을 확보하며, 밴드 이론에 따라 큰 띠틈을 가져 외부 전압이 띠틈을 넘어서면 절연 파괴가 발생하며, 유리에서 세라믹, 고분자 복합 재료 등으로 제작되어 전선, 케이블 등 다양한 분야에 사용된다.
물리학 개념 - 전기 전도체
전기 전도체는 전기를 잘 통하는 물질로, 금속, 전해질, 초전도체, 반도체 등이 있으며, 구리, 은, 알루미늄 등 다양한 재료가 전선 등에 사용된다.

전기 용량
개요
명칭	전기 용량 ( इलेक्ट्रिक कैपेसिटेंस )
다른 이름	정전 용량 캐패시턴스 용량
영어 이름	Electrostatic Capacity
단위
단위	F
다른 단위	μF, nF, pF
SI 기본 단위	F = A² s⁴ kg⁻¹ m⁻²
차원
차원	M⁻¹ L⁻² T⁴ I²
종류	스칼라
정의
정의	C = 전하 / 전압

2. 개념

물체에 전기가 축적되는 대전 현상은 아주 오래 전부터 알려져 있었다. 고대 그리스에서는 나무의 수액이 굳어 화석이 된 호박을 마찰하면 자잘한 물체가 달라붙는 다는 것을 알고 있었다.^[37] 영어 등에서 전기의 의미로 사용되는 일렉트릭(electric)은 그리스어로 호박을 뜻하는 말이었다.^[38] 이와 같이 마찰을 일으켜 물체에 쌓인 전기는 접지를 하지 않으면 그대로 고여 있기 때문에 정전기라고 한다.

18세기 네덜란드 레이던 대학교의 물리학 교수 피터르 판 뮈스헨브룩은 정전기를 저장하는 장치인 라이덴병을 고안하였다. 레이던 대학교에서 처음 만들어졌기 때문에 레이던의 독일식 발음인 라이덴병으로 널리 알려지게 되었다.^[39] 라이덴병은 마찰을 통해 대전된 정전기를 방출하는 축전기로 사용되었다. 라이덴 병에 모인 전기를 손으로 만지면 찌릿한 경험을 할 수 있었고 당시로서는 새로운 볼거리였기 때문에 라이덴병은 과학자들 뿐만 아니라 대중들에게도 유행하였다. 도시마다 라이덴병을 이용한 실험이 유행하였고 180명이 손에 손을 잡고 라이덴병의 전기를 방출하였을 때 모두 찌릿한 경험을 하였다는 기록이 남아있다.^[40] 당시는 전기의 위험성이 사람들에게 알려져 있지 않았기 때문에 이런 실험을 주저없이 하였다. 충전된 라이덴병을 직접 만지는 행위는 지금 기준에선 매우 위험한 행동이다.^[41]

벤저민 프랭클린은 라이덴병 여러 개를 연결하여 라이덴병이 축적할 수 있는 전기용량을 늘렸다. 프랭클린은 이것을 배터리(battery)라고 불렀는데 이 말은 나중에 전지를 가리키는 일반적인 용어가 되었다.^[40]

전기 회로에서 전기를 축적할 목적으로 쓰이는 축전기는 두 개의 금속판이 일정한 간격을 두고 떨어져 있는 형태로 만들어진다. 두 금속판이 적당한 거리를 두고 떨어져 있으면 전기를 일으키는 힘인 기전력 때문에 두 판은 양극과 음극의 극성을 띄면서 둘 사이에 전하가 축적되게 된다. 이 경우에도 두 판 사이에 쌓이는 전하에는 한계가 있으며 이 양을 나타내는 값이 상호 전기용량이다.^[42]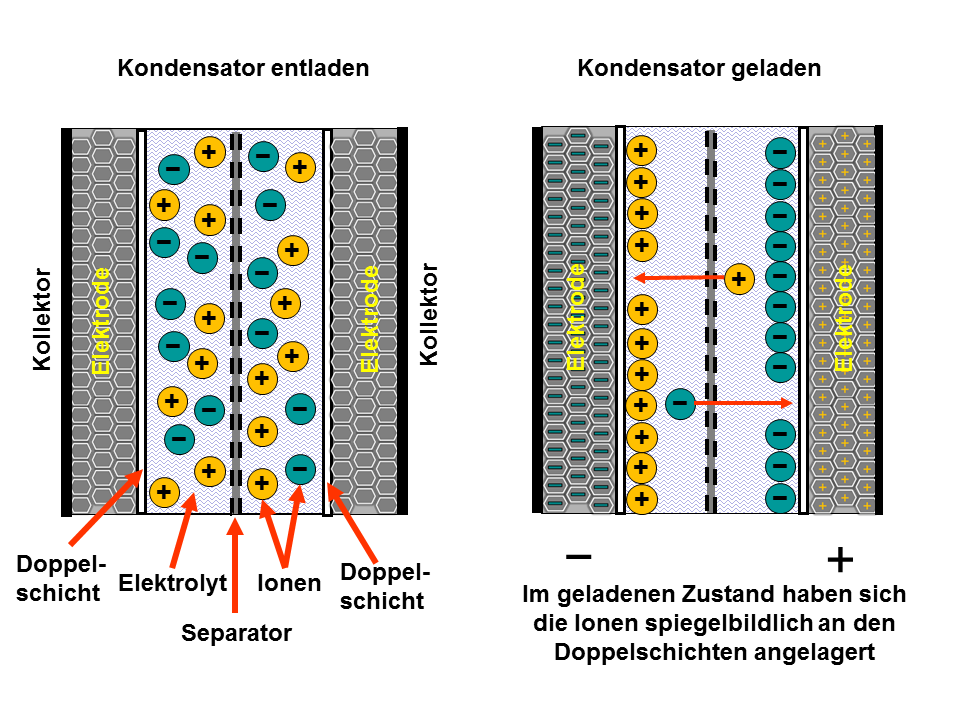

축전기는 두 도체의 사이가 떨어져 있는 형태이기 때문에 직류 전기 회로에서는 처음에는 전기가 흐르다가 전기 용량이 꽉 채워진 포화 상태가 되면 더 이상 전기가 흐르지 않는다. 축전기 내부의 전하가 양쪽 도체의 극성에 의해 완전히 정렬되면 축전기 내부에 전기적 균형이 이루어지기 때문이다. 이렇게 대전된 축전기는 스스로 전하를 보전하고 있기 때문에 전기 회로에 연결하여 방전시킬 수 있다. 이렇게 흐르는 전기를 변위 전류라고 한다. 축전기에 대전되어 있던 전하가 모두 방전되면 전류가 더 이상 흐르지 않는다.^[43] 한편 교류는 일정 주기로 계속하여 극성이 변하기 때문에 축전기 역시 계속하여 충전과 방전을 지속하게 된다. 이 때 축전기의 전기용량은 교류의 주파수와 공진 현상을 보인다.^[44]

정전 용량은 단위 전압당 축적된 전하로 주어진다. 기호는 '''C''', 단위는 '''패럿'''(F)를 사용한다. 어떤 물체에 1 V의 전압을 가했을 때 1 C의 전하를 축적하면 해당 물체의 정전 용량은 1 F이다.

1 F라는 정전 용량은 매우 큰 값이다. 일반적으로 우리 주변에서 사용되는 전자 부품인 콘덴서에서는 1 F의 100만 분의 1(10⁻⁶)인 '''마이크로패럿'''(μF) 또는 1조 분의 1(10⁻¹²)인 '''피코패럿'''(pF)가 많이 사용된다.

3. 정의

전기 용량(C)은 단위 전압(V) 당 대전체가 저장하거나 방출하는 전하(Q)의 양으로 정의된다. 즉, C = Q/V 로 나타낼 수 있다.

국제단위계(SI)에서 전기 용량의 단위는 패럿(F)이며, 1 패럿은 1 볼트(V) 전압에서 1 쿨롬(C)의 전하량을 저장 또는 방출하는 것을 의미한다. 즉, 다음과 같이 표현된다.

:: $F = \frac{C}{V}$

전기 용량은 가우스 법칙에 따라 단위 전압당 전기 선속(Φ)으로 나타낼 수도 있다.

:: $C = \epsilon_0\frac{\Phi}{V}$ (ε₀는 진공의 유전율)

전하는 결국 전자의 움직임이므로, 전기 용량은 물질의 이동 관점에서 다룰 수 있다. 이 경우 축적된 전자 1 mol이 갖는 전하량을 1 F이라고 정의할 수 있다. 전자 1 mol은 아보가드로 상수(N_A)인 6.02214076×10²³ 개의 전자가 모인 양이고, 전자 하나의 기본 전하 ''e''는 1.602×10⁻¹⁹ C 이기 때문에, 1 F은 아래와 같이 계산된다.

:: $1 F = e \cdot N_{A}$

::: $= (1.602 \times 10^{-19} C ) \cdot ( 6.02214076 \times 10^{23} \cdot 1 / mol )$

::: $\approx 96485 C / mol$

일반적인 전기 회로에 사용되는 축전기의 전기 용량은 피코패럿(pF)에서 마이크로패럿(μF) 사이의 값을 갖는다.^[46]

4. 자기 전기 용량

일반적으로 전기 회로에서 사용되는 전기 용량은 인접한 두 도체 사이의 상호 전기 용량을 의미한다. 그러나 고립된 도체 역시 '자기 전기 용량'이라 불리는 전기 용량을 지닌다. 물체는 다른 것과 고립되어 있더라도 대전될 수 있으며 그에 따른 전위차를 갖게 된다.^[47] 대표적인 예로 정전기가 있다. 낙뢰를 일으키는 구름의 대전 역시 자기 전기 용량의 사례이다.

밴더그래프 발전기는 자기 전기 용량을 이용한 정전기 발전기이다.

자기 전기 용량은 고립된 대전체에 쌓이는 정전기의 전압 '''V'''에 대한 대전된 전하의 총량 '''q'''의 비로 나타낼 수 있다.

:

C = \frac{q}{V}

반지름이 '''R''' 인 구형 대전체의 자기 전기 용량은 다음과 같이 간단히 표현할 수 있다.^[48]

:

C = 4 \pi \varepsilon_0 R

여기서 ε₀는 진공 유전율이다.

예를 들어 지름 20cm인 밴더그래프 발전기 표면의 자기 전기 용량은 22.24pF(피코패럿, 10^-12F)이고, 지구의 경우 710µF(마이크로패럿, 10^-6F)이다.^[49]

나선형으로 감긴 코일은 도선이 가까이 붙어 있기 때문에 내부적인 전기 용량을 갖는다. 코일의 이러한 내부적 전기 용량도 종종 자기 전기 용량이라 불리지만,^[50] 코일 내부에 형성되는 것은 기생 전기 용량으로 여기서 말하는 자기 전기 용량과는 전혀 다른 현상이다.

5. 상호 전기용량

전기 회로에서 사용되는 전기 용량은 일반적으로 인접한 두 도체에서 형성되는 상호 전기 용량을 의미한다. 대개는 두 개의 판을 나란히 놓고 그 사이를 유전체로 채운 축전기가 전기 용량의 충전과 방출을 맡는다. 나란히 놓인 두 판 사이에 전하가 축적되기 때문에 "상호"라는 명칭이 붙었다.^[47]

전기 회로에서 전압 ''V'' 가 인가되어 축전기의 양쪽 판에 +''q'' 와 −''q''의 전하가 대전되었다고 하면 상호 전기 용량 ''C''는 다음과 같이 계산된다.

::

C = \frac{q}{V}

전류는 일정 시간 동안 흐른 전하량을 뜻하기 때문에 순간 전류 i(t)는 순간 전압 변화율 d''v''(t)/d''t''와 전기용량 ''C''의 곱으로 표현할 수 있다.

::

i(t) = C \frac{\mathrm{d}v(t)}{\mathrm{d}t}

주어진 전압 ''V''에서 상호 전기 용량 ''C''의 대전으로 발생하는 에너지 ''W''는 다음과 같이 계산된다. 에너지의 단위는 J이다.^[51]

::

W = \frac{1}{2}CV^2 (J)

5. 1. 전기 용량 행렬

세 개 이상의 도체가 관여하는 경우, 전기 용량은 행렬을 통해 계산할 수 있다.^[52] 제임스 클러크 맥스웰은 다중 도체 시스템의 전기 용량을 계산하기 위해 전위 계수를 도입하였다.

맥스웰은 기준점 ''P''를 중심으로 세 개의 도체

Q_1, Q_2, Q_3

로 이루어진 축전기에서 도체 1에 걸리는 전위 계수를 다음과 같이 계산하였다.

::

V_1 = P_{11}Q_1 + P_{12} Q_2 + P_{13}Q_3,

다른 도체에 걸리는 전압 역시 이와 같은 방법으로 계산할 수 있다. 헤르만 폰 헬름홀츠와 윌리엄 톰슨은 전위 계수의 대칭성(

P_{12} = P_{21}

)을 고려하여 엘라스턴스 행렬(전기 용량 행렬의 역행렬)을 정의했다.

::

P_{ij} = \frac{\partial V_{i}}{\partial Q_{j}}

이를 통해 세 개 이상의 도체판이 형성하는 축전기에서 두 도체판 사이의 전기 용량

C_{m}

은 총전하량 ''Q'' 를 전기 용량의 정의(

C_{m}=Q/V

)에 대입하여 계산할 수 있다.

::

C_m = \frac{1}{(P_{11} + P_{22})-(P_{12} + P_{21})}

두 개의 판으로 이루어진 축전기의 경우도 두 판이 완벽하게 대칭이 될 수는 없기 때문에 실제 전기 용량은 위와 같은 전위 계수에 따른 값을 가진다.

계수를 이용하여 표현되는 전기 용량

C_{ij} = \frac{\partial Q_{i}}{\partial V_{j}}

를 전기 용량 행렬이라고 한다.^[53]^[54]^[55] 이 전기 용량 행렬의 역행렬이 엘라스턴스 행렬이다.

6. 축전기에 저장된 에너지

축전기에 저장된 에너지(단위는 줄)는 축전기를 충전하는 데 필요한 일과 같다. 한쪽 판에는 +''q'' 전하를, 다른 한쪽 판에는 -''q'' 전하를 가지고 있는 축전기에서, 전위차 ''V = q/C''를 거슬러 무한소의 전하 ''dq''를 한쪽 판에서 다른 쪽 판으로 이동시키는 데 필요한 일 d''W''는 다음과 같다.^[51]

: $dW = \frac{q}{C}dq$

여기서,

''W''는 일 (단위: 줄)
''q''는 전하량 (단위: 쿨롱)
''C''는 전기 용량 (단위: 패럿)

축전기에 저장된 에너지는 위 공식을 적분하여 구한다. 전하가 없는 축전기(''q''=0)에서 시작하여 각 판에 +''Q''와 -''Q'' 전하가 쌓일 때까지 전하를 옮기는 데 필요한 총 일 ''W''는 다음과 같다.

:

W_{charging} = \int_{0}^{Q} \frac{q}{C} dq = \frac{1}{2}\frac{Q^2}{C} = \frac{1}{2}CV^2 = W_{stored}

7. 축전기와 변위 전류

제임스 클러크 맥스웰은 축전기 같은 곳에서 전하가 모일 때에도 앙페르 회로 법칙이 성립하도록 하기 위해 변위 전류 d'''D'''/dt라는 개념을 고안해 냈다. 맥스웰은 이 개념을 에테르에서 전기 쌍극자의 움직임과 연관지은 다음, 이것이 실재하는 전하의 움직임이라고 해석했다. 변위 전류는 진공에서도 존재하므로, 이 해석에 따르면 진공에서도 어떤 전하가 존재하여야 한다.

맥스웰의 이러한 해석은 오늘날 더 이상 받아들여지지 않는다. 다만, 맥스웰이 추가한 변위 전류 항은 여전히 유효하고, 이는 단순히 자연계의 기본 법칙으로 해석된다. 즉, 변화하는 전기장은 자기장을 만들어낸다.

8. 축전기/인덕터 상보성

수학적으로, 이상적인 축전기는 이상적인 인덕터의 역으로 볼 수 있다. 이는 한 소자(축전기 또는 인덕터)의 전압-전류 공식에서 전압과 전류를 서로 바꾸면 다른 소자의 공식이 되기 때문이다.

9. 축전기의 종류와 응용

대부분의 전자 회로에 사용되는 축전기의 전기 용량은 일반적으로 패러드보다 여러 자릿수 작다. 가장 일반적인 전기 용량 단위는 마이크로 패러드(μF), 나노 패러드(nF), 피코 패러드(pF)이며, 마이크로 회로에서는 펨토 패러드(fF)를 사용한다. 일부 응용 분야에서는 수백 패러드에 달하는 훨씬 더 큰 슈퍼 축전기를 사용하기도 하며, 기생 용량 소자는 펨토 패러드 미만이 될 수도 있다. 과거 문헌에서는 마이크로 패러드(μF)를 "mf" 및 "mfd", 피코 패러드(pF)를 "mmf", "mmfd", "pfd", "μμF"와 같은 패러드의 다른 구식 하위 배수를 사용하기도 한다.^[11]^[12]

전기 용량은 도체의 기하학적 구조와 도체 사이의 절연체의 유전 특성을 알면 계산할 수 있다. 전기 용량은 겹치는 면적에 비례하고, 도체 시트 간의 거리에 반비례한다. 시트가 서로 가까울수록 전기 용량은 커진다.

예를 들어, 면적이 $A$ 이고 거리가 $d$ 인 두 개의 평행판으로 구성된 축전기의 전기 용량은 $d$ 가 $A$ 의 가장 작은 현에 비해 충분히 작으면, 높은 수준의 정확도로 다음과 같이 나타낼 수 있다.

: $C=\varepsilon\frac{A}{d}$

: $\varepsilon=\varepsilon_0 \varepsilon_r,$

이때 각 변수의 의미는 다음과 같다.

변수	설명	단위
$C$	전기 용량	패러드(F)
$A$	두 판의 겹치는 면적	제곱미터(m²)
$\varepsilon_0$	전기 상수 ( $\varepsilon_0 \approx 8.854\times 10^{-12} ~ \mathrm{F{\cdot}m^{-1}}$ )	패러드 퍼 미터(F/m)
$\varepsilon_r$	판 사이 재료의 상대 유전율 (유전 상수) (공기의 경우 $\varepsilon_r \approx 1$ )	무차원
$d$	판 사이의 간격	미터(m)

위 방정식은 ''d''가 판의 다른 치수에 비해 작아서 축전기 영역의 전기장이 균일하고, 주변의 소위 ''프린징 필드''가 전기 용량에 작은 기여만 하는 경우 좋은 근사값을 제공한다.

전기 용량에 대한 방정식을 축전기에 저장된 에너지에 대한 방정식과 결합하면 평판 축전기에 저장된 에너지는 다음과 같다.

: $W_\text{stored} = \frac{1}{2} C V^2 = \frac{1}{2} \varepsilon \frac{A}{d} V^2.$

여기서 $W$ 는 에너지(단위: 줄), $C$ 는 전기 용량(단위: 패러드), $V$ 는 전압(단위: 볼트)이다.

10. 엘라스턴스

전기 용량의 역수를 '''엘라스턴스'''(elastance^영어)라고 한다. 단위는 '''매퍼럿'''(F^-1)이다.

SI 단위는 아니지만, '''다라프'''(daraf^영어)라는 단위가 사용되기도 한다. 이것은 전기 용량의 단위인 퍼럿(farad)을 거꾸로 쓴 것으로, 1936년 아서 에드윈 케넬리가 명명했다. 1매퍼럿은 1다라프와 같다.

11. 정전 용량의 합성

전기 용량을 직렬이나 병렬로 연결하여 합성 전기 용량을 만들 수 있다. 합성 전기 용량은 여러 개의 전기 용량을 하나로 합쳐서 계산한 값을 의미한다.

11. 1. 정전 용량의 병렬 연결

정전 용량을 병렬로 연결하면, 각 정전 용량 ''C_i''에 대해 전체 전압 ''V''가 동일하게 걸린다. 이때의 전하를 ''Q''라고 하면, 합성 정전 용량 ''C''는 다음과 같이 계산된다.

:

C = \frac{Q}{V}  = \frac{V \sum_{i=1}^n C_i}{V} = \sum_{i=1}^n C_i

따라서 합성 정전 용량은 각 정전 용량의 총합과 같다.

11. 2. 정전 용량의 직렬 연결

전기 용량을 직렬로 연결하면 전체에 ''V''의 전압을 가했을 때 각 소자 사이에 전하가 흘러 들어가지 않으므로 전하량이 같아지며, 이를 ''Q''라고 한다. 이때 합성 전기 용량 ''C''는 각 전기 용량 ''C_i''에 전압 ''V_i''가 걸린다고 하면 다음과 같이 나타낼 수 있다.

:

V_i = \frac{Q}{C_i}

:

V=\sum_{i=1}^n V = Q \sum_{i=1}^n \frac{1}{C_i}

:

C=\frac{Q}{V} = \frac{Q}{Q \sum_{i=1}^n \frac{1}{C_i}} =\frac{1}{\sum_{i=1}^n \frac{1}{C_i}}

:

\frac{1}{C} = \sum_{i=1}^n \frac{1}{C_i}

따라서 합성 전기 용량은 각 전기 용량 역수의 총합의 역수와 같다. 즉, 합성 전기 용량의 역수는 각 전기 용량 역수의 합과 같다.

또한, 각 전기 용량의 전압 분담은 다음과 같이 나타낼 수 있다.

:

V_i = \frac{Q}{C_i} = \frac{C}{C_i} V

참조

_[1] 서적 Introduction to Electromagnetic Engineering Dover Publications
_[2] 웹사이트 Definition of 'farad' http://www.collinsdi[...] Collins
_[3] 서적 Electrostatic discharge in electronics https://books.google[...] Research Studies Press
_[4] 웹사이트 Lecture notes: Capacitance and Dieletrics http://www.phys.unsw[...] University of New South Wales
_[5] 서적 Physics for Scientists and Engineers Macmillan
_[6] 간행물 Self capacitance of inductors
_[7] 서적 Classical Electrodynamic John Wiley & Sons
_[8] 서적 A treatise on electricity and magnetism Clarendon Press
_[9] 웹사이트 Capacitance: Charge as a Function of Voltage http://www.av8n.com/[...] 2010-09-20
_[10] 간행물 Capacitance matrix revisited https://www.jpier.or[...] 2021-05-04
_[11] 웹사이트 Capacitor MF-MMFD Conversion Chart http://www.justradio[...]
_[12] 서적 Fundamentals of Electronics https://archive.org/[...] Bureau of Naval Personnel
_[13] 간행물 Capacitance and potential gradients of eccentric cylindrical condensers https://aip.scitatio[...]
_[14] 서적 Classical Electrodynamics Wiley
_[15] 서적 Analysis and computation of electric and magnetic field problems Pergamon Press
_[16] 서적 A Treatise on Electricity and Magnetism Dover
_[17] 간행물 Note on the capacitance of two closely separated spheres
_[18] 서적 Basic Hypergeometric Series Cambridge University Press
_[19] 서적 Classical Electrodynamics Wiley
_[20] 간행물 On the electrical capacity of a long narrow cylinder and of a disk of sensible thickness https://zenodo.org/r[...]
_[21] 간행물 Static boundary problems for a hollow cylinder of finite length. III Approximate formulas
_[22] 간행물 Charge density on thin straight wire, revisited
_[23] 서적 Superlattice to Nanoelectronics Elsevier
_[24] 간행물 Discrete charge dielectric model of electrostatic energy
_[25] 간행물 Capacitive nature of atomic-sized structures
_[26] 간행물 Capacitance: A property of nanoscale materials based on spatial symmetry of discrete electrons http://www.pagesofmi[...] 2014-02-12
_[27] 간행물 Techniques for small-signal analysis of semiconductor devices 1985-10
_[28] 간행물 The physical origin of negative capacitance 1986
_[29] 간행물 Negative capacitance effect in semiconductor devices 1998-10
_[30] 웹사이트 한국물리학회 물리학용어집 https://www.kps.or.k[...]
_[31] 웹사이트 대한화학회 화학술어집 https://new.kcsnet.o[...]
_[32] 문서 축전기의 전기용량 측정 https://file.uos.ac.[...] 서울시립대학교
_[33] 서적 대학물릭학 II 북스힐
_[34] 웹사이트 정전기 발생의 메커니즘(정전기 특집) https://kr.misumi-ec[...] 한국미스미
_[35] 서적 Introduction to Electromagnetic Engineering Dover Publications
_[36] 웹사이트 LC 필터 회로 https://www.chip1sto[...]
_[37] 웹사이트 전기 역사여행 https://www.keri.re.[...]
_[38] 웹사이트 electric https://www.etymonli[...]
_[39] 웹사이트 The Leiden jar https://lorentz.leid[...]
_[40] 뉴스 도구로 읽는 과학사 14. 전기 배터리 https://sojoong.join[...] 2019-08-25
_[41] 웹사이트 전기 위험 https://safety-work.[...]
_[42] 웹사이트 전기회로에서는 내가 주인공! ‘축전기’ https://news.samsung[...]
_[43] 논문 직류전압을 건 평행판 축전기에서 변위전류 고찰 https://koreascience[...]
_[44] 웹사이트 RF 관점에서의 L과 C http://www.rfdh.com/[...]
_[45] 서적 전기와 자기의 밀고 당기기 동아사이언스 2006
_[46] 웹사이트 기본 사항: 커패시터 유형의 특성을 이해하여 커패시터를 적절하고 안전하게 사용 https://www.digikey.[...]
_[47] 서적 Electrostatic discharge in electronics https://books.google[...] Research Studies Press
_[48] 웹사이트 Lecture notes https://web.archive.[...]
_[49] 서적 Physics for Scientists and Engineers Macmillan
_[50] 저널 Self capacitance of inductors
_[51] 웹사이트 Electric Field Energy 전기장 에너지, 전계 에너지 http://www.ktword.co[...]
_[52] 문서 The Maxwell Capacitance Matrix https://www.fastfiel[...] FastFieldSolvers 2020-06
_[53] 서적 A treatise on electricity and magnetism Clarendon Press
_[54] 웹인용 Capacitance : Charge as a Function of Voltage http://www.av8n.com/[...] 2010-09-20
_[55] 저널 Capacitance matrix revisited https://www.jpier.or[...] 2021-05-04

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com