클레인 역설

2. 역사

오스카 클라인은 1929년에 후에 클레인 역설이라고 불리게 된 현상을 설명하는 논문을 발표했는데,^[1] 당시 물리학자들은 상대성 이론과 양자역학을 결합하는 방법, 그리고 물질과 빛의 결합을 이해하는 전자기학을 다루는 데 어려움을 겪고 있었다. 이 역설은 디랙의 초기 시도에서 상대성 이론이 양자역학에 어떻게 추가되었는지에 대한 의문을 제기했다. 이 역설을 해결하기 위해서는 전자기학을 위해 개발된 새로운 양자장론의 발전이 필요했다. 따라서 이 역설의 배경에는 양자역학과 양자 전기역학의 발전이라는 두 가지 흐름이 존재한다.^[7]

보어 모형은 원자 내 전자가 양전하를 띠는 원자핵 주위를 운동한다고 가정했으나, 고전 역학에 따르면 전자는 에너지를 방출하고 원자핵으로 가속되어야 했다.^[8] 보어 모형의 성공은 고전 역학이 옳지 않을 수 있음을 시사했다.^[8]

1926년 에르빈 슈뢰딩거는 전자를 위한 새로운 양자 역학을 개발했지만, 특수 상대성 이론의 효과나 물질과 복사의 상호 작용을 포함하지 않아 불완전했다. 1928년 폴 디랙은 전자의 상대론적 양자 이론을 제시하여 전자 스핀을 예측했지만, 예상보다 두 배 많은 상태를 포함했고, 모두 낮은 에너지를 가졌다.^[8]

클라인은 이러한 추가 상태가 전자가 크고 급격한 정전기적 전위 변화에 부딪힐 때, 장벽 너머에 음전류가 나타나는 터무니없는 결과를 초래함을 발견했다.^[8] 닐스 보어는 이 결과가 갑작스러운 단계와 관련이 있다고 생각했고, 아르놀트 조머펠트는 프리츠 자우터에게 기울어진 단계를 조사하도록 요청했다. 자우터는 보어의 추측을 확인했는데, 역설적인 결과는 전자의 컴프턴 파장과 비슷한 거리에서 큰 전위차(2mc² 초과)가 발생할 때만 나타났다.^[8]

1929년과 1930년 동안 여러 물리학자들이 디랙의 추가 상태를 이해하려 했다.^[7] 헤르만 바일은 이 상태가 양성자에 해당한다고 제안했지만, 디랙은 음전자가 양성자로 변환될 수 없다고 지적하고 추가 상태가 이미 전자로 채워져 있다고 제안했다.^[7] 로버트 오펜하이머와 이고르 탐은 이것이 원자를 불안정하게 만들 것이라고 밝혔다. 1931년 디랙은 이 상태가 새로운 "반전자" 입자에 해당한다고 결론 내렸고, 1932년 칼 앤더슨이 실험적으로 양전자를 발견했다.

역설의 해결은 양자 역학과 함께 발전했지만 복잡성 때문에 속도가 느렸던 양자장론을 필요로 했다. 이 개념은 많은 응용 분야에서 매우 성공적인 맥스웰 방정식의 흑체 복사 스펙트럼을 예측하는 데 실패한다는 막스 플랑크의 시연으로 거슬러 올라간다. 플랑크는 흑체 진동자가 양자 전이에 제한되어야 함을 보여주었다.^[7] 1927년, 디랙은 양자장론을 사용하여 양자 전기역학에 대한 첫 번째 연구를 발표했다. 이 토대를 바탕으로 하이젠베르크, 요르단, 파울리는 1928년과 1929년에 양자화된 맥스웰 방정식에 상대론적 불변성을 통합했다.^[7]

그러나 이 이론이 클레인 역설의 문제에 적용되기까지는 10년이 더 걸렸다. 1941년 프리드리히 훈트는^[9] 역설의 조건 하에서, 단계에서 전하가 반대인 두 전류가 자발적으로 생성된다는 것을 보여주었다. 현대 용어로는 전자와 양전자 쌍이 단계 전위에서 자발적으로 생성된다. 이 결과는 1981년 한센과 라브달에 의해 보다 일반적인 처리를 사용하여 확인되었다.^[10][8] 전통적인 해법은 양자장론의 맥락에서 입자-반입자 쌍 생성 기법을 사용한다.^[10]

2. 1. 디랙 방정식의 등장과 난제

2. 2. 양전자-전자 쌍생성과 양자장론

3. 이론적 설명

3. 1. 무질량 입자의 경우

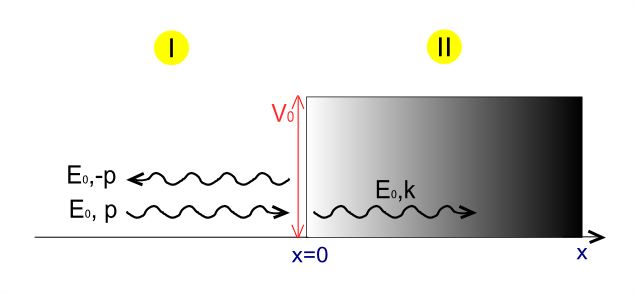
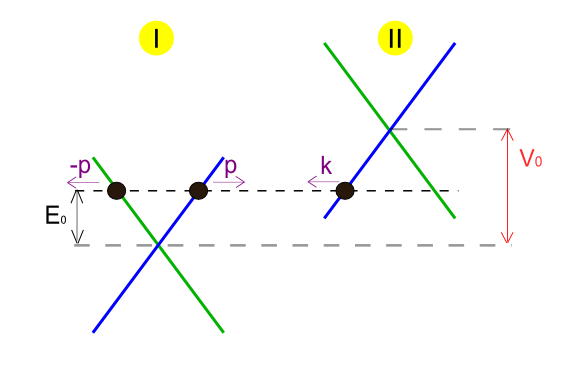
질량이 없고 에너지 이고 운동량 $p$를 가진 상대론적 입자가 높이 $V\_0$의 포텐셜 계단에 접근한다고 가정한다. 입자의 파동 함수 $\backslash psi$는 시간 독립 디락 방정식을 따른다.

::

그리고 $\backslash sigma\_x$는 파울리 행렬이다.

::

입자가 왼쪽에서 전파된다고 가정하면, 계단 전(영역 (1))과 포텐셜 아래(영역 (2))에 두 개의 해를 얻는다.

::$\backslash psi\_1=Ae^\{ipx\}\backslash left(\; \backslash begin\{matrix\}\; 1\; \backslash \backslash \; 1\backslash end\{matrix\}\; \backslash right)+A\text{'}e^\{-ipx\}\backslash left(\; \backslash begin\{matrix\}\; -1\; \backslash \backslash \; 1\backslash end\{matrix\}\; \backslash right)\; ,\backslash quad\; p=E\_0\; \backslash ,$

::$\backslash psi\_2=Be^\{ikx\}\backslash left(\; \backslash begin\{matrix\}\; 1\; \backslash \backslash \; 1\backslash end\{matrix\}\; \backslash right)\; ,\backslash quad\; \backslash left|k\backslash right|=V\_0-E\_0\; \backslash ,$

여기서 계수 , 및 는 복소수이다. 입사 및 투과 파동 함수는 모두 양의 군 속도와 관련이 있으며(그림 1의 파란색 선), 반사 파동 함수는 음의 군 속도와 관련이 있다(그림 1의 녹색 선).

투과 및 반사 계수 $T,\; R$은 확률 진폭 전류에서 파생된다.

디락 방정식과 관련된 확률 전류의 정의는 다음과 같다.

::$J\_i=\backslash psi\_i^\backslash dagger\; \backslash sigma\_x\; \backslash psi\_i,\backslash \; i=1,2\; \backslash ,$

이 경우:

::$J\_1=2\backslash left[\backslash left|\; A\; \backslash right|^2-\backslash left|\; A\text{'}\; \backslash right|^2\backslash right],\; \backslash quad\; J\_2=2\backslash left|\; B\; \backslash right|^2\; \backslash ,$

투과 및 반사 계수는 다음과 같다.

::$R=\backslash frac\; \{\backslash left|A\text{'}\backslash right|^2\}\; \{\backslash left|A\backslash right|^2\},\; \backslash quad\; T=\backslash frac\; \{\backslash left|B\backslash right|^2\}\; \{\backslash left|A\backslash right|^2\}\; \backslash ,$

$x=0$에서 파동 함수의 연속성은 다음을 산출한다.

::$\backslash left|A\backslash right|^2=\backslash left|B\backslash right|^2\; \backslash ,$

::$\backslash left|A\text{'}\backslash right|^2=0\; \backslash ,$

따라서 투과 계수는 1이고 반사는 없다.

이러한 결과는 포텐셜 계단이 질량이 없는 상대론적 입자의 군 속도 방향을 바꿀 수 없다는 해석을 제시한다. 다른 해석으로는 제한 없는 터널링이 포텐셜에서 입자-반입자 쌍의 존재로 인해 발생함을 보여주는 양자장론이 있다.

3. 2. 유질량 입자의 경우

거대한 입자일 경우에도 계산은 유사하게 진행된다. 그 결과는 질량이 없는 입자일 때만큼 놀라운데, 투과 계수는 항상 0보다 크며, 퍼텐셜 계단이 무한대로 갈수록 1에 접근한다.

3. 3. 클라인 영역 (Klein zone)

입자의 에너지가 \( mc^2 < E < Ve - mc^2 \) 범위에 있으면, 완전 반사가 아닌 부분 반사가 일어난다.