쌍둥이 역설
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
쌍둥이 역설은 특수 상대성 이론에서 예측되는 시간 지연 현상으로, 두 쌍둥이 중 한 명이 빠른 속도로 이동한 후 돌아오면 상대적으로 덜 늙는 것처럼 보이는 역설적인 현상을 말한다. 이 역설은 1905년 아인슈타인의 특수 상대성 이론에서 처음 제안되었으며, 1911년 폴 랑주뱅에 의해 쌍둥이의 상황으로 구체화되었다. 쌍둥이 역설은 특수 상대성 이론과 일반 상대성 이론을 통해 해소될 수 있으며, 가속도의 역할, 동시성의 상대성, 시공간 경로 차이 등이 시간 지연에 영향을 미치는 주요 요인으로 작용한다. 상대론적 도플러 효과와 같은 현상을 통해 쌍둥이의 시간 차이를 설명할 수 있으며, 생물학적 노화와 시계 작동의 동등성 또한 쌍둥이 역설을 이해하는 데 중요한 개념이다.
더 읽어볼만한 페이지
- 물리학에 관한 사고 실험 - 동시성의 상대성
동시성의 상대성은 상대적으로 움직이는 기준계에서 공간적으로 분리된 두 사건의 시간 판단이 달라지는 현상으로, 아인슈타인의 특수 상대성 이론에서 절대적인 동시성이 존재하지 않음을 나타내는 핵심 개념이다. - 물리학에 관한 사고 실험 - 맥스웰의 도깨비
맥스웰의 도깨비는 맥스웰이 열역학 제2법칙에 대한 사고 실험으로 제시한 가상의 존재로, 속력이 빠른 분자와 느린 분자를 구별하여 온도 차이를 발생시키는 실험을 통해 엔트로피 감소 가능성을 제시하며 물리학계에서 활발한 논의를 촉발했다. - 물리학의 역설 - 올베르스의 역설
올베르스의 역설은 무한하고 균일한 우주에 무수히 많은 별이 존재할 경우 밤하늘이 밝아야 한다는 역설로, 우주의 유한성, 빛의 속도, 팽창, 적색편이 현상 등으로 해결된다. - 물리학의 역설 - 중력 특이점
중력 특이점은 일반 상대성이론에서 시공간이 정의되지 않고 물리량이 무한대로 발산하는 지점으로, 다양한 형태로 나타나며 이론에 따라 존재가 부정되거나 사건 지평선 뒤에 숨겨져 있다고 여겨지기도 하고 블랙홀의 엔트로피와 관련된 호킹 복사 이론과도 관련된다. - 특수 상대성이론 - 상대론적 양자화학
상대론적 양자화학은 상대성이론을 적용하여 원자와 분자의 구조 및 성질을 연구하는 화학 분야로, 특히 무거운 원소에서 전자의 속도가 빨라 상대론적 효과가 두드러지게 나타나 원자 크기, 결합 에너지, 스펙트럼 등에 영향을 미치며, 금의 색, 수은의 낮은 녹는점 등 여러 현상을 설명하는 데 필요하다. - 특수 상대성이론 - 동시성의 상대성
동시성의 상대성은 상대적으로 움직이는 기준계에서 공간적으로 분리된 두 사건의 시간 판단이 달라지는 현상으로, 아인슈타인의 특수 상대성 이론에서 절대적인 동시성이 존재하지 않음을 나타내는 핵심 개념이다.
| 쌍둥이 역설 | |
|---|---|
| 개요 | |
| 이름 | 쌍둥이 역설 |
| 유형 | 사고 실험 |
| 분야 | 특수 상대성 이론 |
| 관련 개념 | 시간 지연 길이 수축 동시성의 상대성 |
| 설명 | |
| 내용 | 특수 상대성 이론의 시간 지연 효과를 설명하는 사고 실험. 서로 다른 속도로 움직이는 두 쌍둥이의 시간 흐름이 다르게 나타나는 현상을 다룬다. 가속도의 영향으로 대칭성이 깨지면서 발생하는 시간 차이가 핵심이다. |
| 핵심 내용 | 시간 지연: 움직이는 관찰자에게는 시간이 느리게 흐르는 것처럼 보인다. 가속도의 중요성: 방향 전환 시 가속을 받는 쌍둥이에게 시간 차이가 발생한다. 대칭성 깨짐: 가속으로 인해 두 쌍둥이의 상황이 비대칭적으로 변한다. |
| 관련 인물 | |
| 주요 인물 | 앨버트 아인슈타인 폴 랑주뱅 |
| 문제점 및 해결 | |
| 역설의 이유 | 직관과 달리 상대성 이론에서는 시간이 절대적이지 않고 상대적으로 흐르기 때문에 발생한다. |
| 해결 방법 | 가속도를 고려한 분석을 통해 역설이 해소된다. 즉, 가속 운동을 하는 관찰자의 시간 흐름 변화를 정확하게 계산하면 모순이 발생하지 않는다. |
| 참고 문헌 | |
| 관련 서적 | The Modern Revolution in Physics: 현대 물리학 혁명 Modern Physics: 현대 물리학 From Special Relativity to Feynman Diagrams: A Course of Theoretical Particle Physics for Beginners: 특수 상대성 이론부터 파인만 다이어그램까지 Gravitation and Spacetime: 중력과 시공간 Foundations of Modern Cosmology: 현대 우주론의 기초 Albert Einstein's special theory of relativity. Emergence (1905) and early interpretation (1905–1911): 아인슈타인의 특수 상대성 이론 Concepts of Simultaneity: From Antiquity to Einstein and Beyond: 동시성의 개념 Gravity from the Ground Up: An Introductory Guide to Gravity and General Relativity: 중력 기초 |
| 외부 링크 | |
| 추가 정보 | Can Special Relativity Handle Acceleration?: 특수 상대성 이론은 가속도를 다룰 수 있는가? How does relativity theory resolve the Twin Paradox?: 상대성 이론은 쌍둥이 역설을 어떻게 해결하는가? Frequently Asked Questions About Special Relativity - The Twin Paradox: 특수 상대성 이론 FAQ - 쌍둥이 역설 |
2. 역사
알베르트 아인슈타인은 1905년 특수 상대성 이론을 발표하면서 쌍둥이 역설을 처음 제기했다. 그는 두 개의 시계를 A와 B 지점에 놓고, A 지점의 시계를 이동시켜 B 지점에 멈추면 A에서 이동한 시계가 B 지점의 시계보다 늦어진다고 설명했다. 아인슈타인은 이것을 역설이 아닌 특수 상대성 이론의 자연스러운 결과로 보았다.[16][65] 1911년, 아인슈타인은 이 결과를 다시 설명하며, 살아있는 유기체를 예로 들어 여행 후 돌아온 유기체는 거의 변화가 없는 반면, 원래 위치에 있던 유기체는 훨씬 늙어있을 것이라고 했다.[17][18][66][67]
스무 살 쌍둥이 A와 B 중 A는 우주선을 타고, B는 지구에 남는다고 가정하자. A가 우주여행을 마치고 돌아오면 B는 A보다 나이를 더 많이 먹게 된다. A의 관점에서는 B가 움직이는 것이므로 B의 시간이 느리게 가야 하지만, 실제로는 B가 더 늙는다.[68][69]
1911년 폴 랑주뱅은 여행자의 예를 들어 쌍둥이 역설을 설명했다. γ|γ영어 100 (광속의 99.995%)의 로렌츠 인자로 여행하는 여행자는 1년 후 지구로 돌아오면 2년 늙지만, 지구에서는 200년이 지나있다는 것이다. 랑주뱅은 여행자와 지구가 서로 신호를 주고받는 상황을 가정하여, 쌍둥이 역설의 도플러 효과 버전을 제시했다. 그는 여행자만 가속을 겪기 때문에 발생하는 비대칭성이 시간 차이의 원인이며, "속도의 모든 변화, 또는 모든 가속에는 절대적인 의미가 있다"고 주장했다.[19][20][21][68][69][70]
막스 폰 라우에는 헤르만 민코프스키의 시공간 개념을 사용하여 쌍둥이 역설을 설명했다. 그는 관성적으로 움직이는 물체의 세계선이 두 사건 사이의 고유 시간을 최대화한다는 것을 증명하고, 우주 비행사 쌍둥이는 두 개의 별도의 틀로 이동하는 반면, 지구 쌍둥이는 하나의 틀에 남아있다는 사실로 비대칭적인 노화가 설명된다고 썼다.[22][23][24][71][72][73] 핼즈베리 경 등은 가속도를 제거한 "세 형제" 방식을 제안했다. 여행하는 쌍둥이가 자신의 시계 값을 반대 방향으로 이동하는 세 번째 쌍둥이에게 전달하는 방식이다.[73]
아인슈타인과 랑주뱅은 이러한 결과를 문제라고 생각하지 않았다. 아인슈타인은 그것을 "특이하다"고 불렀고, 랑주뱅은 그것을 절대 가속의 결과로 제시했다.[25][74]
3. 쌍둥이 역설의 현상
알베르트 아인슈타인은 1905년에 발표한 특수 상대성 이론에 관한 논문에서 A점과 B점에 놓인 두 개의 정지된 동기화된 시계에 대해, A점의 시계를 직선 AB를 따라 움직여 B점에서 정지시키면, A점에서 이동한 시계는 B점의 시계보다 늦어질 것이라고 추론했다. 그는 이 결과가 A점에서 B점으로의 경로가 다각형 또는 원형인 경우에도 적용된다고 말했다.[65] 아인슈타인은 이것을 특수 상대성 이론의 자연스러운 귀결이며, 패러독스가 아니라고 생각했다.[66][67]
1911년, 폴 랑주뱅은 로렌츠 인자(광속의 99.995%)로 여행하는 여행자의 이야기를 "인상적인 예"로 들었다. 여행자는 1년 동안 발사체 안에 머물고, 그 후 방향을 반전한다. 귀환하면, 여행자는 2살 더 늙지만, 지구에서는 200년이 경과한다.
3. 1. 쌍둥이 역설의 해소
쌍둥이 역설은 특수 상대성 이론과 일반 상대성 이론을 통해 해소될 수 있다. 특수 상대성 이론에 따르면, 빠르게 움직이는 물체의 시간은 느리게 간다. 로런츠 변환에 의해, 지구에 있는 쌍둥이 B가 우주선을 타고 빠르게 이동하는 쌍둥이 A를 보면 A의 시간이 느리게 가는 것처럼 보인다.[65]
:
여기서 c는 광속이며,
:
이다.
그러나 A의 입장에서 보면 B가 움직이는 것이므로 B의 시간이 느리게 가야 한다. 이 역설은 A가 우주 여행 중 가속을 받기 때문에 발생한다. 즉, A와 B의 상황은 대칭적이지 않다.[68][69] 막스 폰 라우에는 헤르만 민코프스키의 시공간 개념을 사용하여, 관성 운동하는 물체의 세계선이 두 사건 사이의 고유 경과 시간을 최대화한다는 것을 증명하였다. 이를 통해 우주 비행사의 쌍둥이 A는 두 개의 서로 다른 관성계로 이동하는 반면, 지구의 쌍둥이 B는 하나의 관성계에 머무르기 때문에 비대칭적인 시간 지연이 발생함을 설명했다.[71][72][73]
알베르트 아인슈타인과 폴 랑주뱅은 이러한 시간 차이가 자기 모순을 일으키지 않는다고 보았다. 아인슈타인은 이를 "기묘"하다고 표현했지만, 랑주뱅은 절대적인 가속의 결과로 설명했다.[74]
3. 1. 1. [[세계선]]
B의 입장에서 B의 1년은 A의 0.6년과 같다. A가 떠난 지 1년 후 B가 '지금'을 생각했을 때, A도 '지금'이라고 생각하는 시점은 A가 떠난 지 0.6년이 되는 시점이다. 이 '지금'을 선으로 이은 것이 파란색 '''동시선'''이다.[1]
그런데 우주선이 방향을 바꾸는 지점에서 동시선의 방향도 바뀐다. 빨간색 선은 A가 지구로 향할 때의 동시선이다. 빨간색 선 중 가장 아래의 선과 파란색 선 중 가장 위의 선이 우주선이 방향을 트는 바로 그 점에서 만난다. 즉, A가 방향을 트는 순간, B의 시간은 '순간적으로' 많이 흘러가게 된다.[1]
3. 1. 2. 일반 상대성 이론의 관점
아인슈타인의 등가 원리에 따르면, 가속도는 중력과 동등하게 취급될 수 있다. 쌍둥이 역설에서 우주선이 방향을 바꾸는 순간 발생하는 "겉보기 중력" 때문에 A의 시간이 B보다 느리게 흘러간다.[7]
좀 더 구체적으로 설명하면, A가 방향을 바꾸는 순간 우주선에는 엄청난 가속이 일어난다. 관성력과 중력이 같다는 등가 원리에 의해 이 순간 우주선에는 엄청난 '겉보기 중력'이 발생한다고 볼 수 있다. 일반 상대성 이론에 따르면 중력이 강할수록 시간은 느려진다. 따라서 우주선이 방향을 바꾸는 순간 A의 시간은 B에 비해 매우 느리게 흘러가게 된다. 결과적으로 A는 B보다 젊은 상태로 지구에 귀환한다.[39]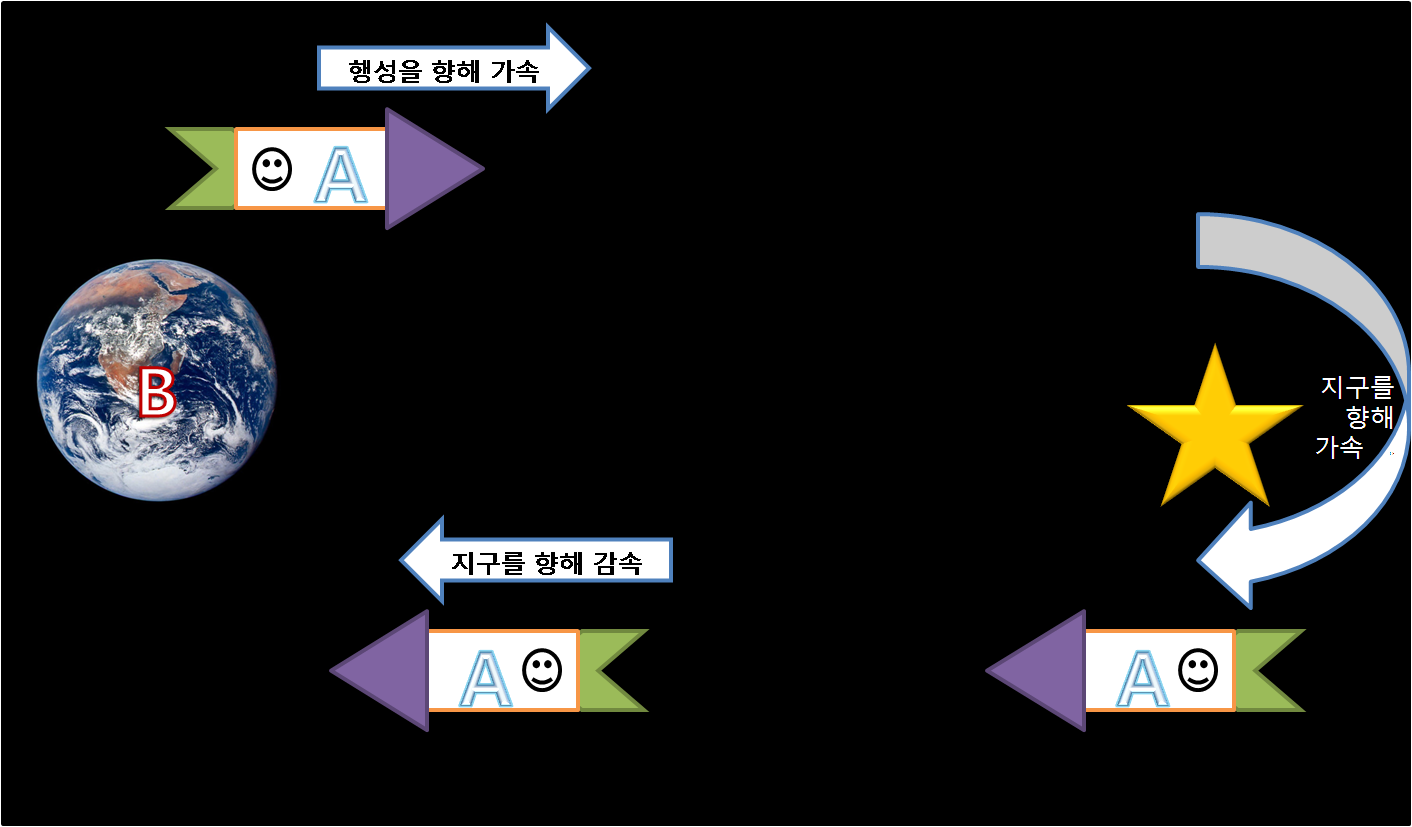
더 현실적인 상황을 고려하여 A의 여행을 세 구간으로 나누어 분석할 수 있다.
| 구간 | 설명 | 겉보기 중력 방향 | 시간 지연 |
|---|---|---|---|
| 1구간 | 지구 출발, 별을 향해 가속 | 지구 방향 | A의 시간이 B보다 느림 |
| 2구간 | 별을 향해 감속 (지구를 향해 가속) | 별 방향 | A의 시간이 B보다 느림 |
| 3구간 | 지구를 향해 감속 | 지구 방향 | A의 시간이 B보다 느림 |
위 표에서 볼 수 있듯이, A가 가속하는 모든 구간에서 겉보기 중력으로 인해 A의 시간은 B보다 느리게 흘러간다.
머무르는 쌍둥이의 시계를 앞당기는 메커니즘은 중력 시간 팽창이다. 관찰자가 관성적으로 움직이는 물체가 자신에 대해 가속되고 있음을 발견하면, 상대성 이론과 관련하여 그 물체는 중력장에 있는 것이다. 전환 시 여행하는 쌍둥이에게 이 중력장은 우주를 채운다. 약한 장 근사에서 시계는 의 속도로 째깍거리며, 여기서 는 중력 퍼텐셜의 차이이다. 이 경우, 이며, 여기서 는 전환 동안 여행하는 관찰자의 가속도이고 는 머무르는 쌍둥이까지의 거리이다. 로켓은 머무르는 쌍둥이 쪽으로 발사되어 그 쌍둥이를 더 높은 중력 퍼텐셜에 놓는다. 쌍둥이 간의 먼 거리 때문에, 머무르는 쌍둥이의 시계는 쌍둥이가 경험하는 고유 시간의 차이를 설명할 수 있을 만큼 충분히 빨라 보이는 것이다.[40]
3. 1. 3. 더 현실적인 가정
가속이 순간적이지 않은 좀 더 현실적인 상황을 위해, A가 여행하는 총 구간을 3개로 나눌 수 있다.- 로켓이 지구에서 출발하여 별을 향해 가속하는 구간 : 1구간
- 로켓이 별을 향해 감속하는 구간 = 지구를 향해 가속하는 구간 : 2구간
- 로켓이 지구를 향해 감속하는 구간 : 3구간
1구간에 있는 A는 가속 운동을 한다. 별을 향해 가속하고 있으므로 지구 방향으로 '겉보기 중력'이 생기고, 이 중력 때문에 A의 시간은 B보다 느려진다.[7][31]
2구간에 있을 때는 지구를 향해 가속하므로, 별 방향으로 겉보기 중력이 생긴다. 이 중력 때문에 역시 A의 시간은 B보다 느려진다.[7][31]
3구간에 있을 때도 1구간과 마찬가지로, 별 쪽으로 가속하는 운동을 하기 때문에 지구 방향으로 겉보기 중력이 생기며 A의 시간은 B보다 느려진다.[7][31]
따라서 A가 가속하는 동안 A의 시간은 B보다 내내 느리게 흘러가게 된다.
4. 특수 상대성 이론에서의 쌍둥이 역설 해소
상대성 원리에 따르면 모든 관성계는 동등하며, 쌍둥이 역설은 여행하는 쌍둥이(A)가 가속을 경험하여 관성계가 바뀌기 때문에 발생한다.[28][29][30]
알베르트 아인슈타인은 특수 상대성 이론 논문에서, 한 시계가 이동 후 멈추면 늦어진다는 결과를 예측했다.[16] 1911년, 아인슈타인은 이 결과를 다시 설명하며, 살아있는 유기체를 이용한 비유를 들었다. 그는 여행하는 유기체가 긴 비행 후 거의 변하지 않은 상태로 돌아올 수 있지만, 원래 위치에 있던 유기체는 이미 새로운 세대로 대체되었을 것이라고 설명했다.[17][18]
폴 랑주뱅은 로렌츠 인자가 ''γ''프랑스어 = 100 (광속의 99.995%)인 여행자의 이야기를 통해 쌍둥이 역설을 설명했다. 여행자는 1년 동안 발사체에 머물다가 방향을 바꾸는데, 돌아오면 2년이 늙었지만 지구에서는 200년이 지났다는 것을 발견한다. 랑주뱅은 여행자와 지구가 서로에게 일정한 속도로 신호를 계속 보내는 상황을 가정하여, 쌍둥이 역설의 도플러 효과 버전을 제시했다. 그는 신호 속도에 대한 상대론적 효과를 이용하여 다른 노화 속도를 설명하고, 여행자만 가속을 겪었기 때문에 발생하는 비대칭성을 강조했다.[19][20][21]
막스 폰 라우에는 헤르만 민코프스키의 시공간 형식을 사용하여 랑주뱅의 설명을 자세히 설명했다. 라우에는 관성적으로 움직이는 물체의 세계선이 두 사건 사이의 고유 시간을 최대화한다는 것을 증명했다. 그는 또한 우주 비행사 쌍둥이는 두 개의 별도의 틀로 이동하는 반면, 지구 쌍둥이는 하나의 틀에 남아 있다는 사실로 비대칭적인 노화가 완전히 설명된다고 썼다.[22][23][24]
아인슈타인과 랑주뱅은 이러한 결과를 문제라고 생각하지 않았다. 아인슈타인은 그것을 "특이하다"고 불렀고, 랑주뱅은 그것을 절대 가속의 결과로 제시했다.[25] 두 사람은 쌍둥이 이야기에서 예시된 시간 차이로부터 자기 모순을 구성할 수 없다고 주장했다.
4. 1. 가속도의 역할
가속도는 쌍둥이 역설에서 중요한 역할을 한다. 비록 가속도를 제거한 사고 실험에서도 시간 차이는 발생하지만, 가속도의 유무는 시간 차이의 크기에 영향을 미친다.[7][31]알베르트 아인슈타인은 1905년 특수 상대성 이론 논문에서 두 시계 중 한 시계가 이동 후 멈추면 늦어진다는 결과를 예측했고, 1911년에는 이를 쌍둥이에 비유하며 자세히 설명했다. 로버트 레스닉은 여행하는 쌍둥이가 돌아왔을 때 그의 쌍둥이 형이 자신보다 훨씬 늙었다는 것을 발견할 것이라고 언급하며, 아인슈타인의 예측을 뒷받침하는 실험이 수행되었다고 덧붙였다.[17][18]
폴 랑주뱅은 로렌츠 인자가 100 (빛의 속도의 99.995%)인 여행자의 이야기를 통해, 여행자가 2년 후 지구에서 200년이 지났음을 발견하는 예를 제시했다. 막스 폰 라우에는 헤르만 민코프스키의 시공간 형식을 사용하여 이를 설명했다.[19][20][21]
오른쪽 그림은 두 쌍둥이의 세계선을 나타낸다. B의 세계선은 ct축과 일치하고, A의 세계선은 >모양이다. A가 방향을 트는 순간, B의 시간은 '순간적으로' 엄청나게 흘러간다. 등가 원리에 따라, 이 순간 우주선에는 엄청난 '겉보기 중력'이 발생하고, 일반 상대성 이론에 의해 중력이 강할수록 시간은 느려진다. 즉, A의 시간은 B에 비해 아주 느리게 흘러가 A는 B보다 젊은 상태로 지구에 귀환한다.
더 현실적인 상황을 위해 A의 여행을 세 구간으로 나누면, 각 구간에서 A는 가속 운동을 하며 겉보기 중력의 영향으로 B보다 시간이 느리게 흘러간다.
일부 해결책에서는 회전 시 여행하는 쌍둥이의 가속도가 중요하다고 하지만,[7] 두 명의 여행자를 상정하여 시계를 동기화하는 경우에도 효과가 나타난다는 점을 지적한다. 이 버전에서는 여행하는 시계의 물리적 가속도는 직접적인 역할을 하지 않는다.[32][33][7] "문제는 세계선의 굽힘 정도가 아니라 그 길이이다".[34]
4. 2. 동시성의 상대성
동시성의 상대성에 따르면 서로 다른 관성 좌표계에서는 동시인 사건들이 다르게 정의된다. 이 때문에 여행하는 쌍둥이가 관성계를 바꿀 때, 지구에 있는 쌍둥이의 시간에 대한 불연속적인 점프가 발생한다.[7][35][36]오른쪽의 민코프스키 다이어그램에서 지구에 있는 쌍둥이(B)의 기준 좌표계는 수직축과 일치한다. 여행하는 쌍둥이(A)는 여행의 첫 번째 구간에서는 오른쪽으로, 두 번째 구간에서는 왼쪽으로 움직인다. 파란색 선은 A가 여행의 첫 번째 구간 동안의 '동시성 평면'을 나타내고, 빨간색 선은 두 번째 구간 동안의 동시성 평면을 나타낸다.
A가 회전하기 직전에 지구에 있는 B의 나이를 계산하면, 원점에서 위쪽 파란색 선까지의 수직축을 따라 간격을 측정한다. 회전 직후 다시 계산하면 원점에서 아래쪽 빨간색 선까지의 간격을 측정하게 된다. 즉, A가 U턴하는 동안 동시성 평면은 파란색에서 빨간색으로 점프하며, 지구에 있는 B의 세계선의 큰 부분을 빠르게 훑게 된다. 결과적으로 A가 출발하는 관성 좌표계에서 도착하는 관성 좌표계로 이동할 때, B의 나이에 불연속적인 점프가 발생하는 것이다. (위의 예시에서 6.4년).
4. 3. 비시공간적 접근
시공간 개념을 사용하지 않고도 쌍둥이 역설을 설명할 수 있다. 우주 비행사(출발 및 귀환)와 지구에 있는 관측자가 전파 신호(광속으로 이동)를 보내는 방식으로 시계 상태를 정기적으로 서로 업데이트하면, 모든 당사자는 "턴어라운드" 지점에서 시작하여 시간 기록의 비대칭성이 점진적으로 증가하는 것을 알 수 있다.[37] "턴어라운드" 전에 각 당사자는 상대방의 시계가 자신의 시계와 다른 방식으로 시간을 기록한다고 간주하지만, 기록된 차이는 두 당사자 간에 대칭적이다. "턴어라운드" 후 기록된 차이는 대칭적이지 않으며, 두 당사자가 재회할 때까지 비대칭성이 점진적으로 증가한다. 마침내 재회하면 이 비대칭성은 두 개의 재회한 시계에 표시되는 실제 차이에서 볼 수 있다.[37]5. 생물학적 노화와 시계 작동의 동등성
화학적 과정, 생물학적 과정, 측정 장치의 기능, 눈과 뇌를 포함하는 인간의 인식, 힘의 전달 등 모든 과정은 빛의 속도에 의해 제약된다. 모든 수준에서 빛의 속도와 원자 수준에서 발생하는 고유한 지연에 의존하는 시계 기능이 존재한다. 따라서 생물학적 노화는 시계 시간 측정과 전혀 다르지 않다.[38] 이는 생물학적 노화가 시계와 같은 방식으로 늦춰질 수 있다는 것을 의미한다.
6. 상대론적 도플러 효과
상대론적 도플러 효과를 통해 쌍둥이가 서로를 관찰할 때 시간 변화를 설명할 수 있다. 쌍둥이가 서로 멀어질 때는 적색 편이가 발생하여 시간이 느리게 가는 것처럼 관측된다. 반대로, 쌍둥이가 서로 가까워질 때는 청색 편이가 발생하여 시간이 빠르게 가는 것처럼 관측된다.
예를 들어, 스무 살 쌍둥이 A와 B 중 A가 0.8c의 속도로 16광년 떨어진 별로 우주여행을 떠나고 B는 지구에 남는 상황을 가정해 보자. 지구에 있는 B의 관점에서 보면, 왕복 여행에는 10년의 시간이 걸린다. 우주선 시계로 측정된 시간은 로렌츠 인자의 역수인 = 0.6만큼 감소한다. 따라서 여행자는 6년만 늙게 된다.
우주선 승무원(A)의 관점에서는 지구와 별 사이의 거리가 0.6 x 4 = 2.4 광년으로 길이 수축이 일어난다. 왕복 여행의 각 절반은 2.4 / 0.8 = 3년이 걸리므로, 총 6년이 걸린다. 결과적으로 여행을 마치고 돌아온 A는 6년, 지구에 남은 B는 10년 늙게 된다.
| 사건 | 지구 (년) | 우주선 (년) |
|---|---|---|
| 출발 | 0 | 0 |
| 왕복 여행 종료 = 귀환 여행 시작 | 5 | 3 |
| 도착 | 10 | 6 |
각 쌍둥이가 서로에게 자신의 모습을 담은 무선 신호를 주기적으로 보낸다고 가정하면, 다음과 같은 현상이 나타난다.
- 멀어질 때:
- 여행하는 쌍둥이(A)는 B의 시간이 정상 속도의 1/3배로 느리게 가는 것처럼 보인다.
- 지구에 있는 쌍둥이(B)는 9년 동안 우주선으로부터 송신기 주파수의 1/3배로 느려진 신호를 받는다.
- 정지 주파수 ''f''rest를 가진 소스에서 멀어질 때 관찰되는 주파수 ''f''obs는 상대론적 도플러 효과에 의해 다음과 같이 주어진다.
:
(''v''/''c'' = 0.8일 때, ''f''obs = (1/3)''f''rest)
- 가까워질 때:
- 여행하는 쌍둥이(A)는 귀환 여정 동안 지구 쌍둥이(B)의 시계가 평소보다 3배 빠르게 진행되는 것처럼 보인다.
- 지구에 있는 쌍둥이(B)는 우주선 귀환 여정이 시작된 후 1년 동안, 화면 속 A의 시계가 빠르게 가는것을 본다.
- 소스가 관찰자를 향해 이동할 때, 관찰되는 주파수는 청색 편이되어 더 높게 나타나며, 다음과 같이 주어진다.
:
(''v''/''c'' = 0.8일 때, ''f''obs = 3''f''rest)
이처럼 상대론적 도플러 효과를 고려하면 쌍둥이 역설에서 나타나는 시간 차이를 명확하게 설명할 수 있다.
6. 1. 도플러 이동 이미지의 비대칭성

왼쪽: 지구에서 우주선으로. 오른쪽: 우주선에서 지구로.
빨간색 선은 저주파 이미지가 수신됨을 나타내고, 파란색 선은 고주파 이미지가 수신됨을 나타낸다.
오른쪽의 ''x''–''t''(시공간) 다이어그램은 지구와 우주선 사이(첫 번째 다이어그램) 및 우주선과 지구 사이(두 번째 다이어그램)를 이동하는 빛 신호의 경로를 보여준다. 이러한 신호는 각 쌍둥이와 그의 나이 시계의 이미지를 다른 쌍둥이에게 전달한다.[7] 발신자의 입장에서 보면, 그는 자신의 시계에 따라 일정한 간격(예: 1시간마다)으로 이것들을 전송한다. 그러나 이러한 신호를 수신하는 쌍둥이의 시계에 따르면, 그들은 일정한 간격으로 수신되지 않는다.
우주선이 0.8''c''의 순항 속도에 도달하면, 각 쌍둥이는 다른 쌍둥이의 수신된 이미지에서 자신의 시간 3초마다 1초가 지나는 것을 보게 된다. 즉, 각자는 다른 시계의 이미지가 느리게 가는 것을 볼 것이고, 이는 단순히 인자 0.6으로 느린 것이 아니라, 빛의 시간 지연이 초당 0.8초씩 증가하기 때문에 더 느리게 나타난다. 이것은 그림에서 붉은색 빛 경로로 표시된다. 어느 시점에서, 각 쌍둥이가 자신의 시간 1초마다 이미지에서 3초가 지나는 것을 볼 수 있도록 각 쌍둥이가 수신하는 이미지가 변경된다. 즉, 수신된 신호는 도플러 이동에 의해 주파수가 증가했다. 이러한 고주파 이미지는 그림에서 파란색 빛 경로로 표시된다.
지구와 우주선의 비대칭성은 이 다이어그램에서 우주선이 더 많은 청색 편이(빠른 노화) 이미지를 수신한다는 사실로 나타난다. 다르게 말하면, 우주선은 여행의 중간 지점(회전 지점, 출발 후 3년)에서 이미지의 적색 편이(이미지의 느린 노화)에서 청색 편이(이미지의 더 빠른 노화)로 변화하는 것을 보며, 지구는 우주선의 이미지가 적색 편이에서 청색 편이로 9년 후에(우주선이 부재하는 기간의 거의 마지막에) 변화하는 것을 본다. 다음 섹션에서 이미지의 또 다른 비대칭성을 보게 될 것이다. 지구 쌍둥이는 적색 편이와 청색 편이 이미지에서 우주선 쌍둥이가 같은 양만큼 나이 드는 것을 보며, 우주선 쌍둥이는 적색 편이와 청색 편이 이미지에서 지구 쌍둥이가 서로 다른 양만큼 나이 드는 것을 본다.
6. 2. 도플러 다이어그램에서 경과 시간 계산
상대론적 도플러 효과를 고려하여 쌍둥이 역설에서 경과 시간을 계산할 수 있다. 각 쌍둥이가 서로에게 자신의 모습을 전송하는 상황을 가정해 보자.출발 직후, 여행하는 쌍둥이는 시간 지연 없이 지구에 있는 쌍둥이를 본다. 도착 시점에는, 우주선에 나타난 지구 쌍둥이의 모습은 발사 1년 후의 모습이다. 이는 지구에서 발사 1년 후의 전파가 4년 후에 별에 도착하여 우주선과 만나기 때문이다. 이 여행 동안, 여행하는 쌍둥이는 자신의 시계가 3년, 화면 속 시계가 1년 진행되는 것을 본다. 즉, 정상 속도의 1/3배로 진행되는 것처럼 보인다. 이는 움직임으로 인한 시간 팽창 효과(0.6의 인수로, 지구에서 5년은 우주선에서 3년)와 빛의 시간 지연 증가 효과(0에서 4년으로 증가)를 결합한 것이다.
정지 주파수 ''f''rest를 가진 소스에서 관찰되는 시계 틱(또는 파면)의 주파수는 소스가 멀어지고 있을 때 다음과 같다.
:
''v''/''c'' = 0.8일 때, ''f''obs = (1/3)''f''rest이다. 이를 상대론적 도플러 효과라고 한다.
지구에 있는 쌍둥이는 9년 동안 우주선으로부터 송신기 주파수의 1/3배로 느려진 신호를 받는다. 이 9년 동안, 화면 속 여행하는 쌍둥이의 시계는 3년 진행된 것으로 보인다. 따라서 두 쌍둥이 모두 자신의 속도보다 1/3배 느린 속도로 형제의 나이가 드는 모습을 보게 된다.
우주선이 지구로 돌아올 때, 지구에 있는 쌍둥이의 시계는 우주선 화면에 "발사 1년 후"를 보여주고, 돌아오는 3년 동안 "발사 10년 후"까지 증가한다. 따라서 화면 속 시계가 평소보다 3배 빠르게 진행되는 것처럼 보인다.
소스가 관찰자를 향해 이동할 때, 관찰되는 주파수는 더 높고("청색 편이") 다음과 같다.
:
''v''/''c'' = 0.8일 때, ''f''obs = 3''f''rest이다.
지구의 화면은 발사 9년 후에 시작되는 귀환 여정을 보여주고, 화면 속 여행하는 시계는 우주선에서 3년이 지났다는 것을 보여준다. 1년 후, 우주선이 집에 도착하고 시계는 6년을 보여준다. 따라서 돌아오는 동안, 두 쌍둥이 모두 형제의 시계가 자신의 시계보다 3배 빠르게 가는 것을 본다.
위의 ''x''–''t''(시공간) 다이어그램은 지구와 우주선 사이(첫 번째 다이어그램) 및 우주선과 지구 사이(두 번째 다이어그램)를 이동하는 빛 신호의 경로를 보여준다.
우주선이 0.8''c''의 순항 속도에 도달하면, 각 쌍둥이는 다른 쌍둥이의 수신된 이미지에서 자신의 시간 3초마다 1초가 지나는 것을 보게 된다. 어느 시점에서, 각 쌍둥이가 자신의 시간 1초마다 이미지에서 3초가 지나는 것을 볼 수 있도록 각 쌍둥이가 수신하는 이미지가 변경된다. 즉, 수신된 신호는 도플러 이동에 의해 주파수가 증가했다.
우주선을 탄 쌍둥이는 3년 동안 저주파수(적색) 영상을 보게 되고, 그 동안 지구에 있는 쌍둥이가 영상 속에서 1년 늙는 것을 보게 된다. 그런 다음 3년 동안의 귀환 여정 동안 고주파수(청색) 영상을 보게 되고, 그 동안 지구에 있는 쌍둥이가 영상 속에서 9년 늙는 것을 보게 된다. 여행이 끝나면 지구에 있는 쌍둥이의 영상은 10년 늙어 있다.
지구에 있는 쌍둥이는 9년 동안 느린(적색) 영상의 우주선 쌍둥이를 보게 되는데, 그 동안 우주선 쌍둥이는 (영상에서) 3년 늙는다. 그런 다음 우주선이 돌아올 때까지 남은 1년 동안 빠른(청색) 영상을 보게 된다. 빠른 영상에서 우주선 쌍둥이는 3년 늙는다. 지구에 의해 수신된 영상에서 우주선 쌍둥이의 총 노화는 6년이므로, 우주선 쌍둥이는 더 젊게 돌아온다(지구에서 10년에 비해 6년).
6. 3. 보이는 것과 계산하는 것의 차이
쌍둥이 역설에서 각 쌍둥이가 보는 것과 실제 시간 변화를 계산하는 것은 구분해야 한다. 상대론적 도플러 효과를 고려하여 실제 시간 변화를 계산해야 한다.출발 직후, 여행하는 쌍둥이는 시간 지연 없이 집에 있는 쌍둥이를 본다. 하지만 도착 시점에는 지구에서 발사 1년 후의 모습이 보이는데, 이는 빛의 속도로 인해 신호가 도달하는 데 시간이 걸리기 때문이다. 이 동안 여행하는 쌍둥이는 자신의 시계가 3년, 지구에 있는 쌍둥이의 시계가 1년 흐른 것을 보게 된다. 즉, 지구에 있는 쌍둥이의 시간이 자신의 시간보다 1/3배 느리게 가는 것처럼 보인다.
집에 있는 쌍둥이 역시 우주선에서 보내는 신호를 받는데, 9년 동안은 우주선 시계가 1/3배 느리게 가는 것으로 보인다. 두 쌍둥이 모두 상대방의 시계가 자신의 시계보다 느리게 간다고 인식하지만, 빛의 지연 시간을 고려하면 실제로는 서로가 서로의 시간보다 60% 느리게 늙고 있다고 계산하게 된다.
우주선이 돌아올 때는 상황이 반전된다. 집에 있는 쌍둥이의 시계는 우주선 화면에 3배 빠르게 가는 것처럼 나타난다. 지구에서 보는 화면에서는 발사 9년 후부터 귀환 여정이 시작되고, 우주선 시계는 3년이 지난 것으로 나타난다. 1년 후 우주선이 도착하면 시계는 6년을 가리킨다. 즉, 돌아오는 동안에는 서로의 시계가 3배 빠르게 가는 것으로 보인다. 빛의 지연 시간 감소를 고려하면, 각 쌍둥이는 상대방이 자신의 60% 속도로 늙는다고 계산한다.
혼동을 피하기 위해, 각 쌍둥이가 보는 것과 계산하는 것을 구분해야 한다. 각자는 상대방의 이미지를 보고, 그 이미지가 과거의 것이며 도플러 효과의 영향을 받았음을 인지한다. 이미지 속 시간은 현재 상대방의 나이가 아니다.
상대방의 나이를 계산하려면, 신호가 방출된 시점의 거리, 즉 동시성을 고려해야 한다. 상대방의 노화 속도를 계산하려면, 도플러 효과를 보정해야 한다. 예를 들어, 고주파 이미지(상대방이 빠르게 늙는 모습)를 받았다면, 이미지 생성 시점에 상대방이 실제로 그렇게 빨리 늙은 것이 아니다. 도플러 효과로 인해 주파수가 증가했음을 고려하여, 실제 노화 속도를 계산해야 한다.
6. 4. 도플러 이동 계산에서의 동시성
쌍둥이 사이의 시간 차이가 어떻게 발생하는지 이해하려면, 특수 상대성 이론에는 '절대적인 현재'라는 개념이 없다는 것을 알아야 한다. 서로 다른 관성 좌표계에서는 동시에 일어나는 사건들이 다를 수 있다. 이러한 동시성의 상대성 때문에 한 관성 좌표계에서 다른 관성 좌표계로 바뀔 때, "현재"로 간주되는 시공간 단면에 대한 조정이 필요하다.
오른쪽 시공간 다이어그램에서 지구에 있는 쌍둥이의 기준 좌표계에서 보면, 쌍둥이의 세계선은 수직축과 일치한다(위치는 공간에서 일정하며 시간만 흐른다). 여행하는 쌍둥이는 여행의 첫 번째 구간에서는 오른쪽으로(검은색 기울어진 선), 두 번째 구간에서는 왼쪽으로 움직인다. 파란색 선은 여행하는 쌍둥이가 여행의 첫 번째 구간 동안의 '동시성 평면'을, 빨간색 선은 두 번째 구간 동안의 동시성 평면을 나타낸다. 회전 직전, 여행하는 쌍둥이는 지구 쌍둥이의 나이를 계산할 때 원점에서 위쪽 파란색 선까지의 간격을 측정한다. 회전 직후에는 원점에서 아래쪽 빨간색 선까지의 간격을 측정한다. 즉, U턴하는 동안 동시성 평면이 파란색에서 빨간색으로 점프하여 지구 쌍둥이의 세계선의 큰 부분을 빠르게 훑는다. 출발하는 관성 좌표계에서 도착하는 관성 좌표계로 이동할 때 지구에 있는 쌍둥이의 나이에 불연속적인 점프가 발생한다.[7][35][36]
아인슈타인의 시계 동기화(시계 격자) 대신, 우주 비행사와 지구에 있는 쪽이 전파 신호(광속으로 이동)를 보내 서로 시계 상태를 정기적으로 업데이트하면, "턴어라운드" 지점에서 시간 기록의 비대칭성이 점진적으로 증가하는 것을 알 수 있다. "턴어라운드" 전에는 각자 상대방의 시계가 다르게 시간을 기록한다고 보지만, 그 차이는 대칭적이다. "턴어라운드" 후에는 차이가 대칭적이지 않고, 재회할 때까지 비대칭성이 점진적으로 증가한다. 이 비대칭성은 재회했을 때 두 시계에 표시되는 실제 차이에서 확인할 수 있다.[37]
공간의 서로 다른 위치에서 발생하는 사건들의 동시성은 프레임에 따라 달라지기 때문에, 각 쌍둥이가 송신자의 시계에 따라 시간 간격이 동일하게 유지된 일련의 정기적인 무선 펄스를 보내는 경우를 생각하는 것이 더 현상학적이다.[7] 이것은 각 쌍둥이가 서로에게 자신의 모습을 비디오로 전송하는 경우와 같다.
상대론적 도플러 효과에 따르면, 정지 주파수 ''f''rest를 가진 소스에서 멀어질 때 관찰되는 주파수 ''f''obs는 다음과 같다.
:
소스가 관찰자를 향해 이동할 때는 다음과 같다.
:
thumb
''x''–''t''(시공간) 다이어그램은 지구와 우주선 사이(첫 번째 다이어그램) 및 우주선과 지구 사이(두 번째 다이어그램)를 이동하는 빛 신호의 경로를 보여준다. 발신자는 자신의 시계에 따라 일정한 간격으로 신호를 보내지만, 수신하는 쌍둥이의 시계에서는 일정한 간격으로 수신되지 않는다.
우주선이 순항 속도에 도달하면, 각 쌍둥이는 다른 쌍둥이의 수신된 이미지에서 자신의 시간 3초마다 1초가 지나는 것을 본다(빛의 시간 지연 증가). 어느 시점에서, 각 쌍둥이가 자신의 시간 1초마다 이미지에서 3초가 지나는 것을 보도록 이미지가 변경된다(도플러 이동으로 주파수 증가).
도플러 이동 계산에서 동시성을 고려해야 하는 이유는, 우주선 쌍둥이가 수신된 도플러 이동 속도를 먼 시계의 느린 속도로 변환할 때, 동시성을 무시하면 오차가 발생하기 때문이다. 그는 이미지에 대해 계산할 수 있는 속도는 지구 쌍둥이의 시계가 이미지를 보낸 순간의 속도이지, 이미지를 수신한 순간의 속도가 아니다. 불균등한 수의 적색 및 청색 이동 이미지를 수신하므로, 적색 및 청색 이동 방출이 지구 쌍둥이에게 동일한 시간 동안 방출되지 않았음을 깨달아야 하며, 따라서 거리의 동시성을 고려해야 한다.
7. 여행하는 쌍둥이의 관점
전환하는 동안, 여행하는 쌍둥이는 가속 좌표계에 있게 된다. 등가 원리에 따르면, 여행자는 머무르는 쌍둥이가 중력 시간 팽창에 의해 중력장에서 자유 낙하하고 여행자는 정지해 있는 것처럼 전환 단계를 분석할 수 있다.[39] 여행자의 관점에서 전환을 무시하고 각 다리에 대한 별도의 계산을 수행하면 지구 시계가 여행자보다 덜 늙는 결과가 나온다. 예를 들어, 지구 시계가 각 다리에서 1일 덜 늙는다면, 지구 시계가 뒤쳐지는 양은 2일이 된다. 전환 시에 일어나는 일에 대한 물리적 설명은 그 두 배인 4일 동안 지구 시계를 앞당기는 반대 효과를 만들어야 한다. 그러면 여행자의 시계는 머무르는 쌍둥이의 좌표계에서 수행된 계산과 일치하여 총 2일 늦어진다.
머무르는 쌍둥이의 시계를 앞당기는 메커니즘은 중력 시간 팽창이다. 관찰자가 관성적으로 움직이는 물체가 자신에 대해 가속되고 있음을 발견하면, 상대성 이론과 관련하여 그 물체는 중력장에 있는 것이다. 전환 시 여행하는 쌍둥이에게 이 중력장은 우주를 채운다. 약한 장 근사에서 시계는 의 속도로 째깍거리며, 여기서 는 중력 퍼텐셜의 차이이다. 이 경우, 이며, 여기서 ''g''는 전환 동안 여행하는 관찰자의 가속도이고 ''h''는 머무르는 쌍둥이까지의 거리이다. 로켓은 머무르는 쌍둥이 쪽으로 발사되어 그 쌍둥이를 더 높은 중력 퍼텐셜에 놓는다. 쌍둥이 간의 먼 거리 때문에, 머무르는 쌍둥이의 시계는 쌍둥이가 경험하는 고유 시간의 차이를 설명할 수 있을 만큼 충분히 빨라 보이는 것이다. 이 속도 증가가 위에서 설명한 동시성 이동을 설명하기에 충분하다.[40]
8. 시공간 경로 차이에 따른 경과 시간 차이
고유 시간 적분을 통해 시간 차이를 정량화할 수 있다.
시계 ''K''를 "집에 머무는 쌍둥이"와 연관시키고, 시계 K'를 여행을 가는 로켓과 연관시킨다. 출발 시점에 두 시계는 모두 0으로 설정된다.
로켓의 총 누적 고유 시간 Δ''τ''는 좌표 시간 Δ''t''의 적분 함수로 주어진다.
:
여기서 ''v''(''t'')는 시계 ''K''에 따라 ''t''의 함수로 된 시계 K'의 ''좌표 속도''이다.
이 적분은 6단계에 대해 계산할 수 있다:[42]
:1단계
:2단계
:3단계
:4단계
:5단계
:6단계
여기서 ''a''는 가속 단계 동안 시계 K'가 느끼는 고유 가속도이며, ''V'', ''a'' 및 ''T''a 사이에는 다음 관계가 성립한다.
:
:
따라서 여행하는 시계 K'는 경과 시간을 다음과 같이 나타낸다.
:
이는 다음과 같이 표현할 수 있다.
:
반면 정지 시계 ''K''는 경과 시간을 다음과 같이 나타낸다.
:
이는 ''a'', ''T''a, ''T''c 및 ''V''의 모든 가능한 값에 대해 시계 K'의 판독값보다 크다.
:
표준 고유 시간 공식에서
:
Δ''τ''는 비관성 (이동하는) 관찰자 K'의 시간을 나타내며, 관성 (집에 머무르는) 관찰자 ''K''의 경과 시간 Δ''t''의 함수이며, 관찰자 K'는 시간 ''t''에서 속도 ''v''(''t'')를 갖는다.
비관성 관찰자 K'가 측정한 양만 사용할 수 있는 경우, 관성 관찰자 ''K''의 경과 시간 Δ''t''를 비관성 관찰자 K'의 경과 시간 Δ''τ''의 함수로 계산하려면 다음 공식을 사용할 수 있다:[43]
:
여기서 ''a(τ)''는 왕복 여행 전체에서 비관성 관찰자 K'가 측정한 (예: 가속도계를 사용하여) 고유 가속도이다. 코시-슈바르츠 부등식을 사용하여 부등식 Δ''t'' > Δ''τ''가 이전 표현에서 따르는 것을 보일 수 있다.
:
가속된 관찰자 K'가 초기 속도가 0인 ''K''에서 출발하는 경우, 일반 방정식은 더 간단한 형태로 축소된다.
:
이는 여행자가 일정한 고유 가속도 단계를 갖는 쌍둥이 역설의 ''매끄러운'' 버전에서 순차적으로 ''a'', −''a'', −''a'', ''a''로 제공되며, 결과는[7]
:
여기서 ''c'' = 1의 관례가 사용되며, 이는 가속도 단계 Δ''t''/4 및 관성 (관성 주행) 단계 0을 갖는 위의 표현식과 일치한다.
9. 우주선에서 경과 시간 계산 방법
Inertial frame of reference영어 관찰자 K의 경과 시간 Δt를 고유 가속도를 이용하여 계산할 수 있다. 시계 ''K''를 "집에 머무는 쌍둥이"와 연관시키고, 시계 K'를 여행을 가는 로켓과 연관시킨다. 출발 시점에 두 시계 모두 0으로 설정한다.
로켓의 이동은 다음과 같이 6단계로 나눌 수 있다.
| 단계 | 설명 |
|---|---|
| 1단계 | 로켓(시계 K/var> 포함)이 시계 K로 측정했을 때 시간 Ta 동안 일정한 고유 가속도 a로 출발하여 속도 V''에 도달한다. |
| 2단계 | 로켓은 시계 K에 따라 시간 Tc 동안 속도 V로 계속 항해한다. |
| 3단계 | 로켓은 시계 K에 따라 시간 Ta 동안 K의 반대 방향으로 엔진을 작동하여 시계 K에 대해 정지한다. 일정한 고유 가속도는 −a의 값을 갖는다. 즉, 로켓은 감속하고 있다. |
| 4단계 | 로켓은 시계 K에 따라 동일한 시간 Ta 동안 K의 반대 방향으로 계속 엔진을 작동하여 K/var>가 다시 K에 대해 동일한 속도 V를 회복하지만 이제 K를 향한다(속도 −V''로). |
| 5단계 | 로켓은 시계 K에 따라 동일한 시간 Tc 동안 속도 V로 K를 향해 계속 항해한다. |
| 6단계 | 로켓은 다시 K의 방향으로 엔진을 작동하여 시계 K에 따라 시간 Ta 동안 일정한 고유 가속도 a로 감속하여 두 시계가 다시 만난다. |
시계 ''K''가 관성적(정지) 상태를 유지한다는 것을 알고, 시계 K'의 총 누적 고유 시간 Δ''τ''는 좌표 시간 Δ''t''의 적분 함수로 주어진다.[42]
:
여기서 ''v''(''t'')는 시계 ''K''에 따라 ''t''의 함수로 된 시계 K'의 ''좌표 속도''이며, 예를 들어 1단계에서 다음과 같이 주어진다.
:
이 적분은 6단계에 대해 계산할 수 있다.[42]
| 단계 | 식 |
|---|---|
| 1단계 | |
| 2단계 | |
| 3단계 | |
| 4단계 | |
| 5단계 | |
| 6단계 |
여기서 ''a''는 가속 단계 동안 시계 K'가 느끼는 고유 가속도이며, ''V'', ''a'' 및 ''T''a 사이에는 다음 관계가 성립한다.
:
:
따라서 여행하는 시계 K'는 경과 시간을 다음과 같이 나타낸다.
:
이는 다음과 같이 표현할 수 있다.
:
반면 정지 시계 ''K''는 경과 시간을 다음과 같이 나타낸다.
:
이는 ''a'', ''T''a, ''T''c 및 ''V''의 모든 가능한 값에 대해 시계 K'의 판독값보다 크다.
:
표준 고유 시간 공식은 다음과 같다.
:
Δ''τ''는 비관성 (이동하는) 관찰자 K'의 시간을 나타내며, 관성 (집에 머무르는) 관찰자 ''K''의 경과 시간 Δ''t''의 함수이며, 관찰자 K'는 시간 ''t''에서 속도 ''v''(''t'')를 갖는다.
비관성 관찰자 K'가 측정한 양만 사용할 수 있는 경우, 관성 관찰자 ''K''의 경과 시간 Δ''t''를 비관성 관찰자 K'의 경과 시간 Δ''τ''의 함수로 계산하려면 다음 공식을 사용할 수 있다.[43]
:
여기서 ''a(τ)''는 왕복 여행 전체에서 비관성 관찰자 K'가 측정한 (예: 가속도계를 사용하여) 고유 가속도이다. 코시-슈바르츠 부등식을 사용하면 다음 부등식이 성립함을 보일 수 있다.
:
여행자가 왕복 여행 동안 일정한 속도 ''v''를 갖는 표준 경우에 무한 가속도 단계를 모델링하기 위해 디랙 델타 함수를 사용하면, 다음 결과가 생성된다.
:
가속된 관찰자 K'가 초기 속도가 0인 ''K''에서 출발하는 경우, 일반 방정식은 더 간단한 형태로 축소된다.
:
이는 여행자가 일정한 고유 가속도 단계를 갖는 쌍둥이 역설의 ''매끄러운'' 버전에서 순차적으로 ''a'', −''a'', −''a'', ''a''로 제공되며, 다음 결과가 나온다.[7]
:
여기서 ''c'' = 1의 관례가 사용되며, 이는 가속도 단계 및 관성 (관성 주행) 단계를 갖는 위의 표현식과 일치한다.
10. 회전하는 버전
밥과 앨리스는 거대한 천체를 원형 궤도로 공전하는 우주 정거장에 탑승하고 있다. 밥은 우주복을 입고 정거장 밖으로 나간다. 앨리스는 이전처럼 정거장 내부에 남아 계속 궤도를 따라 공전하고, 밥은 로켓 추진 시스템을 사용하여 공전을 멈추고 자신이 있던 자리에서 정지한다. 정거장이 한 바퀴를 돌아 밥에게 돌아오면 그는 앨리스와 재회한다. 앨리스는 밥보다 젊어졌다.[44] 회전 가속도 외에도 밥은 정지하기 위해 감속한 다음 다시 가속하여 우주 정거장의 궤도 속도에 맞춰야 한다.
11. 절대 기준틀에서의 쌍둥이 역설
알베르트 아인슈타인은 1905년 특수 상대성 이론에 관한 논문에서 두 개의 시계를 A와 B 지점에 놓고, A 지점의 시계를 이동시켜 B 지점에 멈추면 A에서 이동한 시계가 B 지점의 시계보다 늦어진다고 추론했다. 그는 이 결과가 A에서 B까지의 경로가 다각형이거나 원형인 경우에도 적용된다고 말했다.[16] 1911년, 폴 랑주뱅은 빛의 속도의 99.995%에 해당하는 로렌츠 인자로 여행하는 여행자의 이야기를 통해 "두드러진 예"를 제시했다. 여행자는 자신의 시간으로 1년 동안 발사체에 머물다가 방향을 바꾸는데, 돌아오면 지구에서는 200년이 지났다는 것을 발견하게 된다. 랑주뱅은 신호 속도에 대한 상대론적 효과를 통해 서로 다른 노화 속도를 설명하고, 여행자만 가속을 겪었기 때문에 발생한 비대칭성은 "속도의 모든 변화, 또는 모든 가속에는 절대적인 의미가 있다"는 사실로 설명했다.[19][20][21]
막스 폰 라우에는 헤르만 민코프스키의 시공간 형식을 사용하여 관성적으로 움직이는 물체의 세계선이 두 사건 사이의 고유 시간을 최대화한다는 것을 증명했다. 또한 비대칭적인 노화는 우주 비행사 쌍둥이는 두 개의 별도의 틀로 이동하는 반면, 지구 쌍둥이는 하나의 틀에 남아 있고, 가속 시간은 관성 좌표계의 시간에 비해 임의로 작게 만들 수 있다는 사실로 설명된다고 썼다.[22][23][24]
아인슈타인과 랑주뱅은 이러한 결과를 문제라고 생각하지 않았다. 아인슈타인은 그것을 "특이하다"고 불렀고 랑주뱅은 그것을 절대 가속의 결과로 제시했다.[25] 아인슈타인이나 랑주뱅은 쌍둥이 이야기를 상대론적 물리학의 자기 일관성에 대한 도전으로 보지 않았다. 아인슈타인의 결론은 폴 랑제뱅이 실제적이지만 실험적으로 구별할 수 없는 절대적 기준 틀을 가정하게 만들었다.
1911년, 랑제뱅은 "에테르 내에서의 균일한 이동은 실험적인 의미가 없다. 그러나 이 때문에 에테르의 개념을 포기해야 한다거나, 에테르가 존재하지 않으며 실험적으로 접근할 수 없다고 성급하게 결론내려서는 안 된다. 에테르에 대한 균일한 속도만이 감지될 수 없을 뿐이며, 속도의 변화는... 절대적인 의미를 가진다."라고 썼다.[45]
1913년, 앙리 푸앵카레는 사후 출판된 ''최후의 에세이''에서 "오늘날 일부 물리학자들은 새로운 관례를 채택하려 한다. 그들이 그렇게 해야만 하는 것은 아니며, 이 새로운 관례가 더 편리하다고 생각할 뿐이다. 그것이 전부이다. 그리고 이러한 의견에 동의하지 않는 사람들은 정당하게 옛것을 유지할 수 있다."라며 자신의 입장을 재확인했다.[46]
절대적인 기준 틀을 가정하는 푸앵카레와 헨드릭 로렌츠의 상대성 이론에서는 시계 늦어짐이 현실로 간주되기 때문에, 재회한 시계들 사이의 실제적인 시간 차이로 인해 역설이 발생하지 않는다. 이 해석에서, 우주 전체에 정지해 있는 당사자는 최대의 시간 측정 속도를 가지며 수축되지 않은 길이를 가질 것이다. 존 A. 휠러가 "에테르 이론 B(길이 수축 플러스 시간 수축)"라고 부르는 상대성 이론의 그러한 해석은, 관성 기준 틀 전체에서 대칭적인 측정 뒤에 숨겨진 더 깊은 현실을 단순히 무시한 아인슈타인의 해석만큼 큰 지지를 얻지 못했다. 어느 해석이 다른 해석과 구별되는지를 보여주는 물리적 실험은 없다.[47]
2005년, 로버트 B. 라플린(스탠포드 대학교 물리학 노벨상 수상자)은 공간의 본질에 대해 다음과 같이 썼다: "아인슈타인의 가장 창의적인 작품인 일반 상대성 이론이, 그의 원래 전제[특수 상대성 이론에서]가 그러한 매질이 존재하지 않는다는 것이었음에도 불구하고, 공간을 매질로 개념화하는 것으로 귀결된다는 것은 아이러니하다... '에테르'라는 단어는... 이론 물리학에서 극도로 부정적인 의미를 갖는다. 이는 불행한 일이다... 상대성 이론은 실제로 우주에 스며들어 있는 물질의 존재 여부에 대해 아무것도 말하지 않으며, 그러한 물질은 상대론적 대칭성을 가져야 한다는 것만을 말한다."[48]
''특수 상대성 이론''(1968)에서 A. P. 프렌치는 "우리는 A의 가속도의 현실과, 그것과 관련된 관성력의 관측 가능성에 호소하고 있음을 주목하라. 만약 고정된 별과 멀리 떨어진 은하들의 틀이 존재하지 않는다면, 쌍둥이 역설...과 같은 효과가 존재할까? 대부분의 물리학자들은 그렇지 않다고 말할 것이다. 우리의 궁극적인 관성 기준 틀의 정의는, 실제로 그것이 광대한 우주의 물질에 대해 0의 가속도를 갖는 틀일 수 있다."라고 썼다.[49]
12. 오해
알베르트 아인슈타인은 1905년에 발표한 특수 상대성 이론에 관한 논문에서 두 시계에 대해 언급하며, A점의 시계를 B점으로 이동시키면 B점의 시계보다 늦어진다고 설명했다. 그는 이것이 패러독스가 아닌 특수 상대성 이론의 자연스러운 결과라고 생각했다.[65] 1911년, 아인슈타인은 이 결과를 다시 설명하며, 이동하는 생물은 긴 여행 후에도 거의 변화가 없지만, 정지해 있던 생물은 새로운 세대로 대체되었을 것이라고 말했다.[66][67]
폴 랑주뱅은 1911년에 로렌츠 인자(광속의 99.995%)로 여행하는 여행자의 예를 들어, 여행자가 1년 후 지구로 돌아오면 2살 더 늙지만 지구에서는 200년이 경과한다고 설명했다. 랑주뱅은 여행자와 지구가 일정한 비율로 신호를 주고받는다는 점을 이용해, 쌍둥이 역설의 도플러 이동 버전을 제시했다. 그는 여행자만 가속을 받았기 때문에 비대칭성이 발생하며, "속도의 변화, 또는 가속에는 절대적인 의미가 있기" 때문에 차이가 발생한다고 설명했다.[68][69][70]
막스 폰 라우에는 1911년과 1913년에 랑주뱅의 설명을 자세히 설명하며, 헤르만 민코프스키의 시공간 형식론을 사용하여 관성 운동하는 물체의 세계선이 두 사건 간의 고유 경과 시간을 최대화함을 증명했다. 그는 우주 비행사의 쌍둥이가 두 개의 별도 프레임으로 이동하는 반면, 지구의 쌍둥이는 하나의 프레임에 머무르기 때문에 비대칭적 노화가 발생하며, 가속 시간은 관성 운동 시간에 비해 임의로 작게 만들 수 있다고 설명했다.[71][72][73]
이러한 결과에 대해 아인슈타인과 랑주뱅은 문제 삼지 않았고, 시간차로부터 자기 모순을 구축할 수 없다고 주장했다.[74]
다음은 상대론과 관련된 역설로, "쌍둥이 역설"로 오해되는 경우이다.
- 로켓을 탄 형이 더 늙기 어렵게 된다(우라시마 효과).
- 형이 탄 로켓이 관성 운동을 할 때, 동생의 시점에서는 형이 더 늙기 어렵게 보이고, 형의 시점에서는 동생이 더 늙기 어렵게 보인다.
하지만, 쌍둥이 역설은 '''광속에 가까운 속도'''로 움직인 형이 동생에게 돌아왔을 때 발생하는 현상을 말하며, '''광속에 가까운 속도가 아니면 쌍둥이 역설이 일어나지 않는다는 오해'''를 불러일으키기 쉽다. 형이 동생으로부터 멀어지기만 하면 형이 동생보다 젊어지지만, 시간 지연은 로켓 속도가 광속보다 훨씬 느릴 경우 미미해진다.
특수 상대성 이론에서도 가속도를 가진 대상을 미소 구간으로 나누어 일정한 속도로 취급하면 다룰 수 있다. 이 역설의 본질은 형이 관측자일 때, 도중에 형이 가속도를 가지게 된다는 점이다.
13. 구체적인 예시
이제 막 스무 살이 된 쌍둥이 A와 B가 있다고 가정하자. A는 v=0.8c영어인 속도, 즉 빛의 속도의 80%로 날아가는 우주선을 타고 16광년 떨어진 별로 향하고, B는 지구에 남는다. A가 별에 도착했을 때, B는 20살을 더 먹지만, B가 보았을 때 A의 시계는 12년밖에 흐르지 않는다. A가 다시 지구로 돌아올 때도 마찬가지로, B에게는 20년의 시간이 흐르지만 B가 볼 때는 A가 12년밖에 걸리지 않은 것으로 보인다. 이는 특수 상대성 이론에 따른 당연한 현상이다.[7]
하지만 A가 정지해 있고 B가 v영어의 속도로 멀어지는 상황이라고 생각하면, A는 40년이 지나 60살이 되지만 B는 44살이 된다. 반대로 B의 입장에서는 자신이 60살인데 A는 44살밖에 되지 않는다.
결론적으로 B의 입장에서 본 결과만 옳게 된다. 즉, A가 젊은 채로 지구로 귀환한다.[7]
좀 더 구체적인 예시로, 지구에서 4광년 떨어진 가장 가까운 별까지 v = 0.8c영어의 속도로 여행하는 우주선을 생각해 보자.[26][27]
계산을 쉽게 하기 위해, 우주선은 출발 시 아주 짧은 시간에 최대 속도에 도달하고, 왕복 여행의 끝에서 방향 전환도 아주 짧은 시간에 이루어진다고 가정한다.
지구에 있는 관제소에서는 왕복 여행에 지구 시간으로 10년이 걸릴 것으로 예상한다. 즉, 지구에 남아 있는 사람은 우주선이 돌아올 때 10살 더 늙는다. 우주선 시계로 측정된 시간과 여행자들이 늙는 정도는 로렌츠 인자의 역수인 α = 0.6영어만큼 감소한다. 따라서 여행자들은 돌아올 때 6년만 늙게 된다.
우주선 승무원들은 자신들의 관점에서 지구와 별 사이의 거리가 α d = 0.6 × 4 = 2.4영어 광년(길이 수축)이라고 생각한다. 여행의 각 절반은 3년이 걸리고, 왕복 여행에는 6년이 걸린다. 즉, 그들은 6년을 늙어 고향에 도착하며, 이는 지구에 있는 사람들의 계산과 일치한다.
지구에 체류하는 사람의 좌표계를 K계, 우주선에 타고 있는 사람의 좌표계를 K'계라고 하고, 지구의 영향에 의한 시간 흐름의 변화는 무시한다고 가정한다.
2000년 1월 1일부터 2006년 1월 1일까지의 여행을 6단계로 나누어 생각해보자.
가속과 감속의 물리 현상의 대칭성으로 인해 1, 3, 4, 6단계에서 우주선에서 느끼는 고유 시간은 같다.
참조
[1]
웹사이트
Astronaut Scott Kelly will return from a year in space both older and younger than his twin brother
https://qz.com/37072[...]
2024-10-15
[2]
서적
The Modern Revolution in Physics
https://books.google[...]
Light and Matter
[3]
서적
Modern Physics
https://books.google[...]
Cengage Learning
[4]
서적
From Special Relativity to Feynman Diagrams: A Course of Theoretical Particle Physics for Beginners
https://books.google[...]
Springer Science & Business Media
[5]
서적
Gravitation and Spacetime
https://books.google[...]
Cambridge University Press
[6]
서적
Foundations of Modern Cosmology
https://books.google[...]
Oxford University Press
[7]
학술지
The twin "paradox" and the conventionality of simultaneity
[8]
서적
Albert Einstein's special theory of relativity. Emergence (1905) and early interpretation (1905–1911)
https://archive.org/[...]
Addison–Wesley
[9]
서적
Concepts of Simultaneity: From Antiquity to Einstein and Beyond
https://books.google[...]
The Johns Hopkins University Press
[10]
서적
Gravity from the Ground Up: An Introductory Guide to Gravity and General Relativity
https://books.google[...]
Cambridge University Press
[11]
웹사이트
Can Special Relativity Handle Acceleration?
http://math.ucr.edu/[...]
1996-05-30
[12]
웹사이트
How does relativity theory resolve the Twin Paradox?
https://www.scientif[...]
[13]
서적
The Fundamentals of Physics
John Wiley and Sons
[14]
서적
About Time
Touchstone
[15]
웹사이트
Frequently Asked Questions About Special Relativity - The Twin Paradox
https://www1.phys.vt[...]
2020-05-25
[16]
학술지
On the Electrodynamics of Moving Bodies
http://www.fourmilab[...]
[17]
학술지
Die Relativitäts-Theorie
https://archive.org/[...]
[18]
서적
Introduction to Special Relativity
https://archive.org/[...]
John Wiley & Sons, Inc.
[19]
서적
Space, Time and Einstein: An Introduction
https://books.google[...]
Routledge
[20]
서적
Basic Relativity
https://books.google[...]
Springer Science & Business Media
[21]
학술지
The evolution of space and time
http://amshistorica.[...]
[22]
학술지
Zwei Einwände gegen die Relativitätstheorie und ihre Widerlegung (Two Objections Against the Theory of Relativity and their Refutation)
[23]
서적
Das Relativitätsprinzip (The Principle of Relativity)
Friedrich Vieweg
[24]
학술지
Das Relativitätsprinzip (The Principle of Relativity)
[25]
문서
Quote from Langevin1911, page 82
[26]
서적
Textbook Of Engineering Physics, Part I
https://books.google[...]
PHI Learning Pvt
[27]
서적
Introduction to Relativity
https://books.google[...]
New Age International
[28]
서적
Special relativity: a modern introduction
Physics Curriculum and Instruction
[29]
서적
Modern Physics
Pearson Addison-Wesley
[30]
서적
Introduction to special relativity
Oxford University Press
[31]
서적
Physics
https://archive.org/[...]
Allyn and Bacon
[32]
서적
The Principle of Relativity
Dover Publications
[33]
서적
Introduction to Relativity: For Physicists and Astronomers
https://books.google[...]
Academic Press
[34]
서적
Philosophy of physics : space and time
Princeton University Press
[35]
서적
Spacetime Physics, second edition
W. H. Freeman
[36]
서적
The Principle of Relativity
Dover Publications
[37]
서적
Introductory Special Relativity
Taylor & Francis Inc.
[38]
서적
Spacetime Physics
https://archive.org/[...]
W. H. Freeman
[39]
간행물
Dialog about objections against the theory of relativity
1918-11-29
[40]
학술지
The clock paradox in a static homogeneous gravitational field
2006-02
[41]
학술지
On Radar Time and the Twin 'Paradox'
[42]
학술지
The interstellar traveler
[43]
학술지
Differential aging from acceleration: An explicit formula
[44]
서적
General Relativity: An Introduction for Physicists
https://books.google[...]
Cambridge University Press
[45]
서적
The evolution of space and time
[46]
서적
Mathematics and science: last essays
[47]
서적
Spacetime Physics
W. H. Freeman
[48]
서적
A Different Universe: Reinventing Physics from the Bottom Down
Basic Books
[49]
서적
Special Relativity
W.W. Norton
[50]
서적
The Modern Revolution in Physics
https://books.google[...]
Light and Matter
[51]
서적
Modern Physics
https://books.google[...]
Cengage Learning
[52]
서적
From Special Relativity to Feynman Diagrams: A Course of Theoretical Particle Physics for Beginners
https://books.google[...]
Springer Science & Business Media
[53]
서적
Gravitation and Spacetime
https://books.google[...]
Cambridge University Press
[54]
서적
Foundations of Modern Cosmology
https://books.google[...]
Oxford University Press
[55]
학술지
[56]
학술지
The twin "paradox" and the conventionality of simultaneity
[57]
서적
Albert Einstein's special theory of relativity. Emergence (1905) and early interpretation (1905–1911)
https://archive.org/[...]
Addison–Wesley
[58]
서적
Concepts of Simultaneity: From Antiquity to Einstein and Beyond
https://books.google[...]
The Johns Hopkins University Press
[59]
서적
Gravity from the Ground Up: An Introductory Guide to Gravity and General Relativity
https://books.google[...]
Cambridge University Press
[60]
웹사이트
Can Special Relativity Handle Acceleration?
http://math.ucr.edu/[...]
2017-05-30
[61]
웹사이트
How does relativity theory resolve the Twin Paradox?
https://www.scientif[...]
2017-05-30
[62]
서적
The Fundamentals of Physics
John Wiley and Sons
[63]
서적
About Time
Touchstone
[64]
웹사이트
Frequently Asked Questions About Special Relativity - The Twin Paradox
https://www1.phys.vt[...]
2020-05-25
[65]
학술지
On the Electrodynamics of Moving Bodies
http://www.fourmilab[...]
[66]
학술지
Die Relativitäts-Theorie
https://archive.org/[...]
[67]
서적
Introduction to Special Relativity
https://archive.org/[...]
John Wiley & Sons, Inc.
[68]
서적
Space, Time and Einstein: An Introduction
https://books.google[...]
Routledge
[69]
서적
Basic Relativity
https://books.google[...]
Springer Science & Business Media
[70]
학술지
The evolution of space and time
http://amshistorica.[...]
[71]
논문
Zwei Einwände gegen die Relativitätstheorie und ihre Widerlegung (Two Objections Against the Theory of Relativity and their Refutation)
[72]
서적
Das Relativitätsprinzip (The Principle of Relativity)
Friedrich Vieweg
[73]
논문
Das Relativitätsprinzip (The Principle of Relativity)
[74]
문서
「我々は加速のこの絶対的な特徴が別の形で現れるのを見る事になるだろう。」 (「''Nous allons voir se manifester sous une autre forme ce caractère absolu de l'accélération.''」)
[75]
논문
The clock paradox in a static homogeneous gravitational field
https://arxiv.org/ab[...]
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
