삼각법
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
삼각법은 삼각형의 변과 각 사이의 관계를 연구하는 수학의 한 분야이다. 수메르와 바빌로니아에서 시작되어 고대 그리스, 인도, 이슬람 세계를 거쳐 유럽으로 전파되었으며, 천문학, 항해, 측량 등 다양한 분야에 활용되었다. 삼각비와 삼각함수를 통해 각도와 변의 관계를 정의하며, 사인, 코사인, 탄젠트 등의 함수를 사용한다. 삼각형의 해법, 즉 변과 각의 일부 정보를 통해 나머지 정보를 구하는 데에도 활용되며, 평면 삼각법과 구면 삼각법으로 구분된다. 삼각 함수는 푸리에 급수 및 변환과 같은 수학적 도구의 기초가 되며, 피타고라스 항등식, 오일러 공식 등 다양한 삼각 항등식을 통해 표현된다.
더 읽어볼만한 페이지
- 그리스의 발명품 - 민주주의
민주주의는 국민이 주권을 가지고 국민의 의사에 따라 정치 권력이 행사되는 정치 체제이며, 기본권 존중, 권력 분립, 다수결 원칙을 특징으로 하고 다양한 형태로 나타나며 최근 위협받는다는 우려가 제기된다. - 그리스의 발명품 - 피타고라스 정리
피타고라스 정리는 직각삼각형에서 직각변의 제곱의 합이 빗변의 제곱과 같다는 정리로, a² + b² = c²으로 표현되며, 한 변의 길이를 계산하는 데 사용되고, 여러 지역에서 알려졌으나 피타고라스 학파에 의해 체계화되었다고 전해진다. - 삼각법 - 사인파
사인파는 고조파가 없는 단일 주파수 파형으로, 삼각함수로 표현되며 진폭, 각진동수, 위상 등의 매개변수로 특징지어지고, 푸리에 분석을 통해 복잡한 파형으로 분해 및 합성이 가능하며, 전자공학, 음악, 물리학 등 다양한 분야에서 활용된다. - 삼각법 - 편평률
편평률은 회전타원체의 납작한 정도를 나타내는 척도로, 장반축과 단반축을 이용하여 계산되며, `f = (a - b) / a`, `f' = (a - b) / b`, `n = (a - b) / (a + b)` 세 가지 형태로 정의되고, 지구를 포함한 다른 천체들의 자전 속도와 구성 물질에 따라 다르게 나타난다. - 표시 이름과 문서 제목이 같은 위키공용분류 - 라우토카
라우토카는 피지 비치레부섬 서부에 위치한 피지에서 두 번째로 큰 도시이자 서부 지방의 행정 중심지로, 사탕수수 산업이 발달하여 "설탕 도시"로 알려져 있으며, 인도에서 온 계약 노동자들의 거주와 미 해군 기지 건설의 역사를 가지고 있고, 피지 산업 생산의 상당 부분을 담당하는 주요 기관들이 위치해 있다. - 표시 이름과 문서 제목이 같은 위키공용분류 - 코코넛
코코넛은 코코넛 야자나무의 열매로 식용 및 유지로 사용되며, 조리되지 않은 과육은 100g당 354kcal의 열량을 내는 다양한 영양 성분으로 구성되어 있고, 코코넛 파우더의 식이섬유는 대부분 불용성 식이섬유인 셀룰로오스이며, 태국 일부 지역에서는 코코넛 수확에 훈련된 원숭이를 이용하는 동물 학대 문제가 있다.
| 삼각법 | |
|---|---|
| 삼각법 개요 | |
 | |
| 일반 정보 | |
| 분야 | 수학 |
| 하위 분야 | 기하학 해석학 |
| 역사 | |
| 주요 인물 | 히파르코스 프톨레마이오스 브라마굽타 알-하시브 알-바타니 레기오몬타누스 프랑수아 비에트 아브라함 드 무아브르 레온하르트 오일러 조제프 푸리에 |
| 기본 개념 | |
| 주요 내용 | 삼각 함수 (사인, 코사인, 탄젠트, 역삼각 함수) 삼각 함수의 공식 정확한 삼각 상수 삼각 함수표 단위원 |
| 법칙과 정리 | 정현 코사인 탄젠트 코탄젠트 피타고라스 정리 |
| 미적분학 관련 | |
| 활용 | 삼각 치환 삼각 함수 적분 (역삼각 함수 적분) 삼각 함수 미분 삼각 급수 |
2. 역사
삼각법의 역사는 고대 문명 시대로 거슬러 올라간다. 초기 삼각법은 천문학과 측량, 항해 등의 실제적인 필요에 의해 발전하기 시작했다.
고대 수메르와 바빌로니아에서는 원을 360도로 나누어 각도를 측정하고, 닮은 삼각형 변의 비율을 연구했다.[6][82][83] 헬레니즘 시대 그리스에서는 유클리드, 아르키메데스 등이 원의 현과 원주각의 성질을 기하학적으로 탐구했으며, 기원전 2세기 히파르코스는 최초의 현표(table of chords)를 만들어 천문학 문제 해결에 사용했다. 이후 서기 2세기 프톨레마이오스는 저서 《알마게스트》에서 더 정확하고 체계적인 현표를 제시하여 이후 천 년 이상 서양과 이슬람 천문학에 큰 영향을 미쳤다.[8]
현대적인 사인(sine) 개념은 고대 인도 수학에서 시작되었다. 5세기경 아리아바타는 원주각의 절반과 현의 절반 사이의 관계, 즉 사인 값을 계산하고 이를 체계화했다. 이러한 인도의 지식은 이슬람 황금 시대 학자들에게 전해져 더욱 발전했다. 9세기 알 바타니는 사인을 적극적으로 활용하고 코탄젠트, 탄젠트 등의 개념을 도입했으며, 10세기 아부 알-와파 알-부자니의 연구를 통해 6가지 삼각함수가 모두 사용되기 시작했다. 특히 13세기 페르시아의 학자 나시르 알딘 투시는 삼각법을 천문학에서 분리된 독립적인 수학 분야로 정립하고 구면 삼각법을 체계화하는 데 크게 기여했다.[13][14][15][16]
중세 이슬람 세계에서 발전한 삼각법 지식은 12세기 라틴어 번역을 통해 유럽으로 전파되었다. 15세기 레기오몬타누스는 삼각법을 유럽에 체계적으로 소개하는 중요한 저술을 남겼고,[18] 16세기에는 니콜라우스 코페르니쿠스와 그의 제자 레티쿠스가 삼각법을 연구하고 보급하는 데 기여했다. 레티쿠스는 삼각함수를 직각삼각형의 변의 비율로 정의하는 데 중요한 역할을 했다.[93] 바르톨로메우스 피티스쿠스는 1595년 저서에서 처음으로 '삼각법(Trigonometria)'이라는 용어를 사용했다.[21]
대항해 시대 이후 항해와 지도 제작의 수요가 증가하면서 삼각법의 중요성은 더욱 커졌다.[20][98] 17세기 프랑수아 비에트는 현대적인 삼각함수 기호 도입에 기여했으며, 미적분학의 발달과 함께 삼각함수 이론은 크게 발전했다. 18세기 레온하르트 오일러는 복소수를 삼각법에 도입하고 오일러 공식을 발견하는 등 삼각법을 현대적인 모습으로 발전시키는 데 결정적인 역할을 했다. 이후 푸리에 급수 등의 발견을 통해 삼각법은 물리학, 공학 등 다양한 분야에서 필수적인 도구로 자리 잡게 되었다.
2. 1. 고대 사회

수메르 천문학자들은 원을 360도로 나누어 각도 측정을 연구했다.[6] 이후 바빌로니아인들과 함께 닮은 삼각형의 변의 비율을 연구하고 이러한 비율의 몇 가지 속성을 발견했지만, 이를 삼각형의 변과 각도를 찾는 체계적인 방법으로 발전시키지는 못했다. 예일 대학교의 바빌로니아 컬렉션 No.7289 (기원전 2000년경)에는 정사각형과 두 대각선이 그려져 있으며, 각 길이에는 설형 문자로 60진법으로 기록되어 있다. 이를 통해 계산한 2의 제곱근 근사값은 매우 정확했다. 또한, 기원전 1800년에서 기원전 1650년 사이에 만들어진 것으로 추정되는 점토판인 플림프턴 322에는 피타고라스 수가 기록되어 있다는 해석도 있다. 메소포타미아에서는 신바빌로니아 시대에 천문 관측의 필요성으로 각도를 수치화하는 개념이 발전했으며, 원을 360°로 나누는 도수법이 시작되었다.[82][83] 누비아인들도 비슷한 방법을 사용한 것으로 알려져 있다.[7]
기원전 3세기, 헬레니즘 시대의 수학자인 유클리드와 아르키메데스는 원의 현과 원주각의 속성을 연구했다. 그들은 현대 삼각법 공식과 동등한 정리를 증명했지만, 대수적인 방식이 아닌 기하학적인 방식으로 제시했다. 기원전 140년경 니케아 출신의 히파르코스는 현대의 사인 값표와 유사한 최초의 현표를 만들었으며, 이를 이용해 삼각법과 구면 삼각법 문제를 해결했다. 이 공로로 히파르코스는 "삼각법의 '아버지'"로 불리기도 한다.
서기 2세기에는 이집트 알렉산드리아 출신의 그리스계 천문학자 프톨레마이오스가 그의 저서 ''알마게스트'' 제1권 제11장에 상세한 삼각 함수 표(프톨레마이오스의 현표)를 작성했다.[8] 프톨레마이오스는 오늘날의 사인과는 약간 다르게, 현의 길이를 사용하여 삼각 함수를 정의했다. (예를 들어, 오늘날의 sin(θ) 값은 프톨레마이오스 표에서 각도 2θ에 해당하는 현의 길이를 찾아 2로 나누어 구할 수 있다.) 프톨레마이오스의 표와 연구는 이후 약 1200년 동안 중세 비잔틴, 이슬람 세계, 그리고 서유럽에서 천문학 계산을 수행하는 데 중요한 기준으로 사용되었다.
2. 2. 헬레니즘 시대
기원전 3세기경, 헬레니즘 시대의 수학자 유클리드와 아르키메데스는 원의 현과 원주각의 관계를 깊이 연구했다. 이들은 현대 삼각법 공식과 유사한 정리들을 증명했지만, 당시에는 대수학이 발달하지 않아 기하학적인 방식으로 설명했다.기원전 140년경 니케아 출신의 히파르코스는 삼각법 역사에서 중요한 인물로 평가받는다. 그는 현대의 사인 값 표와 비슷한 최초의 현표(table of chords)를 만들었다. 프톨레마이오스에 따르면 이 표는 7.5° 간격으로 현의 길이를 계산한 것이었다.[84] 히파르코스는 이 표를 이용해 삼각법 문제를 풀고, 구면 삼각법 문제를 해결하기 위해 구면을 평면에 스테레오 투영하는 방법을 사용한 것으로 보인다.[84] 이러한 업적으로 히파르코스는 "삼각법의 아버지"로 불리기도 한다. (다만 히파르코스의 저작은 현재 남아있지 않고, 후대 학자들의 기록을 통해 알려졌다.)
1세기에는 알렉산드리아의 메넬라오스가 구면 삼각법을 체계적으로 연구했다.
서기 2세기, 이집트 알렉산드리아 출신의 그리스계 천문학자 프톨레마이오스는 메넬라오스의 연구를 이어받아 천문학에 응용했다. 그는 자신의 대표 저서인 《알마게스트》(Almagest) 제1권 11장에 매우 상세한 삼각 함수 표, 즉 '프톨레마이오스의 현표'를 제시했다.[8][85] 이 표는 히파르코스의 표처럼 원주각과 현의 관계를 다루었지만, 훨씬 더 정확하고 사용하기 편리했다.[86] 프톨레마이오스는 오늘날의 사인(sin)과는 약간 다르게, 현의 길이를 사용하여 삼각 함수를 정의했다. (현대적인 sin(θ) 값은 프톨레마이오스의 표에서 각의 두 배(2θ)에 해당하는 현의 길이를 찾아 2로 나누어 구할 수 있다.) 프톨레마이오스의 연구와 삼각 함수 표는 이후 약 1200년 동안 중세 비잔틴, 이슬람 세계, 그리고 서유럽에서 천문학 계산의 중요한 기준으로 사용되었다.
2. 3. 인도와 이슬람 세계
사인의 현대적 개념은 인도의 수학 문헌인 ''수르야 시단타''에서 처음 등장했으며, 그 속성은 5세기 인도 수학자이자 천문학자인 아리아바타에 의해 상세히 연구되었다.[6] 그리스 수학이 원의 현과 원주각에 주목한 반면, 인도에서는 원주각의 절반과 현의 절반, 즉 사인 값의 관계에 주목하는 방식으로 변화했다. 아리아바타의 저서 『आर्यभटीय|아리아바티야sa』는 저자가 명확한 인도 최초의 천문학 서적으로, 단위 원에서의 사인 값에 대한 언급이 포함되어 있다. 7세기 천문학자 브라마굽타의 저서 『브라마스푸타시단타』는 이후 아랍 세계로 전해져 삼각법 발전에 영향을 주었다. 이 책은 770년경 إبراهيم الفزاري|이브라힘 알 파자리ar와 야쿠브 이븐 타리크에 의해 아랍어로 번역되어 『زيج السندهند|지 앗신드ar』라는 이름으로 아바스 왕조의 칼리프 만수르에게 헌상되었다.이러한 그리스와 인도의 삼각법 지식은 8세기부터 13세기에 걸쳐 중세 이슬람 세계의 학자들에 의해 번역되고 확장되었다. 이슬람 학자들은 그리스와 인도의 과학 지식을 적극적으로 수용하고 융합하여 독자적인 학문 체계를 구축했다. 9세기 알콰리즈미는 인도의 천문표 『지 앗신드』를 바탕으로 자신만의 زيج|지(천문표)ar를 작성했다. 같은 시기, 페르시아 수학자 하바시 알-하시브 알-마르와지는 최초의 코탄젠트 표를 만들었다.[9][16] 천문학자 알 바타니는 프톨레마이오스의 현 대신 인도의 사인을 중요하게 사용했으며, 코사인, 탄젠트, 코탄젠트 개념을 도입하고 삼각법을 천문학에서 독립된 학문으로 발전시키는 데 중요한 역할을 했다.
10세기에는 페르시아 수학자 아부 알-와파 알-부자니의 저작에서 여섯 종류의 삼각 함수가 모두 사용되었다. 아부 알-와파는 0.25° 간격으로 8자리까지 정확한 사인 표와 탄젠트 값을 계산했으며, 구면 삼각법 분야에서도 중요한 발전을 이루었다.[10][11][12] 카이로의 천문학자 이븐 유누스는 삼각함수의 곱셈과 덧셈 공식에 해당하는 계산법을 개발했다.[91] 이븐 알 하이삼은 삼각법을 광학 연구에 응용하기 시작했다.
13세기 페르시아의 박식가 나시르 알딘 투시는 삼각법을 천문학과 독립된 순수 수학 분야로 확립한 인물로 평가받는다.[13][14][15] 그는 구면 삼각법을 현재의 형태로 체계화했으며,[16] 구면 삼각형에서 직각삼각형의 여섯 가지 경우를 나누어 설명했다. 또한 그의 저서 '섹터 도형에 관하여'에서 평면 및 구면 삼각형에 대한 사인 법칙을 명시하고, 구면 삼각형에 대한 탄젠트 법칙을 발견하여 증명했다.[17] 이처럼 중세 이슬람 세계에서 발전된 삼각 함수와 그 방법론은 알 바타니와 나시르 알딘 투시 같은 학자들의 저작과 프톨레마이오스의 『알마게스트』의 12세기 라틴어 번역을 통해 서유럽으로 전파되었다.
2. 4. 유럽
중세 이슬람 세계에서 발전한 삼각법 지식은 프톨레마이오스의 『알마게스트』나 알 바타니, 투시 등 아랍 학자들의 저작이 12세기 라틴어 번역을 통해 서유럽으로 전해졌다.[92] 알콰리즈미의 천문표는 배스의 아델라드가, 알 바타니의 저작은 체스터의 로버트나 티볼리의 플라토 등이 라틴어로 번역하여 유럽 세계에 소개했다.
15세기 독일 수학자 레기오몬타누스(요하네스 뮐러)는 유럽 초기 삼각법 연구의 중요한 인물이다. 그는 비잔틴 학자이자 추기경인 바실리오스 베사리온의 격려를 받아 1464년 삼각법 입문서인 『모든 종류의 삼각형에 대하여』(De triangulis omnimodisla)를 저술했다.[18] 이 책은 르네상스 시대 유럽 학계에 삼각법을 체계적으로 소개하는 역할을 했다. 또한 그는 1490년에 유럽 최초로 간행된 삼각 함수 표인 『방향표』(Tabula directionumla)를 작성했다.
16세기 초까지도 북유럽에서 삼각법은 널리 알려지지 않았기 때문에, 니콜라우스 코페르니쿠스는 그의 혁명적인 저서 『천구의 회전에 관하여』(1543)에서 두 장에 걸쳐 삼각법의 기본 개념을 설명해야 했다. 코페르니쿠스의 제자인 레티쿠스는 스승의 저서에서 삼각법 부분만을 발췌하여 1542년 『삼각형의 변과 각에 대하여』(De lateribus et angulis triangulorumla)를 출판했다. 레티쿠스는 삼각 함수를 직각삼각형 변의 길이 비율로 정의하는, 오늘날의 삼각비 개념을 도입한 인물로 평가받으며,[93] 방대한 삼각 함수 표를 작성하기도 했다. 바르톨로메우스 피티스쿠스는 레티쿠스의 표를 개선하고,[94] 1595년 저서 『삼각법, 또는 삼각형의 해법에 관한 소론과 증명』(Trigonometria: sive de solutione triangulorum tractatus brevis et perspicuusla)에서 처음으로 "삼각법(Trigonometriala)"이라는 용어를 만들어 사용했다.[21][95][96] 이 단어는 현대 여러 유럽 언어에서 삼각법을 뜻하는 단어의 어원이 되었다.
16세기와 17세기 대항해 시대에는 항해 기술의 발전과 광대한 지역에 대한 정확한 지도 제작의 필요성이 커지면서 삼각법은 수학의 중요한 응용 분야로 부상했다.[20][98] 젬마 프리시우스는 1533년 지도 제작에 관한 책에서 오늘날에도 측량에 사용되는 삼각 측량 방법을 소개했다. 메르카토르는 항해에 유용한 메르카토르 도법을 고안하여 지도학 발전에 크게 기여했다.
17세기 프랑스 수학자 프랑수아 비에트는 레기오몬타누스와 레티쿠스의 연구를 바탕으로 삼각법을 더욱 발전시켰으며, sinθ, cosθ와 같은 현대적인 삼각함수 기호 사용의 토대를 마련한 것으로 평가받는다.[97] 이 시기 미적분학의 발전은 삼각함수 이론에 큰 영향을 미쳤다. 17세기 스코틀랜드 수학자 제임스 그레고리와 18세기 콜린 매클로린의 저작은 삼각 함수 급수의 발전에 영향을 미쳤다.[22][99] 또한, 메르카토르 도법과 관련된 문제였던 정할선 함수의 적분 문제가 17세기 후반 아이작 바로와 그레고리에 의해 독립적으로 해결되었다. sin, cos과 같은 기호가 사용되기 시작한 것도 17세기부터이다.
18세기에 들어 레온하르트 오일러는 복소수를 삼각법에 도입하고, 지수 함수와 삼각 함수 사이의 관계를 나타내는 오일러 공식을 발견하여 삼각법 이론을 혁신적으로 발전시켰다. 그는 또한 일반각에 대한 삼각 함수를 정의하고 sin, cos 기호를 정착시키는 데 기여했다. 브룩 테일러는 함수의 테일러 급수 전개를 정의하여 삼각 함수를 포함한 다양한 함수를 다항함수로 근사하는 길을 열었다.[23][100]
2. 5. 한국
(작성할 내용 없음 - 원본 소스에 해당 섹션 관련 정보 부재)3. 삼각비와 삼각함수
삼각비는 직각 삼각형의 세 변 사이의 비율을 나타낸다. 직각삼각형에서 한 예각의 크기가 정해지면, 삼각형의 크기와 관계없이 변들의 비율은 일정하다. 이는 동일한 예각을 갖는 모든 직각삼각형이 서로 닮음이기 때문이다.[24]
이러한 각도와 변의 비율 사이의 관계를 함수로 나타낸 것이 삼각 함수이다. 가장 기본적인 삼각함수로는 사인(sin), 코사인(cos), 탄젠트(tan)가 있으며, 이들의 역수인 코시컨트(csc), 시컨트(sec), 코탄젠트(cot)도 정의된다.
삼각함수를 이용하면 사인 법칙과 코사인 법칙 등을 통해 임의의 삼각형에 대한 다양한 문제를 해결할 수 있다.[26] 예를 들어, 삼각형의 일부 변의 길이와 각도의 크기를 알면 나머지 변의 길이와 각도를 계산할 수 있다. 삼각함수는 단위 원을 이용하여 직각삼각형을 넘어 임의의 각도에 대해서도 정의될 수 있으며, 이는 삼각법의 활용 범위를 크게 넓힌다.
삼각법은 측량, 천문학, 항해술 등 전통적인 분야뿐만 아니라 물리학, 공학, 음악, 경제학 등 현대의 다양한 학문 및 기술 분야에서 필수적인 도구로 사용된다.
3. 1. 삼각비
삼각비는 직각 삼각형의 변들 사이의 비율이다. 이 비율은 직각 삼각형의 한 예각에만 의존하는데, 동일한 예각을 갖는 두 개의 직각 삼각형은 닮음이기 때문이다.[24] 따라서, 이러한 비율은 특정 각도에 따라 고유한 값을 가지는 함수를 정의하며, 이 함수를 삼각 함수라고 부른다. 그림에서 변의 길이가 각각 ''a'', ''b'', ''h''로 주어질 때, 각도 ''A''의 함수로 아래와 같이 정의된다.
삼각비를 정의하기 위해 사용되는 직각삼각형의 각 변은 다음과 같이 불린다.
- '''빗변''': 직각(90도)의 맞은편에 있는 변이다. 삼각형의 가장 긴 변이며, 기준 각도 ''A''에 인접한 두 변 중 하나이다.
- '''인접변''': 기준 각도 ''A''에 인접한 변 중에서 빗변이 아닌 다른 변이다. '밑변'이라고도 한다.
- '''대변''': 기준 각도 ''A''의 맞은편에 있는 변이다. '높이' 또는 '수직변'이라고도 한다.
주어진 각도 ''A''에 대한 주요 삼각비는 다음과 같다.
- '''사인''' (sin): 각도의 대변과 빗변의 비율이다.
::
- '''코사인''' (cos): 인접변과 빗변의 비율이다.
::
- '''탄젠트''' (tan): 대변과 인접변의 비율이다. 탄젠트는 사인과 코사인의 비율과 같다.
::
이 세 삼각비의 역수는 각각 '''코시컨트'''(csc), '''시컨트'''(sec), '''코탄젠트'''(cot)라고 한다.
- '''코시컨트''' (csc): 사인의 역수. 빗변과 대변의 비율이다.
:
- '''시컨트''' (sec): 코사인의 역수. 빗변과 인접변의 비율이다.
:
- '''코탄젠트''' (cot): 탄젠트의 역수. 인접변과 대변의 비율이다.
:
코사인(cosine), 코탄젠트(cotangent), 코시컨트(cosecant)는 각각 사인(sine), 탄젠트(tangent), 시컨트(secant)의 여각(complementary angle)에 대한 값이기 때문에 이름에 "co-"가 붙었다.[25] 예를 들어, cos ''A'' = sin(90° - ''A'') 와 같은 관계가 성립한다.
=== 기억술 ===
암기법은 삼각법의 정의를 기억하는 데 흔히 사용된다. 특히 직각 삼각형의 사인, 코사인, 탄젠트 비율은 각 비율을 나타내는 영어 단어의 앞 글자를 따서 만든 '''SOH-CAH-TOA'''로 쉽게 외울 수 있다.[27]
- '''S'''ine = '''O'''pposite / '''H'''ypotenuse (사인 = 대변 / 빗변)
- '''C'''osine = '''A'''djacent / '''H'''ypotenuse (코사인 = 인접변 / 빗변)
- '''T'''angent = '''O'''pposite / '''A'''djacent (탄젠트 = 대변 / 인접변)
이 약자를 기억하는 한 가지 방법은 발음 그대로 읽는 것이다(예: 소-카-토아, 크라카토아 화산 이름과 비슷하게).[28] 또 다른 방법은 각 글자로 시작하는 단어를 이용해 문장을 만드는 것이다. 예를 들어 "'''S'''ome '''O'''ld '''H'''ippie '''C'''aught '''A'''nother '''H'''ippie '''T'''rippin' '''O'''n '''A'''cid"(어떤 늙은 히피가 다른 히피가 약에 취해 비틀거리는 것을 잡았다)와 같은 문장을 사용할 수 있다.[29]

| 선분 | 함수 | 값 |
|---|---|---|
| 사인 | ||
| 코사인 | ||
| 탄젠트 | ||
| 코탄젠트 | ||
| 시컨트 | ||
| 코시컨트 | ||
| 버서인(versine) | ||
| 코버서인(coversine) |
3. 2. 삼각함수
삼각비는 직각 삼각형의 변들 사이의 비율이다. 이 비율은 직각 삼각형의 한 예각에만 의존하는데, 동일한 예각을 갖는 두 개의 직각 삼각형은 닮음이기 때문이다.[24]
따라서, 이러한 비율은 함수를 정의하며, 이 함수를 삼각 함수라고 부른다. 구체적으로, 그림에서 변의 길이가 각각 ''a'', ''b'', ''h''로 주어질 때, 알려진 각도 ''A''의 함수로 아래와 같이 정의된다.
다음 정의에서, 빗변은 직각 삼각형에서 90도 각도의 맞은편에 있는 변이다. 이 변은 삼각형의 가장 긴 변이며 각도 ''A''에 인접한 두 변 중 하나이다. 인접변은 각도 ''A''에 인접한 다른 변이다. 대변은 각도 ''A''의 맞은편에 있는 변이다.
- 사인 (sin): 각도의 대변과 빗변의 비율.
:
- 코사인 (cos): 인접변과 빗변의 비율.
:
- 탄젠트 (tan): 대변과 인접변의 비율.
:
이러한 비율의 역수는 각각 코시컨트(csc), 시컨트(sec), 코탄젠트(cot)라고 한다.
:
:
:
코사인, 코탄젠트, 코시컨트는 각각 사인, 탄젠트, 시컨트의 보각(complementary angle)에 대한 함수값이므로 이름에 "co-"가 붙는다.[25]
이러한 함수를 사용하여, 사인 법칙과 코사인 법칙을 이용함으로써 임의의 삼각형에 대한 사실상 모든 질문에 답할 수 있다.[26] 이 법칙들은 두 변과 그 사이의 각도, 두 각도와 한 변, 또는 세 변이 주어졌을 때 나머지 각도와 변을 계산하는 데 사용될 수 있다.
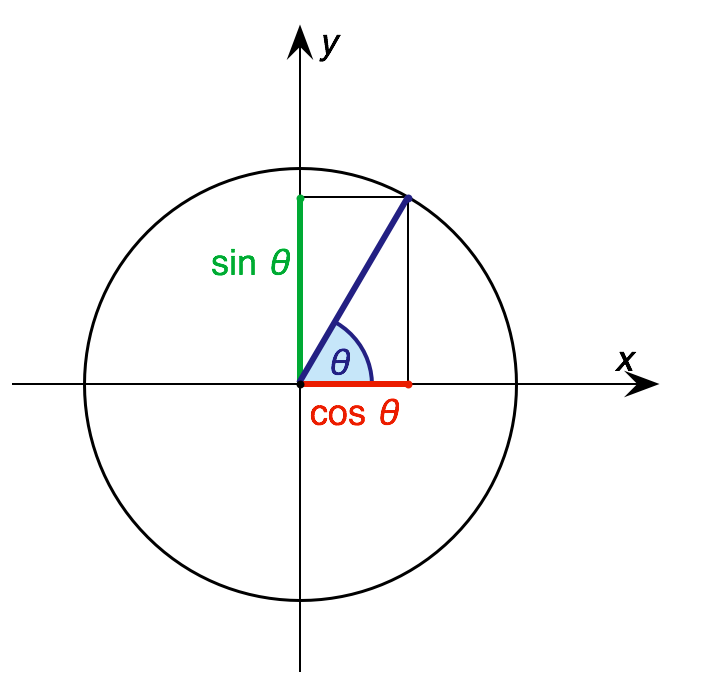

삼각비는 평면의 원점을 중심으로 하는 반지름 1인 원인 단위 원을 사용하여 나타낼 수도 있다.[30] 이 설정에서, 표준 위치에 놓인 각도 ''A''의 동경은 단위 원과 점 (x, y)에서 교차하며, 이때 이고 이다.[30] 이 표현을 통해 아래 표와 같이 일반적으로 사용되는 삼각 함수 값을 계산할 수 있다.[31]
| 함수 | 0 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 사인 | |||||||||
| 코사인 | |||||||||
| 탄젠트 | 정의되지 않음 | ||||||||
| 시컨트 | 정의되지 않음 | ||||||||
| 코시컨트 | 정의되지 않음 | 정의되지 않음 | |||||||
| 코탄젠트 | 정의되지 않음 | 정의되지 않음 |
단위 원을 사용하면 삼각비의 정의를 모든 양수 및 음수 각도로 확장할 수 있다[32](삼각 함수 참조). 다음 표는 여섯 가지 주요 삼각 함수의 그래프 속성을 요약한 것이다.[33][34]
| 함수 | 주기 | 정의역 | 치역 | 그래프 |
|---|---|---|---|---|
| 사인 | -- | |||
| 코사인 | -- | |||
| 탄젠트 | -- | |||
| 시컨트 | -- | |||
| 코시컨트 | -- | |||
| 코탄젠트 | -- |
| 선분 | 함수 | 값 |
|---|---|---|
| 사인 | ||
| 코사인 | ||
| 탄젠트 | ||
| 코탄젠트 | ||
| 시컨트 | ||
| 코시컨트 | ||
| 베르사인 | ||
| 코베르사인 |
삼각 함수는 인류가 처음 만난 초월 함수이다.
3. 3. 역삼각함수
여섯 개의 주요 삼각함수는 주기성을 가지므로 단사 함수(일대일 함수)가 아니다. 따라서 그대로는 역함수를 정의할 수 없다. 하지만 삼각 함수의 정의역을 제한하면 역함수를 만들 수 있다.[35]주요 역삼각함수의 이름, 표기법, 정의, 정의역, 그리고 일반적으로 사용되는 주값(principal value)의 치역은 다음 표와 같다.[35][36]
| 이름 | 표기법 | 정의 | 정의역 x | 치역 y (라디안) | 치역 y (도) |
|---|---|---|---|---|---|
| 아크사인 (arcsine) | y = arcsin(x) | x = sin(y) | −1 ≤ x ≤ 1 | −π/2 ≤ y ≤ π/2 | −90° ≤ y ≤ 90° |
| 아크코사인 (arccosine) | y = arccos(x) | x = cos(y) | −1 ≤ x ≤ 1 | 0 ≤ y ≤ π | 0° ≤ y ≤ 180° |
| 아크탄젠트 (arctangent) | y = arctan(x) | x = tan(y) | 모든 실수 | −π/2 < y < π/2 | −90° < y < 90° |
| 아크코탄젠트 (arccotangent) | y = arccot(x) | x = cot(y) | 모든 실수 | 0 < y < π | 0° < y < 180° |
| 아크시컨트 (arcsecant) | y = arcsec(x) | x = sec(y) | x ≤ −1 또는 x ≥ 1 | 0 ≤ y < π/2 또는 π/2 < y ≤ π | 0° ≤ y < 90° 또는 90° < y ≤ 180° |
| 아크코시컨트 (arccosecant) | y = arccsc(x) | x = csc(y) | x ≤ −1 또는 x ≥ 1 | −π/2 ≤ y < 0 또는 0 < y ≤ π/2 | −90° ≤ y < 0° 또는 0° < y ≤ 90° |
4. 삼각함수의 활용
삼각법은 그 원리가 기하학적 문제 해결에 국한되지 않고, 다양한 과학 및 공학 분야에서 필수적인 도구로 활용된다. 특히 주기적인 현상을 수학적으로 모델링하고 분석하는 데 매우 유용하다.[54]
삼각법의 가장 기본적인 응용 중 하나는 삼각형의 변의 길이나 각의 크기를 구하는 삼각형의 해법이다. 이는 평면 위에서의 계산을 다루는 평면 삼각법뿐만 아니라, 구면 위에서의 계산을 다루는 구면 삼각법으로 확장되어 천문학이나 항해술과 같은 분야에서 중요한 역할을 해왔다.[48][50] 예를 들어, 별이나 행성의 위치를 계산하고[12], 배의 항로를 결정하는 데[51] 구면 삼각법이 필수적이었다.
또한, 삼각함수는 소리나 빛과 같은 파동 현상을 설명하는 데 핵심적인 역할을 한다. 푸리에가 발견한 푸리에 급수와 푸리에 변환은 복잡한 주기 함수나 신호를 단순한 사인과 코사인의 합 또는 적분으로 분해하는 강력한 방법을 제공하며, 이는 물리학, 음향학[58], 광학[58], 통신[56], 신호 처리 등 수많은 분야의 기초가 된다.
이 외에도 삼각법 또는 삼각 함수는 측량[52], 지도 제작[60], 건축[62], 기계 공학, 전기 공학, 토목 공학[60], 컴퓨터 그래픽스[73], 경제학[71], 의료 영상(CT 스캔, 초음파)[64], 음악 이론[60], 측지학, 오디오 합성[61], 전자 공학[60], 생물학[63], 화학[65], 정수론 (및 이를 응용한 암호학)[66], 지진학[58], 기상학[67], 해양학[68], 이미지 압축[69], 음성학[70], 결정학[72], 게임 개발[73] 등 현대 사회의 거의 모든 기술 및 학문 분야에서 광범위하게 응용되고 있다.
4. 1. 삼각형의 해법
삼각형의 세 변과 세 각의 크기 중 일부가 주어졌을 때, 나머지 요소들의 값을 알아내는 것을 삼각형을 푼다(solving triangles)고 하며, 이는 삼각법의 중요한 목표 중 하나이다. 삼각형은 6개의 주요 요소(세 변의 길이, 세 각의 크기) 중 3개의 정보가 주어지면 나머지 요소들이 결정되는 경우가 많다. 이렇게 삼각형을 유일하게 특정할 수 있는 조건을 삼각형의 결정 조건이라고 한다[79][80]. 삼각형을 풀 때는 주로 다음과 같은 법칙들이 사용된다.평면 삼각형의 결정 조건은 주어진 정보의 종류에 따라 다음과 같이 나눌 수 있다. 여기서 S는 변(Side)의 길이, A는 각(Angle)의 크기를 의미한다.
| 조건 | 설명 | 평면 삼각형 결정 여부 |
|---|---|---|
| SSS | 세 변의 길이가 주어짐 | 유일하게 결정됨 |
| SAS | 두 변의 길이와 그 사이의 끼인 각의 크기가 주어짐 | 유일하게 결정됨 |
| ASA | 한 변의 길이와 그 양 끝 각의 크기가 주어짐 | 유일하게 결정됨 |
| AAS | 한 변의 길이와 그 양 끝 각이 아닌 두 각의 크기가 주어짐 | 유일하게 결정됨 (ASA와 동일) |
| ASS | 두 변의 길이와 그 사이의 끼인 각이 아닌 다른 각의 크기가 주어짐 | 두 가지 삼각형으로 결정되거나, 결정되지 않을 수 있음 (그림 1.1 참조) |
| AAA | 세 각의 크기가 주어짐 | 모양은 결정되지만 크기는 결정되지 않음 (무수히 많은 닮음 삼각형 존재) |
이 조건들은 에우클레이데스의 『원론』에서도 기하학적으로 증명되었다. 평면 삼각형은 이처럼 독립적인 3개의 정보로 그 모양과 크기가 결정되므로, 자유도가 3이라고 말한다. (참고로 구면 삼각형에서는 AAA 조건으로도 삼각형이 유일하게 결정된다.)
삼각형을 풀기 위해 사용되는 주요 법칙은 다음과 같다. 아래 공식에서 ''A'', ''B'', ''C''는 삼각형의 각 꼭짓점에서의 각의 크기이며, ''a'', ''b'', ''c''는 각각 각 ''A'', ''B'', ''C''와 마주보는 변의 길이이다.
- '''사인 법칙''' (Sine rule): 임의의 삼각형에서 각 변의 길이를 마주보는 각의 사인 값으로 나눈 비율은 모두 같으며, 이 값은 외접원의 지름(2''R'')과 같다.[77]
:
여기서 는 삼각형의 넓이이고 ''R''은 삼각형의 외접원의 반지름이다.
:
- '''코사인 법칙''' (Cosine rule): 임의의 삼각형에서 한 변의 제곱은 나머지 두 변의 제곱의 합에서 두 변의 길이와 그 끼인 각의 코사인 값을 곱한 것의 두 배를 뺀 값과 같다. 이는 피타고라스 정리를 일반적인 삼각형으로 확장한 것이다.[77]
:
또는 각의 코사인 값에 대해 정리하면 다음과 같다.
:
- '''탄젠트 법칙''' (Tangent rule): 두 변의 길이 차와 합의 비율은, 그 변들과 마주보는 각의 차와 합의 절반에 대한 탄젠트 값의 비율과 같다. 프랑수아 비에트가 개발했으며, 과거 삼각함수표를 사용할 때 코사인 법칙보다 계산이 편리한 경우가 있었다.[76]
:
:
이러한 법칙들을 이용하면 주어진 조건(변의 길이, 각의 크기)으로부터 삼각형의 나머지 요소들을 계산할 수 있다. 또한, 삼각형의 높이, 중선의 길이, 외접원, 내접원, 방심원 등 다른 요소들의 정보가 주어졌을 때도 삼각형을 풀 수 있는 경우가 있다.
4. 2. 평면 삼각법과 구면 삼각법
'''평면 삼각법'''은 평면 위의 삼각형의 변과 각 사이의 관계를 다루는 분야이다.'''구면 삼각법'''은 구면 위의 구면 삼각형의 각과 변의 관계를 연구하는 학문이다. 구면 삼각형은 구면 위의 세 개의 대원의 호로 둘러싸인 도형이다. 대원은 구의 중심을 통과하는 평면으로 구를 잘랐을 때 생기는 원이다. 구면 삼각법의 코사인 법칙과 사인 법칙은 삼각 함수로 정의되며, 역사적으로 천문학과 항해술에 중요하게 이용되었다.
=== 활용 ===
==== 천문학 ====
수 세기 동안 구면 삼각법은 태양, 달, 별의 위치를 파악하고, 일식을 예측하며, 행성의 궤도를 묘사하는 데 사용되어 왔다.[48] 현대에는 삼각 측량 기술이 천문학에서 가까운 별까지의 거리를 측정하는 데 사용되며, 위성 항법 시스템에도 활용된다.[12]
==== 항해술 ====

역사적으로 삼각법은 항해 중 선박의 위도와 경도를 찾고, 항로를 계획하며, 거리를 계산하는 데 필수적이었다.[50] 오늘날에도 삼각법은 GPS나 자율 주행차를 위한 인공 지능과 같은 현대 항해 기술의 기초가 된다.[51]
=== 기본 공식 ===
구면 삼각형의 세 각을 ''A'', ''B'', ''C''라 하고, 각 각에 마주보는 변의 길이를 각각 ''a'', ''b'', ''c''라고 할 때 (그림 참조), 각 변과 각 사이의 관계는 다음과 같은 코사인 법칙으로 나타낼 수 있다.[81]
:
:
:
이는 다음과 같은 형태로도 표현할 수 있다.
:
이 코사인 법칙은 구면 삼각법의 기본적인 공식이며, 다양한 다른 공식들이 이로부터 유도된다.[81]
4. 3. 푸리에 급수/변환과 파동
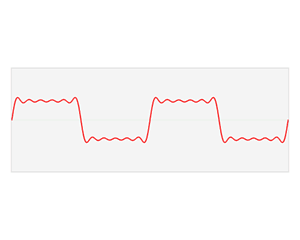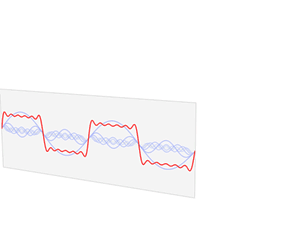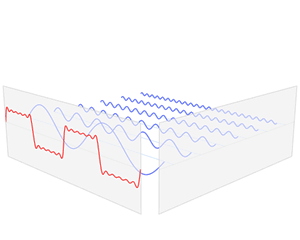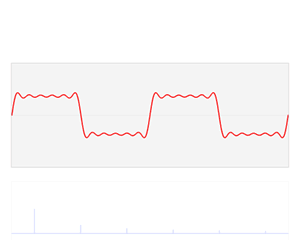
사인 함수와 코사인 함수는 주기 함수 이론의 기본이며,[54] 소리나 빛과 같은 파동을 설명하는 데 사용된다. 푸리에는 모든 연속적인 주기 함수가 삼각 함수의 무한 합으로 표현될 수 있다는 사실을 발견했는데, 이를 푸리에 급수라고 한다.
주기적이지 않은 함수도 푸리에 변환을 통해 사인과 코사인의 적분 형태로 나타낼 수 있다. 이러한 푸리에 급수와 푸리에 변환은 양자 역학[55]이나 통신[56] 등 다양한 분야에서 중요하게 활용된다.
4. 4. 기타 응용 분야
역사적으로 삼각법은 항해 중 항해 선박의 위도와 경도를 찾고, 항로를 계획하며, 거리를 계산하는 데 사용되었다.[50] 오늘날에도 삼각법은 GPS 및 자율 주행차를 위한 인공 지능과 같은 수단을 통해 항해에 활용된다.[51]
토지 측량 분야에서 삼각법은 물체 간의 길이, 면적 및 상대 각도를 계산하는 데 중요한 역할을 한다.[52] 더 넓은 범위에서는 지리학에서 주요 지점 간의 거리를 측정하는 데 사용된다.[53]
사인 함수와 코사인 함수는 주기 함수 이론의 기초를 이루며,[54] 이는 소리나 빛의 파동을 설명하는 데 필수적이다. 푸리에는 모든 연속적인 주기 함수가 삼각 함수의 무한 합으로 표현될 수 있음을 발견했다. 이를 푸리에 급수라고 한다. 비주기적인 함수 역시 푸리에 변환을 통해 사인과 코사인의 적분 형태로 나타낼 수 있으며, 이는 양자 역학[55]이나 통신[56] 등 다양한 분야에서 응용된다.
삼각법은 물리학을 포함한 여러 자연 과학 분야에서 유용하게 쓰인다.[57] 특히 음향학[58]과 광학[58]에서는 음파와 광파를 수학적으로 기술하고, 이들 파동의 경계면 통과나 전달과 관련된 문제를 해결하는 데 삼각법이 사용된다.[59]
이 외에도 삼각법 또는 삼각 함수는 다음과 같은 다양한 분야에서 활용된다.
5. 삼각 항등식
삼각법은 모든 가능한 입력 값에 대해 항상 참이 되는 방정식, 즉 많은 항등식으로 유명하다.[74] 이러한 항등식은 크게 두 가지로 나눌 수 있다.
각도만을 포함하는 항등식은 삼각 함수 공식이라고 하며, 주어진 삼각형의 변과 각도를 모두 관련시키는 방정식은 삼각형 항등식으로 알려져 있다.[75]
5. 1. 피타고라스 항등식
삼각법은 모든 가능한 입력값에 대해 항상 참이 되는 방정식, 즉 많은 항등식으로 유명하다.[74] 이러한 항등식들은 크게 두 가지로 나눌 수 있다.
각도만을 포함하는 항등식은 삼각 함수 공식이라고 하며, 주어진 삼각형의 변과 각도를 모두 관련시키는 방정식은 삼각형 항등식으로 알려져 있다.[75]
피타고라스 항등식은 가장 기본적인 삼각 함수 공식 중 하나로, 다음과 같은 세 가지 형태가 있다.
5. 2. 오일러 공식
오일러 공식은 복소 지수 함수와 삼각 함수를 연결하는 중요한 공식으로, 다음과 같이 표현된다.:
여기서 ''e''는 자연로그의 밑이고, ''i''는 허수 단위 ()이며, ''x''는 라디안으로 측정된 각도이다. 이 공식은 실수 ''x''뿐만 아니라 복소수 변수에 대해서도 성립한다.[38]
복소수 (''x'', ''y''는 실수)에 대한 복소 지수 함수는 오일러 공식을 이용하여 다음과 같이 정의할 수 있다.
:
오일러 공식을 이용하면 사인, 코사인, 탄젠트 함수를 복소 지수 함수 형태로 표현할 수 있으며, 이는 수학적 분석 등 다양한 분야에서 유용하게 활용된다.[39][40][75]
:
:
:
5. 3. 기타 항등식
삼각법은 모든 가능한 입력 값에 대해 항상 참이 되는 방정식, 즉 많은 항등식으로 유명하다.[74]
각도만 포함하는 항등식은 '''삼각 함수 공식'''이라고 부르며, 이와 달리 주어진 삼각형의 변과 각도를 모두 관련시키는 방정식은 '''삼각형 항등식'''으로 알려져 있다.[75]
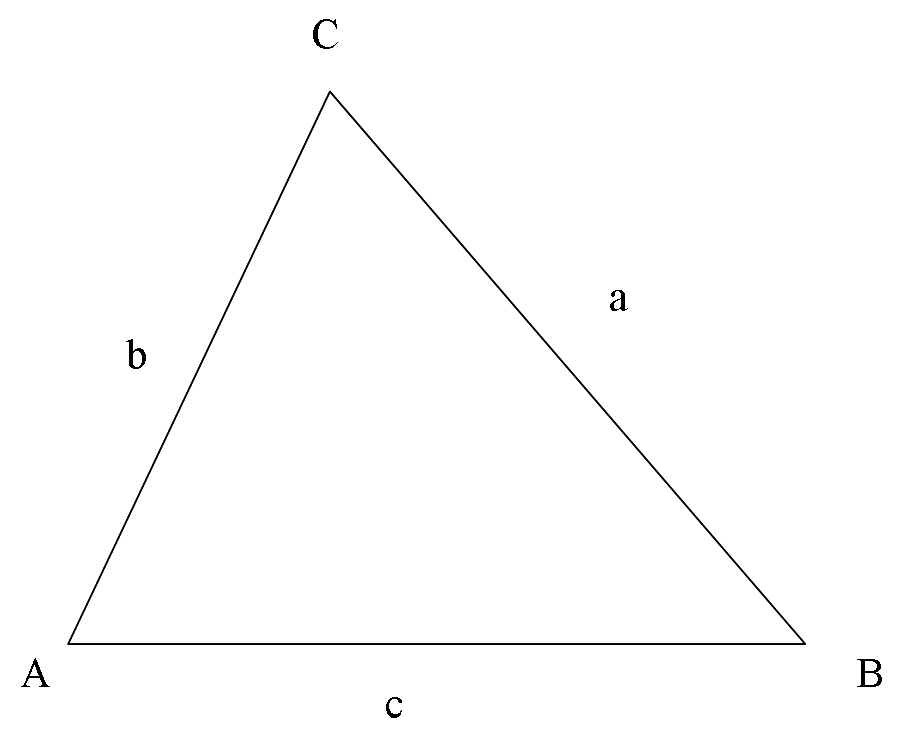
다음 항등식들에서, ''A'', ''B'', ''C''는 삼각형의 각도를 나타내고, ''a'', ''b'', ''c''는 각 각도에 마주보는 삼각형 변의 길이를 의미한다(그림 참조).
참조
[1]
OEtymD
trigonometry
2022-03-18
[2]
서적
Encyclopedia of Science
The Gale Group
2002
[3]
서적
A treatise on trigonometry, plane and spherical: with its application to navigation and surveying, nautical and practical astronomy and geodesy, with logarithmic, trigonometrical, and nautical tables
https://books.google[...]
G. P. Putnam
[4]
서적
Trigonometry For Dummies
https://books.google[...]
John Wiley & Sons
2014-02-24
[5]
서적
Trigonometry
https://books.google[...]
Cengage Learning
2006-03-10
[6]
서적
Cambridge IGCSE Core Mathematics
https://books.google[...]
Hachette UK
[7]
서적
A history of ancient mathematical astronomy. 1
https://books.google[...]
Springer-Verlag
[8]
Citation
Ptolemy's Almagest
Princeton University Press
[9]
서적
Mathematics Across Cultures: The History of Non-western Mathematics
Springer Science+Business Media
[10]
간행물
Mathematical Methods in Abū al-Wafāʾs Almagest and the Qibla Determinations
Cambridge University Press
[11]
뉴스
Islamic astronomy
Scientific American
1986
[12]
서적
Armchair Algebra: Everything You Need to Know From Integers To Equations
https://books.google[...]
Book Sales
2018-02-13
[13]
웹사이트
Nasir al-Din al-Tusi
https://mathshistory[...]
2021-01-08
[14]
서적
the cambridge history of science
https://www.cambridg[...]
Cambridge University Press
2013-10
[15]
Cite encyclopedia
ṬUSI, NAṢIR-AL-DIN i. Biography
http://www.iranicaon[...]
2018-08-05
[16]
웹사이트
trigonometry
http://www.britannic[...]
Encyclopædia Britannica
2008-07-21
[17]
서적
The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook
Princeton University Press
[18]
웹사이트
Johann Müller Regiomontanus
https://mathshistory[...]
2021-01-08
[19]
서적
From Byzantium to Italy. Greek Studies in the Italian Renaissance
London
[20]
서적
The Rainbow of Mathematics: A History of the Mathematical Sciences
W.W. Norton
[21]
서적
Groundbreaking Scientific Experiments, Inventions, and Discoveries of the Middle Ages and the Renaissance
https://books.google[...]
Greenwood Publishing Group
[22]
서적
From Kant to Hilbert Volume 1: A Source Book in the Foundations of Mathematics
https://books.google[...]
OUP Oxford
2005-04-21
[23]
서적
Focus on Curves and Surfaces
https://books.google[...]
Premier Press
2002-11
[24]
서적
Algebra and Trigonometry
https://books.google[...]
Cengage Learning
2015-01-16
[25]
서적
Mathematical Time Capsules: Historical Modules for the Mathematics Classroom
https://books.google[...]
MAA
[26]
서적
Pre-Calculus For Dummies
https://books.google[...]
John Wiley & Sons
[27]
MathWorld
SOHCAHTOA
[28]
서적
Key Maths : GCSE, Higher.
https://www.worldcat[...]
Stanley Thornes Publishers
2001
[29]
서적
Memory: A Very Short Introduction
Oxford
[30]
서적
Precalculus: A Problems-Oriented Approach, Enhanced Edition
https://books.google[...]
Cengage Learning
2009-07-17
[31]
서적
The Complete Idiot's Guide to Calculus
https://books.google[...]
Alpha Books
[32]
서적
Maths: A Student's Survival Guide: A Self-Help Workbook for Science and Engineering Students
https://books.google[...]
Cambridge University Press
2003-09-18
[33]
서적
Mathematics for Electrical Engineering and Computing
https://books.google[...]
Elsevier
2003-06-30
[34]
서적
Calculus of a Single Variable
https://books.google[...]
Cengage Learning
2008-11-10
[35]
서적
Mathematics for Secondary School Teachers
https://books.google[...]
MAA
[36]
서적
Calculus for Scientists and Engineers
https://books.google[...]
Springer
2019-08-03
[37]
서적
Complex Analysis
https://books.google[...]
Springer
2013-03-14
[38]
서적
Digital Signal Processing and Spectral Analysis for Scientists: Concepts and Applications
https://books.google[...]
Springer
2015-12-09
[39]
서적
SIGNALS AND SYSTEMS
https://books.google[...]
PHI Learning
2014-03-24
[40]
서적
Mathematics and Its History
https://books.google[...]
Springer Science & Business Media
2010-07-23
[41]
서적
The History of Mathematical Tables: From Sumer to Spreadsheets
OUP Oxford
2003-10-02
[42]
서적
Trigonometry with calculators
https://books.google[...]
Prindle, Weber & Schmidt
[43]
서적
Instructions for Post-trig and Mannheim-trig Slide Rules
https://books.google[...]
Frederick Post Company
[44]
간행물
Calculator keys—what they do
https://books.google[...]
Bonnier Corporation
1974-04
[45]
서적
Programming Challenges: The Programming Contest Training Manual
https://books.google[...]
Springer Science & Business Media
2006-04-18
[46]
서적
Intel® 64 and IA-32 Architectures Software Developer's Manual Combined Volumes: 1, 2A, 2B, 2C, 3A, 3B and 3C
http://download.inte[...]
Intel
[47]
서적
Elements of Plane and Spherical Trigonometry: With Their Applications to Heights and Distances Projections of the Sphere, Dialling, Astronomy, the Solution of Equations, and Geodesic Operations
https://books.google[...]
Baldwin, Cradock, and Joy
[48]
논문
Mathematical methods in ancient astronomy
[49]
서적
Astronomy: The Solar System and Beyond
https://books.google[...]
Cengage Learning
2009-01-05
[50]
서적
The Practical Mathematician, Containing Logarithms, Geometry, Trigonometry, Mensuration, Algebra, Navigation, Spherics and Natural Philosophy, Etc
https://books.google[...]
1800
[51]
서적
Elements of Robotics
https://books.google[...]
Springer
[52]
서적
Plane Trigonometry and Its Application to Mensuration and Land Surveying: Accompanied with All the Necessary Logarithmic and Trigonometric Tables
https://archive.org/[...]
D. Appleton & Company
[53]
서적
Geographers: Biobibliographical Studies
https://books.google[...]
A&C Black
2015-12-14
[54]
서적
Fourier and Laplace Transforms
https://books.google[...]
Cambridge University Press
2003-08-07
[55]
서적
Visual Quantum Mechanics: Selected Topics with Computer-Generated Animations of Quantum-Mechanical Phenomena
https://books.google[...]
Springer Science & Business Media
2007-05-08
[56]
서적
Applications of Fourier Transforms to Generalized Functions
https://books.google[...]
WIT Press
[57]
서적
Trigonometry for the Physical Sciences
https://books.google[...]
Appleton-Century-Crofts
[58]
서적
College Algebra and Trigonometry: Basics Through Precalculus
https://books.google[...]
Scott, Foresman
[59]
서적
Wave Phenomena
https://books.google[...]
Dover Publications
2014-05-05
[60]
서적
Plane Trigonometry
https://books.google[...]
McGraw-Hill
1992-11-01
[61]
서적
Applications of Digital Signal Processing to Audio and Acoustics
https://books.google[...]
Springer Science & Business Media
2006-04-18
[62]
서적
Architecture and Mathematics from Antiquity to the Future: Volume I: Antiquity to the 1500s
https://books.google[...]
Birkhäuser
2015-02-09
[63]
서적
Essential Skills for GCSE Biology
https://books.google[...]
Hodder Education
2019-07-15
[64]
서적
Medical Imaging: Analysis of Multimodality 2D/3D Images
https://books.google[...]
IOS Press
[65]
서적
Symmetry of Crystals and Molecules
https://books.google[...]
Oxford University Press
[66]
서적
Trigonometric Sums in Number Theory and Analysis
https://books.google[...]
Walter de Gruyter
2008-08-22
[67]
서적
Study Guide for the Course in Meteorological Mathematics: Latest Revision, Feb. 1, 1943
https://books.google[...]
[68]
서적
Oceanography, the past
https://books.google[...]
Springer-Verlag
[69]
웹사이트
JPEG Standard (JPEG ISO/IEC 10918-1 ITU-T Recommendation T.81)
https://www.w3.org/G[...]
International Telecommunication Union
1993
[70]
서적
The Routledge Linguistics Encyclopedia
https://books.google[...]
Routledge
2009-12-04
[71]
서적
Foundations of Mathematical and Computational Economics
https://books.google[...]
Springer Science & Business Media
2011-01-11
[72]
서적
A System of Crystallography, with Its Application to Mineralogy
https://archive.org/[...]
R. Griffin
[73]
서적
Real-World Flash Game Development: How to Follow Best Practices AND Keep Your Sanity
https://archive.org/[...]
CRC Press
2012-11-12
[74]
서적
Trigonometry I/E Sup
https://books.google[...]
Addison Wesley
2002-07
[75]
서적
CONCISE DICTIONARY OF MATHEMATICS
https://books.google[...]
V&S Publishers
2015-01-06
[76]
서적
Trigonometry
https://books.google[...]
Cengage Learning
2010-01-29
[77]
서적
Precalculus
https://books.google[...]
John Wiley & Sons
2010-01-19
[78]
서적
Technical Mathematics with Calculus
https://books.google[...]
Cengage Learning
[79]
웹사이트
Solving Triangles
http://www.mathsisfu[...]
Maths is Fun
2017-03-20
[80]
웹사이트
4.2.1 三角形の決定
http://www.ravco.jp/[...]
2017-03-19
[81]
간행물
球面三角法の簡潔かつ体系的な理解への試み
https://www.gsi.go.j[...]
국토지리원
[82]
서적
The Growth of Physical Science
https://books.google[...]
1947
[83]
문서
Episodes from the Early History of Astronomy
Springer
2001
[84]
문서
Thurston
https://books.google[...]
[85]
서적
Ptolemy's Almagest
Princeton University Press
[86]
문서
Thurston
https://books.google[...]
[87]
문서
『アルマゲスト』薮内清の解説
[88]
웹사이트
ABU’L-WAFĀ BŪZJĀNI
http://www.iranicaon[...]
2017-03-09
[89]
웹사이트
BĪRŪNĪ, ABŪ RAYḤĀN iii. Mathematics and Astronomy
http://www.iranicaon[...]
2017-03-09
[90]
웹사이트
ṬUSI, NAṢIR-AL-DIN ii. AS MATHEMATICIAN AND ASTRONOMER
http://www.iranicaon[...]
2017-03-09
[91]
논문
Islamic Math and Science
https://articles.ads[...]
2017-04-13
[92]
문서
『アルマゲスト』薮内清の解説
[93]
서적
Mathematics in Historical Context
https://books.google[...]
Mathematical Association of America
2017-04-11
[94]
서적
Mathematical Tables and Other Aids to Computation: A Quarterly Journal
https://books.google[...]
National Research Council
[95]
서적
Groundbreaking Scientific Experiments, Inventions, and Discoveries of the Middle Ages and the Renaissance
https://books.google[...]
Greenwood Publishing Group
[96]
서적
数学の歴史
共立出版
[97]
문서
Michel Chasles
https://books.google[...]
[98]
서적
The Rainbow of Mathematics: A History of the Mathematical Sciences
W.W. Norton
[99]
문서
From Kant to Hilbert: a source book in the foundations of mathematics
https://books.google[...]
Oxford University Press US
[100]
문서
Focus on Curves and Surfaces
https://books.google[...]
[101]
웹사이트
《唐開元占經》
https://ctext.org/wi[...]
2020-12-12
[102]
웹사이트
測量全義 (そくりょうぜんぎ)
https://kotenseki.ni[...]
2020-12-10
[103]
논문
イエズス会士と西洋数学の伝入
https://archives.buk[...]
佛教大学中国言語文化研究会
2001-07
[104]
논문
西洋数学に関連した外来書の伝来(2)
http://www.wasan.jp/[...]
近畿数学史学会
2023-10-17
[105]
웹사이트
秘伝地域図法大全書. 上,中,下
https://dl.ndl.go.jp[...]
2020-12-10
[106]
간행물
江戸初期の方位及び角度の概念から見た測量術の形成についての一考察
https://iss.ndl.go.j[...]
国立科学博物館
[107]
간행물
紅毛流として伝来した測量術について(1) (数学史の研究 : RIMS研究集会報告集)
https://hdl.handle.n[...]
京都大学数理解析研究所
[107]
간행물
紅毛流として伝来した測量術について(II) : 三角関数表の伝来と二つの経路 (数学史の研究)
https://hdl.handle.n[...]
京都大学数理解析研究所
[108]
간행물
長井忠三郎と『三角法挙要』 (数学史の研究)
https://hdl.handle.n[...]
京都大学数理解析研究所
2011-04
[109]
간행물
三角法と対数の教材に関する史的考察
https://hdl.handle.n[...]
上越教育大学数学教室
[110]
웹사이트
割円十分標
http://kotenseki.nij[...]
2020-12-12
[111]
논문
阿蘭陀通詞 志筑忠雄の思想 : 近世日本における統一的宇宙観の展開
http://id.nii.ac.jp/[...]
[112]
뉴스
「ホワイトハウス周辺で実弾発砲、新警備システムを試験」
https://www.cnn.co.j[...]
CNN
2017-08-27
[113]
웹인용
보관된 사본
http://dl.dongascien[...]
2018-06-10
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com

