수학적 형태학

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

수학적 형태학은 이미지 처리 및 분석에 사용되는 이론 및 기술 집합이다. 1964년 조르주 마테론과 장 세라에 의해 개발되었으며, 이진 이미지의 집합 연산에서 시작하여 그레이스케일 이미지 및 일반 격자 구조로 확장되었다. 주요 연산자로는 침식, 팽창, 열기, 닫기가 있으며, 이를 통해 이미지의 모양을 변형하고 특징을 추출할 수 있다. 수학적 형태학은 의료 영상 분석, 자율 주행 시스템, 산림 변화 탐지 등 다양한 분야에 응용된다.

더 읽어볼만한 페이지

형태학 - 형태학 (생물학)
형태학은 생물의 형태와 구조를 연구하는 생물학의 한 분야로, 아리스토텔레스의 생물학에서 비롯되어 괴테와 부르다흐 등에 의해 발전했으며, 비교 형태학, 기능 형태학, 실험 형태학 등으로 나뉘어 분류학 및 진화론 연구에 기여한다.
형태학 - 모양
모양은 기하학에서 위치, 크기, 방향, 반사 요소를 제거한 기하학적 정보로, 도형을 이동, 확대, 회전, 반사해도 동일하게 간주되는 점, 선, 평면, 다각형, 원뿔 곡선, 다면체 등의 다양한 기하학적 대상을 지칭하며 합동, 닮음, 동형사상 등의 개념과 프로크루스테스 분석 방법으로 설명하거나 비교된다.
수학적 형태학 - 구조적 요소
구조적 요소는 이진 이미지 처리에서 사용되는 작고 단순한 형태의 집합으로, 유클리드 공간 또는 정수 격자에서의 이진 이미지를 정의하며, 원, 정사각형, 십자 모양 등 다양한 형태를 가질 수 있다.
수학적 형태학 - 가지치기 (형태학)
가지치기는 형태학적 이미지 처리 기법으로, 이미지 골격에서 불필요한 가지를 제거하기 위해 솎아내기, 끝점 찾기, 끝점 팽창, 합집합 단계를 거쳐 3x3 구조적 요소 행렬을 사용한다.
디지털 기하학 - 디지털 이미지
디지털 이미지는 픽셀로 구성된 디지털 데이터 집합으로, 래스터 이미지와 벡터 이미지로 나뉘며 디지털 카메라, 스캐너, 또는 수학적 함수를 통해 생성되고, JPEG와 같은 압축 기술 덕분에 인터넷에서 널리 사용된다.
디지털 기하학 - 가지치기 (형태학)
가지치기는 형태학적 이미지 처리 기법으로, 이미지 골격에서 불필요한 가지를 제거하기 위해 솎아내기, 끝점 찾기, 끝점 팽창, 합집합 단계를 거쳐 3x3 구조적 요소 행렬을 사용한다.

수학적 형태학
개요
수학적 형태학의 예시
분야	이미지 처리, 컴퓨터 비전, 머신 비전
유형	이미지 처리 기술
관련 주제	모폴로지, 격자 이론, 수학적 형태학, 이미지 분할
기본 연산
침식 (Erosion)	이미지의 경계를 침식시키는 연산
팽창 (Dilation)	이미지의 경계를 팽창시키는 연산
열기 (Opening)	침식 후 팽창 연산 (작은 객체 제거에 사용)
닫기 (Closing)	팽창 후 침식 연산 (작은 구멍 메우기에 사용)
응용 분야
이미지 분할	이미지를 여러 영역으로 분할하는 데 사용
특징 추출	이미지에서 특징적인 정보를 추출하는 데 사용
객체 인식	이미지 내의 객체를 식별하고 분류하는 데 사용
노이즈 제거	이미지에서 노이즈를 제거하는 데 사용
이미지 개선	이미지의 품질을 향상시키는 데 사용

2. 역사

수학적 형태학은 1964년 조르주 마테론(Georges Matheron)과 장 세라(Jean Serra)의 공동 연구를 통해 프랑스 파리 국립고등광업학교(École des Mines de Paris)에서 개발되었다. 마테론은 얇은 단면에서 광물 특성을 정량화하는 세라의 박사 학위 논문을 지도했으며, 이 연구는 새로운 실용적 접근 방식뿐만 아니라 적분 기하학 및 위상수학의 이론적 발전을 가져왔다.

1968년, 파리 국립고등광업학교는 마테론과 세라의 주도로 프랑스 퐁텐블로에 ''수학적 형태학 센터(Centre de Morphologie Mathématique)''를 설립했다.

1960년대 후반과 1970년대 대부분 동안, 수학적 형태학은 본질적으로 이진 이미지를 집합으로 처리하여 Hit-or-miss 변환, 팽창, 침식, 열기, 닫기, 입도 분석, 얇게 하기, 골격화, 궁극적 침식, 조건부 이등분선 등 많은 수의 이진 연산자와 기법을 생성하는 데 중점을 두었다. 새로운 이미지 모델을 기반으로 하는 무작위적 접근 방식도 개발되었다. 이 기간의 대부분의 작업은 퐁텐블로에서 개발되었다.

1970년대 중반부터 1980년대 중반까지, 수학적 형태학은 그레이스케일 함수와 이미지로 일반화되었다. 팽창, 침식 등과 같은 주요 개념을 함수로 확장하는 것 외에도, 이러한 일반화는 형태학적 기울기, 톱햇 변환 및 분할 접근 방식인 유역과 같은 새로운 연산자를 생성했다.

1980년대와 1990년대에, 여러 국가의 연구 센터에서 이 방법을 채택하고 조사하기 시작하면서 수학적 형태학은 더 넓은 인정을 받았다. 수학적 형태학은 특히 잡음이 있는 이미지의 비선형 필터링 분야에서 많은 수의 이미지 문제와 응용 분야에 적용되기 시작했다.

1986년, 세라는 이번에는 완전 격자를 기반으로 한 이론적 프레임워크로 수학적 형태학을 더욱 일반화했다. 이러한 일반화는 이론에 유연성을 가져와 컬러 이미지, 비디오, 그래프, 메쉬 등 훨씬 더 많은 구조에 적용할 수 있게 했다. 동시에 마테론과 세라는 새로운 격자 프레임워크를 기반으로 형태학적 필터링에 대한 이론도 정립했다.

1990년대와 2000년대에는 ''연결'' 및 ''레벨링''의 개념을 포함하여 추가적인 이론적 발전이 있었다.

1993년, 제1회 국제 수학적 형태학 심포지엄(ISMM)이 스페인 바르셀로나에서 개최되었다. 그 이후로 ISMM은 2~3년마다 개최되었다: 프랑스 퐁텐블로 (1994); 미국 애틀랜타 (1996); 네덜란드 암스테르담 (1998); 미국 팔로 알토 (2000); 호주 시드니 (2002); 프랑스 파리 (2005); 브라질 리우데자네이루 (2007); 네덜란드 흐로닝언 (2009); 이탈리아 인트라 (베르바니아) (2011); 스웨덴 웁살라 (2013); 아이슬란드 레이캬비크 (2015); 프랑스 퐁텐블로 (2017); 독일 자르브뤼켄 (2019).

2. 1. 초기 (1960년대)

수학적 형태학은 1964년 조르주 마테론(Georges Matheron)과 장 세라(Jean Serra)의 공동 연구를 통해 프랑스 파리 국립고등광업학교(École des Mines de Paris)에서 개발되었다. 마테론은 얇은 단면에서 광물 특성을 정량화하는 세라의 박사 학위 논문을 지도했으며, 이 연구는 새로운 실용적 접근 방식뿐만 아니라 적분 기하학 및 위상수학의 이론적 발전을 가져왔다.

1968년, 파리 국립고등광업학교는 마테론과 세라의 주도로 프랑스 퐁텐블로에 ''수학적 형태학 센터(Centre de Morphologie Mathématique)''를 설립했다.

2. 2. 발전 (1970년대 ~ 1980년대)

1960년대 후반과 1970년대 대부분 동안, 수학적 형태학은 이진 이미지를 집합으로 처리하여 Hit-or-miss 변환, 팽창, 침식, 열기, 닫기, 입도 분석, 얇게 하기, 골격화, 궁극적 침식, 조건부 이등분선 등 많은 수의 이진 연산자와 기법을 생성하는 데 중점을 두었다. 새로운 이미지 모델을 기반으로 하는 무작위적 접근 방식도 개발되었다. 이 기간의 대부분의 작업은 퐁텐블로에서 개발되었다.

1970년대 중반부터 1980년대 중반까지, 수학적 형태학은 그레이스케일 함수와 이미지로 일반화되었다. 팽창, 침식 등과 같은 주요 개념을 함수로 확장하는 것 외에도, 이러한 일반화는 형태학적 기울기, 톱햇 변환 및 분할 접근 방식인 유역과 같은 새로운 연산자를 생성했다.

1980년대와 1990년대에, 여러 국가의 연구 센터에서 이 방법을 채택하고 조사하기 시작하면서 수학적 형태학은 더 넓은 인정을 받았다. 수학적 형태학은 특히 잡음이 있는 이미지의 비선형 필터링 분야에서 많은 수의 이미지 문제와 응용 분야에 적용되기 시작했다.

2. 3. 일반화 및 이론적 발전 (1980년대 후반 ~ 2000년대)

1986년, 장 세라는 완전 격자를 기반으로 한 이론적 프레임워크로 수학적 형태학을 더욱 일반화했다. 이러한 일반화는 이론에 유연성을 가져와 컬러 이미지, 비디오, 그래프, 메쉬 등 훨씬 더 많은 구조에 적용할 수 있게 했다. 동시에 조르주 마테론과 세라는 새로운 격자 프레임워크를 기반으로 형태학적 필터링에 대한 이론도 정립했다.

1990년대와 2000년대에는 ''연결'' 및 ''레벨링''의 개념을 포함하여 추가적인 이론적 발전이 있었다.

2. 4. 국제 수학적 형태학 심포지엄 (ISMM)

수학적 형태학은 1964년 조르주 마테론(Georges Matheron)과 장 세라(Jean Serra)의 공동 연구를 통해 프랑스 파리 국립고등광업학교(École des Mines de Paris)에서 개발되었다. 1993년, 제1회 국제 수학적 형태학 심포지엄(ISMM)이 스페인 바르셀로나에서 개최되었다. 그 이후 ISMM은 2~3년마다 다음의 장소에서 개최되었다:

프랑스 퐁텐블로 (1994)
미국 애틀랜타 (1996)
네덜란드 암스테르담 (1998)
미국 팔로 알토 (2000)
호주 시드니 (2002)
프랑스 파리 (2005)
브라질 리우데자네이루 (2007)
네덜란드 흐로닝언 (2009)
이탈리아 인트라 (베르바니아) (2011)
스웨덴 웁살라 (2013)
아이슬란드 레이캬비크 (2015)
프랑스 퐁텐블로 (2017)
독일 자르브뤼켄 (2019)

3. 이진 형태학

이진 형태학에서 이미지는 어떤 차원 ''d''에 대해 유클리드 공간 $\mathbb{R}^d$ 또는 정수 격자 $\mathbb{Z}^d$ 의 부분 집합으로 간주된다.

== 구조적 요소 ==

수학적 형태학에서 구조적 요소(''B''로 표기)는 이진 이미지를 탐색하여 이미지의 모양에 어떻게 맞거나 맞지 않는지를 판단하는 데 사용되는 간단하고 미리 정의된 모양이다. 구조적 요소는 자체적으로 이진 이미지(즉, 공간 또는 격자의 부분 집합)이다.

구조적 요소의 예시는 다음과 같다:

$E=\mathbb{R}^2$ 일 때, ''B''는 원점을 중심으로 하고 반지름이 ''r''인 열린 원이다.
$E=\mathbb{Z}^2$ 일 때, ''B''는 3x3 사각형으로, ''B''={(-1,-1), (-1,0), (-1,1), (0,-1), (0,0), (0,1), (1,-1), (1,0), (1,1)}이다.
$E=\mathbb{Z}^2$ 일 때, ''B''는 "십자 모양"으로, ''B''={(-1,0), (0,-1), (0,0), (0,1), (1,0)}이다.

== 기본 연산자 ==

병진 불변이다.
단조증가이다. 즉, $A\subseteq C$ 이면 $A\oplus B \subseteq C\oplus B$ 이고 $A\ominus B \subseteq C\ominus B$ 등이다.
팽창은 가환 연산이다.
''E''의 원점이 구조적 요소 ''B''에 있으면 $A\ominus B\subseteq A\circ B\subseteq A\subseteq A\bullet B\subseteq A\oplus B$ 이다.
결합법칙을 만족한다. 즉, $(A\oplus B)\oplus C = A\oplus (B\oplus C)$ 이다. 게다가, 침식은 $(A\ominus B)\ominus C = A\ominus (B\oplus C)$ 이 된다.
침식과 팽창은 쌍대성 $A \oplus B = (A^{c} \ominus B^{s})^{c}$ 을 만족한다.
열기와 닫기도 쌍대성 $A \bullet B = (A^{c} \circ B^{s})^{c}$ 을 만족한다.
팽창은 합집합에서 분배법칙이 성립한다.
침식은 교집합에서 분배법칙이 성립한다.
팽창은 침식의 의사역행렬이고 반대로도 성립한다: $A\subseteq (C\ominus B)$ 이면 $(A\oplus B)\subseteq C$ 이다.
열기와 닫기는 멱등적이다.
열기는 역 확장적이고 닫기는 ''확장적''이다. 즉, $A\circ B\subseteq A$ 이고, $A\subseteq A\bullet B$ 이다.

== 침식 (Erosion) ==

구조적 요소 ''B''에 대한 이진 이미지 ''A''의 침식은 다음과 같이 정의된다:

:

A \ominus B = \{z\in E | B_{z} \subseteq A\}

,

이 때, ''B''_''z''는 ''B''를 벡터 z에 대해서 평행이동한 것이다. 즉,

B_z = \{b+z|b\in B\}

,

\forall z\in E

이다.

구조적 요소 ''B''가 중심을 가지고(예: 원판이나 정사각형), 중심이 ''E''의 원점에 위치하면, ''B''에 대한 ''A''의 침식은 by ''B''가 ''A''의 내부에서 움직일 때의 ''B''의 중심의 자취로 생각할 수 있다. 예를 들어, 원점을 중심으로 하고 한 변의 길이가 10인 정사각형을 원점을 중심으로 하고 반지름이 2인 원판으로 하는 침식은 원점을 중심으로 하고 한 변이 6인 정사각형이다.

''B''에 대한 ''A''의 침식은 다음과 같은 표현으로도 쓸 수 있다:

A \ominus B = \bigcap_{b\in B} A_{-b}

.

진한 파란색 정사각형을 원판으로 침식시킨 것으로, 밝은 파란색 정사각형을 만든다.

적용 예시: 검은 사진의 팩스를 받았다고 가정하자. 전부 새는 펜으로 쓴 것 같아 보인다. 침식 과정은 두꺼운 선을 얇게 만들고 글자 "o"의 구멍을 검출할 수 있다.

한국의 의료 영상 분석에서 침식 연산을 활용하여 종양의 경계를 추출하는 연구 사례가 있다.

== 팽창 (Dilation) ==

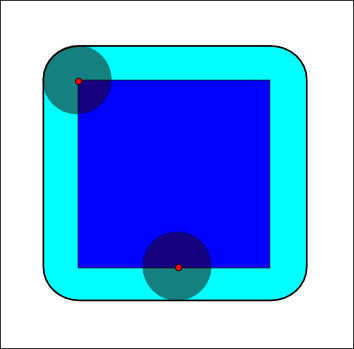
짙은 파란색 사각형을 원판으로 팽창해서 둥근 모서리가 있는 밝은 파란색 사각형을 만든다.

''A''를 구조적 요소 ''B''로 팽창시킨 것은 다음과 같이 정의된다:

::

A \oplus B = \bigcup_{b\in B} A_b,

여기서 ''A''_''b''는 ''A''를 ''b''로 평행이동 시킨 것이다.

팽창은 가환 연산이기 때문에 다음과 같이 쓸 수 있다:

A \oplus B = B\oplus A = \bigcup_{a\in A} B_a

.

''B''가 원점을 중심으로 두고 있다면, ''A''를 ''B''로 팽창시킨 것은 ''B''의 중심이 ''A''의 내부에서 움직일 때 ''B''에 있는 점들의 궤적으로 이해할 수 있다. 크기가 10이고 원점에 중심을 둔 정사각형을 마찬가지로 원점을 중심으로 둔 반지름이 2인 원판으로 팽창시키면 원점을 중심으로 하고 꼭짓점이 둥근 크기가 14인 정사각형이 된다. 둥근 꼭짓점의 반지름은 2이다.

팽창은 다음을 통해서도 얻을 수 있다:

A \oplus B = \{z \in E \mid (B^s)_z \cap A\neq \varnothing\}

, 이 때 ''B''^''s''는 ''B''의 대칭이다. 즉,

B^s=\{x\in E \mid -x \in B\}

이다.

팽창은 침식의 쌍대연산이다. 매우 가는 선으로 그린 그림은 "팽창"하면 두꺼운 선으로 만들 수 있다. 이 말을 파악하기 가장 쉬운 방법은 같은 팩스나 글씨를 더 두꺼운 펜으로 쓴 것을 생각하는 것이다.

한국에서는 자율 주행 시스템의 차선 인식 정확도를 높이는 데 팽창 연산이 활용되기도 한다. 팽창 연산을 통해 차선 이미지를 보정하여, 시스템이 차선을 더욱 정확하게 인식하도록 돕는다.

== 열기 (Opening) ==

''A''를 ''B''로 연 것은 ''A''를 ''B''로 침식하고, 잇따라 ''B''로 팽창 한 것이다:

A \circ B  = (A \ominus B) \oplus B

.

열기는 이렇게도 표현할 수 있다:

A \circ B = \bigcup_{B_x\subseteq A} B_x

. 구조적 요소 ''B''를 이미지 ''A''안에서 움직일 때의 자취로 생각한 것이다. 한 변의 길이가 10인 정사각형의 경우에 반지름이 2인 원판을 구조적 요소일 때, 열기는 한 변의 길이가 10이고 모서리의 반지름이 2인 둥근 사각형이다.

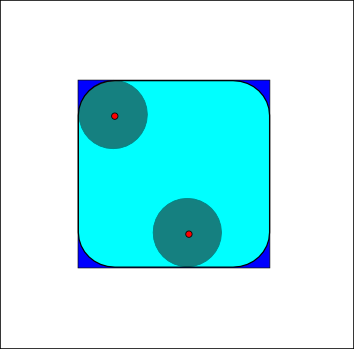
진한 파란색 정사각형을 원판으로 연 것이다, 꼭짓점이 둥근 밝은 파란색 정사각형을 만든다.

적용 예시: 누가 방수 코팅된 종이에 메모를 해서 온통 뿌리에 잔뿌리가 뻩은 것처럼 있다고 가정하자. 이 때, 열기는 본질적으로 내용은 보존하면서 "가는 선"을 제거한다. 부작용은 무엇이든지 둥글게 만든다는 것이다. 뾰족한 모서리는 점차 사라질 것이다.

== 닫기 (Closing) ==

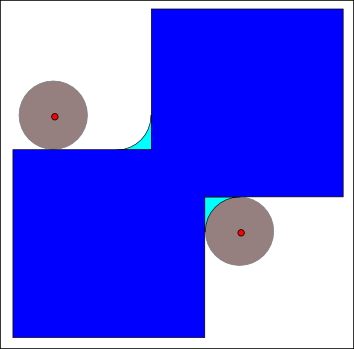
짙은 파란색 도형 (정사각형 두 개의 합집합)을 원판으로 닫은 것은 짙은 파란색과 연한 파란색 영역의 합집합이다.

''A''를 ''B''로 닫은 것은 ''A''를 ''B''로 팽창하고, 잇따라 ''B''로 침식시킨 것이다:

:

A \bullet B  = (A \oplus B) \ominus B

.

닫기는

A \bullet B = (A^{c} \circ B^{s})^{c}

으로도 쓸 수 있고, 여기서 ''X''^''c''는 ''E''에 대한 ''X''의 여집합이고 다(즉,

X^{c}=\{x\in E | x\not \in X\}

이다). 위의 말은 닫기는 이미지 ''A''의 외부에서 움직이는 구조적 요소의 자취의 여집합이라는 것을 의미한다.

== 다른 연산자와 도구 ==

수학적 형태학(Mathematical morphology, MM)은 적중과 비적중 변환, 가지치기 변환, 형태학적 골격, 재생성에 의한 필터링, 궁극적 침식과 조건 이등분, 입도 측정법, 지오데식 거리 함수등의 연산자와 도구를 제공한다.

3. 1. 구조적 요소

수학적 형태학에서 구조적 요소(''B''로 표기)는 이진 이미지를 탐색하여 이미지의 모양에 어떻게 맞거나 맞지 않는지를 판단하는 데 사용되는 간단하고 미리 정의된 모양이다. 구조적 요소는 자체적으로 이진 이미지(즉, 공간 또는 격자의 부분 집합)이다.

구조적 요소의 예시는 다음과 같다:

$E=\mathbb{R}^2$ 일 때, ''B''는 원점을 중심으로 하고 반지름이 ''r''인 열린 원이다.
$E=\mathbb{Z}^2$ 일 때, ''B''는 3x3 사각형으로, ''B''={(-1,-1), (-1,0), (-1,1), (0,-1), (0,0), (0,1), (1,-1), (1,0), (1,1)}이다.
$E=\mathbb{Z}^2$ 일 때, ''B''는 "십자 모양"으로, ''B''={(-1,0), (0,-1), (0,0), (0,1), (1,0)}이다.

3. 2. 기본 연산자

병진 불변이다.
단조증가이다. 즉, $A\subseteq C$ 이면 $A\oplus B \subseteq C\oplus B$ 이고 $A\ominus B \subseteq C\ominus B$ 등이다.
팽창은 가환 연산이다.
''E''의 원점이 구조적 요소 ''B''에 있으면 $A\ominus B\subseteq A\circ B\subseteq A\subseteq A\bullet B\subseteq A\oplus B$ 이다.
결합법칙을 만족한다. 즉, $(A\oplus B)\oplus C = A\oplus (B\oplus C)$ 이다. 게다가, 침식은 $(A\ominus B)\ominus C = A\ominus (B\oplus C)$ 이 된다.
침식과 팽창은 쌍대성 $A \oplus B = (A^{c} \ominus B^{s})^{c}$ 을 만족한다.
열기와 닫기도 쌍대성 $A \bullet B = (A^{c} \circ B^{s})^{c}$ 을 만족한다.
팽창은 합집합에서 분배법칙이 성립한다.
침식은 교집합에서 분배법칙이 성립한다.
팽창은 침식의 의사역행렬이고 반대로도 성립한다: $A\subseteq (C\ominus B)$ 이면 $(A\oplus B)\subseteq C$ 이다.
열기와 닫기는 멱등적이다.
열기는 역 확장적이고 닫기는 ''확장적''이다. 즉, $A\circ B\subseteq A$ 이고, $A\subseteq A\bullet B$ 이다.

== 침식 (Erosion) ==

구조적 요소 ''B''에 대한 이진 이미지 ''A''의 침식은 다음과 같이 정의된다:

:

A \ominus B = \{z\in E | B_{z} \subseteq A\}

,

이 때, ''B''_''z''는 ''B''를 벡터 z에 대해서 평행이동한 것이다. 즉,

B_z = \{b+z|b\in B\}

,

\forall z\in E

이다.

구조적 요소 ''B''가 중심을 가지고(예: 원판이나 정사각형), 중심이 ''E''의 원점에 위치하면, ''B''에 대한 ''A''의 침식은 by ''B''가 ''A''의 내부에서 움직일 때의 ''B''의 중심의 자취로 생각할 수 있다. 예를 들어, 원점을 중심으로 하고 한 변의 길이가 10인 정사각형을 원점을 중심으로 하고 반지름이 2인 원판으로 하는 침식은 원점을 중심으로 하고 한 변이 6인 정사각형이다.

''B''에 대한 ''A''의 침식은 다음과 같은 표현으로도 쓸 수 있다:

A \ominus B = \bigcap_{b\in B} A_{-b}

.

적용 예시: 검은 사진의 팩스를 받았다고 가정하자. 전부 새는 펜으로 쓴 것 같아 보인다. 침식 과정은 두꺼운 선을 얇게 만들고 글자 "o"의 구멍을 검출할 수 있다.

한국의 의료 영상 분석에서 침식 연산을 활용하여 종양의 경계를 추출하는 연구 사례가 있다.

== 팽창 (Dilation) ==

''A''를 구조적 요소 ''B''로 팽창시킨 것은 다음과 같이 정의된다:

::

A \oplus B = \bigcup_{b\in B} A_b,

여기서 ''A''_''b''는 ''A''를 ''b''로 평행이동 시킨 것이다.

팽창은 가환 연산이기 때문에 다음과 같이 쓸 수 있다:

A \oplus B = B\oplus A = \bigcup_{a\in A} B_a

.

''B''가 원점을 중심으로 두고 있다면, ''A''를 ''B''로 팽창시킨 것은 ''B''의 중심이 ''A''의 내부에서 움직일 때 ''B''에 있는 점들의 궤적으로 이해할 수 있다. 크기가 10이고 원점에 중심을 둔 정사각형을 마찬가지로 원점을 중심으로 둔 반지름이 2인 원판으로 팽창시키면 원점을 중심으로 하고 꼭짓점이 둥근 크기가 14인 정사각형이 된다. 둥근 꼭짓점의 반지름은 2이다.

팽창은 다음을 통해서도 얻을 수 있다:

A \oplus B = \{z \in E \mid (B^s)_z \cap A\neq \varnothing\}

, 이 때 ''B''^''s''는 ''B''의 대칭이다. 즉,

B^s=\{x\in E \mid -x \in B\}

이다.

팽창은 침식의 쌍대연산이다. 매우 가는 선으로 그린 그림은 "팽창"하면 두꺼운 선으로 만들 수 있다. 이 말을 파악하기 가장 쉬운 방법은 같은 팩스나 글씨를 더 두꺼운 펜으로 쓴 것을 생각하는 것이다.

한국에서는 자율 주행 시스템의 차선 인식 정확도를 높이는 데 팽창 연산이 활용되기도 한다. 팽창 연산을 통해 차선 이미지를 보정하여, 시스템이 차선을 더욱 정확하게 인식하도록 돕는다.

== 열기 (Opening) ==

''A''를 ''B''로 연 것은 ''A''를 ''B''로 침식하고, 잇따라 ''B''로 팽창 한 것이다:

A \circ B  = (A \ominus B) \oplus B

.

열기는 이렇게도 표현할 수 있다:

A \circ B = \bigcup_{B_x\subseteq A} B_x

. 구조적 요소 ''B''를 이미지 ''A''안에서 움직일 때의 자취로 생각한 것이다. 한 변의 길이가 10인 정사각형의 경우에 반지름이 2인 원판을 구조적 요소일 때, 열기는 한 변의 길이가 10이고 모서리의 반지름이 2인 둥근 사각형이다.

적용 예시: 누가 방수 코팅된 종이에 메모를 해서 온통 뿌리에 잔뿌리가 뻩은 것처럼 있다고 가정하자. 이 때, 열기는 본질적으로 내용은 보존하면서 "가는 선"을 제거한다. 부작용은 무엇이든지 둥글게 만든다는 것이다. 뾰족한 모서리는 점차 사라질 것이다.

== 닫기 (Closing) ==

''A''를 ''B''로 닫은 것은 ''A''를 ''B''로 팽창하고, 잇따라 ''B''로 침식시킨 것이다:

:

A \bullet B  = (A \oplus B) \ominus B

.

닫기는

A \bullet B = (A^{c} \circ B^{s})^{c}

으로도 쓸 수 있고, 여기서 ''X''^''c''는 ''E''에 대한 ''X''의 여집합이고 다(즉,

X^{c}=\{x\in E | x\not \in X\}

이다). 위의 말은 닫기는 이미지 ''A''의 외부에서 움직이는 구조적 요소의 자취의 여집합이라는 것을 의미한다.

3. 2. 1. 침식 (Erosion)

구조적 요소 ''B''에 대한 이진 이미지 ''A''의 침식은 다음과 같이 정의된다:

:

A \ominus B = \{z\in E | B_{z} \subseteq A\}

,

이 때, ''B''_''z''는 ''B''를 벡터 z에 대해서 평행이동한 것이다. 즉,

B_z = \{b+z|b\in B\}

,

\forall z\in E

이다.

구조적 요소 ''B''가 중심을 가지고(예: 원판이나 정사각형), 중심이 ''E''의 원점에 위치하면, ''B''에 대한 ''A''의 침식은 by ''B''가 ''A''의 내부에서 움직일 때의 ''B''의 중심의 자취로 생각할 수 있다. 예를 들어, 원점을 중심으로 하고 한 변의 길이가 10인 정사각형을 원점을 중심으로 하고 반지름이 2인 원판으로 하는 침식은 원점을 중심으로 하고 한 변이 6인 정사각형이다.

''B''에 대한 ''A''의 침식은 다음과 같은 표현으로도 쓸 수 있다:

A \ominus B = \bigcap_{b\in B} A_{-b}

.

적용 예시: 검은 사진의 팩스를 받았다고 가정하자. 전부 새는 펜으로 쓴 것 같아 보인다. 침식 과정은 두꺼운 선을 얇게 만들고 글자 "o"의 구멍을 검출할 수 있다.
(한국 관련 내용 추가) 한국의 의료 영상 분석에서 침식 연산을 활용하여 종양의 경계를 추출하는 연구 사례가 있다.

3. 2. 2. 팽창 (Dilation)

''A''를 구조적 요소 ''B''로 팽창시킨 것은 다음과 같이 정의된다:

::

A \oplus B = \bigcup_{b\in B} A_b,

여기서 ''A''_''b''는 ''A''를 ''b''로 평행이동 시킨 것이다.

팽창은 가환 연산이기 때문에 다음과 같이 쓸 수 있다:

A \oplus B = B\oplus A = \bigcup_{a\in A} B_a

.

''B''가 원점을 중심으로 두고 있다면, ''A''를 ''B''로 팽창시킨 것은 ''B''의 중심이 ''A''의 내부에서 움직일 때 ''B''에 있는 점들의 궤적으로 이해할 수 있다. 크기가 10이고 원점에 중심을 둔 정사각형을 마찬가지로 원점을 중심으로 둔 반지름이 2인 원판으로 팽창시키면 원점을 중심으로 하고 꼭짓점이 둥근 크기가 14인 정사각형이 된다. 둥근 꼭짓점의 반지름은 2이다.

팽창은 다음을 통해서도 얻을 수 있다:

A \oplus B = \{z \in E \mid (B^s)_z \cap A\neq \varnothing\}

, 이 때 ''B''^''s''는 ''B''의 대칭이다. 즉,

B^s=\{x\in E \mid -x \in B\}

이다.

팽창은 침식의 쌍대연산이다. 매우 가는 선으로 그린 그림은 "팽창"하면 두꺼운 선으로 만들 수 있다. 이 말을 파악하기 가장 쉬운 방법은 같은 팩스나 글씨를 더 두꺼운 펜으로 쓴 것을 생각하는 것이다.

한국에서는 자율 주행 시스템의 차선 인식 정확도를 높이는 데 팽창 연산이 활용되기도 한다. 팽창 연산을 통해 차선 이미지를 보정하여, 시스템이 차선을 더욱 정확하게 인식하도록 돕는다.

3. 2. 3. 열기 (Opening)

''A''를 ''B''로 연 것은 ''A''를 ''B''로 침식하고, 잇따라 ''B''로 팽창 한 것이다:

A \circ B  = (A \ominus B) \oplus B

.

열기는 이렇게도 표현할 수 있다:

A \circ B = \bigcup_{B_x\subseteq A} B_x

. 구조적 요소 ''B''를 이미지 ''A''안에서 움직일 때의 자취로 생각한 것이다. 한 변의 길이가 10인 정사각형의 경우에 반지름이 2인 원판을 구조적 요소일 때, 열기는 한 변의 길이가 10이고 모서리의 반지름이 2인 둥근 사각형이다.

적용 예시: 누가 방수 코팅된 종이에 메모를 해서 온통 뿌리에 잔뿌리가 뻩은 것처럼 있다고 가정하자. 이 때, 열기는 본질적으로 내용은 보존하면서 "가는 선"을 제거한다. 부작용은 무엇이든지 둥글게 만든다는 것이다. 뾰족한 모서리는 점차 사라질 것이다.

3. 2. 4. 닫기 (Closing)

''A''를 ''B''로 닫은 것은 ''A''를 ''B''로 팽창하고, 잇따라 ''B''로 침식시킨 것이다:

:

A \bullet B  = (A \oplus B) \ominus B

.

닫기는

A \bullet B = (A^{c} \circ B^{s})^{c}

으로도 쓸 수 있고, 여기서 ''X''^''c''는 ''E''에 대한 ''X''의 여집합이고 다(즉,

X^{c}=\{x\in E | x\not \in X\}

이다). 위의 말은 닫기는 이미지 ''A''의 외부에서 움직이는 구조적 요소의 자취의 여집합이라는 것을 의미한다.

3. 3. 다른 연산자와 도구

수학적 형태학(Mathematical morphology, MM)은 적중과 비적중 변환, 가지치기 변환, 형태학적 골격, 재생성에 의한 필터링, 궁극적 침식과 조건 이등분, 입도 측정법, 지오데식 거리 함수등의 연산자와 도구를 제공한다.

4. 그레이스케일 형태학

그레이스케일 형태학에서, 이미지는 유클리드 공간 또는 그리드 ''E''를

\mathbb{R}\cup\{\infty,-\infty\}

에 매핑하는 함수이다. 여기서

\mathbb{R}

은 실수의 집합이고,

\infty

는 임의의 실수보다 큰 원소이며,

-\infty

는 임의의 실수보다 작은 원소이다.

그레이스케일 구조 요소도 "구조 함수"라고 하는 동일한 형식의 함수이다.

이미지를 ''f''(''x''), 구조 함수를 ''b''(''x''), 그리고 ''b''의 지지체를 ''B''로 표시하면, ''f''를 ''b''로 팽창시키는 그레이스케일 팽창은 다음과 같다.

:

(f \oplus b)(x) = \sup_{y \in B}[f(x - y) + b(y)],

여기서 "sup"은 상한을 나타낸다.

마찬가지로, ''f''를 ''b''로 침식하는 것은 다음과 같다.

:

(f \ominus b)(x) = \inf_{y \in B}[f(x + y) - b(y)],

여기서 "inf"는 하한을 나타낸다.

이진 형태학에서와 마찬가지로, 열림과 닫힘은 각각 다음과 같다.

:

f \circ b = (f \ominus b) \oplus b,

:

f \bullet b = (f \oplus b) \ominus b.

4. 1. 기본 연산

4. 2. 평탄 구조 함수

평탄 구조 함수는 수학적 형태학에서 널리 사용되는 형태로, 다음과 같이 정의된다.

:

b(x) = \begin{cases}0, & x \in B, \\

\infty & \text{그 외},

\end{cases}

여기서

B \subseteq E

이다.

이러한 평탄 구조 함수를 이용하면 팽창과 침식 연산을 단순화할 수 있다. 팽창과 침식은 각각 다음과 같이 표현된다.

:

(f \oplus b)(x) = \sup_{z \in B^s} f(x + z),

:

(f \ominus b)(x) = \inf_{z \in B} f(x + z).

경계가 있고 이산적인 경우(''E''가 그리드이고 ''B''가 경계가 있음), 상한 및 하한 연산은 최댓값 및 최솟값으로 대체 가능하다. 즉, 팽창은 이동 창(구조 함수의 지지대 ''B''의 대칭) 내에서 최댓값을, 침식은 이동 창 ''B'' 내에서 최솟값을 반환하는 순서 통계 필터의 특수한 형태가 된다.

평탄 구조 요소를 사용하는 형태학적 연산은 픽셀 값의 절대적인 수치보다는 상대적인 순서에 의존한다. 따라서 이진 이미지 및 그레이스케일 이미지 처리, 특히 광선 전달 함수를 알 수 없는 경우에 유용하다.

4. 3. 다른 연산자와 도구

형태학적 기울기는 이미지의 각 픽셀에서 팽창(dilation)과 침식(erosion) 연산 결과의 차이를 계산하여 얻어진다. 톱햇 변환은 원래 이미지에서 열기 연산 결과를 뺀 것이나 닫기 연산 결과를 원래 이미지에서 뺀 것이다. 유역 알고리즘은 영상 분할에 사용되는 알고리즘이다.

이러한 연산자들을 결합하여 특징 추출, 이미지 분할, 이미지 선명화, 이미지 필터링, 분류 등 다양한 이미지 처리 작업을 위한 알고리즘을 개발할 수 있다. 예를 들어, 유역 알고리즘은 한국의 위성 이미지를 분석하여 산림 변화를 탐지하거나 도시 확장을 분석하는 데 활용될 수 있다.

이와 함께 연속 형태학도 연구되어야 할 분야이다.

5. 완전 격자에서의 수학적 형태학

완비 격자는 모든 부분 집합이 하한과 상한을 가지는 부분 순서 집합이다. 특히, 최소 원소와 최대 원소 (또는 "전체 집합"이라고도 함)를 포함한다.

== 수반 (Adjunctions) ==

$(L,\leq)$ 을 하한과 상한이 각각 $\wedge$ 과 $\vee$ 로 표시되는 완비 격자라고 하고, 그 우주와 최소 원소는 각각 ''U''와 $\emptyset$ 로 표시한다. 또한, $\{ X_{i} \}$ 를 ''L''의 원소 모음이라고 한다.

팽창은 상한에 대해 분배되고 최소 원소를 보존하는 임의의 연산자 $\delta\colon L\rightarrow L$ 이다. 즉,

$\bigvee_{i}\delta(X_i)=\delta\left(\bigvee_{i} X_i\right)$ ,
$\delta(\emptyset)=\emptyset$ .

침식은 하한에 대해 분배되고 우주를 보존하는 임의의 연산자

\varepsilon\colon L\rightarrow L

이다. 즉,

$\bigwedge_{i}\varepsilon(X_i)=\varepsilon\left(\bigwedge_{i} X_i\right)$ ,
$\varepsilon(U)=U$ .

팽창과 침식은 갈루아 연결을 형성한다. 모든 팽창

\delta

에 대해 다음을 만족하는 유일한 침식

\varepsilon

이 존재한다.

:

X\leq \varepsilon(Y)\Leftrightarrow \delta(X)\leq Y

이는 모든

X,Y\in L

에 대해 성립한다. 마찬가지로, 모든 침식에 대해 위의 연결을 만족하는 유일한 팽창이 존재한다.

두 연산자가 위 연결을 만족하면

\delta

는 팽창,

\varepsilon

는 침식이어야 한다.

위의 연결을 만족하는 팽창과 침식 쌍을 수반(Adjunctions)이라고 하며, 침식은 팽창의 수반 침식(adjoint erosion)이라고 하고 그 반대도 성립한다.

== 열기와 닫기 ==

수반 관계

(\varepsilon,\delta)

에 대해, 형태학적 열기

\gamma \colon L \to L

와 형태학적 닫기

\phi \colon L \to L

는 다음과 같이 정의된다.

:

\gamma = \delta\varepsilon,

:

\phi = \varepsilon\delta.

형태학적 열기와 닫기는 대수적 열기(또는 간단히 열기)와 대수적 닫기(또는 간단히 닫기)의 특수한 경우이다. 대수적 열기는 멱등적이고, 증가하며, 반-확장적인 ''L'' 내의 연산자이다. 대수적 닫기는 멱등적이고, 증가하며, 확장적인 ''L'' 내의 연산자이다.

== 특수한 경우 ==

이진 형태학은 격자 형태학의 특수한 경우이다. 여기서 ''L''은 ''E'' (유클리드 공간 또는 격자)의 멱집합으로, ''E''의 모든 부분 집합의 집합이고,

\leq

는 집합 포함 관계이다. 이 경우, 하한은 집합 교집합이고, 상한은 집합 합집합이다.

그레이스케일 형태학 또한 격자 형태학의 특수한 경우인데, ''L''은 ''E''를

\mathbb{R}\cup\{\infty,-\infty\}

로 매핑하는 함수의 집합이고,

\leq

,

\vee

, 그리고

\wedge

는 각각 점별 순서, 상한, 그리고 하한이다. 즉, ''f''와 ''g''가 ''L''의 함수라면,

f\leq g

는 모든

x\in E

에 대해

f(x)\leq g(x)

인 경우이고; 하한

f\wedge g

는

(f\wedge g)(x)=f(x)\wedge g(x)

로 주어지고; 상한

f\vee g

는

(f\vee g)(x)=f(x)\vee g(x)

로 주어진다.

5. 1. 수반 (Adjunctions)

(L,\leq)

을 하한과 상한이 각각

\wedge

과

\vee

로 표시되는 완비 격자라고 하고, 그 우주와 최소 원소는 각각 ''U''와

\emptyset

로 표시한다. 또한,

\{ X_{i} \}

를 ''L''의 원소 모음이라고 한다.

팽창은 상한에 대해 분배되고 최소 원소를 보존하는 임의의 연산자

\delta\colon L\rightarrow L

이다. 즉,

$\bigvee_{i}\delta(X_i)=\delta\left(\bigvee_{i} X_i\right)$ ,
$\delta(\emptyset)=\emptyset$ .

침식은 하한에 대해 분배되고 우주를 보존하는 임의의 연산자

\varepsilon\colon L\rightarrow L

이다. 즉,

$\bigwedge_{i}\varepsilon(X_i)=\varepsilon\left(\bigwedge_{i} X_i\right)$ ,
$\varepsilon(U)=U$ .

팽창과 침식은 갈루아 연결을 형성한다. 모든 팽창

\delta

에 대해 다음을 만족하는 유일한 침식

\varepsilon

이 존재한다.

:

X\leq \varepsilon(Y)\Leftrightarrow \delta(X)\leq Y

이는 모든

X,Y\in L

에 대해 성립한다. 마찬가지로, 모든 침식에 대해 위의 연결을 만족하는 유일한 팽창이 존재한다.

두 연산자가 위 연결을 만족하면

\delta

는 팽창,

\varepsilon

는 침식이어야 한다.

위의 연결을 만족하는 팽창과 침식 쌍을 수반(Adjunctions)이라고 하며, 침식은 팽창의 수반 침식(adjoint erosion)이라고 하고 그 반대도 성립한다.

5. 2. 열기와 닫기

수반 관계

(\varepsilon,\delta)

에 대해, 형태학적 열기

\gamma \colon L \to L

와 형태학적 닫기

\phi \colon L \to L

는 다음과 같이 정의된다.

:

\gamma = \delta\varepsilon,

:

\phi = \varepsilon\delta.

형태학적 열기와 닫기는 대수적 열기(또는 간단히 열기)와 대수적 닫기(또는 간단히 닫기)의 특수한 경우이다. 대수적 열기는 멱등적이고, 증가하며, 반-확장적인 ''L'' 내의 연산자이다. 대수적 닫기는 멱등적이고, 증가하며, 확장적인 ''L'' 내의 연산자이다.

5. 3. 특수한 경우

이진 형태학은 격자 형태학의 특수한 경우이다. 여기서 ''L''은 ''E'' (유클리드 공간 또는 격자)의 멱집합으로, ''E''의 모든 부분 집합의 집합이고,

\leq

는 집합 포함 관계이다. 이 경우, 하한은 집합 교집합이고, 상한은 집합 합집합이다.

그레이스케일 형태학 또한 격자 형태학의 특수한 경우인데, ''L''은 ''E''를

\mathbb{R}\cup\{\infty,-\infty\}

로 매핑하는 함수의 집합이고,

\leq

,

\vee

, 그리고

\wedge

는 각각 점별 순서, 상한, 그리고 하한이다. 즉, ''f''와 ''g''가 ''L''의 함수라면,

f\leq g

는 모든

x\in E

에 대해

f(x)\leq g(x)

인 경우이고; 하한

f\wedge g

는

(f\wedge g)(x)=f(x)\wedge g(x)

로 주어지고; 상한

f\vee g

는

(f\vee g)(x)=f(x)\vee g(x)

로 주어진다.

6. 응용 분야

참조

_[1] 웹사이트 International Symposium on Mathematical Morphology and Its Applications to Signal and Image Processing https://link.springe[...] 2024-05-17
_[2] 논문 Implementing continuous-scale morphology via curve evolution https://www.cs.techn[...] Pattern Recognition 1993

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com