맨위로가기

구수략

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

《구수략》은 최석정이 1710년에서 1715년 사이에 출판한 것으로 여겨지는 수학서로, 9차 직교 라틴 방진을 포함한 다양한 마방진, 마법진, 지수귀문도 등을 수록하고 있다. 특히, 《구수략》에 제시된 9차 직교 라틴 방진은 레온하르트 오일러보다 60년 이상 앞선 발견으로 국제적으로 인정받고 있으며, '구구모수변궁양도'로 명명되었다.

더 읽어볼만한 페이지

  • 수학 책 - 방법서설
    방법서설은 데카르트가 자신의 학문적 여정과 사색을 담아 이성을 통한 진리 탐구 방법인 데카르트의 방법론을 제시하는 철학 서적으로, 그의 회의주의, 분석 및 종합 규칙, 심신 이원론 등의 사상이 담겨 철학과 과학에 큰 영향을 주었다.
  • 수학 책 - 괴델, 에셔, 바흐
    더글러스 호프스태터의 책 "괴델, 에셔, 바흐"는 괴델의 불완전성 정리, 에셔의 미술, 바흐의 음악을 통해 재귀, 자기 참조, 지능과 의식의 본질을 탐구하며, 다양한 분야를 넘나드는 사유를 제공하여 퓰리처상을 수상하는 등 큰 반향을 일으켰다.
  • 마방진 - 멜랑콜리아 I
    알브레히트 뒤러의 동판화 "멜랑콜리아 I"은 우울을 의인화한 인물과 여러 상징적 오브제를 통해 멜랑콜리아의 복합적인 의미와 예술가의 고뇌, 천재성을 탐구하는 작품이다.
  • 마방진 - 범마방진
    범마방진은 가로, 세로, 대각선뿐 아니라 꺾인 대각선의 숫자 합도 동일한 마방진으로, 행이나 열을 이동시켜도 성질이 유지되며 특정 형태는 존재하지 않고 보조 방진이나 라틴 방진으로 생성 가능하며 동아시아에서 발전하여 현대 수학 및 다양한 분야에 응용된다.
  • 조선의 책 - 동의보감
    동의보감은 허준이 편찬하여 1613년에 간행된 조선 시대의 의서로, 조선 의학과 명나라 의학을 통합하고 실용성을 중시하여 당대 의학 지식을 집대성했으며, 2009년 유네스코 세계기록유산으로 등재되었다.
  • 조선의 책 - 난중일기
    《난중일기》는 이순신이 임진왜란 중 군중에서 직접 쓴 친필 일기로, 전쟁 상황과 개인적인 소회, 사회상 등이 기록된 7권의 일기이며 국보 제76호이자 유네스코 세계기록유산이다.
구수략
개요
분야역사
유형역사서
시대고려 시대
서지 정보
저자미상
창작 시기미상
형태1책
수록 정보고조선부터 고려 고종 때까지의 역대 왕조의 계보와 유사
내용
주요 내용고조선에서 고려에 이르는 역대 왕조의 흥망성쇠를 다룸.
각 왕조의 계보, 주요 사건, 인물 등을 간략하게 기록.
특징고조선을 단군이 세운 국가로 기록.
기자조선과 위만조선에 대한 내용도 포함.
삼국 시대의 건국 과정과 발전 과정을 상세히 기술.
고려의 건국 과정과 주요 사건, 인물 등을 기록.
가치고조선에서 고려에 이르는 한국사의 흐름을 파악하는 데 도움.
당시 사람들의 역사 인식과 사관을 엿볼 수 있는 자료.
전승 정보
현재 소장처국립중앙도서관
보존 상태양호
참고 문헌
참고 문헌한국민족문화대백과사전 - 구수략

2. 수학적 업적

최석정의 주요 수학적 업적은 그의 저서 《구수략》에 집약되어 있다. 《구수략》에는 직교 라틴 방진 외에도 마방진, 마법진, 지수귀문도와 같은 다양한 조합 구조가 수록되어 있다.[6] 최석정은 《구수략》에서 9차 직교 라틴 방진을 제시했는데, 이는 레온하르트 오일러보다 60여 년 앞선 발견으로 국제적으로 인정받고 있다.[2]

2. 1. 직교 라틴 방진

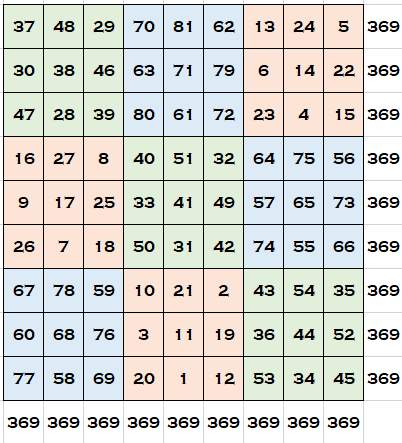
최석정은 《구수략》에서 9차 직교 라틴 방진을 제시했는데, 이는 레온하르트 오일러보다 60여 년 앞선 발견으로 국제적으로 인정받고 있다.[2] 최석정의 9차 직교 라틴 방진 '구구모수변궁양도'는 각 행과 열에 1부터 9까지의 숫자가 중복 없이 배열된 두 개의 라틴 방진으로 구성되어 있으며, 이 두 방진은 서로 직교한다. 구구모수변궁양도를 이용해 만든 마방진은 행과 열의 합이 모두 369로 일정하다.

2. 1. 1. 구구모수변궁양도

다음은 최석정의 9차 직교 라틴 방진 '구구모수변궁양도'이다.[5]

구구모수변궁양도
5, 16, 34, 28, 79, 97, 82, 43, 61, 5
4, 35, 26, 17, 98, 89, 71, 62, 53, 4
6, 24, 15, 39, 87, 78, 93, 51, 42, 6
2, 73, 91, 85, 46, 64, 58, 19, 37, 2
1, 92, 83, 74, 65, 56, 47, 38, 29, 1
3, 81, 72, 96, 54, 45, 69, 27, 18, 3
8, 49, 67, 52, 13, 31, 25, 76, 94, 8
7, 68, 59, 41, 32, 23, 14, 95, 86, 7
9, 57, 48, 63, 21, 12, 36, 84, 75, 9



각 칸에 제시된 두 수는 가로와 세로 방향으로 1부터 9까지이며, 각 행과 열의 합은 45이다. 전체 칸에 있는 수의 총합은 810이다.

두 수를 분리해서 따로 방진을 만들면 모두 라틴 방진이 되며, 이 두 방진은 서로 직교한다.

라틴방진


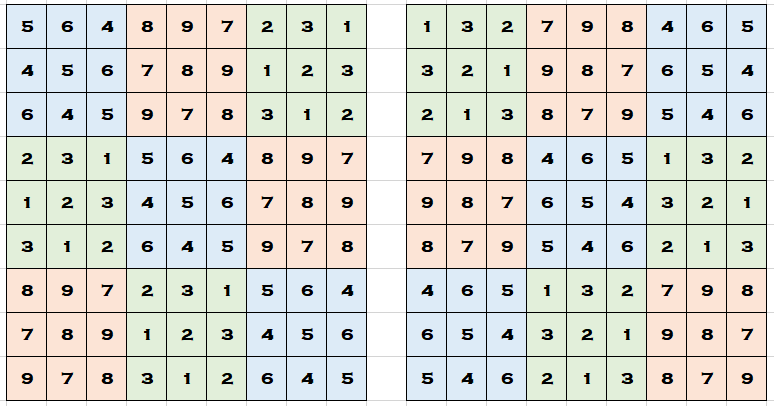
i행, j열에 있는 수를 각각 s_{ij}, t_{ij}라고 할 때, 9\times(s_{ij}-1)+t_{ij}로 계산하면, 열과 행을 더한 값이 모두 369인 마방진이 만들어진다.

마방진

2. 1. 2. 구구모수변궁양도와 마방진

최석정은 1710년~1715년 경 출판된 것으로 여겨지는 수학서 《구수략》에서 9×9 직교 라틴 방진을 구구모수변궁양도(九九母數變宮陽圖)라고 명명하였다.[3][4][5]

최석정의 9차 직교 라틴 방진 '구구모수변궁양도'는 다음과 같다.[5]

5, 16, 34, 28, 79, 97, 82, 43, 61, 5
4, 35, 26, 17, 98, 89, 71, 62, 53, 4
6, 24, 15, 39, 87, 78, 93, 51, 42, 6
2, 73, 91, 85, 46, 64, 58, 19, 37, 2
1, 92, 83, 74, 65, 56, 47, 38, 29, 1
3, 81, 72, 96, 54, 45, 69, 27, 18, 3
8, 49, 67, 52, 13, 31, 25, 76, 94, 8
7, 68, 59, 41, 32, 23, 14, 95, 86, 7
9, 57, 48, 63, 21, 12, 36, 84, 75, 9



모든 칸의 첫 번째와 두 번째에 각각 제시된 수는 가로와 세로 방향으로 1부터 9까지이며, 그 합은 각각 45이다. 가로(세로)줄이 9개 있으므로 총합은 810이다.

두 수를 분리해서 따로 방진을 만들면 모두 라틴 방진이 된다. 두 방진은 서로 직교한다.

i행, j열에 있는 수를 각각 s_{ij}, t_{ij}라고 할 때, 9\times(s_{ij}-1)+t_{ij}로 계산하면 열과 행을 더한 값이 모두 369인 마방진이 만들어진다.

2. 2. 기타

《구수략》에는 직교 라틴 방진 외에도 마방진, 마법진, 지수귀문도와 같은 다양한 조합 구조가 수록되어 있다.[6]

구수략의 지수귀문도

2. 2. 1. 마방진

《구수략》에는 마방진, 마법진, 지수귀문도 등의 구성도가 많이 수록되어 있다.[6]

2. 2. 2. 마법진

마방진과 함께 여러 종류의 마법진이 소개되어 있다.[6]

2. 2. 3. 지수귀문도

마방진, 마법진과 함께 지수귀문도 구성도가 《구수략》에 수록되어 있다.[6]

참조

[1] 웹인용 구수략 https://terms.naver.[...]
[2] 웹인용 반도체 칩에 활용되는 '마방진' 원리…최초로 개발한 건 조선 수학자? / YTN 사이언스 https://www.youtube.[...]
[3] 서적 구수략 1715?
[4] 저널 최석정의 직교라틴방진 http://coding.yonsei[...] 2010-08
[5] 웹인용 최석정의 9차 직교라틴방진 https://terms.naver.[...]
[6] 서적 파워풀한 수학자들 특별한 서재


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com