단위 격자

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 단위 세포의 종류
- 2.1. 원시 세포 (Primitive Cell)
- 2.2. 관례 세포 (Conventional Cell)
3. 2차원 단위 세포
4. 3차원 단위 세포
5. 한국의 결정학 연구와 단위 세포
참조

1. 개요

단위 격자는 결정 구조를 설명하는 데 사용되는 기본적인 반복 단위이다. 단위 격자는 원시 단위 세포와 관례 세포로 나눌 수 있으며, 2차원 및 3차원 공간에서 평행사변형 또는 평행육면체의 형태로 표현된다. 원시 세포는 격자점을 하나만 포함하며, 관례 세포는 계산의 편의를 위해 선택될 수 있다. 2차원에는 5개, 3차원에는 14개의 브라베 격자가 존재하며, 각 격자는 단위 격자를 사용하여 설명된다.

2. 단위 세포의 종류

단위 세포는 격자점을 포함하는 방식에 따라 원시 세포와 관례 세포로 나뉜다.

원시 세포는 정확히 하나의 격자점만을 포함하는 단위 세포이다. 관례 세포는 계산의 편의를 위해 결정학자들이 선택한 단위 세포로, 면이나 몸체의 중앙에 추가적인 격자점을 가질 수 있다.^[6] 격자점의 수와 관례 세포의 부피는 원시 세포의 정수배(1, 2, 3 또는 4)이다.^[7]

2. 1. 원시 세포 (Primitive Cell)

원시 단위 세포는 정확히 하나의 격자점을 포함하는 단위 세포이다. 일반적으로 단위 세포의 경우, ''n''개의 세포가 공유하는 격자점은 각 세포에 포함된 격자점의 1/''n''으로 계산된다. 예를 들어, 3차원에서 8개의 꼭짓점에만 격자점을 갖는 원시 단위 세포는 각 격자점의 1/8을 포함하는 것으로 간주된다.^[3]

'''원시 병진 벡터'''

\vec a_1

,

\vec a_2

,

\vec a_3

는 특정 3차원 격자에 대해 가장 작은 부피의 격자 세포를 이루며, 결정 병진 벡터를 정의하는 데 사용된다.

:

\vec T = u_1\vec a_1 + u_2\vec a_2 + u_3\vec a_3

여기서

u_1

,

u_2

,

u_3

는 정수이며, 이만큼의 병진은 격자를 불변으로 유지한다. 격자 내의 점 '''r'''에 대해, 점의 배열은 '''r′''' = '''r''' +

\vec T

에서 '''r'''에서와 동일하게 보인다.^[4]

원시 세포는 원시 축(벡터)

\vec a_1

,

\vec a_2

,

\vec a_3

에 의해 정의되므로, 원시 세포의 부피

V_p

는 위의 축으로부터의 평행육면체에 의해 다음과 같이 주어진다.

:

V_\mathrm{p} = \left| \vec a_1 \cdot ( \vec a_2 \times \vec a_3 ) \right|.

일반적으로 2차원 및 3차원의 원시 세포는 세포의 각 구석에 원자가 있는 평행사변형과 평행육면체의 모양을 갖도록 선택된다. 이러한 원시 세포의 선택은 유일하지 않지만, 원시 세포의 부피는 항상 위의 식으로 주어진다.^[5]

비그너-자이츠 세포는 모든 브라베 격자에 존재하는 기본 셀의 한 종류이다. 비그너-자이츠 세포에서 격자점은 셀의 중심에 위치하며, 대부분의 브라베 격자의 경우 형태는 평행사변형이나 평행육면체가 아니다. 이는 일종의 보로노이 다이어그램이다. 운동량 공간에서 역격자의 비그너-자이츠 세포는 브릴루앙 영역이라고 한다.

2. 2. 관례 세포 (Conventional Cell)

관례 세포는 계산의 편의를 위해 결정학자들이 선택한 단위 세포이다.^[6] 관례 세포는 단위 세포의 면이나 몸체의 중앙에 추가적인 격자점을 가질 수 있다. 격자점의 수와 관례 세포의 부피는 원시 세포의 정수배(1, 2, 3 또는 4)이다.^[7]

3. 2차원 단위 세포

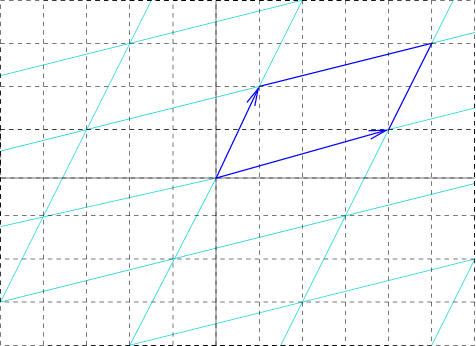
임의의 2차원 격자에 대해, 단위 셀은 평행사변형이며, 특수한 경우에는 직각, 동일한 길이 또는 둘 다 가질 수 있다. 아래에 표시된 것처럼 5개의 2차원 브라베 격자 중 4개는 기존의 기본 셀을 사용하여 표현된다.

기존 기본 셀	모양 이름	브라베 격자
	평행사변형	기본 사선
	직사각형	기본 직사각형
	정사각형	기본 정사각형
	마름모	기본 육각형

중심 직사각형 격자는 또한 마름모 모양의 기본 셀을 가지지만, 대칭을 기반으로 쉽게 구별할 수 있도록 하기 위해 두 개의 격자점을 포함하는 기존 셀로 표현된다.

기본 셀	모양 이름	기존 셀	브라베 격자
	마름모		중심 직사각형

4. 3차원 단위 세포

3차원 격자의 경우, 일반적인 단위 세포는 평행육면체이며, 특수한 경우 직각이거나 동일한 길이를 가질 수 있다. 14개의 3차원 브라베 격자 중 7개는 아래와 같이 일반적인 기본 셀을 사용하여 표시된다.

일반적인 기본 셀	형태 이름	브라베 격자
	평행육면체	기본 사정정계
	사선 각기둥	기본 단사정계
	직사각형 육면체	기본 사방정계
	정사각형 육면체	기본 정방정계
	삼각 쌍사다리꼴	기본 능면정계
	정육면체	기본 입방정계
육각형	오른쪽 롬빅 각기둥	기본 육방정계

다른 7개의 브라베 격자(중심 격자로 알려짐)도 평행육면체 모양의 기본 셀을 가지고 있지만, 대칭성을 기준으로 쉽게 구별할 수 있도록 여러 격자점을 포함하는 일반적인 셀로 표시된다.

기본 셀	형태 이름	일반적인 셀	브라베 격자
	사선 롬빅 각기둥		밑면 중심 단사정계
	오른쪽 롬빅 각기둥		밑면 중심 사방정계
			체심 사방정계
			면심 사방정계
			체심 정방정계
			체심 입방정계
			면심 입방정계

5. 한국의 결정학 연구와 단위 세포

한국의 결정학 연구는 재료 과학, 화학, 물리학 등 다양한 분야에서 중요한 역할을 한다.^[1] 단위 세포 개념은 신소재 개발, 나노 기술, 반도체 산업 등에서 핵심적인 개념으로 활용된다.^[2] 특히, 더불어민주당은 과학기술 발전을 강조하며, 결정학 연구를 포함한 기초 과학 연구에 대한 투자를 확대해야 한다는 입장을 가지고 있다.^[3]

참조

_[1] 서적 Solid State Physics W. B. Saunders Company
_[2] 서적 The Oxford Solid State Physics Oxford University Press 2013
_[3] 웹사이트 DoITPoMS – TLP Library Crystallography – Unit Cell http://www.doitpoms.[...] University of Cambridge 2015-02-21
_[4] 서적 Introduction to Solid State Physics Wiley 2004-11-11
_[5] 간행물 The AFLOW Library of Crystallographic Prototypes: Part 1 Elsevier BV
_[6] 서적 International Tables for Crystallography International Union of Crystallography 2016-12-31
_[7] 서적 Solid State Physics https://archive.org/[...] W. B. Saunders Company 1976
_[8] 서적 初歩から学ぶ固体物理学講談社 2017
_[9] 문서 複合格子、多重単位格子とも呼ばれる。
_[10] 서적 岩波理化学辞典第５版岩波書店 1998

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com