랴푸노프 안정성
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
랴푸노프 안정성은 동역학계의 평형점의 안정성을 분석하는 데 사용되는 개념이다. 랴푸노프 안정은 평형점에서 "충분히 가까이" 시작된 해가 영원히 평형점에 "충분히 가까이" 머무르는 것을 의미하며, 점근적 안정은 랴푸노프 안정성을 만족하고 해가 평형점으로 수렴하는 경우를, 지수적 안정은 해가 지수함수적으로 평형점으로 수렴하는 경우를 의미한다. 랴푸노프 함수는 시스템의 안정성을 판별하는 데 사용되는 스칼라 함수이며, 랴푸노프 안정성 기준, 이산 시간 시스템, 선형 시스템, 입력-상태 안정성 등 다양한 분야에 적용된다. Barbalat의 보조정리는 랴푸노프 함수의 시간 미분 값이 음의 준정부호인 경우에도 점근적 안정성을 판별하는 데 사용된다. 랴푸노프 안정성 이론은 알렉산드르 랴푸노프에 의해 처음 제시되었으며, 제어 이론, 동역학계, 혼돈 이론 등 다양한 분야에서 활용되고 있다.
더 읽어볼만한 페이지
- 삼체 궤도 - 리사주 궤도
리사주 궤도는 특정 천체 시스템 내 라그랑주점을 이용하여 우주선이 안정적으로 임무를 수행하고 데이터를 전송하며 통신을 가능하게 하는 3차원 궤도로, ACE, SOHO, DSCOVR 등의 우주선들이 과학적 임무에 활용했으며 연료 소모가 적고 지속적인 통신이 가능하다는 장점이 있다. - 삼체 궤도 - 헤일로 궤도
헤일로 궤도는 라그랑주점 주변을 공전하는 3차원 주기 궤도로, 지속적인 보정이 필요하지만 지구 그림자 없는 관측, 통신 중계, 우주 탐사 기착지 등 이점이 있어 다양한 우주 임무에 활용되며 한국도 활용을 모색 중이다. - 안정성 이론 - 나비 효과
나비 효과는 초기 조건의 작은 변화가 예측 불가능한 결과로 이어지는 현상을 의미하며, 기상 모의 실험을 통해 발견되었고, 브라질 나비의 날갯짓이 텍사스 토네이도를 유발할 수 있다는 비유로 설명된다. - 안정성 이론 - 평형점
평형점은 미분 방정식 또는 차분 방정식에서 시간이 흘러도 변하지 않는 상태를 나타내는 점으로, 역학계의 안정성을 분석하는 데 중요한 역할을 하며, 쌍곡 평형점, 안정 평형점, 불안정 평형점, 안장점 등으로 분류된다. - 라그랑주 역학 - 조제프루이 라그랑주
조제프루이 라그랑주는 이탈리아 출신의 수학자이자 물리학자로서 변분법, 라그랑주 역학 등을 개발하고 미터법 제정에 참여하며 18~19세기 수학과 역학 발전에 기여했으며, 에펠탑에 그의 이름이 새겨져 있다. - 라그랑주 역학 - 달랑베르의 원리
달랑베르의 원리는 입자계에 작용하는 힘과 운동량의 시간 미분 차이의 합이 구속 조건과 일치하는 가상 변위에 투영될 때 0이 된다는 원리로, 동역학계에서 구속력이 사라짐을 보이며 일반화된 힘에 구속력을 포함할 필요가 없고 열역학에도 적용 가능하다.
2. 정의
유클리드 공간 의 열린집합 위에 정의된 자율 동역학계 를 고려해 보자. 여기서 는 시스템의 상태를 나타내고, 는 립시츠 연속 함수이며 는 원점을 포함하는 열린 집합이라고 가정한다. 또한, 이라고 가정하여 원점이 시스템의 평형점이 되도록 한다. 만약 평형점 가 원점이 아닌 다른 곳에 있다면, 변수 변환 를 통해 평형점을 원점으로 이동시켜 분석할 수 있다.
이러한 동역학계에서 평형점 (또는 일반적인 평형점 )의 안정성은 초기 상태 가 평형점 근처에 있을 때, 시간 가 지남에 따라 해 가 어떻게 거동하는지를 설명하는 중요한 개념이다. 주요 안정성 개념은 다음과 같이 정의된다.
- '''랴푸노프 안정'''(Lyapunov-stableeng): 평형점 근처에서 시작한 해가 시간이 지나도 계속해서 평형점 근처에 머무르는 성질을 의미한다. 즉, 해가 평형점에서 임의로 멀리 벗어나지 않는다.[19][20][21] 이는 안정성의 가장 기본적인 형태로, 단순히 "안정"이라고 불리기도 한다.[20]
- '''점근적으로 안정'''(asymptotically stableeng): 랴푸노프 안정 조건을 만족하면서, 추가적으로 평형점 근처에서 시작한 해가 시간이 무한대로 감에 따라 결국 평형점으로 수렴하는 성질을 의미한다.[18] 즉, 해가 평형점 근처에 머무를 뿐만 아니라 시간이 지나면 평형 상태로 돌아간다.
- '''지수적으로 안정'''(exponentially stableeng): 점근적 안정성보다 더 강한 조건으로, 해가 평형점으로 수렴할 뿐만 아니라 그 수렴 속도가 지수적으로 빠르다는 것을 보장한다.[9][10][11] 즉, 해와 평형점 사이의 거리가 특정 지수 함수보다 빠르게 감소한다.
평형점의 안정성은 시스템의 야코비 행렬의 고유값과 밀접한 관련이 있으며, 특히 평형점에서 야코비안이 안정성 행렬(모든 고유값의 실수부가 음수)이면 평형점은 점근적으로 안정하다.
2. 1. 랴푸노프 안정
유클리드 공간 의 열린집합 위에 정의된 다음과 같은 자율 동역학계를 생각해 보자.:
:
:
여기서 는 립시츠 연속 함수이며, 이라고 가정한다. 즉, 원점 은 계의 평형점이다. (만약 평형점 가 원점이 아니라면, 로 변수 변환을 통해 평형점을 원점으로 이동시킬 수 있다.)
이 동역학계의 평형점 의 안정성은 여러 방식으로 정의될 수 있으며, 그중 가장 기본적인 것이 랴푸노프 안정이다.
평형점 은 다음 조건을 만족할 때 '''랴푸노프 안정'''(Lyapunov-stable영어)이라고 한다:
임의의 에 대해, 적절한 가 존재하여, 만약 초기 상태 가 를 만족하면 (즉, 평형점에 충분히 가깝게 시작하면), 모든 시간 에 대해 해 가 을 만족한다 (즉, 해가 평형점 주변의 반경 안에 계속 머무른다).[19][20][21]
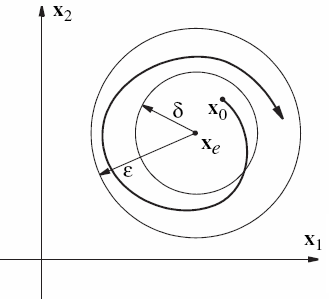
다른 표현으로는, 평형점 의 임의의 근방 에 대해, 에 포함되는 의 또 다른 근방 이 존재하여, 안의 임의의 초기점 에서 시작하는 해 궤도 가 모든 미래 시간 동안 근방 안에 머무를 때, 평형점 는 랴푸노프 안정이라고 정의할 수도 있다.[19][20][21]
개념적으로, 랴푸노프 안정은 평형점에서 "충분히 가까이" ( 거리 이내) 시작된 시스템의 해가 영원히 평형점 주변의 "충분히 가까운" 영역 ( 거리 이내) 안에 머무른다는 것을 의미한다. 여기서 중요한 점은, 우리가 원하는 임의의 작은 오차 범위 을 설정하더라도, 그에 맞는 시작 거리 를 항상 찾을 수 있다는 것이다. 즉, 해가 평형점에서 멀리 벗어나지 않음을 보장한다.
랴푸노프 안정은 단순히 "안정"이라고 불리기도 하지만[20], 다른 종류의 안정성(예: 점근적 안정성, 지수적 안정성)과 구분하기 위해 "랴푸노프의 의미에서 안정"이라고 명시하기도 한다.[22][21] 랴푸노프 안정은 해가 반드시 평형점으로 수렴하는 것을 의미하지는 않는다. 해가 평형점 주변에서 계속 진동하거나 머무르기만 해도 랴푸노프 안정 조건은 만족될 수 있다.
2. 2. 점근적 안정
평형점 가 랴푸노프 안정이고, 추가적으로 평형점 근방에서 시작된 모든 해(trajectory)가 시간이 지남에 따라 평형점으로 수렴하는 성질을 가질 때, 이 평형점을 '''점근적으로 안정'''(asymptotically stable영어)하다고 한다.보다 엄밀하게는, 평형점 가 랴푸노프 안정이고, 어떤 양수 가 존재하여 초기 조건 이 를 만족하면,
:
이 성립할 때, 평형점 는 점근적으로 안정적이다.[18]
이는 랴푸노프 안정성 조건만 만족하는 경우(해 궤도가 평형점 근처를 벗어나지는 않지만 반드시 수렴하지는 않는 경우)보다 더 강한 안정성 조건이다. 점근적 안정성은 평형점 근처에서 시작한 시스템 상태가 시간이 지나면서 결국 평형 상태로 돌아감을 보장한다.
개념적으로 점근적 안정성은 다음과 같이 이해할 수 있다:
- 평형점에 "충분히 가까운" ( 거리 이내) 곳에서 시작된 해는 영원히 "충분히 가까운" ( 거리 이내) 곳에 머물 뿐만 아니라 (랴푸노프 안정성), 시간이 충분히 흐르면 결국 평형점으로 수렴한다.
점근적 안정성은 평형점의 매력성(attractivity영어)과 관련이 깊다. 어떤 궤적 가 '매력적'이라는 것은, 에 충분히 가까이에서 시작하는 모든 궤적 가 시간이 무한대로 갈 때 로 수렴하는 것()을 의미한다. 평형점 가 점근적으로 안정하다는 것은 그 점이 랴푸노프 안정적이면서 동시에 (국소적으로) 매력적이라는 뜻이다. 단, 매력적이라고 해서 반드시 점근적으로 안정적인 것은 아니다. 안정성 조건이 추가로 필요하다.[9][10][11]
선형 시불변 시스템이나 비선형 시스템을 선형화하여 분석할 경우, 평형점에서의 야코비 행렬이 안정성 행렬(즉, 모든 고유값의 실수부가 엄격하게 음수인 행렬)이면 그 평형점은 점근적으로 안정하다.
만약 초기 조건의 제약() 없이 시스템의 모든 해가 평형점 로 수렴한다면, 그 평형점은 '''전역 점근 안정'''(globally asymptotically stable영어)이라고 한다.[19]
때로는 점근적 안정을 단순히 '안정'이라고 부르기도 한다.[18]
2. 3. 지수적 안정
평형점 (또는 일반적인 평형점 )이 점근적으로 안정하고, 추가적으로 특정 조건을 만족할 때 '''지수적으로 안정'''(exponentially stable영어)하다고 한다.[9][10][11] 이는 점근적 안정성보다 더 강력한 안정성 개념으로, 해가 평형점으로 수렴하는 속도에 대한 정보를 제공한다.구체적으로, 어떤 양의 상수 가 존재하여, 초기 상태 가 평형점 에 충분히 가까우면 (), 모든 시간 에 대해 다음 부등식이 성립할 때, 평형점 는 지수적으로 안정하다고 정의된다.
:
이 부등식은 시간이 지남에 따라 해 와 평형점 사이의 거리가 지수적으로 감소하며, 그 감소 속도가 최소한 에 비례함을 의미한다. 상수 는 수렴 속도를 나타낸다.
다른 동등한 정의 방식도 있다. 평형점 이 점근적으로 안정하고, 일 때 다음 조건을 만족하는 양의 상수 가 존재하면 평형점 은 지수적으로 안정하다.
:
개념적으로 랴푸노프 안정성, 점근적 안정성, 그리고 지수적 안정은 다음과 같이 비교할 수 있다.
- '''랴푸노프 안정성''': 평형점 근처에서 시작한 해는 계속해서 평형점 근처에 머무른다. 즉, 해가 멀리 벗어나지 않는다.
- '''점근적 안정성''': 랴푸노프 안정 조건을 만족하며, 추가적으로 평형점 근처에서 시작한 해는 시간이 무한대로 갈 때 평형점으로 수렴한다.
- '''지수적 안정''': 점근적 안정 조건을 만족하며, 해가 평형점으로 수렴하는 속도가 적어도 특정 지수 함수만큼 빠르다는 것이 보장된다. 즉, 수렴 속도에 대한 구체적인 하한값이 존재한다.
선형 시스템의 경우, 평형점에서 시스템의 야코비안 행렬의 모든 고유값의 실수부가 엄격하게 음수이면, 그 평형점은 지수적으로 안정하다. 이는 비선형 시스템의 평형점 근처에서의 안정성을 분석할 때에도 중요한 기준이 된다.
3. 랴푸노프 함수
동역학계의 평형점의 안정 여부는 '''랴푸노프 함수'''(Lyapunov function영어)라는 함수를 찾아 증명할 수 있다.[23]
동역학계 의 평형점이 이라고 가정하자. 그리고 을 을 포함하는 정의역으로 두자. 다음과 같은 조건을 만족하는, 도함수가 연속인 함수 을 고려할 수 있다.
: (함수 값은 평형점에서 0이고, 그 외의 모든 점에서는 양수이다)
: (함수의 시간에 대한 변화율(미분)은 0보다 작거나 같다)
위 두 조건을 만족하는 함수 가 존재하면, 평형점 은 랴푸노프 안정하다고 한다. 만약 두 번째 조건이 더 강하게 (평형점을 제외한 모든 점에서 시간에 대한 변화율이 0보다 작다)을 만족하면, 은 점근적으로 안정하다고 한다. 이러한 함수 를 '''랴푸노프 함수'''라고 부른다.
랴푸노프는 1892년 그의 연구에서 안정성을 증명하는 두 가지 방법을 제안했다.[1] 첫 번째 방법은 해를 급수로 전개하여 제한된 범위 내에서 수렴함을 증명하는 것이고, 두 번째 방법은 현재 랴푸노프 안정성 기준 또는 직접법이라고 불리며, 고전 역학의 포텐셜 함수와 유사한 랴푸노프 함수 를 사용하는 방식이다.
평형점이 인 시스템 에 대해 랴푸노프 함수 는 다음과 같은 성질을 만족해야 한다.
- 은 오직 일 때만 성립한다.
- 은 오직 일 때만 성립한다.
- 모든 에 대해 성립한다. (점근적 안정성을 위해서는 에 대해 이어야 한다.)
이러한 함수 ''V(x)''가 존재하면 시스템은 랴푸노프 안정성을 만족한다. (참고로 조건은 필수적이다. 그렇지 않으면 잘못된 결론을 내릴 수 있다.) 시스템 전체의 안정성(전역적 안정성)을 보장하기 위해서는 "적절성" 또는 "반경 무제한성"이라고 하는 추가적인 조건이 필요하다.
이 분석 방법을 직관적으로 이해하려면 물리적 시스템(예: 진동하는 스프링과 질량)의 에너지를 생각해보면 도움이 된다. 만약 시스템이 시간이 지남에 따라 에너지를 계속 잃고, 잃어버린 에너지가 외부에서 보충되지 않는다면, 시스템은 결국 운동을 멈추고 최종적인 정지 상태에 도달할 것이다. 이 최종 상태를 어트랙터라고 한다. 그러나 실제 물리 시스템의 정확한 에너지를 나타내는 함수를 찾는 것은 어려울 수 있으며, 추상적인 수학적 시스템, 경제 시스템 또는 생물학적 시스템의 경우에는 에너지라는 개념이 직접적으로 적용되지 않을 수도 있다.
랴푸노프는 시스템의 실제 물리적 에너지에 대한 정보가 없더라도, 위에서 정의된 수학적 조건을 만족하는 랴푸노프 함수를 찾을 수 있다면 시스템의 안정성을 증명할 수 있다는 중요한 사실을 발견했다.
4. 이산 시간 시스템
이산 시간 시스템에 대한 안정성 정의는 연속 시간 시스템의 정의와 거의 동일하다. 수학적인 관점에서 정의는 다음과 같다.
(''X'', ''d'')를 거리 공간이라 하고, ''f'' : ''X'' → ''X''를 연속 함수라고 하자. ''X'' 안의 한 점 ''x''가 다음 조건을 만족할 때 랴푸노프 안정(Lyapunov stable영어)이라고 한다.
:
이는 어떤 점 ''x'' 주변의 작은 영역(반경 δ)에서 시작한 다른 점 ''y''들의 궤적(''f''n(''y''))이 시간이 지나도(''n'' ∈ N) 여전히 ''x''의 궤적(''f''n(''x'')) 주변의 특정 영역(반경 ε) 안에 머무른다는 의미이다.
점 ''x''가 그 안정 집합의 내부에 있을 때, 즉 다음 조건을 만족할 때 점근 안정(asymptotically stable영어)이라고 한다.
:
이는 점 ''x'' 주변의 특정 영역(반경 δ)에서 시작한 다른 점 ''y''들의 궤적이 시간이 무한히 흘렀을 때(''n''→∞) 결국 ''x''의 궤적으로 수렴한다는 것을 의미한다.
5. 선형 시스템
선형 상태 공간 모델은 다음과 같이 표현된다.
:
여기서 는 유한한 행렬이며, 의 모든 고유값의 실수 부분이 음수이면 시스템은 점근적으로 안정적이다. 이는 지수적으로 안정적인 것과 같다. 이 조건은 다음 조건과 동일하다.[12]
:
위 식이 어떤 양의 정부호인 대칭 행렬 에 대해 음의 정부호가 되는 것과 같다. (관련 랴푸노프 함수는 이다.)
이와 유사하게, 이산 시간 선형 상태 공간 모델은 다음과 같다.
:
이 시스템은 의 모든 고유값의 절댓값이 1보다 작으면 점근적으로 안정적(사실상 지수적으로 안정적)이다.
이 조건은 스위칭 시스템으로 일반화될 수 있다. 행렬 집합 에 의해 제어되는 선형 스위칭 이산 시간 시스템은 다음과 같다.
:
이 시스템은 집합 의 합동 스펙트럼 반경이 1보다 작으면 점근적으로 안정적(사실상 지수적으로 안정적)이다.
6. 입력-상태 안정성
입력(또는 제어)이 있는 시스템은 다음과 같은 형식으로 표현된다.
:
여기서 입력 `u(t)`는 일반적으로 시간에 따라 변하는 값으로, '제어', '외부 입력', '자극', '교란' 또는 '강제 함수' 등으로 볼 수 있다. 랴푸노프 안정성을 만족하는 평형점 근처의 시스템은 작은 교란이 있더라도 안정성을 유지하는 경향이 있다.[13] 그러나 입력 교란이 더 커지는 경우, 이러한 시스템의 안정성을 분석하는 것은 제어 이론의 주요 주제이며 제어 공학 분야에서 중요하게 다루어진다.
입력이 있는 시스템에서는 시스템의 안정성에 입력이 미치는 영향을 정량적으로 파악하는 것이 중요하다. 이를 위한 주요 분석 방법으로는 선형 시스템에 주로 적용되는 BIBO 안정성(Bounded-Input, Bounded-Output stability)과 비선형 시스템에 적용되는 입력-상태 안정성(Input-to-State Stability, ISS)이 있다. 특히 입력-상태 안정성은 외부 입력이 시스템의 안정성에 미치는 영향을 정량화하는 데 중점을 둔다.
7. 역사
랴푸노프 안정성은 러시아의 수학자 알렉산드르 랴푸노프의 이름을 따서 명명되었다. 랴푸노프는 1892년 하르코프 대학교에서 발표한 박사 학위 논문 《운동의 안정성에 관한 일반적 문제》[24][1]에서 비선형 동역학계의 안정성을 분석하는 전역적 접근 방식을 처음으로 제시하며, 평형점 근처에서의 선형화 방법을 다루었다. 그의 연구는 처음 러시아어로 출판되었고 이후 프랑스어로 번역되었으나, 오랫동안 학계의 주목을 받지 못하였다.[24] 랴푸노프 자신은 천문학 분야, 특히 회전하는 유체 덩어리의 안정성에 관심을 두었으며, 안정성 이론 분야의 후속 연구자를 양성하지 못했다. 그는 1918년 생을 마감했다.
수십 년간 잊혔던 랴푸노프의 이론은 1930년대 러시아-소련의 수학자이자 역학자인 니콜라이 구리예비치 체타예프에 의해 그 중요성이 재발견되었다. 체타예프는 랴푸노프 이론에 중요한 기여를 했으며[2], 많은 학자들은 그를 랴푸노프의 직접적인 학문적 후계자로 여긴다.
랴푸노프 이론은 냉전 시대에 들어서면서 다시 주목받기 시작했다. 특히 항공우주 유도 시스템의 안정성 분석에 랴푸노프의 제2 방법(랴푸노프 함수)이 매우 유용하다는 사실이 밝혀졌기 때문이다. 이러한 시스템들은 강한 비선형성을 가지는 경우가 많아 다른 방법으로는 분석하기 어려웠다.[25][26][27][28][3][4][5][6][7] 이후 랴푸노프 안정성 이론은 제어 이론 및 동역학계 분야에서 활발히 연구되고 응용되었다.
최근에는 랴푸노프의 제1 방법과 관련된 랴푸노프 지수가 혼돈 이론 연구에서 중요한 개념으로 활용되고 있다.[25][26][27][28] 또한, 랴푸노프 안정성 방법은 교통 할당 문제에서 평형 해를 찾는 데에도 적용되고 있다.[8]
8. 응용
랴푸노프 안정성 이론은 1892년 알렉산드르 미하일로비치 랴푸노프가 발표했지만[1], 처음에는 러시아와 프랑스 외에는 거의 주목받지 못했다. 랴푸노프 자신도 천문학 외 분야에는 이 이론을 적용하지 않았고, 그의 연구를 계승한 제자도 없었으며, 1918년 자살로 인해 그의 운명은 매우 비극적이었다. 이로 인해 그의 이론은 수십 년 동안 잊혔다. 1930년대에 이르러서야 러시아의 수학자 니콜라이 구리예비치 체타예프가 랴푸노프 이론의 중요성을 재발견하고 연구를 이어갔다.[2]
랴푸노프 안정성 이론이 본격적으로 주목받기 시작한 것은 냉전 시대였다. 특히 항공우주 분야에서 유도 시스템의 안정성을 분석하는 데 강력한 비선형성을 다룰 수 있는 랴푸노프의 방법(특히 "랴푸노프의 두 번째 방법")이 매우 유용하다는 것이 밝혀지면서 관심이 급증했다. 이후 제어 이론 및 시스템 공학 분야 전반에서 랴푸노프 안정성은 중요한 분석 도구로 자리 잡았으며, 관련 연구와 출판물이 크게 늘어났다.[3][4][5][6][7]
최근에는 카오스 이론 연구가 활발해지면서 혼돈 현상의 예측 불가능성을 측정하는 랴푸노프 지수 개념(랴푸노프의 첫 번째 방법과 관련됨)이 널리 활용되고 있다. 또한, 교통 공학 분야에서 교통 흐름의 평형 상태를 분석하고 예측하는 데 랴푸노프 안정성 방법이 응용되기도 한다.[8]
9. Barbalat의 보조정리
랴푸노프 안정성 기준에서 요구하는 음의 정부호 도함수()를 갖는 랴푸노프 함수를 찾는 것은 어려울 수 있다. 때로는 도함수 가 음의 준정부호()인 함수 를 사용하는 것이 더 용이할 수 있다. 자율 시스템의 경우, 라살의 불변성 원리를 적용하여 점근적 안정성을 증명할 수 있다. 그러나 시스템의 동역학이 시간에 따라 변하는 비자율 시스템에는 이 원리를 직접 적용하기 어렵다.[14]
Barbalat의 보조정리는 이러한 비자율 시스템의 안정성을 분석하는 데 유용한 도구를 제공한다. 즉, 랴푸노프 함수의 시간 미분()이 음의 준정부호인 경우에도 시스템의 점근적 안정성을 판별할 수 있게 해준다. 이 보조정리는 함수와 그 도함수의 극한 관계에 대한 다음 관찰에서 동기를 얻었다. 시간 의 함수 에 대해:
- 이라고 해서 일 때 가 반드시 특정 극한값으로 수렴하는 것은 아니다. (예: )
- 일 때 가 극한값으로 수렴한다고 해서 반드시 인 것은 아니다. (예: )
- 가 아래로 유계이고 감소 함수()이면 극한값으로 수렴하지만, 일 때 가 0으로 수렴하는지는 알 수 없다.
Barbalat의 보조정리는 다음과 같이 기술된다.
: 만약 함수 가 일 때 유한한 극한값을 가지고, 그 도함수 가 균등 연속이라면, 일 때 이다.[15] (참고: 가 유계이면 는 균등 연속이다.)
이 보조정리에는 다른 형태들도 존재한다.
: 이고 일 때, 만약 가 Lp(0, ∞)에 속하고 가 Lq(0, ∞)에 속한다면, 일 때 이다.[16]
: 함수 가 바나흐 공간 의 값을 가지는 균등 연속 함수이고, 가 일 때 유한한 극한값을 가진다고 가정하자. 그러면 일 때 이다.[17]
다음 예시는 Slotine과 Li의 저서 ''응용 비선형 제어''(Applied Nonlinear Control)에서 가져온 것으로, Barbalat 보조정리의 적용을 보여준다.[14]
다음과 같은 비자율 시스템을 고려한다.
:
:
여기서 입력 는 시간의 함수이므로 시스템은 비자율적이다. 입력 는 유계라고 가정한다.
랴푸노프 후보 함수로 를 선택하면, 시간 도함수는 다음과 같다.
:
이므로 는 감소하거나 일정한 값을 유지한다. 이는 임을 의미하며, 따라서 와 는 유계이다.
그러나 는 음의 준정부호이다. 즉, 일 때 이 되지만, 이때 는 0이 아닐 수 있다. 또한 시스템이 비자율적이므로, 라는 사실만으로는 일 때 가 0으로 수렴한다고 결론 내릴 수 없다.
여기서 Barbalat의 보조정리를 사용한다. 의 도함수, 즉 를 계산하면 다음과 같다.
:
앞서 와 가 유계이고, 입력 도 유계라고 가정했으므로, 는 유계이다. 가 유계이면 는 균등 연속이다.
는 아래로 유계(0 이상)이고 감소()하므로 일 때 유한한 극한값으로 수렴한다. Barbalat의 보조정리에 따르면, 가 극한값을 갖고 가 균등 연속이므로, 일 때 이다.
이므로, 은 을 의미하고, 따라서 일 때 이다. 이는 오차 가 0으로 수렴함을 증명한다.
참조
[1]
논문
The General Problem of the Stability of Motion
Univ. Kharkiv
1892
[2]
간행물
On stable trajectories of dynamics
1936
[3]
서적
Устойчивость нелинейных регулируемых систем
Gostekhizdat
[4]
논문
Control System Analysis and Design Via the "Second Method" of Lyapunov: I—Continuous-Time Systems
[5]
서적
Stability by Lyapunov's Second Method with Applications
Academic Press
[6]
논문
Liapunov's method in automatic control theory
[7]
논문
Lyapunov functions for the problem of Lur'e in automatic control
[8]
논문
A continuous day-to-day traffic assignment model and the existence of a continuous dynamic user equilibrium
[9]
서적
Stability of Motion
https://doi.org/10.1[...]
Springer
1967
[10]
서적
(In-)Stability of Differential Inclusions: Notions, Equivalences, and Lyapunov-like Characterizations
https://doi.org/10.1[...]
Springer
2021
[11]
논문
The inadequacy of the method of characteristic exponents for the study of nonlinear differential equations
http://www.mathnet.r[...]
1957
[12]
논문
Global stability in many-species systems
1977
[13]
서적
Theory of Stability of Motion
Gostekhizdat
1952
[14]
서적
Applied Nonlinear Control
Prentice Hall
[15]
간행물
Systèmes d'équations différentielles d'oscillations non Linéaires
[16]
간행물
Variations on Barbălat's Lemma
[17]
간행물
Variations on Barbălat's Lemma
[18]
서적
非線形の力学系とカオス(上)
シュプリンガー・フェアラーク東京
[19]
서적
カオス 第2巻 力学系入門
丸善出版
[20]
서적
力学系入門 原著第2版―微分方程式からカオスまで
共立出版
[21]
서적
力学系2
岩波書店
[22]
서적
カオス現象論
コロナ社
[23]
서적
http://www.egr.msu.e[...]
[24]
저널
[25]
서적
[26]
저널
[27]
서적
[28]
저널
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com