영 타블로

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

영 타블로는 일련의 칸에 숫자를 채워 넣은 도형으로, 조합론, 표현론, 대수 기하학 등 다양한 분야에서 활용된다. 페러스 그림에 숫자를 채워 넣은 형태로, 각 칸의 숫자가 행과 열에서 증가하는 표준 영 타블로, 행에서 감소하지 않고 열에서 증가하는 준표준 영 타블로 등이 있다. 영 타블로는 대칭군의 기약 표현, 일반 선형군의 기약 다항식 표현 등을 분류하는 데 사용되며, 표현의 제한과 유도에 대한 정보를 제공한다. 앨프리드 영에 의해 1900년에 처음 소개되었으며, 슈어 함수의 정의, 로빈슨-션스테드-크누스 대응, 플락틱 모노이드 등과 관련이 있다.

더 읽어볼만한 페이지

대칭함수 - 기본 대칭 다항식
기본 대칭 다항식은 n개의 변수에서 k개의 변수를 선택하여 곱한 모든 항의 합으로 정의되는 대칭 다항식의 일종이며, 대칭 다항식의 환을 생성하고, 비에타의 공식과 행렬의 특성 다항식 등 다양한 분야에 응용된다.
대칭함수 - 대칭 다항식
대칭 다항식은 변수의 순서를 바꾸어도 변하지 않는 다항식으로, 기본 대칭 다항식으로 표현 가능하며, 수학의 여러 분야에서 중요하게 활용된다.
조합론 - 집합의 분할
집합의 분할은 주어진 집합을 서로소인 부분 집합들로 나누는 것이며, 동치 관계와 밀접하게 관련되어 있고, 벨 수로 표현되며, 플레잉 카드를 나누는 것과 같은 예시가 있다.
조합론 - 계승 (수학)
계승은 음이 아닌 정수 n에 대해 1부터 n까지의 자연수를 곱한 값으로, 0의 계승은 1로 정의되며, 대칭군의 크기와 같다는 성질을 통해 기수로 확장될 수 있고, 다중 계승, 지수 계승 등으로 확장 및 응용되어 다양한 분야에서 활용된다.
표현론 - 매케이 화살집
매케이 화살집은 유한군 G의 기약 표현을 꼭짓점으로, 텐서곱 분해를 통해 변을 정의하여 군의 표현론적 구조를 시각적으로 나타내는 도구이다.
표현론 - 보렐-베유-보트 정리
보렐-베유-보트 정리는 복소수 반단순 리 군의 표현론에서 층 코호몰로지를 사용하여 리 군의 기약 표현을 설명하며, 보렐-베유 정리와 보트의 일반화를 포함한다.

영 타블로
개요
유형	조합론적 대상, 표현론적 대상
분야	대수 조합론, 표현론
정의
정의	프로베니우스 표기법, 갈고리 길이, 내용물, 특수화
속성
속성	반전사상, 플레트 다이어그램, 로빈슨-솅스테드-크누스 대응, 슐첸베르거 정리
관련 개념
관련 개념	영 그래프, 분할, 표준 영 타블로, 세미스탠더드 영 타블로, 스펙트럴 격자
일반화
일반화	경로 모형, 결정 콤비나토릭스

2. 정의

'''페러스 그림'''(Ferrers diagram^영어)은 일련의 행들로 이루어진 도형이다. 열들은 왼쪽에 정렬돼 있으며, 아래로 내려갈 수록 그 길이들이 같거나 더 짧다.

'''영 타블로'''(Young tableau^영어)는 페러스 그림에, 각각의 칸에 숫자를 기입한 도형이다.

'''표준 영 타블로'''(standard Young tableau^영어)는 다음 두 조건을 만족시키는 영 타블로다.

각 행에서 오른쪽으로 갈 수록 숫자가 항상 증가한다.
각 열에서 밑으로 갈 수록 숫자가 항상 증가한다.

'''준표준 영 타블로'''(semistandard Young tableau^영어)는 다음 두 조건을 만족시키는 영 타블로다.

각 행에서 오른쪽으로 갈 수록 숫자가 항상 감소하지 않는다.
각 열에서 밑으로 갈 수록 숫자가 항상 증가한다.

주어진 페러스 그림에서,

(i,j)

번째 칸의 '''고리 길이'''(hook length^영어)

\operatorname{hook}(i,j)

는

i'\ge i,j=j'

또는

i'=i,j'\ge j

인 칸

(i',j')

(즉, 주어진 칸의 오른쪽 또는 밑에 있는 칸들. 주어진 칸 자체도 포함한다) 들의 개수다.

2. 1. 페러스 그림 (Ferrers diagram)

'''페러스 그림'''(Ferrers diagram^영어)은 일련의 행들로 이루어진 도형이다. 각 행은 왼쪽 정렬되어 있으며, 아래로 갈수록 길이가 같거나 짧아진다. 열의 길이는 5, 4, 1인 페러스 그림의 예시는 와 같다.

영 다이어그램(특히 점으로 표현될 때에는 페러스 다이어그램)은 왼쪽 정렬된 행으로 배열된 상자 또는 셀의 유한 모음이며, 행의 길이는 감소하지 않는 순서로 정렬된다. 각 행의 상자 수를 나열하면 정수 분할을 이룬다. 예를 들어, 분할 10 = 5 + 4 + 1의 영 다이어그램은 과 같다.

영 다이어그램의 상자에 정수 쌍으로 레이블을 지정할 때, 첫 번째 인덱스는 행을, 두 번째 인덱스는 행 내의 상자를 선택한다. 이러한 다이어그램을 표시하는 데는 영어 표기법과 프랑스어 표기법 두 가지가 있다. 영어 표기법은 각 행을 이전 행 아래에 배치하고, 프랑스어 표기법은 각 행을 이전 행 위에 쌓는다. 는 영어 표기법을, 는 프랑스어 표기법을 따른다.

각 영 다이어그램에 대해 대각선을 따라 세로와 가로를 반전시킨 공액 영 다이어그램이 존재한다. 예를 들어, 분할 10 = 5 + 4 + 1에 해당하는 영 다이어그램의 공액 분할은 10 = 3 + 2 + 2 + 2 + 1이다.

2. 2. 영 타블로 (Young tableau)

영 타블로(Young tableau^영어)는 페러스 그림(Ferrers diagram)의 각 칸에 숫자를 기입한 도형이다. 페러스 그림은 일련의 행들로 이루어진 도형으로, 열들은 왼쪽에 정렬돼 있으며, 아래로 내려갈수록 그 길이들이 같거나 더 짧다.

표준 영 타블로(standard Young tableau^영어)는 다음 두 조건을 만족시키는 영 타블로다.

각 행에서 오른쪽으로 갈 수록 숫자가 항상 증가한다.
각 열에서 밑으로 갈 수록 숫자가 항상 증가한다.

준표준 영 타블로(semistandard Young tableau^영어)는 다음 두 조건을 만족시키는 영 타블로다.

각 행에서 오른쪽으로 갈 수록 숫자가 항상 감소하지 않는다.
각 열에서 밑으로 갈 수록 숫자가 항상 증가한다.

주어진 페러스 그림에서,

(i,j)

번째 칸의 고리 길이(hook length^영어)

\operatorname{hook}(i,j)

는

i'\ge i,j=j'

또는

i'=i,j'\ge j

인 칸

(i',j')

(즉, 주어진 칸의 오른쪽 또는 밑에 있는 칸들. 주어진 칸 자체도 포함한다) 들의 개수다.

영 다이어그램은 왼쪽 정렬된 행으로 배열된 상자 또는 셀의 유한 모음이며, 행의 길이는 감소하지 않는 순서로 정렬된다. 각 행의 상자 수를 나열하면 비음의 정수의 정수 분할을 제공하며, 이는 다이어그램의 총 상자 수이다. 하나의 영 다이어그램이 다른 다이어그램에 포함되는 것은 모든 분할 집합에 대한 부분 순서를 정의하며, 영의 격자로 알려져 있다. 영 다이어그램의 각 열의 상자 수를 나열하면 켤레 또는 전치 분할을 제공한다.

영 다이어그램의 상자에 정수 쌍으로 레이블을 지정할 때, 첫 번째 인덱스는 다이어그램의 행을 선택하고 두 번째 인덱스는 행 내의 상자를 선택한다. 이러한 다이어그램을 표시하는 데 두 가지 규칙이 있는데, ''영어 표기법''과 ''프랑스어 표기법''이 있다. 영어 표기법은 행렬에 사용되는 표기법에 해당하며, 프랑스어 표기법은 데카르트 좌표 규칙에 더 가깝다.

영 타블로는 영 다이어그램의 상자에 전순서 집합인 ''알파벳''에서 가져온 기호로 채워 넣어 얻는다. 대칭군 표현에 대한 원래의 적용에서, 영 타블로는 개의 서로 다른 항목을 가지며, 다이어그램의 상자에 임의로 할당된다. 개의 항목에 대한 서로 다른 표준 영 타블로의 수는 인볼루션 수로 주어진다.

:1, 1, 2, 4, 10, 26, 76, 232, 764, 2620, 9496, ... A000085.

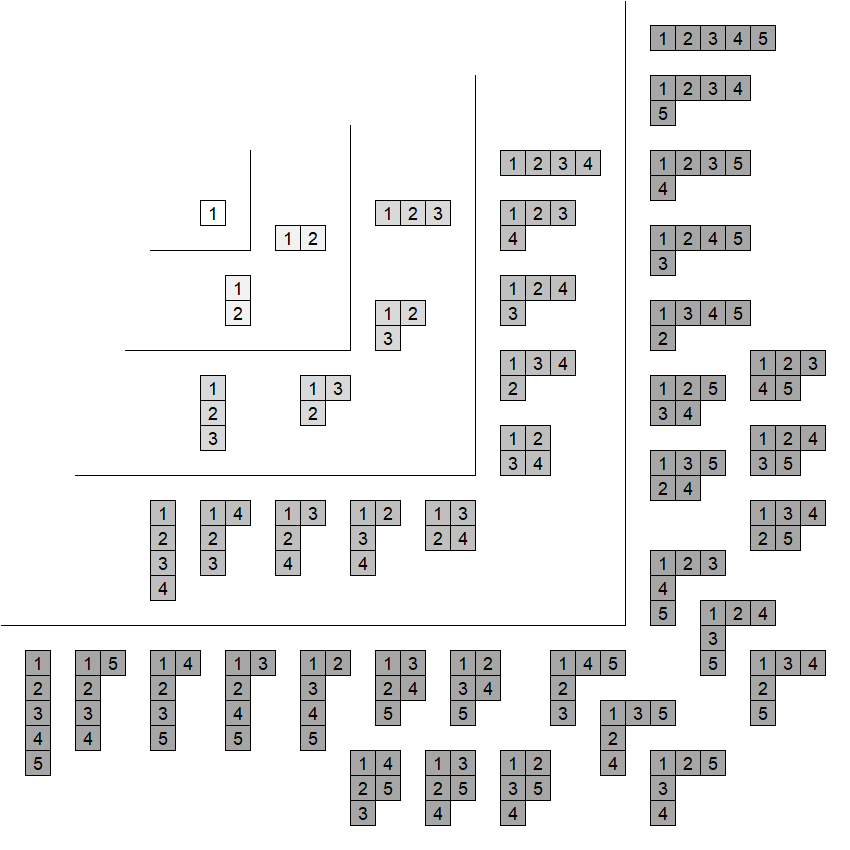
표준 영 타블로에서 정수

k

는

k+1

이

k

바로 아래 행에 나타나면 강하이다. 강하의 합을 타블로의 메이저 인덱스라고 한다.

2. 3. 표준 영 타블로 (standard Young tableau)

페러스 그림(Ferrers diagram)에 각 칸에 숫자를 기입한 도형인 영 타블로는 각 행과 열에서 숫자가 엄격하게 증가하는 경우 표준 영 타블로라고 불린다. 이 조건은 다음과 같이 정의된다.

각 행에서 오른쪽으로 갈 수록 숫자가 항상 증가한다.
각 열에서 밑으로 갈 수록 숫자가 항상 증가한다.

표준 영 타블로에서, 대칭군 표현에 대한 원래의 적용에서, 영 타블로는 n개의 서로 다른 항목을 가지며, 다이어그램의 상자에 임의로 할당된다. n개의 항목에 대한 서로 다른 표준 영 타블로의 수는 인볼루션 수로 주어진다.

:1, 1, 2, 4, 10, 26, 76, 232, 764, 2620, 9496, ...

표준 영 타블로에서 정수 k는 k+1이 k 바로 아래 행에 나타나면 '''강하'''이며, 강하의 합을 타블로의 '''메이저 인덱스'''라고 한다.

2. 4. 준표준 영 타블로 (semistandard Young tableau)

준표준 영 타블로(semistandard Young tableau)는 각 행에서 숫자가 약하게 증가하고, 각 열에서 숫자가 엄격하게 증가하는 영 타블로이다. 각 행을 따라 항목이 약하게 증가하고 각 열을 따라 엄격하게 증가하면 타블로를 '''반표준''' 또는 ''열 엄격''이라고 한다.

반 표준 테이블에서는

각 행에서 숫자는 왼쪽에서 오른쪽으로 감소하지 않는다.
각 열에서 숫자는 위에서 아래로 증가한다.

의 조건을 만족시킨다.

표준 영 타블로는 정확히 가중치(1,1,...,1)의 반표준 타블로이며, 이는 까지의 모든 정수가 정확히 한 번 나타나도록 요구한다.

thumb

2. 5. 고리 길이 (hook length)

주어진 페러스 그림에서,

(i,j)

번째 칸의 '''고리 길이'''(hook length)

\operatorname{hook}(i,j)

는

i'\ge i,j=j'

또는

i'=i,j'\ge j

인 칸

(i',j')

(즉, 주어진 칸의 오른쪽 또는 밑에 있는 칸들. 주어진 칸 자체도 포함한다) 들의 개수다. 예를 들어 잭 함수를 정의할 때, 상자 ''s''의 팔 길이 ''a''_λ(''s'')를 영어 표기법에서 그림 λ에서 ''s''의 오른쪽에 있는 상자의 수로 정의하는 것이 편리하다. 마찬가지로 다리 길이 ''l''_λ(''s'')는 ''s'' 아래에 있는 상자의 수이다. 상자 ''s''의 갈고리 길이는 상자 ''s'' 자체를 포함하여 영어 표기법에서 ''s''의 오른쪽 또는 아래에 있는 상자의 수이다. 즉, 갈고리 길이는 ''a''_λ(''s'') + ''l''_λ(''s'') + 1이다.

2. 6. 켤레 영 타블로 (conjugate Young tableau)

켤레 영 타블로는 영 타블로의 주대각선을 기준으로 뒤집은 형태이다. 영 타블로는 페러스 그림에, 각각의 칸에 숫자를 기입한 도형이다. 페러스 그림(Ferrers diagram)은 일련의 행들로 이루어진 도형이며, 열들은 왼쪽에 정렬돼 있고 아래로 내려갈수록 그 길이들이 같거나 더 짧다.

2. 7. 왜곡 영 타블로 (skew Young tableau)

왜곡 영 타블로(skew Young tableau)는 두 영 타블로의 차집합으로 표현되는 도형이다.^[3] 예를 들어, 모양 (5, 4, 2, 2) / (2, 1)의 왜곡된 타블로는 과 같이 표현된다.

왜곡된 모양은 영 다이어그램 λ가 영 다이어그램 μ를 포함하는 파티션 쌍 (λ, μ)이며, λ/μ로 표기한다. λ = (λ₁, λ₂, ...) 및 μ = (μ₁, μ₂, ...) 이면, 모든 i에 대해 μ_i ≤ λ_i인 경우에 다이어그램 포함 관계가 성립한다. 왜곡된 모양 λ/μ의 왜곡된 다이어그램은 λ와 μ의 영 다이어그램의 집합론적 차이, 즉 λ의 다이어그램에는 속하지만 μ의 다이어그램에는 속하지 않는 사각형 집합이다.^[3]

모양 λ/μ의 왜곡된 타블로는 해당 왜곡된 다이어그램의 사각형을 채움으로써 얻어진다. 각 행을 따라 값이 약하게 증가하고 각 열을 따라 엄격하게 증가하면 반표준이며, 왜곡된 다이어그램의 사각형 수에서 1까지의 모든 숫자가 정확히 한 번 나타나면 표준이다. 파티션에서 해당 영 다이어그램으로의 맵은 주입적이지만, 왜곡된 모양에서 왜곡된 다이어그램으로의 맵은 그렇지 않다. 따라서 왜곡된 다이어그램의 모양은 채워진 사각형 집합만으로는 항상 결정될 수 없다.^[3]

영 타블로는 μ가 빈 파티션 (0)인 왜곡된 타블로로 식별될 수 있다.^[4]

3. 표현론에서의 응용

대칭군 표현론도 참조

영 도표는 복소수에 대한 대칭군의 기약 표현과 일대일 대응을 이룬다. 영 도표는 표현론을 구성하는 영 대칭자를 지정하는 편리한 방법을 제공한다.^[5]^[6] 표현에 대한 많은 사실들은 해당 도표에서 유추할 수 있다. 표현의 차원을 결정하고 제한된 표현을 결정하는 두 가지 예시를 설명한다. 두 경우 모두, 표현의 일부 속성은 도표만 사용하여 결정할 수 있음을 알 수 있다. 영 타블로는 원자, 분자 및 고체의 양자 화학 연구에서 대칭군을 사용하는 데 관련된다.

영 도표는 또한 일반 선형군의 기약 다항식 표현 또는 특수 선형군의 기약 표현 또는 특수 유니타리군의 기약 복소 표현을 매개변수화한다. 이 경우 표준 타블로 대신 최대 n까지의 항목이 있는 준표준 타블로가 핵심적인 역할을 한다. 특히 표현의 차원을 결정하는 것은 그러한 타블로의 수이다.

영 타블로는 대칭군의 복소수체 상의 기약 표현과 일대일 대응을 가진다. 이는 기약 표현을 구성하는 영 대칭자()를 특정하는 데 유용하다. 대응하는 영 타블로로부터 표현에 관한 많은 사실을 추론할 수 있다. 표현의 차원을 결정하는 예와 표현의 제한에 관한 예, 두 가지를 기술한다. 두 예 모두에서, 해당 영 타블로를 사용하는 것만으로 표현의 어떤 성질을 결정할 수 있음을 알 수 있다.

'''대칭군 (Symmetric group)'''

대칭군 $S_n$ 의 복소수 기약 표현은 총 $n$ 개의 칸을 가지는 페러스 그림과 일대일 대응한다.^[7] 이 경우, 주어진 페러스 그림에 대응하는 표현의 차원은 페러스 그림에 대응하는 표준 영 타블로의 수와 같으며, 이는 갈고리 길이 공식으로 계산할 수 있다. 즉, 각 칸의 숫자는 $1,\dots,n$ 가운데 하나이고 숫자가 중복되지 않아야 하며, $S_n$ 기약 표현의 차원은 다음과 같다.^[8]

: $\dim r=\frac{n!}{\prod_{i,j}\operatorname{hook}(i,j)}$

여기서 $\operatorname{hook}(i,j)$ 는 상자 $(i,j)$ 의 갈고리 길이로, 오른쪽에 있는 같은 행의 상자 수와 아래에 있는 같은 열의 상자 수에 1(상자 자체)을 더한 값이다.

예를 들어, S₄의 기약 표현들은 다음과 같이 분류할 수 있다.

페러스 그림	고리 길이	S₄ 표현 차원
□□□□	4321	1
□□□ □	421 1	3
□□ □□	32 21	2
□□ □ □	41 2 1	3
□ □ □ □	4 3 2 1	1

분할 10 = 5 + 4 + 1의 경우, 각 상자의 갈고리 길이는 위 그림과 같으며, 대응하는 기약 표현의 차원은 다음과 같다.

: $\dim\pi_\lambda = \frac{10!}{7\cdot5\cdot 4 \cdot 3\cdot 1\cdot 5\cdot 3\cdot 2\cdot 1\cdot1} = 288.$

'''선형군과 유니터리 군 (Linear and Unitary groups)'''

일반선형군 $GL(n,\mathbb C)$ 의 복소수 기약 표현은 각 열의 길이가 $n$ 이하인 페러스 그림과 일대일 대응한다. 이 경우, 주어진 페러스 그림에 대응하는 표현의 차원은 페러스 그림에 대응하는 준표준 영 타블로의 수와 같으며, 각 칸의 숫자는 $1,\dots,n$ 가운데 하나이다. 차원은 다음 공식으로 계산할 수 있다.

: $\dim r=\prod_{(i,j)}\frac{n-i+j}{\operatorname{hook}(i,j)}$

특수선형군 $SL(n,\mathbb C)$ 의 복소수 기약 표현은 각 열의 길이가 $n$ 미만인 페러스 그림과 일대일 대응하며, 표현의 차원은 일반선형군의 경우와 같다. 특수 유니터리 군 $SU(n)$ 의 복소화는 특수선형군 $SL(n,\mathbb C)$ 이므로, 특수 유니터리 군의 복소수 기약 표현도 특수선형군과 마찬가지로 분류할 수 있다.

페러스 그림	고리 길이	SU(n) 표현 차원
·	·	1
□	1	$n$
□□	21	$n(n+1)/2$
□ □	2 1	$n(n-1)/2$
□□□	321	$n(n+1)(n+2)/6$
□□ □	31 1	$n(n^2-1)/3$
□ □ □	3 2 1	$n(n-1)(n-2)/6$

이들 표현들은 ''N''차원 기본 표현의 적절한 (반)대칭 곱들로 만들 수 있다. ''N''차원 기본 표현의 지표(index)를 사용하여 표현하면 다음과 같다.

같은 행에 속한 지수들은 모두 완전 대칭화한다.
같은 열에 속한 지수들은 모두 완전 반대칭화한다.

예를 들어,

:

i⃞ j⃞ k⃞
l⃞ m⃞

의 꼴의 영 타블로는

:

T^{ijklm}

꼴의 텐서에 대응한다. 이는

:

T^{ijklm}=T^{(ijk)(lm)}=T^{[i|jk|l]m}=T^{i[j|kl|m]}

의 꼴의 (반)대칭성을 가진다.

'''직교군 (Orthogonal group)'''

직교군의 텐서 표현은 영 타블로를 이용하여 분류할 수 있다. 각 열의 길이가

\lfloor n/2\rfloor

이하인 페러스 그림에 대응되며,

n

이 짝수이고 길이가

n/2

인 열이 존재한다면, 같은 영 타블로에 자기쌍대(self-dual, SD) 및 반자기쌍대(anti-self-dual, ASD) 두 개의 기약 표현이 대응한다.^[10]

주어진 페러스 그림에 대응하는 SO(''n'') 텐서 표현의 차원은 내용 함수(content function)를 통해 계산할 수 있다.^[10]

i

번째 열의 길이를

r_i

,

i

번째 행의 길이를

c_i

라고 할 때, 내용 함수는 다음과 같이 정의된다.^[10]

:

C(i,j)=\begin{cases}r_i+r_j-i-j&i\ge j\\-c_i-c_j+i+j-2&i

SO(''n'') 텐서 표현의 차원은 다음과 같다.^[10]

:

\dim r=\sum_{(i,j)}\frac{n+C(i,j)}{\operatorname{hook}(i,j)}

만약

n

이 짝수이며 길이가

n/2

인 행이 있다면, (반)자기쌍대 조건을 가하면 차원은 위 공식의 ½이다.

영 타블로의 각 칸은

n

차원 벡터 지표에 대응한다. 같은 행에 속한 지표들은 모두 대칭화하며, 같은 행에 속한 임의의 한 쌍의 지표에 대하여 대각합이 0이다. 같은 열에 속한 지표들은 모두 반대칭화한다.

SO(''n'')은 스피너 표현을 갖는다. 스피너 표현은 모든 가능한 감마 행렬 축약이 0이어야 한다.^[9]

예를 들어, SU(2)=Spin(3)의 기약 표현은 다음과 같이 나타낼 수 있다.

스핀	0	½	1	1½	2	2½	3	3½
차원	1	2	3	4	5	6	7	8
SU(2) 영 타블로	·	□	□□	□□□	□□□□	□□□□□	□□□□□□	□□□□□□□
SO(3) 영 타블로	·	· (s)	□	□ (s)	□□	□□ (s)	□□□	□□□ (s)

Spin(6)=SU(4)와 Spin(4)=SU(2)×SU(2)의 기약 표현 또한 영 타블로를 통해 나타낼 수 있다.

'''심플렉틱 군 (Symplectic group)'''

짝수 $n$ 에 대하여, USp(''n'')의 경우에도 영 타블로를 사용하여 표현을 분류할 수 있다.^[9] 이 경우

: $\operatorname{USp}(n)\subset\operatorname{SU}(n)$

을 사용해, 특수 유니터리 군의 경우와 마찬가지로 표현들을 분류할 수 있다. USp(''n'')의 텐서 표현은 각 열의 길이가 $n/2$ 이하인 페러스 그림과 대응한다.

페러스 그림 $\lambda$ 의 행의 길이가 $r_1,r_2,\dots$ 이며, 열의 길이가 $c_1,c_2,\dots$ 라고 할 때, '''내용 함수'''(content function^영어)를 다음과 같이 정의한다.^[10]

: $C(i,j)=\begin{cases}r_i+r_j-i-j+2&i>j\\$

c_i-c_j+i+j&i\le j

\end{cases}

그러면 USp(''n'') 표현의 차원은 다음과 같다.^[10]

:

\dim r=\prod_{(i,j)}\frac{n+C(i,j)}{\operatorname{hook}(i,j)}

영 타블로의 각 칸은

n

차원 벡터 지표에 대응한다. 이 경우 같은 행에 속한 지표들은 모두 대칭화하고, 같은 열에 속한 지표들은 모두 반대칭화하며,

\omega_{\mu\nu}

에 의한 축약이 모두 0이다.

예를 들어, SO(5)=USp(4)의 표현들은 다음과 같이 나타낼 수 있다.

차원	1	4	5	10	14	16
SO(5) 영 타블로	·	· (s)	□	□ □	□□	□ (s)
USp(4) 영 타블로	·	□	□ □	□□	□□ □□	□□ □

3. 1. 대칭군 (Symmetric group)

대칭군

S_n

의 복소수 기약 표현은 총

n

개의 칸을 가지는 페러스 그림과 일대일 대응한다.^[7] 이 경우, 주어진 페러스 그림에 대응하는 표현의 차원은 페러스 그림에 대응하는 표준 영 타블로의 수와 같으며, 이는 갈고리 길이 공식으로 계산할 수 있다. 즉, 각 칸의 숫자는

1,\dots,n

가운데 하나이고 숫자가 중복되지 않아야 하며,

S_n

기약 표현의 차원은 다음과 같다.^[8]

:

\dim r=\frac{n!}{\prod_{i,j}\operatorname{hook}(i,j)}

여기서

\operatorname{hook}(i,j)

는 상자

(i,j)

의 갈고리 길이로, 오른쪽에 있는 같은 행의 상자 수와 아래에 있는 같은 열의 상자 수에 1(상자 자체)을 더한 값이다.

예를 들어, S₄의 기약 표현들은 다음과 같이 분류할 수 있다.

페러스 그림	고리 길이	S₄ 표현 차원
□□□□	4321	1
□□□ □	421 1	3
□□ □□	32 21	2
□□ □ □	41 2 1	3
□ □ □ □	4 3 2 1	1

분할 10 = 5 + 4 + 1의 경우, 각 상자의 갈고리 길이는 위 그림과 같으며, 대응하는 기약 표현의 차원은 다음과 같다.

: $\dim\pi_\lambda = \frac{10!}{7\cdot5\cdot 4 \cdot 3\cdot 1\cdot 5\cdot 3\cdot 2\cdot 1\cdot1} = 288.$

3. 2. 선형군과 유니터리 군 (Linear and Unitary groups)

일반선형군

GL(n,\mathbb C)

의 복소수 기약 표현은 각 열의 길이가

n

이하인 페러스 그림과 일대일 대응한다. 이 경우, 주어진 페러스 그림에 대응하는 표현의 차원은 페러스 그림에 대응하는 준표준 영 타블로의 수와 같으며, 각 칸의 숫자는

1,\dots,n

가운데 하나이다. 차원은 다음 공식으로 계산할 수 있다.

:

\dim r=\prod_{(i,j)}\frac{n-i+j}{\operatorname{hook}(i,j)}

특수선형군

SL(n,\mathbb C)

의 복소수 기약 표현은 각 열의 길이가

n

미만인 페러스 그림과 일대일 대응하며, 표현의 차원은 일반선형군의 경우와 같다. 특수 유니터리 군

SU(n)

의 복소화는 특수선형군

SL(n,\mathbb C)

이므로, 특수 유니터리 군의 복소수 기약 표현도 특수선형군과 마찬가지로 분류할 수 있다.

페러스 그림	고리 길이	SU(n) 표현 차원
·	·	1
□	1	$n$
□□	21	$n(n+1)/2$
□ □	2 1	$n(n-1)/2$
□□□	321	$n(n+1)(n+2)/6$
□□ □	31 1	$n(n^2-1)/3$
□ □ □	3 2 1	$n(n-1)(n-2)/6$

이들 표현들은 ''N''차원 기본 표현의 적절한 (반)대칭 곱들로 만들 수 있다. ''N''차원 기본 표현의 지표(index)를 사용하여 표현하면 다음과 같다.

같은 행에 속한 지수들은 모두 완전 대칭화한다.
같은 열에 속한 지수들은 모두 완전 반대칭화한다.

예를 들어,

:

i⃞ j⃞ k⃞
l⃞ m⃞

의 꼴의 영 타블로는

:

T^{ijklm}

꼴의 텐서에 대응한다. 이는

:

T^{ijklm}=T^{(ijk)(lm)}=T^{[i|jk|l]m}=T^{i[j|kl|m]}

의 꼴의 (반)대칭성을 가진다.

3. 3. 직교군 (Orthogonal group)

직교군의 텐서 표현은 영 타블로를 이용하여 분류할 수 있다. 각 열의 길이가

\lfloor n/2\rfloor

이하인 페러스 그림에 대응되며,

n

이 짝수이고 길이가

n/2

인 열이 존재한다면, 같은 영 타블로에 자기쌍대(self-dual, SD) 및 반자기쌍대(anti-self-dual, ASD) 두 개의 기약 표현이 대응한다.^[10]

주어진 페러스 그림에 대응하는 SO(''n'') 텐서 표현의 차원은 내용 함수(content function)를 통해 계산할 수 있다.^[10]

i

번째 열의 길이를

r_i

,

i

번째 행의 길이를

c_i

라고 할 때, 내용 함수는 다음과 같이 정의된다.^[10]

:

C(i,j)=\begin{cases}r_i+r_j-i-j&i\ge j\\-c_i-c_j+i+j-2&i

SO(''n'') 텐서 표현의 차원은 다음과 같다.^[10]

:

\dim r=\sum_{(i,j)}\frac{n+C(i,j)}{\operatorname{hook}(i,j)}

만약

n

이 짝수이며 길이가

n/2

인 행이 있다면, (반)자기쌍대 조건을 가하면 차원은 위 공식의 ½이다.

영 타블로의 각 칸은

n

차원 벡터 지표에 대응한다. 같은 행에 속한 지표들은 모두 대칭화하며, 같은 행에 속한 임의의 한 쌍의 지표에 대하여 대각합이 0이다. 같은 열에 속한 지표들은 모두 반대칭화한다.

SO(''n'')은 스피너 표현을 갖는다. 스피너 표현은 모든 가능한 감마 행렬 축약이 0이어야 한다.^[9]

예를 들어, SU(2)=Spin(3)의 기약 표현은 다음과 같이 나타낼 수 있다.

스핀	0	½	1	1½	2	2½	3	3½
차원	1	2	3	4	5	6	7	8
SU(2) 영 타블로	·	□	□□	□□□	□□□□	□□□□□	□□□□□□	□□□□□□□□
SO(3) 영 타블로	·	· (s)	□	□ (s)	□□	□□ (s)	□□□	□□□ (s)

Spin(6)=SU(4)와 Spin(4)=SU(2)×SU(2)의 기약 표현 또한 영 타블로를 통해 나타낼 수 있다.

3. 4. 심플렉틱 군 (Symplectic group)

짝수

n

에 대하여, USp(''n'')의 경우에도 영 타블로를 사용하여 표현을 분류할 수 있다.^[9] 이 경우

:

\operatorname{USp}(n)\subset\operatorname{SU}(n)

을 사용해, 특수 유니터리 군의 경우와 마찬가지로 표현들을 분류할 수 있다. USp(''n'')의 텐서 표현은 각 열의 길이가

n/2

이하인 페러스 그림과 대응한다.

페러스 그림

\lambda

의 행의 길이가

r_1,r_2,\dots

이며, 열의 길이가

c_1,c_2,\dots

라고 할 때, '''내용 함수'''(content function^영어)를 다음과 같이 정의한다.^[10]

:

C(i,j)=\begin{cases}r_i+r_j-i-j+2&i>j\\

c_i-c_j+i+j&i\le j

\end{cases}

그러면 USp(''n'') 표현의 차원은 다음과 같다.^[10]

:

\dim r=\prod_{(i,j)}\frac{n+C(i,j)}{\operatorname{hook}(i,j)}

영 타블로의 각 칸은

n

차원 벡터 지표에 대응한다. 이 경우 같은 행에 속한 지표들은 모두 대칭화하고, 같은 열에 속한 지표들은 모두 반대칭화하며,

\omega_{\mu\nu}

에 의한 축약이 모두 0이다.

예를 들어, SO(5)=USp(4)의 표현들은 다음과 같이 나타낼 수 있다.

차원	1	4	5	10	14	16
SO(5) 영 타블로	·	· (s)	□	□ □	□□	□ (s)
USp(4) 영 타블로	·	□	□ □	□□	□□ □□	□□ □

4. 표현의 제한과 유도

대칭군 S_''n''^영어의 ''n''개 원소에 대한 표현은 S_''n''−1^영어의 ''n'' − 1개 원소에 대한 대칭군의 표현이기도 하다. 그러나 S_''n''^영어의 기약 표현은 S_''n''−1^영어에 대해 기약적이지 않을 수 있다. 대신에, S_''n''−1^영어에 대해 기약적인 여러 표현의 직합일 수 있다. 이러한 표현들은 그 후 유도 표현의 인수(factor)라고 불린다.

주어진 ''n''의 분할파티션/partition^영어 ''λ''에 해당하는 ''S''_''n''의 주어진 기약 표현의 이러한 제한 표현의 분해를 결정하는 문제는 다음과 같이 답한다. 단 하나의 상자만 제거하여 모양이 ''λ''인 도표에서 얻을 수 있는 모든 영 다이어그램의 집합을 형성한다(이 상자는 행과 열의 끝에 있어야 한다). 그러면 제한 표현은 해당 다이어그램에 해당하는 ''n'' − 1/S_''n''−1}}의 기약 표현의 직합으로 분해되며, 각 표현은 합에 정확히 한 번 나타난다.

}}의 부분군으로 간주할 수 있다. 이로부터 임의의 ''n''차 대칭군 }}의 표현 는 차 대칭군 V/S_''n''−1}}의 표현으로 간주할 수 있다. 이것을 표현 }}의 기약 표현에 대응하는 영 도표가 주어졌을 때, 그 제한의 직합 성분으로 나타나는 기약 표현에 대응하는 영 도표를 결정하는 것이 문제가 된다.

그 답은 대칭군 }}의 표현의 영 도표에서 상자 하나를 제거하고 그 결과가 여전히 올바른 영 도표가 되는 경우의 영 도표에 대응하는 것과 일치한다.

한편, 대칭군 }}의 부분군 W/S_''n''−1}}의 표현 }}의 표현으로 "올릴" 수 있다. 이를 '''유도 표현'''()이라고 부른다. 일반적으로 기약 표현의 유도 표현은 기약이라고는 할 수 없기 때문에, 부분군 S_''n''−1^영어의 기약 표현에 해당하는 영 도표가 주어졌을 때, 그 유도 표현의 직합 성분으로 나타나는 기약 표현에 해당하는 영 도표를 결정하는 것이 문제가 된다.

그 답은, S_''n''−1^영어의 표현의 영 도표에 상자 하나를 추가해도 그 결과가 여전히 올바른 영 도표가 되는 경우의 영 도표에 일치한다.

4. 1. 표현의 제한 (Restriction)

대칭군 S_''n''의 ''n''개 원소에 대한 표현은 S_''n''−1의 ''n'' − 1개 원소에 대한 대칭군의 표현이기도 하다. 그러나 S_''n''의 기약 표현은 S_''n''−1에 대해 기약적이지 않을 수 있다. 대신에, S_''n''−1에 대해 기약적인 여러 표현의 직합일 수 있다. 이러한 표현들은 유도 표현의 인수(factor)라고 불린다.

주어진 ''n''의 분할파티션/partition^영어 ''λ''에 해당하는 S_''n''의 주어진 기약 표현의 제한 표현의 분해를 결정하는 문제는 다음과 같이 답한다. 단 하나의 상자만 제거하여 모양이 ''λ''인 도표에서 얻을 수 있는 모든 영 다이어그램의 집합을 형성한다(이 상자는 행과 열의 끝에 있어야 한다). 그러면 제한 표현은 해당 다이어그램에 해당하는 S_''n''−1의 기약 표현의 직합으로 분해되며, 각 표현은 합에 정확히 한 번 나타난다.

''n'' − 1개의 요소의 대칭군 S_''n''−1은 자연스럽게 ''n''개의 요소의 대칭군 S_''n''의 부분군으로 간주할 수 있다. 이로부터 임의의 ''n''차 대칭군 S_''n''의 표현 ''V''는 ''n'' − 1차 대칭군 S_''n''−1의 표현으로 간주할 수 있다. 이것을 표현 ''V''의 '''제한'''(restriction)이라고 한다. 일반적으로 기약 표현의 제한은 기약이 된다고는 할 수 없다. 대칭군 S_''n''의 기약 표현에 대응하는 영 도표가 주어졌을 때, 그 제한의 직합 성분으로 나타나는 기약 표현에 대응하는 영 도표를 결정하는 것이 문제가 된다.

그 답은 대칭군 S_''n''의 표현의 영 도표에서 상자 하나를 제거하고 그 결과가 여전히 올바른 영 도표가 되는 경우의 영 도표에 대응하는 것과 일치한다.

4. 2. 표현의 유도 (Induction)

한편, 대칭군 S_n^영어의 부분군 S_n-1^영어의 표현 ''W''를 S_n^영어의 표현으로 "올릴" 수 있다. 이를 '''유도 표현'''(induced representation^영어)이라고 부른다. 일반적으로 기약 표현의 유도 표현은 기약이라고는 할 수 없기 때문에, 부분군 S_n-1^영어의 기약 표현에 해당하는 영 도표가 주어졌을 때, 그 유도 표현의 직합 성분으로 나타나는 기약 표현에 해당하는 영 도표를 결정하는 것이 문제가 된다.

그 답은, S_n-1^영어의 표현의 영 도표에 상자 하나를 추가해도 그 결과가 여전히 올바른 영 타블로가 되는 경우의 영 도표에 일치한다.

5. 역사

영국의 수학자 앨프리드 영/Alfred Young^영어이 1900년에 영 타블로의 개념을 도입하였다.^[11]

6. 응용

영 타블로는 조합론, 표현론, 대수 기하학 등 다양한 분야에서 응용된다. 슈어 함수의 정의 및 항등식은 영 타블로를 세는 방법을 통해 도출되었다.

죄 드 타캥과 로빈슨-션스테드-크누스 대응 등 타블로에 대한 여러 조합 알고리즘이 알려져 있다. 라스코와 슈첸베르거는 모든 준표준 영 타블로 집합에 결합적 연산을 부여하여 플락틱 모노이드라는 구조를 만들었다.

표현론에서 크기가 ''k''인 표준 영 타블로는 ''k''개의 문자에 대한 대칭군의 기약 표현에서 기저를 설명한다. 일반 선형군의 유한 차원 기약 표현에서 표준 단항 기저는 {1, 2, ..., ''n''} 알파벳 위에서 고정된 형태의 준표준 영 타블로 집합에 의해 매개변수화된다. 이는 불변론에 중요한 결과를 가져왔으며, 호지의 그래스만 다양체의 동차 좌표환에 대한 연구를 시작으로, 지안-카를로 로타, 데 콘치니, 프로체시, 아이젠버드 등이 더 깊이 연구했다. 리틀우드-리차드슨 규칙은 특정 왜곡 준표준 타블로를 통해 일반 선형군의 기약 표현의 텐서 곱을 기약 성분으로 분해하는 방법을 설명한다.

대수 기하학에서는 그래스만 다양체와 플래그 다양체에 대한 슈베르트 미적분학에 응용된다. 특정 코호몰로지류는 슈베르트 다항식으로 표현될 수 있으며, 이는 영 타블로를 통해 설명 가능하다.

참조

_[1] 서적 The Art of Computer Programming, Vol. III: Sorting and Searching Addison-Wesley
_[2] 간행물 On quantitative substitutional analysis https://zenodo.org/r[...]
_[3] 문서
_[4] 문서
_[5] 서적 Molecular Symmetry and Spectroscopy https://volumesdirec[...] NRC Research Press, Ottawa
_[6] 서적 The Symmetric Group in Quantum Chemistry CRC Press, Boca Raton, Florida
_[7] 서적 Group Theory: Birdtracks, Lie's, and Exceptional Groups http://birdtracks.eu[...] Princeton University Press
_[8] 문서
_[9] 웹인용 Group theory for physicists http://astro.sunysb.[...] 2013-11-22
_[10] 저널 Hook–content formulae for symplectic and orthogonal tableaux
_[11] 맥튜터 Alfred Young 2001-09

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com