위너 확률 과정
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
위너 확률 과정은 확률 과정의 한 종류로, 시간의 흐름에 따라 무작위적으로 변화하는 현상을 수학적으로 모델링하는 데 사용된다. 이 과정은 평균 0, 분산 t인 정규 분포를 따르는 독립 증분과 연속적인 경로를 가지며, 다양한 분야에서 응용된다. 물리학에서는 브라운 운동, 확산 현상, 양자역학의 경로 적분 등에 활용되며, 수리 금융에서는 옵션 가격 모델링에 중요한 역할을 한다.
유한 차원 유클리드 공간과 확률 공간이 주어졌을 때, 다음 조건들을 만족시키는 확률 과정을 위너 확률 과정(Wiener stochastic process영어)이라고 정의한다.
2. 정의
위너 확률 과정은 다음과 같은 특성들로 정의된다:[3]
과정이 독립 증분을 갖는다는 것은 일 경우 과 가 독립적인 확률 변수이며, 유사한 조건이 ''n''개의 증분에 대해서도 성립한다는 의미이다.
이러한 정의는 마팅게일 관점에서도 설명될 수 있는데, 위너 과정은 과 이차 변동 (이는 또한 마팅게일임을 의미)을 갖는 거의 확실하게 연속적인 마팅게일이라는 것이다.
또한, 위너 과정은 카르후넨-로에브 정리를 사용하여 계수가 독립적인 ''N''(0, 1) 확률 변수인 사인 급수로 표현될 수 있다.[4]
위너 과정은 평균이 0이고 분산이 1이며 델타 상관 관계("백색")를 갖는 가우시안 과정의 정적분 (시간 0에서 시간 ''t''까지)으로도 정의할 수 있다.
돈스커의 정리에 따르면, 위너 과정은 무작위 보행 또는 정상 독립 증분을 갖는 다른 이산 시간 확률 과정의 스케일링 극한으로 구성될 수 있다.[5]
2. 1. 조건
위너 확률 과정은 다음 조건들을 만족시킨다:
위너 과정 ''Wt''는 다음 조건으로 특징지어진다:[3]
3. 연산
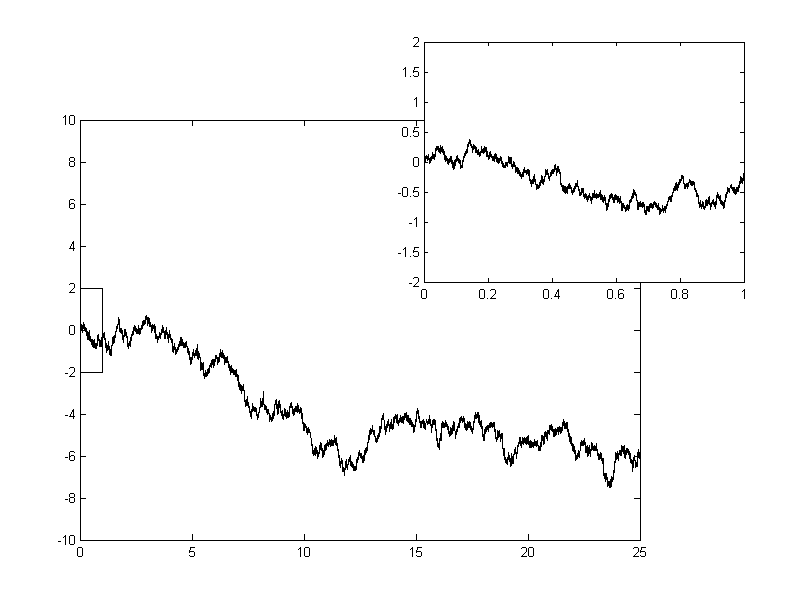
위너 확률 과정 이 주어졌을 때, 확률 과정
:
역시 위너 확률 과정을 이룬다. 즉, 그 그래프는 일종의 프랙털을 이룬다.
가 유클리드 공간 값의 위너 확률 과정이라고 하자. 그렇다면, 임의의 부분 벡터 공간 에 대하여, 역시 값의 위너 확률 과정이다.
임의의 직교 행렬 및 값의 위너 확률 과정 에 대하여, 역시 값의 위너 확률 과정이다.
4. 특징
과정이 독립 증분을 갖는다는 것은 일 경우 과 가 독립적인 확률 변수이며, 유사한 조건이 ''n''개의 증분에 대해서도 성립한다는 의미이다.
이 외에도, 위너 과정은 다음과 같은 특징을 갖는다.
:
:가 임의의 0이 아닌 상수 에 대해 비너 과정임을 의미한다.
무조건부 확률 밀도 함수는 고정된 시간 에서 평균 = 0, 분산 = ''t''인 정규 분포를 따른다.
:
기댓값은 0이다.
:
분산은 이다.
:
이 결과는 증가분이 0을 중심으로 하는 정규 분포를 갖는다는 정의에서 즉시 따른다. 따라서
:
공분산과 상관 관계 (단, ):
:
이러한 결과는 중첩되지 않는 증분이 독립적이라는 정의에서 비롯되며, 상관관계가 없다는 속성만 사용된다.
4. 1. 조건 (확률 1)
4. 2. 추가 특징
위너 과정은 다음과 같은 추가 특징을 갖는다.
:
5. 성질
위너 확률 과정 은 다음과 같은 성질을 갖는다.
- 자기 유사성: 위너 확률 과정의 그래프는 프랙털과 같은 자기 유사성을 보인다. 즉, 확률 과정 역시 위너 확률 과정을 이룬다.
- 벡터 공간: 가 유클리드 공간 값의 위너 확률 과정일 때, 임의의 부분 벡터 공간 에 대하여, 역시 값의 위너 확률 과정이다.
- 직교 행렬: 임의의 직교 행렬 및 값의 위너 확률 과정 에 대하여, 역시 값의 위너 확률 과정이다.
- 확률 밀도 함수: 고정된 시간 에서 무조건부 확률 밀도 함수는 평균 = 0, 분산 = 인 정규 분포를 따른다.
:
- 기댓값: 기댓값은 0이다.
:
- 분산: 분산은 이다.
:
- 공분산 및 상관 관계: 공분산과 상관 관계는 일 때, 다음과 같다.
:
- 표현: 에 대해, (여기서 는 독립적인 표준 정규 변수)로 표현 가능하다.
- 푸리에 급수 표현: 무작위 푸리에 급수를 사용하여 브라운 운동 경로를 표현할 수 있다.[7]
- 실행 최대값:
- 실행 최대값 와 의 결합 분포는 다음과 같다.
:
- 실행 최대값의 무조건부 분포는 절단 정규 분포의 확률 밀도 함수와 같으며 다음과 같다.
:
:
- 시간 에서 위너 과정이 값을 가질 때, 구간 에서 최대값의 조건부 확률 분포를 계산할 수 있다.
- 스케일링: 모든 에 대해, 과정 는 또 다른 위너 과정이다.
- 시간 반전: 과정 ()는 ()와 동일한 분포를 갖는다.
- 시간 역전: 과정 는 또 다른 위너 과정이다.
- 사영 불변성: 비너 과정은 PSL(2,R)의 사영군에 대해 불변이다.
- 등각 불변성: 2차원 위너 과정은 정칙 함수에 대해 시간 변화된 위너 과정이다.
- 독립 증분: 위너 과정은 독립 증분을 가지며, 인 임의의 , 에 대해, 는 정규 분포 를 따른다.
- 마팅게일: 위너 과정은 거의 확실히 연속인 마팅게일이며 이고 2차 변분 가 되는 것으로 특징지어진다.
- 스펙트럼 표현: 위너 과정은 계수가 표준 정규 분포 를 따르는 독립적인 확률 변수인 정현 급수로 표현되는 스펙트럼 표현을 갖는다.
- 확률 수렴: 평균 0, 분산 1의 독립 동일 분포인 이산 시간 연쇄의 스케일링 극한은 위너 과정에 확률 수렴한다().
- 재귀성: 위너 과정은 1차원 또는 2차원에서 재귀적이지만, 3차원 이상에서는 과도적이다.
- 스케일 불변성: 위너 과정은 스케일 불변이다.
5. 1. 브라운 마팅게일
특정 편미분 방정식을 만족하는 다항식 ''p''(''x'', ''t'')에 대해, 확률 과정 ''M''''t'' = ''p'' ( ''W''''t'', ''t'' )는 마팅게일이 된다. (여기서 Wt는 위너 확률 과정을 나타낸다.)[1]이는 모든 브라운 마팅게일이 연속적이라는 일반적인 정리의 특별한 경우에 해당한다.[1]
5. 1. 1. 2차 변동 마팅게일
만약 다항식 ''p''(''x'', ''t'')가 다음의 편미분 방정식을 만족한다면:
다음 확률 과정
:
는 마팅게일이다.
'''예시:''' 는 마팅게일이며, 이는 ''W''의 2차 변동이 ''t''와 같음을 보여준다. 따라서 ''W''가 (−''c'', ''c'')에서 최초 이탈 시간의 기댓값은 ''c''2와 같다.
더 일반적으로, 모든 다항식 ''p''(''x'', ''t'')에 대해 다음 확률 과정은 마팅게일이다.
:
여기서 ''a''는 다항식이다.
:
'''예시:''' ''p''(''x'',''t'') = (''x''2 - ''t'')2, ''a''(''x'',''t'') = 4''x''2; 다음 과정
:
는 마팅게일이며, 이는 [0, ''t'']에서 마팅게일 의 2차 변동이 다음 값과 같음을 보여준다.
:
5. 1. 2. 국소 마팅게일
만약 다항식 ''p''(''x'', ''t'')가 다음의 편미분 방정식을 만족한다면:(''∂''/''∂t'' + 1/2 ''∂''2/''∂x''2) ''p''(''x'',''t'') = 0
다음 확률 과정
:''M''''t'' = ''p'' ( ''W''''t'', ''t'' )
는 마팅게일이다.
'''예시:''' ''W''''t''2 − ''t''는 마팅게일이며, 이는 ''W''의 2차 변동이 ''t''와 같음을 보여준다. 따라서 ''W''가 (−''c'', ''c'')에서 최초 이탈 시간의 기댓값은 ''c''2와 같다.
더 일반적으로, 모든 다항식 ''p''(''x'', ''t'')에 대해 다음 확률 과정은 마팅게일이다.
:''M''''t'' = ''p'' ( ''W''''t'', ''t'' ) − ∫0''t'' ''a''(''W''''s'',''s'') d''s'',
여기서 ''a''는 다항식이다.
:''a''(''x'',''t'') = (''∂''/''∂t'' + 1/2 ''∂''2/''∂x''2) ''p''(''x'',''t'').
'''예시:''' ''p''(''x'',''t'') = (''x''2 − ''t'')2, ''a''(''x'',''t'') = 4''x''2; 다음 과정
:( ''W''''t''2 − ''t'' )2 − 4 ∫0''t'' ''W''''s''2 d''s''
는 마팅게일이며, 이는 [0, ''t'']에서 마팅게일 ''W''''t''2 − ''t''의 2차 변동이 다음 값과 같음을 보여준다.
:4 ∫0''t'' ''W''''s''2 d''s''.
다항식보다 더 일반적인 함수 ''p''(''x'', ''t'')에 대해서는 국소 마팅게일을 참조한다.
''A''를 위너 과정과 관련된 사건이라고 하고(보다 형식적으로는 함수 공간에서 위너 측도와 관련하여 가측인 집합), ''X''''t''를 시간 구간 [0, ''t'']에서 위너 과정이 주어졌을 때 ''A''의 조건부 확률이라고 하자(보다 형식적으로는 [0, ''t'']에서 주어진 부분 궤적과의 연결이 ''A''에 속하는 궤적 집합의 위너 측도). 그러면 과정 ''X''''t''는 연속적인 마팅게일이다. 마팅게일 성질은 정의로부터 즉시 따르지만, 연속성은 매우 특별한 사실로, 모든 브라운 마팅게일이 연속적이라는 일반적인 정리의 특별한 경우이다. 브라운 마팅게일은 정의에 따라 브라운 여과에 적응된 마팅게일이며, 브라운 여과는 정의에 따라 위너 과정에 의해 생성된 여과이다.
6. 표본 경로의 성질
비너 측도를 갖는 함수 ''w''의 집합에서, 위너 과정의 경로(표본 함수)는 거의 확실하게 이러한 모든 속성을 갖는다.[8]
6. 1. 질적 특성
- 모든 ε > 0에 대해, 함수 ''w''는 (0, ε)에서 (엄밀히) 양수와 (엄밀히) 음수 값을 모두 갖는다.[8]
- 함수 ''w''는 어디에서나 연속이지만, 어디에서도 미분 가능하지 않다 (바이어슈트라스 함수와 같이).[8]
- 모든 에 대해, 는 거의 확실하게 -홀더 연속이 아니며, 거의 확실하게 -홀더 연속이다.[8]
- 함수 ''w''의 국소 극대 지점은 조밀한 가산 집합이며, 극댓값은 쌍별로 다르다. 각 국소 극댓값은 다음과 같은 의미에서 날카롭다. 만약 ''w''가 에서 국소 극댓값을 갖는다면