은닉 마르코프 모형

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 정의
- 3.1. 용어
4. 구조
5. 항아리를 이용한 설명
6. 추론 문제에의 응용
7. 구체적인 예제
8. 은닉 마르코프 모형의 학습
9. 확장
10. 수학적 서술
11. 응용
12. 개념 보충 설명
13. 소프트웨어
참조

1. 개요

은닉 마르코프 모형(HMM)은 관찰할 수 없는 은닉 상태를 추론하는 데 사용되는 통계적 모델이다. 1960년대 후반 레너드 바움에 의해 연구가 시작되어, 음성 인식, 계산 언어학, 생물 정보학 등 다양한 분야에 적용된다. HMM은 마르코프 연쇄를 기반으로 하며, 전이 확률과 출력 확률을 사용하여 은닉 상태와 관찰 값 사이의 관계를 모델링한다. 필터링, 다듬질, 가장 가능성이 높은 설명 추론 등의 추론 문제를 해결하는 데 사용되며, 바움-웰치 알고리즘과 같은 기법을 통해 학습될 수 있다.

더 읽어볼만한 페이지

은닉 마르코프 모형 - Folding@home
Folding@home은 단백질 폴딩 연구를 위해 전 세계 컴퓨터 자원을 활용하여 알츠하이머병, 헌팅턴병 등 질병 연구에 기여하는 분산 컴퓨팅 프로젝트이다.
통계 이론 - 로지스틱 회귀
로지스틱 회귀는 범주형 종속 변수를 다루는 회귀 분석 기법으로, 특히 이항 종속 변수에 널리 사용되며, 오즈에 로짓 변환을 적용하여 결과값이 0과 1 사이의 값을 가지도록 하는 일반화 선형 모형의 특수한 경우이다.
통계 이론 - 정보 엔트로피
정보 엔트로피는 확률 변수의 불확실성을 측정하는 방법으로, 사건 발생 가능성이 낮을수록 정보량이 커진다는 원리에 기반하며, 데이터 압축, 생물다양성 측정, 암호화 등 다양한 분야에서 활용된다.
마르코프 모형 - 강화 학습
강화 학습은 에이전트가 환경과의 상호작용을 통해 누적 보상을 최대화하는 최적의 정책을 학습하는 기계 학습 분야이며, 몬테카를로 방법, 시간차 학습, Q-러닝 등의 핵심 알고리즘과 탐험과 활용의 균형, 정책 경사법 등의 다양한 연구 주제를 포함한다.
마르코프 모형 - 칼만 필터
칼만 필터는 잡음이 있는 측정값들을 이용하여 선형 동적 시스템의 상태를 추정하는 재귀 필터로, 예측과 보정 단계를 반복하며 항법 시스템, 레이더 추적, 컴퓨터 비전 등 다양한 분야에 응용된다.

은닉 마르코프 모형
개요
유형	통계 모형
분야	기계 학습 자연 언어 처리 유전체학 음성 인식
모형
구조	마르코프 연쇄
가시성	부분적으로 보이는 상태
변수	상태 변수 관측 변수
응용 분야	음성 인식 필기 인식 생물정보학 유전체학 시계열 분석
관련 항목
관련 개념	마르코프 모형 베이즈 네트워크 칼만 필터 파티클 필터
개발 및 연구
주요 학자	레너드 E. 바움 제임스 D. 라비너 셸던 M. 케슬러 아서 롤 스타라토노비치
참고 자료	https://scholar.google.com/scholar?q=levinson+hidden+markov+model+tutorial&hl=en&as_sdt=0&as_vis=1&oi=scholart https://web.archive.org/web/20120206123155/http://www.cs.northwestern.edu/~pardo/publications/pardo-birmingham-aaai-05.pdf https://www.nature.com/articles/nmeth.1906
관련 논문	https://doi.org/10.1093/genetics/165.4.2213 https://doi.org/10.1038/nmeth.1906

2. 역사

안드레이 마르코프(Andrey Andreyevich Markov; 1856-1922)는 1906년 마르코프 '연쇄'라는 단어를 처음 언급한 이론을 발표하였으며,^[80] 1913년에는 이를 이용하여 러시아 문자들의 순서에 대한 연구를 진행하였다. 1931년에는 안드레이 콜모고로프(Andrey Kolmogorov)가 마르코프 연쇄의 상태 공간을 가산 무한 집합으로 확장시켜 이 이론을 일반화하였다. 마르코프 연쇄는 20세기 초반 물리학계의 중요한 연구 주제였던 브라운 운동과 에르고딕 가설과 연관성이 있는 것으로 밝혀져 많은 관심을 받았으나, 정작 마르코프 자신은 해당 마르코프 연쇄를 큰 수의 법칙을 서로 의존적인 사건들로 확장시키는 수학적 일반화의 관점을 선호하였다. 확률 및 통계학에서 마르코프 연쇄는 주로 이산 상태 공간을 가지며 마르코프 특성을 따르는 확률 과정을 의미한다.

1940년대 계산 과학의 급격한 발전과 더불어, 비선형적이고 확률적인 시스템들의 해를 찾기 위한 알고리즘을 개발하기 위해 많은 과학자들이 이 분야에 뛰어들었다. 전향-후향 재귀법(forward-backward recursion)과 주변 다듬질 확률(marginal smoothing probability)등에 대한 이론이 루슬란 스트라토노비치(Ruslan L. Stratonovich)에 의해 1950년대 후반 최초로 논의되었고^[67], 1960년대 후반 레너드 바움(Leonard E. Baum)에 의해 은닉 마르코프 모형의 모수들을 찾아내는 바움-웰치 알고리즘이 발표되면서 은닉 마르코프 모형에 대한 연구가 활발히 진행되기 시작하였다.^[29]^[30]^[31]^[32]^[33] 1967년 앤드루 비터비(Andrew Viterbi)는 동적 프로그래밍을 이용하여 관찰된 사건들이 도출될 확률이 가장 높은 은닉 상태들의 순서를 찾아내는 비터비 알고리즘을 발표하였다. HMM의 첫 번째 응용 분야 중 하나는 1970년대 중반부터 시작된 음성 인식이었다.^[34]^[35]^[36]^[37] 언어학적 관점에서 은닉 마르코프 모델은 확률적 정규 문법과 동일하다.^[38]

1980년대 후반에 HMM은 생물학적 서열, 특히 DNA 분석에 적용되기 시작했다.^[39] 이후, 생물 정보학 분야에서 널리 사용되고 있다.^[40]

은닉 마르코프 모형은 1970년대 음성 인식 분야에서 응용되기 시작하였으며,^[34]^[35]^[36]^[37] 1980년대 후반에는 DNA의 서열을 분석하는 데 사용되기 시작하였다.^[81] 이후, 생물 정보학 분야에서 널리 사용되고 있다.^[40] 현대에는 음성 인식, 계산언어학, 생물정보학등에 사용되고 있다.^[81]

2. 1. 마르코프 연쇄

안드레이 마르코프(Andrey Andreyevich Markov; 1856-1922)는 1906년 마르코프 '연쇄'라는 단어를 처음 언급한 이론을 발표하였으며,^[80] 1913년에는 이를 이용하여 러시아 문자들의 순서에 대한 연구를 진행하였다. 1931년에는 안드레이 콜모고로프(Andrey Kolmogorov)가 마르코프 연쇄의 상태 공간을 가산 무한 집합으로 확장시켜 이 이론을 일반화하였다. 마르코프 연쇄는 20세기 초반 물리학계의 중요한 연구 주제였던 브라운 운동과 에르고딕 가설과 연관성이 있는 것으로 밝혀져 많은 관심을 받았으나, 정작 마르코프 자신은 해당 마르코프 연쇄를 큰 수의 법칙을 서로 의존적인 사건들로 확장시키는 수학적 일반화의 관점을 선호하였다. 확률 및 통계학에서 마르코프 연쇄는 주로 이산 상태 공간을 가지며 마르코프 특성을 따르는 확률 과정을 의미한다.

2. 2. 은닉 마르코프 모형으로의 발전

1940년대 계산 과학의 급격한 발전과 더불어, 비선형적이고 확률적인 시스템들의 해를 찾기 위한 알고리즘을 개발하기 위해 많은 과학자들이 이 분야에 뛰어들었다. 전향-후향 재귀법(forward-backward recursion)과 주변 다듬질 확률(marginal smoothing probability)등에 대한 이론이 루슬란 스트라토노비치(Ruslan L. Stratonovich)에 의해 1950년대 후반 최초로 논의되었고^[67], 1960년대 후반 레너드 바움(Leonard E. Baum)에 의해 은닉 마르코프 모형의 모수들을 찾아내는 바움-웰치 알고리즘이 발표되면서 은닉 마르코프 모형에 대한 연구가 활발히 진행되기 시작하였다.^[29]^[30]^[31]^[32]^[33] 1967년 앤드루 비터비(Andrew Viterbi)는 동적 프로그래밍을 이용하여 관찰된 사건들이 도출될 확률이 가장 높은 은닉 상태들의 순서를 찾아내는 비터비 알고리즘을 발표하였다. HMM의 첫 번째 응용 분야 중 하나는 1970년대 중반부터 시작된 음성 인식이었다.^[34]^[35]^[36]^[37] 언어학적 관점에서 은닉 마르코프 모델은 확률적 정규 문법과 동일하다.^[38]

1980년대 후반에 HMM은 생물학적 서열, 특히 DNA 분석에 적용되기 시작했다.^[39] 이후, 생물 정보학 분야에서 널리 사용되고 있다.^[40]

2. 3. 은닉 마르코프 모형의 응용

은닉 마르코프 모형은 1970년대 음성 인식 분야에서 응용되기 시작하였으며,^[34]^[35]^[36]^[37] 1980년대 후반에는 DNA의 서열을 분석하는 데 사용되기 시작하였다.^[81] 이후, 생물 정보학 분야에서 널리 사용되고 있다.^[40] 현대에는 음성 인식, 계산언어학, 생물정보학등에 사용되고 있다.^[81]

3. 정의

$x$ : 잠재 변수의 상태

$y$ : 가능한 관측값

$a$ : 상태 전이 확률

$b$ : 출력 확률]]

그림 1은 은닉 마르코프 모델의 일반적인 구성을 나타낸다. 확률 변수 $x(t)$ 는 시각 $t$ 에서의 잠재 변수이다. 확률 변수 $y(t)$ 는 시각 $t$ 에서의 관측값이다. 화살표는 조건부 확률 간의 의존 관계를 나타낸다.

그림 2는 잠재 변수의 상태 수가 3 ( $x(t)\in\left\{x_1, x_2, x_3\right\}$ ), 관측값의 상태 수가 4 ( $y(t)\in\{y_1, y_2, y_3, y_4\}$ )인 은닉 마르코프 모델을 나타낸다.

시각 $t$ 에서의 잠재 변수 $x(t)$ 의 조건부 확률 분포는 잠재 변수 $x(t-1)$ 에만 의존한다. $x(t-2)$ 및 그 이전의 상태는 영향을 미치지 않는다. 이를 (단순) 마르코프 성질이라고 한다. 또한, 관측값 $y(t)$ 는 $x(t)$ 에만 의존한다 (시각 $t$ 가 같은 것에 주의). 여기서 생각하는 것과 같은 표준적인 은닉 마르코프 모델에서는 잠재 변수 $x(t)$ 는 이산적이며, 관측값 $y(t)$ 는 연속적이거나 이산적일 수 있다.

은닉 마르코프 모델의 매개변수는 '''전이 확률'''과 '''출력 확률'''의 두 종류이다. 전이 확률은 시각 $t-1$ 에서의 잠재 변수에서 시각 $t$ 에서의 잠재 변수로의 상태 전이를 나타낸다. 그림 2에서 전이 확률은 $a_{ij}$ 로, 출력 확률은 $b_{ij}$ 로 표시된다.

잠재 변수의 상태 공간은 $N$ 개의 값을 취하는 이산 분포이다 (그림 2에서는 $N=3$ ). 이는 시각 $t$ 에서 잠재 변수가 가질 수 있는 $N$ 개의 값 각각에 대해, 시각 $x(t+1)$ 에서 잠재 변수가 가질 수 있는 $N$ 개의 값으로의 전이 확률이 존재한다는 것을 의미한다. 결과적으로 전체 $N^2$ 개의 전이 확률이 있다 (그림 2에서는 그 중 $a_{12}, a_{21}, a_{23}$ 만 나타낸다). 이 $N\times N$ 행렬을 마르코프 행렬이라고 한다. 확률의 공리에 따라 특정 상태에서 다른 상태로의 전이 확률의 합은 1이다. 따라서 특정 상태에서 어떤 전이 확률은 나머지 확률이 알려지면 결정되므로, $N\times (N-1)$ 개의 전이 매개변수가 있게 된다.

이에 더하여, $N$ 개의 각 상태에 대해 잠재 변수의 특정 시점에서 관측값의 분포를 지배하는 출력 확률의 집합이 있다 (그림 2에서는 $M=4$ 이고, $3\times 4$ 의 출력 확률 $b_{ij}$ 가 있다). 예를 들어, 관측값이 이산 분포이고 $M$ 개의 값을 취할 때, 개별 잠재 변수에 $M-1$ 개의 매개변수가 있으므로, 전체적으로 $N\times (M-1)$ 개의 출력 매개변수가 있다. 또는, 관측값이 임의의 혼합 가우스 분포를 따르는 $M$ 차원 벡터인 경우, 평균값에 대해 $M$ 개와, 공분산 행렬에 $M(M+1)/2$ 개의 매개변수가 있으므로, 총 $N(M + M(M+1)/2) = NM(M+3)/2 = O(NM^2)$ 개의 출력 매개변수가 있다.

실제로, $M$ 이 작지 않은 한, 관측 벡터의 개별 요소 간의 공분산 특성에 제약을 두는 것이 현실적이다. 예를 들어 요소별로 독립적이라든지, 조금 더 제약을 완화하여 인접한 몇몇 요소를 제외하고는 독립적이라든지 하는 것을 생각할 수 있다.

3. 1. 용어

은닉 마르코프 모형에서 모든 시간에 대하여 은닉 변수(hidden variable)

x(t)

의 값이 주어질 때, 특정 시간

t

에서의 은닉 변수

x(t)

의 조건부 확률 분포는 오직 은닉 변수

x(t-1)

에만 의존한다. 그 이전의 시간들 (

< t-1

)은

x(t)

에 영향을 주지 않는데, 이를 마르코프 특성이라 한다. 이와 비슷하게 시간

t

에서 관측된 변수

y(t)

의 값은 오직 은닉 변수

x(t)

에만 영향을 받는다.

과정

X_n

(또는

X_t

)의 상태를 ''은닉 상태''라고 하며,

\operatorname{\mathbf{P}}\bigl(Y_n \in A \mid X_n=x_n\bigr)

(또는

\operatorname{\mathbf{P}}\bigl(Y_t \in A \mid X_t \in B_t\bigr))

를 ''출력 확률'' 또는 ''방출 확률''이라고 한다.

4. 구조

x^영어: 잠재 변수의 상태

y^영어: 가능한 관측값

a^영어: 상태 전이 확률

b^영어: 출력 확률]]

그림 1은 은닉 마르코프 모델의 일반적인 구성을 나타낸다. 확률 변수 $x(t)$ 는 시각 $t$ 에서의 잠재 변수이다. 확률 변수 $y(t)$ 는 시각 $t$ 에서의 관측값이다. 화살표는 조건부 확률 간의 의존 관계를 나타낸다.

그림 2는 잠재 변수의 상태 수가 3 ( $x(t)\in\left\{x_1, x_2, x_3\right\}$ ), 관측값의 상태 수가 4 ( $y(t)\in\{y_1, y_2, y_3, y_4\}$ )인 은닉 마르코프 모델을 나타낸다.

시각 $t$ 에서의 잠재 변수 $x(t)$ 의 조건부 확률 분포는 잠재 변수 $x(t-1)$ 에만 의존한다. $x(t-2)$ 및 그 이전의 상태는 영향을 미치지 않는다. 이를 (단순) 마르코프 성질이라고 한다. 또한, 관측값 $y(t)$ 는 $x(t)$ 에만 의존한다 (시각 $t$ 가 같은 것에 주의). 여기서 생각하는 것과 같은 표준적인 은닉 마르코프 모델에서는 잠재 변수 $x(t)$ 는 이산적이며, 관측값 $y(t)$ 는 연속적이거나 이산적일 수 있다.

은닉 마르코프 모델의 매개변수는 '''전이 확률'''과 '''출력 확률'''의 두 종류이다. 전이 확률은 시각 $t-1$ 에서의 잠재 변수에서 시각 $t$ 에서의 잠재 변수로의 상태 전이를 나타낸다. 그림 2에서 전이 확률은 $a_{ij}$ 로, 출력 확률은 $b_{ij}$ 로 표시된다.

잠재 변수의 상태 공간은 $N$ 개의 값을 취하는 이산 분포이다 (그림 2에서는 $N=3$ ). 이는 시각 $t$ 에서 잠재 변수가 가질 수 있는 $N$ 개의 값 각각에 대해, 시각 $x(t+1)$ 에서 잠재 변수가 가질 수 있는 $N$ 개의 값으로의 전이 확률이 존재한다는 것을 의미한다. 결과적으로 전체 $N^2$ 개의 전이 확률이 있다 (그림 2에서는 그 중 $a_{12}, a_{21}, a_{23}$ 만 나타낸다). 이 $N\times N$ 행렬을 마르코프 행렬이라고 한다. 확률의 공리에 따라 특정 상태에서 다른 상태로의 전이 확률의 합은 1이다. 따라서 특정 상태에서 어떤 전이 확률은 나머지 확률이 알려지면 결정되므로, $N\times (N-1)$ 개의 전이 매개변수가 있게 된다.

이에 더하여, $N$ 개의 각 상태에 대해 잠재 변수의 특정 시점에서 관측값의 분포를 지배하는 출력 확률의 집합이 있다 (그림 2에서는 $M=4$ 이고, $3\times 4$ 의 출력 확률 $b_{ij}$ 가 있다). 예를 들어, 관측값이 이산 분포이고 $M$ 개의 값을 취할 때, 개별 잠재 변수에 $M-1$ 개의 매개변수가 있으므로, 전체적으로 $N\times (M-1)$ 개의 출력 매개변수가 있다. 또는, 관측값이 임의의 혼합 가우스 분포를 따르는 $M$ 차원 벡터인 경우, 평균값에 대해 $M$ 개와, 공분산 행렬에 $M(M+1)/2$ 개의 매개변수가 있으므로, 총 $N(M + M(M+1)/2) = NM(M+3)/2 = O(NM^2)$ 개의 출력 매개변수가 있다.

실제로, $M$ 이 작지 않은 한, 관측 벡터의 개별 요소 간의 공분산 특성에 제약을 두는 것이 현실적이다. 예를 들어 요소별로 독립적이라든지, 조금 더 제약을 완화하여 인접한 몇몇 요소를 제외하고는 독립적이라든지 하는 것을 생각할 수 있다.

4. 1. 은닉 변수

은닉 변수 ''x''(''t'')는 마르코프 성질을 가지며, 이전 시간 ''t'' - 1에서의 은닉 변수 ''x''(''t'' - 1)에만 조건부 의존성을 갖는다. 즉, 특정 시간 ''t''에서의 은닉 변수 ''x''(''t'')의 조건부 확률 분포는 오직 ''x''(''t'' - 1)에만 의존하고, 그 이전 시간들은 ''x''(''t'')에 영향을 주지 않는다.

마찬가지로, 시간 ''t''에서 관측된 변수 ''y''(''t'')의 값은 오직 은닉 변수 ''x''(''t'')에만 영향을 받는다.

표준 은닉 마르코프 모델에서 은닉 변수의 상태 공간은 이산적이며, 전이 확률과 방출 확률(또는 출력 확률)이라는 두 가지 유형의 매개변수를 갖는다. 전이 확률은 시간 ''t'' - 1에서의 은닉 상태를 고려하여 시간 ''t''에서의 은닉 상태가 선택되는 방식을 제어하며, 방출 확률은 은닉 변수의 상태가 주어졌을 때 특정 시간에서의 관측 변수의 분포를 제어한다.

4. 2. 은닉 변수의 상태 공간

은닉 마르코프 모형(HMM)의 표준적인 형태에서 은닉 변수의 상태 공간은 이산적이다. 반면 관측값들은 이산적이거나 연속적일 수 있다. 이산적인 경우는 주로 범주 분포를 따르고, 연속적인 경우는 주로 정규 분포를 따른다. 은닉 마르코프 모형의 모수(parameter)로는 전이 확률(transition probability)과 출력 확률(emission probability)의 두 종류가 있다. 전이 확률은 시간 ''t''-1에서의 은닉 상태가 주어졌을 때 시간 ''t''에서의 은닉 상태가 선택되는데 영향을 주며, 출력 확률은 주어진 상태 ''x''(''t'')에서 특정한 결과값 ''y''(''t'')이 관측될 확률 분포를 나타낸다.

은닉 변수 ''x''(''t'')의 시간 ''t''에서의 조건부 확률 분포는 모든 시간에서의 은닉 변수 ''x''의 값을 고려했을 때, ''x''(''t'' - 1)의 값에만 의존하며, 시간 ''t'' - 2 및 그 이전의 값은 영향을 미치지 않는다. 이를 마르코프 성질이라고 한다. 마찬가지로, 관측 변수 ''y''(''t'')의 값은 은닉 변수 ''x''(''t'')의 값에만 의존한다.

표준 유형의 은닉 마르코프 모델에서 은닉 변수의 상태 공간은 이산적이며, 관측치는 이산적(일반적으로 범주형 분포에서 생성됨)이거나 연속적(일반적으로 가우시안 분포에서 생성됨)일 수 있다. 전이 확률은 시간 ''t''에서의 은닉 상태가 시간 ''t''-1에서의 은닉 상태를 고려하여 선택되는 방식을 제어한다.

은닉 상태 공간은 범주형 분포로 모델링된 ''N''개의 가능한 값 중 하나로 구성되는 것으로 가정한다. 시간 ''t''에서 은닉 변수가 있을 수 있는 각 ''N''개의 가능한 상태에 대해, 이 상태에서 시간 ''t''+1에서 은닉 변수의 각 ''N''개의 가능한 상태로의 전이 확률이 있으며, 총 ''N''²개의 전이 확률이 있다. 주어진 상태에서 전이 확률의 합은 1이어야 한다. 따라서, ''N'' × ''N'' 전이 확률 행렬은 마르코프 행렬이다.

각 ''N''개의 가능한 상태에 대해 은닉 변수의 상태가 주어졌을 때 특정 시간에서의 관측 변수의 분포를 제어하는 방출 확률 집합이 있다. 예를 들어, 관측 변수가 ''M''개의 가능한 값을 갖는 이산적이고 범주형 분포에 의해 제어되는 경우, 모든 은닉 상태에 대해 총 ''N''(''M''-1)개의 방출 매개변수가 있을 것이다.

4. 3. 전이 확률

은닉 상태 공간은 범주 분포로 모델링 될 수 있는 N개의 가능한 상태들 중 하나로 구성되어 있다고 가정된다. 각각의 시간 t에서 은닉 변수는 총 N개의 가능한 상태들을 가질 수 있고, 시간 t+1에는 은닉 변수가 N개의 가능한 상태로 전이할 확률이 존재한다. 따라서 이러한 확률은 N²개의 전이 확률로써 표현될 수 있다. 이때 한 상태의 전이 확률의 합은 항상 1이 되어야 한다. 따라서 N x N 전이 확률 행렬은 마르코프 행렬이다. 다른 전이 확률들을 모두 알고 있을 때 마지막 전이 확률은 당연하게 도출될 수 있기 때문에 전체 전이 모수(transition parameter)의 수는 N(N-1)이다.

4. 4. 출력 확률

출력 확률은 주어진 은닉 상태에서 특정 결과값이 관측될 확률 분포를 나타낸다. 각 상태에 대해, 관측 변수 분포를 제어하는 출력 확률 집합이 존재한다. 이 집합의 크기는 관측 변수의 특성에 따라 결정된다.

예를 들어, 관측 변수가 범주 분포를 따르고 M개의 가능한 값을 가질 경우, M-1개의 독립적인 모수가 존재한다. 따라서 모든 은닉 상태에 대한 전체 출력 모수 개수는 N(M-1)개가 된다.

반면, 관측 변수가 다변량 정규분포를 따르는 M차원 벡터일 경우, 평균에 영향을 주는 M개의 모수와 공분산 행렬에 영향을 주는 $\frac {M(M+1)} 2$개의 모수가 존재한다. 따라서 전체 $N\left(M + \frac{M(M+1)}{2}\right) = \frac {NM(M+3)} 2 = O(NM^2)$개의 출력 모수가 존재한다. 이 경우, M 값이 작지 않다면 관측 벡터의 각 원소를 서로 독립으로 가정하거나, 서로 독립이면서 고정된 수의 인접 원소를 가진다는 가정 등을 통해 공분산의 특징을 제한하는 것이 실용적이다.

4. 5. 출력 확률의 확률 분포

은닉 마르코프 모형은 마르코프 과정에 기반하여 상태들이 특정한 확률 분포에 따라 결과들을 출력하는 모델을 만들 수 있다. 이러한 확률 분포의 예시 중 하나로 정규 분포가 있으며, 이 경우 출력 확률이 정규 분포를 따른다고 이야기 할 수 있다. 출력된 결과값이 둘 이상의 혼합 정규 분포에 의해 표현된다면 훨씬 더 복잡한 시스템을 표현할 수도 있다. 이 경우 특정 결과가 관찰될 확률은 정규 분포들 중에서 하나를 선택할 확률과 그 정규 분포에서 해당 관측 값을 출력할 확률의 곱이 된다.

5. 항아리를 이용한 설명

은닉 마르코프 모형은 복원 추출을 하는 항아리 문제의 일반화로 설명될 수 있다.^[82] 관측자에게 보이지 않는 방 안에 요정이 있고, 방에는 여러 개의 항아리(X1, X2, X3, ...)가 있다. 각 항아리에는 고유한 이름표(y1, y2, y3, ...)가 붙은 공들이 섞여 있으며, 이 구성은 알려져 있다. 요정은 특정 규칙에 따라 항아리를 선택하고, 그 안에서 무작위로 공을 하나 꺼내 컨베이어 벨트에 올려놓는다. 관측자는 벨트 위의 공들의 순서만 볼 수 있고, 공이 뽑힌 항아리의 순서는 알 수 없다.^[7]

그림 1. 은닉 마르코프 모형의 확률적 매개변수 (예시)
''X'' — 상태
''y'' — 가능한 관측
''a'' — 상태 전이 확률
''b'' — 출력 확률

요정이 항아리를 선택하는 규칙은 마르코프 특성을 따른다. 즉, n번째 공을 뽑기 위해 선택하는 항아리는 무작위 숫자와 (n-1)번째 공을 뽑기 위해 선택한 항아리에만 영향을 받는다. 이전의 항아리 선택은 현재 항아리 선택에 직접적인 영향을 주지 않으므로, 이는 마르코프 과정이라고 불린다.

마르코프 과정 자체는 관측 불가능하며, 컨베이어 벨트 위의 공의 나열만 관측 가능하다. 따라서 이를 "은닉 마르코프 과정"이라고 한다. 관찰자는 각 항아리의 구성을 알고, 세 개의 공(y1, y2, y3)을 관측했더라도, 세 번째 공이 어떤 항아리에서 뽑혔는지 확신할 수 없다. 다만, 각 항아리에서 세 번째 공이 뽑혔을 가능도와 같은 정보는 계산할 수 있다.

6. 추론 문제에의 응용

5 3 2 5 3 2

4 3 2 5 3 2

3 1 2 5 3 2

가장 가능성이 높은 시퀀스는 각 경우에 대한 상태 시퀀스와 관찰의 결합 확률을 평가하여 찾을 수 있습니다 (여기서는 관련된 화살표의 불투명도에 해당하는 확률 값을 단순히 곱하여). 일반적으로 이 유형의 문제(즉, 관찰 시퀀스에 대한 가장 가능성이 높은 설명을 찾는 문제)는 비터비 알고리즘을 사용하여 효율적으로 해결할 수 있습니다.]]

6. 1. 일련의 사건들이 관찰될 확률에 대한 추론

점선 아래에 있는 출력 시퀀스가 관측되었을 때, 이것이 어떤 상태 시퀀스에 의해 얻어진 것인가를 생각하면, 그림에 표시된 상태 전이와 출력 확률의 화살표로부터, 다음 상태 시퀀스가 후보가 된다.

5 3 2 5 3 2

4 3 2 5 3 2

3 1 2 5 3 2

각 후보에 대해, 상태 시퀀스와 관측 시퀀스의 결합 확률을 구함으로써, 가장 있을 법한 (즉, 최우도의) 상태 시퀀스를 구할 수 있다. 일반적으로 이러한 최우도 관측 시퀀스 문제는 비터비 알고리즘으로 효율적으로 풀 수 있다.

]]

모델의 매개변수가 알려져 있을 때, 특정 출력 시퀀스가 얻어질 확률을 구한다. 이는 가능한 상태 시퀀스에 대한 확률의 총합에 의해 얻어진다.

길이

L

의 관측값 시퀀스

:

Y=y(0), y(1),\dots,y(L-1)

의 확률은, 잠재 상태 시퀀스

:

X=x(0), x(1), \dots, x(L-1)

의 확률의 총합을 사용하여 다음과 같이 주어진다.

:

P(Y)=\sum_{X}P(Y\mid X)P(X)

동적 계획법의 원리를 적용하면, 이 문제는 전방 알고리즘으로 효율적으로 처리할 수 있다.

6. 1. 1. 전향 알고리즘 (Forward algorithm)

[[File:https://cdn.onul.works/wiki/source/195097e610c_2f93faaf.png|오른쪽|섬네일|250px|전향 알고리즘을 위한 은닉 마르코프 모형 예제

N = 5, T = 5, t = 4, j = 3

]]

전향 알고리즘은 은닉 마르코프 모형이

N

개의 상태를 가질 때, 시간

t

에서 각 상태들의 확률 분포를 구하는 방법이다.

은닉 마르코프 모형을 상태와 시간으로 나열하면 이들은 격자 모양을 가지게 되는데,

전향 알고리즘은 시간

t

와 상태

i

에 도달할 때까지 모든 경로의 확률의 합을 계속해서 보관하며 다음 시간

t+1

을 구할 때 이 정보를 이용한다.

특정 시간

t

에서 특정 사건

j

가 관찰될 확률은 시간

t-1

까지의 각 상태에 있을 확률들을 알면

시간

t-1

의 각 상태들로부터 시간

t

로의 전이 확률의 합과 시간

t

의 상태에서 사건

j

를 관찰할 확률의 곱으로 표현이 가능하다.

전체 상태가

N

개라고 할 때 특정 시간

t

에서 특정 상태

j

에 있을 확률을 수식으로 나타내면 다음과 같다.

:

\alpha_t(j) = \sum\limits_{i=1}^N \alpha_{t-1}(i) a_{ij}b_j(o_t)

이때

a_{ij}

는

i

상태에서

j

상태로의 전이 확률을 나타내며,

b_j(o_t)

는 j 상태에서 관측값

o_t

을 얻을 확률이다.

예시로 주어진 은닉 마르코프 모형에서 시간 t = 4일 때 상태 3에서 관측값 4를 얻을 확률은 위 수식을 통해 다음과 같이 표현 가능하다.

:

\alpha_4 (3) = [\alpha_3(1) * a_{13} + \alpha_3(2) * a_{23} + \alpha_3(3) * a_{33} + \alpha_3(4) * a_{43} + \alpha_3(5) * a_{53}] * b_3(o_4)

이를 계산하기 위한

\alpha_3 (i)

는

\alpha_2 (i)

들로부터 구할 수 있고

\alpha_2 (i)

는

\alpha_1 (i)

들로부터 구할 수 있다.

:

t = 1

에서의 확률 분포인

\alpha_1 (i)

에 대한 값은 초기 상태 분포

\pi_i

로부터

\alpha_1 (i) = \pi_i b_i (o_1)

의 식을 통해 계산한다.

6. 2. 특정 은닉 변수에 대한 확률 추론

일련의 결과들

y(1),\dots,y(t)

가 관측되었을 때, 주어진 모델에 대한 가정하에 특정한 은닉 변수들에 대한 확률을 계산하는 문제들이다. 관련된 여러 작업은 모델의 매개변수와 관찰 시퀀스

y(1),\dots,y(t)

가 주어졌을 때, 하나 이상의 잠재 변수의 확률에 대해 묻는다. 모델 파라미터와 관측 시퀀스가 주어졌을 때, 하나 또는 그 이상의 잠재 변수의 확률을 구하는 다음과 같은 문제가 있다.

== 필터링 (Filtering) ==

필터링 문제는 관찰된 결과들과 이에 대한 확률 모델의 변수들이 주어졌을 때 가장 마지막 은닉 변수의 확률 분포를 묻는다. 좀 더 자연스럽게 설명하자면, 은닉 마르코프 모형의 관점에 의하여 관찰된 사건

y(1),\dots,y(t)

들이 특정 확률 과정에 의해 일련의 순서로 은닉 변수

x(n)

를 거쳐가면서 도출되었다고 가정했을 때 가장 마지막에 도달한 은닉 변수에 대해 기술하는 것으로 여겨질 수 있다.

수식으로는

:

P(x(t)\ |\ y(1),\dots,y(t))

의 값을 구하는 것으로 표현될 수 있다.

해당 문제는 전향 알고리즘을 이용하여 효율적으로 풀 수 있다. 모델의 매개변수와 관측 시퀀스가 주어졌을 때, 시퀀스 마지막에 있는 잠재 변수의 은닉 상태에 대한 분포, 즉

P(x(t)\ |\ y(1),\dots,y(t))

를 계산하는 것이 이 작업의 목표이다. 이 작업은 잠재 변수 시퀀스가 시간의 특정 지점에서 프로세스가 거치는 기본적인 상태로 간주되고, 각 지점에서 해당 관측값이 주어질 때 사용된다. 따라서, 마지막 시점에서의 프로세스 상태에 대해 묻는 것은 자연스러운 질문이다. 이 문제는 정방향 알고리즘을 사용하여 효율적으로 처리할 수 있다. 예를 들어, 이 알고리즘을 은닉 마르코프 모델에 적용하여

\mathrm{P}\big( h_t \ | v_{1:t} \big)

를 결정할 수 있다. 이 문제는 모델 파라미터와 관측 시퀀스가 주어졌을 때, 시퀀스의 마지막에서의 잠재 변수 상태의 확률 분포, 즉

P(x(t)\ |\ y(1),\dots,y(t))

를 구하는 것이다. 이 문제는 일반적으로, 잠재 변수의 시퀀스가 어떤 프로세스의 배후 상태에 있고, 그 프로세스는 각 시각의 관측값에 관해 어떤 과정이 시각의 시퀀스에 따라 전이하는 것으로 여겨지는 경우에 사용된다. 따라서 마지막 시점에서의 프로세스 상태를 아는 것이 자연스럽다.

== 다듬질 (Smoothing) ==

다듬질은 필터링과 유사한 개념이나, 가장 마지막 은닉 변수가 아니라 확률 과정 중간의 은닉 변수에 대해 묻는다는 점에서 차이가 있다. 즉, 다듬질은 k < t 인 k에 대하여 P(x(k) | y(1), …, y(t))를 구하는 과정이라고 할 수 있다. 필터링과 마찬가지로 관찰된 사건들이 특정 확률 과정에 의해 은닉 변수를 거쳐가며 도출된다는 관점에서, 특정 시간 t에서 k만큼 상태에서의 확률 분포를 묻는 것으로 이해할 수 있다.

해당 문제는 전향-후향 알고리즘으로 은닉 변수의 다듬질된 값을 구해낼 수 있다. 이는 필터링과 유사하지만 시퀀스의 중간 어딘가에 있는 잠재 변수의 분포에 대해 묻는다. 즉, P(x(k) | y(1), …, y(t))를 k < t에 대해 계산한다. 위에서 설명한 관점에서, 이는 시간 ''t''를 기준으로 과거의 시점 ''k''에 대한 숨겨진 상태에 대한 확률 분포로 생각할 수 있다. 전향-후향 알고리즘은 모든 숨겨진 상태 변수에 대한 다듬질 값을 계산하는 데 좋은 방법이다. 필터링이 시퀀스의 마지막 상태를 구하는 데 반해, 다듬질(smoothing)는 시퀀스의 중간 시점에서의 잠재 변수의 확률 분포, 즉 어떤 시점 k < t에서의 P(x(k) | y(1), …, y(t))를 구하는 것이다.

== 가장 가능성이 높은 설명에 대한 추론 ==

이 문제는 필터링이나 다듬질과는 달리, 특정한 관찰 결과들의 나열이 주어졌을 때 고려할 수 있는 전체 은닉 변수들에 대한 결합 확률들의 분포를 묻는다. 보통 이러한 유형의 문제는 필터링이나 다듬질이 적용되기 힘든 다른 종류의 문제들을 은닉 마르코프 모형을 이용하여 풀 때 적용가능하다. 가장 대표적인 예로는 품사 추론이 있다. 품사 추론이란 특정한 단어들의 나열이 주어졌을 때, 해당 단어들의 품사들을 추론하는 문제이다. 이 문제에 은닉 마르코프 모형을 적용한다면 관찰된 결과는 주어진 단어들의 나열에 해당하고, 은닉 변수들은 단어들의 품사로서 생각될 수 있다. 만약 이 문제에 필터링이나 다듬질 기법을 적용한다면 오직 한 단어의 품사만을 고려하게 되지만, 앞서 언급한 방법론은 각각의 품사들을 전체적인 문맥을 고려하여 추론하게 된다.

해당 방법론은 가능한 모든 은닉 변수들의 나열중 가장 확률이 높은 것을 찾는 문제로 귀결되는데, 이는 비터비 알고리즘으로 해결될 수 있다.

6. 2. 1. 필터링 (Filtering)

필터링 문제는 관찰된 결과들과 이에 대한 확률 모델의 변수들이 주어졌을 때 가장 마지막 은닉 변수의 확률 분포를 묻는다. 좀 더 자연스럽게 설명하자면, 은닉 마르코프 모형의 관점에 의하여 관찰된 사건

y(1),\dots,y(t)

들이 특정 확률 과정에 의해 일련의 순서로 은닉 변수

x(n)

를 거쳐가면서 도출되었다고 가정했을 때 가장 마지막에 도달한 은닉 변수에 대해 기술하는 것으로 여겨질 수 있다.

수식으로는

P(x(t)\ |\ y(1),\dots,y(t))

의 값을 구하는 것으로 표현될 수 있다.

해당 문제는 전향 알고리즘을 이용하여 효율적으로 풀 수 있다. 모델의 매개변수와 관측 시퀀스가 주어졌을 때, 시퀀스 마지막에 있는 잠재 변수의 은닉 상태에 대한 분포, 즉

P(x(t)\ |\ y(1),\dots,y(t))

를 계산하는 것이 이 작업의 목표이다. 이 작업은 잠재 변수 시퀀스가 시간의 특정 지점에서 프로세스가 거치는 기본적인 상태로 간주되고, 각 지점에서 해당 관측값이 주어질 때 사용된다. 따라서, 마지막 시점에서의 프로세스 상태에 대해 묻는 것은 자연스러운 질문이다.

이 문제는 정방향 알고리즘을 사용하여 효율적으로 처리할 수 있다. 예를 들어, 이 알고리즘을 은닉 마르코프 모델에 적용하여

\mathrm{P}\big( h_t \ | v_{1:t} \big)

를 결정할 수 있다.

이 문제는 모델 파라미터와 관측 시퀀스가 주어졌을 때, 시퀀스의 마지막에서의 잠재 변수 상태의 확률 분포, 즉

P(x(t)\ |\ y(1),\dots,y(t))

를 구하는 것이다. 이 문제는 일반적으로, 잠재 변수의 시퀀스가 어떤 프로세스의 배후 상태에 있고, 그 프로세스는 각 시각의 관측값에 관해 어떤 과정이 시각의 시퀀스에 따라 전이하는 것으로 여겨지는 경우에 사용된다. 따라서 마지막 시점에서의 프로세스 상태를 아는 것이 자연스럽다. 이 문제는 전방 알고리즘으로 효율적으로 풀 수 있다.

6. 2. 2. 다듬질 (Smoothing)

다듬질은 필터링과 유사한 개념이나, 가장 마지막 은닉 변수가 아니라 확률 과정 중간의 은닉 변수에 대해 묻는다는 점에서 차이가 있다. 즉, 다듬질은 k < t 인 k에 대하여 P(x(k) | y(1), …, y(t))를 구하는 과정이라고 할 수 있다. 필터링과 마찬가지로 관찰된 사건들이 특정 확률 과정에 의해 은닉 변수를 거쳐가며 도출된다는 관점에서, 특정 시간 t에서 k만큼 상태에서의 확률 분포를 묻는 것으로 이해할 수 있다.

해당 문제는 전향-후향 알고리즘으로 은닉 변수의 다듬질된 값을 구해낼 수 있다. 이는 필터링과 유사하지만 시퀀스의 중간 어딘가에 있는 잠재 변수의 분포에 대해 묻는다. 즉, P(x(k) | y(1), …, y(t))를 k < t에 대해 계산한다. 위에서 설명한 관점에서, 이는 시간 ''t''를 기준으로 과거의 시점 ''k''에 대한 숨겨진 상태에 대한 확률 분포로 생각할 수 있다.

전향-후향 알고리즘은 모든 숨겨진 상태 변수에 대한 다듬질 값을 계산하는 데 좋은 방법이다. 필터링이 시퀀스의 마지막 상태를 구하는 데 반해, 다듬질(smoothing)는 시퀀스의 중간 시점에서의 잠재 변수의 확률 분포, 즉 어떤 시점 k < t에서의 P(x(k) | y(1), …, y(t))를 구하는 것이다. 이는 전향-후향 알고리즘으로 효율적으로 풀 수 있다.

6. 2. 3. 가장 가능성이 높은 설명에 대한 추론

이 문제는 필터링이나 다듬질과는 달리, 특정한 관찰 결과들의 나열이 주어졌을 때 고려할 수 있는 전체 은닉 변수들에 대한 결합 확률들의 분포를 묻는다. 보통 이러한 유형의 문제는 필터링이나 다듬질이 적용되기 힘든 다른 종류의 문제들을 은닉 마르코프 모형을 이용하여 풀 때 적용가능하다. 가장 대표적인 예로는 품사 추론이 있다. 품사 추론이란 특정한 단어들의 나열이 주어졌을 때, 해당 단어들의 품사들을 추론하는 문제이다. 이 문제에 은닉 마르코프 모형을 적용한다면 관찰된 결과는 주어진 단어들의 나열에 해당하고, 은닉 변수들은 단어들의 품사로서 생각될 수 있다. 만약 이 문제에 필터링이나 다듬질 기법을 적용한다면 오직 한 단어의 품사만을 고려하게 되지만, 앞서 언급한 방법론은 각각의 품사들을 전체적인 문맥을 고려하여 추론하게 된다.

해당 방법론은 가능한 모든 은닉 변수들의 나열중 가장 확률이 높은 것을 찾는 문제로 귀결되는데, 이는 비터비 알고리즘으로 해결될 수 있다.

6. 3. 통계적 유의성

통계적 유의성은 은닉 마르코프 모형에서 특정한 결과들의 나열이 관찰되었을 때, 해당 결과가 어떠한 상태 은닉 변수들의 조합으로부터 비롯되었을 확률이 어느 정도인지를 나타내는 지표가 된다.^[83] 전향 알고리즘의 경우 이는 어떠한 귀무 분포에 대한 은닉 마르코프 모형의 확률을 구하는 문제로서 표현될 것이고, 비터비 알고리즘을 사용한 경우에는 가장 높은 확률을 갖는 은닉 변수 순서를 구하는 문제로 표현될 것이다. 이러한 맥락에서 통계적 유의성은 은닉 마르코프 모형이 가설과 특정 결과값에 대한 연관성을 평가하는데 사용된 경우 거짓 양성률을 나타내는 것으로 생각될 수 있다.^[83]

어떤 귀무 가설 분포에서 추출된 시퀀스가 특정 출력 시퀀스보다 크거나 같은 HMM 확률(전방 알고리즘의 경우) 또는 최대 상태 시퀀스 확률(비터비 알고리즘의 경우)을 가질 확률에 대한 질문도 흥미로울 수 있다.^[8] HMM이 특정 출력 시퀀스에 대한 가설의 관련성을 평가하는 데 사용될 때, 통계적 유의성은 해당 출력 시퀀스에 대한 가설을 기각하지 못하는 것과 관련된 위양성률을 나타낸다.^[8]

7. 구체적인 예제

영희와 철수는 멀리 떨어져 살고 있어 전화로만 안부를 주고받는다. 철수는 '걷기', '쇼핑', '집안 청소' 중 하나를 날씨에 따라 결정하는데, 영희는 철수가 사는 지역의 날씨를 정확히 알지 못하고 대략적인 경향만 알고 있다. 영희는 철수와의 통화 내용, 즉 철수의 행동 관찰을 통해 그 지역의 날씨를 예측하려 한다.

영희는 날씨가 마르코프 연쇄로 동작한다고 가정한다. 날씨는 '비(Rainy)'와 '맑음(Sunny)' 두 가지 상태를 가지지만, 영희는 이를 직접 관찰할 수 없으므로 은닉 상태이다. 철수는 날씨에 따라 걷거나, 쇼핑을 하거나, 청소를 하며, 영희는 이를 통해 날씨를 추측한다.

영희는 철수 지역의 일반적인 날씨 경향과 철수가 특정 날씨에 주로 하는 행동을 알고 있다. 즉, 은닉 마르코프 모형의 모수를 알고 있으며, 이는 파이썬으로 다음과 같이 표현된다.

```python

states = ('Rainy', 'Sunny')

observations = ('walk', 'shop', 'clean')

start_probability = {'Rainy': 0.6, 'Sunny': 0.4}

transition_probability = {

'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3},

'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6},

}

emission_probability = {

'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},

'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},

}

```

`start_probability`는 철수가 처음 전화했을 때 은닉 마르코프 모형이 어떤 상태에 있을지에 대한 영희의 믿음이다. (영희는 철수가 사는 지역이 주로 비가 온다는 것을 알고 있다.)
`transition_probability`는 마르코프 연쇄에서 날씨 변화를 나타낸다. 예를 들어 오늘 비가 오면 내일 맑을 확률은 30%이다.
`emission_probability`는 철수가 매일 어떤 행동을 할지 나타낸다. 비가 오면 철수는 50% 확률로 청소를 하고, 맑으면 60% 확률로 산책을 한다.

이와 유사한 예시는 비터비 알고리즘 페이지에서 더 자세히 설명되어 있다.

8. 은닉 마르코프 모형의 학습

관찰 결과의 나열이 주어졌을 때 은닉 마르코프 모형의 모수를 학습하는 과정은 해당 결과가 나올 확률을 극대화시키는 전이 확률과 출력 확률을 구하는 것이다. 이 과정은 대체로 주어진 관찰 결과에 기반하여 최대 가능도 방법으로 유도한다.^[84] 이러한 문제를 정확히 풀 수 있는 쉬운 알고리즘은 알려지지 않았지만, 바움-웰치 알고리즘이나 Baldi-Chauvin 알고리즘 등을 통해 국지적 극댓값들은 효율적으로 계산될 수 있다.^[84] 바움-웰치 알고리즘은 기대값 최대화 알고리즘(EM 알고리즘)의 특별한 경우이다.^[84]

$X_t$ 가 시간 $t$ 에서 가능한 값들이 $N$ 개 존재한다고 하자. $P(X_t|X_{t-1})$ 가 시간 $t$ 에 대해 독립적이라고 가정한다면 전이 확률은 시간독립적 전이 확률 행렬 $A$ 로 표현될 수 있다.

: $A=\{a_{ij}\}=P(X_t=j|X_{t-1}=i)$ .

초기 분포( $t=1$ )와 관찰된 결과는 각각 $\pi_i=P(X_1 = i)$ 과 $Y= (Y_1=y_1,Y_2=y_2,...,Y_t=y_t)$ 의 형태로서 주어진다.

관측된 결과변수 $Y_t$ 는 가능한 $K$ 개의 값들 중 하나를 취한다. 따라서 특정한 시간 $t$ 의 상태 $j$ 에서 어떠한 결과가 관측될 확률은 아래와 같이 기술될 수 있다.

: $b_j(y_t)=P(Y_t=y_t|X_t=j)$ .

또한 가능한 모든 상태 $X_t$ 와 결과 값 $Y_t$ 의 조합은 $K$ x $N$ 크기의 행렬 $B=\{b_j(y_i)\}$ 로 기술된다.

따라서 은닉 마르코프 모형은 $\theta = (A,B,\pi)$ 와 같이 기술된다. 바움-웰치 알고리즘은 $\theta^* = \max_{\theta} P(Y|\theta)$ 의 국지적 극댓값을 찾는데, 이는 곧 주어진 관찰 결과가 도출될 확률을 극대화하는 은닉 마르코프 모형의 모수 $\theta$ 를 찾는 과정이라 할 수 있다.^[84]

은닉 마르코프 모델(HMM)이 시계열 예측에 사용되는 경우, 단일 최대 우도 모델을 찾는 것보다 마르코프 연쇄 몬테카를로 (MCMC) 샘플링과 같은 더 정교한 베이즈 추론 방법이 정확성과 안정성 측면에서 더 유리한 것으로 입증되었다.^[9] MCMC는 상당한 계산 부하를 부과하기 때문에, 계산 확장성이 또한 중요한 경우, 대안으로 베이즈 추론에 대한 변분 근사를 사용할 수 있다.^[10]

9. 확장

9. 1. 연속적 상태 공간으로의 확장

은닉 마르코프 모형은 은닉 변수의 상태 공간을 연속적으로 확장할 수 있다.^[41]^[42] 모든 변수들이 선형적이고 가우시안 분포를 따르는 마르코프 프로세스가 선형 동적 시스템이 되는 것이 그러한 확장의 예시이다. 이와 같은 선형 동적 시스템은 칼만 필터를 이용하여 정확한 추론이 가능하다.^[41]^[42] 그러나 일반적으로 연속 은닉 변수에 대한 은닉 마르코프 모형에서의 정확한 추론은 불가능하며, 확장 칼만 필터나 입자 필터와 같은 근사 방법이 사용되어야 한다.^[41]^[42]

9. 2. 다양한 사전 분포로의 확장

은닉 마르코프 모형(HMM)은 생성 모델로, 관찰 값과 은닉 상태 사이의 결합 분포를 나타낸다. 이는 은닉 상태(전이 확률)의 사전 분포와 주어진 상태에서의 관찰 값(결과 확률)의 조건 분포로 표현될 수 있다.^[85]^[43] 기본 알고리즘은 전이 확률에 대한 균등 사전 분포를 가정하지만, 다른 사전 분포를 사용할 수도 있다.

전이 확률이 범주 분포를 따를 때, 디리클레 분포가 켤레 사전 분포로 사용될 수 있다.^[85]^[43] 일반적으로 대칭 디리클레 분포가 사용되며, 집중 모수를 통해 전이 행렬의 밀도나 희소성을 조절한다. 집중 모수가 1이면 균등 분포가 되고, 1보다 크면 밀집 행렬, 1보다 작으면 희소 행렬이 생성된다.^[85]^[43]

두 단계의 디리클레 분포를 사전 분포로 사용할 수도 있다. 상위 디리클레 분포가 하위 디리클레 분포의 매개변수를 제어하고, 하위 분포는 전이 확률을 제어하는 방식이다.^[85]^[43] 상위 분포의 집중 모수는 상태의 밀도나 희소성을 결정한다. 이러한 방식은 비지도 품사 태깅과 같이 일부 품사가 다른 품사보다 더 자주 나타나는 경우에 유용하다.^[85]^[43]

디리클레 분포 대신 디리클레 과정을 사전 분포로 사용할 수 있다. 이 경우 잠재적으로 무한한 수의 상태를 고려할 수 있다.^[85]^[43] 두 단계 디리클레 과정을 사용하는 계층적인 디리클레 과정 은닉 마르코프 모형(HDP-HMM)이 제안되었다.^[85]^[43] HDP-HMM은 "무한 은닉 마르코프 모델"이라고도 불렸으며, "계층적 디리클레 과정"^[44]에서 더 형식화되었다. 이러한 모델의 모수는 깁스 샘플링이나 기댓값 최대화 알고리즘의 확장 버전을 통해 학습할 수 있다.^[85]^[43]

9. 3. 판별 모델을 이용한 확장

표준 은닉 마르코프 모형의 생성 모형 대신 판별 모형을 사용할 수 있다. 이 모델은 관측값에 주어진 은닉 상태의 조건부 분포를 직접 모델링한다. 최대 엔트로피 마르코프 모형(Maximum-entropy Markov model)이 그 예시 중 하나인데, 로지스틱 회귀를 사용하여 상태의 조건부 분포를 모델링한다. 이러한 모델은 관찰 값들의 임의의 특징들을 모델링 할 수 있다는 장점이 있다. 예를들어, 관찰 값과 근처 관찰 값의 조합이나 주어진 은닉 상태로부터 어떤 거리에 있는 임의의 관찰 값의 실제에서의 근처 관찰 값의 특징은 은닉 상태의 값을 결정하는데 사용될수 있다. 또한, 이러한 특징에 대해 각각 서로에 대해 통계적으로 독립일 필요가 없다. 그러나 은닉 상태들에 놓일 수 있는 사전 분포들의 종류는 엄격하게 제한되며, 임의의 관찰 값을 보는 것의 확률을 예측하는 것은 불가능하다는 단점이 있다.

선형-연쇄 조건부 무작위장은 최대 엔트로피 마르코프 모형의 방향 그래프 모델과 비슷한 모델들 보다는 비방향 그래프 모델을 사용하며, 레이블 편향 문제로 고통받지 않아도 된다는 장점이 있지만, 훈련이 느릴 수 있다는 단점이 있다.

9. 4. 차례곱 은닉 마르코프 모형

차례곱 은닉 마르코프 모형(factorial hidden Markov model)은 하나의 관측값이

K

개의 독립적인 마르코프 연쇄와 관련되는 것을 허용한다.^[45] 이는 각 연쇄가

N

개의 상태를 가진다고 가정할 때,

N^K

개의 상태를 가진 하나의 은닉 마르코프 모형과 동등하다. 길이

T

인 상태열에 대한 전방 비터비 알고리즘은

O(N^{2k}T)

의 복잡도를 가지며, 따라서 이런 모델을 학습하는 것은 무척 어렵다.^[45] 정확한 해를 찾기 위하여 접합 트리 알고리즘이 사용될 수 있으나 이는

O(N^{K+1}KT)

의 복잡도를 가진다.^[45] 현실적인 사용을 위해서는 변분법을 이용한 접근과 같은 근사화 방법이 사용될 수 있다.^[45]

9. 5. 삼중 마르코프 모형

삼중 마르코프 모형은 특수 데이터를 모델링하기 위한 보조적인 과정을 추가한 모델이다.^[46] 이 모델의 다양한 변형 형태들이 제안되었다.^[46] 증거 이론과 삼중 마르코프 모형 사이에 흥미로운 연관성이 있으며,^[47] 이를 통해 마르코프 맥락에서 데이터를 융합하고^[48] 비정상 데이터를 모델링할 수 있다.^[49]^[50]

10. 수학적 서술

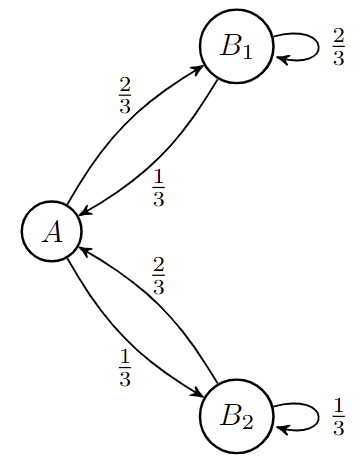
마르코프 전이 행렬과 상태에 대한 불변 분포가 주어지면, 부분 이동 집합에 확률 측도를 부과할 수 있다. 예를 들어, 상태 A^영어, B₁^영어, B₂^영어에 대해 주어진 마르코프 체인을 고려하고, 불변 분포는 이다. B₁^영어, B₂^영어 사이의 구분을 무시함으로써, 이 부분 이동 공간은 A^영어, B₁^영어, B₂^영어에서 A^영어, B^영어의 다른 부분 이동 공간으로 투영되며, 이 투영은 또한 확률 측도를 A^영어, B^영어의 부분 이동에 대한 확률 측도로 투영한다.

흥미로운 점은 A^영어, B^영어의 부분 이동에 대한 확률 측도가 A^영어, ''B''^''n''/B}}에 대한 마르코프 체인에 의해 생성되지 않는다는 것이다. 직관적으로 이것은 긴 가 됨을 점점 더 확신하게 되기 때문이다. 즉, 시스템의 관측 가능한 부분은 과거의 무언가에 의해 무한히 영향을 받을 수 있다.^[60]^[61]

반대로, 6개의 기호에 대한 부분 이동 공간이 존재하며, 2개의 기호에 대한 부분 이동으로 투영되어 더 작은 부분 이동에 대한 모든 마르코프 측도가 어떤 차수에서도 마르코프가 아닌 전사 측도를 갖는다.^[61]

10. 1. 보편적 서술

기본적인 비 베이지안 은닉 마르코프 모형은 다음과 같이 서술될 수 있다. 상태의 수를 ''N'', 관찰의 수를 ''T''라고 할 때, 상태와 관련된 관찰을 위한 결과 모수는

\theta_{i=1 \dots N}

, 상태 ''i''에서 상태 ''j''로 가는 확률은

\phi_{i=1 \dots N, j=1 \dots N}

로 표현된다.

\boldsymbol\phi_{i=1 \dots N}

는

-\phi_{i,1 \dots N}

로 구성된 ''N''차원 벡터이며, 그 합은 1이 되어야 한다. 시간 ''t''에서 관찰의 상태는

x_{t=1 \dots T}

, 시간 ''t''에서의 관찰은

y_{t=1 \dots T}

로 나타낸다. ''θ''에 대해 모수화 된 관찰의 확률 분포는

F(y|\theta)

이다.

x_{t=2 \dots T}

는

\operatorname{Categorical}(\boldsymbol\phi_{x_{t-1}})

분포를 따르며,

y_{t=1 \dots T}

는

F(\theta_{x_t})

분포를 따른다.^[60]^[61]

초기 상태

x_1

의 사전 분포는 정해지지 않았으며, 일반적인 학습 모델들은 이산적인 연속균등분포를 따른다고 가정한다. 베이지안 설정에서 모든 모수는 확률 변수와 관련되며, 결과 모수들을 위한 공유 초 모수는 ''α'', 전이 모수들을 위한 공유 초 모수는 ''β''로 표현된다. 는 로 모수화 된 결과 모수들의 사전 확률 분포를 나타내며,

\theta_{i=1 \dots N}

는

H(\alpha)

분포를,

\boldsymbol\phi_{i=1 \dots N}

는

\operatorname{Symmetric-Dirichlet}_N(\beta)

분포를 따른다.

마르코프 전이 행렬과 상태에 대한 불변 분포가 주어지면, 부분 이동 집합에 확률 측도를 부과할 수 있다. 예를 들어, 상태

A, B_1, B_2

에 대한 마르코프 체인에서

B_1, B_2

사이의 구분을 무시하면, 이 부분 이동 공간은

A, B_1, B_2

에서

A, B

의 다른 부분 이동 공간으로 투영되며, 이 투영은 확률 측도를

A, B

의 부분 이동에 대한 확률 측도로 투영한다. 그러나

A, B

의 부분 이동에 대한 확률 측도는

A, B

에 대한 마르코프 체인에 의해 생성되지 않는다. 긴

B^n

의 시퀀스를 관찰하면

Pr(A | B^n) \to \frac 23

가 되기 때문에 시스템의 관측 가능한 부분은 과거의 무언가에 의해 무한히 영향을 받을 수 있다.^[60]^[61]

10. 2. 단순 혼합 모델과의 비교

은닉 마르코프 모형(HMM)에서 각 관찰의 분포는 해당 상태에서 혼합 컴포넌트로의 상태를 가지는 혼합 밀도이다. 은닉 마르코프 모형을 혼합 모델과 비교하면 다음과 같다.

혼합 모델은 N개의 혼합 컴포넌트와 T개의 관찰로 구성된다. θ_i=1...N은 i번째 관찰 분포의 매개변수, Φ_i=1...N은 혼합 편중(컴포넌트 i의 사전 확률)을 나타낸다. Φ는 Φ_1...N으로 구성된 N차원 벡터이며, 그 합은 1이 된다. x_t=1...T는 관찰 t의 컴포넌트, y_t=1...T는 관찰 t를 의미한다. F(y|θ)는 θ로 매개화된 관찰의 확률 분포이다.

비 베이지안 혼합 모델:

		$x_{t=1 \dots T}$		~		$\operatorname{Categorical}(\boldsymbol\phi)$
		$y_{t=1 \dots T}$		~		$F(\theta_{x_t})$

베이지안 혼합 모델:

$\theta_{i=1 \dots N}$	~	$H(\alpha)$
$\boldsymbol\phi$	~	$\operatorname{Symmetric-Dirichlet}_N(\beta)$
$x_{t=1 \dots T}$	~	$\operatorname{Categorical}(\boldsymbol\phi)$
$y_{t=1 \dots T}$	~	$F(\theta_{x_t})$

여기서 α는 컴포넌트 모수들을 위한 공유 초 모수, β는 혼합 편중들을 위한 공유 초 모수, H(θ|α)는 α로 매개화된 컴포넌트 모수의 사전 확률 분포를 나타낸다.

마르코프 전이 행렬과 상태에 대한 불변 분포가 주어지면, 부분 이동 집합에 확률 측도를 부과할 수 있다. 예를 들어, 상태 A, B₁, B₂에 대한 마르코프 체인에서 불변 분포가 π = (2/7, 4/7, 1/7)일 때, B₁, B₂ 사이의 구분을 무시하면 A, B₁, B₂에서 A, B로 투영될 수 있다. 이 투영은 확률 측도를 A, B의 부분 이동에 대한 확률 측도로 투영한다.

그러나 A, B의 부분 이동에 대한 확률 측도는 A, B에 대한 마르코프 체인에 의해 생성되지 않는다. 긴 Bⁿ의 시퀀스를 관찰하면 Pr(A | Bⁿ) → 2/3가 되기 때문에 시스템의 관측 가능한 부분은 과거에 의해 무한히 영향을 받을 수 있다.^[60]^[61]

10. 3. 예시

은닉 마르코프 모형(HMM)의 수학적 서술을 구체화하기 위해 정규 분포와 Categorical 관찰을 따르는 HMM의 예시를 살펴본다.

관찰 결과들이 정규 분포를 따르는 비 베이지안 및 베이지안 은닉 마르코프 모형은 다음과 같다.

		수식		설명
N	상태의 수
T	관찰의 수
$\phi_{i=1 \dots N, j=1 \dots N}$	상태 i에서 상태 j로 가는 확률
$\boldsymbol\phi_{i=1 \dots N}$	$\phi_{i,1 \dots N}$ 로 구성된 N-차원 벡터; 합이 $1$ 이 되어야 한다.
$\mu_{i=1 \dots N}$	상태 i와 관련된 관찰들의 평균
$\sigma^2_{i=1 \dots N}$	상태 i와 관련된 관찰들의 편차
$x_{t=1 \dots T}$	시간 t에서 관찰의 상태
$y_{t=1 \dots T}$	시간 t에서의 관찰
$x_{t=2 \dots T}$	$\operatorname{Categorical}(\boldsymbol\phi_{x_{t-1}})$
$y_{t=1 \dots T}$	$\mathcal{N}(\mu_{x_t}, \sigma_{x_t}^2)$

베이지안 은닉 마르코프 모형의 경우, 추가적으로 다음 변수들이 정의된다.

		수식		설명
β	전이 행렬의 밀도를 조절하는 집중 초 모수
$\mu_0, \lambda$	각 상태의 평균들의 공유 초 모수
$\nu, \sigma_0^2$	각 상태의 편차들의 공유 초 모수
$\boldsymbol\phi_{i=1 \dots N}$	$\operatorname{Symmetric-Dirichlet}_N(\beta)$
$\mu_{i=1 \dots N}$	$\mathcal{N}(\mu_0, \lambda\sigma_i^2)$
$\sigma_{i=1 \dots N}^2$	$\operatorname{Inverse-Gamma}(\nu, \sigma_0^2)$

Categorical 관찰을 따르는 비 베이지안 및 베이지안 은닉 마르코프 모형은 다음과 같다.

		수식		설명
N	상태의 수
T	관찰의 수
$\phi_{i=1 \dots N, j=1 \dots N}$	상태 i에서 상태 j로 가는 확률
$\boldsymbol\phi_{i=1 \dots N}$	$\phi_{i,1 \dots N}$ 로 구성된 N-차원 벡터; 합이 $1$ 이 되어야 한다.
V	Categorical 관찰들의 차원 (예: 단어 어휘의 크기)
$\theta_{i=1 \dots N, j=1 \dots V}$	j 번째 아이템을 관찰하는 상태 i를 위한 확률
$\boldsymbol\theta_{i=1 \dots N}$	$\theta_{i,1 \dots V}$ 로 구성된 V-차원 벡터; 합이 $1$ 이 되어야 한다.
$x_{t=1 \dots T}$	시간 t에서 관찰의 상태
$y_{t=1 \dots T}$	시간 t에서의 관찰
$x_{t=2 \dots T}$	$\operatorname{Categorical}(\boldsymbol\phi_{x_{t-1}})$
$y_{t=1 \dots T}$	$\text{Categorical}(\boldsymbol\theta_{x_t})$

베이지안 은닉 마르코프 모형의 경우, 추가적으로 다음 변수들이 정의된다.

		수식		설명
α	각 상태에 대한 $\boldsymbol\theta$ 의 공유 집중 초 모수
β	전이 행렬의 밀도를 조절하는 집중 초 모수
$\boldsymbol\phi_{i=1 \dots N}$	$\operatorname{Symmetric-Dirichlet}_N(\beta)$
$\boldsymbol\theta_{1 \dots V}$	$\operatorname{Symmetric-Dirichlet}_V(\alpha)$

베이지안 특징에서 ''β'' (집중 모수)는 전이 행렬의 밀도를 조절한다. 높은 ''β'' 값(1 이상)에서는 특정 상태의 전이를 조절하는 확률들이 비슷해져, 다른 많은 상태로 전이될 확률이 높아진다. 즉, 감춰진 상태들의 마르코프 연쇄 경로는 매우 임의적이다. 반면 낮은 ''β'' 값에서는 소수의 가능한 전이만 상당한 확률을 가지므로, 감춰진 상태들의 경로는 어느 정도 예측 가능하다.^[60]^[61]

마르코프 전이 행렬과 상태에 대한 불변 분포가 주어지면, 부분 이동 집합에 확률 측도를 부여할 수 있다. 예를 들어, 상태 $A, B_1, B_2$ 에 대한 마르코프 체인에서 불변 분포가 $\pi = (2/7, 4/7, 1/7)$ 일 때, $B_1, B_2$ 사이의 구분을 무시하면 $A, B_1, B_2$ 에서 $A, B$ 로 투영할 수 있다. 이 투영은 확률 측도를 $A, B$ 의 부분 이동에 대한 확률 측도로 투영한다.

하지만 $A, B$ 의 부분 이동에 대한 확률 측도는 $A, B$ 에 대한 마르코프 체인에 의해 생성되지 않는다. 긴 $B^n$ 시퀀스를 관찰하면 $Pr(A | B^n) \to \frac 23$ 가 됨을 확신하게 되므로, 시스템의 관측 가능한 부분은 과거에 의해 무한히 영향을 받을 수 있다.^[60]^[61]

10. 4. 두 단계 베이지안 은닉 마르코프 모형

은닉 마르코프 모형(HMM)에서 전이 행렬에 대한 사전 매개변수를 추가하여 모델을 확장할 수 있다. 이는 두 단계 베이지안 은닉 마르코프 모형으로, 전이 행렬의 밀도와 특정 상태로의 전이 확률을 독립적으로 조절할 수 있게 한다.^[60]^[61]

기존 모델에서는 전이 행렬의 밀도를 조절하는 집중 초모수 와, 이에 따른 대칭 디리클레 분포를 따르는 전이 확률 벡터

\boldsymbol\phi_{i=1 \dots N}

를 사용했다.

두 단계 모델에서는 다음과 같은 변수들이 추가된다.

변수	설명
	얼마나 많은 상태들이 본질적으로 존재할지를 조절하는 집중 초모수
	전이 행렬의 밀도를 조절하는 집중 초모수
	주어진 상태의 본질적 확률을 명시하는 -차원 벡터. ~ $\operatorname{Symmetric-Dirichlet}_N(\gamma)$
$\boldsymbol\phi_{i=1 \dots N}$	$\operatorname{Dirichlet}_N(\beta N \boldsymbol\eta)$ 를 따름

: 상태들의 확률 분포를 나타낸다. 특정 상태의 확률이 높을수록 해당 상태로 전이할 가능성이 커진다.
: 의 밀도를 조절한다. 1보다 크면 모든 상태가 비슷한 사전 확률을 갖는 밀집한 벡터가 되고, 1보다 작으면 소수의 상태만 가능한 밀도가 낮은 벡터가 된다.
: 전이 행렬의 밀도를 조절한다. 가 1보다 크면, 벡터들은 밀도가 높아지고 확률 질량이 모든 상태에 고르게 퍼진다. 반면, 가 1보다 작으면, 벡터들은 밀도가 낮아지고, 확률 질량은 소수의 상태에 집중된다.

를 사용하여 특정 상태가 더 선호되도록 설정할 수 있다. 만약 의 값들이 불균형하면, 특정 상태가 다른 상태보다 높은 확률을 갖게 되어, 시작 상태와 관계없이 해당 상태로의 전이가 자주 발생한다.

이와 같이 두 단계 모델은 전체 전이 행렬의 밀도와 특정 전이가 가능한 상태의 밀도를 독립적으로 조절할 수 있다.

부분 이동 집합에 확률 측도를 부여할 수 있다. 예를 들어, 상태

A, B_1, B_2

를 갖는 마르코프 체인에서 불변 분포가

\pi = (2/7, 4/7, 1/7)

일 때,

B_1, B_2

를

B

로 투영하면,

A, B

에 대한 확률 측도는 마르코프 체인에 의해 생성되지 않는다. 긴

B^n

시퀀스를 관찰하면

Pr(A | B^n) \to \frac 23

가 되므로, 시스템의 관측 가능한 부분은 과거에 의해 무한히 영향을 받을 수 있다.^[60]^[61]

11. 응용

HMM은 직접 관찰할 수 없는 데이터 시퀀스를 복구하는 것이 목표인 많은 분야에 적용될 수 있다(하지만 시퀀스에 의존하는 다른 데이터는 있음). 적용 분야는 다음과 같다.

계산 금융^[11]^[12]
단분자 운동 분석^[13]
신경 과학^[14]^[15]
암호 해독
음성 인식, Siri 포함^[16]
음성 합성
품사 태깅
스캔 솔루션의 문서 분리
기계 번역
부분 방전
유전자 예측
필기 인식^[17]
생체 시퀀스 정렬
시계열 분석
활동 인식
단백질 폴딩^[18]
시퀀스 분류^[19]
변이 바이러스 탐지^[20]
시퀀스 모티프 발견 (DNA 및 단백질)^[21]
DNA 혼성화 역학^[22]^[23]
크로마틴 상태 발견^[24]
수송 예측^[25]
태양 복사 조도 변동성^[26]^[27]^[28]

11. 1. 음성 인식에의 응용

은닉 마르코프 모형(HMM)은 음성 인식 분야에서 널리 사용된다.^[16] 주어진 음성이 어떤 문자열에서 비롯되었는지를 판단하는 데 사용될 수 있다. 은닉 마르코프 모형의 관점에서 음성은 "특정한 문자열로부터 도출된 출력 변수"로 여겨질 수 있다. 따라서 은닉 마르코프 모형의 최적해를 찾는 과정은 "관찰된 출력 변수(음성)를 가장 잘 설명하는 은닉 상태(문자열)"을 찾는 과정이라고 할 수 있다. 이러한 모델은 비터비 알고리즘을 이용하여 최적해를 찾을 수 있다.

11. 2. 생물정보학에의 응용

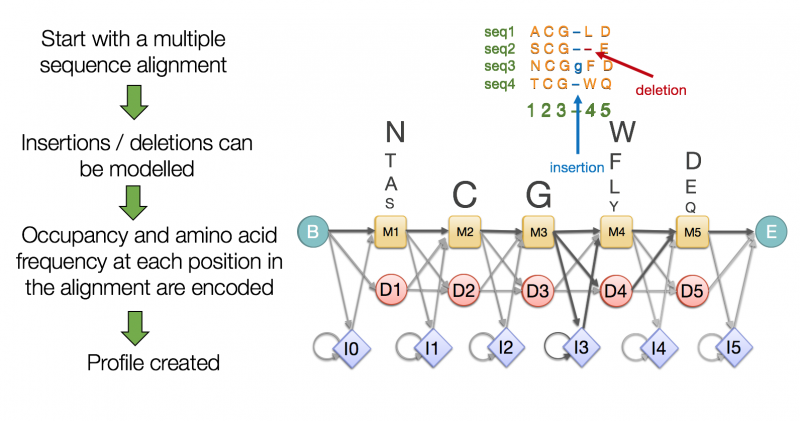
은닉 마르코프 모형은 생물정보학에서 유전자 예측, 다중 서열 정렬, DNA 서열 에러 모델링, 단백질 2차 구조 예측, ncRNA 식별, 비코딩 RNA의 위치 확인 등에 사용되는 대표적인 도구이다.^[86]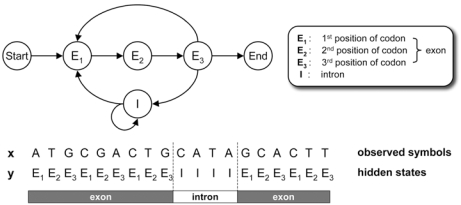

위 그림은 주어진 유전자 서열에서 엑손과 인트론의 통계적 차이점을 밝혀내기 위한 은닉 마르코프 모형의 예시이다.^[86] 엑손에서 발견된 코돈의 첫번째, 두번째, 세번째 염기를 의미하는

E_1

,

E_2

,

E_3

와 인트론의 염기를 의미하는

I

의 4개의 상태를 가진다. 이 모델은 여러개의 코돈을 내포한 다수의 엑손과 다양한 길이의 인트론을 표현할 수 있다.

11. 3. 금융공학에의 응용

은닉 마르코프 모형(HMM)은 금융 시계열 데이터 분석에 응용될 수 있다.^[11]^[12] 몇몇 연구에서는 은닉 마르코프 모형이 대부 은행 고객 특성 모델링에서 K-최근접 이웃 알고리즘보다 더 나은 성과를 보였다고 주장한다.^[87]

11. 4. 기타 널리 사용되는 분야

은닉 마르코프 모형은 직접 관측할 수 없는 데이터 열과 이에 의존하는 다른 데이터들이 있을 때 데이터 열을 복원하는 것을 목표로 하는 다양한 분야에 적용 가능하다.^[88] 응용분야로는 단분자의 운동 분석,^[88] 암호해독, 음성 합성, 품사 추론, 스캔 된 문서의 분할, 기계 번역, 서열 정렬, 시계열 분석, 사람 행동 분석,^[89] 단백질 접힘,^[90] 변성 바이러스 탐지^[91] 등이 있다.

11. 5. 응용 시 고려해야 할 사항들

은닉 마르코프 모형에는 상태들의 전이 구성에 따라 몇 가지 알려진 모델들이 있다. 이때 주어진 문제에 따라 적합한 아키텍처를 선택하는 것은 중요하다. 가장 널리 쓰이는 모델로는 에르고딕(ergodic) 모델과 좌우(left-to-right) 모델이 있다.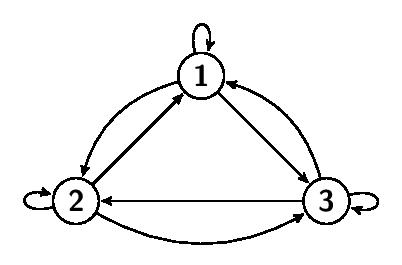

좌우 모델은 어떤 상태로 들어가면 뒤로 돌아갈 수 없다는 특징이 있다. 따라서 철수와 영희 문제에 좌우 모델을 선택한다면, 오늘의 날씨가 맑고(Sunny) 내일 비가 온다면(Rainy) 모레 이후로는 맑은 날씨가 나타날 수 없게 되므로, 이는 잘못된 선택이다. 반면 음성 인식이나 온라인 필기 인식처럼 어떤 부분 패턴이 지나간 후에 그것이 다시 나타나지 않는 상황에서는 좌우 모델이 많이 사용된다.

12. 개념 보충 설명

Mark Stamp 저, San Jose State University의 [http://www.cs.sjsu.edu/~stamp/RUA/HMM.pdf 은닉 마르코프 모형에 대한 자세한 설명].
[https://web.archive.org/web/20120415032315/http://www.ee.washington.edu/research/guptalab/publications/EMbookChenGupta2010.pdf EM과정에 기반한 은닉 마르코프 모형 계산].
[https://web.archive.org/web/20111005202130/http://www.tristanfletcher.co.uk/SAR%20HMM.pdf 전환 자기회귀 은닉 마르코프 모형 (Switching Autoregressive 또는 SAR HMM)].
[http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html 은닉 마르코프 모형 튜토리얼].
[http://www.cs.brown.edu/research/ai/dynamics/tutorial/Documents/HiddenMarkovModels.html 은닉 마르코프 모형] "간단한 수학을 이용한 설명 페이지".
[http://jedlik.phy.bme.hu/~gerjanos/HMM/node2.html 은닉 마르코프 모형].
은닉 마르코프 모형 : 기초와 응용 [http://www.eecis.udel.edu/~lliao/cis841s06/hmmtutorialpart1.pdf Part 1], [http://www.eecis.udel.edu/~lliao/cis841s06/hmmtutorialpart2.pdf Part 2] (V. Petrushin 작성).
제이슨 아이스너의 강의 [http://videolectures.net/hltss2010_eisner_plm/video/2/ Video] 와 [http://www.cs.jhu.edu/~jason/papers/eisner.hmm.xls interactive spreadsheet].
Statistical–mechanical lattice models for protein–DNA binding in chromatin^영어.

13. 소프트웨어

매트랩을 위한 은닉 마르코프 모형 툴박스는 케빈 머피가 제작하였다.
은닉 마르코프 모형 툴킷 (HTK)은 은닉 마르코프 모형의 제작 및 조작에 유용한 툴킷박스이다.
R을 위한 은닉 마르코프 모형은 "이산 은닉 마르코프 공간에서 추론을 하기 위한 도구"이다.
HMMlib은 은닉 마르코프 모형 기능을 제공하는 최적화된 라이브러리이다.
parredHMMlib은 전향 알고리즘과 비터비 알고리즘에 대한 병렬적 구현으로, 상태 공간이 작을 때 매우 빠르다.
zipHMMlib은 전향 알고리즘의 반복되는 작업을 크게 단순화시킨 일반적인 은닉 마르코프 모형 라이브러리이다.
GHMM 라이브러리는 GHMM 라이브러리 프로젝트의 홈페이지에서 확인할 수 있다.
The hmm package는 "은닉 마르코프 모형을 구현한 하스켈 라이브러리"이다.
조지아 공대 동작 인식 툴킷(GT2K)도 활용 가능하다.
비터비 모델을 계산해주는 온라인 은닉 마르코프 모형 페이지도 있다.
OpenCV 기반 은닉 마르코프 모형 클래스도 제공된다.
MLPACK은 은닉 마르코프 모형을 C++로 구현한 라이브러리이다.

참조

_[1] 웹사이트 Google Scholar https://scholar.goog[...]
_[2] 논문 Real-Time American Sign Language Visual Recognition From Video Using Hidden Markov Models http://www.cc.gatech[...] MIT 1995-02
_[3] 간행물 Modeling Form for On-line Following of Musical Performances http://www.cs.northw[...] 2005-07
_[4] 간행물 Use of hidden Markov models for partial discharge pattern classification https://ieeexplore.i[...] 2003-04
_[5] 논문 Modeling linkage disequilibrium and identifying recombination hotspots using single-nucleotide polymorphism data. 2003-12
_[6] 논문 ChromHMM: automating chromatin-state discovery and characterization 2012-03
_[7] 논문 A tutorial on Hidden Markov Models and selected applications in speech recognition http://www.ece.ucsb.[...] 1989-02
_[8] 논문 Error statistics of hidden Markov model and hidden Boltzmann model results
_[9] 간행물 Parallel stratified MCMC sampling of AR-HMMs for stochastic time series prediction http://1drv.ms/b/s!A[...] 2016
_[10] 논문 A variational Bayesian methodology for hidden Markov models utilizing Student's-t mixtures http://users.iit.dem[...] 2018-03-11
_[11] 논문 Parallel Optimization of Sparse Portfolios with AR-HMMs
_[12] 논문 A novel corporate credit rating system based on Student's-t hidden Markov models
_[13] 논문 Solving Ion Channel Kinetics with the QuB Software 2013
_[14] 논문 Spatiotemporally Resolved Multivariate Pattern Analysis for M/EEG 2022
_[15] 논문 Motor-like neural dynamics in two parietal areas during arm reaching https://www.scienced[...] 2021-10-01
_[16] 서적 The Master Algorithm: How the Quest for the Ultimate Learning Machine Will Remake Our World https://archive.org/[...] Basic Books 2015
_[17] 간행물 "Recognition of handwritten word: first and second order hidden Markov model based approach" https://www.academia[...] 1989
_[18] 논문 The Complex Folding Network of Single Calmodulin Molecules
_[19] 논문 A Hidden Markov Model Variant for Sequence Classification
_[20] 논문 Hunting for metamorphic engines
_[21] 논문 DNA motif elucidation using belief propagation
_[22] 논문 Improved Optical Multiplexing with Temporal DNA Barcodes 2019-05-17
_[23] 논문 Programming Temporal DNA Barcodes for Single-Molecule Fingerprinting 2019-04-10
_[24] 웹사이트 ChromHMM: Chromatin state discovery and characterization http://compbio.mit.e[...] 2018-08-01
_[25] arXiv Modeling and Forecasting the Evolution of Preferences over Time: A Hidden Markov Model of Travel Behavior 2011-05
_[26] 논문 The stochastic two-state solar irradiance model (STSIM) 1998-02
_[27] 논문 A Markov-chain probability distribution mixture approach to the clear-sky index 2018-08
_[28] 논문 An N-state Markov-chain mixture distribution model of the clear-sky index 2018-10
_[29] 논문 Statistical Inference for Probabilistic Functions of Finite State Markov Chains
_[30] 논문 An inequality with applications to statistical estimation for probabilistic functions of Markov processes and to a model for ecology http://projecteuclid[...]
_[31] 논문 Growth transformations for functions on manifolds
_[32] 논문 A Maximization Technique Occurring in the Statistical Analysis of Probabilistic Functions of Markov Chains
_[33] 논문 An Inequality and Associated Maximization Technique in Statistical Estimation of Probabilistic Functions of a Markov Process
_[34] 논문 The DRAGON system—An overview
_[35] 논문 Design of a linguistic statistical decoder for the recognition of continuous speech
_[36] 서적 Hidden Markov Models for Speech Recognition Edinburgh University Press
_[37] 서적 Spoken Language Processing Prentice Hall
_[38] 서적 Grammatical Inference and Applications Springer 1994
_[39] 논문 Maximum Likelihood Alignment of DNA Sequences
_[40] 간행물 Durbin 1998
_[41] 논문 Inference in finite state space non parametric Hidden Markov Models and applications https://doi.org/10.1[...] 2016-01-01
_[42] 논문 Fundamental Limits for Learning Hidden Markov Model Parameters https://ieeexplore.i[...] 2023-03
_[43] 문서 The infinite hidden Markov model
_[44] 문서 Hierarchical dirichlet processes
_[45] 논문 Factorial Hidden Markov Models
_[46] 논문 Chaı̂nes de Markov Triplet http://www.numdam.or[...]
_[47] 논문 Multisensor triplet Markov chains and theory of evidence
_[48] 웹사이트 Boudaren et al. http://asp.eurasipjo[...] 2014-03-11
_[49] 웹사이트 Lanchantin et al. https://ieeexplore.i[...]
_[50] 웹사이트 Boudaren et al. https://ieeexplore.i[...]
_[51] 웹사이트 Visual Workflow Recognition Using a Variational Bayesian Treatment of Multistream Fused Hidden Markov Models https://ieeexplore.i[...] 2012-07
_[52] 논문 A Reservoir-Driven Non-Stationary Hidden Markov Model
_[53] 문서 Reservoir computing approaches to recurrent neural network training
_[54] 문서 Equivalence between LC-CRF and HMM, and Discriminative Computing of HMM-Based MPM and MAP
_[55] 문서 Hidden markov chains, entropic forward-backward, and part-of-speech tagging
_[56] 문서 Deriving discriminative classifiers from generative models
_[57] 문서 On discriminative vs. generative classifiers: A comparison of logistic regression and naive bayes
_[58] 서적 Panel Analysis: Latent Probability Models for Attitude and Behaviour Processes Elsevier
_[59] 서적 Latent Markov models for longitudinal data https://sites.google[...] Chapman and Hall/CRC
_[60] 웹사이트 Sofic Measures: Characterizations of Hidden Markov Chains by Linear Algebra, Formal Languages, and Symbolic Dynamics https://web.archive.[...]
_[61] 간행물 Hidden Markov processes in the context of symbolic dynamics 2010-01-13
_[62] 논문 Statistical Inference for Probabilistic Functions of Finite State Markov Chains https://www.jstor.or[...] 2023-04-05
_[63] 논문 An inequality with applications to statistical estimation for probabilistic functions of Markov processes and to a model for ecology http://projecteuclid[...]
_[64] 논문 Growth transformations for functions on manifolds https://www.scribd.c[...] 2011-11-28
_[65] 논문 A Maximization Technique Occurring in the Statistical Analysis of Probabilistic Functions of Markov Chains
_[66] 논문 An Inequality and Associated Maximization Technique in Statistical Estimation of Probabilistic Functions of a Markov Process
_[67] 논문 Conditional Markov Processes
_[68] 논문 Statistical Inference for Probabilistic Functions of Finite State Markov Chains http://projecteuclid[...] 2011-11-28
_[69] 논문 An inequality with applications to statistical estimation for probabilistic functions of Markov processes and to a model for ecology http://projecteuclid[...]
_[70] 논문 Growth transformations for functions on manifolds http://www.scribd.co[...] 2011-11-28
_[71] 저널 A Maximization Technique Occurring in the Statistical Analysis of Probabilistic Functions of Markov Chains http://projecteuclid[...]
_[72] 저널 An Inequality and Associated Maximization Technique in Statistical Estimation of Probabilistic Functions of a Markov Process
_[73] 문서 Real-Time American Sign Language Visual Recognition From Video Using Hidden Markov Models http://www.cc.gatech[...] MIT 1995-02
_[74] 간행물 Modeling Form for On-line Following of Musical Performances http://www.cs.northw[...] AAAI-05 Proc. 2005-07
_[75] 저널 Use of hidden Markov models for partial discharge pattern classification http://ieeexplore.ie[...] 2003-04
_[76] 저널 Multisensor triplet Markov chains and theory of evidence http://www.sciencedi[...]
_[77] 저널 Dempster-Shafer fusion of multisensor signals in nonstationary Markovian context http://asp.eurasipjo[...]
_[78] 저널 Unsupervised restoration of hidden non stationary Markov chain using evidential priors http://ieeexplore.ie[...]
_[79] 저널 Unsupervised segmentation of random discrete data hidden with switching noise distributions http://ieeexplore.ie[...] 2012-10
_[80] 문서 Extension of the law of large numbers to dependent quantities Izv. Fiz.-Matem. Obsch. Kazan Univ.(2nd Ser)
_[81] 저널 Maximum Likelihood Alignment of DNA Sequences
_[82] 저널 A tutorial on Hidden Markov Models and selected applications in speech recognition http://www.ece.ucsb.[...] 1989-02
_[83] 저널 Error statistics of hidden Markov model and hidden Boltzmann model results
_[84] 서적 A Gentle Tutorial of the EM Algorithm and its Application to Parameter Estimation for Gaussian Mixture and Hidden Markov Models International Computer Science Institute
_[85] 저널 Hierarchical Dirichlet Processes 2006
_[86] 문서 Hidden Markov Models and their Applications in Biological Sequence Analysis http://www.ncbi.nlm.[...]
_[87] 문서 Gaussian mixture based HMM for human daily activity recognition using 3D skeleton features, Model-Based Clustering With Hidden Markov Models and its Application to Financial Time-Series Data http://ieeexplore.ie[...]
_[88] 저널 SOLVING ION CHANNEL KINETICS WITH THE QuB SOFTWARE 2013
_[89] 간행물 Gaussian mixture based HMM for human daily activity recognition using 3D skeleton features http://ieeexplore.ie[...] 2013-06-19
_[90] 저널 The Complex Folding Network of Single Calmodulin Molecules
_[91] 저널 Hunting for metamorphic engines

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com