헨더슨-하셀바흐 방정식

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
- 2.1. 헨더슨과 하셀발흐의 방정식 개발
3. 정의 및 유도
- 3.1. 정의
- 3.2. 유도
4. 가정, 한계 및 응용
- 4.1. 염기에 대한 적용
- 4.2. 생물학적 응용
  - 4.2.1. 항상성과 혈액 완충 시스템
  - 4.2.2. 해양 산성화
참조

1. 개요

헨더슨-하셀바흐 방정식은 화학 및 생리학 분야에서 널리 사용되는 공식으로, 용액의 pH를 산의 산 해리 상수(pKa)와 산 및 짝염기의 농도 비율과 연관시킨다. 로렌스 조셉 헨더슨과 카를 알베르트 하셀발흐가 개발했으며, 헨더슨은 탄산 수소염 완충 용액의 수소 이온 농도를 계산하는 방정식을 유도했고, 하셀발흐는 이를 로그 대수식으로 재표현하여 방정식을 완성했다. 이 방정식은 완충 용액의 pH 계산, 생물학적 시스템의 pH 조절, 해양 산성화 연구 등 다양한 분야에 적용된다.

더 읽어볼만한 페이지

평형화학 - 헤모글로빈
헤모글로빈은 척추동물 혈액에서 산소를 운반하는 주요 단백질로, 헴과 글로빈이 결합된 4개의 소단위체로 구성된 사량체 구조를 가지며, 헴의 철 성분이 산소와 결합하여 폐에서 조직으로 산소를, 조직에서 이산화탄소와 양성자를 운반하고, 산소 결합은 여러 요인에 의해 영향을 받으며, 유전자 돌연변이는 헤모글로빈병증을 유발하고, 농도와 기능은 질병 진단에 활용되며, 다양한 생물종에서 발견된다.
평형화학 - 해리 (화학)
해리는 분자, 복합체, 또는 이온이 더 작은 구성 요소로 분리되는 과정을 의미하며, 해리 상수는 화학 평형 상태에서 반응의 정도를 측정하는 데 사용된다.
방정식 - 피타고라스 정리
피타고라스 정리는 직각삼각형에서 직각변의 제곱의 합이 빗변의 제곱과 같다는 정리로, a² + b² = c²으로 표현되며, 한 변의 길이를 계산하는 데 사용되고, 여러 지역에서 알려졌으나 피타고라스 학파에 의해 체계화되었다고 전해진다.
방정식 - 케플러 방정식
케플러 방정식은 천체의 궤도를 기술하는 초월 방정식으로, 행성의 위치를 결정하는 데 사용되며 평균 이상, 편심 이상, 이심률 간의 관계를 나타낸다.
분석화학 - 도가니
도가니는 금속이나 기타 물질을 고온에서 가열, 용융, 정련하는 데 사용되는 용기로, 기원전 6~5천년경에 등장하여 구리 제련에 사용되었으며, 현대에는 다양한 재료와 형태로 제작되어 화학 분석, 금속 제련 등 다양한 분야에서 활용된다.
분석화학 - 미량 원소
미량 원소는 지구과학에서 지각 내 극미량 원소를, 생물학에서 생명 활동에 필수적이나 함량이 적은 원소를 뜻하며, 두 분야의 정의는 다르나 극소량으로 존재하며 중요한 역할을 한다는 공통점이 있고, 생물학적으로는 철보다 함량이 적은 원소를 지칭하며, 인체 필수 미량 원소 결핍 및 과다 섭취는 건강 문제를 야기하므로 적정량 섭취가 중요하다.

헨더슨-하셀바흐 방정식
일반 정보
이름	헨더슨-하셀바흐 방정식
분야	생화학
용도	완충 용액의 pH 추정
관련 항목	산해리 상수 (pKₐ)

2. 역사

헨더슨-하셀바흐 방정식은 로렌스 조셉 헨더슨과 카를 알베르트 하셀발흐 두 과학자에 의해 개발되었다.^[2]

2. 1. 헨더슨과 하셀발흐의 방정식 개발

로렌스 조셉 헨더슨은 생화학자였고, 카를 알베르트 하셀발흐는 pH를 연구한 생리학자였다.^[2]^[3]

1908년, 로렌스 조셉 헨더슨^[4]은 탄산 수소염 완충 용액의 수소 이온 농도를 계산하는 방정식을 유도했는데, 이를 재정리하면 다음과 같다.

[H⁺] [HCO₃^–] = K [CO₂] [H₂O]

1909년 쇠렌 페테르 로리츠 쇠렌센이 pH 용어를 도입했고, 이를 통해 카를 알베르트 하셀발흐는 헨더슨의 방정식을 로그 대수식으로 재표현할 수 있었으며,^[5] 이로 인해 헨더슨-하셀발흐 방정식이 탄생했다.

3. 정의 및 유도

산(HA)의 해리 반응식 HA → H⁺ + A^- 에서 평형상수(K_a)는 다음과 같이 표현된다.^[8]

:K_a = [A^-][H⁺]/[HA]

이를 [H⁺]에 대해 정리하면 다음과 같다.

:[H⁺] = K_a × ([HA]/[A^-])

양변에 -log를 취하면 다음과 같다.

:-log[H⁺] = -log K_a - log([HA]/[A^-])

pH = -log[H⁺], pK_a = -log K_a 이므로, 위 식은 다음과 같이 변환된다.

:pH = pK_a + log([A^-]/[HA])

이는 또한 다음과 같이 표현할 수 있다.

:pH = pK_a + log([염기성형]/[산성형])

3. 1. 정의

완충 용액은 산과 그 산의 짝염기 염 용액으로 구성된다. 예를 들어, 아세트산과 아세트산 나트륨을 혼합한 용액이 이에 해당한다. 헨더슨-하셀바흐 방정식은 이러한 혼합 용액의 pH를 산의 산 해리 상수(''K''_a) 및 용액 내 각 성분의 농도와 연관시킨다.

이 방정식을 유도하기 위해 다음과 같은 몇 가지 가정을 단순화한다.

'''가정 1''': 산 HA는 일양성자산이며, 다음 반응식에 따라 해리된다.

:

\ce{HA <=> H^+ + A^-}

:

\mathrm{C_A = [A^-] + [H^+][A^-]/K_a}

:

\mathrm{C_H = [H^+] + [H^+][A^-]/K_a}

여기서 C_A는 산의 분석 농도, C_H는 용액에 첨가된 수소 이온의 농도, [X]는 화학종 X의 농도를 나타낸다. H⁺는 수화된 히드로늄 이온을, K_a는 산 해리 상수를 의미한다. 헨더슨-하셀바흐 방정식은 연속적인 p''K'' 값의 차이가 최소 3 이상인 다염기성 산에만 적용 가능한데, 인산이 그 예이다.

'''가정 2''': 물의 자동 이온화는 무시할 수 있다. 이는 pH가 7에 가까울 때는 엄밀히 유효하지 않지만, 물의 자동 이온화 상수(K_w)를 고려하여 수소에 대한 질량 균형 방정식을 확장하면,

\mathrm{K_w/[H^+]}

항은 근사적으로 생략할 수 있다.

'''가정 3''': 염 MA는 용액에서 완전히 해리된다. 예를 들어 아세트산 나트륨은 다음과 같이 해리된다.

:

\mathrm{Na(CH_3CO_2) \rightarrow Na^ + + CH_3CO_2^-}

이때 나트륨 이온 농도([Na⁺])는 무시할 수 있다. 이는 1:1 전해질에서는 타당하지만, 황산 마그네슘(MgSO₄)처럼 이온쌍을 형성하는 고전하 이온의 염에는 적용되지 않는다.

'''가정 4''': 활동도 계수의 몫(

\Gamma

)은 계산에 포함된 실험 조건에서 상수이다.

열역학적 평형 상수(

K^*

)는 다음과 같이 농도의 몫과 활동도 계수의 몫(

\Gamma

)의 곱으로 표현된다.

:

K^* = \frac{ [\ce{H+}][\ce{A^-}]} { [\ce{HA}] } \times \frac{ \gamma_{\ce{H+}} \gamma _{\ce{A^-}}} {\gamma _{HA} }

여기서 대괄호 안의 수량은 비해리된 산(HA), 수소 이온(H⁺), 음이온(A⁻)의 농도를,

\gamma

는 각 화학종의 활동도 계수를 나타낸다. 활동도 계수의 몫이 농도 및 pH와 무관한 상수라고 가정하면, 해리 상수(''K''_a)는 농도의 몫으로 표현할 수 있다.

:

K_a = \frac{K^*}{\Gamma} = \frac{[\ce{H+}][\ce{A^-}]}{[\ce{HA}]}

위 식을 정리하면 헨더슨-하셀바흐 방정식은 다음과 같다.

:

\textrm{pH} = \textrm{p}K_{\mathrm{a}}+ \log \frac{[\textrm{A}^-]}{[\textrm{HA}]}

여기서,

\textrm{p}K_\mathrm{a}

는

-\log K_\mathrm{a}

이고,

K_\mathrm{a}

는 산 해리 상수이다. 일반적인 브뢴스테드-로우리 산-염기 반응에서,

:

\mbox{HA} + \mbox{H}_{2}\mbox{O} \rightleftharpoons \mbox{H}_{3}\mbox{O}^+ + \mbox{A}^-

:

\mathrm{p}K_{\mathrm{a}} = - \log K_\mathrm{a} = - \log \frac{[\mathrm{H_3O}^{+}][\mathrm{A^{-}}]}{[\mathrm{HA}] ~ \mathrm{mol~L^{-1}}}

\mbox{A}^-

는 산 HA의 짝염기를 나타내며, [염기]나 [산]과 같이 괄호가 붙은 양은 몰 농도를 나타낸다.

위의 등식과 유사하게, 다음 등식들도 성립한다.

:

\textrm{pOH} = \textrm{p}K_{\mathrm{b}}+ \log \frac{[\textrm{BH}^+]}{[\textrm{B}]}

:

\textrm{pH} = \textrm{p}K_{\mathrm{a}}+ \log \frac{[\textrm{B}]}{[\textrm{BH}^+]}

위의 식에서,

\textrm{p}K_\mathrm{b}

는

-\log K_\mathrm{b}

이며,

K_\mathrm{b}

는 염기 해리 상수이다. 또한, BH⁺는 염기 B의 짝산이다.

3. 2. 유도

산(HA)의 해리 반응식 HA → H⁺ + A^- 에서 평형상수(K_a)는 다음과 같이 표현된다.^[8]

:K_a = [A^-][H⁺]/[HA]

이를 [H⁺]에 대해 정리하면 다음과 같다.

:[H⁺] = K_a × ([HA]/[A^-])

양변에 -log를 취하면 다음과 같다.

:-log[H⁺] = -log K_a - log([HA]/[A^-])

pH = -log[H⁺], pK_a = -log K_a 이므로, 위 식은 다음과 같이 변환된다.

:pH = pK_a + log([A^-]/[HA])

이는 또한 다음과 같이 표현할 수 있다.

:pH = pK_a + log([염기성형]/[산성형])

헨더슨-하셀바흐 방정식은 산 해리 상수 식으로부터 유도되며, 이 과정에서 몇 가지 가정이 사용된다.^[8]
가정:1. 산 HA는 일염기성이며 다음과 같이 해리된다.

:

\ce{HA <=> H^+ + A^-}

:

\mathrm{C_A = [A^-] + [H^+][A^-]/K_a}

:

\mathrm{C_H = [H^+] + [H^+][A^-]/K_a}

(C_A: 산의 분석 농도, C_H: 용액에 첨가된 수소 이온 농도, [X]: 화학 물질 X의 농도, H⁺: 수화된 히드로늄 이온, K_a: 산 해리 상수)

2. 물의 자동 이온화는 무시한다.

3. 염 MA는 용액에서 완전히 해리된다. (예: 아세트산 나트륨의 경우

\mathrm{Na(CH_3CO_2) \rightarrow Na^ + + CH_3CO_2^-}

)

4. 활동도 계수의 몫(

\Gamma

)은 계산에 포함된 실험 조건에서 상수이다.

열역학적 평형 상수(

K^*

)는 다음과 같다.

:

K^* = \frac{ [\ce{H+}][\ce{A^-}]} { [\ce{HA}] } \times \frac{ \gamma_{\ce{H+}} \gamma _{\ce{A^-}}} {\gamma _{HA} }

(대괄호 안: 비해리된 산 HA, 수소 이온 H⁺, 음이온 A^-의 농도,

\gamma

: 해당 활동도 계수). 활동도 계수의 몫이 상수라고 가정하면, 해리 상수 ''K''_a는 다음과 같이 농도의 몫으로 표현할 수 있다.^[8]

:

K_a = \frac{K^*}{\Gamma} = \frac{[\ce{H+}][\ce{A^-}]}{[\ce{HA}]}

위 식의 양변에 로그를 취하고 정리하면 헨더슨-하셀바흐 방정식을 얻을 수 있다.

:

\begin{align}K_\mathrm{a} &= \frac{a_{\mathrm{H}^{+}}a_{\mathrm{A}^{-}}}{a_{\mathrm{HA}}} \\\log K_\mathrm{a} &= \log a_{\textrm{H}^{+}} + \log \frac{a_{\mathrm{A}^{-}}}{a_{\mathrm{HA}}} \\

\mathrm{p}K_\mathrm{a} &= -\mathrm{pH} + \log \frac{a_{\mathrm{A}^{-}}}{a_{\mathrm{HA}}} \\

\mathrm{pH} &= \mathrm{p}K_\mathrm{a} + \log \frac{[\mathrm{A}^-]}{[\mathrm{HA}]}\end{align}

4. 가정, 한계 및 응용

완충 용액은 산과 그 산의 짝염기 염 용액으로 구성된다. 예를 들어, 산은 아세트산일 수 있고, 염은 아세트산 나트륨일 수 있다. 헨더슨-하셀바흐 방정식은 두 성분의 혼합물을 포함하는 용액의 pH를 산의 산 해리 상수(''K''_a) 및 용액 내 종의 농도와 관련시킨다.

이 방정식을 유도하기 위해 몇 가지 단순화 가정을 해야 한다.

'''가정 1''': 산 HA는 일염기성이며 다음과 같은 방정식에 따라 해리된다.

: $\ce{HA <=> H^+ + A^-}$

: $\mathrm{C_A = [A^-] + [H^+][A^-]/K_a}$

: $\mathrm{C_H = [H^+] + [H^+][A^-]/K_a}$

C_A는 산의 분석 농도이고, C_H는 용액에 첨가된 수소 이온의 농도이다. 물의 자체 해리는 무시된다. 대괄호 안의 수량 [X]는 화학 물질 X의 농도를 나타낸다. H⁺ 기호는 수화된 히드로늄 이온을 나타낸다. ''K''_a는 산 해리 상수이다. 헨더슨-하셀바흐 방정식은 연속적인 p''K'' 값의 차이가 최소 3인 다염기성 산에만 적용할 수 있다. 인산이 그러한 산이다.

'''가정 2''': 물의 자동 이온화는 무시할 수 있다. 이 가정은 엄밀히 말해 pK_w(물의 자동 이온화 상수) 값의 절반인 pH 7에 가까운 값에서는 유효하지 않다. 이 경우, 수소에 대한 질량 균형 방정식은 물의 자체 이온화를 고려하여 확장해야 한다.

: $\mathrm{C_H = [H^+] + [H^+][A^-]/K_a + K_w/[H^+]}$

그러나 $\mathrm{K_w/[H^+]}$ 항은 근사적으로 생략할 수 있다.

'''가정 3''': 염 MA는 용액에서 완전히 해리된다. 예를 들어, 아세트산 나트륨의 경우 다음과 같다.

: $\mathrm{Na(CH_3CO_2) \rightarrow Na^ + + CH_3CO_2^-}$

나트륨 이온 농도 [Na⁺]는 무시할 수 있다. 이는 1:1 전해질에는 적용되지만, 황산 마그네슘(MgSO₄)과 같이 이온쌍을 형성하는 더 높은 전하를 가진 이온의 염에는 해당하지 않는다.

'''가정 4''': 활동도 계수의 몫( $\Gamma$ )은 계산에 포함된 실험 조건에서 상수이다.

열역학적 평형 상수( $K^*$ )는 다음과 같다.

: $K^* = \frac{ [\ce{H+}][\ce{A^-}]} { [\ce{HA}] } \times \frac{ \gamma_{\ce{H+}} \gamma _{\ce{A^-}}} {\gamma _{HA} }$

이는 농도의 몫 $\frac{ [\ce{H+}][\ce{A^-}]} { [\ce{HA}] }$ 과 활동도 계수의 몫( $\Gamma$ = $\frac{ \gamma_{\ce{H+}} \gamma _{\ce{A^-}}} {\gamma _{HA} }$ )의 곱이다. 이 식에서 대괄호 안의 양은 비해리된 산(HA), 수소 이온(H⁺), 음이온(A⁻)의 농도를 나타내며, $\gamma$ 는 해당 활동도 계수이다. 활동도 계수의 몫이 농도 및 pH와 무관한 상수라고 가정하면, 해리 상수(''K''_a)는 농도의 몫으로 표현할 수 있다.

: $K_a = \frac{K^*}{\Gamma} = \frac{[\ce{H+}][\ce{A^-}]}{[\ce{HA}]}$

4. 1. 염기에 대한 적용

염기 B의 양성자화에 대한 평형 상수^[1]는 다음과 같다.

:

이때 회합 상수 ''K''_b는 짝산 BH⁺의 해리 상수와 관련되어 있다.

:

\mathrm{pK_a = \mathrm{pK_w} - \mathrm{pK_b}}

\mathrm{pK_w}

값은 약 25 °C에서 14이다. 이 근사는 정확한 값을 모를 때 사용할 수 있다. 따라서, 헨더슨-하셀바흐 방정식은 수정 없이 염기에 사용할 수 있다.^[1]
수정사항:

화학식 표현을 `` 템플릿을 사용하여 가독성을 높였습니다.
`` 템플릿을 제거하고, 일반 텍스트로 변경했습니다.
들여쓰기 문법(`:`)을 제거하고, 일반적인 문단 형태로 변경했습니다. (위키백과에서는 들여쓰기가 토론 등에서 사용되며, 일반적인 문서 본문에는 사용하지 않습니다.)
문맥에 맞게 윗첨자, 아랫첨자 문법을 수정했습니다.
기타 오탈자를 수정했습니다.

4. 2. 생물학적 응용

생물학에서 헨더슨-하셀바흐 방정식은 생체 내 pH 조절 기작을 설명하는 데 중요하게 사용된다. 특히, 혈액의 pH는 항상성을 통해 일정하게 유지되며, 이는 탄산수소 이온(

\mathrm{HCO_3^-}

)과 탄산(

\mathrm{H_2CO_3}

) 사이의 평형 반응을 통해 조절된다. 이 과정에서 탄산수소 시스템이 중요한 역할을 한다.

또한, 헨더슨-하셀바흐 방정식은 해양 산성화와 같이 지구 환경 변화를 이해하는 데에도 응용될 수 있다.

4. 2. 1. 항상성과 혈액 완충 시스템

항상성을 통해 생물학적 용액의 pH는 평형의 위치를 조절하여 일정하게 유지된다.^[9]

:

\ce{HCO3-} + \mathrm{H^+} \rightleftharpoons \ce{H2CO3} \rightleftharpoons \ce{CO2} + \ce{H2O}

여기서 HCO}}는 탄산수소 이온이고, H}}는 탄산이다. 탄산은 이산화 탄소와 물로부터 가역적으로 형성된다. 그러나 물에 대한 탄산의 용해도를 초과할 수 있다. 이런 경우 이산화 탄소 기체가 방출되므로 대신 다음 방정식을 사용할 수 있다.

:

\mathrm{[H^+] [HCO_3^-]} = \mathrm{K^m [CO_2(g)]}

CO는 기체로 방출되는 이산화 탄소를 나타낸다. 생화학에서 널리 사용되는 이 방정식에서 K은 화학 및 용해도 평형 모두와 관련된 혼합 평형 상수이다. 다음과 같이 나타낼 수 있다.

:

\mathrm{pH} = 6.1 + \log_{10}  \left ( \frac{[\mathrm{HCO}_3^-]}{0.0307 \times P_{\mathrm{CO}_2}} \right )

여기서 HCO}}는 혈장 내 탄산수소의 몰 농도이고 P^영어는 상등액 기체 내 이산화 탄소의 분압이다. H}}의 농도는 CO에 의존하며, 이는 다시 P^영어에 의존한다.^[9]

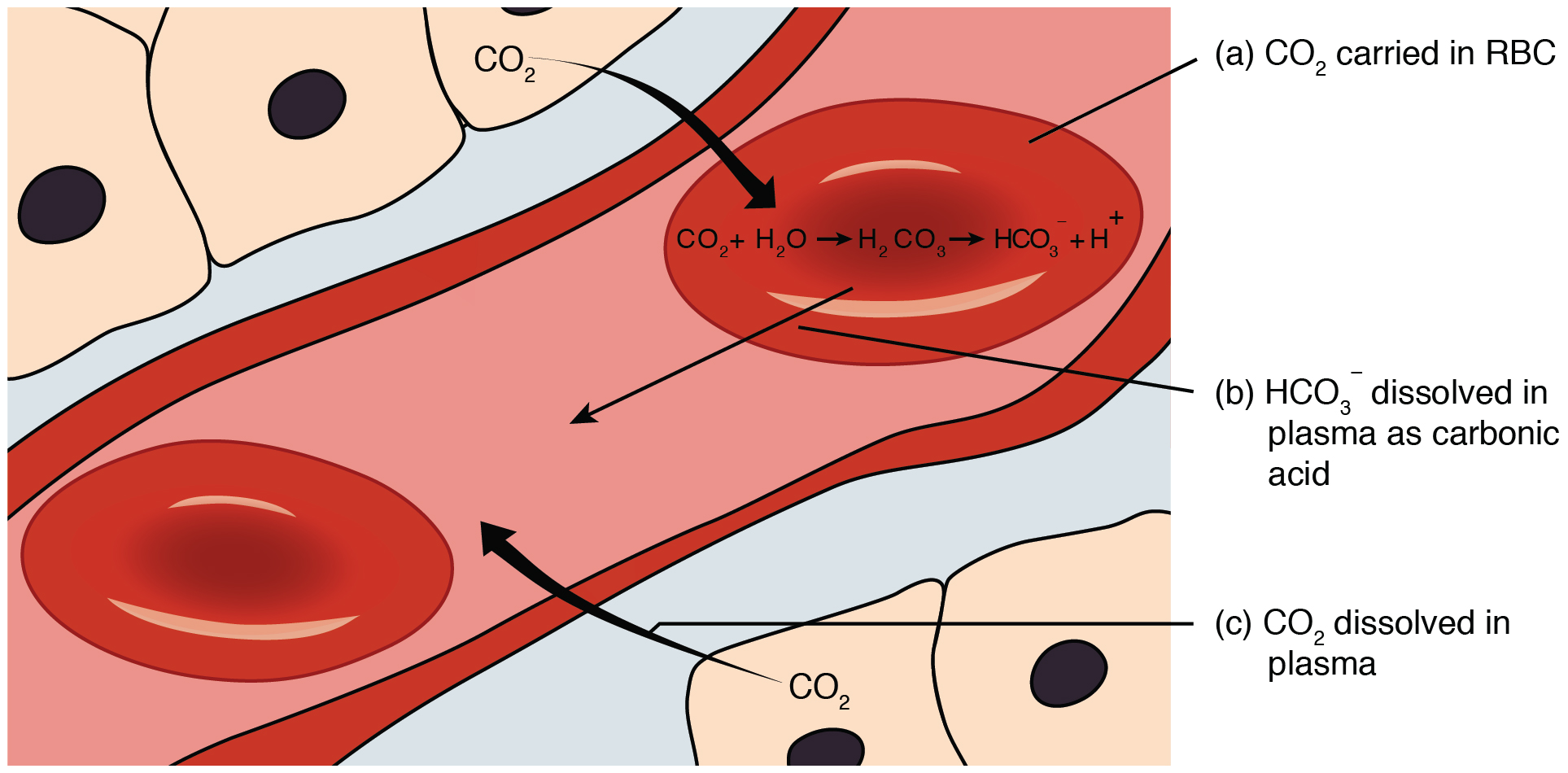
이산화 탄소는 세포 호흡의 부산물로서 혈액에 용해된다. 혈액에서 적혈구에 흡수되어 탄산염 완충 시스템에 의해 탄산으로 전환된다. 대부분의 탄산은 탄산수소와 수소 이온으로 해리된다.

신체에 존재하는 완충 시스템 중 하나는 혈장 완충 시스템이다. 이것은 H}}인 탄산과 HCO}}인 탄산수소가 함께 작용하여 탄산수소 시스템을 형성한다.^[10] 이것은 카르복실산이 폐에서 CO와 평형을 이루기 때문에 생리학적 pH인 7.4 근처에서 효과적이다.^[9] 혈액이 신체를 통과하면서 젖산 발효와 단백질 이화 작용으로부터의 NH3 양성자화 등과 같은 다양한 과정에서 H+를 얻고 잃는다.^[9] 이 때문에 H}}가 조직을 통과하면서 혈액 내에서 변한다. 이것은 폐에서 CO의 분압 변화와 관련이 있으며, 더 많은 또는 더 적은 CO가 필요하다면 호흡 속도의 변화를 유발한다.^[9] 예를 들어, 혈액 pH가 감소하면 뇌간이 더 빈번한 호흡을 수행하도록 유발한다. 헨더슨-하셀바흐 방정식은 이러한 평형을 모델링하는 데 사용될 수 있다. 효소가 최적으로 작동하도록 하기 위해 이 pH 7.4를 유지하는 것이 중요하다.^[10]

생명을 위협하는 산증 (낮은 pH로 인해 메스꺼움, 두통, 심지어 혼수 상태, 경련이 발생하는 낮은 혈액 pH)은 낮은 pH에서 효소의 기능 부족으로 인해 발생한다.^[10] 헨더슨-하셀바흐 방정식으로 모델링된 바와 같이, 심각한 경우에는 정맥 내 탄산수소 용액을 투여하여 이를 되돌릴 수 있다. CO의 분압이 변하지 않으면, 이 탄산수소 용액의 첨가는 혈액 pH를 높일 것이다.

4. 2. 2. 해양 산성화

바다는 pH를 8.1에서 8.3 사이로 유지하기 위한 자연 완충 시스템을 포함하고 있다.^[11] 바다의 완충 시스템은 탄산염 완충 시스템으로 알려져 있다.^[12] 탄산염 완충 시스템은 탄산염을 완충제로 사용하여 이산화탄소(

\mathrm{CO_2}

)를 중탄산염으로 변환하는 일련의 반응이다.^[12] 탄산염 완충 반응은 수소 이온을 소모하여^[13] 일정한 H+ 농도를 유지하도록 도와주며, 그로 인해 일정한 pH를 유지한다.^[12]

바다는 인간이 대기 중의 이산화탄소(

\mathrm{CO_2}

)를 증가시킴으로써 해양 산성화를 겪고 있다.^[14] 대기 중으로 방출되는 이산화탄소(

\mathrm{CO_2}

)의 약 30%가 바다에 흡수되고,^[14] 이산화탄소(

\mathrm{CO_2}

) 흡수의 증가는 H+ 이온 생성의 증가로 이어진다.^[15] 대기 중 이산화탄소(

\mathrm{CO_2}

)의 증가는 바다에서 이산화탄소(

\mathrm{CO_2}

)가 물과 반응하여 탄산을 생성하고, 탄산이 H+ 이온과 중탄산염 이온을 방출하기 때문에 H+ 이온 생성을 증가시킨다.^[15] 전반적으로, 산업 혁명 이후 바다는 '''이산화탄소(

\mathrm{CO_2}

)''' 생산 증가로 인해 pH가 약 0.1 pH 단위 감소했다.^[12]

해양 산성화는 탄산염으로 만들어진 껍질을 가진 해양 생물에 영향을 미친다. 더 산성인 환경에서는 유기체가 탄산염 껍질을 성장시키고 유지하기가 더 어렵다.^[12] 해양 산성화의 증가는 탄산염 껍질을 가진 유기체의 성장과 번식을 감소시킬 수 있다.^[12]

참조

_[1] 서적 General Chemistry Prentice Hall 2002
_[2] 웹사이트 Henderson-Hasselbalch Equation - an overview {{!}} ScienceDirect Topics https://www.scienced[...] 2024-11-02
_[3] 웹사이트 Henderson-Hasselbalch Approximation https://chem.librete[...] 2024-11-02
_[4] 논문 Concerning the relationship between the strength of acids and their capacity to preserve neutrality
_[5] 웹사이트 Biochemistry {{!}} Definition, History, Examples, Importance, & Facts {{!}} Britannica https://www.britanni[...] 2024-11-02
_[6] 서적 Fundamentals of Analytical Chemistry Brooks/Cole 2004
_[7] 논문 Henderson–Hasselbalch Equation: Its History and Limitations
_[8] 서적 Lehninger principles of biochemistry Macmillan Learning 2021
_[9] 서적 Lehninger principles of biochemistry Macmillan Learning 2021
_[10] 논문 Bench-to-bedside review: A brief history of clinical acid–base 2004-04-30
_[11] 웹사이트 Researching ocean buffering fact sheet https://www.uwa.edu.[...] 2024-11-03
_[12] 웹사이트 What is ocean acidification? {{!}} NIWA https://niwa.co.nz/o[...] 2024-11-04
_[13] 웹사이트 How does seawater buffer or neutralize acids created by scrubbing? – EGCSA.com https://www.egcsa.co[...] 2024-11-04
_[14] 웹사이트 Ocean acidification {{!}} National Oceanic and Atmospheric Administration https://www.noaa.gov[...] 2024-11-04
_[15] 웹사이트 Ocean Acidification {{!}} NRDC https://www.nrdc.org[...] 2024-11-04
_[16] 뉴스 Henderson-Hasselbach equation {{!}} biochemistry https://www.britanni[...] 2017-11-12
_[17] 웹인용 Henderson-Hasselbach Equation https://www.merckman[...] 2017-11-12

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com