마르코프 수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 마르코프 나무
- 2.1. 마르코프 삼중항 생성
- 2.2. 피보나치 수 및 펠 수와의 관계
3. 마르코프 수의 성질
4. 마르코프 정리
5. 행렬 표현
참조

1. 개요

마르코프 수는 디오판토스 방정식 x² + y² + z² = 3xyz의 정수 해로, 마르코프 나무를 통해 생성된다. 이 수는 피보나치 수, 펠 수와 관련이 있으며, 특정 성질을 가진다. 예를 들어, 마르코프 수의 소수 약수는 4를 법으로 할 때 3과 합동이 아니며, 짝수 마르코프 수는 32의 배수보다 2 더 크다. 단일성 추측, 점근적 근사, 라그랑주 수와의 관계 등 다양한 수학적 개념과 연결되어 연구된다.

더 읽어볼만한 페이지

디오판토스 근사 - 리우빌 수
리우빌 수는 유리수로 특별히 잘 근사될 수 있는 무리수이며, 초월수임을 증명하는 데 사용될 수 있고, 리우빌 상수는 리우빌 수의 예시이다.
디오판토스 근사 - 균등분포 정리
균등분포 정리는 수론과 역학계에서 수열의 균등 분포를 다루는 중요한 개념으로, 헤르만 바일 등에 의해 처음 증명되었고, 제곱수 수열 및 소수 수열의 균등 분포 증명, 일반화된 등분포 정리로 발전했으며, 현대에도 연구가 진행되고 있다.
피보나치 수 - 레오나르도 피보나치
레오나르도 피보나치는 힌두-아라비아 숫자 체계를 유럽에 소개하고 피보나치 수열을 제시하여 중세 수학 발전에 기여했으며, 상업 발달을 돕는 《산반서》를 저술하고 황금비와 관련된 피보나치 수열이 다양한 분야에서 활용되도록 했다.
피보나치 수 - 피보나치 힙
피보나치 힙은 최소 힙 속성을 가진 트리들의 집합으로, 각 노드의 차수를 특정 로그 값 이하로 유지하여 효율적인 삽입, 병합, 최소값 검색 연산을 지원하며, 다익스트라 알고리즘과 같은 그래프 알고리즘의 성능 향상에 활용된다.
디오판토스 방정식 - 펠 방정식
펠 방정식은 제곱수가 아닌 양의 정수 n에 대해 $x^2-ny^2=1$ 꼴로 표현되는 디오판토스 방정식이며, 이차 수체에서 노름이 1인 원소를 찾는 문제로 해석되고, 자명한 해 외에 항상 정수해를 가지며, 해는 연분수 전개를 통해 구할 수 있고, 무리 제곱근의 유리 근삿값과 관련되어 고대부터 연구되었다.
디오판토스 방정식 - 베주 항등식
베주 항등식은 주 아이디얼 정역에서 두 원소의 최대공약수를 그 두 원소의 정수 배의 합으로 나타낼 수 있다는 정리이며, 확장 유클리드 알고리즘을 통해 베주 계수를 구할 수 있고, 정수, 다항식 등 다양한 대수적 구조로 확장 가능하다.

2. 마르코프 나무

마르코프 삼중항은 (1, 1, 1)에서 시작하는 이진 트리 구조를 형성하며, 이 구조를 마르코프 나무라고 부른다.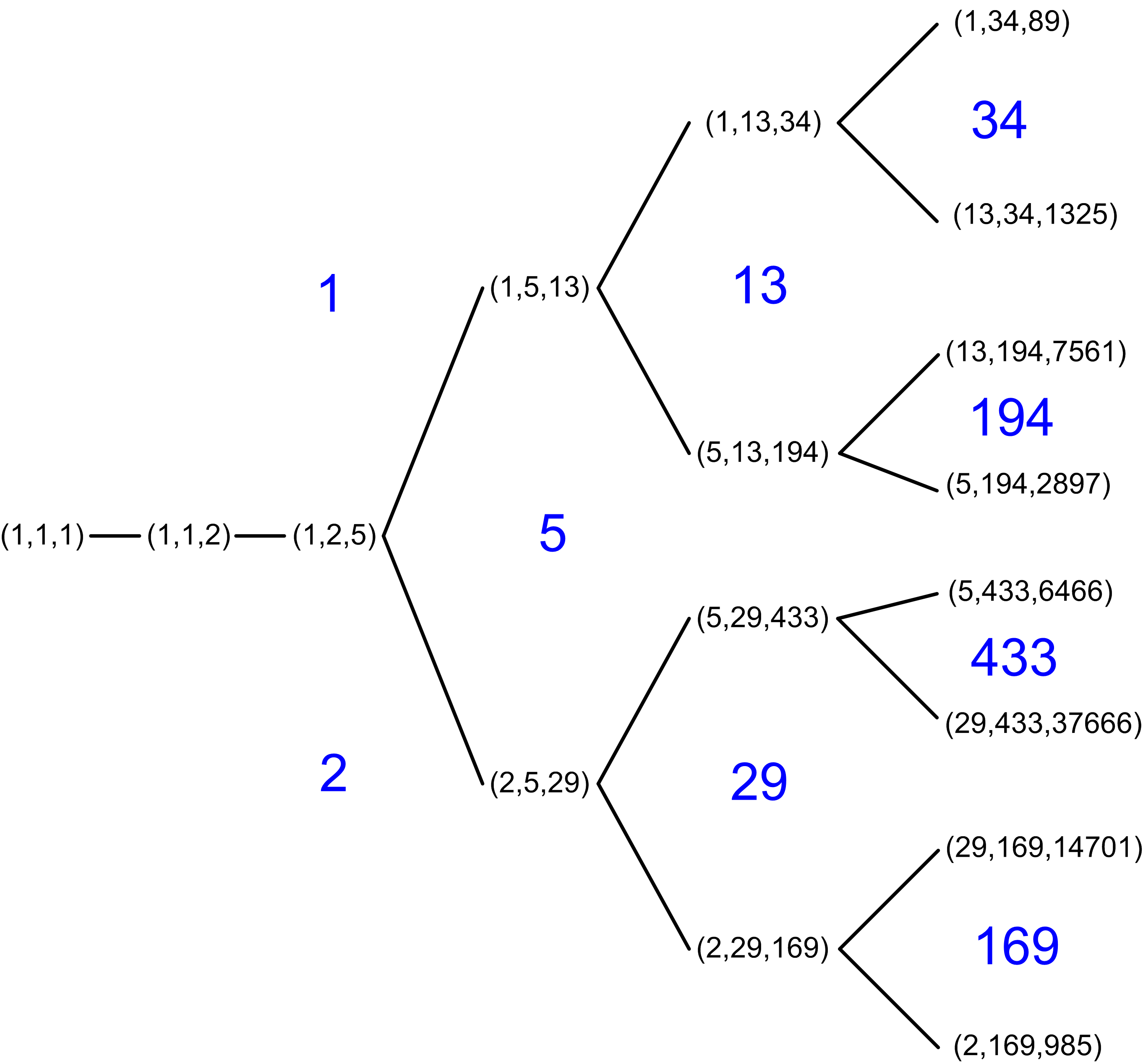

2. 1. 마르코프 삼중항 생성

새로운 마르코프 삼중항(''x'', ''y'', ''z'')은 기존 삼중항으로부터 두 가지 방법으로 얻을 수 있다. 첫째, ''x'', ''y'', ''z''를 순열하여 삼중항을 ''x'' ≤ ''y'' ≤ ''z''가 되도록 정규화할 수 있다. 둘째, (''x'', ''y'', ''z'')가 마르코프 삼중항이면 (''x'', ''y'', 3''xy'' − ''z'')도 마르코프 삼중항이다. 이 연산을 두 번 적용하면 원래 삼중항으로 돌아간다.^[1]

각 정규화된 마르코프 삼중항을 이로부터 얻을 수 있는 1, 2 또는 3개의 정규화된 삼중항에 연결하면, 처럼 (1,1,1)에서 시작하는 그래프가 만들어진다. 이 그래프는 연결성 (그래프 이론)을 가지며, 모든 마르코프 삼중항은 이러한 연산을 통해 (1,1,1)에 연결될 수 있다.^[1] 예를 들어 (1, 5, 13)에서 시작하면, ''z''를 1, 5, 13으로 설정했을 때 마르코프 나무에서 세 이웃 (5, 13, 194), (1, 13, 34), (1, 2, 5)를 얻는다.

(1, 1, 2)에서 시작하여 변환의 각 반복 전에 ''y''와 ''z''를 교환하면 피보나치 수가 포함된 마르코프 삼중항이 나열된다. 같은 삼중항에서 각 반복 전에 ''x''와 ''z''를 교환하면 펠 수가 포함된 삼중항이 나온다.

2의 영역에 인접한 모든 마르코프 수는 홀수 인덱스 펠 수(또는 2''n''² − 1이 제곱수인 수)이며, 1의 영역에 인접한 모든 마르코프 수는 홀수 인덱스 피보나치 수이다.^[2] 따라서 다음과 같은 형태의 무한히 많은 마르코프 삼중항이 존재한다.

:

(1, F_{2n-1}, F_{2n+1}),\,

여기서 ''F''_''k''는 ''k''번째 피보나치 수이다. 마찬가지로 다음과 같은 형태의 무한히 많은 마르코프 삼중항이 존재한다.^[2]

:

(2, P_{2n-1}, P_{2n+1}),\,

여기서 ''P''_''k''는 ''k''번째 펠 수이다.

2. 2. 피보나치 수 및 펠 수와의 관계

마르코프 나무에서 2의 영역에 인접한 마르코프 수는 홀수 인덱스 펠 수(2''n''² - 1이 제곱수인 수^[2])이며, 1의 영역에 인접한 마르코프 수는 홀수 인덱스 피보나치 수이다.^[2] 따라서 다음과 같은 형태의 무한히 많은 마르코프 삼중항이 존재한다.^[2]

(1, ''F''_2''n''-1, ''F''_2''n''+1)

여기서 ''F''_''k''는 ''k''번째 피보나치 수이다. 마찬가지로 다음과 같은 형태의 무한히 많은 마르코프 삼중항이 존재한다.^[2]

(2, ''P''_2''n''-1, ''P''_2''n''+1)

여기서 ''P''_''k''는 ''k''번째 펠 수이다.

3. 마르코프 수의 성질

두 개의 가장 작은 특이 삼중항 (1, 1, 1)과 (1, 1, 2)를 제외하면, 모든 마르코프 삼중항은 서로 다른 세 정수로 구성된다.^[3]

3. 1. 단일성 추측 (Unicity Conjecture)

프로베니우스가 1913년에 언급했듯이^[4], 단일성 추측은 주어진 마르코프 수 ''c''에 대해 ''c''를 가장 큰 요소로 갖는 정규화된 해가 정확히 하나 존재한다는 것이다.^[3] 이 추측에 대한 수학적 증명이 주장되었지만, 정확한 증명은 없는 것으로 보인다.^[5] 마틴 아이그너^[6]는 단일성 추측의 여러 약한 변형을 연구했다. 그의 고정 분자 추측은 2020년에 Rabideau와 Schiffler에 의해 증명되었고,^[7] 고정 분모 추측과 고정 합 추측은 2023년에 Lee, Li, Rabideau 및 Schiffler에 의해 증명되었다.^[8]

3. 2. 모듈러 합동 관계

마르코프 수의 소수 약수는 4를 법으로 할 때 3과 합동이 아니며, 이는 홀수인 마르코프 수가 4의 배수보다 1 더 크다는 것을 의미한다.^[9] 또한

m

이 마르코프 수이면

9m^2-4

의 소수 약수 중 4를 법으로 할 때 3과 합동인 것은 없다. 짝수 마르코프 수는 32의 배수보다 2 더 크다.^[10]

3. 3. 점근적 근사

돈 자기에는 1982년 논문에서 ''n''번째 마르코프 수(m_n)가 점근적으로 다음과 같이 주어진다고 추측했다.^[11]

:m_n = ⅓ e^C√n+o(1)^영어 (C = 2.3523414972...)

더욱이 그는 원래의 디오판토스 방정식의 근사인 x² + y² + z² = 3xyz + 4/9^영어가 f(t)^영어 = 아크코사인 쌍곡선(3t^영어/2)로 표현될 때 f(x) + f(y) = f(z)^영어와 동등하다고 지적했다.^[11] 이 추측은 1995년 그레그 맥셰인과 이고르 리빈에 의해 쌍곡 기하학의 기술을 사용하여 증명되었다.^[12]

''n''번째 라그랑주 수는 다음 공식을 사용하여 ''n''번째 마르코프 수로부터 계산할 수 있다.

:L_n = √(9 - 4/m_n²)^영어

마르코프 수는 (고유하지 않은) 제곱 쌍의 합이다.

3. 4. 라그랑주 수와의 관계

''n''번째 라그랑주 수는 다음 공식을 사용하여 ''n''번째 마르코프 수로부터 계산할 수 있다.^[11]

:

L_n = \sqrt{9 - {4 \over {m_n}^2}}.\,

마르코프 수는 (고유하지 않은) 제곱 쌍의 합이다.^[11]

4. 마르코프 정리

마르코프는 다음 사실을 보였다.

: $f(x,y) = ax^2+bxy+cy^2$

부호가 정해지지 않은 이진 이차 형식이고, 실수 계수를 가지며, 판별식 $D = b^2-4ac$ 를 가질 때, 다음을 만족하는 정수 ''x'', ''y''가 존재하여 ''f''는 0이 아닌 값을 가지며, 그 절댓값은 최대

: $\frac{\sqrt D}{3}$

이다. 단, ''f''가 다음과 같은 형태의 ''마르코프 형식''일 경우에는 예외이다.^[13] 상수와 곱해진 형식

: $px^2+(3p-2a)xy+(b-3a)y^2$

이며, 다음을 만족한다.

: $\begin{cases} 0$

여기서 (''p'', ''q'', ''r'')은 마르코프 삼중항이다.

5. 행렬 표현

행렬에 대한 대각합 함수를 tr로 표기했을 때, ''X''와 ''Y''가 SL₂(''' $\mathbb{C}$ ''')에 속한다면 다음 식이 성립한다.^[14]

: $\operatorname{tr}(X) \operatorname{tr}(Y) \operatorname{tr}(XY) + \operatorname{tr}(XYX^{-1}Y^{-1}) + 2 = \operatorname{tr}(X)^2 + \operatorname{tr}(Y)^2 + \operatorname{tr}(XY)^2$

만약 $\operatorname{tr}(XYX^{-1}Y^{-1}) = -2$ 라면, 다음이 성립한다.^[14]

: $\operatorname{tr}(X) \operatorname{tr}(Y) \operatorname{tr}(XY) = \operatorname{tr}(X)^2 + \operatorname{tr}(Y)^2 + \operatorname{tr}(XY)^2$

특히, ''X''와 ''Y''가 정수 항목을 가진다면 tr(''X'')/3, tr(''Y'')/3, tr(''XY'')/3는 마르코프 삼중항이다. 만약 ''X''⋅''Y''⋅''Z'' = I이면 tr(''XtY'') = tr(''Z'')이다. 따라서 더 대칭적으로, 만약 ''X'', ''Y'', 그리고 ''Z''가 SL₂( $\mathbb{Z}$ )에 속하고 ''X''⋅''Y''⋅''Z'' = I이며 그들 중 둘의 교환자의 대각합이 −2이면, 그들의 대각합/3은 마르코프 삼중항이다.^[14]

참조

_[1] 서적 1957
_[2] OEIS
_[3] 서적 1957
_[4] 논문 Über die Markoffschen Zahlen 1913
_[5] 서적 2004
_[6] 서적 2013
_[7] 논문 Continued fractions and orderings on the Markov numbers 2020
_[8] 논문 On the ordering of the Markov numbers 2023
_[9] 서적 2013
_[10] 논문 Congruence and Uniqueness of Certain Markov Numbers http://journals.impa[...]
_[11] 논문 On the Number of Markoff Numbers Below a Given Bound
_[12] 논문 Simple curves on hyperbolic tori
_[13] 서적 1957
_[14] 서적 2013
_[15] 논문 First memory http://gdz.sub.uni-g[...]
_[16] 논문 Second memory http://gdz.sub.uni-g[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com

마르코프 수
마르코프 수
정의	방정식 x² + y² + z² = 3xyz의 양의 정수 해
다른 이름	마르코프 삼중항의 구성원
역사
창시자	Andrey Markoff
발표 연도	1879년
성질
발생 방식	마르코프 트리에서 발생
최소 마르코프 수	1
마르코프 수 중 소수	2, 5, 13, 29, 169, 433, 985, 5741, 6469, 7561, 14929, 21325, 140437, 237785, 419341, 543337, 3056065, 5142293, 6621809, 22107313, 23545001, 48647677, 67162781, 145224497, 417328633, 807546121, 1054406569
수열	1, 2, 5, 13, 29, 34, 89, 169, 194, 233, 433, 610, 985, 1325, 1597, 2897, 3682, 5741, 6466, 7561, 9077, 12701, 15125, 21325, 22649, 28657, 43261, 48382, 64661, 67657, 75025, 81009, 109441, 119305, 135137, 140437, 237785, 253970, 300169, 301037, 341561, 396401, 410405, 419341, 495205, 543337, 621337, 714281, 756098, 793129, 902377, 1090681, 1220021, 1307921, 1432049, 1540049, 1771193, 2048390, 22107313, 23545001, 3056065, 3290449, 3895009, 4036001, 4134037, 4181821, 4627393, 5142293, 5535881, 6468361, 6621809, 8164049, 8624665, 8626757, 10284581, 10923202, 11071681, 12936721, 13243601, 13930729, 14044321, 145224497, 158626577, 171305809, 242666201, 273240269, 323316601, 325687841, 352283437, 378355757, 382386866, 417328633, 470912737, 489002522, 546472849, 651377641, 698687329, 764773721, 807546121, 834653369, 903364441, 1054406569
OEIS	A002559
관련 항목
관련 개념	마르코프 상수
관련 정리	마르코프 정리
참고 문헌	Markoff, A. (1879). "First memory". Mathematische Annalen. 15 (3–4): 381–406. doi:10.1007/BF02086269. S2CID 179177894. Markoff, A. (1880). "Second memory". Mathematische Annalen. 17 (3): 379–399. doi:10.1007/BF01446234. S2CID 121616054.
같이 보기	라그랑주 수