뱀 완전열

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
- 2.1. 뱀 보조정리의 명제
- 2.2. 연결 사상의 구성
3. 성질
- 3.1. 자연성
- 3.2. 호몰로지 긴 완전열
4. 예
5. 뱀 보조정리의 증명
6. 역사
7. 그룹 범주에서의 뱀 보조정리
참조

1. 개요

뱀 완전열은 아벨 범주에서 핵과 여핵을 연결하는 완전열을 말하며, 연결 사상을 통해 구성된다. 이는 가환 다이어그램에서 뱀과 같은 모양을 가지며, 텐서곱의 불완전성을 설명하는 데 사용될 수 있다. 뱀 보조정리는 자연성을 가지며, 호몰로지 긴 완전열을 구성하는 데 활용된다. 마이어-피토리스 열과 복시테인 준동형은 뱀 완전열의 예시이며, 1955년 데이비드 앨빈 북스바움에 의해 처음 등장했다.

더 읽어볼만한 페이지

보조정리 - 베주 항등식
베주 항등식은 주 아이디얼 정역에서 두 원소의 최대공약수를 그 두 원소의 정수 배의 합으로 나타낼 수 있다는 정리이며, 확장 유클리드 알고리즘을 통해 베주 계수를 구할 수 있고, 정수, 다항식 등 다양한 대수적 구조로 확장 가능하다.
보조정리 - 모스 이론
모스 이론은 미분다양체 위의 함수의 임계점과 지표를 이용하여 다양체의 위상수학적 성질을 연구하는 이론으로, 함수값에 따른 부분공간 변화를 관찰하여 다양체의 호몰로지를 계산하고 위상수학적 성질을 밝히는 데 응용된다.
호몰로지 대수학 - 미분 등급 대수
미분 등급 대수는 체 위의 등급 대수와 미분의 순서쌍으로, 대수적 위상수학 및 호모토피 이론에서 활용되며, 등급 대수에 차수, 라이프니츠 규칙, 멱영성을 만족하는 미분을 추가하여 정의됩니다.
호몰로지 대수학 - 가환 그림
가환 그림은 대상, 사상, 경로 또는 합성으로 이루어진 구조로, 대수학에서 사상의 종류를 화살표 기호로 나타내고 점선 화살표로 사상의 존재성을 표시하며, 부분 다각형 그림이 가환적일 때 전체 그림이 가환적이라고 정의되고, 범주론에서 함자로 해석되며 호몰로지 대수학에서 사상의 성질 증명에 활용된다.

뱀 완전열

2. 정의

아벨 범주에서 가환 다이어그램과 완전열을 이용하여 뱀 보조정리를 정의한다. 아벨 군의 범주나 주어진 체 위의 벡터 공간의 범주 등에서 뱀 보조정리가 성립한다.

2. 1. 뱀 보조정리의 명제

아벨 범주에서, 다음과 같은 그림이 가환한다고 하자.

여기에서 각 행은 완전열이며 0은 영 대상이다. 이 경우, 세 사상

a

,

b

,

c

의 핵과 여핵들로 구성된 6항 완전열이 존재하며, 이를 '''뱀 완전열'''이라고 한다.^[4]

:

\ker a\to\ker b\to\ker c\xrightarrow d\operatorname{coker}a\to\operatorname{coker}b\to\operatorname{coker}c

이 완전열에서,

d

를 '''연결 사상'''(connecting morphism^영어)이라고 한다.

나아가, 사상 ''f''가 단사 사상이면,

\ker a \to \ker b

또한 단사 사상이며, ''g''가 전사 사상이면,

\operatorname{coker} b \to \operatorname{coker} c

또한 전사 사상이다.

여기서 코핵은 다음과 같다:

\operatorname{coker}a = A'/\operatorname{im}a

,

\operatorname{coker}b = B'/\operatorname{im}b

,

\operatorname{coker}c = C'/\operatorname{im}c

.

2. 2. 연결 사상의 구성

아벨 군 범주나 환 위의 가군의 경우, 연결 사상

d

는 다음과 같이 구체적으로 구성할 수 있다.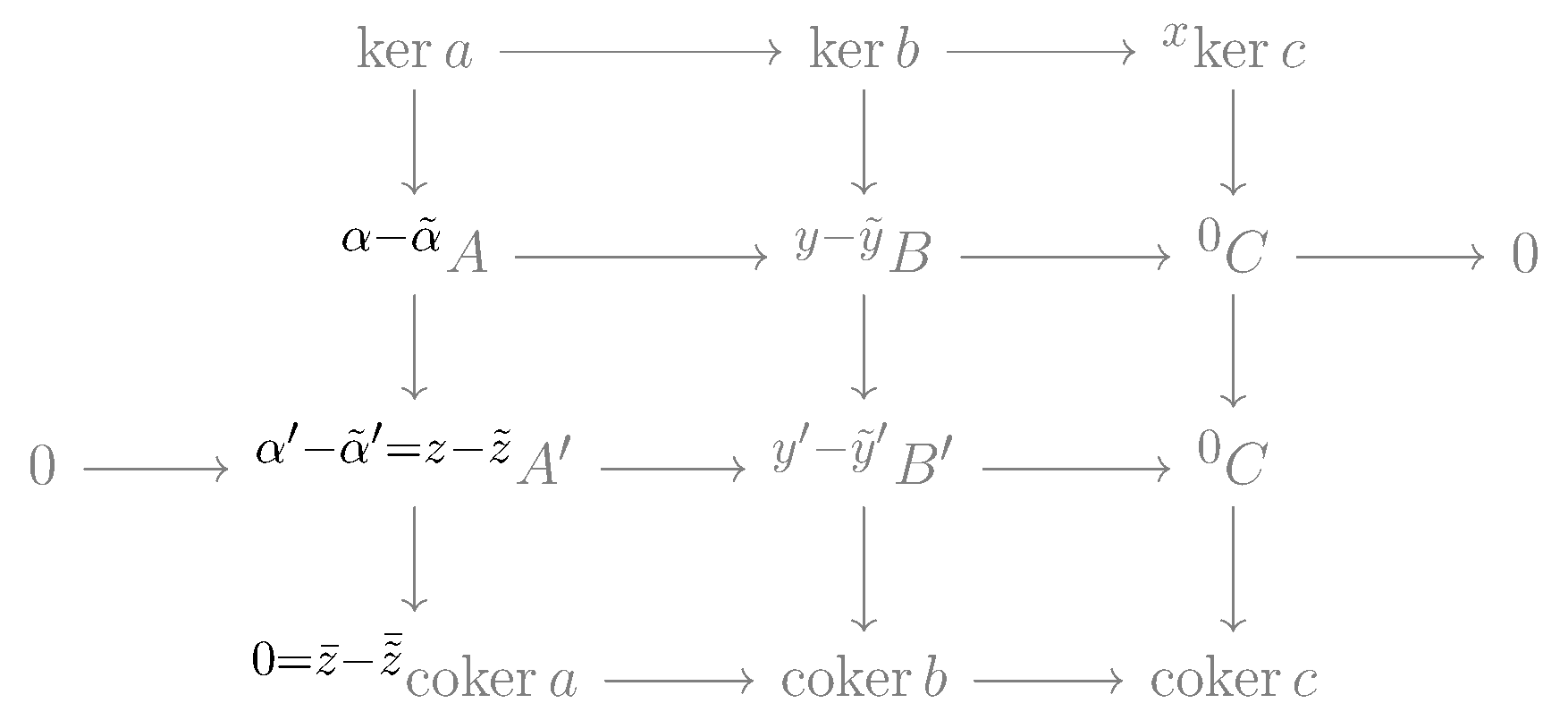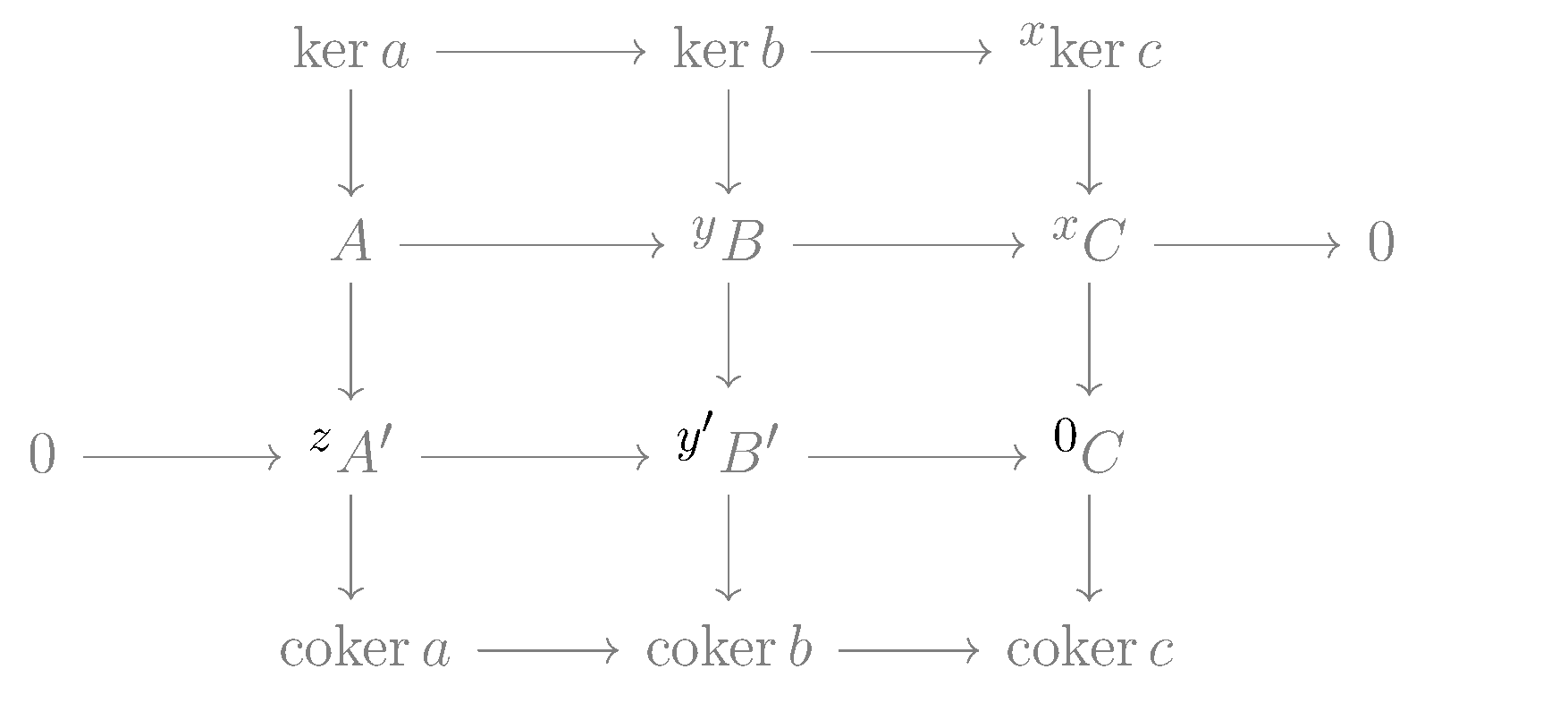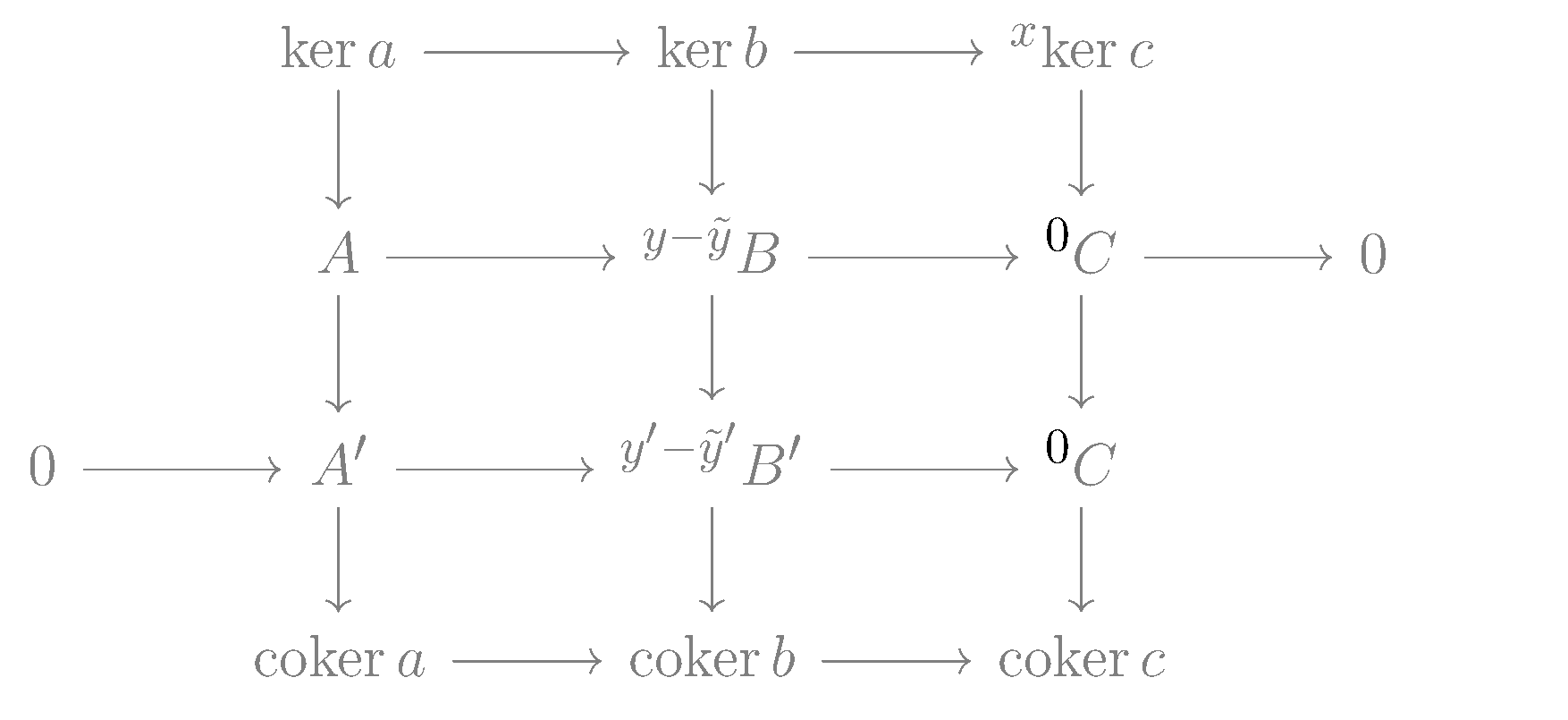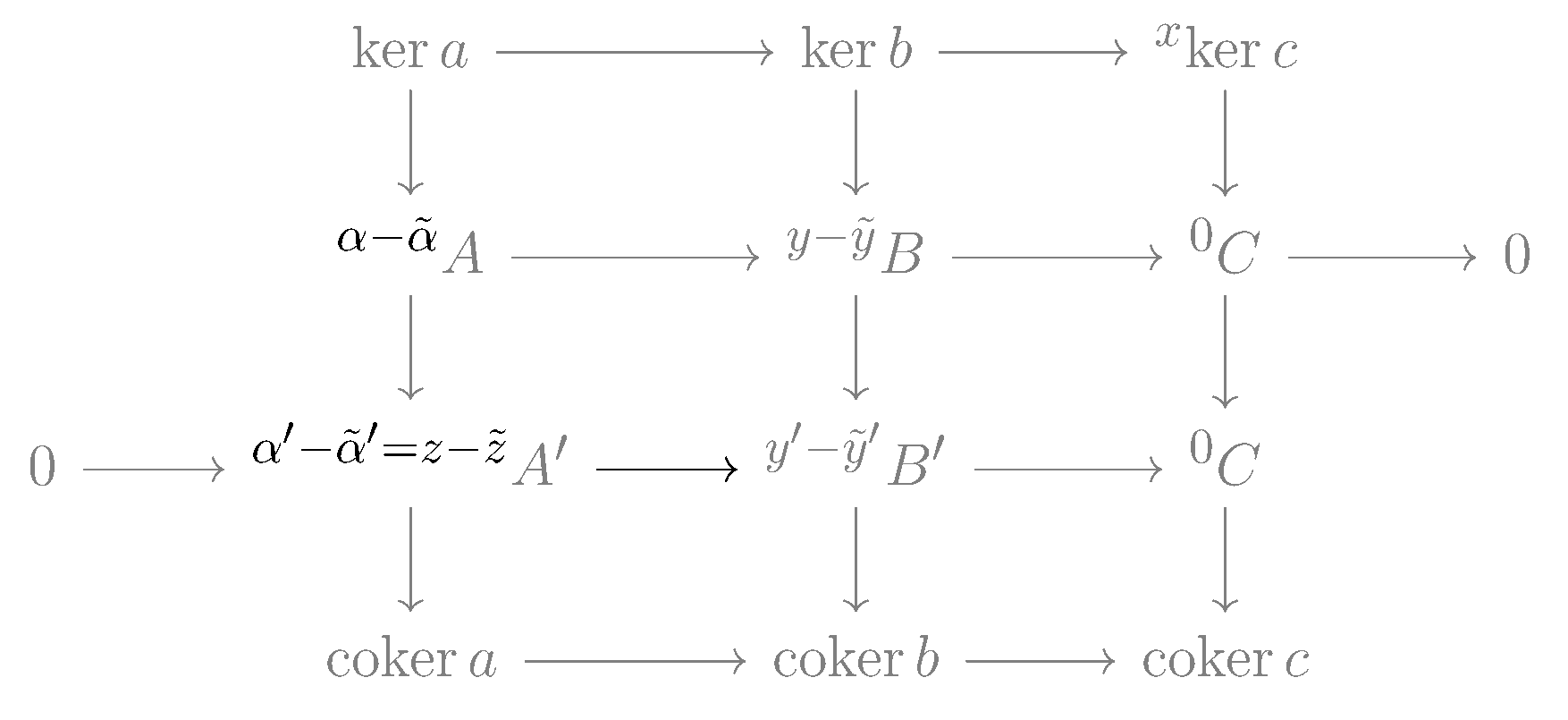

1. ker ''c''의 원소 ''x''를 선택하고, 이를 ''C''의 원소로 간주한다.

2. ''g''가 전사 함수이므로, ''g''(''y'') = ''x''인 ''B''의 원소 ''y''가 존재한다.

3. 가환 다이어그램의 가환성에 의해,

g'(b(y)) = c(g(y)) = c(x) = 0

이다. (''x''는 ''c''의 핵에 속하므로)

4. 따라서 ''b''(''y'')는 ''g' ''의 핵에 있다.

5. 아래쪽 행이 완전열이므로, ''f'' '(''z'') = ''b''(''y'')를 만족하는 ''A' ''의 원소 ''z''가 존재한다.

6. ''f'' '의 단사 사상 성질에 의해 ''z''는 유일하다.

7. ''d''(''x'') = ''z'' + ''im''(''a'') 로 정의한다.

이때, ''d''는 ''y''의 선택에 의존하지 않고 ''x''에만 의존하며, 준동형사상이다. 또한, 이렇게 구성된 연결 사상

d

에 의해 만들어지는 긴 열은 완전열이 된다. 이는 다이어그램 체이싱을 통해 확인할 수 있다.^[1]

일반적인 아벨 범주의 경우, 미첼의 임베딩 정리를 사용하여 위와 같은 방식으로 증명할 수 있다.

3. 성질

뱀 보조정리에서 유도되는 완전열은 몇 가지 중요한 성질을 갖는다.

위 그림에 대응하는 뱀 완전열에서 다음이 성립한다.

(가) 만약 $f$ 가 단사 사상이라면 $\ker a\to\ker b$ 도 단사 사상이다.
(나) $g'$ 이 전사 사상인 경우 $\operatorname{coker}b\to\operatorname{coker}c$ 도 전사 사상이다.

이들은 서로 쌍대적이다. 즉, 아벨 범주

\mathcal A

에서의 명제 (가)는 반대 범주

\mathcal A^{\operatorname{op}}

에서의 명제 (나)와 같다.

임의의 아벨 범주(아벨 군의 범주나 주어진 체 위의 벡터 공간의 범주 등)에서, 아래와 같은 가환 도형

을 생각해보자. 이때, 두 행이 완전하고, 0은 영 대상이다. 그러면 ''a'', ''b'', ''c''의 핵이나 여핵과 관련된 다음과 같은 완전열

\ker a \; {\color{Gray}\longrightarrow} \ker b \; {\color{Gray}\longrightarrow} \ker c \; \overset{d}{\longrightarrow} \operatorname{coker}a \; {\color{Gray}\longrightarrow} \operatorname{coker}b \; {\color{Gray}\longrightarrow} \operatorname{coker}c

이 존재한다. 또한, 사상 ''f''가 단사 사상이면, 사상 ker ''a'' → ker ''b''도 단사 사상이며, ''g''가 전사 사상이면, coker ''b'' → coker ''c''도 전사 사상이다.^[4]

3. 1. 자연성

뱀 보조정리는 자연 변환의 의미에서 "자연스럽다". 즉, 두 개의 가환 다이어그램이 주어지고, 그 다이어그램들이 완전열을 이룰 때, 뱀 보조정리를 통해 얻어지는 두 개의 긴 완전열은 서로 가환하는 다이어그램을 통해 관련된다.

정확한 행을 가진 가환도표라면, 뱀 보조정리를 "앞쪽"과 "뒤쪽"에 적용하여 두 개의 긴 완전 순서를 얻을 수 있다. 이것들은 다음과 같은 형태의 가환도표에 의해 관련된다.

3. 2. 호몰로지 긴 완전열

사슬 복합체의 짧은 완전열이 주어졌을 경우, 뱀 완전열들이 이어져 더 긴 완전열을 얻는다. 이를 짧은 완전열에 대응하는 '''호몰로지 긴 완전열'''(homology long exact sequence^영어)이라고 한다.

아벨 범주에서, 사슬 복합체

A_\bullet

,

B_\bullet

,

C_\bullet

가 주어졌다고 하고, 이들이 다음과 같은 짧은 완전열을 이룬다고 하자.

:

0\to A_\bullet\xrightarrow\alpha B_\bullet\xrightarrow\beta C_\bullet\to0

'''지그재그 정리'''(zigzag 補助定理, zigzag lemma^영어)에 따르면, 다음과 같은 긴 완전열이 존재한다.^[4]

:

\cdots\to\operatorname H_{n+1}(C)\to\operatorname H_n(A)\xrightarrow{\alpha_*}\operatorname H_n(B)\xrightarrow{\beta_*}\operatorname H_n(C)\to\operatorname H_{n-1}(A)\to\cdots

뱀 보조정리 또는 도롱뇽 정리를 사용하여 호몰로지 긴 완전열을 구성할 수 있다.

4. 예

아벨 범주에서 가환 그림의 각 행이 완전열이고 0이 영 대상일 때, 세 사상 $a$ , $b$ , $c$ 의 핵과 여핵들로 구성된 6항 완전열이 존재하며, 이를 '''뱀 완전열'''이라고 한다.^[4]

: $\ker a\to\ker b\to\ker c\xrightarrow d\operatorname{coker}a\to\operatorname{coker}b\to\operatorname{coker}c$

여기서 $d$ 는 '''연결 사상'''이라고 불린다. 뱀 완전열은 도롱뇽 정리를 사용하여 증명할 수 있다.^[5]

4. 1. 마이어-피토리스 열

대수적 위상수학에서 마이어-피토리스 열은 뱀 완전열의 일종이다.^[1]

4. 2. 복시테인 준동형

대수적 위상수학에서 복시테인 준동형은 뱀 보조정리의 연결 사상의 한 예시이다.^[1]

4. 3. 텐서곱의 불완전성

체 ''k'' 위의 벡터 공간 V에 대한 짧은 완전열이 주어졌을 때, 텐서곱을 취하면 일반적으로 완전열이 유지되지 않는다. 뱀 보조정리는 이러한 텐서곱의 불완전성을 설명하는 데 사용될 수 있다.^[1]

k

를 체로,

V

를

k

-벡터 공간으로 놓고,

t:V \to V

는

k

-선형 변환이라 하자.

V

와

k

를

k[t]

위에서 텐서곱하면 다음과 같다.

:

V \otimes_{k[t]} k = V \otimes_{k[t]} (k[t]/(t)) = V/tV = \operatorname{coker}(t) .

k

-벡터 공간의 짧은 완전열

0 \to M \to N \to P \to 0

이 주어지면, 텐서곱을 통해

M \otimes_{k[t]} k \to N \otimes_{k[t]} k \to P \otimes_{k[t]} k \to 0

의 완전열을 유도할 수 있지만, 열

0 \to M \otimes_{k[t]} k \to N \otimes_{k[t]} k \to P \otimes_{k[t]} k \to 0

은 일반적으로 완전하지 않다.

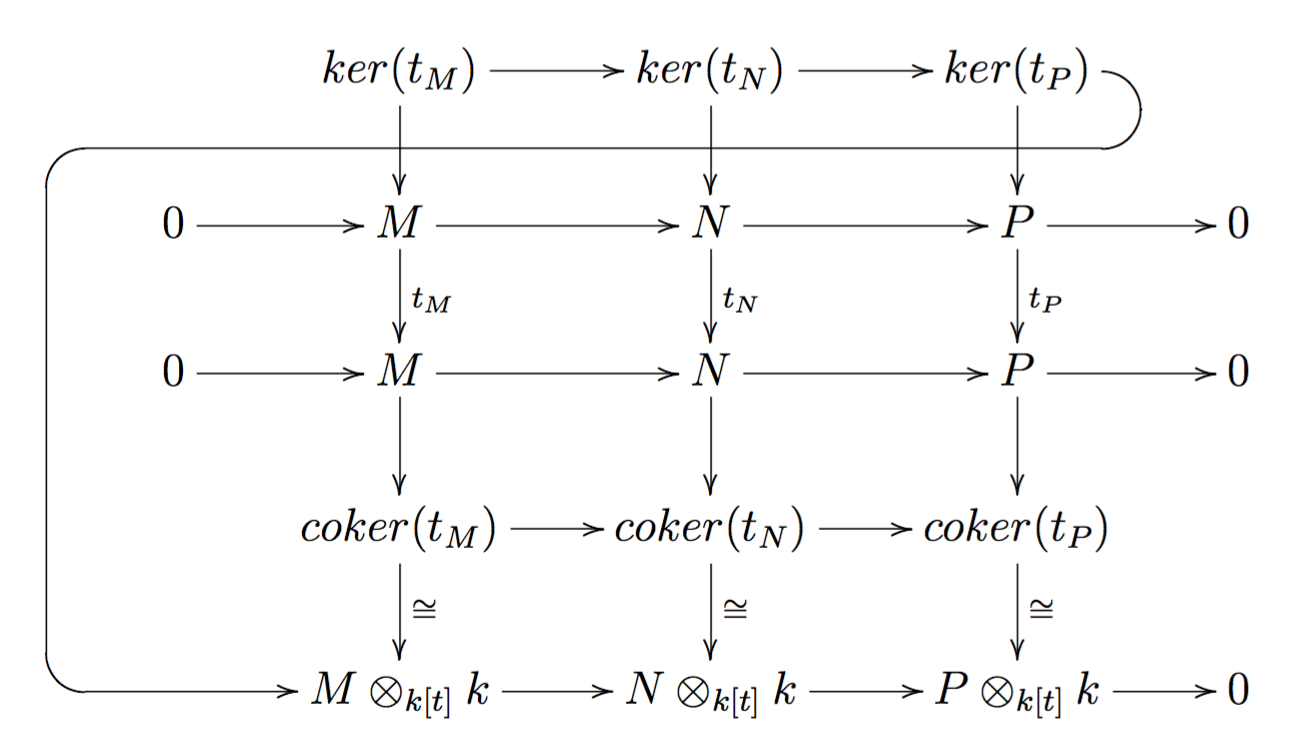
위의 다이어그램에 뱀 보조정리를 적용하면,

\ker(t_M) \to \ker(t_N) \to \ker(t_P) \to M \otimes_{k[t]} k \to N \otimes_{k[t]} k \to P \otimes_{k[t]} k \to 0

의 완전열을 얻을 수 있다. 즉, 뱀 보조정리는 텐서곱이 완전열을 보존하지 못하는 현상을 보여준다.^[1]

5. 뱀 보조정리의 증명

아벨 범주에서, 다음과 같은 그림이 가환한다고 하자.

여기에서 각 행은 완전열이며 0은 영 대상이다. 이 경우, 세 사상 $a$ , $b$ , $c$ 의 핵과 여핵들로 구성된 6항 완전열이 존재하며, 이를 '''뱀 완전열'''이라고 한다.^[4]

: $\ker a\to\ker b\to\ker c\xrightarrow d\operatorname{coker}a\to\operatorname{coker}b\to\operatorname{coker}c$

이 완전열에서, $d$ 를 '''연결 사상'''(connecting morphism^영어)이라고 한다.

연결 사상 $d$ 는 만약 $\mathcal A$ 가 아벨 군 범주의 부분 범주라고 할 경우 구체적으로 다음과 같이 구성할 수 있다.

'''연결 사상의 구성:'''

우선, 임의의 $\gamma\in\ker c\subseteq C$ 에 대하여 다음과 같은 원소들을 정의한다.

$g(\beta)=\gamma$ 인 임의의 $\beta\in B$ (이는 $g$ 가 전사 사상이므로 가능하다)
$g'(b(\beta))=c(g(\beta))=c(\gamma)=0$ 이므로, $b(\beta)\in\ker g'\subseteq B'$ 가 된다.
$0\to A'\to B'\to C'$ 가 완전열이므로, (다시 말해, $\operatorname{im}f' = \ker g'$ 이고 $f'$ 이 단사 사상이므로) $f'(\alpha')=b(\beta)$ 인 $\alpha'\in A'$ 이 유일하게 존재한다.

그렇다면, 연결 사상

d

는 다음과 같다.

:

d\colon \gamma\mapsto \alpha'+\operatorname{im}a

이는

\beta\in B

의 선택에 의존하지 않으며, 또한 연결 사상을 통해 얻는 열이 완전열임을 보일 수 있다.

뱀 완전열의 존재는 도롱뇽 정리를 사용하여 증명할 수 있다.^[5]

'''증명:'''

그림의 위에 핵을, 밑에 여핵을 추가하여 다음과 같은 그림을 만들자.

:

\begin{matrix}&& 0 && 0 && 0 \\&& \downarrow && \downarrow && \downarrow \\&& \ker a &\to & \ker b &\to & \ker c \\&& \downarrow && \downarrow && \downarrow \\&& A  & \to &  B &\to & C &\to &0\\&& \downarrow && \downarrow && \downarrow \\0&\to & A' &\to & B' &\to & B' \\&& \downarrow && \downarrow && \downarrow \\&& \operatorname{coker}a &\to & \operatorname{coker}b &\to & \operatorname{coker}c \\&& \downarrow && \downarrow && \downarrow \\&& 0 && 0 && 0\end{matrix}

이제, 다음 세 명제를 증명하면 된다.

(가): $_= (\ker b) \cong 0$
(나): $_=(\operatorname{coker}b) \cong 0$
(다): $(\ker c)_\square \cong {}^\square (\operatorname{coker}a)$ . 이는 $\operatorname{coker} (\operatorname{ker}b \to \ker c) = (\ker c)_\square$ 이며, $\ker (\operatorname{coker}a\to\operatorname{coker}b) = {}^\square (\operatorname{coker}a)$ 이기 때문이다. 이 동형 사상은 연결 사상에 해당한다.

이제, 완전성을 사용하여 다음 교외 사상들이 동형 사상임을 보일 수 있다.

:

\begin{matrix}&& 0_\square && 0_\square && 0_\square \\&& \swarrow && \swarrow && \swarrow \\&& ^\square \bullet_\square &\nearrow & ^\square \bullet_\square &\nearrow & ^\square \bullet_\square \\&& \swarrow && \swarrow && \swarrow \\&& ^\square \bullet_\square & \nearrow & ^\square \bullet_\square &\nearrow &^\square \bullet_\square &\nearrow &^\square 0\\&& \swarrow && \swarrow && \swarrow \\0_\square &\nearrow & ^\square \bullet_\square &\nearrow & ^\square \bullet_\square &\nearrow & ^\square \bullet_\square \\&& \swarrow && \swarrow && \swarrow \\&& ^\square \bullet_\square &\nearrow & ^\square \bullet_\square &\nearrow & ^\square \bullet_\square \\&& \swarrow && \swarrow && \swarrow \\&& ^\square0 && ^\square0 && ^\square0\end{matrix}

\ker b\to \ker c

를 중심으로 하는 도롱뇽 완전열 및

\operatorname{coker}b\to \operatorname{coker}c

를 중심으로 하는 도롱뇽 완전열을 사용하면, 아래 그림에 추가된 교내 사상이 추가로 동형 사상임을 알 수 있다.

:

\begin{matrix}&& 0_\square && 0_\square && 0_\square \\&& \swarrow && \color{Red}\swarrow && \swarrow \\&& ^\square \bullet_\square &\nearrow & \overset\square{\underset={\scriptstyle\color{Red}\downarrow}} \underset\to\bullet_\square &\nearrow & ^\square \bullet_\square \\&& \swarrow && \swarrow && \color{Green}\swarrow \\&& ^\square \bullet_\square & \nearrow & ^\square \bullet_\square &\color{Green}\nearrow &^\square \bullet_\square &\nearrow &^\square 0\\&& \swarrow && \color{Green}\swarrow && \swarrow \\0_\square &\nearrow & ^\square \bullet_\square &\color{Green}\nearrow & ^\square \bullet_\square &\nearrow & ^\square \bullet_\square \\&& \color{Green}\swarrow && \swarrow && \swarrow \\&& ^\square \bullet_\square &\nearrow & \overset\square{\underset={\scriptstyle\downarrow}} \underset{\color{Cyan}\to}\bullet_\square &\nearrow & ^\square \bullet_\square \\&& \swarrow && \color{Cyan}\swarrow && \swarrow \\&& ^\square0 && ^\square0 && ^\square 0\end{matrix}

이제, (가) ~ (다)의 증명은 다음과 같이 간단하다.

(가): 위의 그림에서 붉게 칠한 동형 사상 $0\cong 0_\square \to {}^\square(\ker b)\to {}_=(\ker b)$
(나): 위의 그림에서 하늘색으로 칠한 동형 사상 $0\cong {}^\square 0\leftarrow (\operatorname{coker} b)_\square \leftarrow {}_=(\operatorname{coker}b)$
(다): 위의 그림에서 녹색으로 칠한 동형 사상 $(\ker c)_\square \to {}^\square C \leftarrow B_\square \to {}^\square B'\leftarrow A_\square \to {}^\square(\operatorname{coker}a)$

핵 사이의 사상과 여핵 사이의 사상은, 도식의 가환성에 의해 주어진 (수평) 사상으로부터 자연스럽게 유도된다. 두 유도된 열의 완전성은 원래 도식의 행의 완전성으로부터 쉽게 유도된다. 보조정리의 중요한 내용은, 완전열을 완성시키는 '연결 준동형' ''d'' 가 존재한다는 것이다.

아벨 군이나 어떤 환 위의 가군의 경우, 사상 ''d''는 다음과 같이 구성할 수 있다. ker ''c''의 원소 ''x''를 취하고, 그것을 ''C''의 원소로 본다. ''g''는 전사이므로, 어떤 ''B''의 원소 ''y''가 존재하여, ''g''(''y'') = ''x''이다. 도식의 가환성에 의해,

g'(b(y)) = c(g(y))=c(x)=0 \!

이고 (''x''는 ''c''의 핵에 속해 있기 때문에), 따라서 ''b''(''y'')는 ''g' ''의 핵에 속한다. 아래 행이 완전하므로, ''A' ''의 원소 ''z''가 존재하여, ''f'' '(''z'') = ''b''(''y'')이다. ''z''는 ''f'' '의 단사성에 의해 유일하다. 그래서 ''d''(''x'') = ''z'' + ''im''(''a'')로 정의한다. 다음을 확인해야 한다. ''d''는 well-defined (즉, ''d''(''x'')는 ''x''에만 의존하며, ''y''의 선택에 의존하지 않음)이고, ''d''는 준동형이며, 그리고 얻어지는 긴 열이 실제로 완전하다는 것이다.

이 과정이 완료되면, 아벨 군이나 환 위의 가군에 대한 정리가 증명된다. 일반적인 경우에는, 원소 대신에 사상 및 소거의 성질을 사용하여 논의를 다시 작성할 수 있다. 또는 미첼의 매장 정리를 이용할 수도 있다.

6. 역사

뱀 완전열은 연결 사상이 가환 그림에서 마치 뱀처럼 구불거리는 모양을 하므로 이러한 이름이 붙었다.^[4] 아래 그림은 뱀의 모습을 묘사하고 있다.

데이비드 앨빈 북스바움은 1955년 논문에서 아벨 범주의 개념을 도입하였는데, 이 논문에서 이미 뱀 정리가 등장한다.^[6]

뱀 완전열의 존재 증명은 클로디아 와일(Claudia Weill) 감독의 1980년 미국 영화 《뉴욕 소나타》(It’s My Turn)의 도입부에 등장한다.^[4] 이 영화에서 수학 교수 케이트 건징어(Kate Gunzinger, 질 클레이버그 분)는 이 정리를 강의 중에 증명한다.

7. 그룹 범주에서의 뱀 보조정리

그룹 범주에서 코커널의 정의에 따라 뱀 보조정리의 성립 여부가 달라진다. 만약 코커널을 오른쪽 잉여류로 대체하면, 뱀 보조정리는 여전히 유효하다. 그러나 이 경우 몫은 군이 아니라 점 집합이다.^[2]

교대군 A₅는 대칭군 S₃와 동형인 부분군을 포함하며, 이는 다시 순환군의 반직접곱으로 나타낼 수 있다. 즉, S₃ ≃ C₃ ⋊ C₂이다.^[2] 이를 통해 다음과 같은 가환 다이어그램을 만들 수 있다.

1	→	C₃	→	C₃	→	1
↓		↓		↓
1 →	1	→	S₃	→	A₅

여기서 중간 열은 완전열이 아니다. 왜냐하면 C₂는 반직접곱에서 정규 부분군이 아니기 때문이다.^[2]

A₅는 단순군이므로, 오른쪽 수직 화살표는 자명한 코커널을 갖는다. 한편 몫군 S₃/C₃는 C₂와 동형이다. 따라서 뱀 보조정리에 따른 수열은 다음과 같다.

:1 → 1 → 1 → 1 → C₂ → 1

그러나 이 수열은 완전하지 않다.^[2]

참조

_[1] Harvnb
_[2] 웹사이트 Extensions of C2 by C3 https://people.maths[...] 2021-11-06
_[3] 논문 The Topological Snake Lemma and Corona Algebras http://www.emis.de/j[...]
_[4] 서적 An introduction to homological algebra http://www.math.rutg[...] Cambridge University Press 1994
_[5] 저널 On diagram-chasing in double complexes http://www.tac.mta.c[...] 2012
_[6] 저널 Exact categories and duality

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com