정백이십포체
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
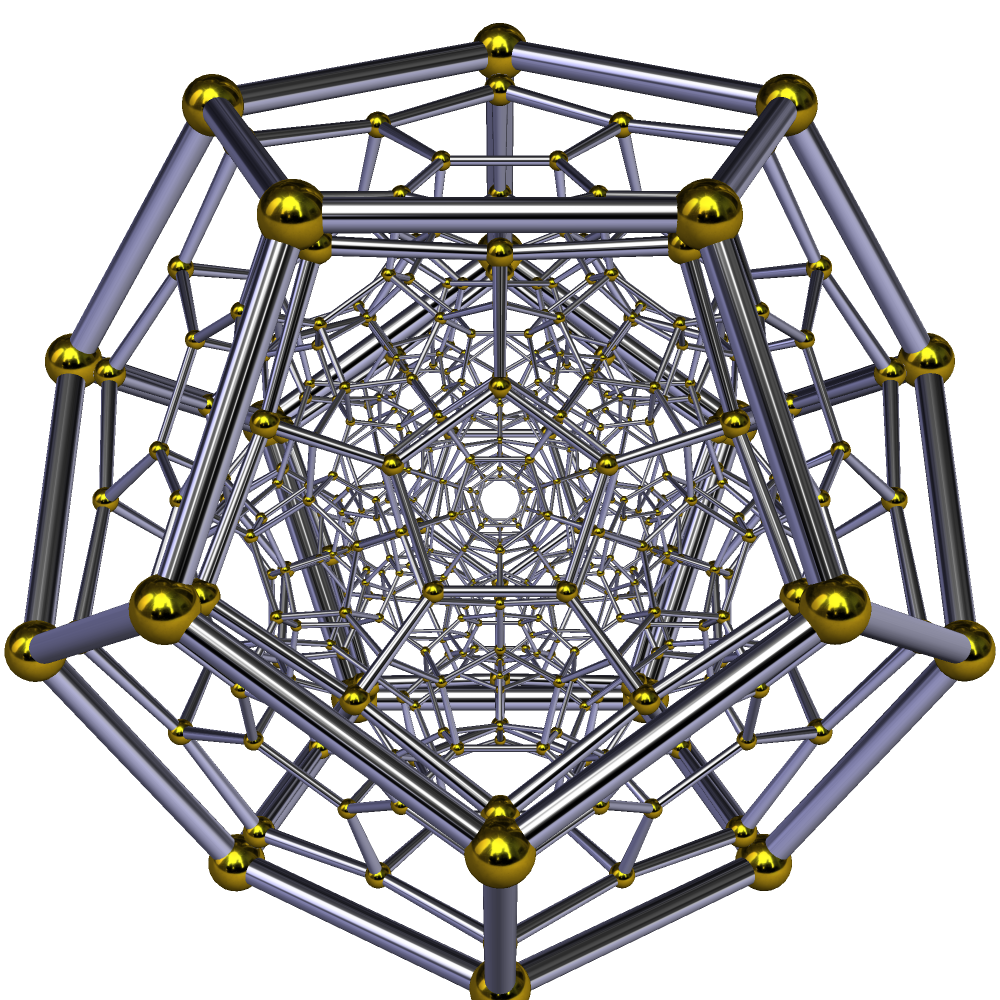
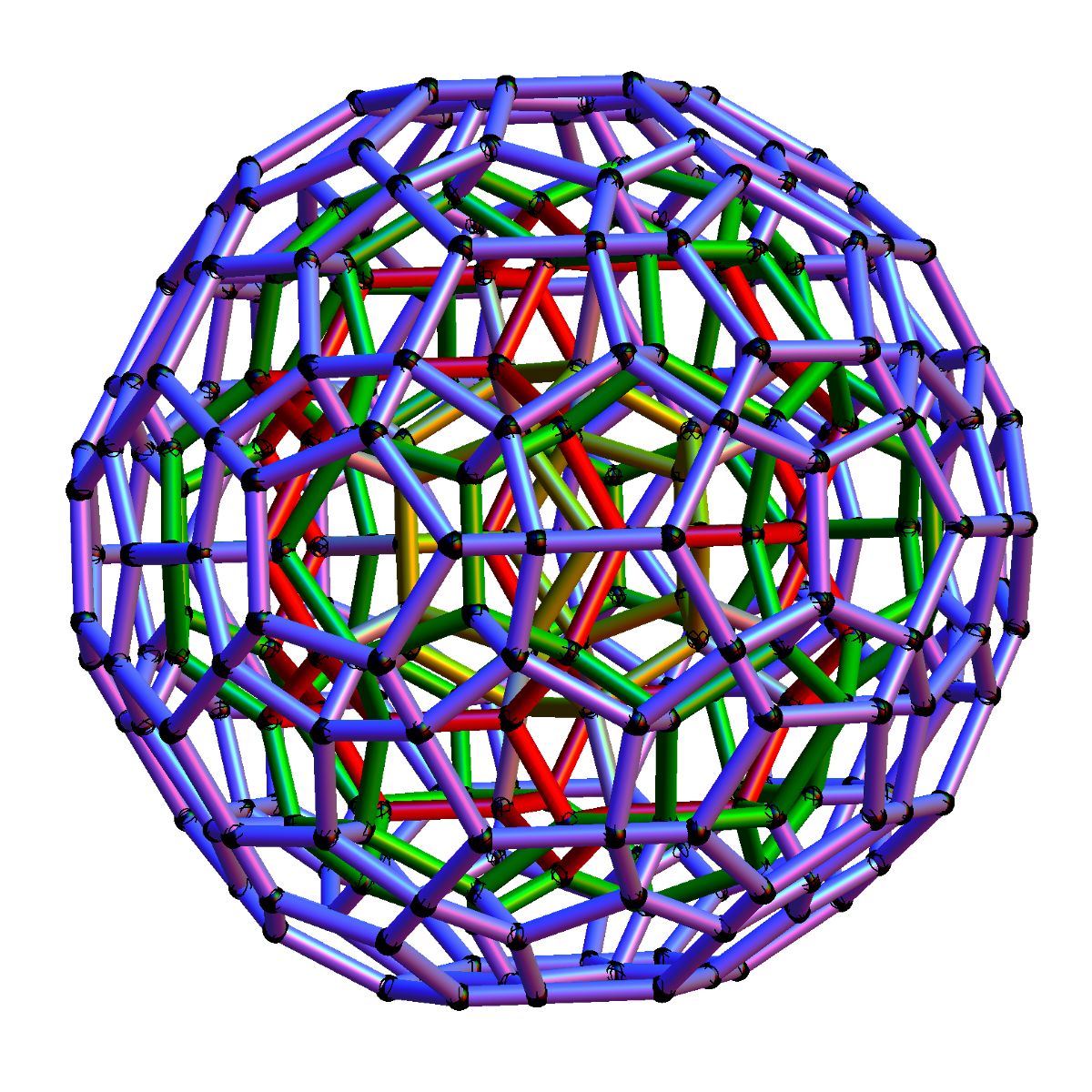
정백이십포체는 120개의 정십이면체 세포로 구성된 4차원 정다포체이다. 6개의 볼록 정규 4-다포체 시퀀스에서 여섯 번째로, 600개의 꼭짓점, 1200개의 모서리, 720개의 면을 갖는다. 120-포체는 600-포체의 쌍대 다포체이며, 600-포체, 24-포체, 초정육면체, 16-포체 등 다른 다포체들과의 관계를 가진다. 슐레겔 도표, 입체 투영, 원근 투영, 직교 투영 등 다양한 방법으로 시각화할 수 있으며, H₄ 대칭을 갖는 15개의 정다포체 중 하나이다.
더 읽어볼만한 페이지
| 정백이십포체 | |
|---|---|
| 개요 | |
 | |
| 종류 | 볼록 정다포체 |
| 순서 | 32 |
| 다음 | 33 |
| 슐레플리 기호 | {5,3,3} |
| 콕서터 다이어그램 | node_1 5 node 3 node 3 node |
| 면 | 120개 {5,3} |
| 모서리 | 1200개 |
| 꼭짓점 | 600개 |
| 페트리 다각형 | 30각형 |
| 콕서터 그룹 | H₄, [3,3,5] |
| 꼭짓점 도형 | 정사면체 |
| 쌍대 | 육백포체 |
| 성질 | 볼록, 등각, 등변, 등면 |
| 상세 정보 | |
| 면 구성 | 120개의 십이면체 |
| 변 구성 | 각 변에 3개의 십이면체와 3개의 오각형이 만남 |
| 꼭짓점 구성 | 각 꼭짓점에 4개의 십이면체, 6개의 오각형, 4개의 변이 만남 |
| 이면각 | 144° |
| 명칭 | |
| 영어 명칭 | Regular hecatonicosachoron |
| 다른 영어 명칭 | hyperdodecahedron |
2. 기하학적 구조
정백이십포체는 6개의 볼록 정규 4-다포체 시퀀스에서 여섯 번째(크기와 복잡성 순서)이다. 120-포체는 이전 도형(및 이중 도형)인 600-포체의 열 개의 개별 인스턴스(또는 다섯 개의 분리된 인스턴스)로 분해될 수 있다. 600-포체가 이전 도형인 24-포체의 스물다섯 개의 개별 인스턴스(또는 다섯 개의 분리된 인스턴스)로 분해될 수 있는 것처럼, 24-포체는 이전 도형인 초정육면체 (8-포체)의 세 개의 개별 인스턴스로 분해될 수 있으며, 8-포체는 이전 도형(및 이중 도형)인 16-포체의 두 개의 분리된 인스턴스로 분해될 수 있다. 120-포체는 16-포체의 675개의 개별 인스턴스(75개의 분리된 인스턴스)를 포함한다.
이전 도형의 인스턴스에서 각각을 구성하는 역방향 절차는 이전 도형의 반지름을 보존하지만 일반적으로 더 작은 모서리 길이를 가진 후속 도형을 생성한다. 600-포체의 모서리 길이는 반지름의 약 ~0.618배(역 황금비)이지만, 120-포체의 모서리 길이는 반지름의 약 ~0.270배이다.
120-포체가 600-포체의 쌍대이므로, 600개의 꼭지점을 각 600개의 사면체 세포의 부피 중심에 위치시켜 600-포체로부터 구성할 수 있다. 단위 장반경의 600-포체로부터, 이로 인해 약간 더 작은 장반경과 정확히 1/4의 모서리 길이를 가진 120-포체가 생성된다.
상호적으로, 단위 반경 120-포체는 각 정십이면체 세포의 중심을 600-포체 120개 꼭지점 중 하나에 배치하여 600-포체 바로 바깥에 구성할 수 있다.
따라서 단위 반경 120-포체는 선행체인 단위 반경 600-포체로부터 세 단계를 거쳐 상호적으로 구성할 수 있다.
120-포체는 내접하는 600-포체를 포함하기 때문에, 같은 반지름의 자체 쌍대를 포함한다. 120-포체는 다섯 개의 서로 소인 600-포체(두 가지 방법으로 다섯 개의 서로 소인 600-포체를 고를 수 있는 열 개의 중첩된 내접 600-포체)를 포함하므로, 자체 쌍대의 화합물(두 가지 방법으로)로 볼 수 있다. 각 내접 600-포체의 꼭짓점은 120-포체의 꼭짓점이며, (쌍대적으로) 각 십이면체 세포 중심은 각 내접 600-포체의 사면체 세포 중심이다.
120-포체의 십이면체 세포는 그 안에 내접하는 600-포체의 사면체 세포를 가지고 있다. 120-포체가 다섯 개의 600-포체의 화합물인 것처럼(두 가지 방법으로), 십이면체는 다섯 개의 정사면체의 화합물이다(두 가지 방법으로).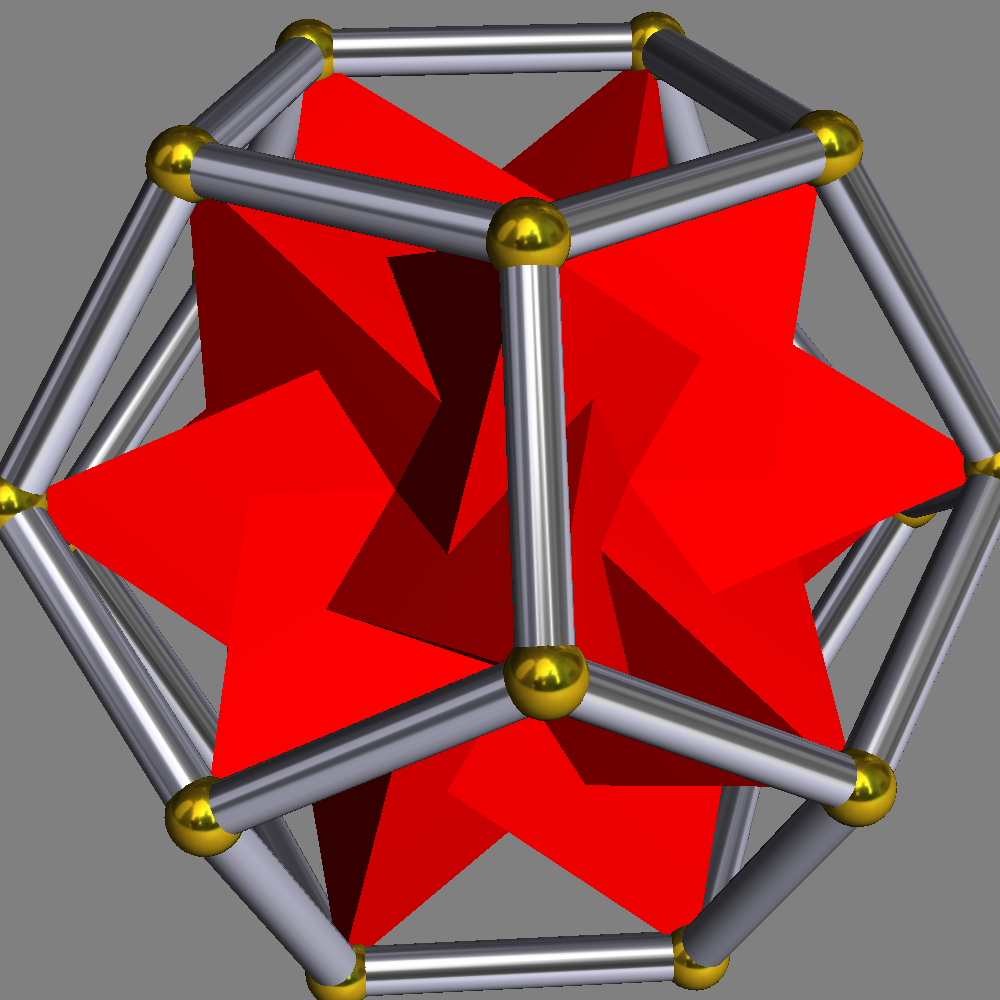
두 개의 반대 사면체가 정육면에 내접할 수 있고, 다섯 개의 정육면체가 십이면체에 내접할 수 있으므로, 다섯 개의 정육면에 있는 열 개의 사면체가 십이면체에 내접할 수 있다. 즉, 각 세트가 20개의 모든 꼭짓점을 덮고 각 꼭짓점이 두 개의 사면체(각 세트에서 하나씩, 하지만 정육면체의 반대 쌍은 분명히 아님)에 있는, 두 개의 반대 세트가 있다. 이것은 120-포체가, 그 많은 내부 특징 중, 열 개의 600-포체의 화합물로서 전체 120-포체와 차원적으로 유사한, 120개의 열 개의 사면체의 화합물을 포함하고 있음을 보여준다.
열 개의 모든 사면체는 임의의 하나의 사면체의 두 개의 키랄 다섯 번의 클릭 회전을 통해 생성될 수 있다. 각 십이면체 세포에서 하나의 사면체 세포는 120-포체에 내접하는 열 개의 600-포체 각각에서 나온다. 따라서 전체 120-포체는, 모든 열 개의 내접 600-포체를 가지고, 단 하나의 600-포체의 세포를 회전시켜 생성할 수 있다.
120-포체는 내접하는 600-포체를 포함하고 있기 때문에, 어떤 종류의 4-각뿔을 600-포체의 세포에 배치하여 구성하는 것이 가능하다는 또 다른 결과가 있다.
각 600-포체의 120개의 사면체 세포만이 120-포체의 십이면체에 내접할 수 있으며, 나머지 480개의 사면체는 십이면체 세포에 걸쳐 있다. 각 십이면체 내접 사면체는 5개의 사면체 클러스터의 중심 세포이며, 그 주위에 면 결합된 다른 4개는 십이면체 내부에 부분적으로만 놓여 있다. 중심 사면체는 십이면체 내부에 부분적으로만 놓여 있는 추가 12개의 사면체 세포와 모서리 결합되어 있다. 중심 세포는 십이면체 외부에 완전히 놓여 있는 다른 40개의 사면체 세포와 꼭지점 결합되어 있다.
또 다른 구성 방법은 사원수와 바일 군 궤도의 정십이면체 대칭을 사용하여, 순서가 120인 것을 사용한다.
구성 행렬은 정백이십포체를 나타낸다.
아래는 ''k''-면 요소와 ''k''-도형으로 확장된 구성이다.
| H4 | k-면 | fk | f0 | f1 | f2 | f3 | k-도형 | 비고 | |
|---|---|---|---|---|---|---|---|---|---|
| A3 | ( ) | f0 | 600 | 4 | 6 | 4 | {3,3} | H4/A3 = 14400/24 = 600 | |
| A1A2 | { } | f1 | 2 | 1200 | 3 | 3 | {3} | H4/A2A1 = 14400/6/2 = 1200 | |
| H2A1 | {5} | f2 | 5 | 5 | 720 | 2 | { } | H4/H2A1 = 14400/10/2 = 720 | |
| H3 | {5,3} | f3 | 20 | 30 | 12 | 120 | ( ) | H4/H3 = 14400/120 = 120 |
- 포(구성 입체): 정십이면체 120개로 구성되어 있다.
- 면: 720장의 각 정오각형에 정십이면체 2개가 모인다.
- 변: 1200개의 각 변에 정오각형 3장, 정십이면체 3개가 모인다.
- 꼭짓점: 600개의 각 꼭짓점에 변 4개, 정오각형 6장, 정십이면체 4개가 모인다.
- 면, 변, 꼭짓점에 모이는 도형의 수는 각각의 모양에 따라, 선분의 단점의 수(파스칼의 삼각형의 제3단), 정삼각형의 꼭짓점과 변의 수(제4단), 정사면체의 꼭짓점과 변과 면의 수(제5단)와 같다.
- 쌍대: 정육백포체
- 슐레플리 기호: {5,3,3}
2. 1. 구성 요소
정백이십포체는 6개의 볼록 정규 4-다포체 시퀀스에서 여섯 번째(크기와 복잡성 순서)이다. 120-포체는 이전 도형(및 이중 도형)인 600-포체의 열 개의 개별 인스턴스(또는 다섯 개의 분리된 인스턴스)로 분해될 수 있다. 600-포체가 이전 도형인 24-포체의 스물다섯 개의 개별 인스턴스(또는 다섯 개의 분리된 인스턴스)로 분해될 수 있는 것처럼, 24-포체는 이전 도형인 초정육면체 (8-포체)의 세 개의 개별 인스턴스로 분해될 수 있으며, 8-포체는 이전 도형(및 이중 도형)인 16-포체의 두 개의 분리된 인스턴스로 분해될 수 있다. 120-포체는 16-포체의 675개의 개별 인스턴스(75개의 분리된 인스턴스)를 포함한다.이전 도형의 인스턴스에서 각각을 구성하는 역방향 절차는 이전 도형의 반지름을 보존하지만 일반적으로 더 작은 모서리 길이를 가진 후속 도형을 생성한다. 600-포체의 모서리 길이는 반지름의 약 ~0.618배(역 황금비)이지만, 120-포체의 모서리 길이는 반지름의 약 ~0.270배이다.
120-포체가 600-포체의 쌍대이므로, 600개의 꼭지점을 각 600개의 사면체 세포의 부피 중심에 위치시켜 600-포체로부터 구성할 수 있다. 단위 장반경의 600-포체로부터, 이로 인해 약간 더 작은 장반경과 정확히 1/4의 모서리 길이를 가진 120-포체가 생성된다.
상호적으로, 단위 반경 120-포체는 각 정십이면체 세포의 중심을 600-포체 120개 꼭지점 중 하나에 배치하여 600-포체 바로 바깥에 구성할 수 있다.
따라서 단위 반경 120-포체는 선행체인 단위 반경 600-포체로부터 세 단계를 거쳐 상호적으로 구성할 수 있다.
120-포체는 내접하는 600-포체를 포함하기 때문에, 같은 반지름의 자체 쌍대를 포함한다. 120-포체는 다섯 개의 서로 소인 600-포체(두 가지 방법으로 다섯 개의 서로 소인 600-포체를 고를 수 있는 열 개의 중첩된 내접 600-포체)를 포함하므로, 자체 쌍대의 화합물(두 가지 방법으로)로 볼 수 있다. 각 내접 600-포체의 꼭짓점은 120-포체의 꼭짓점이며, (쌍대적으로) 각 십이면체 세포 중심은 각 내접 600-포체의 사면체 세포 중심이다.
120-포체의 십이면체 세포는 그 안에 내접하는 600-포체의 사면체 세포를 가지고 있다. 120-포체가 다섯 개의 600-포체의 화합물인 것처럼(두 가지 방법으로), 십이면체는 다섯 개의 정사면체의 화합물이다(두 가지 방법으로).
두 개의 반대 사면체가 정육면에 내접할 수 있고, 다섯 개의 정육면체가 십이면체에 내접할 수 있으므로, 다섯 개의 정육면에 있는 열 개의 사면체가 십이면체에 내접할 수 있다. 즉, 각 세트가 20개의 모든 꼭짓점을 덮고 각 꼭짓점이 두 개의 사면체(각 세트에서 하나씩, 하지만 정육면체의 반대 쌍은 분명히 아님)에 있는, 두 개의 반대 세트가 있다. 이것은 120-포체가, 그 많은 내부 특징 중, 열 개의 600-포체의 화합물로서 전체 120-포체와 차원적으로 유사한, 120개의 열 개의 사면체의 화합물을 포함하고 있음을 보여준다.
열 개의 모든 사면체는 임의의 하나의 사면체의 두 개의 키랄 다섯 번의 클릭 회전을 통해 생성될 수 있다. 각 십이면체 세포에서 하나의 사면체 세포는 120-포체에 내접하는 열 개의 600-포체 각각에서 나온다. 따라서 전체 120-포체는, 모든 열 개의 내접 600-포체를 가지고, 단 하나의 600-포체의 세포를 회전시켜 생성할 수 있다.
120-포체는 내접하는 600-포체를 포함하고 있기 때문에, 어떤 종류의 4-각뿔을 600-포체의 세포에 배치하여 구성하는 것이 가능하다는 또 다른 결과가 있다.
각 600-포체의 120개의 사면체 세포만이 120-포체의 십이면체에 내접할 수 있으며, 나머지 480개의 사면체는 십이면체 세포에 걸쳐 있다. 각 십이면체 내접 사면체는 5개의 사면체 클러스터의 중심 세포이며, 그 주위에 면 결합된 다른 4개는 십이면체 내부에 부분적으로만 놓여 있다. 중심 사면체는 십이면체 내부에 부분적으로만 놓여 있는 추가 12개의 사면체 세포와 모서리 결합되어 있다. 중심 세포는 십이면체 외부에 완전히 놓여 있는 다른 40개의 사면체 세포와 꼭지점 결합되어 있다.
또 다른 구성 방법은 사원수와 바일 군 궤도의 정십이면체 대칭을 사용하여, 순서가 120인 것을 사용한다.
구성 행렬은 정백이십포체를 나타낸다.
아래는 ''k''-면 요소와 ''k''-도형으로 확장된 구성이다.
| H4 | k-면 | fk | f0 | f1 | f2 | f3 | k-도형 | 비고 | |
|---|---|---|---|---|---|---|---|---|---|
| A3 | ( ) | f0 | 600 | 4 | 6 | 4 | {3,3} | H4/A3 = 14400/24 = 600 | |
| A1A2 | { } | f1 | 2 | 1200 | 3 | 3 | {3} | H4/A2A1 = 14400/6/2 = 1200 | |
| H2A1 | {5} | f2 | 5 | 5 | 720 | 2 | { } | H4/H2A1 = 14400/10/2 = 720 | |
| H3 | {5,3} | f3 | 20 | 30 | 12 | 120 | ( ) | H4/H3 = 14400/120 = 120 |
- 포(구성 입체): 정십이면체 120개로 구성되어 있다.
- 면: 720장의 각 정오각형에 정십이면체 2개가 모인다.
- 변: 1200개의 각 변에 정오각형 3장, 정십이면체 3개가 모인다.
- 꼭짓점: 600개의 각 꼭짓점에 변 4개, 정오각형 6장, 정십이면체 4개가 모인다.
- 면, 변, 꼭짓점에 모이는 도형의 수는 각각의 모양에 따라, 선분의 단점의 수(파스칼의 삼각형의 제3단), 정삼각형의 꼭짓점과 변의 수(제4단), 정사면체의 꼭짓점과 변과 면의 수(제5단)와 같다.
- 쌍대: 정육백포체
- 슐레플리 기호: {5,3,3}
2. 2. 꼭짓점 좌표
4차원 공간의 원점에 중심을 둔 정백이십포체의 데카르트 좌표는 긴 반지름(중심에서 꼭짓점까지)에 따라 서로 다른 좌표계에서 나타난다. 정백이십포체는 긴 반지름 √8 = 2√2 ≈ 2.828을 가지며, 변의 길이는 4−2φ = 3−√5 ≈ 0.764이다.이 좌표계에서 600개의 꼭짓점 좌표는 다음과 같다.
| 24 | (0, 0, ±2, ±2) | 24-포체 | 600-점 정백이십포체 |
|---|---|---|---|
| 64 | (±φ, ±φ, ±φ, ±φ−2) | ||
| 64 | (±1, ±1, ±1, ±√5) | ||
| 64 | (±φ−1, ±φ−1, ±φ−1, ±φ2) | ||
| 96 | (0, ±φ−1, ±φ, ±√5) | 스너브 24-포체 | |
| 96 | (0, ±φ−2, ±1, ±φ2) | 스너브 24-포체 | |
| 192 | (±φ−1, ±1, ±φ, ±2) |
여기서 φ는 황금비, (1 + √5)/2 ≈ 1.618이다.
정단위 반지름 120-포체는 모서리 길이 }} ≈ 0.270을 갖는다. 이 좌표계에서 120-포체는 표준 방향으로 꼭짓점이 위로 향하게 놓인다.
120-포체의 600개 꼭짓점의 정단위 반지름 좌표는 5-포체의 5개 꼭짓점, 24-포체의 24개 꼭짓점, 600-포체의 120개 꼭짓점의 모든 가능한 사원수 곱이다. 정규 볼록 4-포체의 정단위 반지름 좌표는 사원수 곱셈으로 관련된다. 정규 4-포체는 서로의 합성물이므로, 그 데카르트 4-좌표(사원수) 집합은 서로의 집합 곱이다.
또 다른 구성 방법은 사원수와 바일 군 궤도의 정십이면체 대칭을 사용하는 것이다.
2. 3. 현
120-셀의 모서리는 600-셀, 24-셀, 16-셀의 모서리와 같이 단일 중심 평면에서 정규 큰 원 다각형을 형성하지 않는다. 5-셀 및 8-셀 테서랙트의 모서리와 마찬가지로, 지그재그 페트리 다각형을 형성한다. 120-셀의 페트리 다각형은 삼십각형 {30} 지그재그 왜곡 다각형이다. 120-셀은 1200개의 모서리의 80개의 서로 다른 30-각형 페트리 다각형을 포함하며, 20개의 분리된 30-각형 페트리 다각형으로 분할될 수 있다. 페트리 30-각형은 한 원형 궤도 과정에서 9번 큰 원 축을 중심으로 비틀리며, 600-셀 모서리(#3 현)가 페트리 다각형에서 9개의 꼭짓점 떨어져 있는 꼭짓점 쌍을 연결하는 삼십각별 {30/9}3{10/3}의 화합물로 볼 수 있다.120-셀은 30개의 모서리 원주를 갖기 때문에, 모서리 길이에서 지름에 이르기까지 15개의 서로 다른 현 길이를 갖는다. 120-셀의 15개 번호가 매겨진 현은 이 30-꼭짓점 헬리컬 링에서 두 꼭짓점 사이의 거리로 나타난다. 이러한 15개의 서로 다른 4-공간을 통한 피타고라스 거리는 링에서 두 개의 가장 가까운 꼭짓점을 연결하는 120-셀 모서리 길이(#1 현)에서 링에서 두 개의 대척점(가장 먼) 꼭짓점을 연결하는 120-셀 축 길이(지름)(#15 현)까지 다양하다.
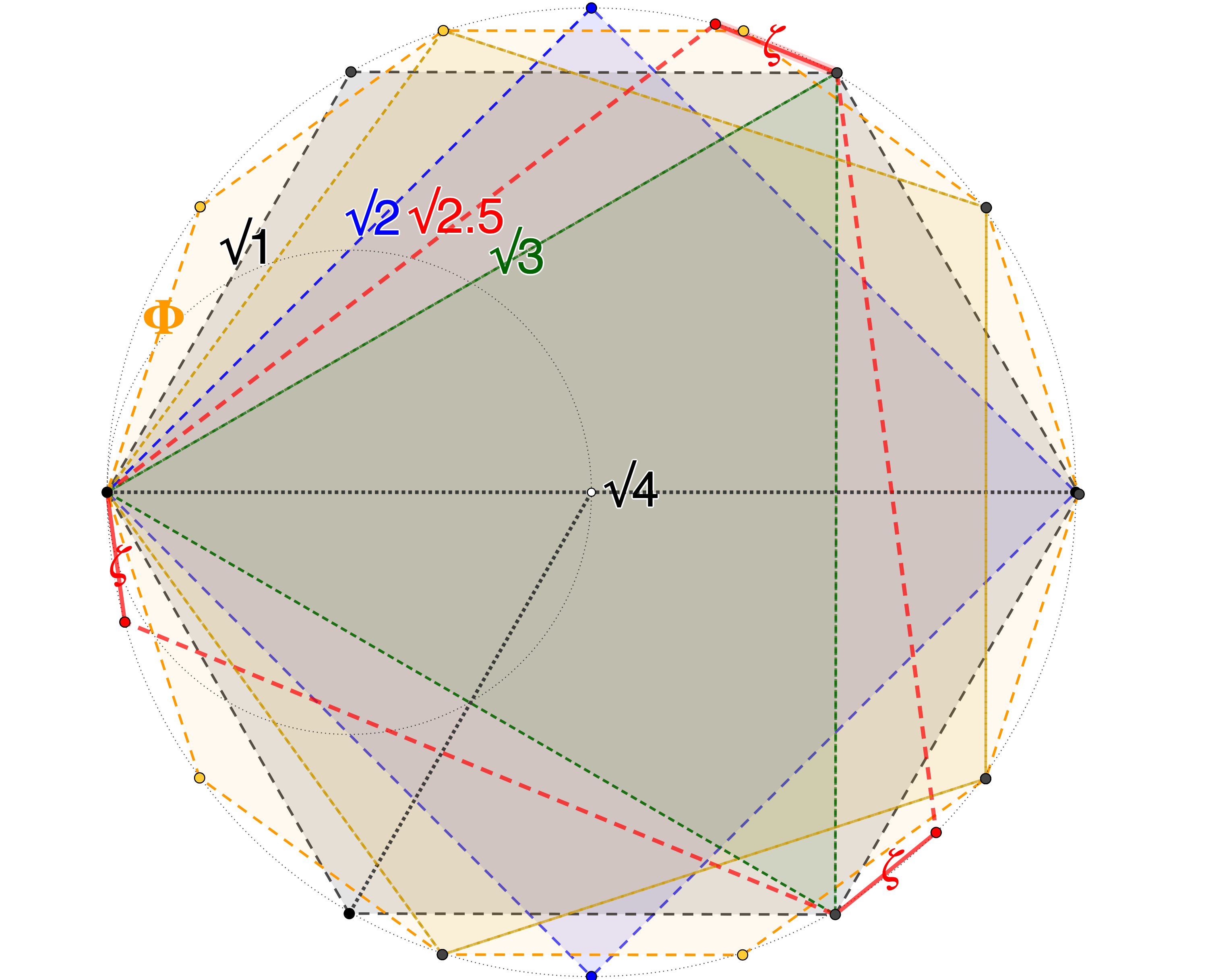
길이 ≈ 0.270인 120-셀 모서리는 불규칙한 큰 육각형에서만 발생하며, 이는 길이 }}의 모서리도 갖는다. 120-셀의 1200개 모서리 자체로는 큰 원 다각형을 형성하지 않지만, 내접된 정규 5-셀의 모서리와 번갈아 가며 400개의 불규칙한 큰 육각형을 형성한다.
120-셀은 또한 별도로 설명된 동일한 중심 평면에서 이러한 여러 큰 원 다각형의 화합물을 포함한다. 화합물의 의미는 120-셀 모서리 및 특성 회전과 같다. 정규 5-셀, 8-셀 초입방체, 24-셀 및 120-셀의 회전은 모두 동일한 회전 평면, 즉 24-셀의 육각형 중심 평면에 놓여 있다.
600점 120-셀은 120점 600-셀의 모든 8개의 서로 다른 현 길이, 두 개의 추가 중요한 현을 갖는다. 즉, 자체적인 더 짧은 모서리와 120개의 내접된 정규 5-셀의 모서리이다. 단위 반지름 120-셀에는 120개의 분리된 정규 5-셀이 내접되어 있다. 모서리 길이는 이다. 5-셀과 120-셀을 제외한 정규 4-포체는 현(#8 현)을 포함하지 않는다.
120-셀에는 10개의 서로 다른 내접된 600-셀이 포함되어 있으며, 이는 두 가지 방법으로 5개의 분리된 600-셀로 간주될 수 있다. 각 현은 분리된 600-셀의 두 꼭짓점을 연결하므로 분리된 24-셀, 8-셀 및 16-셀을 연결한다. 5-셀 모서리와 120-셀 모서리 모두 분리된 600-셀의 꼭짓점을 연결한다. 분리된 600-셀에서 동일한 종류의 해당 다포체는 클리포드 평행이며 떨어져 있다. 각 5-셀은 5개의 분리된 600-셀 각각에서 하나의 꼭짓점을 포함한다.
이 두 개의 추가 현은 120-셀에 특징적인 등각 회전을 제공하며, 1200개의 모서리와 내접된 정규 5-셀의 반대 1200개 모서리의 불변 평면에서 120-셀의 특징적인 등각 회전이 발생한다. 또한 120-셀에 특징적인 큰 원 다각형, 즉 세 개의 120-셀 모서리가 세 개의 5-셀 모서리와 번갈아 가며 나타나는 "불규칙한" 큰 육각형을 제공한다.
2. 4. 내부 다포체 간의 관계
정백이십포체는 다른 정 볼록 4차원 다포체들의 조합으로 구성된다. 정 1-, 2-, 3-, 4차원 다포체 간의 모든 관계는 정백이십포체 내에서 나타난다. 이는 모든 다포체가 부분인 4차원 직소 퍼즐과 같다. 정백이십포체를 구성하는 여러 방법이 있지만, 결국 한 가지 방식으로만 조립된다.정 1-포체는 정백이십포체의 구성 다포체에서 15개의 서로 다른 길이로만 나타난다. 알렉산드로프의 유일성 정리에 따라, 서로 다른 모양의 볼록 다면체는 고유한 거리 공간을 가지므로, 각 정 4차원 다포체는 이 15개 코드의 고유한 부분 집합을 가진다.
정십육포체, 정팔포체, 정이십사포체에서는 이 15개의 코드 중 4개만 나타난다. 4개의 , , , 는 정이십사포체와 그 구성 요소들을 만드는 데 충분하다. 정이십사포체는 이 4개의 코드와 그로부터 만들 수 있는 모든 정다포체의 조합에 대한 고유한 해답이다.
15개의 코드 중 4개가 더 정육백포체를 만드는 데 필요하다. 4개의 는 의 함수인 무리수 분수의 제곱근이다. 정육백포체는 이 8개의 코드와 그로부터 만들 수 있는 모든 정다포체의 조합에 대한 고유한 해답이다. 정이십사포체에서 발생하지 않고 정육백포체에서 발견되는 새로운 부분 중 주목할 만한 것은 오각형과 정이십면체이다.
15개의 모든 코드와 아래에 나열된 15개의 다른 고유한 코드 거리가 정백이십포체에서 나타난다. 정육백포체에서 발생하지 않고 정백이십포체에서 발견되는 새로운 부분 중 주목할 만한 것은 코드]]}}이다. 정오포체(4-심플렉스 정 4차원 다포체)와 다른 정 4차원 다포체 간의 관계는 정백이십포체에서 직접적으로 나타난다. 정백이십포체의 600개 점은 120개의 서로 분리된 5개 점 정오포체의 조합이며, 5개의 서로 분리된 120개 점 정육백포체의 조합이기도 하다(두 가지 방법). 각 정오포체는 5개의 서로 분리된 정육백포체, 따라서 각 5개의 서로 분리된 정이십사포체, 정팔포체, 정십육포체에 하나의 꼭짓점을 가진다. 각 정오포체는 다른 정 4차원 다포체의 각 5개의 서로 분리된 인스턴스를 연결하는 고리이다(두 가지 방법).
2. 5. 사면체로 감소된 120-포체
600개의 점을 가진 120-포체는 5개의 서로소인 내접 600-포체를 가지고 있으므로, 그 중 하나인 120개의 점을 가진 600-포체를 제거하여 불규칙한 480개의 점을 가진 4-포체를 만들 수 있다. 120-포체의 각 십이면체 셀은 20개의 꼭지점 중 4개를 제거하여 사면체 감소 십이면체라고 하는 불규칙한 16개의 점을 가진 다면체를 만든다. 이는 제거된 4개의 꼭지점이 십이면체에 내접한 사면체를 형성하기 때문이다. 십이면체의 꼭짓점 도형이 삼각형이므로, 각 절단된 꼭짓점은 삼각형으로 대체된다. 12개의 오각형 면은 각 오각형의 한 꼭짓점이 제거되고 두 모서리가 오각형의 대각선 현으로 대체되므로 12개의 사다리꼴로 대체된다. 사면체 감소 십이면체는 16개의 꼭짓점과 16개의 면을 갖는다: 12개의 사다리꼴 면과 4개의 정삼각형 면.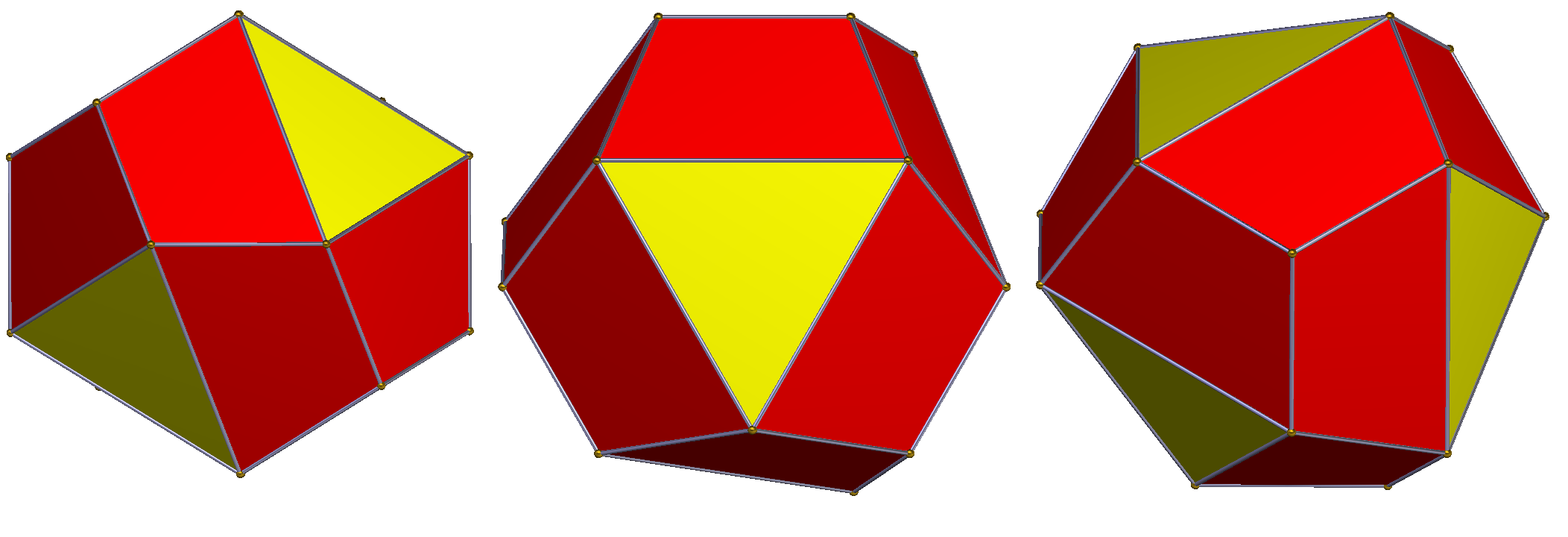
120-포체의 꼭짓점 도형이 사면체이므로, 각 절단된 꼭짓점은 사면체로 대체되어 120개의 사면체 감소 십이면체 셀과 120개의 정사면체 셀이 남는다. 정십이면체와 사면체 감소 십이면체는 모두 30개의 모서리를 가지며, 정 120-포체와 사면체 감소 120-포체는 모두 1200개의 모서리를 갖는다.
'''480개의 점을 가진 감소 120-포체'''는 셀이 사면체로 감소되었기 때문에 '''사면체 감소 120-포체''', 꼭짓점이 120-포체에 내접한 600-포체를 형성했기 때문에 '''600-포체 감소 120-포체''', 또는 120개의 꼭짓점을 제거하면 120개의 내접 정 5-포체 각각에서 한 꼭짓점이 제거되어 120개의 정사면체가 남기 때문에 '''정 5-포체 감소 120-포체'''라고 부를 수 있다.
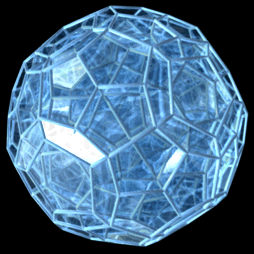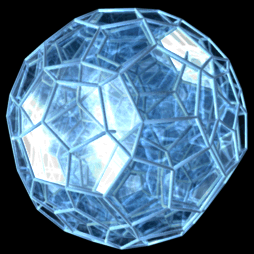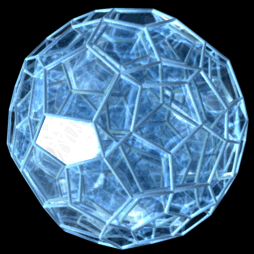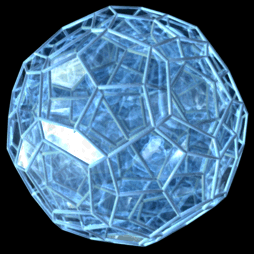
3. 투영
120-포체는 120개의 십이포체 세포로 구성된다. 십이포체는 마주보는 평행한 면을 가지는데, 이는 초정육포체와 24-포체의 세포와 공유하는 특징이다. 십이포체는 4번째 방향으로 구부러진 직선으로 면 대 면으로 쌓아 10개의 세포를 둘레로 하는 대원을 만들 수 있다. 이 10-세포 구조로부터 층상 입체 투영과 얽혀 있는 고리 구조(이산 호프 올림)를 사용한 두 가지 시각화 방법을 사용할 수 있다.
3. 1. 슐레겔 도표
3. 2. 입체 투영
세포 위치는 초구적 묘사에 적합하다. 임의의 십이면체를 선택하고 "북극"이라고 명명한다. 12개의 대원 경선(세포 4개 길이)이 3차원에서 방사상으로 뻗어나가 다섯 번째 "남극" 세포에서 수렴한다. 이 골격은 120개의 세포 중 50개(2 + 4 × 12)를 차지한다.북극에서 시작하여 9개의 위도층으로 정백이십포체를 구성할 수 있다. 이는 지구의 2-구면 지형을 암시한다. 극점을 제외하고 각 층의 세포 중심점은 별도의 2-구면에 위치하며, 적도 중심점은 대 2-구면에 위치한다. 30개의 적도 세포의 중심점은 정이십면십이면체의 꼭짓점을 형성하며, 위에서 설명한 경선은 각 오각형 면의 중심을 통과한다.
| 층 # | 세포 수 | 설명 | 위도 | 지역 |
|---|---|---|---|---|
| 1 | 세포 1개 | 북극 | 0° | 북반구 |
| 2 | 세포 12개 | 첫 번째 경선 세포층 / "북극권" | 36° | |
| 3 | 세포 20개 | 비경선 / 간질 | 60° | |
| 4 | 세포 12개 | 두 번째 경선 세포층 / "북회귀선" | 72° | |
| 5 | 세포 30개 | 비경선 / 간질 | 90° | 적도 |
| 6 | 세포 12개 | 세 번째 경선 세포층 / "남회귀선" | 108° | 남반구 |
| 7 | 세포 20개 | 비경선 / 간질 | 120° | |
| 8 | 세포 12개 | 네 번째 경선 세포층 / "남극권" | 144° | |
| 9 | 세포 1개 | 남극 | 180° | |
| 합계 | 세포 120개 | colspan="3" | |
2, 4, 6, 8층의 세포는 극점 세포의 면 위에 위치한다. 3층과 7층의 세포는 극점 세포의 꼭짓점 바로 위에 위치한다. 5층의 세포는 극점 세포의 모서리 위에 위치한다.
3. 3. 원근 투영
4차원 정백이십포체의 단순 회전을 수행하는 4차원 정백이십포체의 3차원 투영은 다음과 같다.| 4차원 정백이십포체의 단순 회전을 수행하는 4차원 정백이십포체의 3차원 투영 | |
|---|---|
 |  |
| 4차원 공간의 3-구 외부에서 본 모습. | 3-구의 3차원 표면 내부. |
이 렌더링에서는 정백이십포체의 모서리만 나타나며, 다른 모든 현은 표시되지 않는다. 정백이십포체의 복잡한 내부 부분은 모든 그림에서 완전히 보이지 않는다.
이러한 투영은 4차원의 특정 시점에서 원근 투영을 사용하여 모델을 3차원 그림자로 투영한다. 따라서 더 크게 보이는 면과 셀은 4차원 시점에 더 가까울 뿐이다.
슐레겔 도표는 특정 셀의 ''위''에 있는 시점을 선택하여 평평해진 차원의 깊이를 보여주기 위해 원근법을 사용하며, 따라서 해당 셀을 모델의 외피로 만들고, 다른 셀이 그 안에 더 작게 나타나도록 한다. 입체 투영은 동일한 접근 방식을 사용하지만, 구형 다포체를 3-구의 타일링으로 나타내면서 곡선 모서리로 표시된다.
| 투영 | 십이면체 | 정백이십포체 |
|---|---|---|
| 슐레겔 도표 | 평면에 12개의 오각형 면 |  3차원 공간에 120개의 십이면체 셀 |
| 입체 투영 | 투명한 면 포함 |
| 향상된 원근 투영 | |
|---|---|
| 중심에서 꼭짓점까지의 거리의 5배 거리에서 셀 우선 원근 투영 | |
| 중심에서 꼭짓점까지의 거리의 5배 거리에서 꼭짓점 우선 원근 투영 | |
3. 4. 직교 투영
120-포체의 직교 투영은 특정 시야 방향에 대한 두 개의 정규 직교 기저 벡터를 정의하여 2D로 수행할 수 있다. 30각 투영은 1963년 B. L. 칠튼에 의해 제작되었다. H3 십각형 투영은 반 오스 다각형의 평면을 보여준다.| H4 | - | F4 |
|---|---|---|
 [30] (Red=1) |  [20] (Red=1) |  [12] (Red=1) |
| H3 | A2 / B3 / D4 | A3 / B2 |
 [10] (Red=5, orange=10) |  [6] (Red=1, orange=3, yellow=6, lime=9, green=12) |  [4] (Red=1, orange=2, yellow=4, lime=6, green=8) |
3차원 직교 투영 또한 세 개의 정규 직교 기저 벡터를 사용하여 3D 모델로 만들고, 2D 이미지에 대한 특정 원근법을 투영하여 만들 수 있다.
 3D 등각 투영 |  애니메이션 4D 회전 |
4. 관련 다포체 및 벌집
4. 1. H₄ 다포체
120-포체는 H4 대칭 [3,3,5]를 갖는 15개의 정다포체 및 균일 다포체 중 하나이다.| H4 고른 다포체 군 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
4. 2. {p,3,3} 다포체
120-포체는 세 개의 정다포체와 유사하다. 5-포체 {3,3,3}와 유클리드 4차원 공간의 초정육면체 {4,3,3}, 그리고 쌍곡 공간의 육각형 타일 벌집 {6,3,3}이 있다. 이들 모두는 사면체 꼭짓점 도형 {3,3}을 갖는다.| 볼록 고른 다포체 | 유클리드 고른 벌집 | 쌍곡 고른 벌집 |
|---|---|---|
| 120px120px120px120px | 120px120px120px120px | 120px120px120px120px |
| {3,3,3} | {4,3,3} | {6,3,3} |
4. 3. {5,3,p} 다포체
정백이십포체는 십이면체 세포를 가진 4차원 다포체 및 벌집의 시퀀스 중 일부이다.| 차원 | 그림 | 이름 | 슐레플리 기호 | 콕서터 다이어그램 | 정점 | 변 | 면 | 세포 |
|---|---|---|---|---|---|---|---|---|
| 3 | 120px | {5,3,5} | ∞ | ∞ | ∞ | ∞ | ||
| 4 | 120px | {4,3,3} | 16 | 32 | 24 | 8 | ||
| 4 | 120px | {5,3,3} | 600 | 1200 | 720 | 120 | ||
| 4 | 120px | {3,3,3} | 5 | 10 | 10 | 5 | ||
| 4 | 120px | {3,3,4} | 8 | 24 | 32 | 16 | ||
| 4 | 120px | {3,4,3} | 24 | 96 | 96 | 24 | ||
| 4 | 120px | {3,3,5} | 120 | 720 | 1200 | 600 |
5. 한국과의 관련성
참조
[1]
서적
Geometries and Transformations
2018
[2]
서적
The Geometry of Art and Life
1977
[3]
서적
Mathematics and Its History
2010
[4]
서적
Symmetrical Hamiltonian manifolds on regular 3D and 4D polytopes
https://archive.brid[...]
Mathartfun.com
2005-07
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com