십각형

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정십각형
3. 대칭
4. 분할
5. 엇각 십각형
6. 기타 십각형 관련 사항
참조

1. 개요

십각형은 열 개의 변과 꼭짓점을 가진 다각형을 의미하며, 특히 모든 변의 길이가 같고 내각이 144°인 정십각형을 가리킨다. 정십각형은 슐레플리 기호 {10}으로 나타내며, 절단된 오각형으로도 구성할 수 있다. 넓이는 변의 길이, 내접원 또는 외접원의 반지름을 이용하여 계산할 수 있으며, 자와 컴퍼스로 작도가 가능하다. 정십각형은 Dih₁₀ 대칭을 가지며, 평행사변형으로 분할되거나 다양한 고차원 다포체의 페트리 다각형으로 나타날 수 있다. 엇각 십각형은 동일 평면에 존재하지 않는 십각형으로, 오각 기둥 반대 다면체 등에서 볼 수 있다. 십각형은 판크라스 격투기 링, 기리 타일, 소설, 건축물 등 다양한 분야에서 활용된다.

더 읽어볼만한 페이지

10 - 데카폴
10 - 마갈궁
마갈궁은 염소와 물고기 꼬리 형상의 별자리로, 힌두교 신화의 괴어 마카라를 의미하며 인도 점성술에서 유래하여 동아시아에 전해져 토성의 거주지로 여겨지고 인도에서는 축제로 기념된다.
작도가능한 다각형 - 정삼각형
정삼각형은 세 변의 길이가 같고 모든 내각이 60°인 삼각형으로, 이등변삼각형의 특수한 형태이며 내심, 외심, 무게중심이 일치하는 특징을 가진다.
작도가능한 다각형 - 오각형
다섯 변으로 이루어진 다각형인 오각형은 변의 길이와 각의 크기가 모두 같은 정오각형을 포함하며, 정오각형은 컴퍼스와 자로 작도할 수 있고 자연에서도 발견된다.
변의 수에 따른 다각형 - 오각형
다섯 변으로 이루어진 다각형인 오각형은 변의 길이와 각의 크기가 모두 같은 정오각형을 포함하며, 정오각형은 컴퍼스와 자로 작도할 수 있고 자연에서도 발견된다.
변의 수에 따른 다각형 - 육각형
육각형은 여섯 변과 꼭짓점으로 이루어진 다각형으로, 특히 모든 변과 각이 같은 정육각형은 평면 테셀레이션이 가능하고 벌집 구조, 건축, 자연 현상, 한국 전통 문양 등 다양한 분야에서 활용된다.

십각형
십각형 정보
정십각형
변	10
꼭짓점	10
슐레플리 기호	{10}
성질	볼록, 주기적
정십각형의 정보
내각	144°
성질	볼록
면적
공식	(5/2) * a^2 * cot(π/10) = (5/2) * a^2 * √(5 + 2√5) ≒ 7.694208843 * a^2 (a는 변의 길이)
작도
십각형 작도

2. 정십각형

정'''정십각형'''은 모든 변의 길이가 같고, 모든 내각의 크기가 같은 십각형이다. 정십각형의 한 내각의 크기는 144°이며, 중심각과 외각은 36°이다.^[1] 슐레플리 기호는 {10}이며,^[2] 절단된 오각형, t{5}으로도 구성할 수 있다.

십각형은 종종 (부분적인) 5겹 대칭을 가진 타일링에 나타난다.

: $\cos\frac{2\pi}{10} = \cos\frac{\pi}{5} =\cos 36^\circ=\frac{\sqrt5+1}{4}$

정십각형은 작도가능한 다각형으로, 컴퍼스와 자를 사용하여 작도할 수 있다. 정오각형을 작도한 후, 각 꼭짓점에서 외접원의 중심을 잇는 반직선을 그려 새로운 꼭짓점을 찾고, 이들을 연결하여 정십각형을 작도할 수 있다.^[4]

2. 1. 넓이

한 변의 길이가 ''a''인 정십각형의 넓이 ''A''는 다음과 같다.^[3]

:A^영어 = 2.5a2 cot|π/10^영어 = 2.5a2 √(5 + 2√5)^영어 ≈ 7.694208843a^2

아포테마(내접원의 반지름) ''r''을 사용하면, 넓이는 다음과 같다.

:A^영어 = 10tan|π/10^영어 r2^영어 = 2r2√(5(5 - 2√5))^영어 ≈ 3.249196962r^2

외접원의 반지름 ''R''을 사용하면, 넓이는 다음과 같다.

:A^영어 = 5sin|π/5^영어 R2^영어 = 2.5R2√(5 - √5)/2^영어 ≈ 2.938926261R^2

다른 공식은 A = 2.5da^영어인데, 여기서 ''d''는 평행한 변 사이의 거리, 즉 십각형이 한 변을 밑변으로 세워져 있을 때의 높이, 또는 십각형의 내접원의 지름이다. 간단한 삼각법에 의해,

:d = 2a(cos(3π/10) + cos(π/10))^영어

그리고 이것은 대수식으로 다음과 같이 쓸 수 있다.

:d = a√(5 + 2√5)^영어

정십각형의 경우, 중심각과 외각은 36 °이며, 내각은 144°가 된다.

2. 2. 한 변의 길이와 외접원의 반지름

정십각형에서 한 변의 길이

a

와 외접원의 반지름

R

사이의 관계를 나타낸 그림이다.

삼각형 $E_{10}E_1M$ 은 길이가 $R$ 인 두 변과 길이 $a$ 인 밑변을 가진 이등변삼각형이다.
반지름이 $a$ 인 원을 $E_1$ 을 중심으로 그리면, 이 원은 선분 $]M\,E_{10}[$ 과 점 $P$ 에서 만난다. (그림에는 표시되지 않음).
삼각형 ${E_{10}E_1P}\;$ 는 꼭짓점 $E_1$ 에서 밑각 $m\angle E_1 E_{10} P = m\angle E_{10} P E_1 = 72^\circ \;$ 를 갖는 이등변삼각형이다.
따라서 $m\angle P E_1 E_{10} = 180^\circ -2\cdot 72^\circ = 36^\circ \;$ 이다. 또한 $\; m\angle M E_1 P = 72^\circ- 36^\circ = 36^\circ\;$ 이므로, $\; E_1 M P\;$ 는 꼭짓점 $P$ 를 갖는 이등변삼각형이다. 이 삼각형의 다리 길이는 $a$ 이므로, 선분 $[P\,E_{10}]$ 의 길이는 $R-a$ 이다.
이등변삼각형 $E_{10} E_1 M\;$ 과 $P E_{10} E_1\;$ 은 꼭짓점에서 같은 각도 36°를 가지므로 닮음이다. 따라서 $\;\frac{a}{R}=\frac{R-a}{a}$ 이다.
위 식에서 $R,a >0$ 이므로, 양변에 $Ra$ 를 곱하면 이차방정식 $\;a^2=R^2-aR\;$ 을 얻는다.
이 이차방정식에서 변의 길이 $a\,$ 에 대한 양의 해는 $\;a=\frac{R}{2}(-1+\sqrt{5})$ 이다.

따라서 정십각형은 자와 컴퍼스로 작도할 수 있다.

;추가 결론:

\;R=\frac{2a}{\sqrt{5}-1}=\frac{a}{2}(\sqrt{5}+1)\;

이고, 삼각형

\Delta\,E_{10} E_1 M\,

의 높이(즉,

[M\,D]

의 길이)는

h = \sqrt{R^2-(a/2)^2}=\frac{a}{2}\sqrt{5+2\sqrt{5}}\;

이며, 삼각형의 면적은

A_\Delta=\frac{a}{2}\cdot h = \frac{a^2}{4}\sqrt{5+2\sqrt{5}}

이다.

외접원과 변의 길이가 주어졌을 때, 십각형 작도에서 황금비는 선분을 외분하는 결정적인 요소가 된다.

주어진 외접원을 이용하여 작도할 때, G를 중심으로 하고 반지름이 인 원호는 황금비에 따라 선분 를 나눈다.

:

\frac{\overline{AM}}{\overline{MH}} = \frac{\overline{AH}}{\overline{AM}} = \frac{1+ \sqrt{5}}{2} = \Phi \approx 1.618 \text{.}

주어진 변의 길이를 이용하여 작도할 때,^[6] D를 중심으로 하고 반지름이 인 원호는 황금비에 따라 선분 를 나눈다.

:

\frac{\overline{E_1 E_{10}}}{\overline{E_1 F}} = \frac{\overline{E_{10} F}}{\overline{E_1 E_{10}}} = \frac{R}{a} = \frac{1+ \sqrt{5}}{2} =\Phi \approx 1.618 \text{.}

정십각형에서 한 변의 길이와 외접원의 반지름의 비는 황금비이다. 외접원의 반지름을 ''R'', 한 변의 길이를 ''a''라고 할 때,

\;R=\frac{2a}{\sqrt{5}-1}=\frac{a}{2}(\sqrt{5}+1)\;

관계가 성립한다.

2. 3. 작도

정십각형은 작도가능한 다각형으로, 컴퍼스와 자를 사용하여 작도할 수 있다. 정오각형을 작도한 후, 각 꼭짓점에서 외접원의 중심을 잇는 반직선을 그려 새로운 꼭짓점을 찾고, 이들을 연결하여 정십각형을 작도할 수 있다.^[4]

정십각형을 작도하는 방법은 다음과 같다.

1. 정오각형 작도 방법을 이용하여 원 안에 정오각형을 작도한다.

2. 정오각형의 각 꼭짓점에서 원의 중심을 지나 원의 반대편까지 선을 연장한다. 이때 각 선이 원과 만나는 지점이 정십각형의 꼭짓점이 된다.

3. 정오각형의 다섯 꼭짓점과 새로 생긴 꼭짓점을 번갈아 연결하면 정십각형이 완성된다.

이는 정오각형을 점대칭으로 중심에 대해 대칭 이동하면 중심이 같은 ''합동''인 오각형이 되고, 두 오각형이 총 십각형의 꼭짓점을 이루기 때문이다.^[4]

3. 대칭

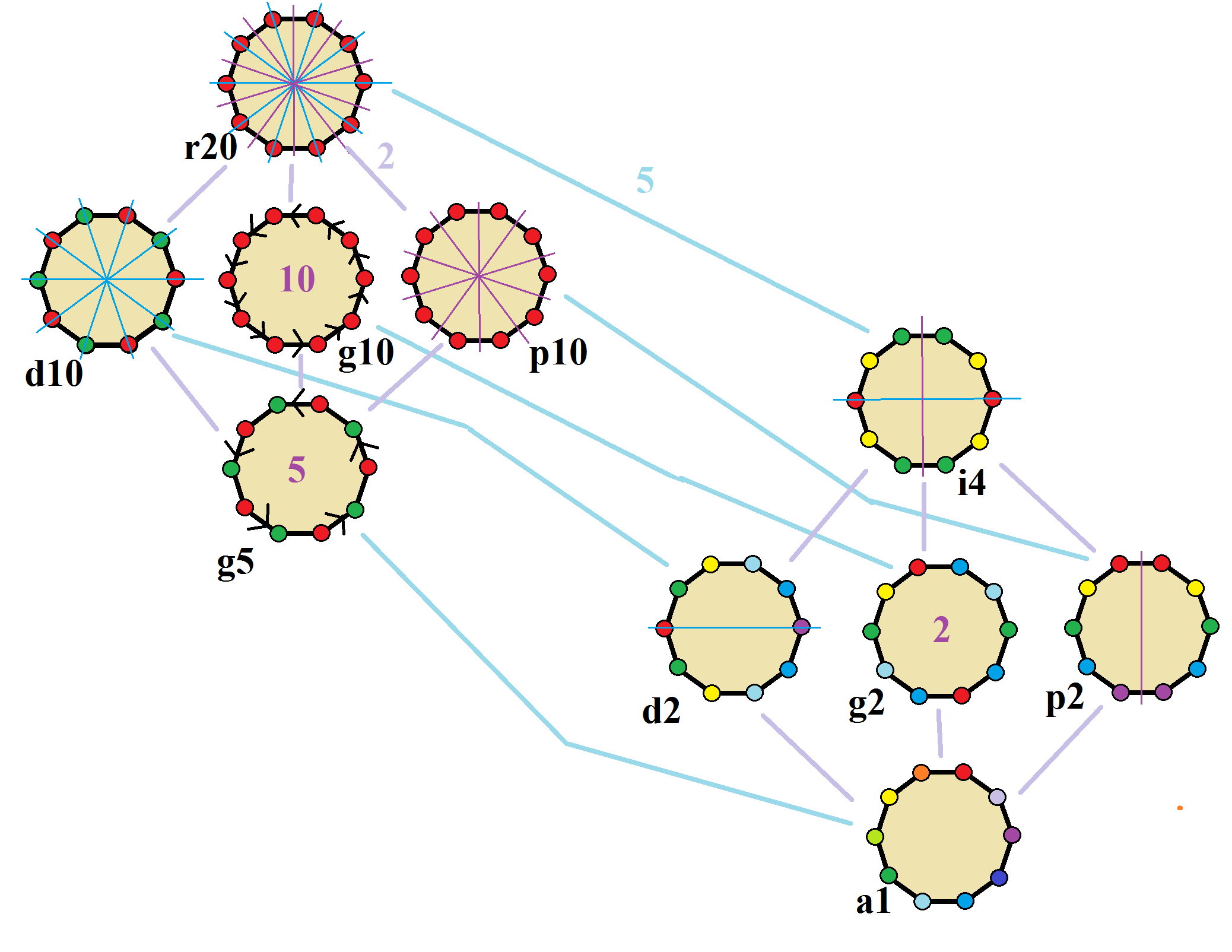
정십각형의 대칭. 꼭짓점은 대칭 위치에 따라 색상이 지정되어 있으며, 파란색 거울은 꼭짓점을, 보라색 거울은 변을 통과한다. 회전 차수는 중앙에 표시되어 있다.

정십각형은 20차 Dih₁₀ 대칭을 가진다. Dih₅, Dih₂, Dih₁의 3개의 부분군 이면각 대칭과 Z₁₀, Z₅, Z₂, Z₁의 4개의 순환군 대칭이 있다.

이 8개의 대칭은 십각형에서 10개의 서로 다른 대칭으로 볼 수 있는데, 이는 반사선이 꼭짓점 또는 변을 통과할 수 있기 때문이다. 존 콘웨이는 이를 문자와 군의 차수로 표기한다.^[7] 정규 형태의 전체 대칭은 '''r20'''이며, 대칭이 없는 것은 '''a1'''로 표기된다. 이면각 대칭은 꼭짓점을 통과하는지('''d'''는 대각선), 변을 통과하는지('''p'''는 수직), 또는 변과 꼭짓점 모두를 통과하는지('''i''')에 따라 구분된다. 중간 열의 순환 대칭은 중심 회전 차수에 따라 '''g'''로 표기된다.

각 부분군 대칭은 불규칙한 형태에 대해 하나 이상의 자유도를 허용한다. '''g10''' 부분군만이 자유도가 없지만 유향 변으로 볼 수 있다.

가장 높은 대칭 불규칙 십각형은 긴 변과 짧은 변이 번갈아 나타날 수 있는 5개의 거울로 구성된 등각 십각형인 '''d10'''과, 변의 길이는 같지만 꼭짓점이 두 개의 서로 다른 내부 각도를 번갈아 나타내는 등축 십각형인 '''p10'''이다. 이 두 형태는 서로의 쌍대 다각형이며 정십각형 대칭 차수의 절반을 갖는다.

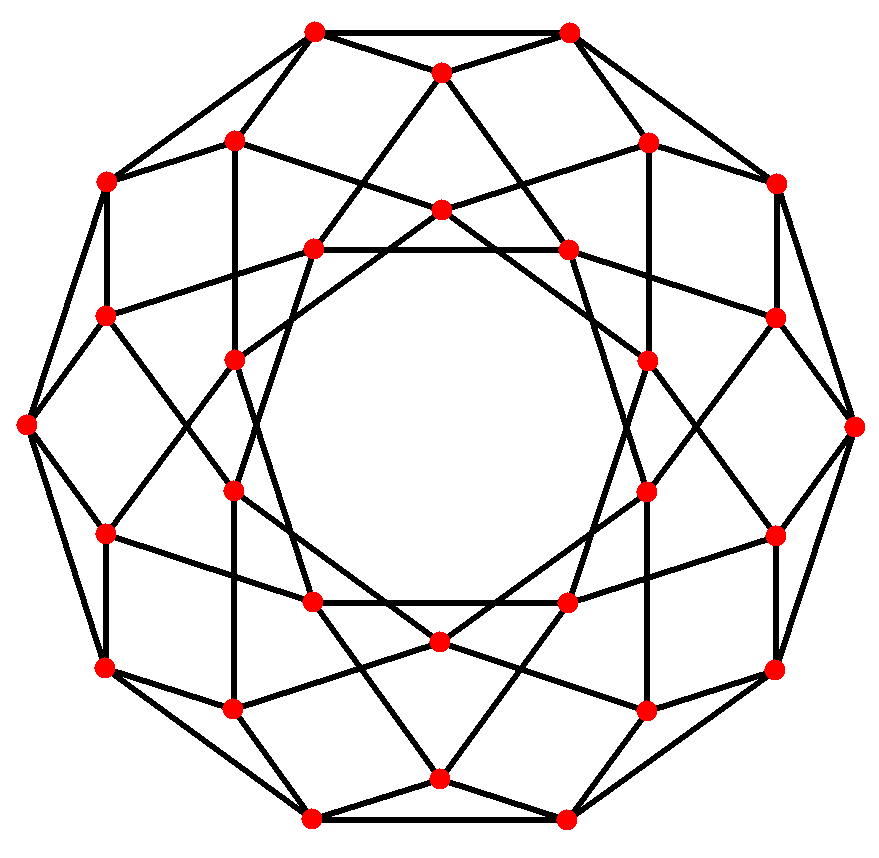
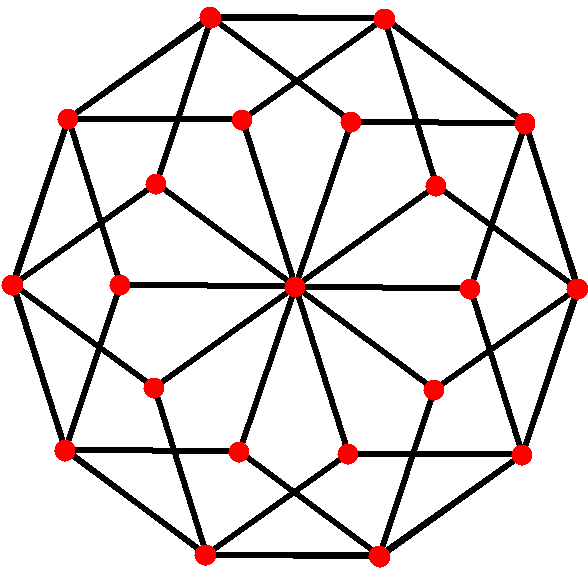
4. 분할

정십각형은 10개의 마름모로 분할할 수 있다. 이는 5-정육면체의 페트리 다각형 투영 평면에서 80개의 면 중 10개로 볼 수 있다. 코셰터는 모든 존오곤(마주보는 변이 평행하고 길이가 같은 2''m''각형)이 ''m''(''m''-1)/2 개의 평행사변형으로 분할될 수 있다고 말한다.^[8] 특히, 이는 짝수 개의 변을 가진 정다각형에 적용되며, 이 경우 평행사변형은 모두 마름모꼴이다. 정''십각형''의 경우, ''m''=5이며, 10개의 마름모로 나눌 수 있다. 이 분해는 마름모 삼십면체의 30개 면 중 10개를 기반으로 한다.

10개의 마름모로 분할된 정십각형
5-정육면체

5. 엇각 십각형

'''엇각 십각형'''은 동일 평면에 존재하지 않는 10개의 꼭짓점과 모서리를 가진 엇각 다각형이다. 이러한 십각형의 내부는 일반적으로 정의되지 않는다. '''엇각 지그재그 십각형'''은 두 개의 평행한 평면 사이에서 꼭짓점이 번갈아 나타난다.

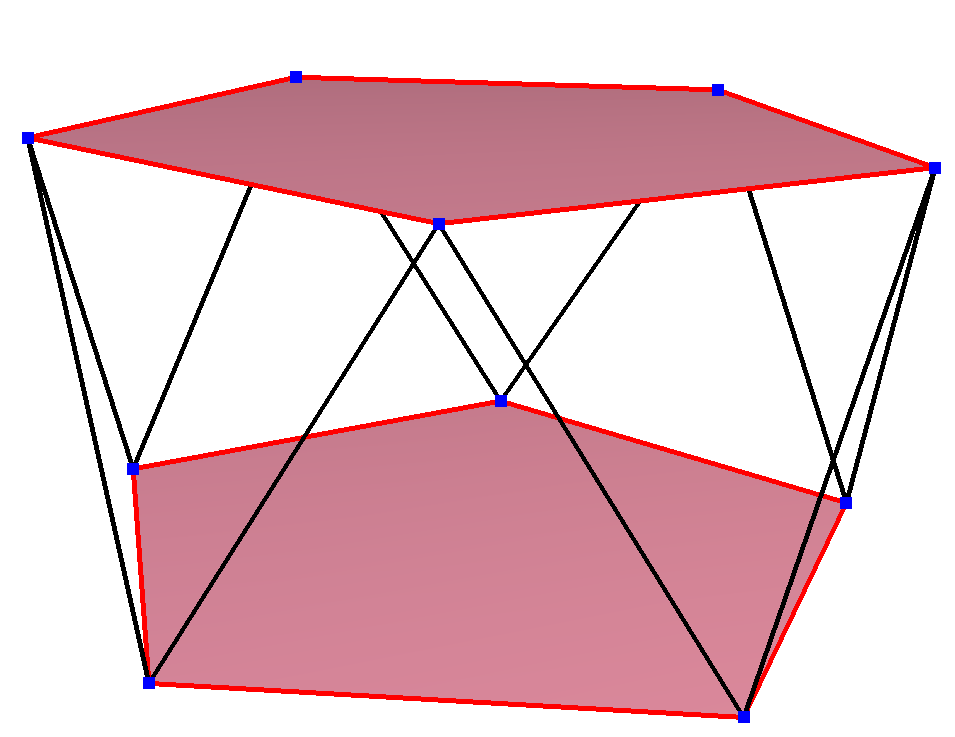
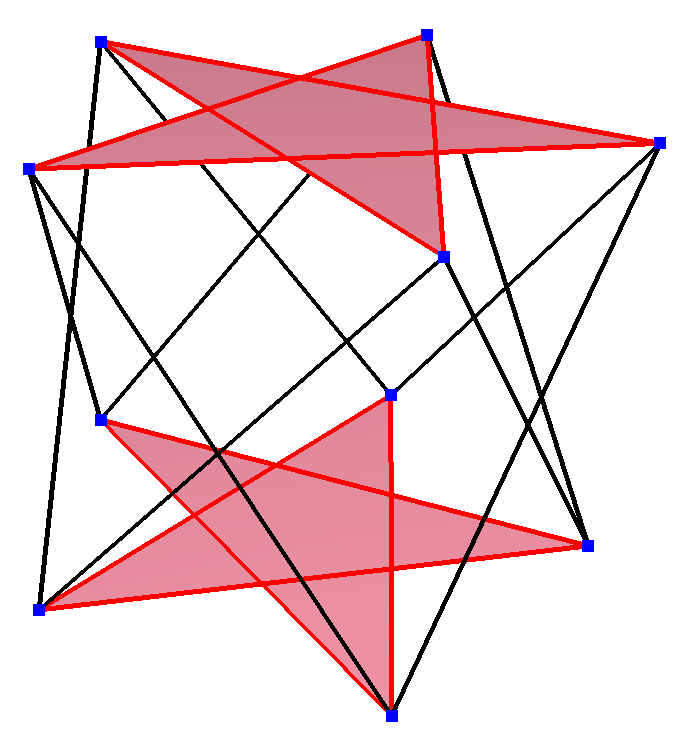
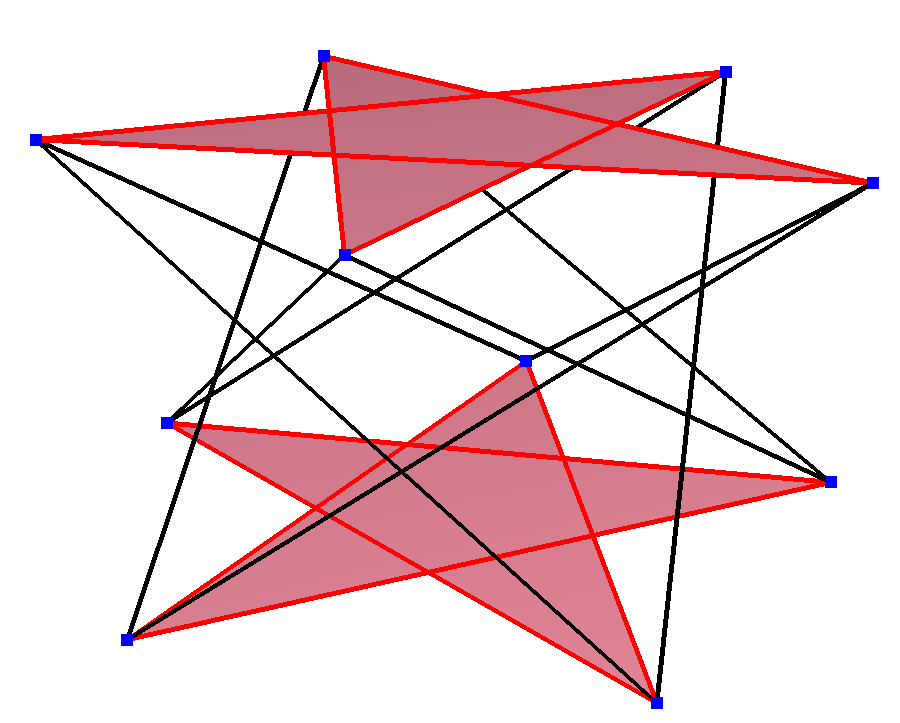
'''정규 엇각 십각형'''은 꼭짓점-추이적이며 모서리 길이가 같다. 3차원에서는 지그재그 엇각 십각형이 되며, 동일한 D_5d, [2⁺,10] 대칭, 차수 20을 가진 오각 기둥 반대 다면체, 오각 별 기둥 반대 다면체, 오각 별 교차 반대 다면체의 꼭짓점과 옆면 모서리에서 볼 수 있다.

3개의 정규 엇각 지그재그 십각형
{5}#{ }	{5/2}#{ }	{5/3}#{ }

정규 엇각 십각형은 오각 기둥 반대 다면체, 오각 별 기둥 반대 다면체, 오각 별 교차 반대 다면체의 지그재그 모서리로 볼 수 있다.

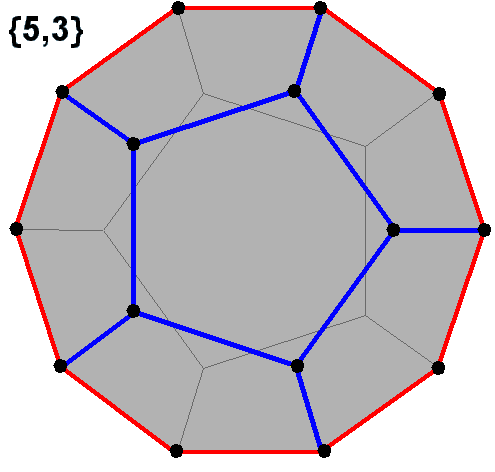
이들은 또한 이십면체 대칭을 가진 다음 네 개의 볼록 다면체에서도 볼 수 있다. 이러한 투영의 둘레에 있는 다각형은 정규 엇각 십각형이다.

5-겹 축에 대한 다면체의 직교 투영
정십이면체	정이십면체	이십이면체	마름모 삼십면체

6. 기타 십각형 관련 사항

일본의 종합 격투기 단체인 판크라스 등에서 사용되는 철망으로 만들어진 십각형 링(케이지)을 "데카곤"이라고 부른다.^[10]
기리 타일(英語版)은 이슬람 건축에서 바닥이나 벽 등을 타일로 덮을 때 사용되는 5가지 타일 패턴 중 하나이며, 그 중 십각형이 존재한다.
아야츠지 유키토의 추리 소설 『십각관의 살인』에는 십각형 건물이 등장한다.^[10]
나고야시 미나토구에 있는 "라라포토 나고야 미나토 아클루스"의 야외 무대 지붕이 십각형인 것에서 "데카곤"이라고 불린다.
대한민국의 종합격투기 단체 ROAD FC 또한 정십각형 형태의 링을 사용한다.

참조

_[1] 서적 The A to Z of Mathematics: A Basic Guide https://books.google[...] John Wiley & Sons
_[2] 서적 Polyhedron Models https://books.google[...] Cambridge University Press
_[3] 서적 The elements of plane and spherical trigonometry https://books.google[...] Society for Promoting Christian Knowledge
_[4] 서적 Geometric Construction of the Regular Decagon and Pentagon Inscribed in a Circle https://books.google[...] The Open Court Publishing Co.
_[5] 서적 Euclid's Plane Geometry, Books III–VI, Practically Applied, or Gradations in Euclid, Part II https://books.google[...] London: Simpkin, Marshall,& CO. 2016-02-10
_[6] 간행물 Regelmäßiges Zehneck, → 3. Section "Formeln, Ist die Seite a gegeben ..." http://www.mathemati[...] 2016-02-10
_[7] 서적 The Symmetries of Things
_[8] 문서 Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
_[9] 문서 Coxeter, Regular polytopes, 12.4 Petrie polygon, pp. 223-226.
_[10] 웹사이트 『十角館の殺人』綾辻行人 http://www.webdoku.j[...] WEB本の雑誌 2018-08-29

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com