일반 상대성이론

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

일반 상대성이론은 1915년 알베르트 아인슈타인이 발표한 중력 이론으로, 시공간의 기하학적 구조를 통해 중력을 설명한다. 뉴턴의 만유인력의 법칙을 대체하며, 빛의 굴절, 중력 적색편이, 천체의 궤도 변화 등 다양한 현상을 예측하고 설명한다. 일반 상대성이론은 고전 역학의 한계를 극복하고 특수 상대성이론과 일관성을 유지하며, 중력파의 존재를 예측하는 등 천체물리학과 우주론 발전에 기여했다. 현재까지 실험적으로 검증되었지만, 양자 이론과의 통합, 암흑 에너지 및 암흑 물질 문제 등 해결해야 할 과제도 남아있다.

더 읽어볼만한 페이지

1915년 과학 - 1915년 2월 14일 일식
1915년 2월 14일 일식은 금환 일식이며, 반년 주기, 메토닉 주기, 사로스 주기, 이넥스 주기의 일부로 다양한 시간대와 매개변수를 갖는다.
1915년 과학 - 1915년 8월 10일 일식
1915년 8월 10일에 발생한 금환 일식은 크기 1.0397, 가림 1.0421, 감마 0.2083, 중심 시간 03:25:15.7 UT, 사로스 주기 145의 매개변수를 가졌으며, 중국 동반부, 한반도, 일본 등에서 부분 일식으로, 금환대는 태평양, 하와이, 괌, 오가사와라 제도 하하지마섬 등에서 관측되었다.
알베르트 아인슈타인 - 광전 효과
광전 효과는 빛이 물질에 닿을 때 전자가 방출되는 현상으로, 빛 에너지가 광자라는 덩어리로 양자화되어 있고, 아인슈타인의 광양자 가설로 설명되며, 다양한 기술에 응용되지만 문제도 야기한다.
알베르트 아인슈타인 - 보스-아인슈타인 응축
보스-아인슈타인 응축은 극저온에서 보존 입자들이 가장 낮은 에너지 상태로 응축되어 새로운 물질 상을 형성하는 현상으로, 1995년 실험적으로 관측되어 노벨 물리학상을 수상했으며, 초유체 현상과 같은 특이한 양자 현상을 보이며 다양한 분야에서 응용 가능성을 가진다.
중력 - 중력 가속도
중력 가속도는 물체가 중력에 의해 가속되는 정도를 나타내는 값으로, 자유 낙하하는 물체의 가속도와 같으며, 지구의 경우 자전에 의한 원심력으로 인해 적도에서 가장 작고 극에서 가장 크게 나타난다.
중력 - 만유인력의 법칙
만유인력의 법칙은 모든 질량을 가진 물체들이 서로를 끌어당기는 힘에 대한 법칙으로, 뉴턴은 질량에 비례하고 거리의 제곱에 반비례한다는 것을 제시했으며, 케플러의 행성 운동 법칙을 설명하고 뉴턴 역학의 기초가 되었으나, 일반 상대성 이론이 등장하면서 저중력 한계로 여겨진다.

일반 상대성이론
일반 상대성이론
개요
분야	중력 이론
기본 정보
발표	1915년
창시자	알베르트 아인슈타인
이전 이론	아이작 뉴턴의 만유인력의 법칙
후속 이론	양자 중력 (미완성)
주요 내용
기본 가정	등가 원리
시공간	시공간의 곡률
중력	시공간의 곡률에 의한 효과
수학적 기술
주요 방정식	아인슈타인 방정식
관련 개념	텐서 리만 기하학 미분기하학
주요 예측 및 현상
시간 지연	중력장에서의 시간 지연
빛의 휨	중력 렌즈 효과
블랙홀	강력한 중력장
중력파	시공간의 떨림
우주론	우주의 팽창 설명
실험적 검증
아인슈타인의 예측	다양한 실험과 관측으로 검증됨
GPS	GPS 시스템의 정확도에 필수적
응용 분야
천체물리학	블랙홀, 중성자별 연구
우주론	우주의 기원과 진화 연구
GPS 기술	정밀한 위치 정보 제공
미래 기술	중력파를 이용한 새로운 기술 개발 가능성
관련 인물
주요 과학자	알베르트 아인슈타인 카를 슈바르츠실트 조르주 르메트르 로저 펜로즈 스티븐 호킹

2. 역사적 배경

갈릴레오 갈릴레이의 자유낙하 법칙과 요하네스 케플러의 행성운동법칙에서 시작된 중력 연구는, 아이작 뉴턴의 만유인력의 법칙으로 이어졌다. 뉴턴의 만유인력 법칙은 지구에서의 낙하 현상과 행성들의 움직임을 설명했지만, 19세기 말 위르뱅 르베리에가 수성의 근일점 이동 문제를 제기하면서 한계가 드러났다. 또한, 마이클 패러데이가 제안한 장(Field) 개념은 기존의 원격 작용을 대체하며 중력 이론의 수정을 요구했다.^[2]

1905년 알베르트 아인슈타인은 특수 상대성이론을 발표했고, 1908년 헤르만 민코프스키는 4차원 시공간 개념을 도입하여 상대성이론을 체계화했다. 아인슈타인은 1907년 등가원리를 착안, 중력을 시공간의 기하학으로 설명해야 한다는 결론에 도달했다. 1915년, 리만 기하학을 이용하여 일반 상대성 이론을 완성했다.^[3]^[4]^[5]^[6]

일반 상대성 이론은 수성의 근일점 이동 문제를 해결했을 뿐만 아니라, 1919년 아서 스탠리 에딩턴의 1919년 5월 29일 일식 관측 실험을 통해 그 정당성이 입증되었다.

이 실험의 성공은 아인슈타인을 세계적인 과학자로 만들었다.^[11]^[12]^[13]

일반 상대성 이론은 빌럼 더시터르, 알렉산드르 프리드만, 조르주 르메트르 등의 연구를 통해 현대 물리 우주론의 탄생에 기여했다.^[9]^[10] 제2차 세계 대전 이후, 퀘이사, 펄서 등 새로운 천체 발견과 함께 천체 물리학 및 우주론 연구의 핵심 이론으로 자리 잡았다.^[14]^[15]^[16]^[17]

2. 1. 한국 관련 내용

한국에서는 일반 상대성 이론에 대한 연구와 교육이 이루어지고 있다. 1986년 이철훈 교수가 "일반상대론" 교재를 출판하여 일반 상대성 이론의 대중화에 기여했다. 2003년에는 이열 교수가 "시간공간의 물리학" 교재를 통해 일반 상대성 이론을 더욱 쉽게 설명했다.

한국천문연구원(KASI)은 중력파 검출을 위한 국제 협력 연구에 참여하고 있으며, 한국중력파연구협력단(KGWG)은 국내 중력파 연구를 주도하고 있다. 한국과학기술원(KAIST) 등 국내 대학에서도 일반 상대성 이론 및 관련 분야 연구가 활발히 진행되고 있다.

3. 고전 역학에서 일반 상대론으로

16세기 갈릴레오 갈릴레이의 자유낙하 법칙과 요하네스 케플러의 행성운동법칙을 거쳐, 17세기 영국의 아이작 뉴턴은 만유인력의 법칙을 도입하여 자신의 저서 『자연철학의 수학적 원리』에 자세히 설명하였다. 그의 만유인력은 지표면에서의 자유낙하 현상과 태양계 행성들의 운동 규칙을 통합적으로 기술하였다.

만유인력의 법칙은 처음으로 중력에 대하여 수학적으로 체계화된 설명을 제공했을 뿐만 아니라, 19세기까지 태양계 안에서 천체의 운동을 설명하는 데에 매우 성공적이었다. 특히 존 쿠치 애덤스와 위르뱅 르베리에는 천왕성의 궤도로부터 이론적으로 예측되는 미지의 행성의 궤도를 계산하였는데, 이윽고 그 자리에서 1846년 해왕성이 발견되었다.

뉴턴 법칙의 한계로는, 우선 르베리에가 수성의 근일점 이동량이 뉴턴 중력의 예측을 벗어난다는 것을 발견하여 1859년 천문학계에 보고하였다. 그 오차는 100년에 43''(각초, arc second)라는 매우 작은 양이었으나, 만유인력의 수식으로는 이것을 설명할 수 없었다. 이론적으로는, 마이클 패러데이가 제시한 장(Field) 개념이 기존의 원격 작용(Action at a distance)을 대체하면서 오래된 중력 이론 또한 장 이론으로 수정할 필요성이 생겼다.

한편, 1905년 고전 역학과 전자기학끼리 발생하는 모순, 특히 광속의 문제를 해결하려는 과정에서 새로운 역학 체계인 상대성 이론이 등장하였다. 알베르트 아인슈타인의 상대성 원리에 기반하여 전자기학의 맥스웰 방정식의 형태를 관성 좌표계에서 고정시키기 위해 시간과 공간의 개념이 크게 바뀌었다. 이후 1908년 헤르만 민코프스키는 시간과 공간을 합친 4차원 시공간을 도입하여 상대성 이론을 더욱 체계적으로 재구성하였다.

상대성 이론의 성공과 영향력은 지대했다. 그 중 중력, 즉 만유인력 법칙을 상대성 이론으로 재구성하는 것은 가장 어려운 작업이었다. 개념적으로 만유인력 법칙은 장 개념이 아닌 원격 작용, 즉 정보의 즉각적인 전달에 의존하기 때문에 명백히 수정이 필요했지만 단순한 방법의 수정은 매우 엉성했다. 특히 상대성 이론에서 관성이 에너지에 의존한다는 특성으로 인해 모든 물체가 동일한 가속도로 낙하한다는 갈릴레이의 원리를 설명하기 어려웠다.

이러한 난관들에 대해서는 많은 학자들의 다양한 시도가 있었지만 현재까지 그대로 남아있는 유산은 일부이다. 아인슈타인의 경우 1907년 중력장을 좌표계의 가속으로 대체할 수 있다는 등가 원리를 고안해냈고, 이를 바탕으로 했을 때 중력을 기존의 역학적 기술에서 벗어나 시공간의 기하학으로 설명해야 한다는 결론에 도달했다. 따라서 이것을 완전히 기술하기 위해서는 리만 기하학(비유클리드 기하학)이라는 복잡한 수학이 필요했고, 결국 1915년에 이르러 일반 상대성 이론을 완성했다.

일반 상대론은 르베리에가 발견했던 수성의 근일점 운동 편차를 추가 가설 없이 정확하게 설명하는 등 실험적으로도 우월성을 입증하면서 물리학의 새로운 표준 중력 이론으로 자리잡았다. 특히, 1919년 5월 영국의 아서 스탠리 에딩턴 등에 의해 이루어진 개기일식 원정 실험의 성공은 물리학의 세대 교체를 가장 극적으로 보여주는 상징적 장면으로 여겨지며, 아인슈타인을 전례없는 세계적 스타 과학자로 만들어주었다. 일반 상대론은 태양계 내부의 중력 현상을 더욱 완벽하게 설명할 뿐만 아니라, 현대적인 물리 우주론을 탄생시켰다.

일반 상대론은 고전 물리학과의 공통점과 차이점을 살펴봄으로써 이해될 수 있다. 고전 역학과 뉴턴의 중력 법칙이 기하학적 기술을 허용한다는 사실을 확인하고, 이러한 기술과 특수 상대론의 법칙들을 조합하면 일반 상대론을 발견법적으로 유도할 수 있다.

앙리 푸앵카레의 1905년 전자의 역학 이론은 중력을 포함한 모든 힘에 적용된 상대론적 이론이었다. 그는 상대성이론이 "우리의 측정 방법에 기인한 것"이라고 제안했다. 그의 이론에서 그는 중력파가 빛의 속도로 전파된다는 것을 보여주었다.^[2] 곧 아인슈타인은 중력을 자신의 상대론적 틀에 통합하는 방법을 고안하였다. 1907년, 자유 낙하 관찰자를 포함하는 간단한 사고 실험으로 시작하여, 8년에 걸쳐 상대론적 중력 이론을 찾기 위한 탐험을 시작했다. 수많은 우회와 잘못된 시작 끝에 그의 연구는 1915년 11월 프로이센 과학 아카데미에 현재 아인슈타인 장 방정식으로 알려진 것을 발표하는 것으로 절정에 달했는데, 이는 아인슈타인의 일반 상대성이론의 핵심을 이룬다.^[3] 이 방정식은 공간과 시간의 기하학이 존재하는 물질과 방사선의 영향을 받는 방식을 명시한다.^[4] 비유클리드 기하학의 한 버전인 리만 기하학은 아인슈타인이 중력에 대한 자신의 물리적 아이디어를 맞추는 핵심 수학적 틀을 제공하여 일반 상대성이론을 개발하는 데 기여했다.^[5]

아인슈타인 장 방정식은 비선형 미분 방정식이며 풀기 어려운 것으로 여겨진다. 아인슈타인은 이론의 초기 예측을 계산하는 데 근사 방법을 사용했다. 하지만 1916년, 천체물리학자 카를 슈바르츠실트는 아인슈타인 장 방정식의 첫 번째 비자명한 정확한 해인 슈바르츠실트 계량을 발견했다. 이 해는 중력 붕괴의 마지막 단계에 대한 설명과 오늘날 블랙홀로 알려진 객체에 대한 기반을 마련했다. 같은 해, 전하를 띈 객체에 대한 슈바르츠실트 해를 일반화하기 위한 첫 단계가 이루어졌고, 결국 라이스너-노르드스트룀 계량으로 이어졌는데, 이는 현재 전하를 띈 블랙홀과 관련이 있다.^[7] 1917년, 아인슈타인은 자신의 이론을 우주 전체에 적용하여 상대론적 우주론 분야를 시작했다. 그는 당시의 사고방식에 따라 정적인 우주를 가정하고, 기존 장 방정식에 새로운 매개변수인 우주 상수를 추가하여 이러한 관측적 가정을 맞추었다.^[8] 그러나 1929년에 에드윈 허블과 다른 사람들의 연구는 우주가 팽창하고 있음을 보여주었다. 이는 1922년 알렉산드르 프리드만이 발견한 팽창하는 우주론적 해로 쉽게 설명되며, 우주 상수를 필요로 하지 않는다. 조르주 르메트르는 이러한 해를 사용하여 우주가 극도로 뜨겁고 밀도가 높은 초기 상태에서 진화했다는 빅뱅 모델의 초기 버전을 공식화했다.^[9] 아인슈타인은 나중에 우주 상수를 자신의 인생에서 가장 큰 실수라고 선언했다.^[10]

일반 상대성이론은 뉴턴 중력보다 분명히 우월했고, 특수 상대성이론과 일치하며 뉴턴 이론으로는 설명되지 않는 여러 효과를 설명했다. 아인슈타인은 1915년에 자신의 이론이 임의의 매개변수 없이 수성의 수성 근일점 세차 운동을 어떻게 설명하는지 보여주었고,^[11] 1919년 아서 에딩턴이 이끄는 탐험대가 1919년 5월 29일 일식 동안 태양에 의한 별빛의 굴절에 대한 일반 상대성이론의 예측을 확인하면서,^[12] 아인슈타인은 즉시 유명해졌다.^[13] 그러나 이 이론은 약 1960년부터 1975년 사이에 일어난 발전까지 이론 물리학 및 천체물리학의 주류 밖에 머물렀다.^[14] 물리학자들은 블랙홀의 개념을 이해하기 시작했고, 퀘이사를 이러한 객체의 천체 물리학적 현상 중 하나로 식별했다.^[15] 더욱 정확한 태양계 테스트는 이론의 예측력을 확인했고,^[16] 상대론적 우주론도 직접적인 관측 테스트에 적합하게 되었다.^[17]

일반 상대성이론은 놀라운 아름다움을 가진 이론이라는 평판을 얻었다.^[18]^[19]^[20] 수브라마니안 찬드라세카르는 일반 상대성이론이 프랜시스 베이컨이 말한 "비율의 이상함"을 나타낸다고 언급했다. 그것은 이전에 완전히 독립적인 것으로 여겨졌던 기본 개념(공간과 시간 대 물질과 운동)을 병치한다. 찬드라세카르는 또한 아인슈타인이 정확한 이론을 찾는 과정에서 오직 등가 원리와 중력에 대한 적절한 설명은 기하학적이어야 한다는 자신의 감각에 의존했기 때문에, 아인슈타인이 자신의 이론에 도달하는 방식에는 "계시의 요소"가 있었다고 언급했다.^[21]

일반 상대성 이론에서는 다음을 예측한다.

;중력 렌즈 효과

: 중력장 안에서는 빛이 굴절되어 진행한다. 아서 에딩턴은 1919년 5월 29일 일식 때, 태양 근처를 지나는 별빛의 굴절이 뉴턴 역학으로 예상되는 것의 2배임을 관측으로 확인하여, 일반 상대성 이론이 옳다는 것을 입증했다.

;수성의 근일점 이동

: 뉴턴 역학만으로는 수성 궤도의 어긋남 (근일점 이동의 크기)의 관측값을 완전히 설명할 수 없었지만, 일반 상대성 이론이 해결책을 제시하여, 태양의 질량에 의한 시공간의 뒤틀림에 원인이 있음을 보였다.

;중력파

: 시공간의 뒤틀림 (중력장)의 변동이 전파되는 현상. 선형 근사가 유효한 약한 중력파의 전파 속도는 광속이다. 아인슈타인에 의한 예측 발표 100주년인 2016년에, 미국의 LIGO에 의해 직접 관측되었다.

;팽창 우주

: 시공간은 팽창 또는 수축하며, 정지해 있지 않다. 빅뱅 우주를 이끌어낸다.

;블랙홀

: 제한된 공간에 큰 질량이 집중되면, 빛조차 탈출할 수 없는 블랙홀이 형성된다.

;중력에 의한 적색 편이

: 강한 중력장에서 방출되는 빛의 파장이 원래 파장보다 늘어지는 현상.

;시간 지연

: 강한 중력장에서 측정하는 시간의 흐름 (고유 시간)이, 약한 중력장에서 측정하는 시간의 흐름보다 늦다.

일반 상대성 이론은 관성력과 중력을 결합하는 등가 원리의 아이디어를 기반으로 한다. 등가 원리란, 외부를 관측할 수 없는 상자 안의 관찰자는, 자신에게 작용하는 힘이 상자가 균일하게 가속되기 때문에 생기는 관성력인지, 상자 외부에 있는 질량에 의해 생기는 중력인지 구분할 수 없다는 주장이다.

상대론에 따르면 공간은 시공간 연속체이며, 일반 상대성 이론에서는 그 시공간 연속체가 균일하지 않고 뒤틀린 것이 된다. 즉, 질량이 시공간을 뒤틀리게 함으로써 중력이 생긴다고 생각한다. 그렇다면, 질량 주변의 시공간은 뒤틀려 있으므로, 빛은 직진하지 않고, 시간의 흐름도 영향을 받는다. 이것이 중력 렌즈나 시간 지연과 같은 현상으로 관측된다. 또한 질량이 이동하는 경우, 그 이동에 따라 시공간의 뒤틀림이 이동·전파되기 때문에 중력파가 생기는 것도 예측된다.

아인슈타인 방정식으로부터 얻어지는 시공간은, 블랙홀의 존재나 팽창 우주 모델 등, 아인슈타인 자신조차 그 해석을 거부할 정도의 놀라운 묘사이다. 그러나 블랙홀이나 초기 우주의 특이점의 존재도 이론으로 내포하고 있으며, 특이점의 발생은 일반 상대성 이론 자체를 붕괴시킨다. 장래에는 양자 중력 이론이 완성됨으로써, 이 어려움은 해결될 것으로 기대된다.

아인슈타인 방정식은 미분 방정식으로 주어지기 때문에 국소적인 이론이지만, 마치 전자기학에서의 국소적인 맥스웰 방정식으로부터 대역적인 쿨롱의 법칙을 유도할 수 있는 것처럼, 아인슈타인 방정식은 정적인 뉴턴의 만유 인력의 법칙을 포함하고 있다. 만유 인력의 법칙과의 주요 차이점은 다음 3가지이다.

# 중력은 순식간에 전달되는 것이 아니라 빛과 같은 속도(광속)로 전달된다.

# 중력에서 중력이 발생한다(비선형 상호 작용).

# 질량을 가진 물체의 가속 운동에 의해, 중력파가 방출된다.

여기서, 3.은 하전 입자가 가속 운동함으로써 전자기파가 방출되는 것과 유사하다. 이것은 만유 인력의 법칙이나 쿨롱의 법칙에, 운동하는 대상의 자기 중력이나 전하의 효과를 도입한 것에 대응한다.

일반 상대성 이론에서의 시공간은 수학적으로 각 점의 접벡터 공간에 민코프스키 계량을 넣은 4차원 다양체 ( 로렌츠 다양체 )이며, 아인슈타인 방정식을 만족한다.

따라서 각 점의 접벡터 공간은 특수 상대성 이론에 따르는 민코프스키 공간이며, 접벡터 공간은 수학적으로 테일러 전개의 1차 항에 대응한다.

이는 즉, 일반 상대성 이론의 측면에서 볼 때, 특수 상대성 이론이란 시공간 상의 임의로 고정된 한 점의 근방에서 일반 상대성 이론을 1차 근사한 것임을 의미한다. 또한, ( 우주항이 없는 ) 아인슈타인 방정식에 등장하는 각 항 ( 곡률이나 에너지-운동량 텐서 )은 2차 미분에 관련된 항이며, 1차 근사인 특수 상대성 이론에는 등장하지 않는다.

반대로 특수 상대성 이론의 측면에서 일반 상대성 이론을 보면, 특수 상대성 이론의 수학적 정식화인 민코프스키 공간은 모든 점에 동일한 민코프스키 계량을 넣은 평탄한 로렌츠 다양체이다.

이 로렌츠 다양체 상에서는 곡률이 모든 점에서 0이므로, 이 사실을 ( 우주항이 없는 ) 아인슈타인 방정식에 대입하면, 이 공간에서는 에너지-운동량 텐서가 0임을 의미한다.

또한, 평탄한 로렌츠 다양체 상에서는 공변 미분과 일반적인 미분이 일치하므로, 모든 선형 좌표에서 크리스토펠 기호는 0이다. 크리스토펠 기호는 물리학적으로 중력에 대응하므로, 이는 즉 모든 선형 좌표에서 중력이 0임을 의미한다.

이상에서 특수 상대성 이론이란, 에너지-운동량 텐서의 영향을 무시할 수 있을 정도로, 즉 우주 전체에 비하면 미소한 영역에서의 이론이며, 공간의 곡률도 영역의 미소함 때문에 무시할 수 있는 경우의 이론이라고 할 수 있다.

3. 1. 뉴턴 중력의 기하학

기하학적 뉴턴 중력이 흥미로울 수 있지만, 그 기초인 고전 역학은 (특수) 상대성 역학의 극한 경우일 뿐이다.^[32] 대칭성의 관점에서 보면, 중력을 무시할 수 있는 경우 물리학은 고전 역학의 갈릴레이 불변성이 아닌 특수 상대성 이론처럼 로렌츠 불변성을 따른다. (특수 상대성 이론을 정의하는 대칭성은 푸앵카레 군이며, 여기에는 평행 이동, 회전, 부스트 및 반사가 포함된다.) 두 이론 간의 차이점은 광속에 가까운 속도와 고에너지 현상을 다룰 때 두드러진다.^[33]

로렌츠 대칭성과 함께 추가적인 구조가 작용한다. 이들은 빛원뿔 (

)의 집합에 의해 정의된다. 빛원뿔은 인과 관계 구조를 정의한다. 각 사건 A에 대해, 빛보다 빠르게 이동할 필요가 없는 신호나 상호 작용을 통해 A에 영향을 미치거나 영향을 받을 수 있는 사건(그림의 사건 B와 같은)과 그러한 영향이 불가능한 사건(그림의 사건 C와 같은)의 집합이 존재한다. 이러한 집합은 관측자에 의존하지 않는다.^[34] 자유 낙하하는 입자의 세계선과 함께, 빛원뿔은 시공간의 반 리만 계량을 (최소한 양의 스칼라 인수로) 재구성하는 데 사용할 수 있다. 수학적 용어로, 이것은 등각 구조^[35] 또는 등각 기하학을 정의한다.

특수 상대성 이론은 중력이 없는 상태에서 정의된다. 실용적인 적용을 위해 중력을 무시할 수 있을 때는 적절한 모델이다. 중력을 고려하고 자유 낙하 운동의 보편성을 가정하면, 전역 관성 좌표계가 존재하지 않는다. 대신 자유 낙하하는 입자와 함께 움직이는 근사적인 관성 좌표계가 존재한다. 시공간의 언어로 번역하면, 중력이 없는 관성 좌표계를 정의하는 직선 시간꼴은 서로에 대해 곡선으로 변형되어 중력을 포함하려면 시공간 기하학의 변화가 필요함을 시사한다.^[36]

우선, 자유 낙하하는 새로운 국소 좌표계가 특수 상대성 이론의 법칙이 성립하는 좌표계와 일치하는지 여부는 불분명하다. 그러나 특수 상대성 이론적 좌표계에 대한 다른 가정을 사용하여 중력 적색 편이에 대한 다른 예측을 도출할 수 있다. 실제 측정 결과는 자유 낙하하는 좌표계에서 빛이 특수 상대성 이론에서와 같이 전파된다는 것을 보여준다.^[37] 이 진술의 일반화, 즉 특수 상대성 이론의 법칙이 자유 낙하(및 회전하지 않는) 좌표계에서 잘 근사적으로 성립한다는 것은 아인슈타인 등가 원리로 알려져 있으며, 이는 특수 상대성 이론적 물리학을 일반화하여 중력을 포함하는 데 중요한 지침이 된다.^[38]

동일한 실험 데이터는 중력장에서 시계로 측정된 시간, 즉 고유 시간이 특수 상대성 이론의 규칙을 따르지 않는다는 것을 보여준다. 시공간 기하학의 언어로, 그것은 민코프스키 계량으로 측정되지 않는다. 뉴턴의 경우와 마찬가지로, 이것은 보다 일반적인 기하학을 시사한다. 작은 규모에서는 자유 낙하하는 모든 좌표계가 동일하고 대략 민코프스키적이다. 결과적으로, 우리는 이제 민코프스키 공간의 곡선 일반화를 다루고 있다. 기하학을 정의하는 계량 텐서, 특히 길이와 각도가 어떻게 측정되는지는 특수 상대성 이론의 민코프스키 계량이 아니라 반 리만 계량으로 알려진 일반화이다. 또한, 각 리만 계량은 자연스럽게 하나의 특정 종류의 연결, 즉 레비-치비타 접속과 관련되며, 이것이 실제로 등가 원리를 만족하고 공간을 국소적으로 민코프스키적(즉, 적절한 국소 좌표계에서 계량은 민코프스키적이고, 그 1차 편미분 및 연결 계수는 사라짐)으로 만드는 연결이다.^[39]

3. 2. 상대론적 일반화

기하학적 뉴턴 중력은 고전 역학의 특수한 경우일 뿐이며, (특수) 상대론적 역학으로 일반화될 수 있다.^[32] 중력을 무시할 수 있는 경우, 물리학은 특수 상대론에서처럼 로렌츠 불변성을 따르며, 고전 역학에서의 갈릴레이 불변성을 따르지 않는다. 특수 상대론의 대칭성은 푸앵카레 군으로, 평행 이동, 회전, 부스트 및 반사를 포함한다. 이 둘의 차이는 빛의 속력에 근접하는 속력과 고에너지 현상을 다룰 때 두드러진다.^[33]

로런츠 대칭성과 함께, 광추() 집합으로 정의되는 추가적인 구조가 개입된다. 광추는 인과 구조를 결정한다. 각 사건 A에 대하여, 빛보다 빠르지 않은 속력의 신호나 상호작용을 통해 A에 영향을 주거나 A로부터 영향을 받을 수 있는 사건들의 집합(그림의 사건 B처럼)과, 그러한 상호작용이 가능하지 않은 사건들의 집합(그림의 사건 C처럼)으로 나뉜다. 이 집합들은 관측자에 독립적이다.^[34] 자유낙하하는 입자들의 세계선과 결합하여, 광추들은 시공간의 준-리만기하학적 메트릭 구조를 (적어도 양수의 스칼라 곱셈인자까지는) 재구성하는 데 쓰일 수 있다. 이는 등각 구조^[35] 또는 등각 기하학을 정의한다.

특수 상대론은 중력이 없는 상황에서 정의되지만, 중력을 도입하고 자유 낙하 운동의 보편성을 가정하면, 대역적인 관성 좌표계는 존재하지 않는다. 대신, 자유 낙하하는 입자들과 함께 움직이는 근사적 관성 좌표계들이 존재한다. 중력의 영향을 받지 않는 관성 좌표계에서의 똑바른 시간꼴 세계선들은 서로에 대해 휘어진 세계선들로 변형되며, 이는 중력의 개입이 시공간 기하학에 어떤 변화를 요구함을 시사한다.^[36]

선험적으로, 새로운 자유 낙하 국소 좌표계가 특수 상대론의 법칙들이 성립하는 기준계와 일치하는지 분명히 밝힐 수는 없다. 하지만 특수 상대론적 좌표계(지표 고정, 혹은 자유 낙하)에 관하여 다른 가정을 사용하면, 중력 적색편이에 관한 다른 예측을 유도할 수 있다. 실제 측정 결과는 자유 낙하 좌표계가 바로 빛이 특수 상대론에서처럼 전파되는 좌표계임을 보여준다.^[37] 이 진술의 일반화, 즉 특수 상대론의 법칙들이 자유 낙하하는 (그리고 회전하지 않는) 좌표계에서 충분한 근사로 성립한다는 것은 아인슈타인 등가 원리로 알려져 있으며, 이는 특수 상대론적 물리학을 중력을 포함하도록 일반화하는 데 있어서 결정적인 지도 원리이다.^[38]

위와 동일한 실험 자료는 중력장에 놓인 시계로 측정한 시간(엄밀히 말하자면 고유 시간)이 특수 상대론의 법칙을 따르지 않음을 보여준다. 시공간 기하학의 관점에서, 이는 민코프스키 계량으로 측정되지 않는다. 뉴턴 중력에서 살펴보았듯이, 이는 보다 일반적인 기하학을 시사한다. 작은 척도에서, 자유 낙하하는 모든 기준계는 동등하며 근사적으로 민코프스키 메트릭을 따른다. 결과적으로, 우리는 민코프스키 공간의 휘어진 일반화를 다루고 있는 것이다. 기하(특히, 길이와 각도의 측정 방식)를 결정하는 계량 텐서는 특수 상대론의 민코프스키 메트릭이 아니라 그 일반화, 즉 반 리만 계량이다. 더 나아가, 각각의 리만기하학적 메트릭은 자연스럽게 특정 종류의 접속과 연관되는데, 이것이 곧 레비-치비타 접속이며 사실 등가 원리를 만족시키며 공간이 국소적으로 민코프스키 공간이도록 만드는 접속이다(즉, 적당한 국소 좌표계에서 메트릭은 민코프스키 메트릭이며, 그 일계 편미분과 접속 계수는 사라진다).^[39]

3. 3. 아인슈타인의 방정식

중력의 원천은 뉴턴 중력에서는 질량이지만, 특수 상대성 이론에서는 에너지-운동량 텐서이다.^[40] 아인슈타인 방정식은 이 에너지-운동량 텐서와 리치 텐서를 연결하여 중력을 기하학적으로 설명한다.^[40]

아인슈타인 방정식은 다음과 같다.

:

G_{\mu\nu}\equiv R_{\mu\nu} - {\textstyle 1 \over 2}R\,g_{\mu\nu} = \kappa T_{\mu\nu}\,

$G_{\mu\nu}$ : 아인슈타인 텐서
$R_{\mu\nu}$ : 리치 텐서
$R$ : 스칼라 곡률
$g_{\mu\nu}$ : 계량 텐서
$\kappa$ : 상수
$T_{\mu\nu}$ : 에너지-운동량 텐서

여기서

\kappa

는

\kappa=\frac{8\pi G}{c^4}

이며,

G

는 뉴턴의 중력 상수,

c

는 진공에서 빛의 속도이다.^[42]

이 방정식은 비선형 미분 방정식으로, 일반적인 해를 구하기 어렵다고 알려져 있다.^[7]

일반 상대성 이론에서 자유 낙하하는 입자의 세계선은 휘어진 시공간의 측지선이다. 측지선 방정식은 다음과 같다.^[40]

:

{d^2 x^\mu \over ds^2}+\Gamma^\mu {}_{\alpha \beta}{d x^\alpha \over ds}{d x^\beta \over ds}=0,

여기서

s

는 운동의 스칼라 매개변수(예: 고유 시간)이고,

\Gamma^\mu {}_{\alpha \beta}

는 크리스토펠 기호이다.

3. 4. 일반 상대론에서의 총력

일반 상대성 이론에서 유효 중력 퍼텐셜 에너지는 뉴턴 중력 항, 원심력 항, 상대론적 효과 항의 합으로 주어진다. 총력은 이 유효 중력 퍼텐셜 에너지의 기울기로 계산된다.^[24]^[25]

3. 5. 일반 상대론의 대안

동일한 전제에서 출발하지만, 추가적인 법칙이나 제약을 통해 다른 장 방정식을 유도하는 일반 상대론의 대안 이론들이 존재한다. 이러한 예로는 화이트헤드의 이론, 브란스-딕 이론, 텔레병렬, f(R) 중력, 아인슈타인-카르탄 이론 등이 있다.^[45]

4. 주요 결과

일반 상대성이론은 여러 가지 비고전적 효과를 예측하며, 이는 실험적으로 검증되었다. 주요 결과는 다음과 같다.

'''중력 렌즈 효과''': 중력장 안에서 빛이 굴절되어 진행한다. 아서 에딩턴은 1919년 5월 29일 일식 때, 태양 근처를 지나는 별빛의 굴절이 뉴턴 역학으로 예상되는 것의 2배임을 관측하여 일반 상대성이론이 옳다는 것을 입증했다.
'''수성의 근일점 이동''': 뉴턴 역학만으로는 수성 궤도의 근일점 이동 크기를 완전히 설명할 수 없었지만, 일반 상대성이론은 태양의 질량에 의한 시공간의 뒤틀림으로 이를 설명했다.
'''중력파''': 시공간의 뒤틀림(중력장)의 변동이 전파되는 현상이다. 선형 근사가 유효한 약한 중력파의 전파 속도는 광속이다. 아인슈타인의 예측 발표 100주년인 2016년에, 미국의 LIGO에 의해 직접 관측되었다.
'''팽창 우주''': 시공간은 팽창 또는 수축하며 정지해 있지 않다. 이는 빅뱅 우주론으로 이어진다.
'''블랙홀''': 제한된 공간에 큰 질량이 집중되면 빛조차 탈출할 수 없는 블랙홀이 형성된다.
'''중력에 의한 적색 편이''': 강한 중력장에서 방출되는 빛의 파장이 원래 파장보다 늘어지는 현상이다.
'''시간 지연''': 강한 중력장에서 측정하는 시간의 흐름(고유 시간)이 약한 중력장에서 측정하는 시간의 흐름보다 늦다.

일반 상대성이론은 관성력과 중력을 결합하는 등가 원리를 기반으로 한다. 등가 원리에 따르면, 외부를 관측할 수 없는 상자 안의 관찰자는 자신에게 작용하는 힘이 상자의 균일한 가속 때문인지, 아니면 외부 질량에 의한 중력 때문인지 구분할 수 없다.

상대성이론에 따르면 공간은 시공간 연속체이며, 일반 상대성이론에서는 이 시공간 연속체가 균일하지 않고 뒤틀려 있다. 즉, 질량이 시공간을 뒤틀리게 하여 중력이 발생한다. 질량 주변의 시공간은 뒤틀려 있으므로 빛은 직진하지 않고 시간의 흐름도 영향을 받는다. 이는 중력 렌즈나 시간 지연 현상으로 관측된다. 또한 질량이 이동하면 시공간의 뒤틀림이 이동 및 전파되어 중력파가 발생한다.

아인슈타인 방정식으로 얻어지는 시공간은 블랙홀이나 팽창 우주 모델과 같이, 아인슈타인 자신도 해석을 거부할 정도로 놀라운 모습을 보인다. 그러나 블랙홀이나 초기 우주의 특이점 또한 이론에 내포되어 있으며, 특이점의 발생은 일반 상대성이론 자체를 붕괴시킨다. 미래에는 양자 중력 이론이 완성되어 이러한 어려움이 해결될 것으로 기대된다.

4. 1. 근사 법칙으로서의 만유인력

Newton^영어의 만유인력 법칙은 중력장 또는 시공간의 곡률이 매우 약한 경우, 일반 상대론의 근사 법칙으로 간주된다. 일반 상대론에서 측지선 방정식은 뉴턴 역학의 운동 방정식으로 근사된다. 포스트 뉴턴 이론(PPN theory)에서 만유인력은 1차 근사로서의 지위를 갖는다.^[49]

일반 상대성 이론에서 질량

M

인 중심 천체 주위를 공전하는 질량

m

인 물체의 유효 중력 퍼텐셜 에너지는 다음과 같다.

:

U_f(r)=-\frac{GMm}{r}+\frac{L^2}{2mr^2}-\frac{GML^2}{mc^2r^3}

여기서

L

은 각운동량이다. 이때 보존력의 총합은 그 그래디언트의 음수를 취해 다음과 같이 나타낼 수 있다.

:

F_f(r)=-\frac{GMm}{r^2}+\frac{L^2}{mr^3}-\frac{3GML^2}{mc^2r^4}

첫 번째 항은 뉴턴 중력의 힘을 나타내며, 역제곱 법칙으로 기술된다. 두 번째 항은 원운동에서의 원심력을 나타낸다. 세 번째 항은 상대론적 효과를 나타낸다.^[43]^[44]

뉴턴 이론은 약 200년 동안 가장 정확한 중력 이론이었다. 따라서 고전 역학에 대응하는 상황, 즉 중력장 또는 시공간의 곡률이 매우 약한 경우 뉴턴 이론으로 근사되는 것은 자연스럽다. 이를 수식으로 표현하면 다음과 같다.

:

g_{\mu\nu} = \eta_{\mu\nu} + h_{\mu\nu}, \quad |h_{\mu\nu}| \ll 1

이 경우, 측지선 방정식은 다음과 같이 근사된다.

:

\begin{aligned} \frac{d^2x^i}{dt^2} &= -\Gamma^i_{00} = -\frac{1}{2}\eta^{ii}(2g_{0i,0}-g_{00,i}) \\ & \approx -\frac{1}{2}\frac{\partial g_{00}} {\partial x^i}\end{aligned}

따라서,

g_{\mu\nu}

는 등가 원리와 같이 실제로 중력장을 일반화함과 동시에 뉴턴 역학을 근사 법칙으로 포함한다는 것을 알 수 있다. 더 나아가, 아인슈타인 방정식을 근사시키면 다음과 같다.

:

\begin{aligned} R_{00} & \approx \frac{\partial \Gamma^i_{00}}{\partial x^i} \\ &= \kappa \left(T_{00}-\frac{1}{2}g_{00}T\right) = \frac{1}{2}\kappa \rho \end{aligned}

이는 정확하게 뉴턴 중력의 푸아송 방정식과 일치한다.

4. 2. 빛과 관련된 현상

일반 상대성이론은 빛의 경로와 파장이 중력장의 영향을 받는다고 예측한다. 빛은 멀리 떨어진 천체의 정보를 전달해주는데, 일반 상대성이론에 따르면 빛이 지구에 도달하면서 중력 퍼텐셜의 차이로 인해 파장이 변화하거나 궤적이 휠 수 있다.^[231] 이러한 효과들은 관측 천문학에서 반드시 고려해야 하는 요소이다.

중력 적색편이: 빛이 강한 중력장에서 빠져나올 때 파장이 길어지는 현상이다. 등가원리에 의해 예측 가능하며, 중력 퍼텐셜 차이에 비례한다.
광선의 굴절: 빛이 질량이 큰 천체 주변을 지나갈 때 경로가 휘는 현상이다. 일반 상대성이론은 뉴턴 역학보다 두 배 더 큰 굴절을 예측하며, 1919년 5월 29일 일식 때 아서 에딩턴의 관측으로 검증되었다.^[230]

일반 상대성 이론에서 광선 굴절량(

\Delta

)은 다음과 같이 주어진다.^[230]

:

\Delta = \frac{4GM}{c^2 R}

:(

G

- 중력 상수,

M

- 천체의 질량,

R

- 천체와 광선의 수직거리,

c

- 진공에서의 광속)

콤팩트한 천체(회색으로 표시) 근처를 지나는 빛(파란색으로 표시된 위치에서 방출)의 굴절

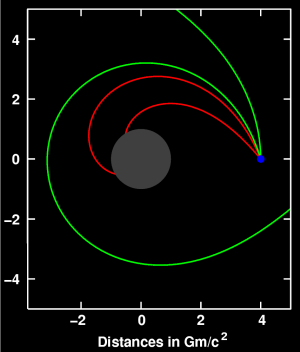
일반 상대성 이론은 빛의 경로가 별 근처를 지날 때 시공간의 곡률을 따라갈 것이라고 예측한다. 이 효과는 처음에는 태양을 지나는 별이나 멀리 떨어진 퀘이사의 빛이 굴절되는 것을 관찰하여 확인되었다.^[72]

4. 2. 1. 중력 적색편이

질량이 큰 물체의 표면에서 탈출하는 빛의 파동의 중력 적색 편이를 개략적으로 나타낸 그림

중력장이 강한 곳에서 방출된 빛은 파장이 길어지는 적색 편이 현상을 겪는다. 이를 중력 적색편이라고 한다. 중력 적색편이는 중력 퍼텐셜의 차이에 의해 발생하며, 등가원리를 통해 예측할 수 있다.^[231]

등가원리에 따르면, 중력장 내에서 자유낙하하는 관찰자는 중력장이 없는 관성계의 관찰자와 같다.^[231] 중력장이 없는 관성계에서는 빛의 변형이 일어나지 않으므로, 자유낙하하는 관찰자는 도플러 효과를 관측할 수 없다. 하지만 승강기 밖의 정지한 관찰자는 빛의 청색편이를 예상한다. 승강기가 자유낙하를 시작할 때 빛이 출발했다면, 빛이 이동하는 동안 승강기 천장은 가속되어 빛에 대한 청색편이가 발생하기 때문이다.

이러한 모순을 해결하기 위해 중력장이 청색편이를 상쇄하는 적색편이를 일으킨다고 생각할 수 있다. 이 중력 적색편이(

\frac{\Delta \omega}{\omega}

)는 중력 퍼텐셜의 차이(

\Delta \Phi

)에 의해 다음과 같이 나타낼 수 있다.^[231]

:

\frac{\Delta \omega}{\omega} = -\frac{\Delta \Phi}{c^2}

따라서 빛 방출기와 감지기가 서로 정지해 있는 상황에서는 청색편이로 상쇄되지 않는 중력 적색편이가 관측된다.

등가 원리가 성립하면,^[63] 중력은 시간의 흐름에 영향을 미친다. 중력 우물로 보내진 빛은 청색 편이되고, 중력 우물에서 벗어나는 빛은 적색 편이된다. 이를 통틀어 중력 주파수 이동이라고 한다. 일반적으로 질량이 큰 물체에 가까운 과정은 멀리 떨어진 과정보다 느리게 진행되며, 이를 중력 시간 지연이라고 한다.^[64]

중력 적색 편이는 실험실^[65] 및 천문학적 관측^[66]으로 측정되었다. 지구 중력장에서의 중력 시간 지연은 원자 시계로 여러 번 측정되었고,^[67] GPS(Global Positioning System) 작동의 부수 효과로 지속적으로 검증된다.^[68] 쌍성 펄서 관측은 더 강한 중력장에서의 검증을 제공한다.^[69] 모든 결과는 일반 상대성이론과 일치한다.^[70] 그러나 현재 정확도 수준으로는 일반 상대성 이론과 등가 원리가 유효한 다른 이론을 구별할 수 없다.^[71]

4. 2. 2. 중력 시간지연

등가 원리에 따르면,^[63] 중력은 시간의 흐름에 영향을 미친다. 중력 우물로 보내진 빛은 청색 편이되고, 반대 방향으로 보내진 빛(즉, 중력 우물에서 벗어나는 빛)은 적색 편이된다. 이 두 효과를 통틀어 중력 주파수 이동이라고 한다. 보다 일반적으로, 질량이 큰 물체에 가까운 과정은 멀리 떨어진 과정과 비교할 때 더 느리게 진행된다. 이 효과를 중력 시간 지연이라고 한다.^[64]

중력 적색 편이는 실험실에서^[65] 그리고 천문학적 관측을 사용하여 측정되었다.^[66] 지구의 중력장에서의 중력 시간 지연은 원자 시계를 사용하여 수없이 측정되었으며,^[67] GPS(Global Positioning System) 작동의 부수 효과로 지속적인 검증이 제공된다.^[68] 더 강한 중력장에서의 테스트는 쌍성 펄서의 관측으로 제공된다.^[69] 모든 결과는 일반 상대성 이론과 일치한다.^[70] 그러나 현재 정확도 수준에서는 이러한 관측만으로는 등가 원리가 유효한 일반 상대성 이론과 다른 이론을 구별할 수 없다.^[71]

빛의 감지기가 빛의 방출기에 대해 정적인 상황에서 서로 다른 진동수를 얻는 이유는, 파면의 개수는 동일하지만 빛의 감지기와 빛의 방출기가 서로 다른 시간 단위를 갖기 때문이다. 즉, 서로 다른 중력 퍼텐셜에 위치한 시계에서는 서로 다른 빠르기로 시침이 움직인다. 진동수는 그 곳의 고유 시간에 반비례하므로,

\omega \sim \frac{1}{d\tau}

이며, 이를 중력 적색편이 식에 집어넣으면,

d\tau_1 = \left(1+\frac{\Phi_1-\Phi_2}{c^2}\right)d\tau_2

의 식을 얻을 수 있다.^[232]

자동차 등의 위치를 실시간으로 측정하여 표시하는 내비게이션 시스템은 GNSS의 대표적인 예인 GPS 등을 이용하며, GPS 위성 등에 탑재된 원자 시계를 기반으로 생성되는 항법 신호에 의존하고 있다.

GPS 위성으로부터 신호를 수신하는 장치에서는 다양한 요인에 의한 보정을 수행하는데, GPS 위성의 시계와의 동기화와 관련하여 지표면에 대해 고속으로 운동하는 GPS 위성의 특수 상대론 효과에 의한 지표면에서 본 시간 지연과 지구의 중력장에 의한 지상의 시간 지연, 즉 일반 상대론 효과에 의한 위성의 시계 진행이 포함된다.^[227]

GPS 위성의 궤도 속도는 초속 약 4킬로미터로 고속이기 때문에, 특수 상대성 이론에 의해 시간의 진행이 미세하게나마 늦어진다. 한편, GPS 위성의 고도는 약 2만 킬로미터로, 지구의 중력장의 영향이 작기 때문에, 일반 상대성 이론에 의해 지상보다 시간의 진행이 빨라진다. 이처럼 특수 상대성 이론과 일반 상대성 이론은 서로 반대되는 효과를 가져온다. 이러한 상대론적 보정을 하지 않고 하루 동안 방치하면, 위치 정보가 약 11 킬로미터나 벗어날 정도의 시각차가 발생하기 때문에, 상대론적 보정은 GPS 시스템의 운용에 필수적이다.^[228]

4. 2. 3. 광선의 굴절

빛은 질량이 큰 천체 주변을 통과하면서 궤적이 꺾이는 광선 굴절 현상을 겪는다. 이러한 현상은 등가 원리만으로도 예측할 수 있지만, 일반 상대성이론은 뉴턴 역학 예측의 두 배에 해당하는 굴절량을 예측한다. 일반 상대론에 따르면 광선 굴절량(

\Delta

)은 다음과 같이 주어진다.^[230]

:

\Delta = \frac{4GM}{c^2 R}

:(

G

- 중력 상수,

M

- 천체의 질량,

R

- 천체와 광선의 수직거리,

c

- 진공에서의 광속)

이때, 광선이 별의 표면을 스쳐 지나가는 경우, 즉

R

이 별의 반지름과 같은 경우에 광선 굴절 효과가 가장 크다. 따라서 이 효과를 가장 크게 확인하기 위해서는 별이 (천구 상에서) 태양 곁에 있을 때, 특히 태양빛을 제거하기 위해 개기일식 상황을 활용해야 한다.^[230]

아인슈타인은 1915년 태양에 의한 별빛의 이동량을 1.75''로 예측했고, 뉴턴 역학에 따른 이동량은 0.87''였다. 1919년 5월 29일 일어난 개기일식 때 아서 에딩턴이 촬영한 사진들을 분석한 결과는 일반 상대론의 예측을 지지하는 것으로 나타났다.^[230] 이 결과는 1979년 재검증되었다.^[233]

일반 상대성 이론은 빛의 경로가 별 근처를 지날 때 시공간의 곡률을 따라갈 것이라고 예측한다. 이 효과는 처음에는 태양을 지나는 별이나 멀리 떨어진 퀘이사의 빛이 굴절되는 것을 관찰하여 확인되었다.^[72]

빛의 굴절과 관련된 예측은 빛이 고전 물리학에서 빛이 이동하는 직선의 일반화인 광선 또는 영 측지선을 따른다는 사실에서 비롯된다.^[73] 적절한 시공간 모델(외부 슈바르츠실트 해 또는 질량이 하나 이상인 경우 후 뉴턴 전개)을 검토하면, 빛의 전파에 대한 중력의 여러 효과가 나타난다. 빛의 굽힘은 자유 낙하의 보편성을 빛으로 확장하여 얻을 수도 있지만,^[75] 이러한 계산에서 나오는 굴절 각도는 일반 상대성 이론에서 제공하는 값의 절반에 불과하다.^[76]

4. 3. 천체의 궤도

일반 상대성이론에서 천체의 운동은 아인슈타인 방정식의 특수해 위에 놓인 측지선을 분석하여 파악한다. 만유인력에서는 천체의 궤도가 닫힌 타원 궤적을 따르지만, 일반 상대성이론에서는 궤도가 조금씩 회전하는 근일점의 세차운동이 나타난다.^[234]^[235]

태양계에서는 수성에서 이 효과가 두드러지며, 이는 1859년 프랑스의 천문학자 르베리에에 의해 보고되었고, 아인슈타인이 1915년 자신의 이론으로 설명했다. 펄서 쌍성계에서는 이 효과가 훨씬 크게 관측된다.

일반 상대성이론은 또한 중력파 방출로 인한 궤도 감쇠를 예측한다. 이 효과는 1974년 헐스와 테일러가 발견한 헐스-테일러 쌍성계에서 처음 확인되었으며, 중력파의 간접 증거로 받아들여졌다.

4. 3. 1. 근일점 세차운동

일반 상대성이론에서, 행성 궤도의 근일점은 공전 방향으로 회전하는 세차운동을 보인다. 궤도는 타원이 아니라, 초점을 중심으로 회전하는 타원과 유사하여 장미 곡선과 같은 모양을 만든다. 이 효과는 1회 공전 당

:

\varepsilon = 24\pi^3\frac{a^2}{T^2c^2(1-e^2)}

:(

T

- 공전 주기,

a

- 궤도 장반경,

e

- 궤도 이심률,

c

- 진공에서의 광속)

으로 나타난다. 궤도의 이심률이 클수록 효과가 커진다.

태양계에서는 수성의 효과가 특히 두드러지며, 100년 동안 43arcsec 정도의 근일점 세차운동이 이루어진다. 1859년 프랑스의 천문학자 르베리에가 이 효과를 보고했고,^[11] 아인슈타인이 1915년 일반 상대성이론으로 이 문제를 설명했다.^[89] 금성에서는 4arcsec, 지구에서는 1arcsec 정도이다.

펄서 쌍성계에서는 이 효과가 훨씬 크게 관측된다. 예를 들어 헐스-테일러 쌍성계(PSR B1913+16)에서는 공전 주기가 7시간 45분이고, 근일점 이동량은 1년에 4.2° 정도이다.^[234]^[235]

4. 3. 2. 궤도 감쇠와 중력파

일반 상대성이론에서는 질량의 변동에 따라 중력파가 예측된다. 중력파는 시공간의 물결 같은 진동이 주변 공간으로 퍼지는 것이다. 중력파는 매우 작아서 직접 검출은 비교적 최근에야 이루어졌으며, 이전에는 궤도 반경이 점차 감소하는 '''궤도 감쇠(orbital decay)''' 효과를 통해 간접적으로 존재가 검증되었다. 궤도 반경은 계의 퍼텐셜 에너지에 의해 결정되는데, 회전에 따라 중력파가 방출되면 퍼텐셜 에너지가 감소하여 궤도 반경과 주기가 감소한다.

이 효과는 1974년 헐스와 테일러가 발견한 펄사 쌍성계(PSR B1913+16)에서 최초로 확인되었다. 이 쌍성계는 시간이 지남에 따라 공전 주기가 감소하여 궤도 크기가 감소하는 것을 확인할 수 있다.^[236] 궤도 감쇠의 양은 일반 상대성이론이 중력파 방출에 따른 효과로 계산한 것과 일치하며, 이때 중력파의 총 방출량은 이다. 이 결과는 중력파의 간접 증거로 받아들여져 1993년 헐스와 테일러는 노벨 물리학상을 수상했다.

일반 상대성 이론에 따르면, 쌍성계는 중력파를 방출하여 에너지를 잃는다. 이로 인해 궤도를 도는 두 천체 사이의 거리가 줄어들고, 궤도 주기도 짧아진다. 태양계나 일반적인 쌍성에서는 이 효과가 너무 작아서 관측하기 어렵지만, 두 중성자별이 궤도를 도는 좁은 쌍성 펄서의 경우에는 그렇지 않다. 펄서는 매우 정확한 시계 역할을 할 수 있는 규칙적인 전파 펄스를 방출하여 궤도 주기를 정밀하게 측정할 수 있다. 중성자별은 매우 압축되어 상당한 양의 에너지가 중력파로 방출된다.^[96]

중력파 방출로 인한 궤도 주기의 감소를 처음 관측한 것은 헐스와 테일러가 PSR1913+16을 이용하여 발견하였다. (1974년) 이는 중력파의 첫 번째 간접적 탐지였으며, 이들은 이 업적으로 1993년 노벨 물리학상을 수상했다.^[97] 이후, 두 별 모두 펄서인 PSR J0737−3039 등 여러 쌍성 펄서가 발견되었으며, 2021년에는 16년간의 관측 끝에 일반 상대성 이론과 일치하는 것으로 보고되었다.^[95]

5. 주요 적용

일반 상대성이론은 중성자별이나 블랙홀과 같이 고전적인 이론으로는 충분히 설명되지 않는 천체들을 설명하는 데 사용된다.^[2] 고전 역학에서는 천체의 중력에 밀도만이 관여하지만, 일반 상대론에서는 압력 또한 관여하며, 중성자별과 같이 밀도가 매우 클 경우 압력 또한 그에 의한 영향을 무시할 수 없을 만큼 커진다.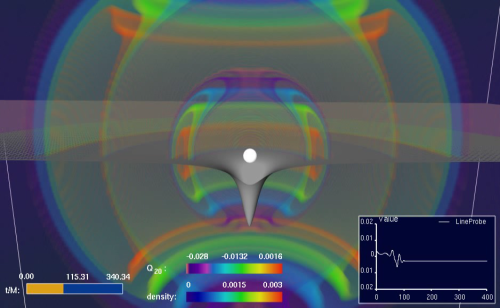

일반 상대성 이론 방정식에 기반한 시뮬레이션: 중력파를 방출하면서 블랙홀을 형성하기 위해 붕괴하는 별

일반 상대성이론은 다음과 같은 현상들을 예측한다.

중력 렌즈 효과: 중력장 안에서는 빛이 굴절되어 진행한다.
수성의 근일점 이동: 뉴턴 역학만으로는 수성 궤도의 어긋남을 완전히 설명할 수 없었지만, 일반 상대성 이론은 태양의 질량에 의한 시공간의 뒤틀림으로 그 원인을 설명했다.
중력파: 시공간의 뒤틀림(중력장)이 광속으로 전파되는 현상.
블랙홀: 제한된 공간에 큰 질량이 집중되면 빛조차 탈출할 수 없는 블랙홀이 형성된다.
중력에 의한 적색 편이: 강한 중력장에서 방출되는 빛의 파장이 늘어지는 현상.
시간 지연: 강한 중력장에서 측정하는 시간의 흐름(고유 시간)이 약한 중력장에서보다 늦게 흐른다.

일반 상대성이론은 우주의 기원과 진화를 설명하는 데 사용된다. 1929년 확인된 허블-르메트르 법칙은 외부 은하들이 거리에 비례하여 지구로부터 멀어지는 현상을 우주 공간 자체의 팽창으로 설명한다.

우주 마이크로파 배경 (ESA and the Planck Collaboration)

5. 1. 천체 물리학

일반 상대성이론은 중성자별이나 블랙홀과 같이 고전적인 이론으로는 충분히 설명되지 않는 천체들을 설명하는 데 사용된다.^[2] 고전 역학에서는 천체의 중력에 밀도만이 관여하지만, 일반 상대론에서는 압력 또한 관여하며, 중성자별과 같이 밀도가 매우 클 경우 압력 또한 그에 의한 영향을 무시할 수 없을 만큼 커진다.

물체의 질량과 반지름의 비율이 충분히 커지면 일반 상대성 이론은 빛조차도 탈출할 수 없는 공간인 블랙홀의 형성을 예측한다. 현재 받아들여지는 항성 진화 모델에서 약 1.4 태양 질량의 중성자별과 수십 태양 질량 정도의 항성 블랙홀은 거대한 별의 진화의 최종 단계로 여겨진다.^[121] 일반적으로 은하는 중심에 수백만에서 수십 억 개의 태양 질량을 가진 하나의 초대질량 블랙홀을 가지고 있으며,^[122] 그 존재는 은하 및 더 큰 우주 구조의 형성에 중요한 역할을 한 것으로 여겨진다.^[123]

천문학적으로, 컴팩트 천체의 가장 중요한 특성은 중력 에너지를 전자기 복사로 변환하는 매우 효율적인 메커니즘을 제공한다는 것이다.^[124] 강착, 즉 먼지나 기체 물질이 항성 또는 초대질량 블랙홀로 떨어지는 현상은 일부 눈부시게 밝은 천문학적 물체, 특히 은하 규모의 다양한 종류의 활동 은하핵과 마이크로퀘이사와 같은 항성 크기의 물체를 설명하는 것으로 여겨진다.^[125] 특히 강착은 거의 광속으로 우주로 뿜어져 나가는 고에너지 입자의 집중된 빔인 상대론적 제트로 이어질 수 있다.^[126] 일반 상대성 이론은 이 모든 현상을 모델링하는 데 중심적인 역할을 하며,^[127] 관측은 이론이 예측한 특성을 가진 블랙홀의 존재에 대한 강력한 증거를 제공한다.^[128]

일반 상대성 이론은 다음과 같은 현상들을 예측한다.

중력 렌즈 효과: 중력장 안에서는 빛이 굴절되어 진행한다. 아서 에딩턴은 1919년 5월 29일 일식 때, 태양 근처를 지나는 별빛의 굴절이 뉴턴 역학으로 예상되는 것의 2배임을 관측으로 확인하여, 일반 상대성 이론이 옳다는 것을 입증했다.
수성의 근일점 이동: 뉴턴 역학만으로는 수성 궤도의 어긋남( 근일점 이동)을 완전히 설명할 수 없었지만, 일반 상대성 이론은 태양의 질량에 의한 시공간의 뒤틀림으로 그 원인을 설명했다.
중력파: 시공간의 뒤틀림( 중력장)이 광속으로 전파되는 현상. 2016년, 미국의 LIGO에 의해 직접 관측되었다.
블랙홀: 제한된 공간에 큰 질량이 집중되면 빛조차 탈출할 수 없는 블랙홀이 형성된다.
중력에 의한 적색 편이: 강한 중력장에서 방출되는 빛의 파장이 늘어지는 현상.
시간 지연: 강한 중력장에서 측정하는 시간의 흐름(고유 시간)이 약한 중력장에서보다 늦게 흐른다.

5. 2. 물리 우주론

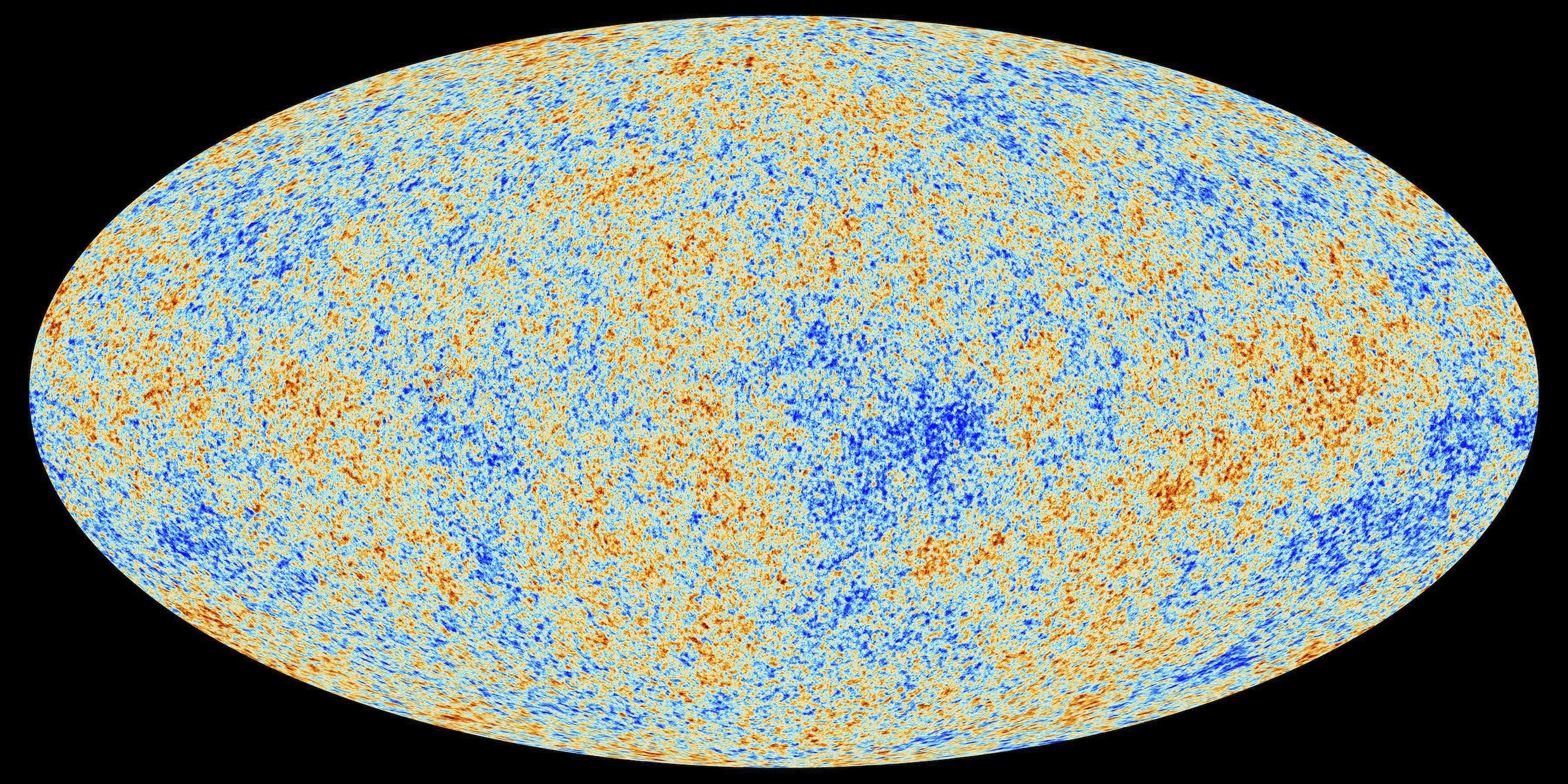
일반 상대성이론은 우주의 기원과 진화를 설명하는 데 사용된다. 우주 공간이 균일하고 등방적이라는 가정 하에 도입된 FLRW 계량은 우주 모델의 기본이 된다.^[57] 1929년 확인된 허블-르메트르 법칙은 외부 은하들이 거리에 비례하여 지구로부터 멀어지는 현상을 우주 공간 자체의 팽창으로 설명한다.

빅뱅 우주론은 우주 탄생 38만년 후 전자들이 원자에 붙잡히면서 빛이 흩어져 현재 2.7K의 우주 마이크로파 배경으로 관측될 것이라고 예측했고, 이는 1965년 펜지어스와 윌슨에 의해 발견되었다.

우주 마이크로파 배경의 불균일도 분포를 통해 우주 공간의 곡률을 판단할 수 있는데, 관측 결과 우주의 곡률은 거의 0이다. 기존 빅뱅 모델의 지평선 문제와 평탄성 문제를 해결하기 위해 1980년대 인플레이션 우주론이 등장하여 우주 초기 급격한 팽창을 제시하였다.

1998년 Ia형 초신성 관측 결과는 우주가 가속팽창한다는 증거를 제시하였고, 이를 설명하기 위해 암흑 에너지 개념이 도입되었다.^[142]

현재 우주론 모델은 아인슈타인 방정식을 기반으로 하며, 우주 상수

\Lambda

를 포함한다.

:

R_{\mu\nu} - {\textstyle 1 \over 2}R\,g_{\mu\nu} + \Lambda\ g_{\mu\nu} = \frac{8\pi G}{c^{4}}\, T_{\mu\nu}

여기서 ''

g_{\mu\nu}

''는 시공간 계량 텐서이다.^[131] 이 방정식의 등방성 및 균질한 해인 프리드만-르메트르-로버트슨-워커 해를 통해^[132] 물리학자들은 빅뱅 단계에서 진화한 우주를 모델링할 수 있다.^[133]

6. 관련 이론

일반 상대성 이론은 실험적으로 성공했지만, 양자장론과 관련하여 여러 가지로 확장될 수 있다. 일반 상대성 이론에 비틀림을 더하면 아인슈타인-카르탕 이론이 되고, 중력상수를 스칼라장으로 바꾸면 브랜스-딕 이론이 된다. 추가 차원을 도입하여 다른 상호작용을 포함시키는 칼루차-클라인 이론과 초대칭을 도입한 초중력 이론도 있다. 초끈이론에서는 아인슈타인-힐베르트 작용을 자연스럽게 얻을 수 있으며, 고리 양자 중력은 아인슈타인-힐베르트 작용을 양자화하는 것에서 시작한다.

6. 1. 관련 확장 이론

일반 상대성이론과 동일한 전제에서 출발하지만, 추가적인 법칙이나 제약을 통해 다른 장 방정식을 유도하는 다양한 확장 이론들이 존재한다.^[24]^[25] 예를 들어 화이트헤드의 이론, 브랜스-딕 이론, 텔레평행성(Teleparallelism), f(R) 중력, 아인슈타인-카르탕 이론 등이 있다.

현대 물리학의 또 다른 기둥인 양자 이론은 기초 입자에서 고체 물리학에 이르기까지 물질을 이해하는 기본 이론이다.^[183] 그러나 양자 이론과 일반 상대성 이론을 통합하는 문제는 여전히 미해결 과제이다.

일반적인 양자장론은 평평한 민코프스키 공간에서 정의되는데, 이는 약한 중력장에서 미시적 입자의 거동을 설명하는 데 적합하다.^[184] 중력이 강하지만 양자화가 필요하지 않은 상황을 설명하기 위해 굽은 시공간에서의 양자장론이 연구되고 있다.^[185] 이 이론은 블랙홀 증발과 호킹 복사를 설명하고, 블랙홀 열역학에서 중요한 역할을 한다.^[186]^[187]

칼라비-야우 다양체의 투영, 끈 이론에서 제시된 추가 차원을 콤팩트화하는 방법 중 하나

양자 중력은 물질의 양자적 설명과 시공간의 기하학적 설명 사이의 일관성을 요구하며, 블랙홀 내부와 초기 우주를 설명하기 위해 필요한 이론이다.^[188]^[189]

끈 이론은 점입자가 아닌 미세한 1차원 끈에 대한 양자 이론으로, 모든 입자와 상호작용을 통일적으로 설명할 수 있다고 여겨진다.^[195]^[196] 끈 이론은 초중력과 결합하여 M-이론이라는 11차원 모델을 형성하며, 이는 양자 중력의 유력한 후보로 간주된다.^[198]^[199]

정준 양자화 절차를 통해 루프 양자 중력이라는 또 다른 접근 방식이 제시되었다.^[200] 아쉬테카 변수를 도입하여 휠러-드윗 방정식을 유도하고, 공간을 스핀 네트워크라는 웹 구조로 표현한다.^[201]^[202]

이 외에도 인과적 동적 삼각분할,^[204] 인과 집합,^[205] 트위스터 모델^[206] 등 다양한 양자 중력 이론들이 연구되고 있다.^[190]^[207] 그러나 이러한 이론들은 여전히 해결해야 할 문제들이 많고, 실험적 검증이 어렵다는 공통적인 한계를 가지고 있다.^[208] 초끈 이론의 경우에는 입자를, 길이를 가진 "끈"으로 재가정함으로써 자외선 발산 문제를 해결하고 있지만, 실험적인 뒷받침이 매우 부족하여 아직 가설의 영역을 벗어나지 못하고 있다.

7. 결론 및 전망

일반 상대성 이론은 실험적으로 성공적인 이론이지만, 몇 가지 확장 가능성과 해결해야 할 과제가 남아있다. 우선, 양자장론과의 통합 문제이다. 비틀림을 더한 아인슈타인-카르탕 이론, 중력상수를 스칼라장으로 확장한 브랜스-딕 이론, 추가 차원을 도입한 칼루차-클라인 이론, 초대칭을 도입한 초중력 이론 등이 그 예시이다. 초끈이론에서는 아인슈타인-힐베르트 작용을 자연스럽게 얻을 수 있으며, 고리 양자 중력은 아인슈타인-힐베르트 작용을 양자화하는 방식으로 접근한다.

쿠르트 괴델은 닫힌 시간꼴 곡선(CTCs)을 포함하는 아인슈타인 방정식의 해를 제시하여 시간 여행의 가능성을 열었으나, 극단적인 물리적 조건이 필요하며 추가적인 물리 법칙으로 제거될 수 있을지는 미지수이다. 스티븐 호킹은 연대기 보호 가설을 통해 시간 여행을 막는 가정을 제안했다. 알큐비에르 드라이브와 같은 워프 드라이브를 제시하는 해도 있지만, 특이한 물질 분포와 반고전적 불안정성을 겪는 문제가 있다.^[149]

양자 중력 문제와 시공간 특이점의 실재, 암흑 에너지와 암흑 물질의 존재는 새로운 물리학의 필요성을 시사한다.^[211] 수학적 상대론 연구자들은 특이점의 본질과 아인슈타인 방정식의 근본적인 속성을 연구하고 있으며,^[212] 수치 상대론 연구자들은 블랙홀 병합과 같은 현상을 컴퓨터 시뮬레이션으로 연구한다.^[213]

2015년 9월 14일, Advanced LIGO 팀은 중력파의 직접 검출에 성공하였다.^[83]^[214]^[215] 이는 일반 상대성 이론의 예측을 다시 한번 확인시켜 준 중요한 사건이다. 일반 상대성 이론은 도입된 지 1세기가 넘었지만, 여전히 활발한 연구 분야로 남아있다.^[216]

참조

_[1] 웹사이트 GW150914: LIGO Detects Gravitational Waves http://www.black-hol[...] 2016-04-18
_[2] 논문 Poincaré 1905
_[3] 웹사이트 General relativity http://www-history.m[...] 1996-05
_[4] 논문 Pais 1982
_[5] 서적 Relativity: Modern Large-Scale Structures of the Cosmos 2008
_[6] 간행물 Entwurf einer verallgemeinerten Relativitätstheorie und einer Theorie der Gravitation (Outline of a Generalized Theory of Relativity and of a Theory of Gravitation) http://www.pitt.edu/[...] 1913
_[7] 논문 Schwarzschild 1916
_[8] 논문 Einstein 1917
_[9] 논문 Hubble 1929
_[10] 논문 Gamow 1970
_[11] 논문 Pais 1982
_[12] 논문 Kennefick 2005
_[13] 논문 Pais 1982
_[14] 논문 Thorne 2003
_[15] 논문 Israel 1987
_[16] 문서 Orbital effects and the relativity of direction
_[17] 문서 Cosmology
_[18] 논문 Landau 1975
_[19] 논문 Wald 1984
_[20] 논문 Rovelli 2015
_[21] 논문 Chandrasekhar 1984
_[22] 논문 Engler 2002
_[23] 서적 Relativity – The Special and General Theory https://books.google[...] Read Books Ltd 2011
_[24] 논문 Ehlers 1973
_[25] 웹사이트 Gravity and Me: The force that shapes our lives https://www.bbc.co.u[...] 2021-03-26
_[26] 논문 Arnold 1989
_[27] 논문 Ehlers 1973
_[28] 논문 Will 1993
_[29] 논문 Wheeler 1990
_[30] 논문 Ehlers 1973
_[31] 논문 Ehlers 1973
_[32] 논문 Giulini 2005
_[33] 논문 Giulini 2006
_[34] 논문 Rindler 1991
_[35] 논문 Ehlers 1973
_[36] 간행물 Harvnb Ehlers 1973 sec. 1.4, Harvnb Schutz 1985 sec. 5.1
_[37] 간행물 Harvnb Ehlers 1973 pp=17ff; a derivation can be found in Harvnb Mermin 2005 loc=ch. 12
_[38] 간행물 Harvnb Rindler 2001 loc=sec. 1.13; for an elementary account, see Harvnb Wheeler 1990 loc=ch. 2; there are, however, some differences between the modern version and Einstein's original concept used in the historical derivation of general relativity, cf. Harvnb Norton 1985
_[39] 간행물 Harvnb Ehlers 1973 loc=sec. 1.4
_[40] 간행물 Harvnb Ehlers 1973 p=16, Harvnb Kenyon 1990 loc=sec. 7.2, Harvnb Weinberg 1972 loc=sec. 2.8
_[41] 간행물 Harvnb Ehlers 1973 pp=19–22; for similar derivations, see sections 1 and 2 of ch. 7 in Harvnb Weinberg 1972. The Einstein tensor is the only divergence-free tensor that is a function of the metric coefficients, their first and second derivatives at most, and allows the spacetime of special relativity as a solution in the absence of sources of gravity, cf. Harvnb Lovelock 1972
_[42] 간행물 Harvnb Kenyon 1990 loc=sec. 7.4
_[43] 서적 Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity John Wiley
_[44] 서적 Relativity, Gravitation and Cosmology: a Basic Introduction Oxford and New York: Oxford University Press
_[45] 간행물 Harvnb Brans Dicke 1961, Harvnb Weinberg 1972 loc=sec. 3 in ch. 7, Harvnb Goenner 2004 loc=sec. 7.2, and Harvnb Trautman 2006
_[46] 간행물 Harvnb Wald 1984 loc=ch. 4, Harvnb Weinberg 1972 loc=ch. 7
_[47] 간행물 Harvnb Poisson 2004a
_[48] 간행물 Harvnb Wheeler 1990 p=xi
_[49] 간행물 Harvnb Wald 1984 loc=sec. 4.4
_[50] 간행물 Harvnb Wald 1984 loc=sec. 4.1
_[51] 간행물 Harvnb Giulini 2007
_[52] 간행물 section 5 in ch. 12 of Harvnb Weinberg 1972
_[53] 간행물 Introductory chapters of Harvnb Stephani Kramer MacCallum Hoenselaers 2003
_[54] 간행물 Harvnb Geroch 1996
_[55] 간행물 Harvnb Stephani Kramer MacCallum Hoenselaers 2003; a more recent review can be found in Harvnb MacCallum 2006
_[56] 간행물 Harvnb Chandrasekhar 1983 loc=ch. 3,5,6
_[57] 간행물 Harvnb Narlikar 1993 loc=ch. 4, sec. 3.3
_[58] 간행물 Harvnb Hawking Ellis 1973 loc=ch. 5
_[59] 간행물 Harvnb Lehner 2002
_[60] 간행물 Harvnb Wald 1984 loc=sec. 4.4
_[61] 간행물 Harvnb Will 1993 loc=sec. 4.1 and 4.2
_[62] 간행물 Harvnb Will 2006 loc=sec. 3.2, Harvnb Will 1993 loc=ch. 4
_[63] 간행물 Harvnb Rindler 2001 pp=24–26 vs. pp. 236–237 and Harvnb Ohanian Ruffini 1994 pp=164–172
_[64] 간행물 Harvnb Rindler 2001 pp=24–26; Harvnb Misner Thorne Wheeler 1973 loc=§ 38.5
_[65] 간행물 Harvnb Pound Rebka 1959, Harvnb Pound Rebka 1960; Harvnb Pound Snider 1964
_[66] 간행물 Harvnb Greenstein Oke Shipman 1971; the most recent and most accurate Sirius B measurements are published in Harvnb Barstow, Bond et al. 2005.
_[67] 간행물 Harvnb Hafele Keating 1972a and Harvnb Hafele Keating 1972b
_[68] 간행물 Harvnb Ashby 2002 and Harvnb Ashby 2003
_[69] 간행물 Harvnb Stairs 2003 and Harvnb Kramer 2004
_[70] 간행물 Harvnb Ohanian Ruffini 1994 loc=sec. 4.2
_[71] 서적
_[72] 서적
_[73] 서적
_[74] 서적
_[75] 서적
_[76] 서적
_[77] 서적
_[78] 서적
_[79] 논문 Näherungsweise Integration der Feldgleichungen der Gravitation http://einstein-anna[...] 2016-02-12
_[80] 논문 Über Gravitationswellen http://einstein-anna[...] 2016-02-12
_[81] 논문 Einstein's gravitational waves found at last http://www.nature.co[...] 2016-02-11
_[82] 논문 Observation of Gravitational Waves from a Binary Black Hole Merger
_[83] 웹사이트 Gravitational waves detected 100 years after Einstein's prediction https://www.nsf.gov/[...] 2016-02-11
_[84] 서적
_[85] 서적
_[86] 서적
_[87] 서적
_[88] 서적
_[89] 서적
_[90] 서적
_[91] 서적
_[92] 서적
_[93] 서적
_[94] 서적
_[95] 논문 Strong-Field Gravity Tests with the Double Pulsar https://link.aps.org[...] 2021-12-13
_[96] 서적
_[97] 서적
_[98] 서적
_[99] 서적
_[100] 서적
_[101] 서적
_[102] 서적
_[103] 서적
_[104] 서적
_[105] 서적
_[106] 논문
_[107] 논문
_[108] 논문
_[109] 논문
_[110] 논문
_[111] 논문
_[112] 논문
_[113] 논문
_[114] 논문
_[115] 논문
_[116] 간행물 The international pulsar timing array project: using pulsars as a gravitational wave detector 2010
_[117] 논문
_[118] 웹사이트 LISA pathfinder overview http://www.esa.int/e[...] ESA 2012-04-23
_[119] 논문
_[120] 논문
_[121] 논문
_[122] 논문
_[123] 논문
_[124] 논문
_[125] 논문
_[126] 논문
_[127] 논문
_[128] 논문
_[129] 논문
_[130] 논문
_[131] 논문
_[132] 논문
_[133] 논문
_[134] 논문
_[135] 논문
_[136] 논문
_[137] 논문
_[138] 논문
_[139] 논문
_[140] 논문
_[141] 논문 Evidence for dark matter
_[142] 논문
_[142] 논문 Accessible overview
_[142] 논문
_[142] 논문
_[143] 논문 Good introduction
_[143] 논문 Recent review
_[144] 논문
_[144] 논문
_[145] 논문
_[146] 문서 potential function
_[146] 문서 inflaton
_[147] 논문
_[148] 논문
_[149] 간행물 Semiclassical instability of dynamical warp drives 2009-06-15
_[150] 간행물 Gravitational waves in general relativity: VII. Waves from axisymmetric isolated systems
_[151] 간행물 Asymptotic symmetries in gravitational theory
_[152] arXiv Lectures on the Infrared Structure of Gravity and Gauge Theory
_[153] 논문
_[153] 서적
_[153] 서적
_[154] 서적
_[154] 서적
_[155] 논문
_[155] 논문
_[156] 논문
_[156] 서적
_[156] 서적
_[156] 논문
_[157] 논문
_[157] 서적
_[157] 서적
_[157] 논문
_[157] 논문
_[158] 논문
_[158] 논문
_[158] 논문
_[158] 서적
_[158] 논문
_[159] 논문
_[159] 논문
_[160] 논문
_[160] 논문
_[160] 논문
_[161] 서적
_[162] 서적 Horizons
_[162] 논문 Unruh effect
_[162] 논문
_[163] 서적
_[163] 서적
_[164] 논문
_[164] 서적
_[165] 논문
_[165] 서적
_[166] 논문
_[166] 서적
_[167] 문서 caustic (mathematics)
_[167] 문서 eikonal approximation
_[168] 문서 trapped null surface
_[168] 논문
_[169] 논문
_[170] 논문
_[170] 논문
_[170] 논문
_[171] 논문
_[171] 서적
_[171] 논문
_[172] 서적
_[173] 논문
_[173] 서적
_[174] 논문
_[174] 논문
_[174] 서적
_[174] 논문
_[175] 논문
_[175] 논문
_[176] 서적
_[177] 논문
_[178] 논문
_[179] 서적
_[180] 서적
_[181] 서적
_[182] 논문
_[183] 서적
_[184] 서적
_[185] 서적
_[186] 서적
_[187] 서적
_[188] 서적
_[189] 서적
_[190] 서적
_[191] 논문
_[192] 논문
_[193] 논문
_[194] 서적
_[195] 논문
_[196] 서적
_[197] 서적
_[198] 서적
_[199] 논문
_[200] 논문
_[201] 서적
_[202] 논문
_[203] 논문
_[204] 서적
_[205] 서적
_[206] 서적
_[207] 서적
_[208] 서적
_[209] 서적
_[210] 서적
_[211] 서적
_[212] 논문
_[213] 논문
_[214] 논문
_[215] 논문
_[216] 논문
_[217] 논문
_[218] 서적
_[219] 논문
_[220] 논문
_[221] 논문
_[222] 논문
_[223] 논문
_[224] 논문
_[225] 서적
_[226] 논문
_[227] 논문
_[228] 논문
_[229] 서적
_[230] 서적
_[231] 문서 section #Quantum gravity
_[211] 문헌 Cosmology
_[212] 문헌
_[213] 문헌
_[214] 문헌
_[215] 문헌
_[216] 문헌 Living Reviews in Relativity
_[217] 문헌 場の古典論
_[218] 문헌 選集2 [A2]一般相対性理論および重力論の草案 (1914)
_[219] 문헌 Über den Einfluß der Schwerkraft auf die Ausbreitung des Lichtes
_[220] 문헌 Entwurf einer verallgemeinerten Relativitätstheorie und einer Theorie der Gravitation
_[221] 논문 Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie
_[222] 문헌 Die Grundlage der allgemeinen Relativitätstheorie
_[223] 논문 Hamiltonsches Prinzip und allgemeine Relativitätstheorie
_[224] 문헌
_[225] 문헌
_[226] 문헌
_[227] 문헌
_[228] 논문 Relativity and the Global Positioning System American Institute of Physics
_[229] 논문 Centennial Review of General Relativity https://www.semantic[...] 2016
_[230] 서적 123. A Determination of the Deflection of Light by the Sun's Gravitational Field, from Observations Made at the Total Eclipse of May 29, 1919 http://dx.doi.org/10[...] Harvard University Press 1979-12-31
_[231] 서적
_[232] 서적
_[233] 저널 Gravitational deflection of light: a re-examination of the observations of the solar eclipse of 1919 https://articles.ads[...]
_[234] 저널 TIMING MEASUREMENTS OF THE RELATIVISTIC BINARY PULSAR PSR B1913+16 http://dx.doi.org/10[...] 2010-09-24
_[235] 저널 Gravitational Waves from an Orbiting Pulsar http://dx.doi.org/10[...] 1981-10
_[236] 저널 TIMING MEASUREMENTS OF THE RELATIVISTIC BINARY PULSAR PSR B1913+16 http://dx.doi.org/10[...] 2010-09-24

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com