자이페르트-판 캄펀 정리

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 예
4. 동치인 정식화
5. 일반화
6. 역사
참조

1. 개요

자이페르트-판 캄펀 정리는 위상 공간과 그 공간을 덮는 두 부분 공간의 기본군 사이의 관계를 설명하는 정리이다. 이 정리는 기본군뿐만 아니라 기본 준군에 대해서도 일반화될 수 있다. 특히, 공간이 두 열린 부분 공간의 합집합으로 표현될 때, 각 부분 공간의 기본군과 교집합의 기본군 사이의 관계를 통해 전체 공간의 기본군을 계산할 수 있다. 자이페르트-판 캄펀 정리는 원의 기본군 계산과 같은 문제 해결에 활용되며, 쐐기합 공간, 종수 n인 곡면의 기본군 계산에도 적용된다. 이 정리는 군의 표현을 통해 더 명확하게 표현될 수 있으며, 기본 준군을 사용하여 더 일반적인 경우로 확장될 수 있다. 이 정리는 헤르베르트 자이페르트와 에흐베르튀스 판 캄펀이 증명했으며, 로널드 브라운에 의해 기본 준군에 대해 일반화되었다.

더 읽어볼만한 페이지

대수적 위상수학 정리 - 렙셰츠 초평면 정리
렙셰츠 초평면 정리는 복소수체 위의 사영 대수다양체 $X$ 와 초평면의 교집합 $Y$ 에 대해, $X\setminus Y$ 가 매끄러운 다양체일 때, 특이 호몰로지 군, 특이 코호몰로지 군, 호모토피 군 사이의 특정 군 준동형들이 동형사상 또는 전사 함수가 됨을 보이는 정리이며, 상대 호몰로지 군, 상대 코호몰로지 군, 상대 호모토피 군의 소멸 정리와 동치이다.
대수적 위상수학 정리 - 보편 계수 정리
보편 계수 정리는 대수적 위상수학에서 호몰로지 군과 코호몰로지 군 사이의 관계를 Tor 및 Ext 함자를 통해 설명하며, 호몰로지 및 코호몰로지 보편 계수 정리로 나뉘고 여러 따름정리를 유도하거나 구체적인 예제 계산에 활용된다.
대수적 위상수학 - 매시 곱
매시 곱은 미분 등급 대수 원소에 대한 연산으로 코호몰로지 곱으로 파악하기 어려운 위상수학적 불변량을 측정하며, 2항 곱과 3항 곱을 일반화한 형태로 불확정성을 가지지만, 브루니안 링크, 보로메오 고리 연구 및 꼬인 K-이론 등 다양한 분야에 응용된다.
대수적 위상수학 - 톰 공간
톰 공간은 파라콤팩트 공간 위의 벡터 다발을 이용하여 구성되며, 르네 톰에 의해 도입되었고, 톰 동형을 통해 기저 공간의 코호몰로지와 관계를 가지며 특성류 이론 등에서 중요한 역할을 한다.

자이페르트-판 캄펀 정리

2. 정의

위상 공간 $X$ 와 이 공간을 덮는 두 부분 공간 $A, B\subseteq X$ 가 주어졌고, 다음 조건이 성립한다고 가정하자.

$\operatorname{int}A\cup\operatorname{int}B=X$

또한, 부분 공간

C\subseteq X

가 다음 조건을 만족시킨다고 하자.

$A$ 또는 $B$ 또는 $A\cap B$ 의 임의의 경로 연결 성분과의 교집합은 공집합이 아니다.

그렇다면, '''자이페르트-판 캄펀 정리'''에 따르면 다음 명제들이 성립한다.

$C$ 는 $X$ 의 모든 경로 연결 성분들과 교차한다.
포함 관계에 의하여 유도되는 다음과 같은 기본 준군의 사상들은 준군 범주에서의 밂을 이룬다.

:

\begin{matrix}\Pi_1(A\cap B,C)&\to& \Pi_1(A,C)\\\downarrow&&\downarrow\\\Pi_1(B,C)&\to&\Pi_1(X,C)\end{matrix}

특히,

A

와

B

가 경로 연결 공간이며,

C=\{c\}\subseteq A\cap B

는 한원소 집합이며,

A\cap B

는 공집합이 아닌 경로 연결 공간이라고 하자. 그렇다면

X

는 경로 연결 공간이며, 다음과 같은, 기본군의 (군의 범주에서의) 밂이 존재한다.

:

\begin{matrix}\pi_1(A\cap B,c)&\to& \pi_1(A,c)\\\downarrow&&\downarrow\\\pi_1(B,c)&\to&\pi_1(X,c)\end{matrix}

''X''가 두 열린 경로 연결 부분 공간 ''U''₁, ''U''₂의 합집합인 위상 공간이라고 하자. ''U''₁ ∩ ''U''₂가 경로 연결되어 있고 공집합이 아니며, ''x''₀를 모든 기본군들의 기저로 사용할 ''U''₁ ∩ ''U''₂의 점이라고 하자. ''U''₁과 ''U''₂를 ''X''에 포함하는 사상은 준동형 사상

j_1:\pi_1(U_1,x_0)\to \pi_1(X,x_0)

와

j_2:\pi_1(U_2,x_0)\to \pi_1(X,x_0)

를 군 준동형 사상으로 유도한다. 그러면 ''X''는 경로 연결되어 있고

j_1

과

j_2

는 가환 푸시 아웃 다이어그램을 형성한다.

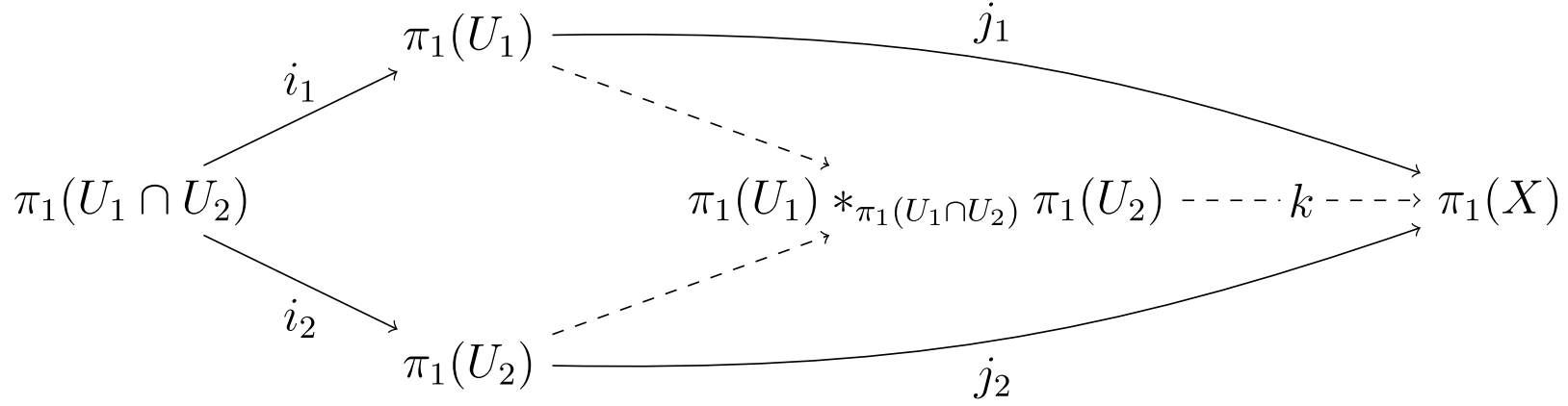
자연 사상 ''k''는 동형 사상이다. 즉, ''X''의 기본군은

\pi_1(U_1\cap U_2, x_0)

의 합병과 함께 ''U''₁과 ''U''₂의 기본군의 자유곱이다.^[1]

일반적으로 이 정리에서 포함에 의해 유도된 사상은 그 자체가 단사가 아니며, 더 정확한 진술은 군의 푸시 아웃의 관점에서 이루어진다.

위상 공간 ''X''가 두 부분 공간 ''X''₁, ''X''₂의 내부로 덮여 있고, ''A''가 ''X''₁, ''X''₂ 및 ''X''₀ = ''X''₁ ∩ ''X''₂의 각 경로 성분을 만나는 집합이라고 할 때, ''A''는 ''X''의 각 경로 성분을 만나고, 포함에 의해 유도된 사상의 다이어그램 '''P'''는 군군의 범주에서 푸시 아웃 다이어그램이다.^[4]

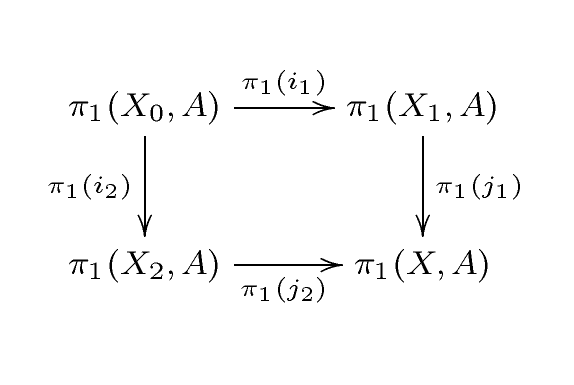
''X''가 부분 집합의 가족

\{U_\lambda : \lambda \in \Lambda\}

의 내부의 합으로 덮이는 경우, 만약 ''A''가

U_\lambda

집합의 모든 1, 2, 3-겹 교집합의 각 경로 성분을 만난다면, ''A''는 ''X''의 모든 경로 성분을 만나고, 포함에 의해 유도된 사상의 다이어그램

:

\bigsqcup_{(\lambda,\mu) \in \Lambda^2} \pi_1(U_\lambda \cap U_\mu, A) \rightrightarrows \bigsqcup_{\lambda \in \Lambda} \pi_1(U_\lambda, A)\rightarrow \pi_1(X,A)

은 군군의 범주에서 코이퀄라이저이다.

알렉산더 그로텐디크는 Esquisse d'un Programme에서 다음과 같이 언급하였다.

원은 대수적 위상수학에서 가장 중요하고 기본적인 예시이지만, 위에 제시된 정리로는 기본군을 계산할 수 없다. 그 이유는, 원은 연결된 공통 부분을 갖는 두 개의 열린 집합의 합집합으로는 실현될 수 없다는 데에 있다. 이 문제는, 기하학적인 상황에 따라 선택한 기점들의 '''집합'''

A

위의 기본 아군

\pi_1(X,A)

를 사용함으로써 해결할 수 있다. 원의 경우에는, 두 개의 기점을 선택하면 된다.^[20]

이 아군은

A \cap X

의 점들을 잇는

X

내의 곡선들의 양 끝단에 상대적인 (양 끝단을 고정하는) 호모토피류로 이루어진다. 특히,

X

가 수축 가능 공간이고,

A

가

X

의 서로 다른 두 점으로 이루어져 있을 때,

\pi_1(X,A)

는

\mathcal I

로 종종 표기되는 아군과 동형임을 쉽게 알 수 있다. 이 아군은 두 개의 꼭짓점과 각 꼭짓점 사이에 정확히 하나의 사상으로 이루어진다. 이 아군은, 군의 이론에서 정수의 군이 수행하는 것과 유사한 역할을 아군의 이론에서 수행한다.^[21] 아군

\mathcal I

는 또한 아군의 호모토피 개념을 생각할 수 있게 한다. 즉, 이는 아군의 범주에서의 '''단위 구간 대상'''이다.

위상 공간

X

가 두 개의 부분 공간

X_1

과

X_2

의 내부로 덮이고, 기점 집합

A

는

X_1

과

X_2

와

X_0=X_1 \cap X_2

의 모든 호상 연결 성분과 교차한다고 가정한다. 이 때

A

는

X

의 모든 호상 연결 성분과 교차하며, 포함에 의해 유도된 사상으로 이루어진 그림

P

는 아군의 범주의 푸시 아웃 그림이 된다.^[22]

3. 예

자이페르트-판 캄펀 정리는 원, 구, 쐐기합, 종수 n인 곡면 등과 같이 더 간단한 공간으로 분해할 수 있는 위상 공간의 기본군을 계산하는 데 사용될 수 있다.^[2]

이러한 예시들은 하위 섹션에서 자세히 다루고 있으므로, 여기서는 간략하게 언급만 하고 넘어간다.

3. 1. 원

원

\mathbb S^1=\mathbb R/\mathbb Z

의 기본군은 무한 순환군

\mathbb Z

이다. 이를 보이기 위해, 원을 두 개의 겹치는 열린 집합으로 나눈다.

:

A=(-1/3,2/3)/\mathbb Z\subsetneq\mathbb S^1

:

B=(1/3,4/3)/\mathbb Z\subsetneq\mathbb S^1

이때,

A

와

B

의 교집합은 두 개의 연결된 성분으로 구성된다.

:

C=\{0,1/2\}/\mathbb Z\subsetneq A\cap B

A

,

B

,

A\cap B

의 밑점 집합

C

에서의 기본 준군은 다음과 같다. (항등 사상은 생략)

:

\Pi_1(A,C)\colon \overset{0}\bullet{\xrightarrow\phi\atop\xleftarrow[\phi^{-1}]{}}\overset{1/2}\bullet

:

\Pi_1(B,C)\colon \overset{0}\bullet{\xrightarrow{\phi'^{-1}}\atop\xleftarrow[\phi']{}}\overset{1/2}\bullet

:

\Pi_1(A\cap B,C)\colon \overset{0}\bullet\qquad\overset{1/2}\bullet

원의 기본군은

A

와

B

의 준군들의 쌍대곱이다. 여기서

\phi'\circ\phi\colon 0\to 0

는 항등 사상이 아닌 사상이므로,

\hom(0,0)

및

\hom(1/2,1/2)

는 모두 무한 순환군

\mathbb Z

이다.

0

과

1/2

는

\Pi_1(\mathbb S^1,\{0,1/2\})

에서 서로 동형이므로,

\mathbb S^1

의 기본군은 무한 순환군이다.^[2]

하지만, 원은 연결된 교집합을 갖는 두 개의 열린 집합의 합으로는 표현할 수 없기 때문에, 이 방법으로는 원의 기본군을 직접 계산할 수 없다. 이 문제는 기저점의 집합

A

에 대한 기본 군군

\pi_1(X,A)

를 사용하여 해결할 수 있다. 원의 경우 두 개의 기저점을 사용한다.^[2]

3. 2. 구

2차원 이상의 구

S^2

에서, 북극과 남극을 각각 나타내는 ''n''과 ''s''에 대해 열린 집합

A = S^2\setminus \{n\}

과

B = S^2\setminus \{s\}

를 선택한다. 그러면 ''A'', ''B'' 및 ''A'' ∩ ''B''가 열린 경로 연결 집합이라는 속성을 갖는다.

''A'' ∩ ''B''를 ''A''와 ''B''로 포함시키고, 그 다음 ''A''와 ''B''를

S^2

로 포함시키는 가환도표가 있으며, 각 부분 공간의 기본군 간의 상응하는 준동형사상 도표가 있음을 알 수 있다. 자이페르트-판 캄펀 정리를 적용하면 다음과 같은 결과를 얻는다.

:

\pi_1(S^2)=\pi_1(A)\cdot\pi_1(B)/\ker(\Phi).

그러나 ''A''와 ''B''는 모두 위상동형이며, 이는 단일 연결인 '''R'''²와 위상동형이므로 ''A''와 ''B'' 모두 자명군을 갖는다. 이로부터

S^2

의 기본군이 자명하다는 것을 알 수 있다.

3. 3. 쐐기합 공간

두 개의 점 있는 공간

(X,x)

와

(Y,y)

가 주어졌을 때, 두 밑점을 동일시하여

X \coprod Y

의 몫을 취함으로써 쐐기합

(X\vee Y,p)

을 구성할 수 있다.

만약

x

가 수축 가능한 열린 근방

U \subset X

을 갖고,

y

가 수축 가능한 열린 근방

V \subset Y

를 갖는다면 (예를 들어

X

와

Y

가 CW 복합체인 경우), 반 캄펜 정리를

X \vee Y

에 적용할 수 있다. 이때 두 개의 열린 집합으로

X \vee V

와

U \vee Y

를 취하면, 쐐기합의 기본군은 두 공간의 기본군의 자유곱과 같다는 결론을 얻는다.

:

\pi_1(X\vee Y, p)\cong \pi_1(X,x)*\pi_1(Y,y)

.

점(하나만으로 이루어진 공간)의 기본군은 자명하므로, 반 캄펜 정리는 위 식이 군의 동형임을 보여준다.

3. 4. 종수 n인 곡면

종수 ''n'' 방향성 곡면 ''S''의 기본군은 ''종수-n 곡면군''이라고도 불린다. ''S''는 표준 기본 다각형을 사용하여 구성할 수 있다. 다각형 내부의 원판을 열린 집합 ''A''로, ''A''의 중심점을 제외한 ''S''의 여집합을 ''B''로 선택하면, ''A''와 ''B''의 교집합은 환면이 되어 원과 호모토피 동치이며 기본군이 정수군과 같다. 이때,

\pi_1(A \cap B)

를

\pi_1(A)

로 포함시키는 것은 임의의 생성자를 자명한 원소로 보내지만,

\pi_1(A \cap B)

를

\pi_1(B)

로 포함시키는 것은 자명하지 않다.

\pi_1(B)

는 ''B'' (한 점이 삭제된 ''S'')를 다음과 같이 변형 수축시켜 계산할 수 있다.

:

A_1 B_1 A_1^{-1} B_1^{-1} A_2 B_2 A_2^{-1} B_2^{-1} \cdots A_n B_n A_n^{-1} B_n^{-1}.

이 공간은 2''n''개의 원의 쐐기합(원의 부케)과 같고, 기본군은 2''n''개의 생성자를 갖는 자유군과 동형이다. 생성자는 루프

\{A_1,B_1,\dots,A_n,B_n\}

이고, 유일한 관계는 다음과 같다.

:

A_1 B_1 A_1^{-1} B_1^{-1} A_2 B_2 A_2^{-1} B_2^{-1} \cdots A_n B_n A_n^{-1} B_n^{-1} = 1.

따라서 종수 n인 곡면의 기본군은 다음과 같이 표현된다.

:

\left \langle A_1,B_1,\dots,A_n,B_n\left | A_1B_1A_1^{-1}B_1^{-1}\cdots A_nB_nA_n^{-1}B_n^{-1}\right. \right \rangle.

4. 동치인 정식화

조합군론의 언어를 사용하면, 자이페르트-판 캄펀 정리는 군의 표현(group presentation)을 통해 더 명확하게 표현될 수 있다. $X$ 가 위상 공간, $U$ 와 $V$ 가 $X$ 의 열린 경로 연결 부분 공간이며, $U\cap V$ 가 공집합이 아니고 경로 연결되어 있으며, $w\in U\cap V$ 일 때, $\pi_1(X,w)$ 는 $\pi_1(U,w)$ 와 $\pi_1(V,w)$ 의 융합곱이다. (반드시 단사일 필요는 없는) 준동형사상 $I:\pi_1(U\cap V, w)\to \pi_1(U,w)$ 와 $J:\pi_1(U\cap V, w)\to \pi_1(V,w)$ 에 관하여, 주어진 군 표현은 다음과 같다.

: $\begin{align}\pi_1(U,w) &= \langle u_1,\dots,u_k \mid\alpha_1,\dots,\alpha_l\rangle \\\pi_1(V,w) &= \langle v_1,\dots,v_m \mid \beta_1,\dots,\beta_n\rangle \\\pi_1(U\cap V,w) &= \langle w_1,\dots,w_p \mid \gamma_1,\dots,\gamma_q\rangle\end{align}$

이때 융합곱은 다음과 같이 표현될 수 있다.

: $\pi_1(X,w) = \left\langle u_1,\dots,u_k, v_1,\dots,v_m \left | \alpha_1,\dots,\alpha_l, \beta_1,\dots,\beta_n, I(w_1)J(w_1)^{-1},\dots,I(w_p)J(w_p)^{-1} \right. \right\rangle.$

범주론에서 $\pi_1(X,w)$ 는 군의 범주에서 다음 다이어그램의 밂이다.

: $\pi_1(U,w)\gets\pi_1(U\cap V,w)\to\pi_1(V,w).$

5. 일반화

이 정리는 기본 준군(fundamental groupoid)을 사용하여 더 일반적인 경우로 확장될 수 있다. 기본 준군은 대수기하학에도 나타나며, 알렉산더 그로텐디크의 연구에서 중요한 역할을 한다.^[17]

로널드 브라운은 기점 집합 `A` 위의 기본 준군 $\pi_1(X,A)$ 를 사용하여, 연결되지 않은 경우로 이 정리를 일반화하였다.^[24]

위상 공간 `X`가 두 부분 공간 `X`₁, `X`₂의 내부로 덮여 있고, `A`가 `X`₁, `X`₂ 및 `X`₀ = `X`₁ ∩ `X`₂의 각 경로 성분을 만나는 집합이라고 하자. 그러면 `A`는 `X`의 각 경로 성분을 만나고, 포함에 의해 유도된 사상의 다이어그램

-|]]

은 군군의 범주에서 푸시 아웃 다이어그램이다.^[4]^[22]

이 정리는 위상수학에서 추상대수학으로의 전이를 제공하여 기본 군군

\pi_1(X,A)

을 완전히 결정한다. 그런 다음 대수학과 조합론을 사용하여 어떤 기저점에서 기본군을 결정해야 한다.

이 정리의 한 해석은 호모토피 1-형태를 계산한다는 것이다.

`X`가 부분 집합의 가족

\{U_\lambda : \lambda \in \Lambda\}

의 내부의 합으로 덮이는 경우, `A`가

U_\lambda

집합의 모든 1, 2, 3-겹 교집합의 각 경로 성분을 만난다면, `A`는 `X`의 모든 경로 성분을 만나고, 포함에 의해 유도된 사상의 다이어그램

:

\bigsqcup_{(\lambda,\mu) \in \Lambda^2} \pi_1(U_\lambda \cap U_\mu, A) \rightrightarrows \bigsqcup_{\lambda \in \Lambda} \pi_1(U_\lambda, A)\rightarrow \pi_1(X,A)

은 군군의 범주에서 코이퀄라이저이다.

알렉산더 그로텐디크는 다음과 같이 언급했다.

임의의 덮개에 대한 정리는, `A`가 덮개 집합의 세 겹 교차점을 모두 만나는 제한을 두어, 브라운과 압둘 라작 살레의 논문에 제시되어 있다.^[10]^[24]

6. 역사

헤르베르트 자이페르트^[25]와 에흐베르튀스 판 캄펀^[27]이 이 정리를 증명하였다. 로널드 브라운(Ronald Brown^영어)이 이를 기본 준군에 대하여 일반화하였다.^[28]

이 정리는 로널드 브라운에 의해 기본 군군 $\pi_1(X,A)$ 를 밑점 집합 ''A''에 사용하여 비연결 경우로 확장되었다. 임의의 덮개에 대한 정리는, ''A''가 덮개 집합의 세 겹 교차점을 모두 만나는 제한을 두어, 브라운과 압둘 라작 살레의 논문에 제시되어 있다.^[10] 기본 군에 대한 정리와 증명은 일부 군군 방법을 사용하여 J. 피터 메이의 책에도 제시되어 있다.^[11]

밑점 집합에 대한 기본 군군의 응용은 요르단 곡선 정리, 덮개 공간 및 궤도 공간에 대해 로널드 브라운의 책에 제시되어 있다.^[12]

이 정리의 고차원 버전은 호모토피 유형에 대한 정보를 제공하며, 고차원 군 이론 및 군군에 대한 논문에 제시되어 있다.^[13] 비가환적인 두 번째 상대 호모토피 군을 계산하는 2차원 Van Kampen 정리는 로널드 브라운과 필립 J. 히긴스에 의해 제시되었다.^[14]

기본 군은 대수기하학에도 나타나며, 알렉산더 그로텐디크의 첫 번째 부아 마리 대수기하학 세미나 (SGA1)의 주요 주제이다. Van Kampen 정리의 한 버전이 여기에 나타나며, 대수적 위상수학과는 매우 다른 방식으로, 즉 강하 이론에 의해 증명된다.^[17]

참조

_[1] 서적 Introduction to topological manifolds Springer 2011
_[2] 논문 Groupoids and Van Kampen's theorem
_[3] 웹사이트 Groupoids in Mathematics http://groupoids.org[...]
_[4] 서적 Topology and Groupoids. http://groupoids.org[...] Booksurge PLC 2006
_[5] 서적 Categories and Groupoids Van Nostrand 1971
_[6] 서적 Topology and Groupoids. Booksurge PLC 2006
_[7] 서적 Nonabelian Algebraic Topology: filtered spaces, crossed complexes, cubical homotopy groupoids European Mathematical Society Tracts 2011-08
_[8] 웹사이트 Higher-dimensional, generalized Van Kampen theorems (HD-GVKT) http://planetphysics[...] 2024-10-15
_[9] 문서
_[10] 간행물 A Van Kampen theorem for unions of nonconnected spaces
_[11] 서적 A Concise Introduction to Algebraic Topology
_[12] 서적 Topology and Groupoids Booksurge 2006
_[13] 웹사이트 Higher-dimensional group theory http://www.bangor.ac[...] 2007
_[14] 간행물 On the connection between the second relative homotopy groups of some related spaces
_[15] 문서 Nonabelian algebraic topology: filtered spaces, crossed complexes, cubical homotopy groupoids http://groupoids.org[...] EMS Tracts in Mathematics 20011
_[16] 간행물 Van Kampen theorems for diagrams of spaces
_[17] 문서 Algèbre et théories galoisiennes Cassini 2005
_[18] 논문 Groupoids and Van Kampen's theorem http://planetmath.or[...]
_[19] 서적 Introduction to topological manifolds https://www.worldcat[...] Springer 2011
_[20] 논문 Groupoids and Van Kampen's theorem http://planetmath.or[...]
_[21] 웹사이트 Groupoids in Mathematics http://groupoids.org[...]
_[22] 서적 Topology and Groupoids. http://groupoids.org[...] Booksurge PLC 2006
_[23] 서적 Introduction to topological manifolds https://www.worldcat[...] Springer 2011
_[24] 논문 A van Kampen theorem for unions of nonconnected spaces
_[25] 저널
_[26] 저널 http://www.maths.ed.[...]
_[27] 저널 https://archive.org/[...]
_[28] 저널

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com