로런츠 힘

3. 구성 요소

많은 고전 전자기학 교재에서는 로런츠 힘 법칙을 전기장 '''E'''^영어와 자기장 '''B'''^영어의 ''정의''로 사용한다.^[4][5][6] 구체적으로, 로런츠 힘은 다음과 같은 경험적 명제로 이해된다.

> 주어진 시점과 시간에 있는 시험 전하에 작용하는 전자기력 '''''F'''^영어''는 그 전하 ''''q''^영어''와 속도 '''''v'''^영어''의 특정 함수이며, 다음 함수 형태로 정확히 두 벡터 '''''E'''^영어''와 '''''B'''^영어''로 매개변수화할 수 있다.

> :$\backslash mathbf\{F\}\; =\; q(\backslash mathbf\{E\}+\backslash mathbf\{v\}\; \backslash times\; \backslash mathbf\{B\})$

이는 빛의 속도에 가까운 입자(즉, '''v'''^영어의 크기 1=)에도 유효하다.^[7] 따라서 두 벡터장 '''E'''^영어와 '''B'''^영어는 공간과 시간 전체에 걸쳐 정의되며, 이것을 "전기장"과 "자기장"이라고 한다. 힘을 경험할 전하가 존재하든 그렇지 않든, 시험 전하가 받는 힘과 관련하여 공간과 시간의 모든 곳에서 장이 정의된다.

전기장 $\backslash boldsymbol\{E\}(t,\backslash boldsymbol\{x\})$과 자기선속밀도(자기장) $\backslash boldsymbol\{B\}(t,\backslash boldsymbol\{x\})$ 속에서 운동하는 하전입자(위치 $\backslash boldsymbol\{r\}(t)$, 속도 $\backslash boldsymbol\{v\}(t)$, 전하 $q$)에 작용하는 전자기적인 힘 $\backslash boldsymbol\{F\}(t)$는

:$\backslash boldsymbol\{F\}(t)\; =\; q\backslash boldsymbol\{E\}(t,\backslash boldsymbol\{r\}(t))\; +\; q\backslash boldsymbol\{v\}\; \backslash times\; \backslash boldsymbol\{B\}(t,\backslash boldsymbol\{r\}(t))$

= q \big\{ \boldsymbol{E}(t,\boldsymbol{r}(t)) + \boldsymbol{v} \times \boldsymbol{B}(t,\boldsymbol{r}(t)) \big\}

이며, 이 $\backslash boldsymbol\{F\}$를 로렌츠 힘이라고 한다. 여기서, 「×」는 벡터곱이다.

상기 식에서 우변 제1항은 전기장 내에서 하전입자가 받는 힘이며, 쿨롱 법칙이라고도 한다. 제2항은 비오-사바르 법칙을 일반화한 형태이다. 제2항은 자기장 내에서 하전입자가 받는 힘 $q\backslash boldsymbol\{v\}\; \backslash times\; \backslash boldsymbol\{B\}$이지만, 로런츠 힘이라는 용어가 이 항만을 가리키는 경우도 있다.

하전입자가 가속운동을 하고 있는 경우, 그 하전입자 자신에 의한 전자기장의 효과가 존재하지만, 그 영향은 매우 작은 경우가 많으므로 일반적으로 무시되거나 매우 작은 것으로 취급된다. (참고: 제동 복사, 라머 공식 방사의 반작용, 아브라함-로렌츠 힘)

3. 1. 전기력

3. 2. 자기력

4. 로런츠 힘의 방향

로런츠 힘의 방향은 전기장과 자기장의 방향, 그리고 하전 입자의 속도에 의해 결정된다.

플라스마 내의 전기를 띤 입자(예: 전자 또는 이온)의 자기장 내 운동은 '''유도 중심'''이라고 하는 점을 중심으로 하는 비교적 빠른 원운동과 이 점의 비교적 느린 '''표류'''의 중첩으로 취급될 수 있다. 표류 속도는 전하 상태, 질량 또는 온도에 따라 다른 종류의 입자에 대해 다를 수 있으며, 전류 또는 화학적 분리가 발생할 수 있다.

전기장에 의한 힘은 전기장과 평행하며, 자기장에 의한 힘은 플레밍의 왼손 법칙이나 오른손 법칙으로 나타낸다.

4. 1. 전기장에 의한 힘의 방향

4. 2. 자기장에 의한 힘의 방향

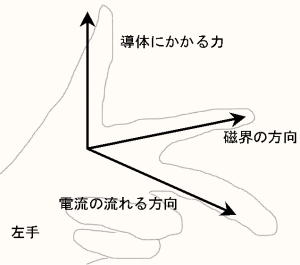
5. 로런츠 힘과 일

로런츠 힘이 하전 입자에 한 일은 다음과 같이 계산된다.

:$\backslash mathrm\{d\}W\; =\; \backslash boldsymbol\{F\}\; \backslash cdot\; \backslash mathrm\{d\}\backslash boldsymbol\{r\}\; =\; q\; (\backslash boldsymbol\{E\}\; +\backslash boldsymbol\{v\}\; \backslash times\; \backslash boldsymbol\{B\})\backslash cdot\; \backslash mathrm\{d\}\backslash boldsymbol\{r\}$

위 식에서 자기장에 의한 힘의 항은 다음과 같다.

:$\backslash mathrm\{d\}W\_\{\backslash mathrm\{m\}\}\; =\; q\; (\backslash boldsymbol\{v\}\; \backslash times\; \backslash boldsymbol\{B\})\backslash cdot\; \backslash mathrm\{d\}\backslash boldsymbol\{r\}\; =\; q\; (\backslash boldsymbol\{v\}\; \backslash times\; \backslash boldsymbol\{B\})\; \backslash cdot\; \backslash boldsymbol\{v\}\; ~\; \backslash mathrm\{d\}t$

= 0

즉, 자기장은 일을 하지 않는다.

전기장에 의한 힘의 항은 다음과 같다.

:$\backslash mathrm\{d\}W\_\{\backslash mathrm\{e\}\}\; =\; q\; \backslash boldsymbol\{E\}\; \backslash cdot\; \backslash mathrm\{d\}\backslash boldsymbol\{r\}\; =\; q\; \backslash boldsymbol\{E\}\; \backslash cdot\; \backslash boldsymbol\{v\}\; ~\; \backslash mathrm\{d\}t$

= w\, \mathrm{d}t

이 전기장에 의한 일의 양은 거시적으로 보면 줄열에 상당한다.

자기장에 의한 힘은 속도와 직교하는 방향으로 발생하므로, 운동 방향을 바꿀 뿐 입자의 운동 에너지는 변하지 않는다. 에너지의 이동은 전기장에 의해 발생한다.

5. 1. 전체 일

• 자기장에 의한 힘의 항은 다음과 같다.

• 즉, 자기장은 일을 하지 않는다.

• 전기장에 의한 힘의 항은 다음과 같다.

• 이 전기장에 의한 일의 양은 거시적으로 보면 줄열에 해당한다.

5. 2. 자기력에 의한 일

5. 3. 전기력에 의한 일

6. 역사

18세기 중반, 전자기력에 대한 초기 연구가 시작되었다. 1760년 요한 토비아스 마이어 등은 자기 극에 작용하는 힘을 연구했고,^[12] 1762년 헨리 캐번디시는 전하를 띤 물체 사이의 힘이 역제곱 법칙을 따른다고 주장했다.^[13] 그러나 실험적 증거는 불충분했다. 1784년 샤를 오귀스탱 드 쿨롱이 비틀림 저울을 사용하여 역제곱 법칙을 실험적으로 증명했다.^[14]

1820년 한스 크리스티안 외르스테드가 전류가 흐르는 도선 주위에 자기장이 형성됨을 발견한 직후, 앙드레 마리 앙페르는 두 전류 요소 사이의 힘의 각 의존성에 대한 공식을 고안했다.^[15][16]

전기장과 자기장의 현대적 개념은 마이클 패러데이의 이론, 특히 그의 힘줄 개념에서 처음으로 등장했으며, 이후 켈빈 경과 제임스 클러크 맥스웰에 의해 완전한 수학적 설명이 주어졌다.^[18] 맥스웰은 1865년에 자신의 장 방정식 공식을 통해 전류와 관련된 로런츠 힘 방정식의 형태를 확인했다.^[19]

J. J. 톰슨은 맥스웰의 장 방정식에서 움직이는 대전된 물체에 작용하는 전자기력을 유도하려 했다. 1881년 톰슨은 외부 자기장으로 인한 입자에 작용하는 힘을 다음과 같이 제시했다.^[20][21]

:$\backslash mathbf\{F\}\; =\; \backslash frac\{q\}\{2\}\backslash mathbf\{v\}\; \backslash times\; \backslash mathbf\{B\}.$

톰슨은 공식의 기본 형태는 맞았지만, 계산 오류와 불완전한 설명으로 인해 공식 앞에 1/2이라는 잘못된 배율 인수가 붙었다. 올리버 헤비사이드는 현대적인 벡터 표기법을 발명하여 맥스웰의 장 방정식에 적용했고, 1885년과 1889년에 톰슨의 유도 과정에서 발생한 실수를 수정하여 움직이는 대전된 물체에 작용하는 자기력의 올바른 형태를 얻었다.^[20][22][23]

1895년,^[24][25] 헨드릭 로런츠는 전기장과 자기장 모두에서 총 힘에 대한 기여를 포함하는 전자기력 공식의 현대적인 형태를 유도했다. 로런츠는 물질과 발광 에테르를 구분하고 미시적 규모에서 맥스웰 방정식을 적용하여 현재 로런츠 힘으로 불리는 정확하고 완전한 형태의 힘 법칙을 유도했다.^[26][27]

7. 상대론적 표현

로런츠 힘은 상대성 이론에서도 중요한 역할을 한다. 상대론적으로 로런츠 힘을 기술하면 다음과 같다.

:$\backslash dot\{p\}\_\backslash mu\; =\; -q\backslash dot\{X\}^\backslash nu\; F\_\{\backslash nu\backslash mu\}(X)$

여기서 $X$는 입자의 상대론적 위치, $p$는 입자의 상대론적 4원 운동량이며, 점은 운동 매개변수에 의한 미분이다. $F$는 전장과 자장을 합친 전자기장 텐서로, 그 성분은 다음과 같다.

:$(F\_\{01\},\; F\_\{02\},\; F\_\{03\})\; =(-E\_1/c,\; -E\_2/c,\; -E\_3/c),~$

(F_{23}, F_{31}, F_{12}) =(B_1, B_2, B_3)

위치의 미분은 비상대론적 속도 $\backslash boldsymbol\{v\}$에 의해 다음과 같이 표현된다.

:$\backslash dot\{X\}^\backslash mu\; =\; (c\backslash dot\{t\},\; \backslash dot\{t\}\backslash boldsymbol\{v\})$

이 식의 공간 성분은 다음과 같다.

:$\backslash dot\{\backslash boldsymbol\{p\}\}\; =q\backslash dot\{t\}\; \backslash boldsymbol\{E\}(t,\backslash boldsymbol\{r\})$

+q\dot{t}\boldsymbol{v}\times\boldsymbol{B}(t,\boldsymbol{r})

비상대론적 힘 $\backslash boldsymbol\{f\}$는 다음과 같이 유도된다.

:$\backslash boldsymbol\{f\}\; =\backslash frac\{d\backslash boldsymbol\{p\}\}\{dt\}$

= \frac{\dot{\boldsymbol{p}}}{\dot{t}}

= q\boldsymbol{E}(t,\boldsymbol{r})

+q\boldsymbol{v}\times\boldsymbol{B}(t,\boldsymbol{r})

7. 1. 공변 형태

7. 2. 시공간 대수 (STA)

• $\backslash mathbf\{E\}\; =\; \backslash left(\backslash mathcal\{F\}\; \backslash cdot\; \backslash gamma\_0\backslash right)\; \backslash gamma\_0$
• $i\backslash mathbf\{B\}\; =\; \backslash left(\backslash mathcal\{F\}\; \backslash wedge\; \backslash gamma\_0\backslash right)\; \backslash gamma\_0$

8. 응용

로런츠 힘은 다양한 장치에 응용된다.

• 사이클로트론 및 기타 원형 경로 입자 가속기
• 질량 분석기
• 속도 필터
• 마그네트론
• 로런츠 힘 속도 측정법
• 전동기
• 레일건
• 선형 모터
• 라우드스피커
• 자기 플라즈마 역추진기
• 발전기
• 단극 발전기
• 선형 교류 발전기

8. 1. 전동기 및 발전기

• 전동기
• 발전기
• 단극 발전기
• 선형 교류 발전기
• 레일건
• 선형 모터
• 라우드스피커
• 자기 플라즈마 역추진기

8. 2. 입자 가속기

8. 3. 질량 분석기

8. 4. 기타 응용

• 사이클로트론 및 기타 원형 경로 입자 가속기
• 질량 분석기
• 속도 필터
• 마그네트론
• 로런츠 힘 속도 측정법

• 전동기
• 레일건
• 선형 모터
• 라우드스피커
• 자기 플라즈마 역추진기
• 발전기
• 단극 발전기
• 선형 교류 발전기

참조

_[1] 웹사이트 Geomagnetism Frequently Asked Questions http://www.ngdc.noaa[...] National Geophysical Data Center 2013-10-21
_[2] 웹사이트 International system of units (SI) http://physics.nist.[...] National Institute of Standards and Technology 2012-05-09
_[3] 서적 Maxwell's Equations https://books.google[...] John Wiley & Sons 2009-11-16
_[4] 문서 See, for example, Jackson, pp. 777–8.
_[5] 서적 Gravitation https://archive.org/[...] W.H. Freeman & Co
_[6] 서적 Electromagnetism John Wiley & Sons
_[7] 서적 Electromagnetism John Wiley & Sons
_[8] 서적 Carl Friedrich Gauss Werke. Fünfter Band Königliche Gesellschaft der Wissenschaften zu Göttingen
_[9] 문서 See Griffiths, page 204.
_[10] 웹사이트 website of the Lorentz Institute http://ilorentz.org/[...]
_[11] 서적 Introduction to electrodynamics https://archive.org/[...] Prentice Hall
_[12] 서적 Encyclopedia of the Enlightenment Fitzroy Dearborn Publishers
_[13] 서적 The New Cambridge Modern History Volume 8: The American and French Revolutions, 1763–93 Cambridge University Press
_[14] 서적 A History of Electricity and Magnetism https://archive.org/[...] Burndy Library
_[15] 서적 Hidden Attraction : The History And Mystery Of Magnetism https://archive.org/[...] Oxford University Press
_[16] 서적 Electrodynamics from Ampère to Einstein https://archive.org/[...] Oxford University Press
_[17] 서적 Hidden Attraction : The History And Mystery Of Magnetism https://archive.org/[...] Oxford University Press
_[18] 서적 Electrodynamics from Ampère to Einstein https://archive.org/[...] Oxford University Press
_[19] 서적 Maxwell's Equations https://books.google[...] Wiley-IEEE
_[20] 서적 Oliver Heaviside https://books.google[...] JHU Press
_[21] 학술지 XXXIII. On the electric and magnetic effects produced by the motion of electrified bodies https://doi.org/10.1[...] 1881-04-01
_[22] 서적 Electrodynamics from Ampère to Einstein https://archive.org/[...] Oxford University Press
_[23] 학술지 On the Electromagnetic Effects due to the Motion of Electrification through a Dielectric http://en.wikisource[...] 1889-04-01
_[24] 서적 Flash of the Cathode Rays: A History of J J Thomson's Electron CRC Press
_[25] 서적 Versuch einer Theorie der electrischen und optischen Erscheinungen in bewegten Körpern
_[26] 서적 Electrodynamics from Ampère to Einstein https://archive.org/[...] Oxford University Press
_[27] 서적 A History of the Theories of Aether and Electricity: From the Age of Descartes to the Close of the Nineteenth Century Longmans, Green and Co.
_[28] 문서 See Jackson, page 2. The book lists the four modern Maxwell's equations, and then states, "Also essential for consideration of charged particle motion is the Lorentz force equation, {{math|1='''F''' = ''q''('''E''' + '''v''' × '''B''')}}, which gives the force acting on a point charge ''q'' in the presence of electromagnetic fields."
_[29] 문서 See Griffiths, page 326, which states that Maxwell's equations, "together with the [Lorentz] force law...summarize the entire theoretical content of classical electrodynamics".
_[30] 웹사이트 Physics Experiments https://web.archive.[...] 2018-08-14
_[31] 문서 See Griffiths, pages 301–3.
_[32] 서적 Electromagnetic theory https://books.google[...] Jones and Bartlett
_[33] 서적 Electrodynamics of continuous media; Volume 8 ''Course of Theoretical Physics'' http://worldcat.org/[...] Butterworth-Heinemann
_[34] 서적 Introduction to electromagnetic engineering https://books.google[...] Dover Publications
_[35] 서적 Elements of electromagnetics https://books.google[...] Oxford University Press
_[36] 서적 Classical Mechanics McGraw Hill
_[37] 서적 The variational principles of mechanics 1986-01-00
_[38] 문서 Chapter 11
_[39] 웹사이트 SpaceTime Calculus https://davidhestene[...]